Построение параболы по методу наименьших квадратов

Вид материала

Документы

Подобный материал:

• Ф. И. Эджоурт один из известнейших ученых, первый кто попытался применить методы, которые, 243.09kb.
• Тема: Построение, 96.98kb.
• И. А. Пахнутов Рассмотрены вычислительные аспекты обобщенного метода наименьших квадратов, 39.76kb.
• Лабораторная работа по теме: метод наименьших квадратов, 231.91kb.
• Задачи на построение. Геометрические места точек, 10.53kb.
• Решение : Составляем функцию для зависимости, 10.81kb.
• Свойства оценок параметров, получаемых с помощью наименьших квадратов, 47.59kb.
• «Математические методы в химии» Общая трудоёмкость дисциплины составляет, 22.21kb.
• Метод наименьших квадратов, 238.98kb.
• Линейная регрессия и метод наименьших квадратов, 177.63kb.

Построение параболы по методу наименьших квадратов


Чтобы понять, как одна величина 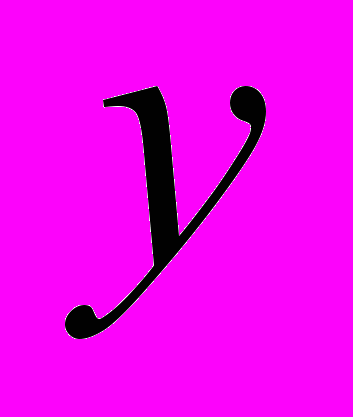зависит от другой величины 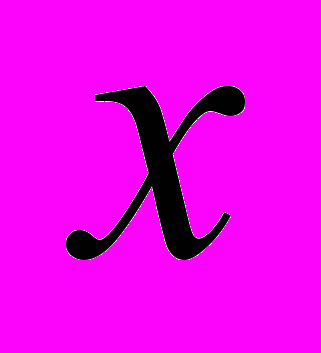, например

• длина стержня 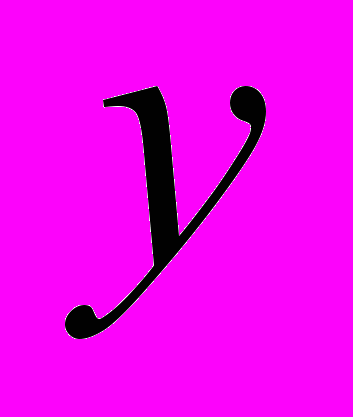от температуры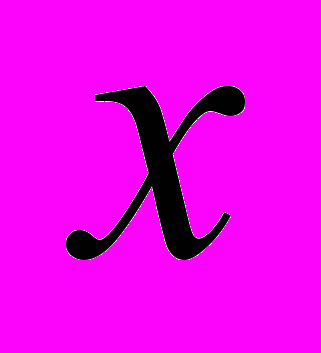
  
• показатель преломления 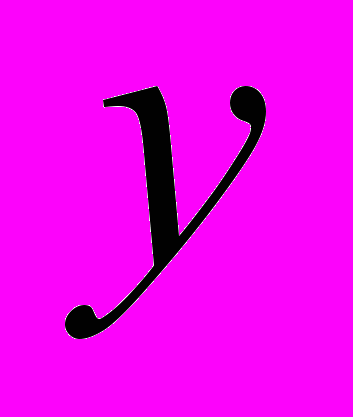данного материала от длины световой волны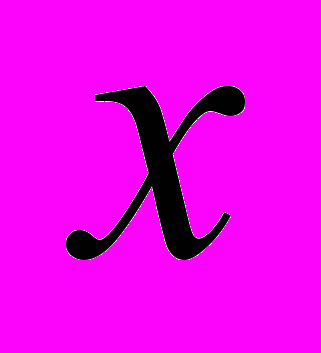
  
• высота свободно падающего тела 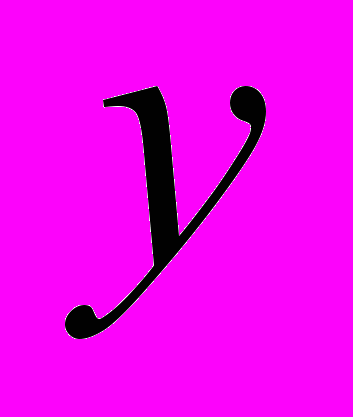от времени ,
  

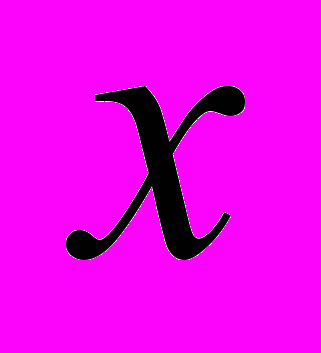мы проводим ряд экспериментов и получаем следующую таблицу.

		…		…
		…		…

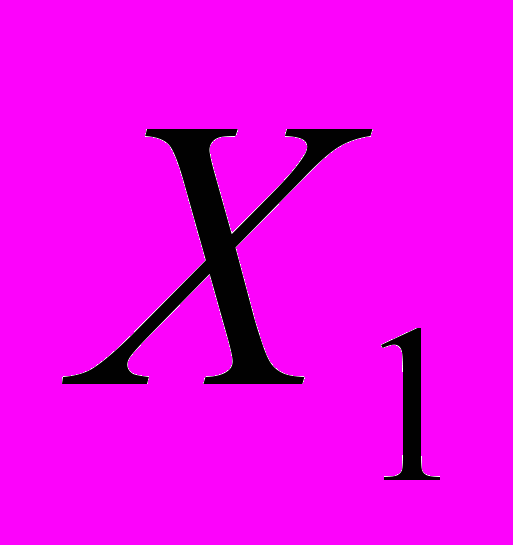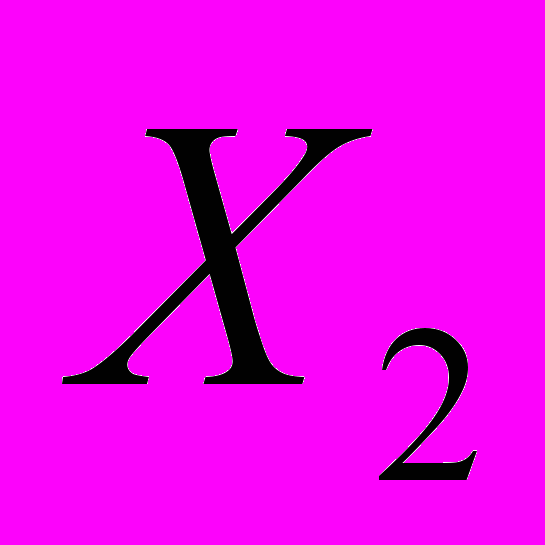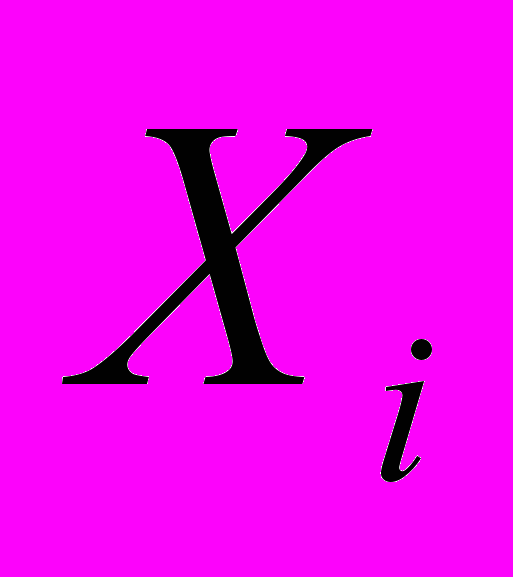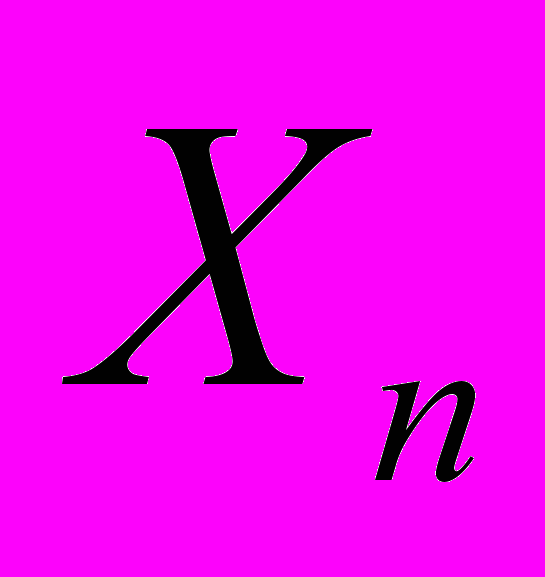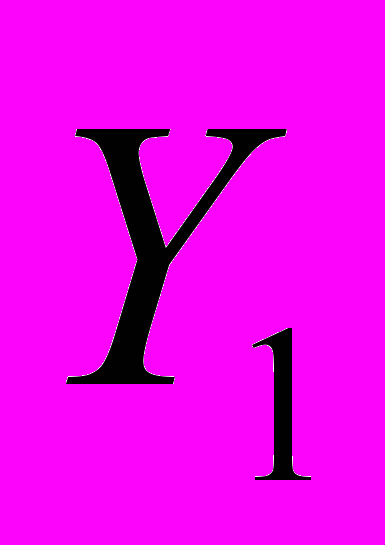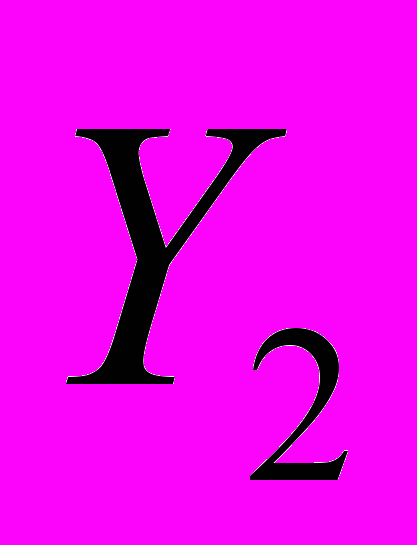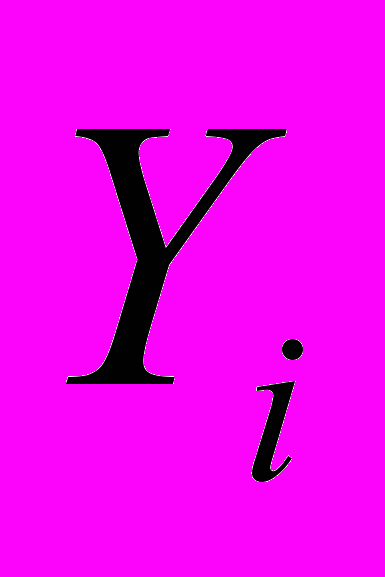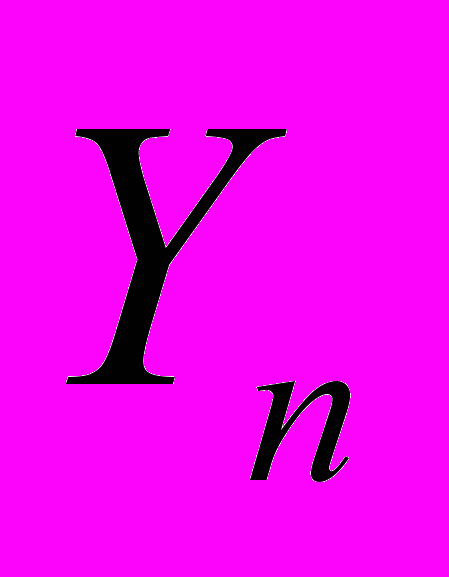Д
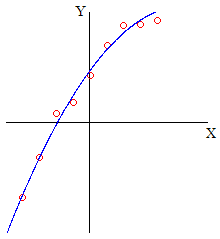
ля наглядного представления этих данных их следует изобразить на координатной плоскости, нанеся на нее 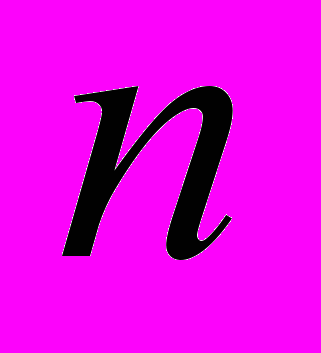точек с координатами .


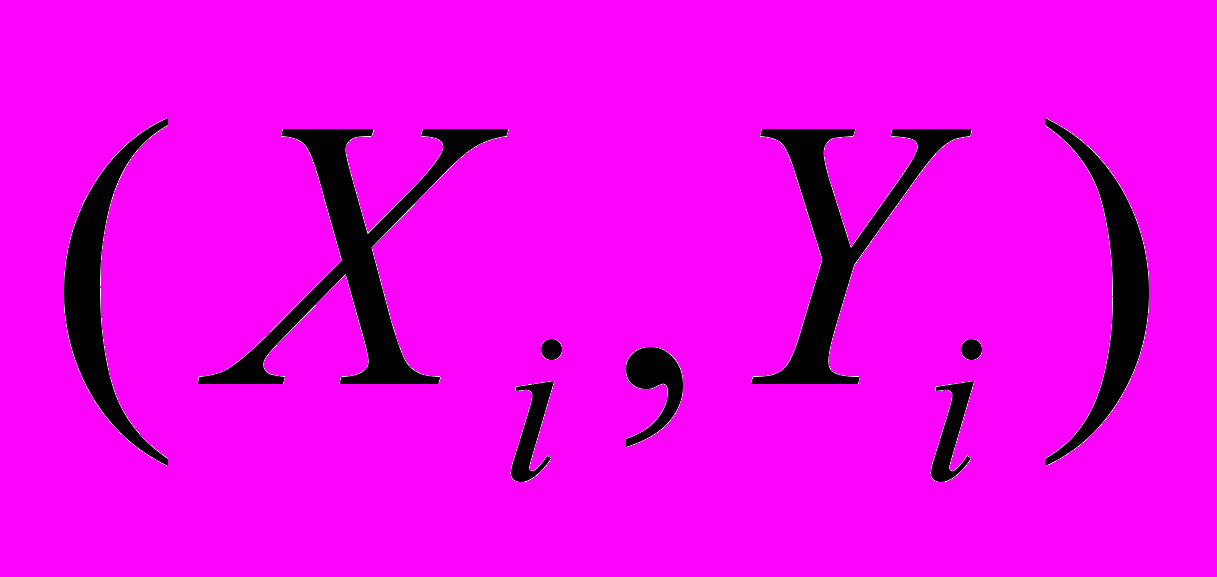Может оказаться, что полученные точки расположены вдоль некоторой параболы, и мы можем предположить, что зависимость между величинам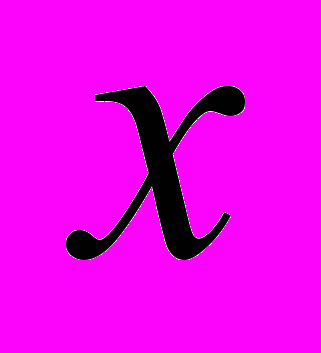и и 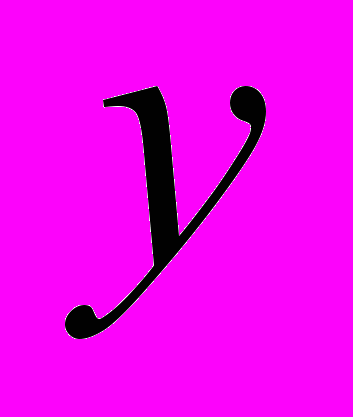квадратичная. И только ошибки измерений вызывают некоторые небольшие отклонения полученных экспериментальных точек от некоторой параболы. Возникает задача нахождения параболы, которая лучше всего описывает эти экспериментальные данные.

Запишем уравнение параболы в виде

(1) .

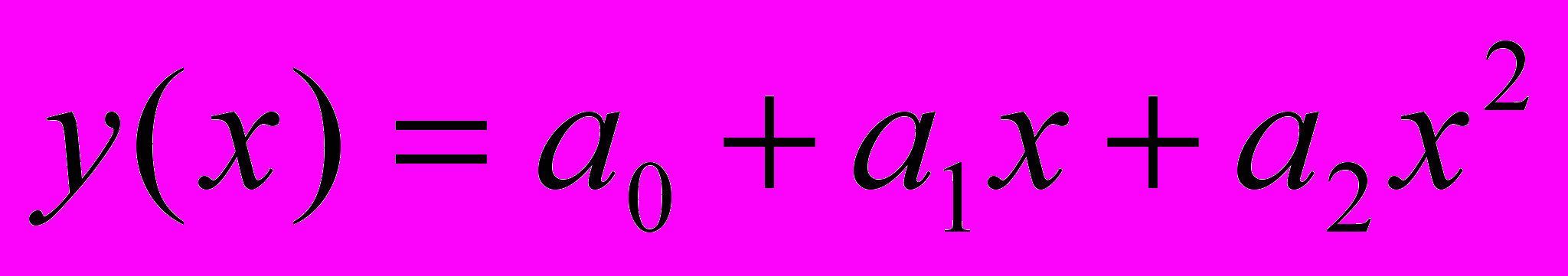И тогда задача нахождения наилучшей параболы сводится к задаче нахождения ее коэффициентов 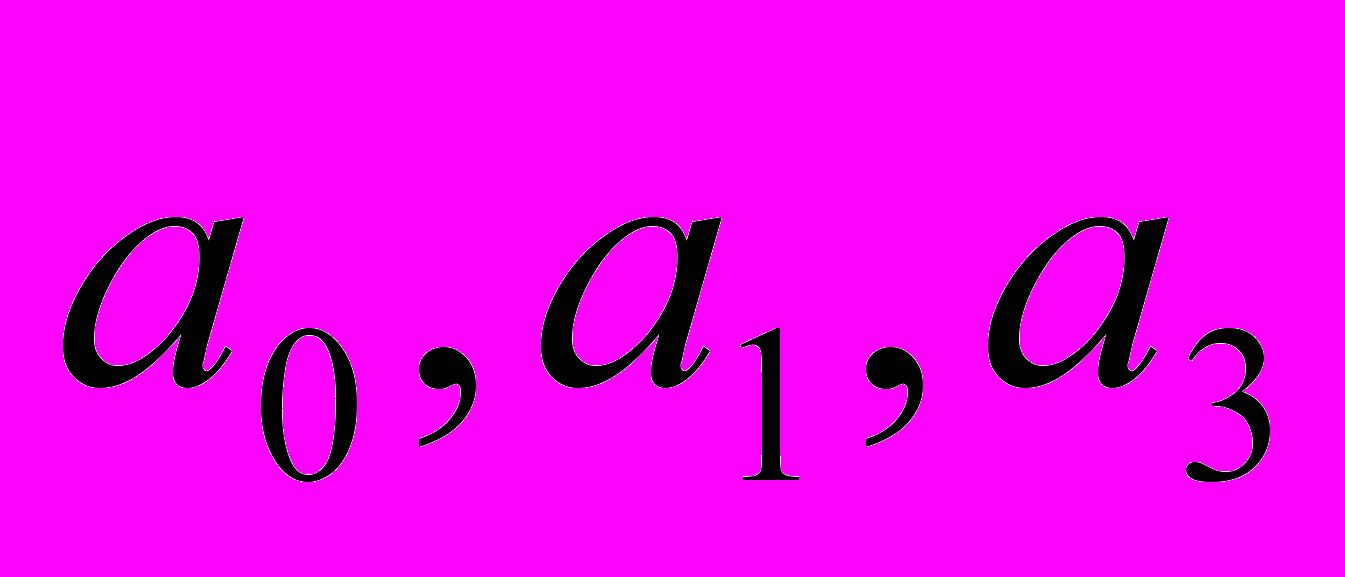. Какую же параболу следует считать наилучшей? Чтобы ответить на этот вопрос, для каждой точки 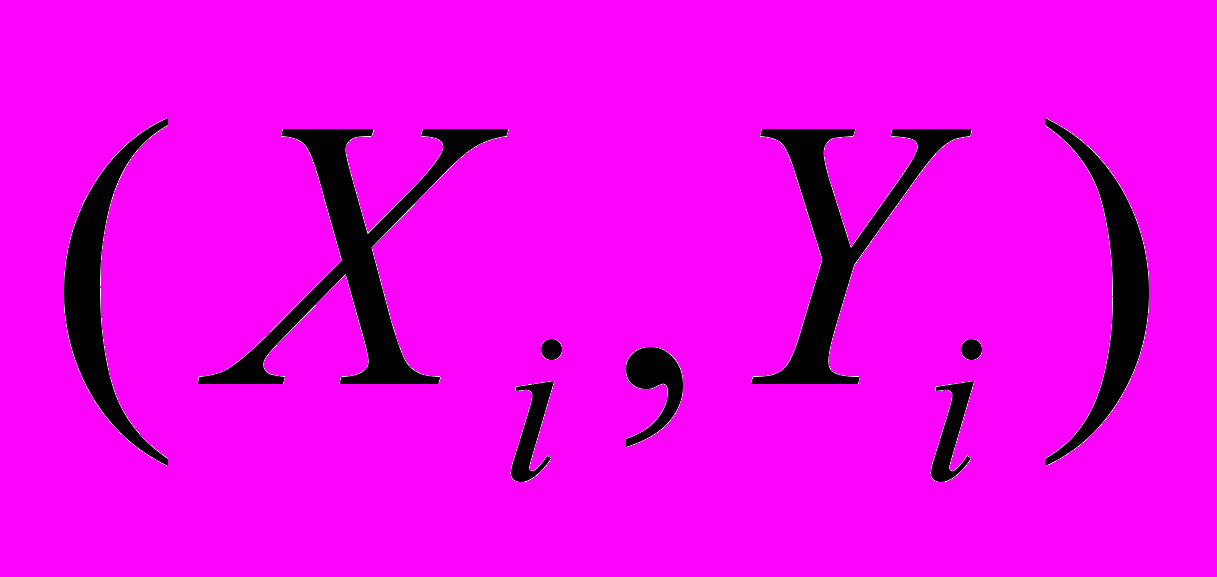вычислим отклонение по вертикали от параболы, заданной уравнением (1), до этой точки

.

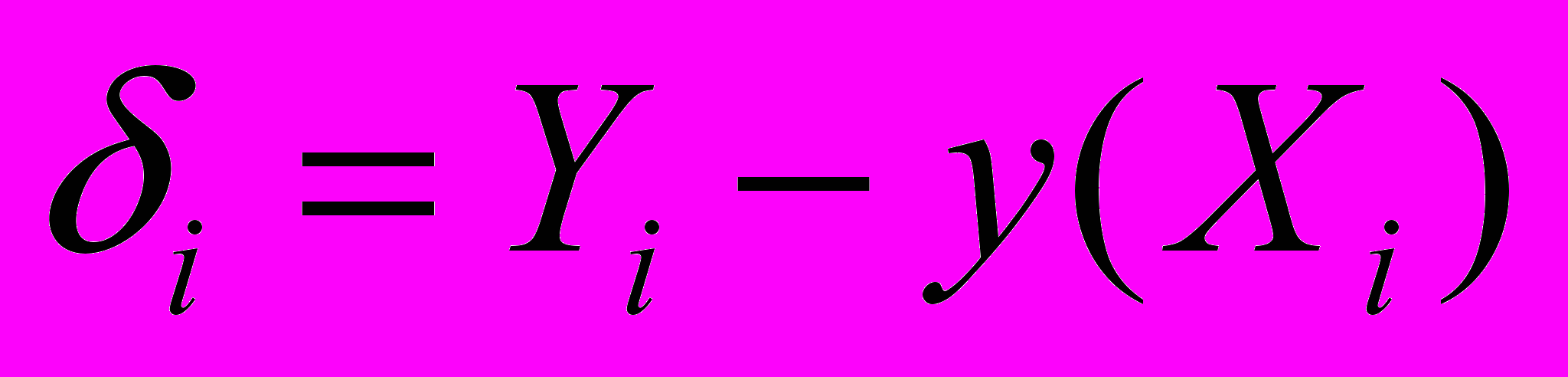Эти расстояния, измеренные по вертикали, называются невязками. Для параболы, наилучшим образом описывающей наши данные, каждая из этих невязок должна быть мала – они должны быть малы в совокупности. В качестве критерия малости невязок выбирается сумма их квадратов

.

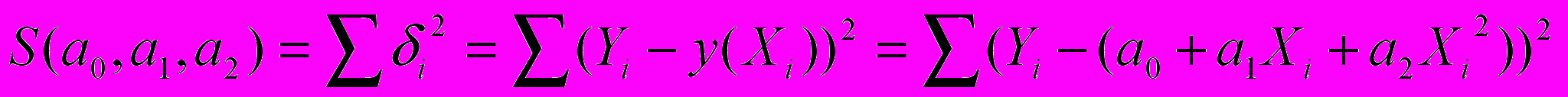Чем меньше эта сумма, тем лучше парабола 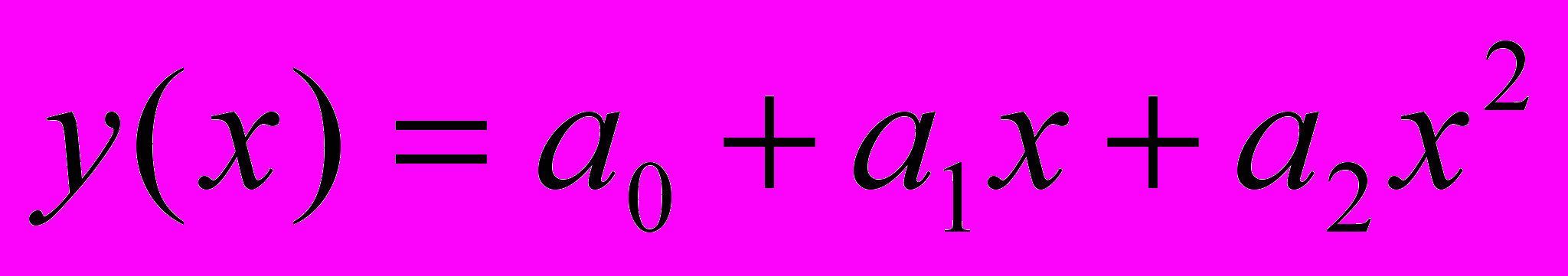описывает наши данные. Таким образом, наилучшая парабола – это та, для которой сумма минимальна.

Минимум суммы ищем, приравнивая ее частные производные нулю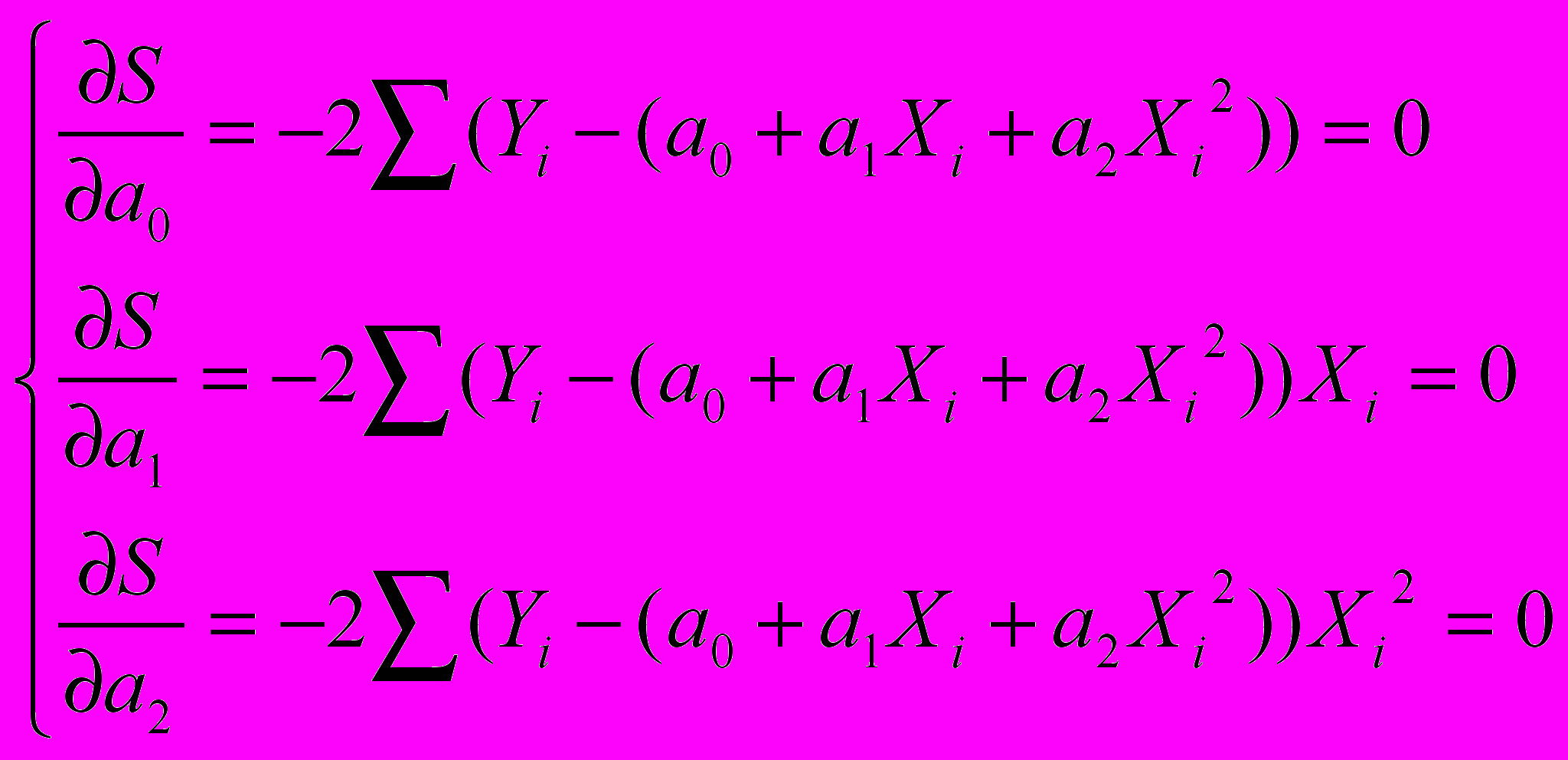

.

Или

.

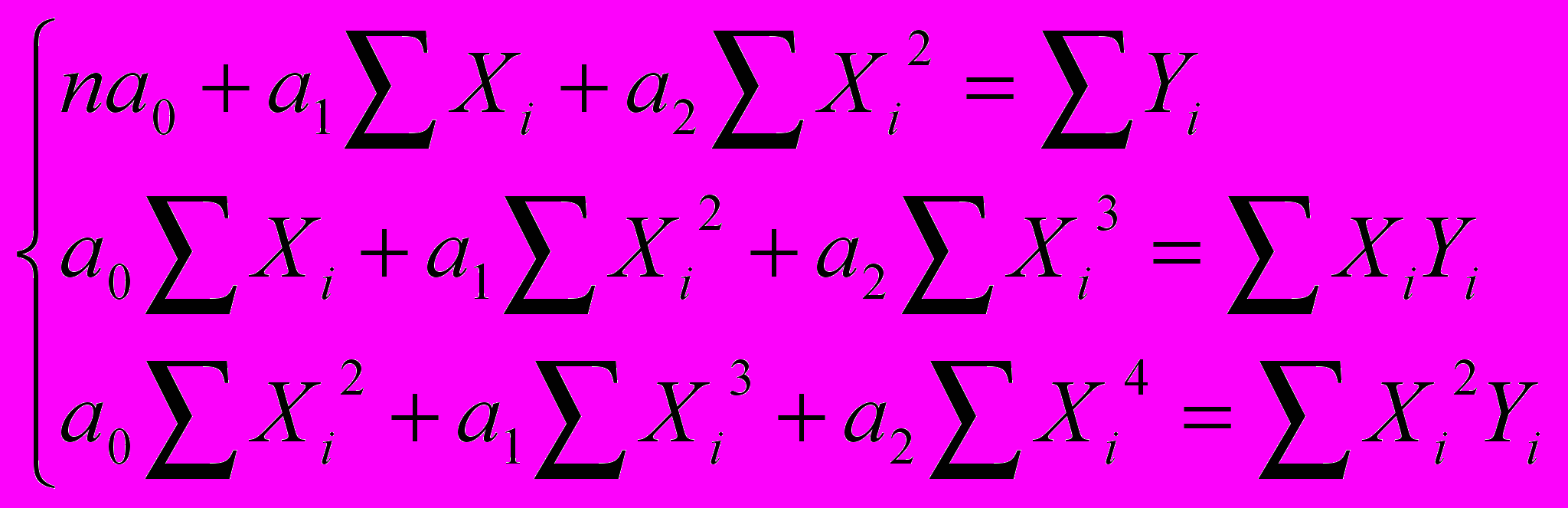Это система из трех уравнений с тремя неизвестными 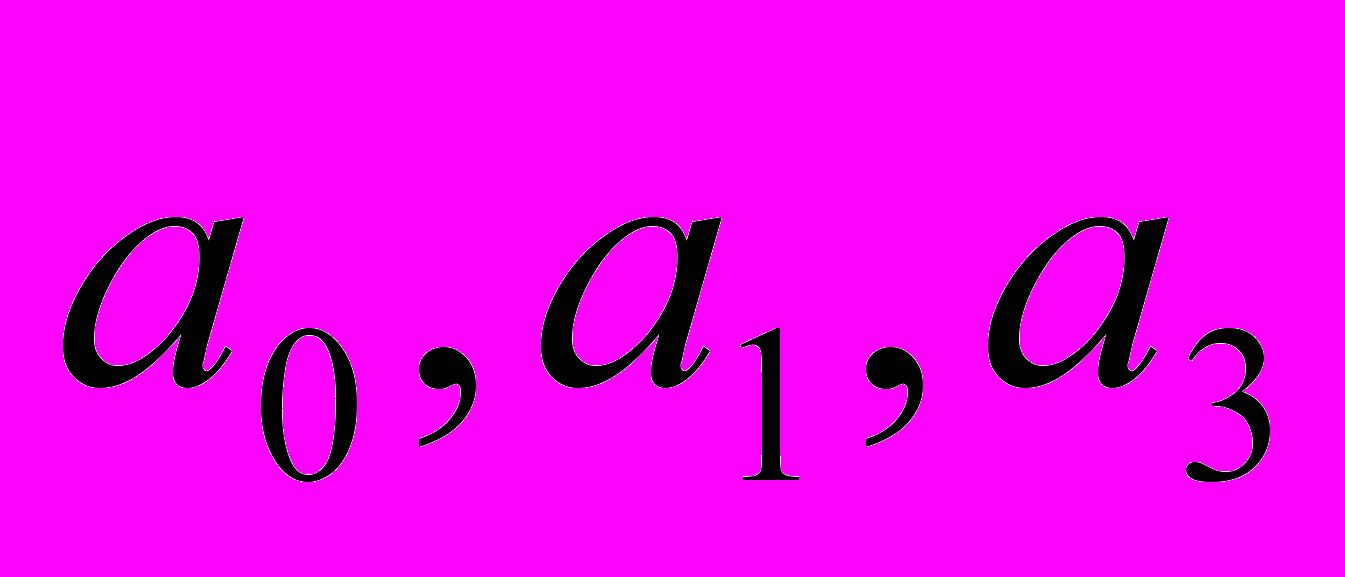, после решения которой получаем параболу 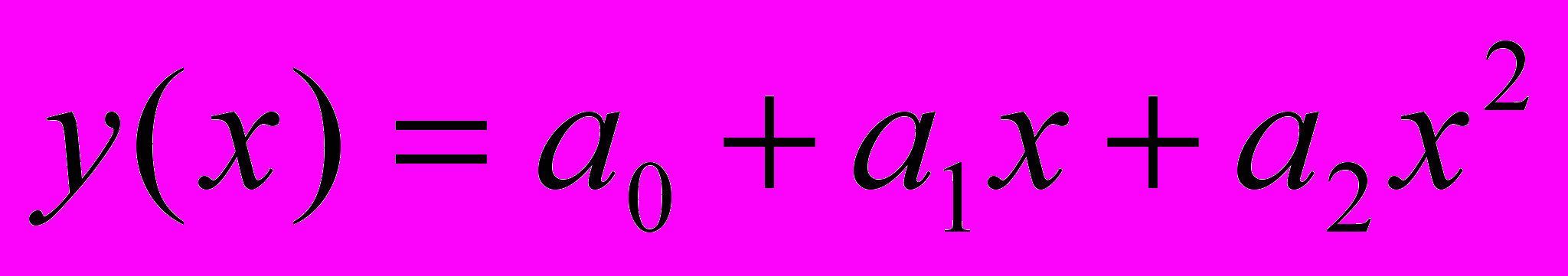, наилучшим образом описывающую наши данные по методу наименьших квадратов.

Аналогичным образом может быть построен кубический многочлен 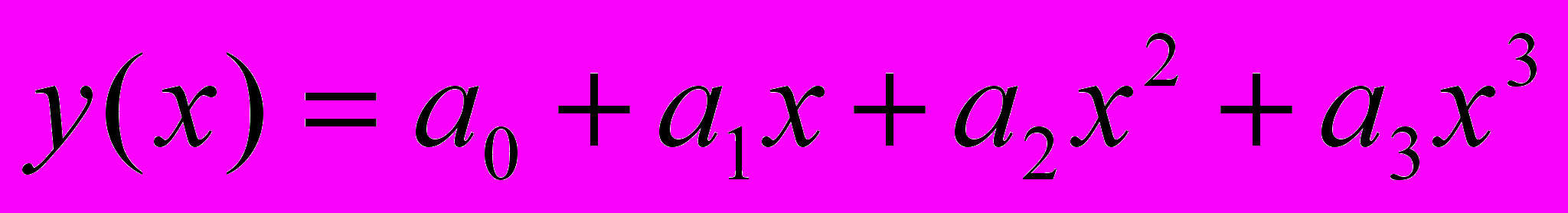, наилучшим образом описывающую наши данные по методу наименьших квадратов. Его коэффициенты являются решением следующей системы из четырех уравнений с четырьмя неизвестными

.

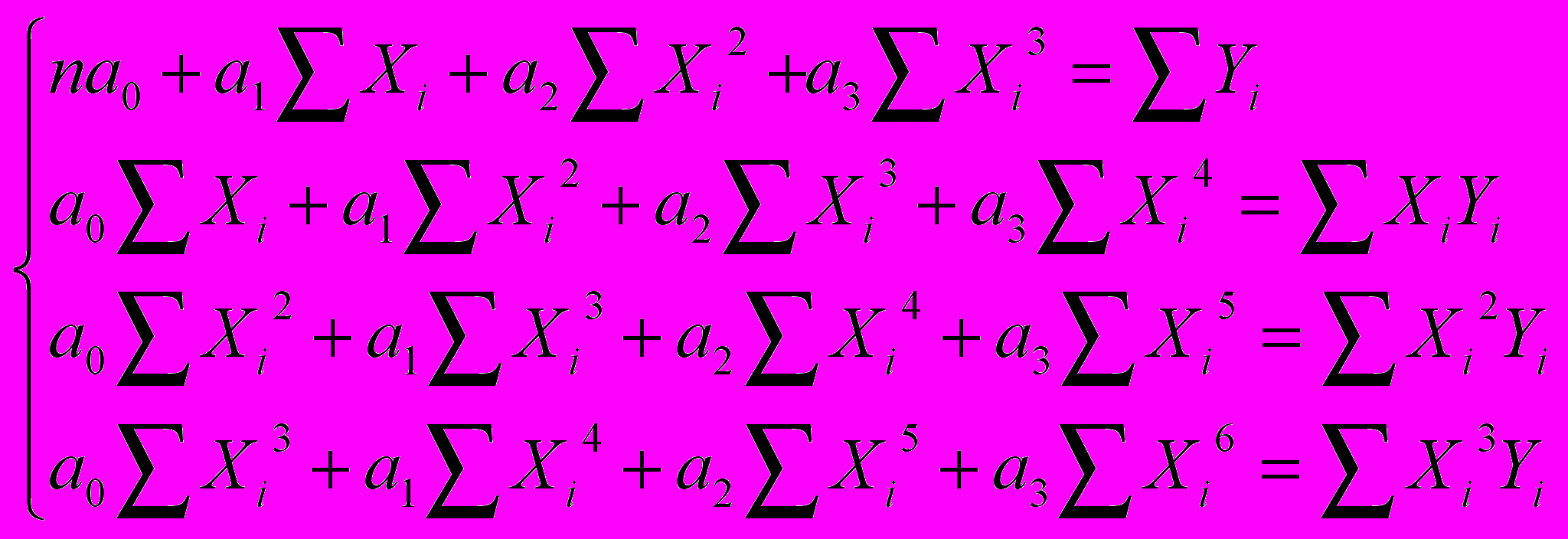В Mathcad имеются собственные средства, реализующие метод наименьших квадратов – это функции regress и interp.