Тимчасова навчальна програма з дисципліни бухгалтерський облік та статистика для студентів денної І заочної форми навчання спеціальності 130102 "Агрономія"
| Вид материала | Документы |
СодержаниеТема 3. Середні величини та показники варіації Тема 4. Ряди динаміки |
- Робоча навчальна програма з дисципліни "статистика" для студентів спеціальності "Облік, 432.81kb.
- Робоча навчальна програма дисципліни "Вища освіта І Болонський процес" для студентів, 406.21kb.
- Навчавчальна програма курсу «історія україни» для студентів денної (заочної) форми, 213.67kb.
- Іуправління Кафедра "Облік І аудит", 310.08kb.
- Навчальна програма курсу для студентів спеціальності «Книгознавство, бібліотекознавство, 465.09kb.
- Робоча програма, методичні вказівки та індивідуальні завдання до вивчення дисципліни, 574.82kb.
- Науково методичне видання, 160.21kb.
- Методичні рекомендації для самостійної роботи Для студентів денної І заочної форми, 516.83kb.
- Сагайдачного Кафедра «Облік І аудит», 141.13kb.
- Робоча програма, методичні вказівки та індивідуальні завдання до вивчення дисципліни, 703.92kb.
Тема 3. Середні величини та показники варіації
Середні величини – це узагальнюючі кількісні показники, що характеризують типові розміри варіюючих ознак якісно однорідних сукупностей.
Загальні принципи застосування середніх величин:
1. При визначені середньої величини в кожному конкретному випадку необхідно виходити із якісного змісту усередненої ознаки, враховуючи взаємозалежність ознак, що вивчаються.
2. Середня величина повинна, перш за все, розраховуватись по однорідній сукупності.
3. Загальні середні повинні підкріплюватись груповими середніми. Наприклад, аналіз динаміки продуктивності окремих тварин показує, що загальна середня продуктивність знижується.
4. Необхідно обґрунтувати вибір одиниць сукупності, для яких розраховується середня.
Середні величини діляться на два класи:
- ступеневі: середня арифметична, середня гармонійна, середня геометрична, середня квадратична, середня кубічна та ін.
- структурні: мода, медіана.
Найбільш поширеним видом середніх величин є середня арифметична. Її застосовують тоді, коли загальний об’єм варіюючої ознаки для всієї сукупності становить суму індивідуальних значень усередненої ознаки. Розрізняють середню арифметичну просту і зважену.
С
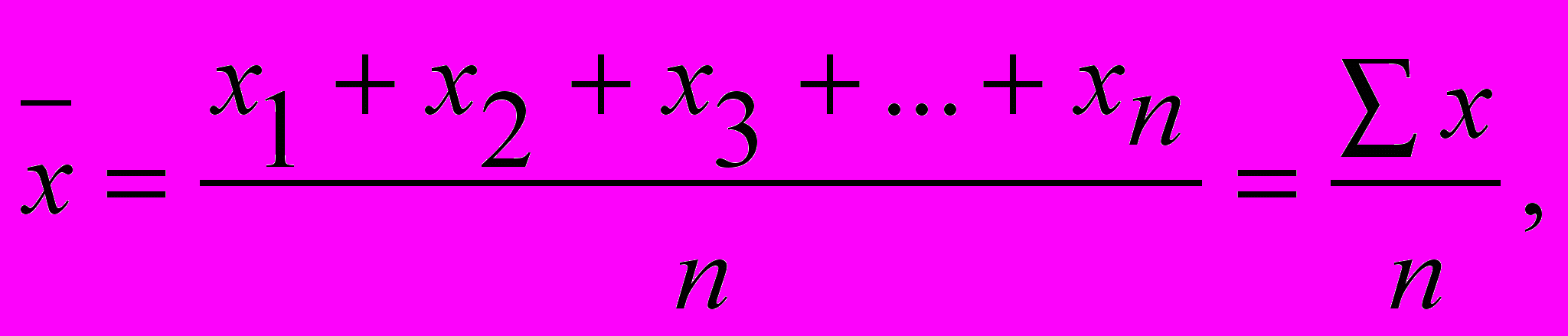
ередню арифметичну просту застосовують тоді, коли відомі індивідуальні значення усередненої ознаки у кожної одиниці сукупності. Її визначають за формулою:
де
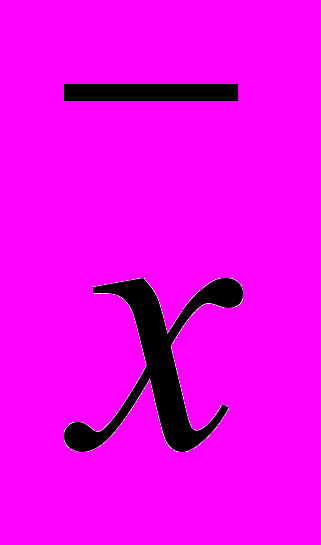– середнє значення ознаки; x – варіанти;
n – кількість варіантів.
Середню арифметичну зважену обчислюють тоді, коли окремі значення усередненої ознаки повторюються в досліджуваній сукупності неоднакове число разів, а також для обчислення середньої із середніх при різному обсязі сукупності.
С
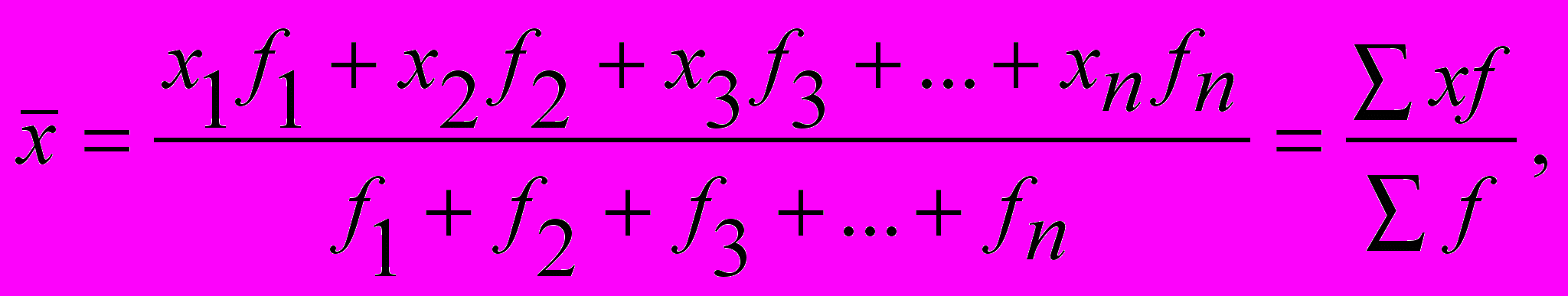
ередню арифметичну зважену визначають за такою формулою:
де f – частоти (ваги).
Середню гармонійну використовують для узагальненої характеристики ознаки тоді, коли відомі окремі значення досліджуваної ознаки і обсяги явищ, а частоти невідомі. Формула середньої гармонічної простої має вигляд:
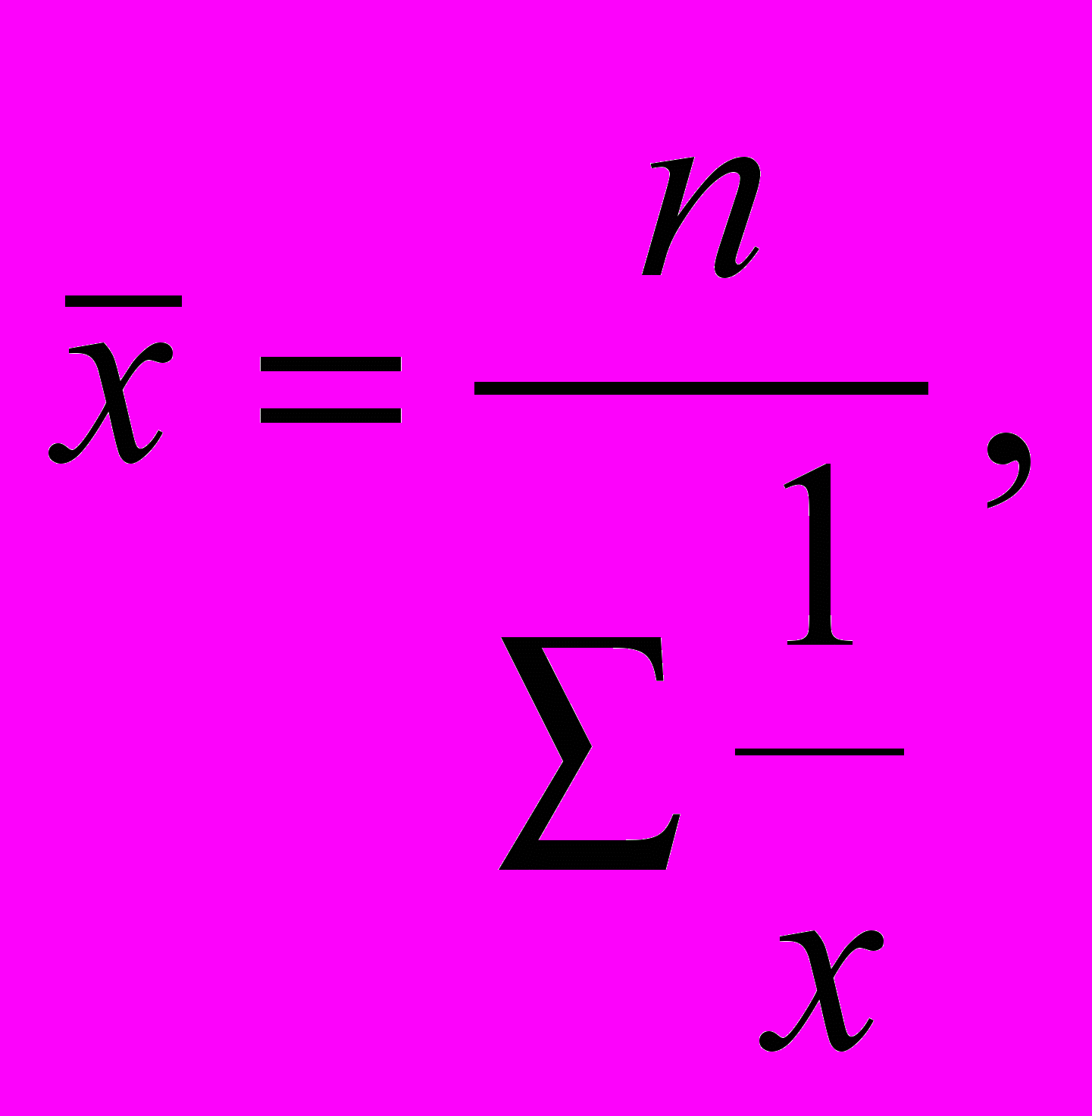
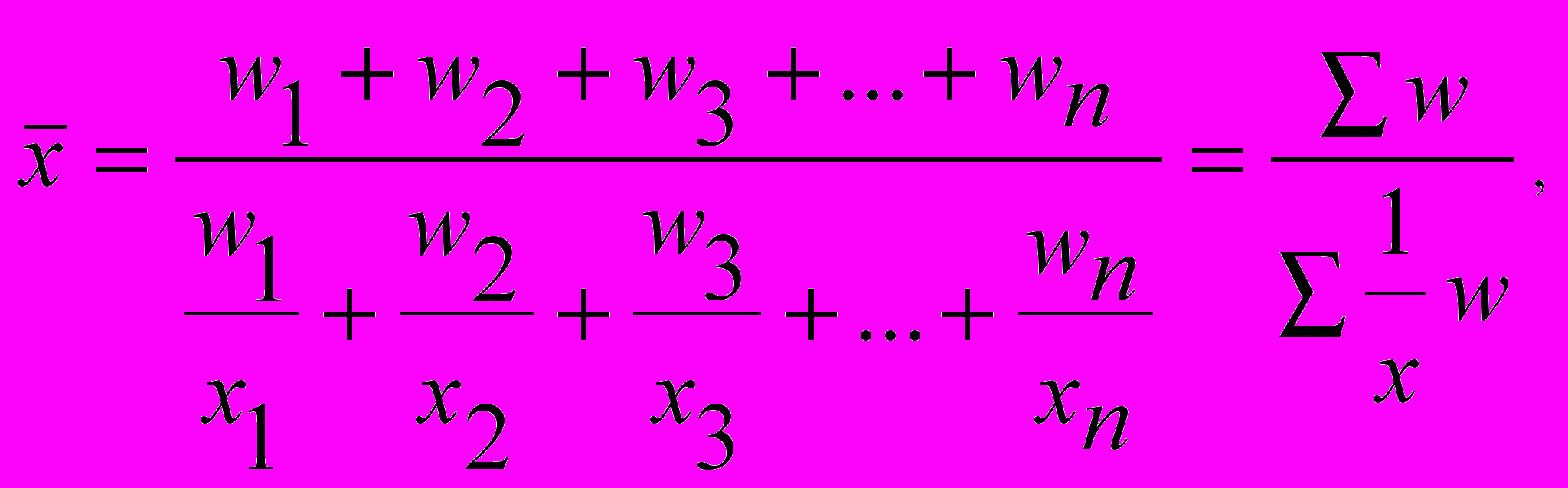
Середня гармонійна зважена:
де w – вага (xf = w; f =w/x ).
Для характеристики величин варіюючої ознаки використовують моду і медіану, які відносять до структурних середніх величин.
Варіація – це зміна розміру ознаки у статистичній сукупності. Для характеристики варіації використовують такі показники: розмах варіації, середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.
Тема 4. Ряди динаміки
Усі природні і суспільні явища перебувають у постійному русі та розвитку.
Процес розвитку явищ у часі називають динамікою, а статистичні величини, які характеризують зміну явищ у часі – рядами динаміки.
Обов'язковими елементами рядів динаміки є моменти або періоди часу (певне число місяця, день, місяць, рік), до яких належать досліджувані показники і рівні ряду, що характеризують розмір явища.
Залежно від характеру досліджуваних явищ розрізняють два види рядів динаміки: моментні і періодичні. Моментні ряди динаміки характеризують стан явища на певні періоди: на 1 січня, на кінець року і т. д. Наприклад, земельна площа, поголів'я визначають на 1.01 щороку. Періодичні (інтервальні) характеризують розміри явищ за певні періоди: доби, декаду, місяць, рік тощо. Особливістю періодичних рядів динаміки є те, що їх рівні можна підсумувати.
Якщо ряд моментний має однакові проміжки, то середній рівень такого ряду обчислюють за формулою середньої хронологічної:
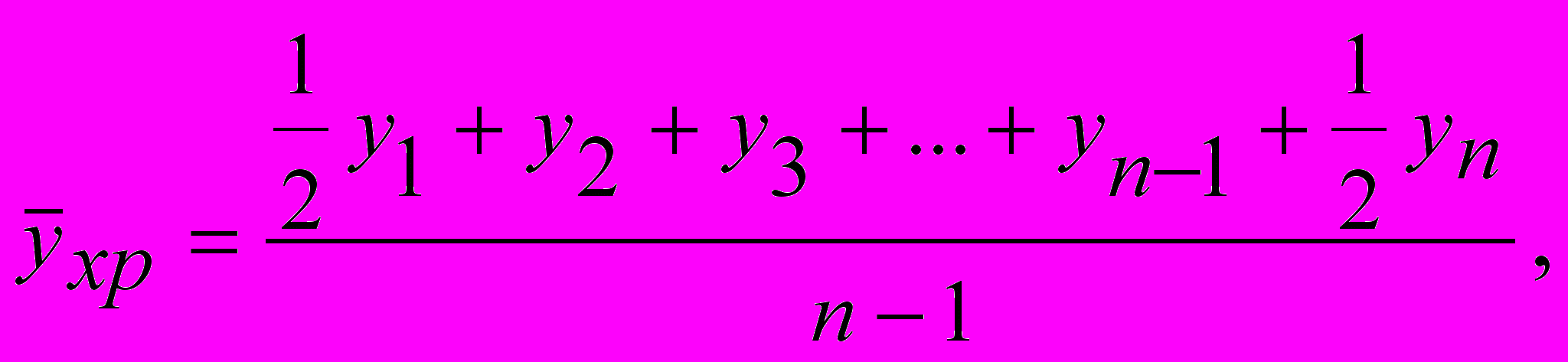
де y1, y2, yn – рівні ряду;
n – кількість рівнів.
Якщо моментний ряд має нерівні інтервали, то середній рівень визначають за формулою середньої арифметичної
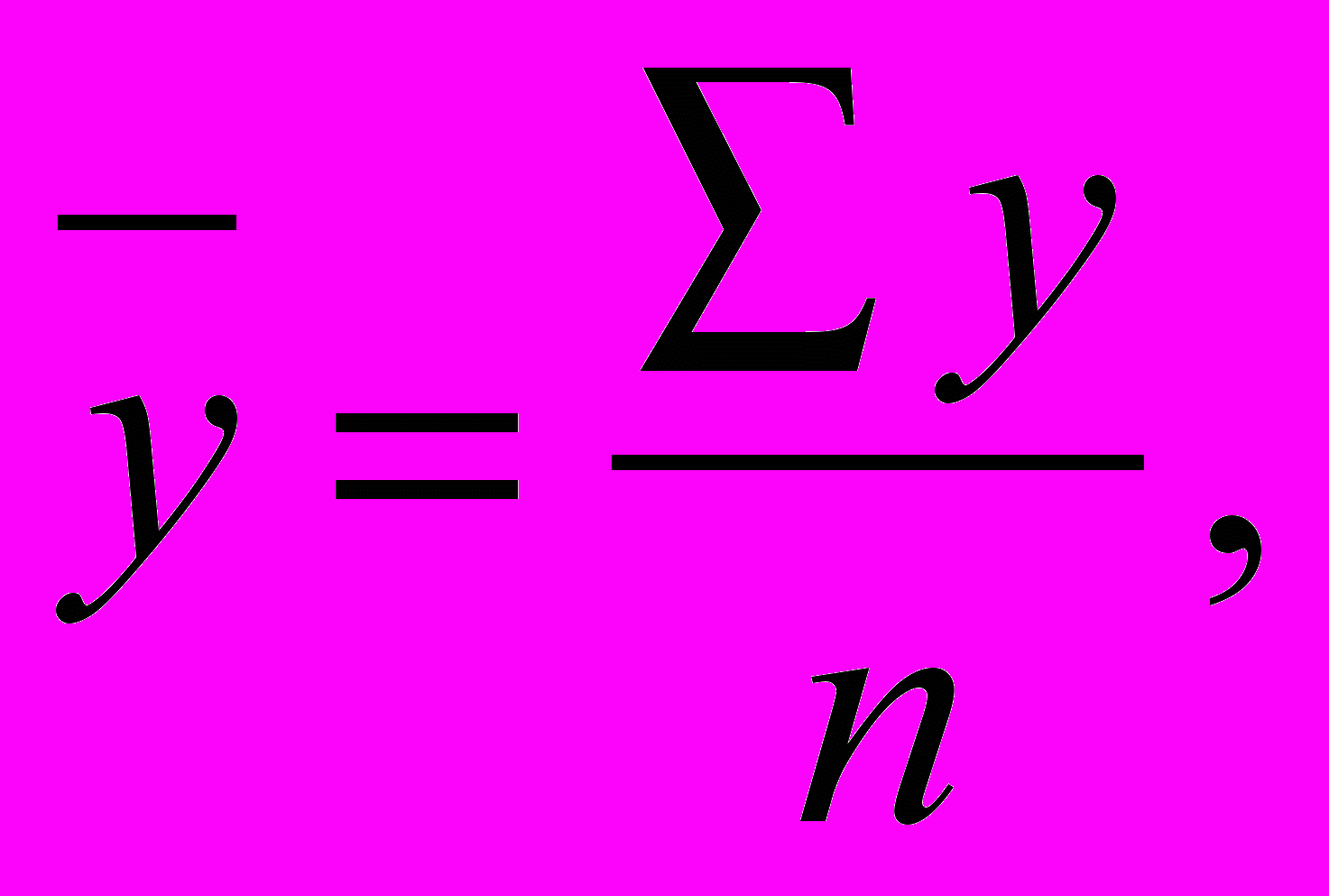
д
е y – рівні ряди; n – кількість рівнів.
Важливою умовою при побудові рядів динаміки є порівнянність рівнів ряду, які характеризують кількісну сторону досліджуваного явища. При порівнянні величин динамічного ряду відмінність їх має відображувати тільки зміни явища і не залежати від причин, пов'язаних з їх підрахунком.
Для характеристики динамічних рядів використовують такі показники: абсолютний приріст, темпи росту, темпи приросту, абсолютне значення одного процента приросту.