Приёмы триз на уроках учебный мозговой штурм – (умш)
| Вид материала | Урок |
- Методы генерирования идей, 68.5kb.
- «Мозговой штурм», 69.21kb.
- Принцип реализации метода «мозговой штурм» в курсе «методы экологических исследований», 54.46kb.
- Длительность программы: 24 часа (3 дня) Методы: Лекция, мозговой штурм, фасилитация,, 17.46kb.
- 3. Метод мозгового штурма, 428.24kb.
- М. А. Жужа Ключевые слова: олимпиадные задачи по физике, приёмы составления задач,, 94.17kb.
- Том числе и организационных, исторически называемая триз (теория решения изобретательских, 539.37kb.
- Экзаменационный стресс, 78.84kb.
- Тематическое планирование для 7 класс, 26.14kb.
- Российская ассоциация триз конкурс "триз 2012" Международная ассоциация триз российская, 75.63kb.
ПРИЁМЫ ТРИЗ - НА УРОКАХ
УЧЕБНЫЙ МОЗГОВОЙ ШТУРМ – (УМШ)
Это – один из наиболее интересных приёмов решения творческих, эвристических задач. Эта перспективная форма учебной деятельности применима к любым возрастам.
Целью данного приёма является развитие творческого мышления. Этот приём – хорошее дополнение и противовес репродуктивным формам работы. Учащиеся тренируют умения кратко и чётко выражать свои мысли, слышать и слушать друг друга. Есть возможность поддержать трудного ученика, обратив внимание на его идею. УМШ вызывает большой интерес учеников, на его основе можно организовать деловую игру.
Технология приёма. Штурм проводится в группах по 5-9 человек. Основное правило на первом этапе – никакой критики! Выбранный ведущий следит за поступающими идеями, чтобы ничего не было упущено. Секретарь – фиксирует идеи. Проводится первичное обсуждение и уточнение условия задачи. Время, обычно до 20 минут, желательно фиксировать на доске.
1-ый этап. «СОЗДАНИЕ БАНКА ИДЕЙ».
Главная его цель – наработать как можно больше возможных решений. В том числе – необычных, «диких». Затем – перерыв, в котором можно обсудить штурм с рефлексивной позиции: какие были сбои, допускались ли нарушения правил штурма, почему.
2-ой этап. «АНАЛИЗ ИДЕЙ».
Все высказанные идеи группа рассматривает критически. При этом придерживается основного правила: в каждой идее желательно найти что-то полезное, рациональное, возможность усовершенствовать идею или хотя бы применить её в других условиях.
3-ий этап. «ОБРАБОТКА РЕЗУЛЬТАТОВ».
Группа выбирает 2-3 самых интересных решения (можно включить и «дикие»), назначает спикера и он рассказывает о них классу. Если целью группы был поиск как можно большего числа решений, то оглашаются все идеи, решения.
Пример использования приёма «Мозговой штурм» на уроке алгебры в 8 классе по теме: «Преобразование выражений, содержащих квадратные корни»
Ситуация: Над вашей Компанией нависла угроза
банкротства, в случае не выполнения
следующего задания:
Докажите, что выражения
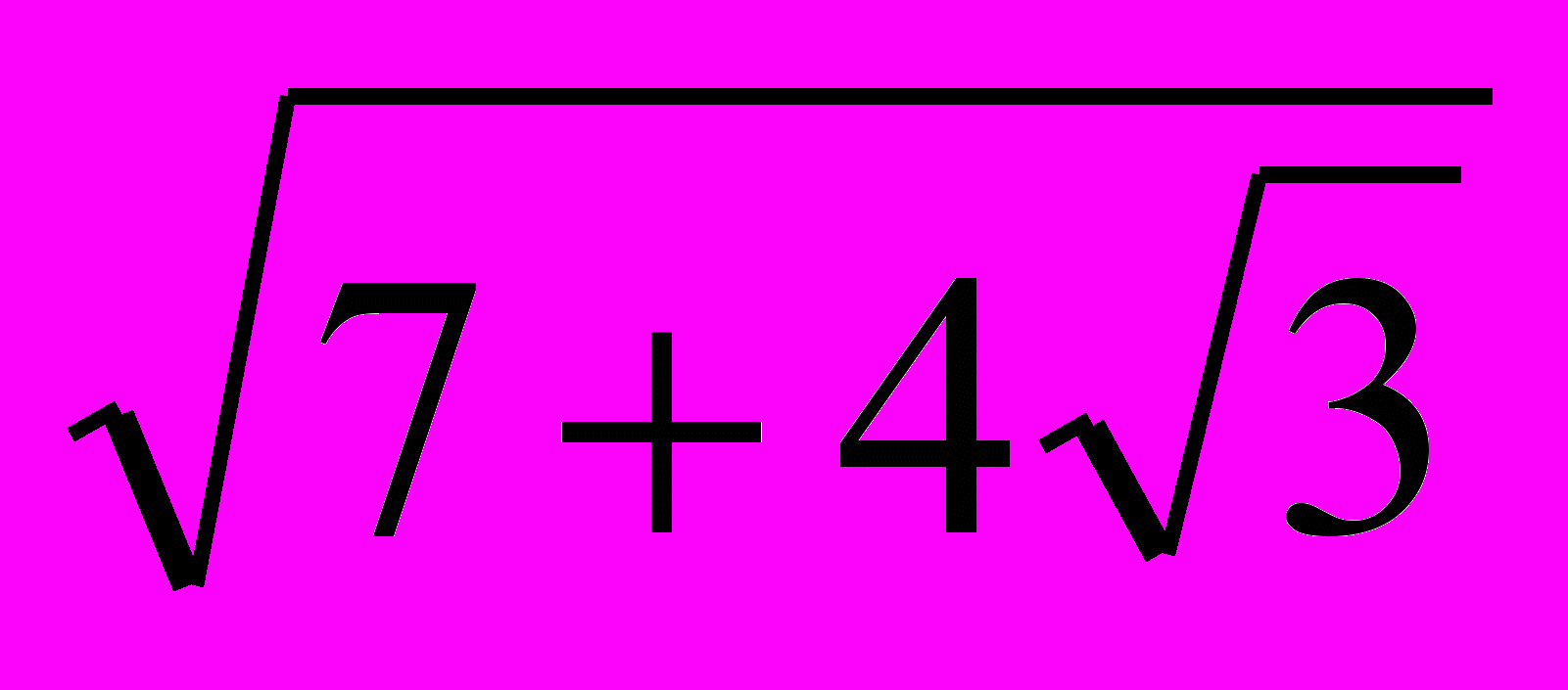 и
и 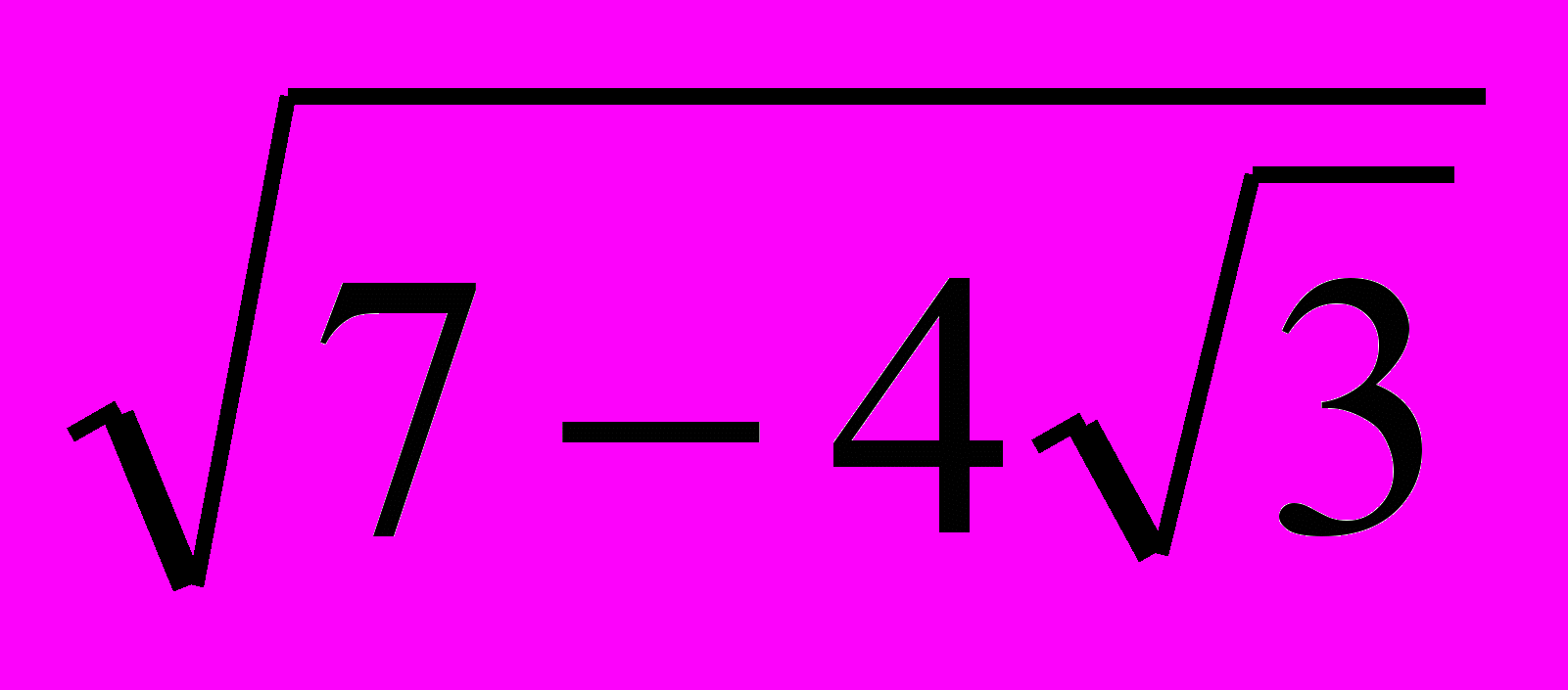
являются натуральными числами
Подсказка: отсутствует.
