Geum.ru

Лекция 1

Вид материалаЛекция

Содержание


AB=. Объединение AB ={x:xA или xB}.
Несчетные множества
Квантор Субъект Связка Предикат
Все, каждый, любой, произвольный
A (условие) , из него выводится свойство B
Подобный материал:

Лекция 1

Глава 1. Ведение


§1. Некоторые понятия теории множеств и математической логики

1.Множество, операции над множествами, обозначения

Множество - совокупность некоторых различимых объектов. Задать множество - задать признаки, характеризующие эти объекты.

Примеры:

N - натуральные числа [a,b] - отрезок

Z - целые числа (a, b) – интервал, (a,b],[a,b) - полуинтервалы

Q - рациональные числа

R - вещественные числа

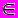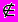x E, x E

Подмножество A  E

- пустое множество E,EE

Обозначение множества перечислением - {a, b, c}

Обозначение множества указанием характеризующего свойства - { x : x удовлетворет свойству P}. Пример: N={xZ:x>0}

[a,b]={x: axb}

Дополнение (разность) E\A={xE:xA}

Пересечение AB ={x:xA и xB}. Если два множества не пересекаются. то это можно записать в виде AB=.

Объединение AB ={x:xA или xB}.

Произведение множеств AB ={(x,y):xA и yB}.

Пример R2 = R  R - плоскость.

2. Отображение, взаимно-однозначное соответствие, счетное и несчетные множества

Даны множества A и B. Отображение A в B (или функция определенная на A со значениями в B) - соответствие или закон (обозначим его f ), которое каждому a 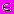A сопоставляет единственное b  B, A B, f: A  B, b = f(a).

a - прообраз, b - образ при отображении f.

Отображение из A в B называется взаимно-однозначным, если

1) разные элементы из A имеют разные образы

2) каждый элемент из B является образом некоторого элемента из A

Эквивалентные множества A  B или множества одинаковой мощности, если существует взаимно-однозначное соответствие между элементами этих множеств.

Счетное множество A  N

Пример: Множество рациональных чисел счетно.

Одно из простейших свойств счетных множеств

Объединение конечного или счетного числа счетных множеств является счетным множеством.

Несчетные множества

Бесконечное множество, не являющееся счетным, называется несчетным. Множество [0,1] имеет большую мощность, чем N. Множество мощности континиума. Множество действительных чисел R - несчетное множество.

R  [ 0, 1 ]

3. Некоторые понятия математической логики (Дж. Маллас Пролог)

При описании логики Аристотеля употребляется понятие суждение. Суждение представляет собой законченную мысль, выраженную средствами естественного языка и (согласно Аристотелю) состоит из четырех элементов:

Квантор Субъект Связка Предикат
Все числа являются не рациональными

Некоторые натуральные числа - четны

В последнем случае подразумевается связка “являются”. В первом случае обычно говорят также: “Все числа не являются рациональными”. Вместо термина предикат мы будем использовать также термин свойство. Противоположное свойство P или отрицание свойства P обозначается значком 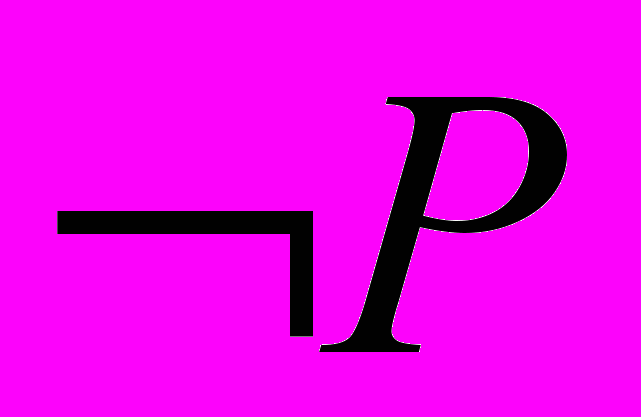или .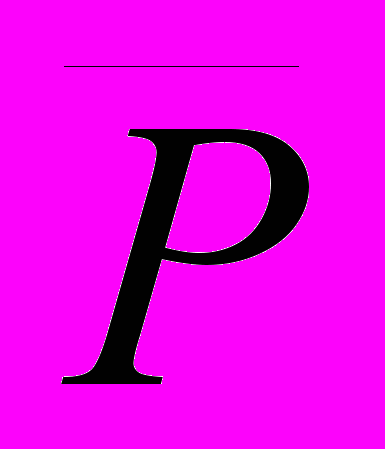


В традиционной логике допускаются два типа суждений, каждый из которых характеризует возможные отношения между двумя классами (классом субъектов и классом предикатов):

Все S являются P ( каждый из S удовлетворяет свойству P )

Некоторые из S являются P ( существует представитель из S, удовлетворяющий свойству P )

Здесь S обозначает класс субъектов, а P - класс предикатов ( или некоторое свойство, характеризующее этот класс ). Все, каждый, любой, произвольный называются универсальным квантором или квантором общности. Квантор общности обозначается значком . Некоторые из, существует - экзистенциальные кванторы. Квантор существования обозначается значком . Таким образом, основные типы суждений можно записать в следующей форме ( логической связке соответствует символ двоеточия ):
  1. xS:P
  2. xS:P

Предикат и субъект в суждении могут быть составными, в частности они сами могут быть суждениями. Например, рассмотрим высказывание:

>0 >0 x,|x-x0|< : |f(x)-2|<.

Это высказывание следует читать так: Для любого эпсилон больше нуля существует дельта больше нуля, что для всех икс, удовлетворяющих неравеству …, выполнено неравенство …. Это суждение является составным и может быть разложено на простейшие суждения следующим образом:

S1 : P1, где S1-класс, S1={xR,x>0}, P1 - предикат,

P1=(S2 : P2), где S2=S1, P2 - предикат,

P2=(xS3: P3), S3= S3()={xR:|x-x0|<}, P3 - предикат,

Прямая и обратная теоремы, эквивалентность, метод математической индукции

Структура простейшей теоремы выглядит следующем образом: дано свойство A (условие) , из него выводится свойство B (заключение).

В этом случае говорят A влечет B , A B ( последняя запись подразумевает на самом деле истинность выражения A B).

Если к тому же B A, то говорят, что верна и обратная теорема и пишут AB, при этом A и B называются эквивалентными.

Теорема. Отрицание суждения должно строится по следующим формальным правилам:

1. квантор заменяется на квантор

2. квантор заменяется на квантор

3. предикат P заменяется на свое отрицание.

Пример:

>0 >0 x,|x-x0|< : |f(x)-2|<.

его отрицание

>0 >0 x,|x-x0|< : |f(x)-2|.

Доказательство достаточно провести для двух типов простейших суждений:

1. x: P

2. x: P,

где P некоторое суждение. Для таких суждений сформулированная теорема достаточно очевидна.

Метод математической индукции

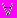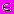Емеется последовательность свойств Pn. Если доказано свойство P1 и Pk Pk+1, то Pn справедливы для n N.

Пример: Доказать индукцией равенство Cnk + Cnk+1=Cn+1k+1, .