Домашнее задание Докажите, что при любом натуральном (Литвиненко, Мордкович) Докажите, что при любом натуральном (Литвиненко, Мордкович)
| Вид материала | Документы |
- Домашнее задание по теме «Методика обучения математическим доказательствам. Различные, 42.98kb.
- Докажите, что значение выражения не зависит от значения переменной при всех ее допустимых, 13.18kb.
- -, 2072.97kb.
- Овозможности дистанционного воздействия на подсознание субъекта, 25.93kb.
- Учение о воскрешении, 492.05kb.
- Библиотека Альдебаран, 3050.29kb.
- Пояснительная записка Данная учебная программа ориентирована на учащихся 7 класса, 476.73kb.
- Карточка №1 урок №1 Прочитайте описание донской природы. Какова роль этих описаний, 57.94kb.
- При наличии в собственности личного подсобного хозяйства получение доходов от него, 5.09kb.
- Предметом изучения макроэкономики не являются: а вопросы индексации заработной платы, 622kb.
Совместный разбор
- Докажите, что при любом натуральном

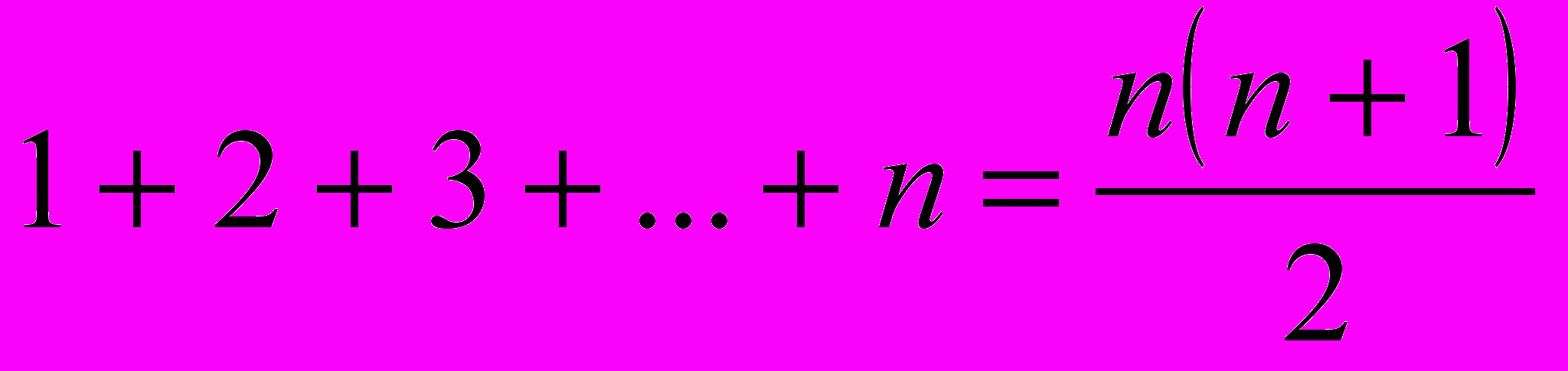
- Доказать, что
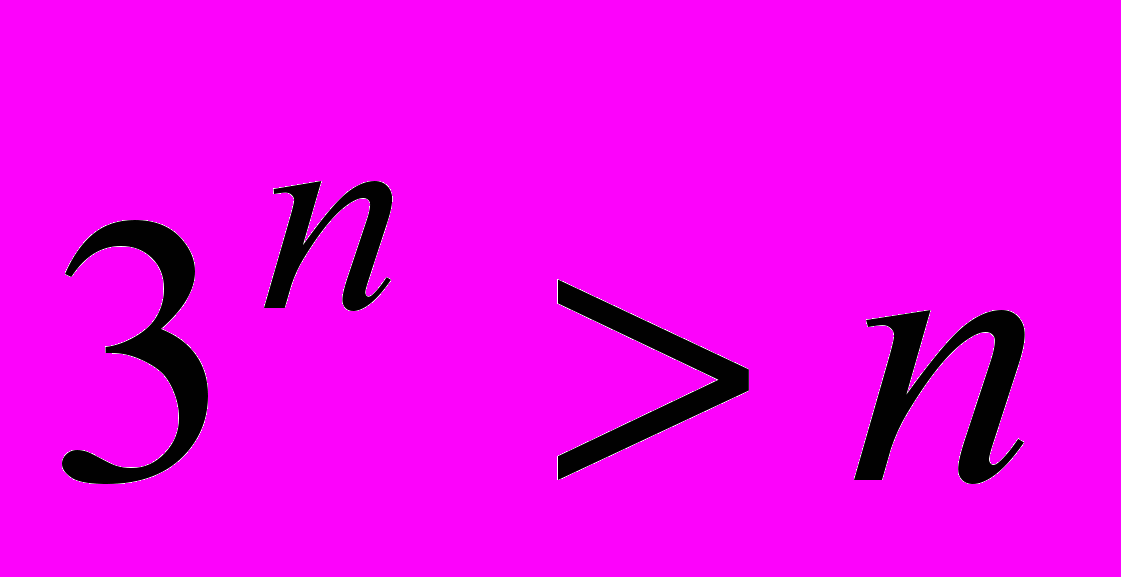 , гд е
, гд е  - любое натуральное число.
- любое натуральное число.
- Докажите, что при любом натуральном

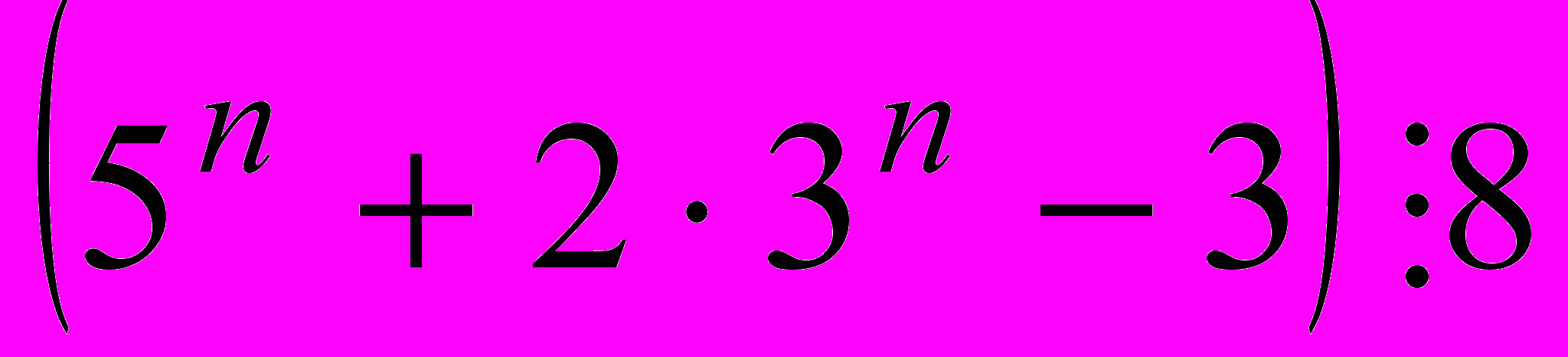 .
.
Домашнее задание
- Докажите, что при любом натуральном

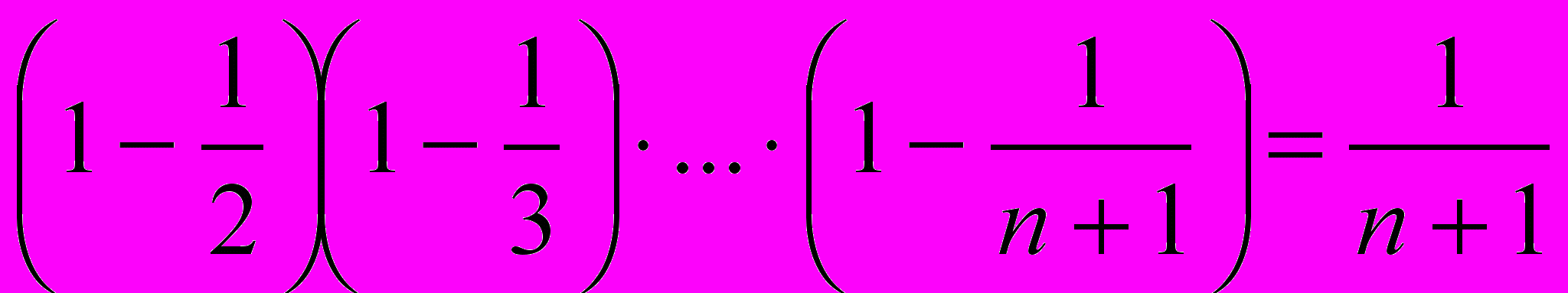 (Литвиненко, Мордкович)
(Литвиненко, Мордкович)
- Докажите, что при любом натуральном

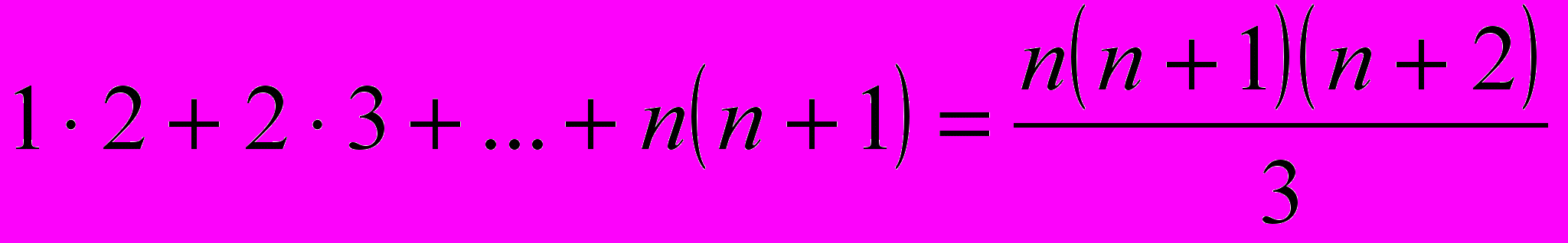 (Литвиненко, Мордкович)
(Литвиненко, Мордкович)
- Докажите, что при любом натуральном

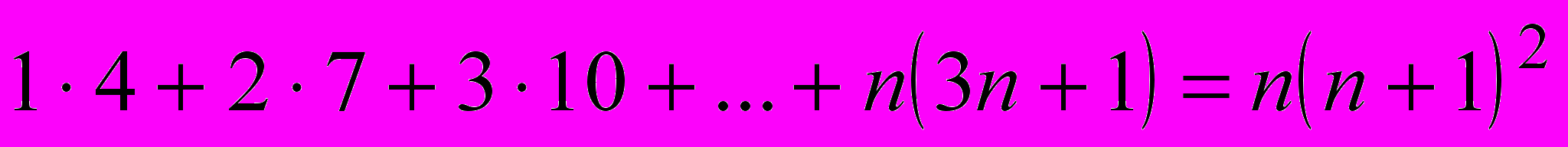 (Литвиненко, Мордкович)
(Литвиненко, Мордкович)
- Докажите, что при любом натуральном

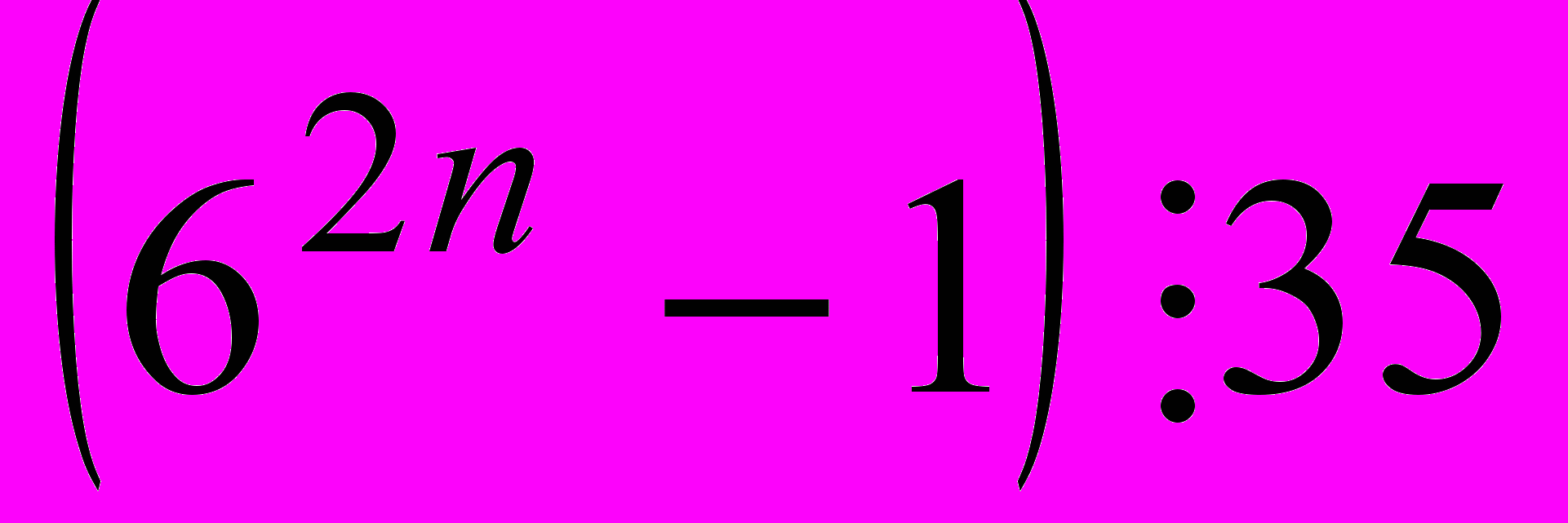 . (Литвиненко, Мордкович)
. (Литвиненко, Мордкович)
- Докажите, что при любом натуральном

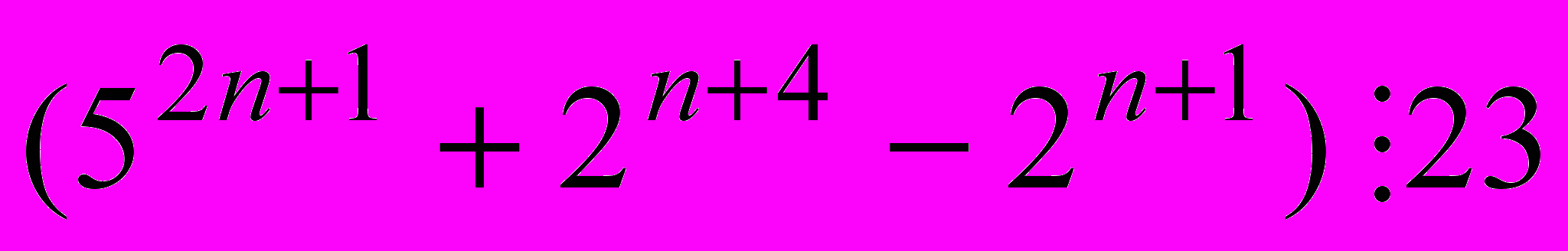 (Литвиненко, Мордкович)
(Литвиненко, Мордкович)
- Докажите, что при любом натуральном

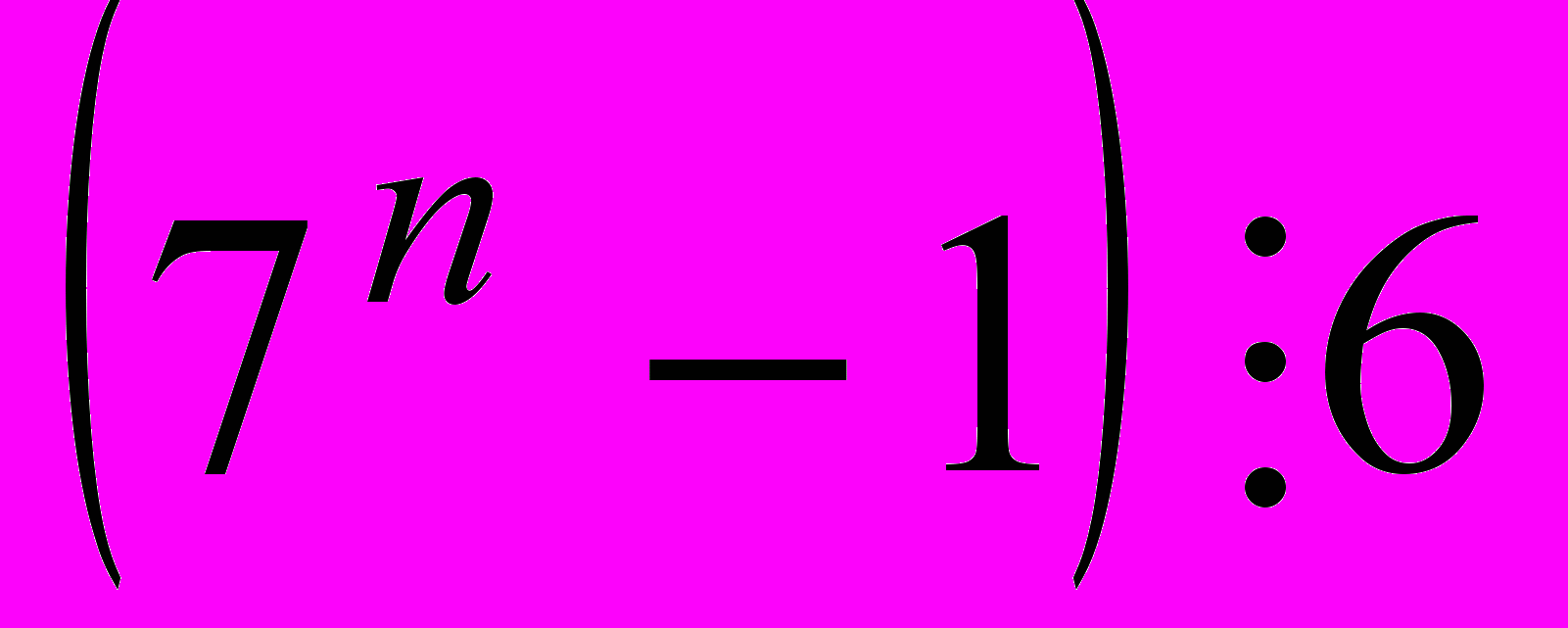 (Бахтина)
(Бахтина)
Для обязательного самостоятельного решения
- Докажите, что при любом натуральном

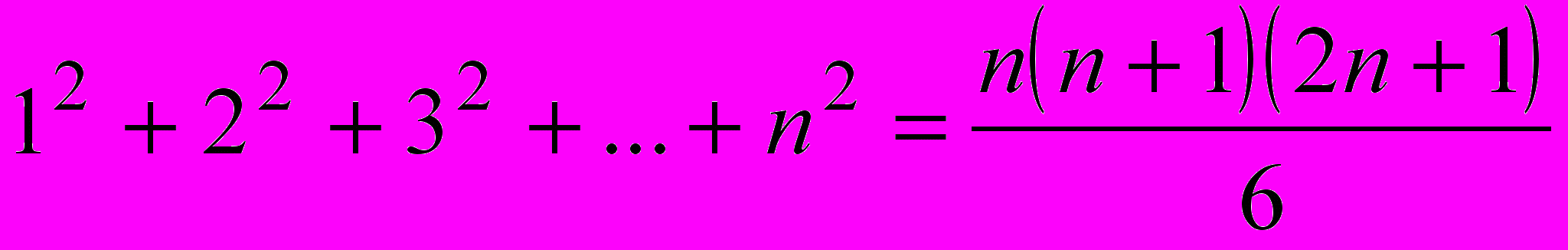 (Звавич 3600)
(Звавич 3600)
- Докажите, что при любом натуральном

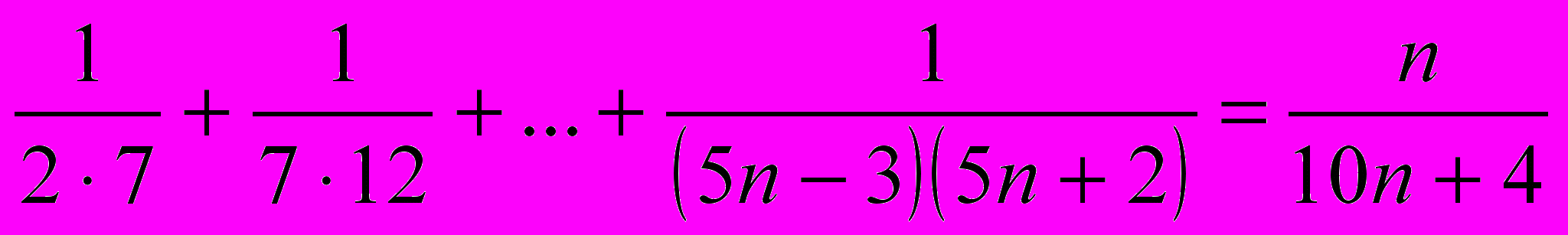 (Звавич 3600)
(Звавич 3600)
- Докажите, что при любом натуральном

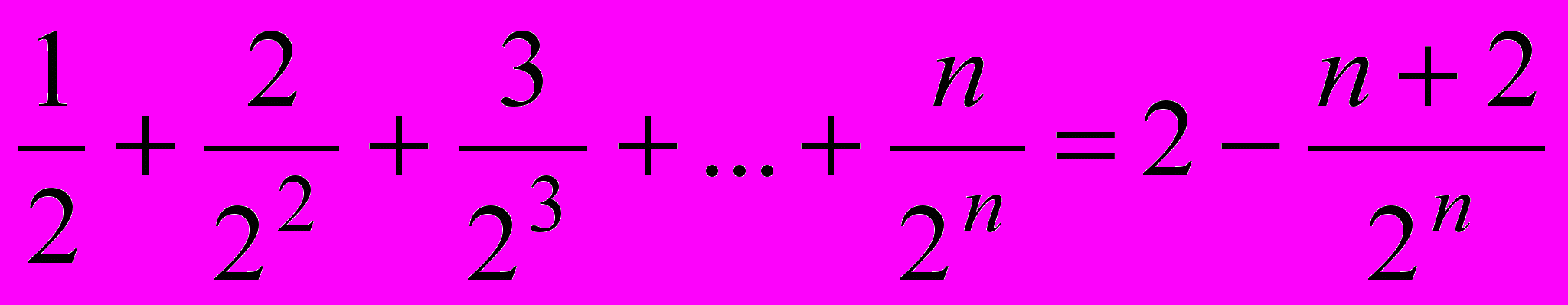 (звавич 3600)
(звавич 3600)
- Докажите, что при любом натуральном

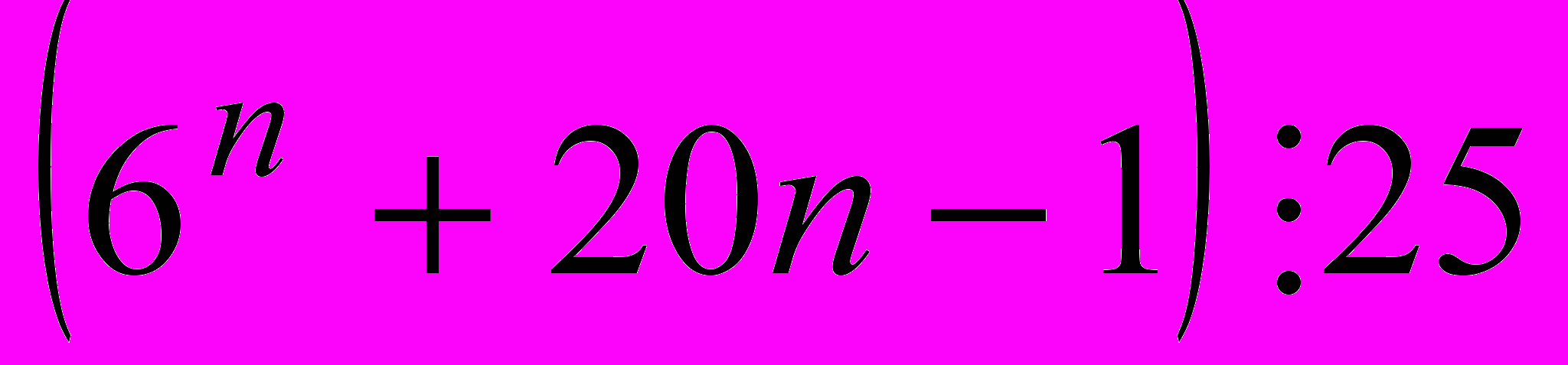 (звавич 3600)
(звавич 3600)
- Докажите, что при любом натуральном
 все члены последовательности
все члены последовательности 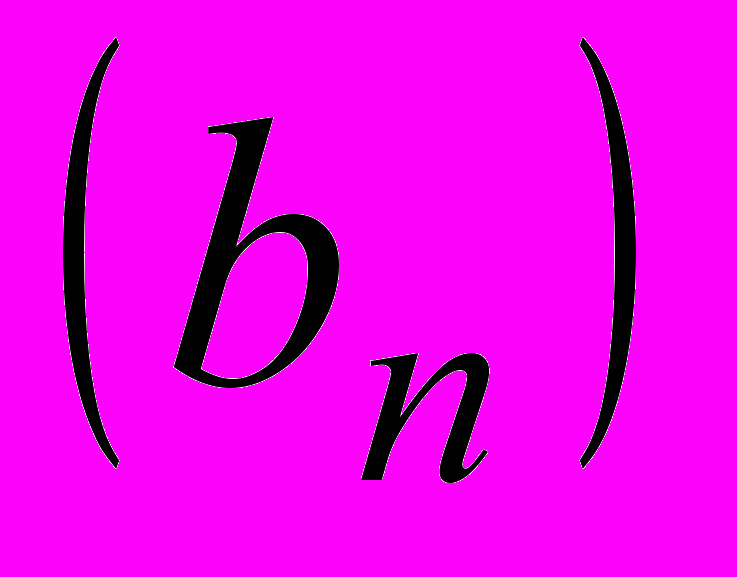 , где
, где 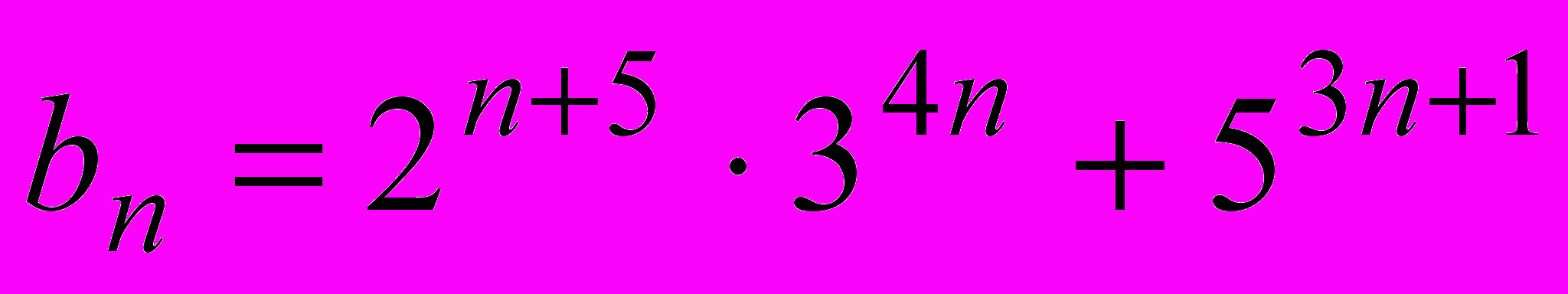 делятся на 37 (звавич3600)
делятся на 37 (звавич3600)
- Докажите, что при любом натуральном

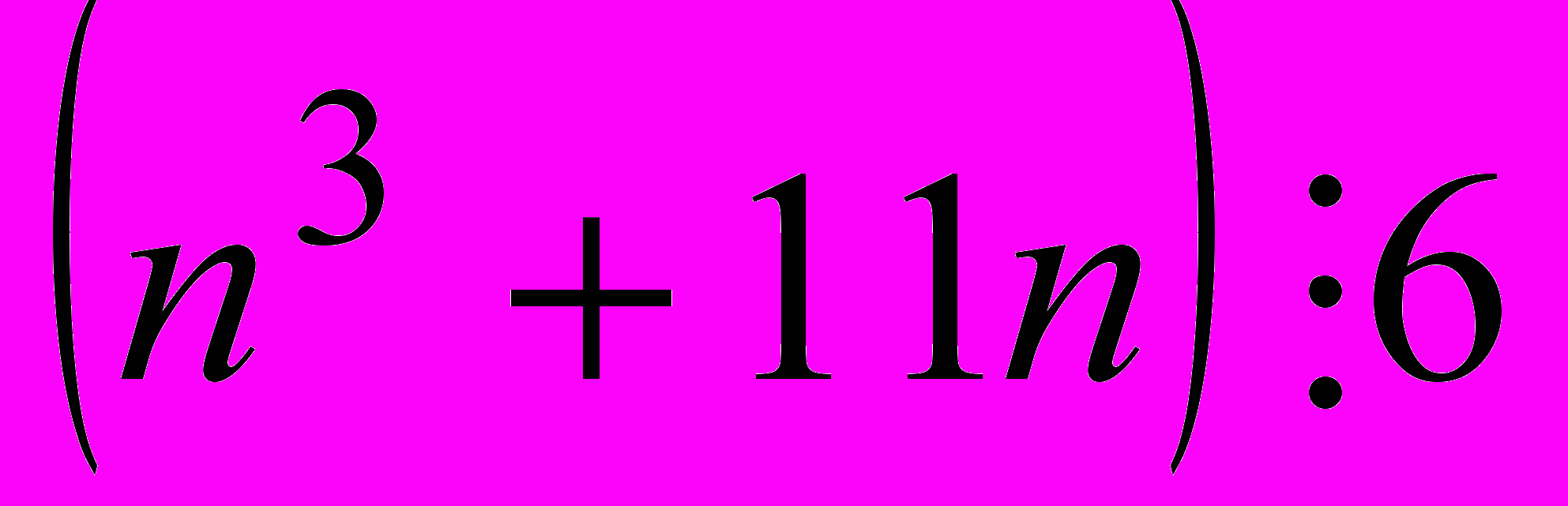 . (Бахтина)
. (Бахтина)
- Докажите, что при любом натуральном

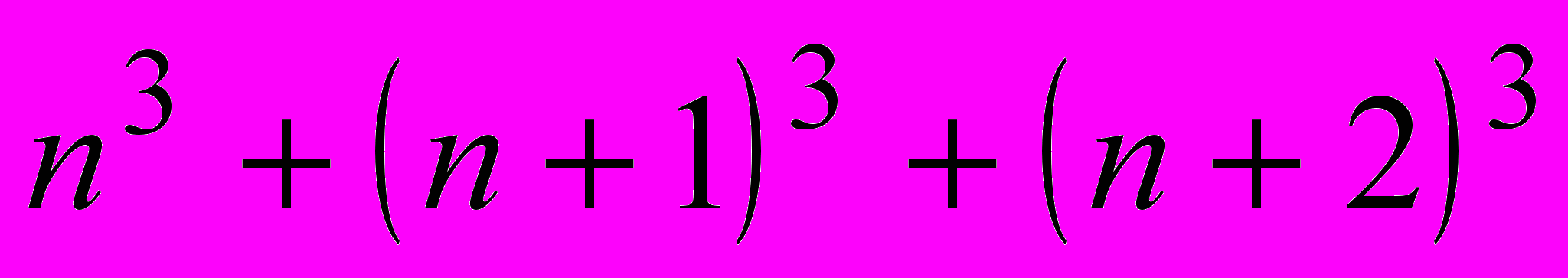 делится на 9. (Генкин)
делится на 9. (Генкин)
- Докажите, что при любом натуральном

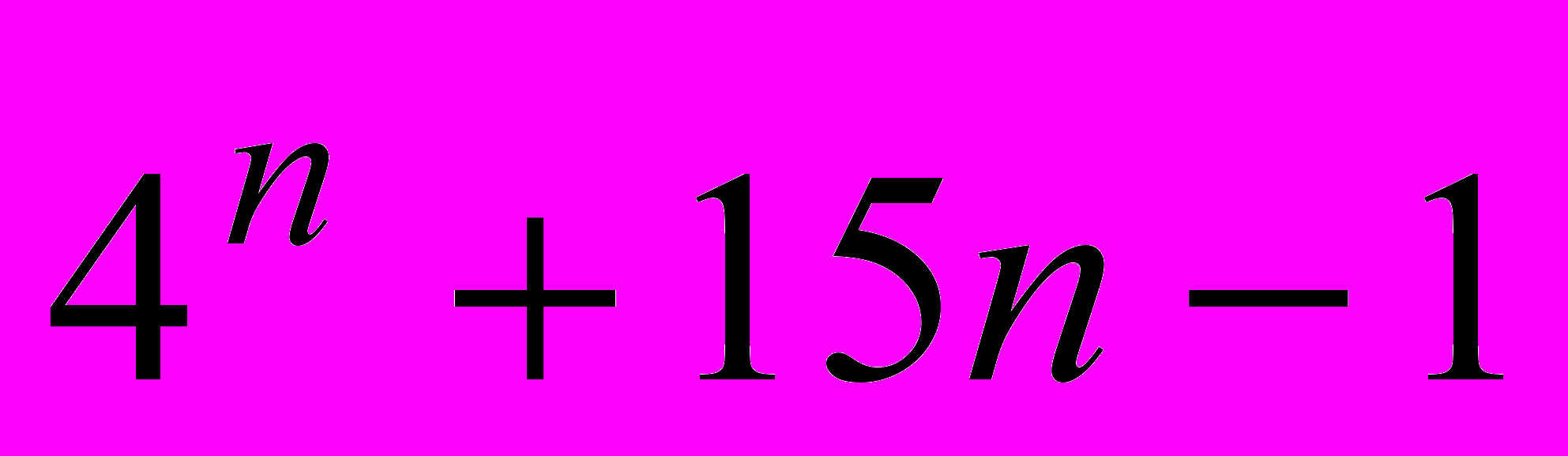 делится на 9. (Генкин)
делится на 9. (Генкин)
- Докажите, что при любом натуральном

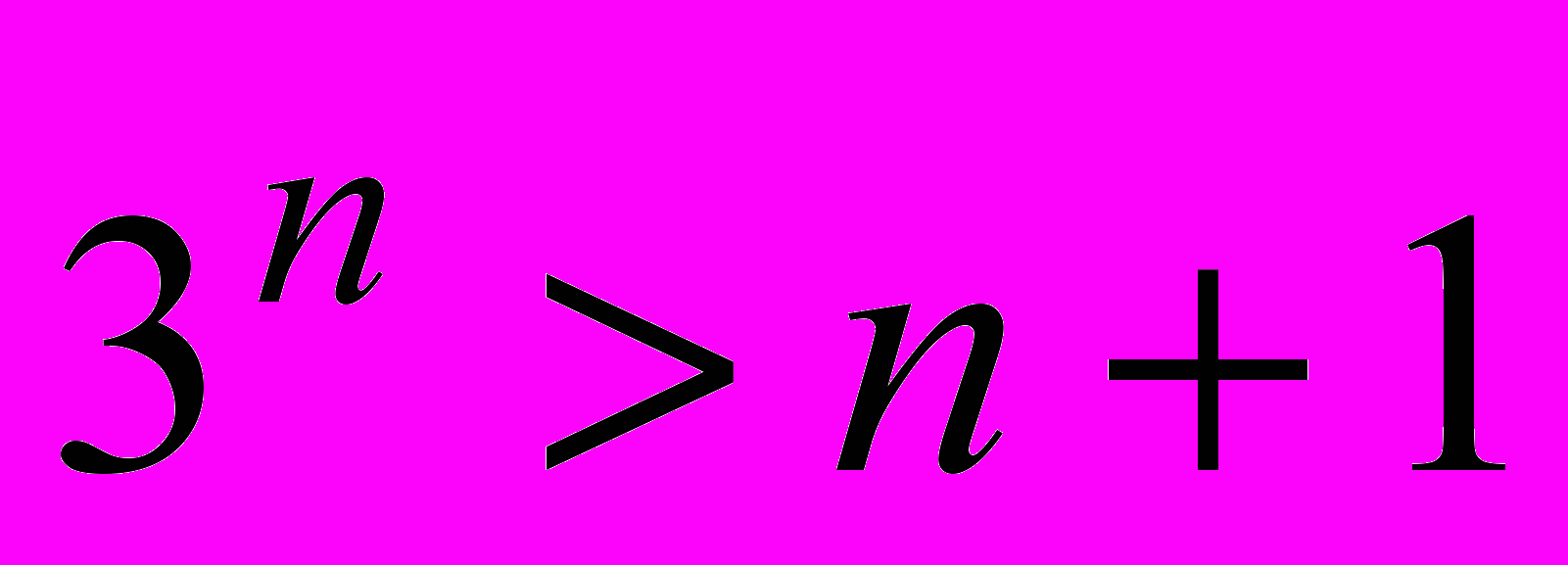 (звавич 3600)
(звавич 3600)
- Докажите, что при любом натуральном

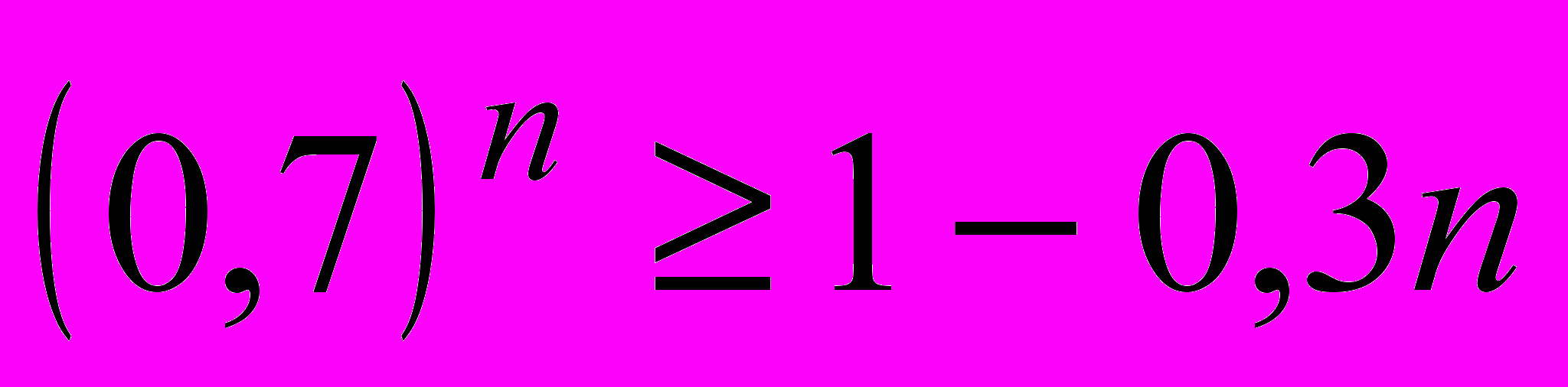 (звавич 3600)
(звавич 3600)
- Доказать, что
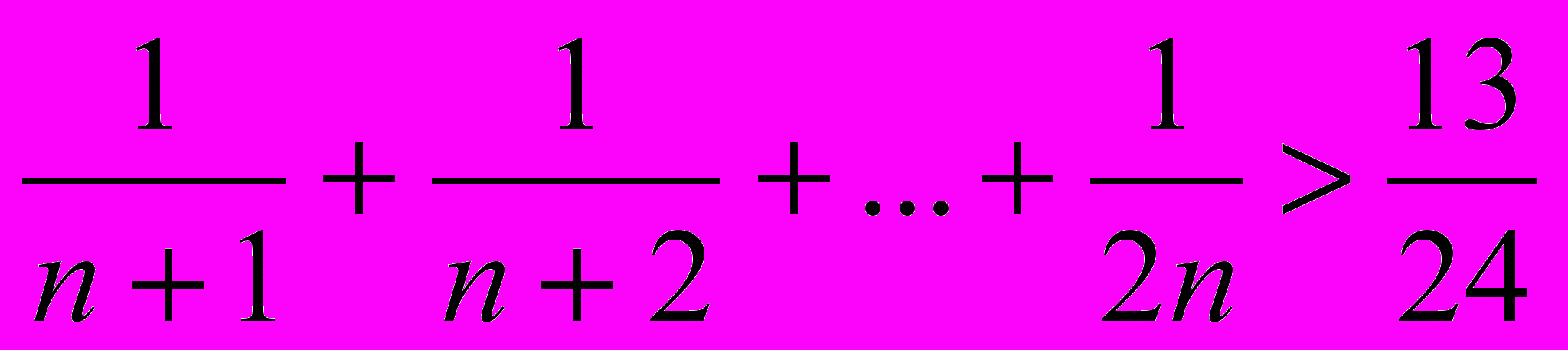 ,
, 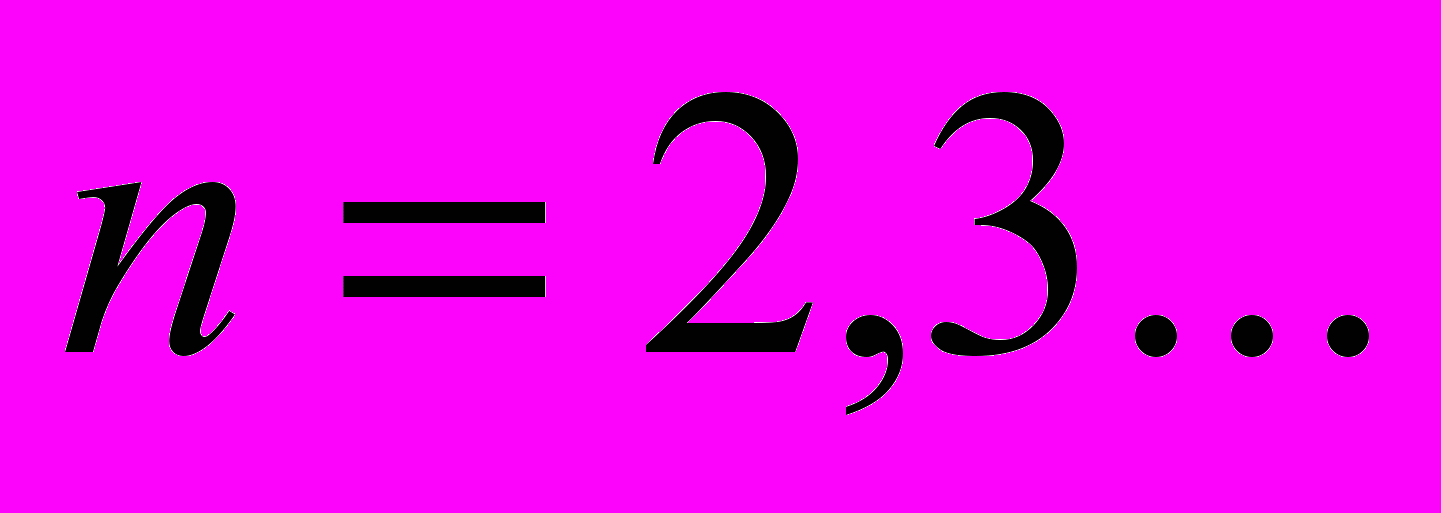 (Генкин)
(Генкин)
- Пусть
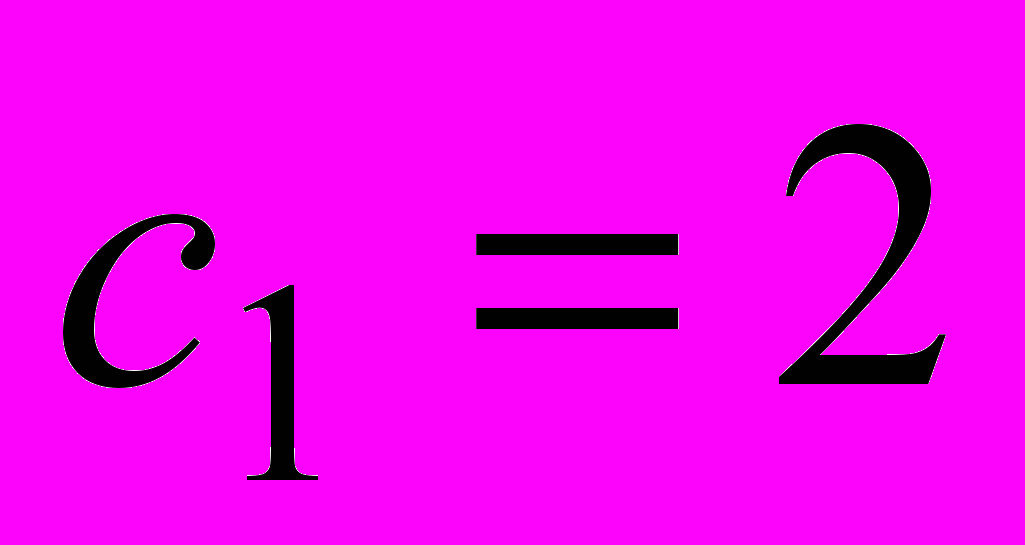 ,
, 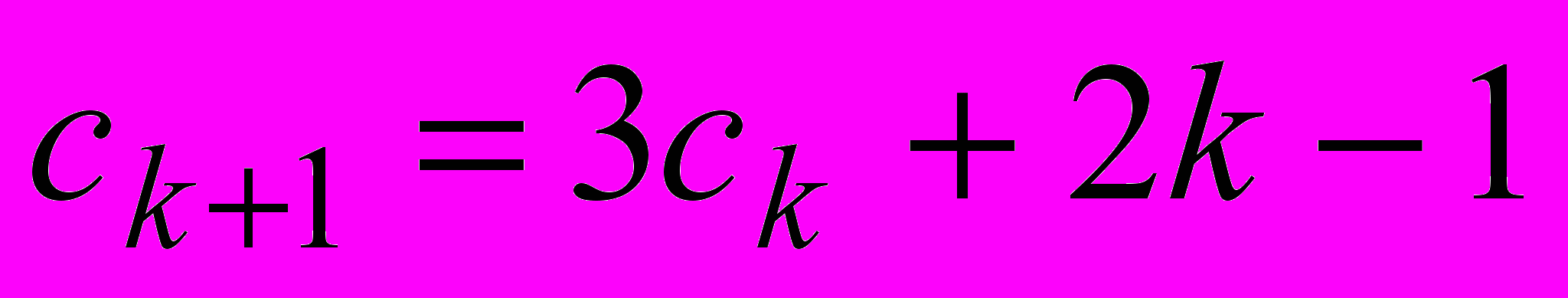 . Докажите, что при любом натуральном
. Докажите, что при любом натуральном 
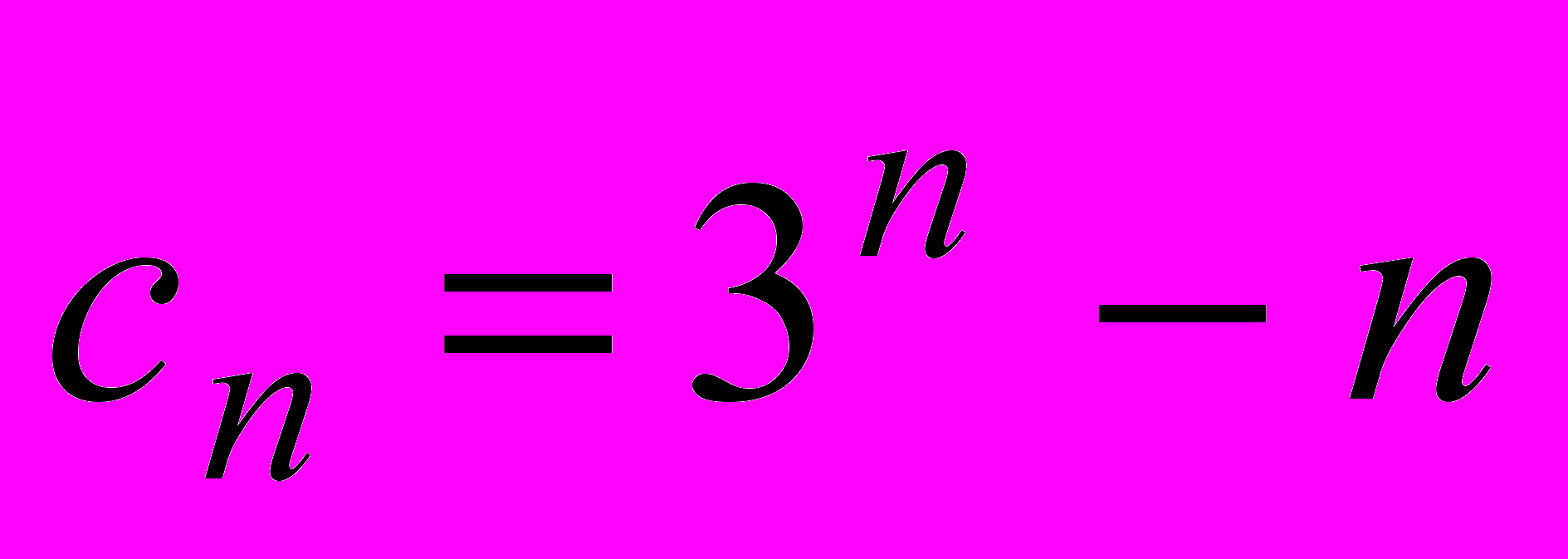 .
.
- Докажите, что любое натуральное число можно представить как сумму нескольких разных степеней двойки (возможно, включая и нулевую) (Генкин)
- Кусок бумаги разрешается рвать на 4 или на 6 кусков. Докажите, что по этим правилам его можно разорвать на любое число кусков, начиная с девяти. (Генкин)
- Даны
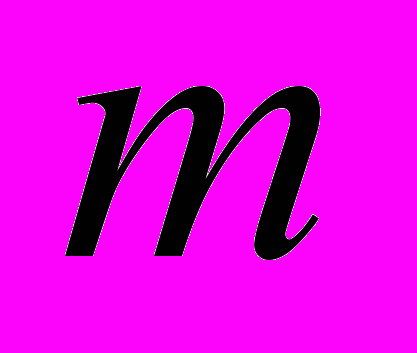 монет одинакового достоинства, среди которых имеется одна фальшивая, весящая меньше настоящей, Докажите, что если количество монет удовлетворяет неравенству
монет одинакового достоинства, среди которых имеется одна фальшивая, весящая меньше настоящей, Докажите, что если количество монет удовлетворяет неравенству 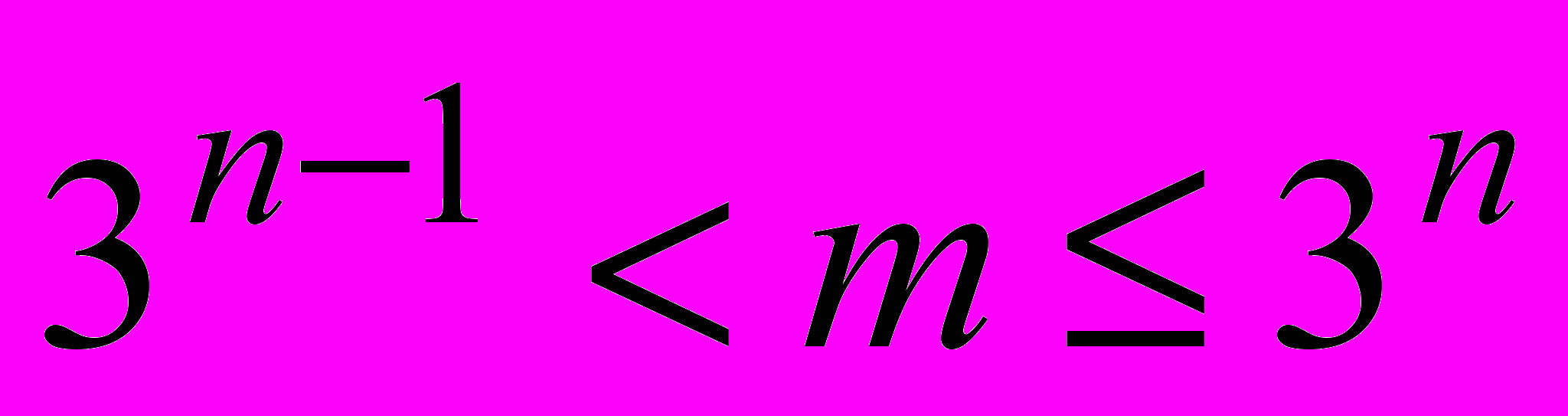 , то за
, то за  взвешиваний можно найти фальшивую монету. (звавич3600)
взвешиваний можно найти фальшивую монету. (звавич3600)
- Докажите, что квадрат можно разрезать на
 квадратов для любого
квадратов для любого  , начиная с 6. (Генкин)
, начиная с 6. (Генкин)
- Дано:
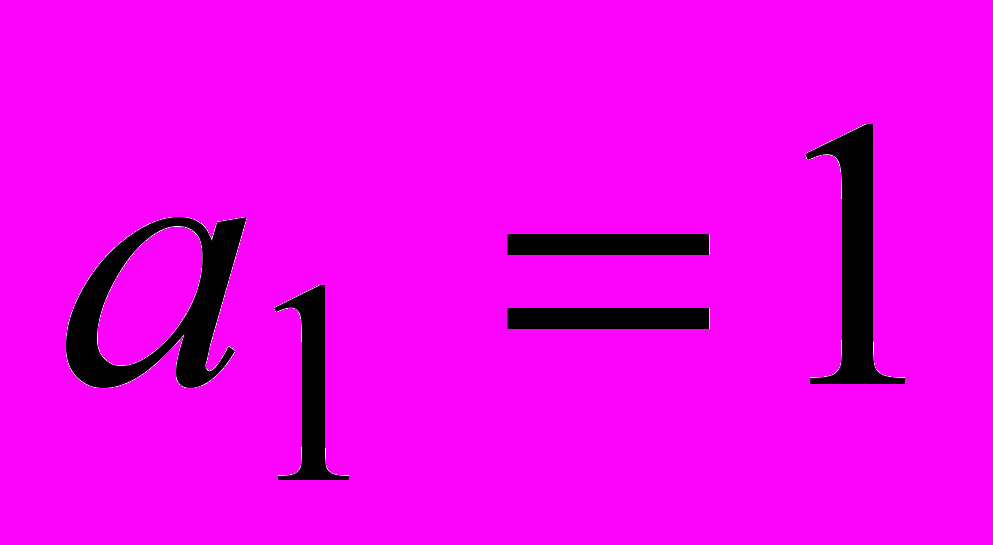 ,
, 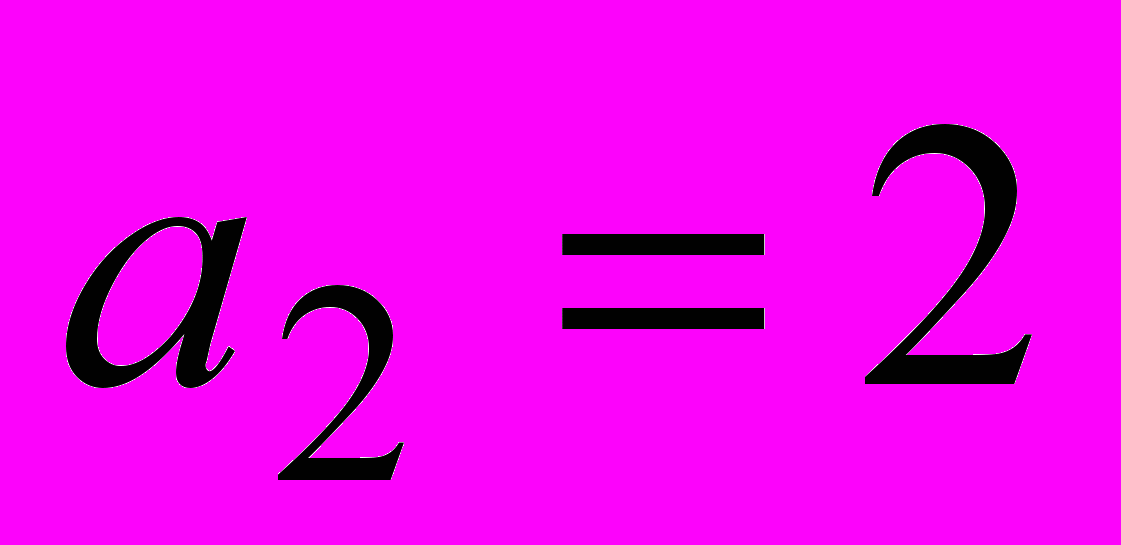 ,
, 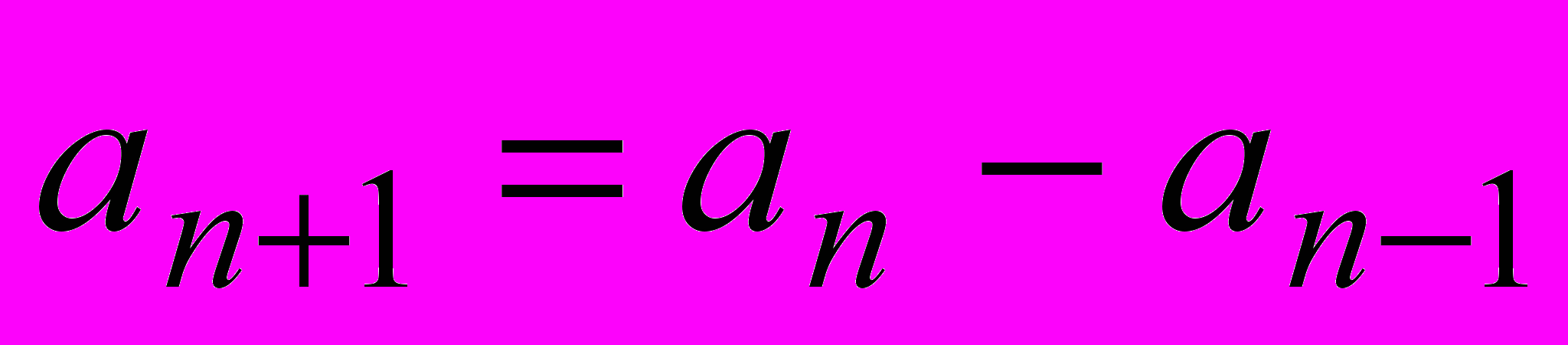 при всех
при всех 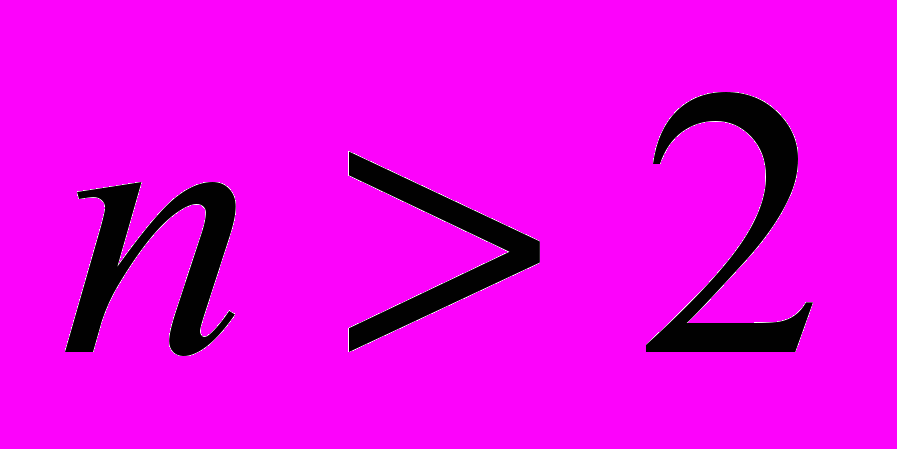 . Докажите, что
. Докажите, что 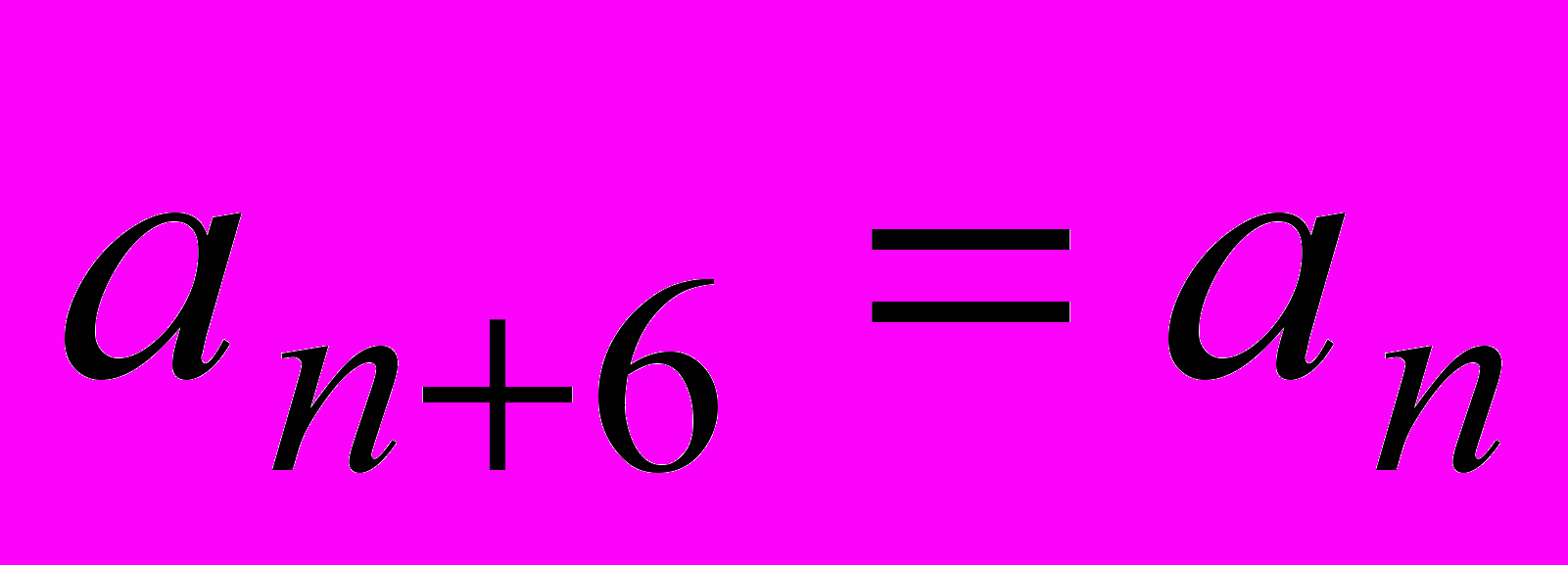 при любом натуральном
при любом натуральном  . (Генкин)
. (Генкин)
- Дан ряд чисел Фибоначчи:
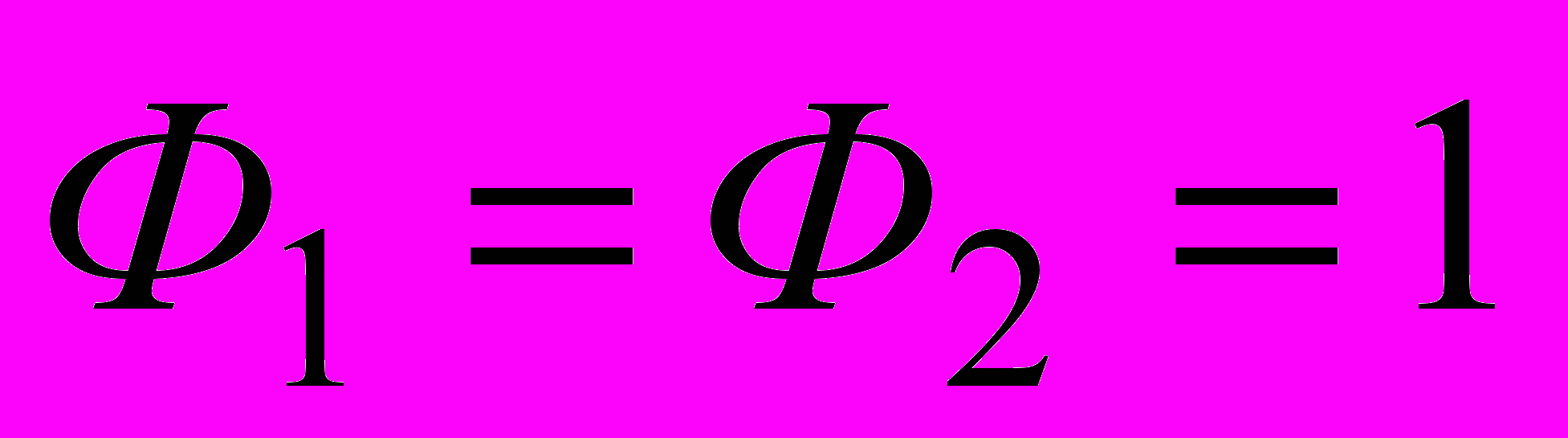 и
и 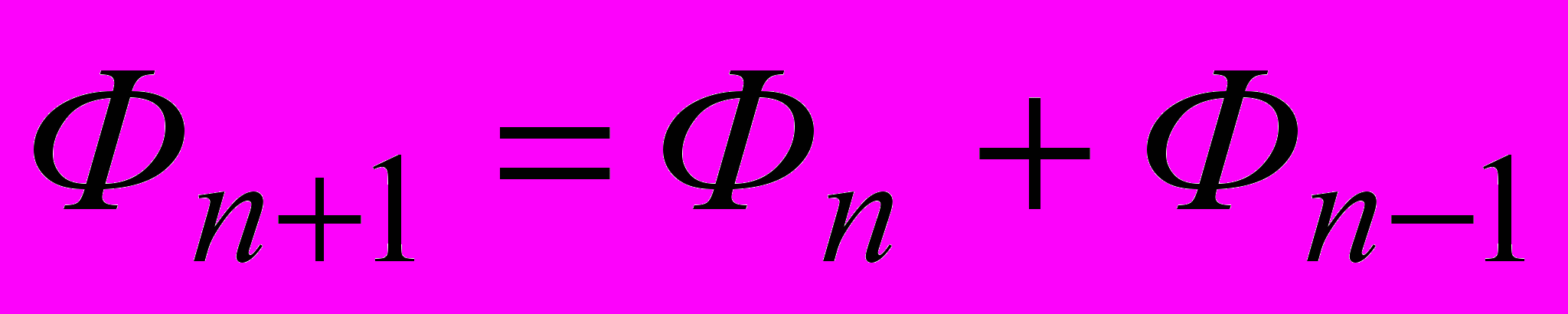 при всех
при всех 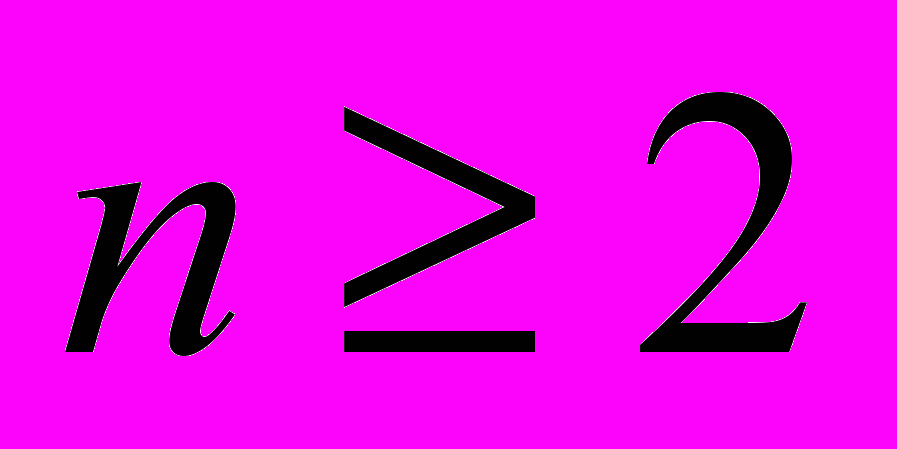 . Докажите, что любое натуральное число можно представить как сумму нескольких различных чисел Фибоначчи. (Генкин)
. Докажите, что любое натуральное число можно представить как сумму нескольких различных чисел Фибоначчи. (Генкин)
- Докажите, что в выпуклом
 -угольнике
-угольнике 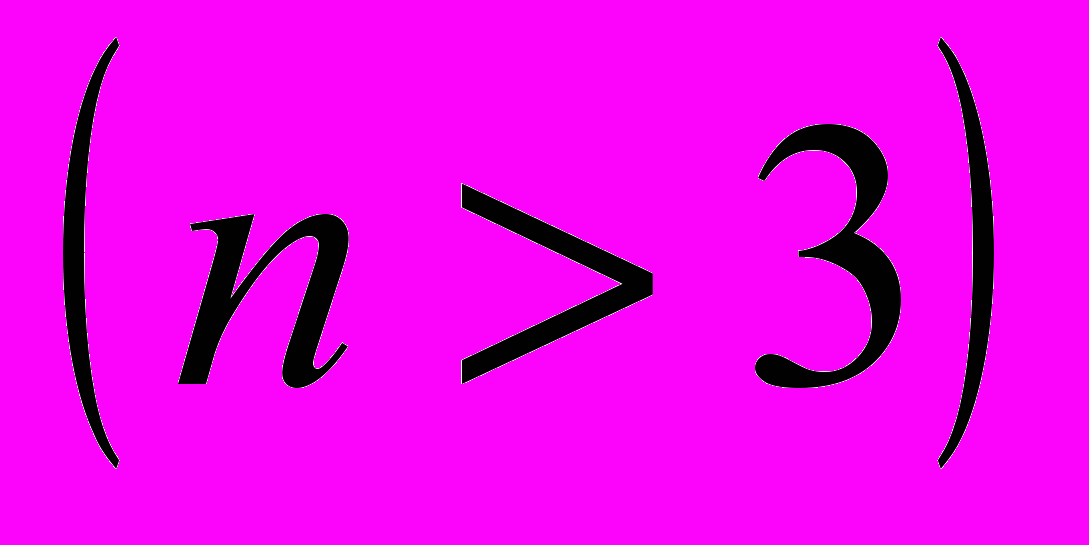 ровно
ровно 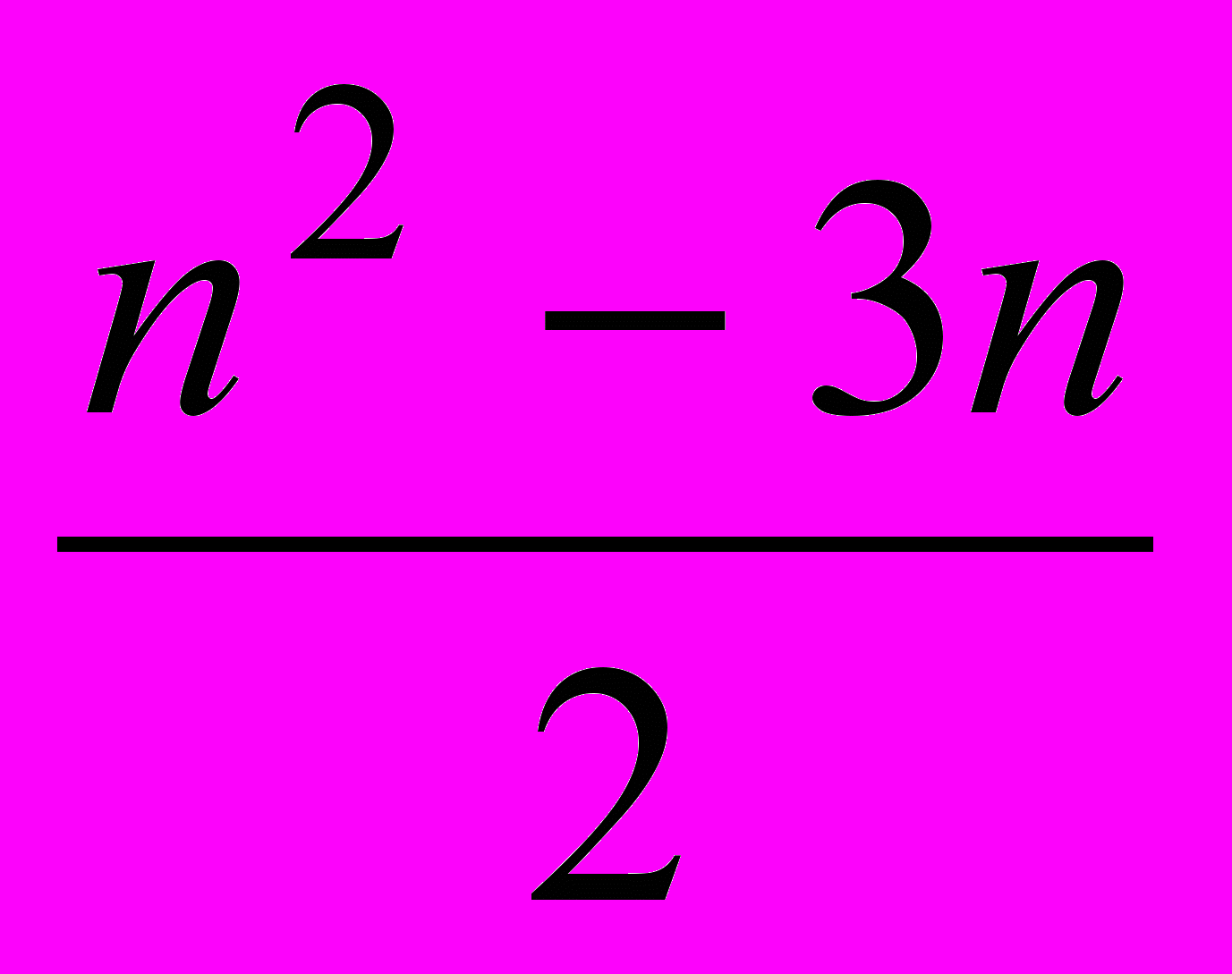 диагоналей (звавич 3600)
диагоналей (звавич 3600)
- Пусть
 - произвольное натуральное число. Докажите, что число
- произвольное натуральное число. Докажите, что число 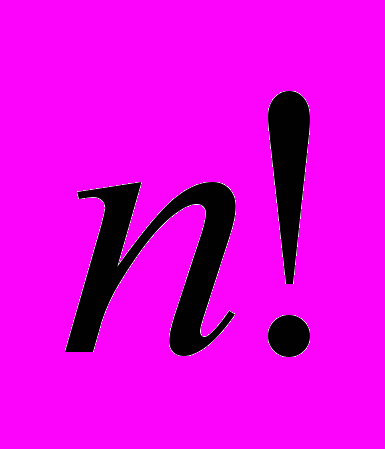 представимо в виде произведения двух натуральных чисел, различающихся между собой не более чем вдвое. (Савин 2000)
представимо в виде произведения двух натуральных чисел, различающихся между собой не более чем вдвое. (Савин 2000)
- Докажите, что если
 - натурально число, большее 1, то
- натурально число, большее 1, то 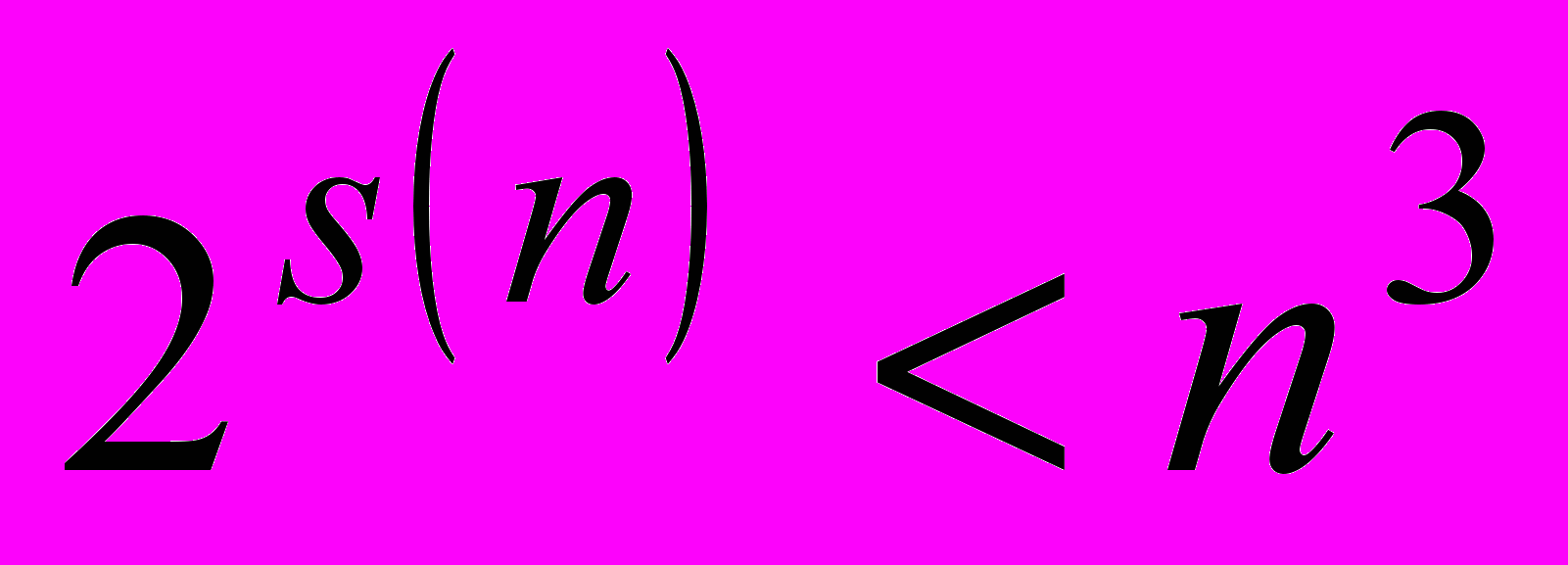 , где
, где 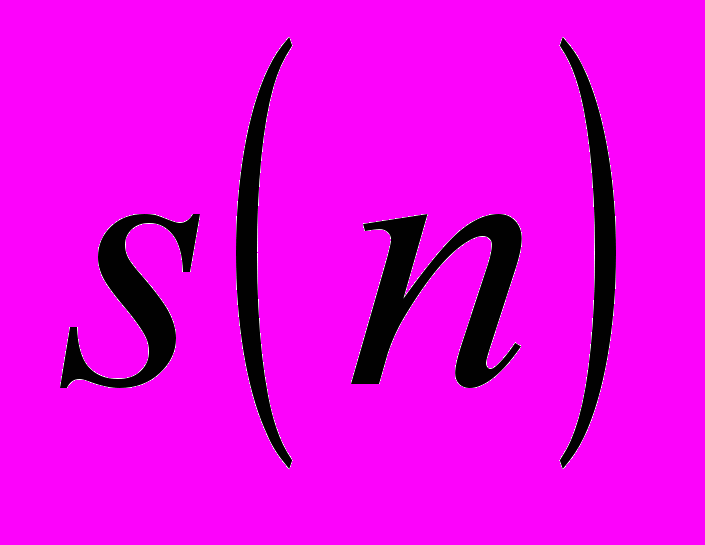 - сумма цифр числа
- сумма цифр числа  .(Савин 1999)
.(Савин 1999)
Дополнительные задачи
- Даны два взаимно простых натуральных числа
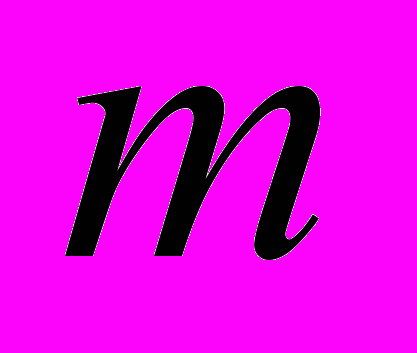 и
и  , а также число 0. Имеется калькулятор, который умеет выполнять лишь одну операцию: вычисление среднего арифметического двух целых чисел, если они имеют одинаковую четность. Докажите, что при помощи этого калькулятора можно получить все натуральные числа от 1 до
, а также число 0. Имеется калькулятор, который умеет выполнять лишь одну операцию: вычисление среднего арифметического двух целых чисел, если они имеют одинаковую четность. Докажите, что при помощи этого калькулятора можно получить все натуральные числа от 1 до  . (Генкин)
. (Генкин)
- Докажите, что
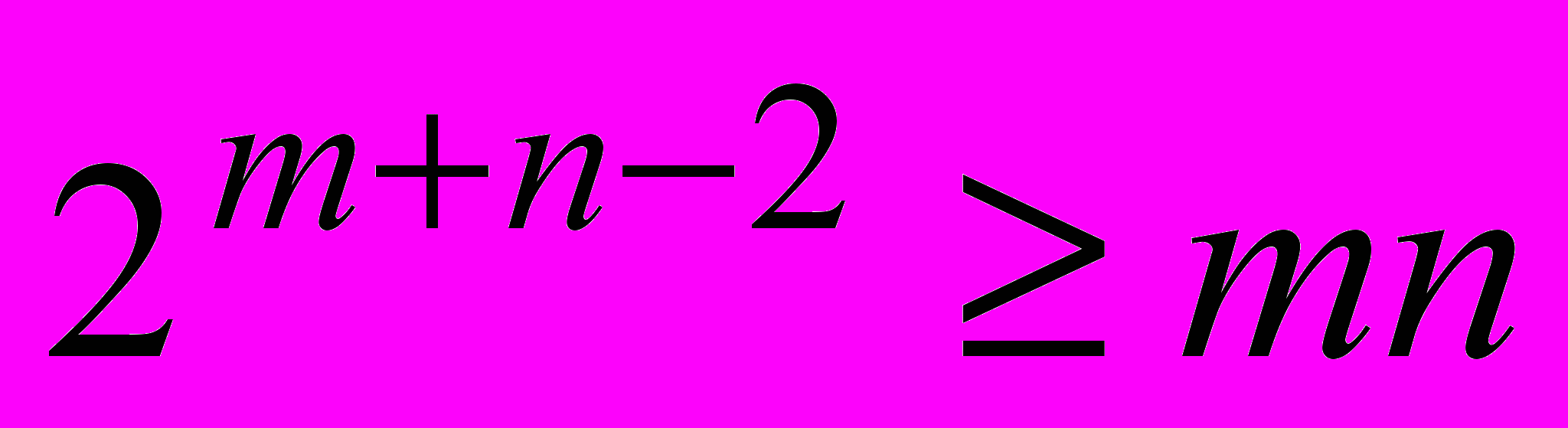 при любых натуральных
при любых натуральных 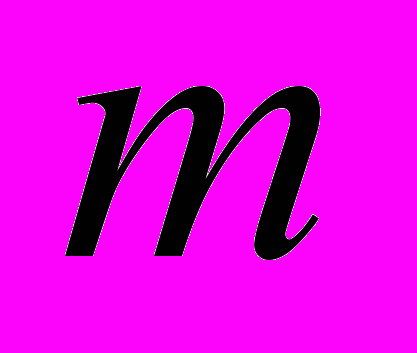 и
и  . (Генкин)
. (Генкин)
- Из квадрата
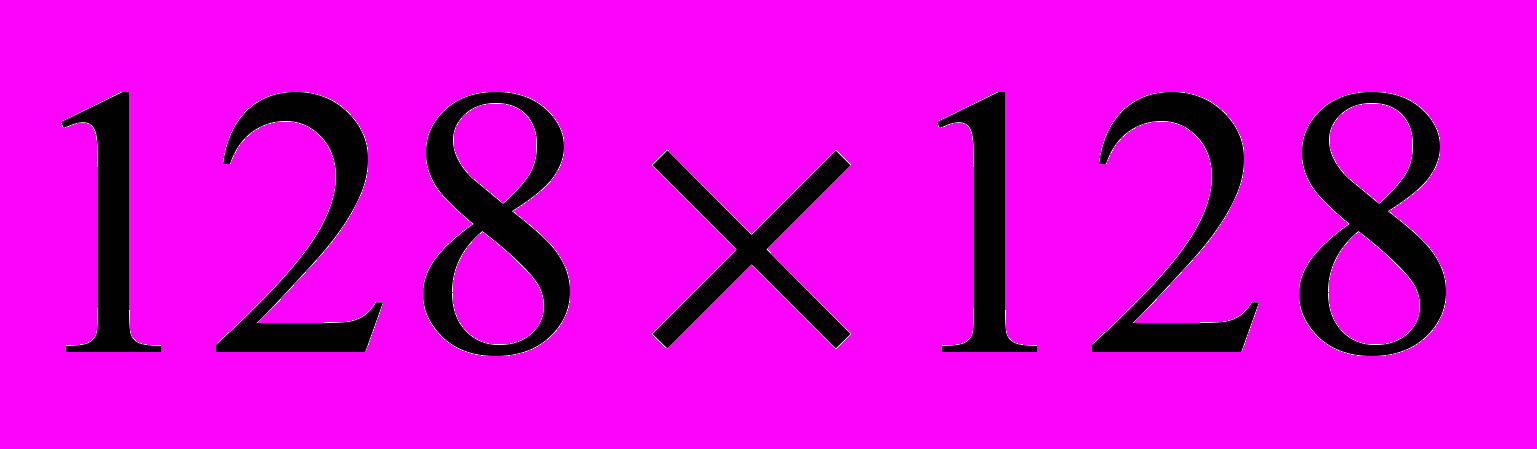 вырезали одну клетку. Докажите, что эту фигуру можно замостить уголками из трех клеток. (Ковальджи)
вырезали одну клетку. Докажите, что эту фигуру можно замостить уголками из трех клеток. (Ковальджи)
- Докажите, что предпоследняя цифра десятичной записи любой степени тройки четна. (Ковальджи)
- Дано несколько квадратов. Докажите, что их можно разрезать на такие части, из которых удастся сложить один квадрат. (Генкин)
- Докажите, что
 -е число Фибоначчи делится на 3 тогда и только тогда, когда
-е число Фибоначчи делится на 3 тогда и только тогда, когда  делится на 4. (Генкин)
делится на 4. (Генкин)
- Докажите, что модуль суммы любого числа слагаемых не превосходит суммы модулей этих слагаемых. (Генкин)
- Докажите, что
 различных точек на прямой определяют ровно
различных точек на прямой определяют ровно 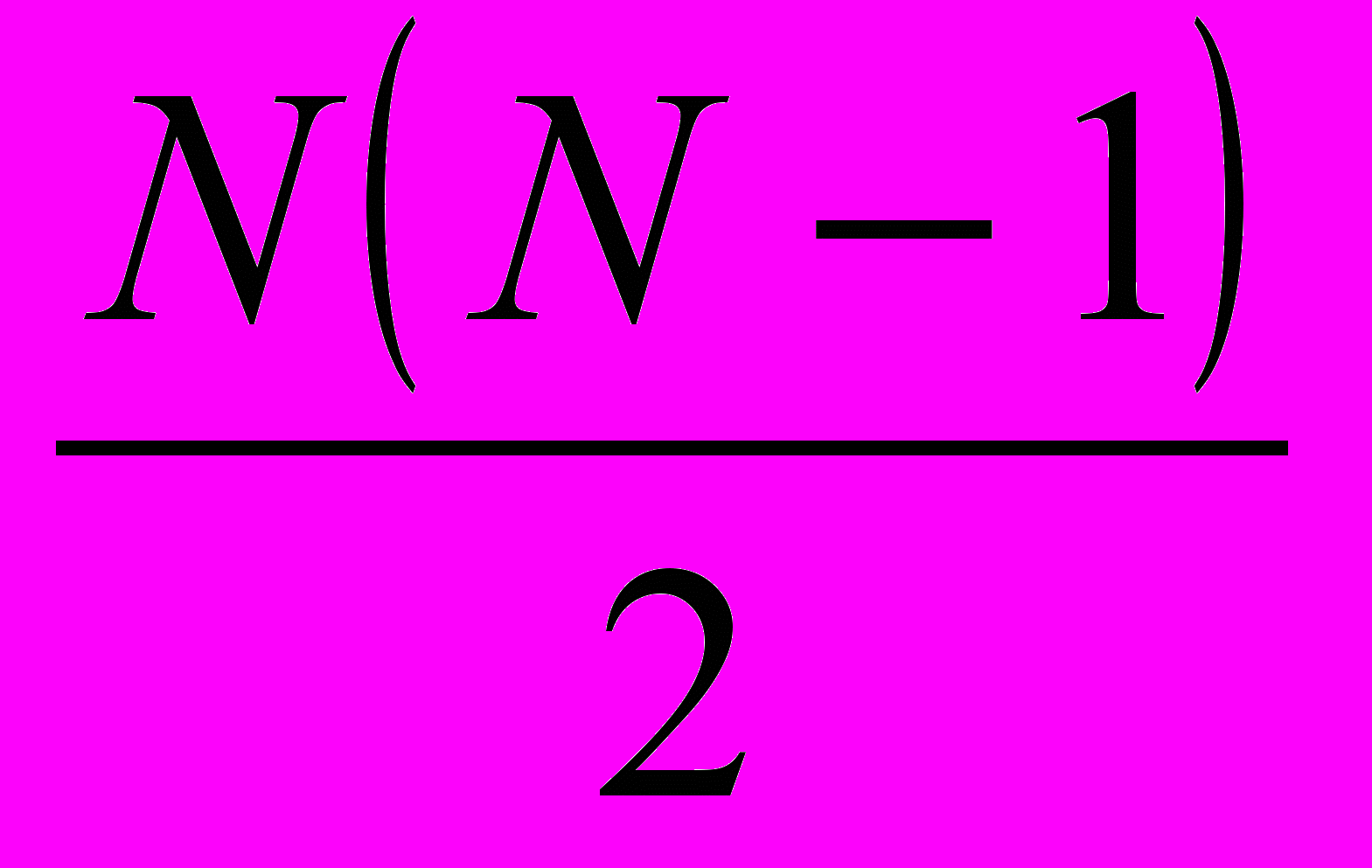 отрезков с концами в этих точках. (звавич 3600)
отрезков с концами в этих точках. (звавич 3600)
- Двенадцать чисел 1, 2, 3, 4, …12 – произвольным образом записаны на окружности. Одним ходом разрешается поменять местами два соседних числа, если модуль их разности больше 1. Докажите, что за конечное число ходов все числа могут быть расставлены в естественном порядке. (МГО)
- В шахматном клубе посетители могут играть в шахматы друг с другом или с компьютером. Вчера в клубе было
 человек, каждый из них сыграл не более
человек, каждый из них сыграл не более  партий, и любые двое, не игравшие друг с другом, сыграли в сумме не более
партий, и любые двое, не игравшие друг с другом, сыграли в сумме не более  партий. Докажите, что всего было сыграно не более
партий. Докажите, что всего было сыграно не более 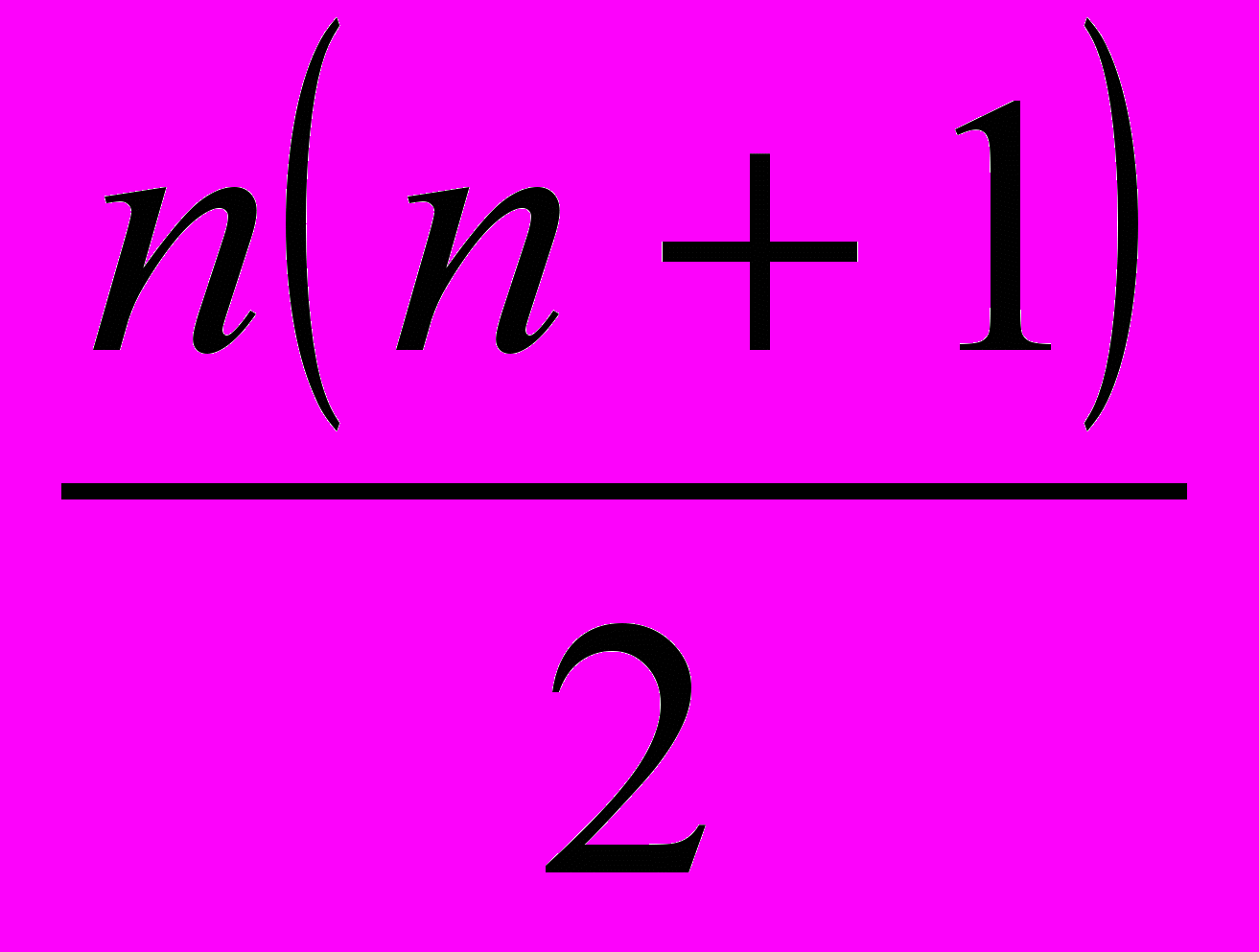 партий. (Питер 2001)
партий. (Питер 2001)
