Geum.ru

Открытые задачи на метод математической индукции

Вид материалаДокументы
Подобный материал:
Открытые задачи на метод математической индукции


Здесь собраны задачи, в которых нет готовых утверждений. Сначала надо эти утверждения получить (угадать с помощью численного эксперимента и аналогий), а потом уже доказывать методом математической индукции.



  1. С помощью картинки угадайте формулу для суммы первых 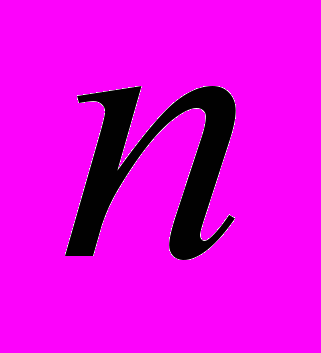натуральных чисел. Докажите её. Сформулируйте и докажите аналогичное утверждение про сумму первых 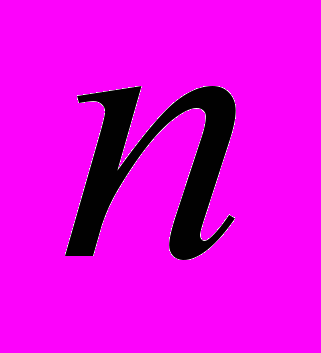чётных чисел; первых 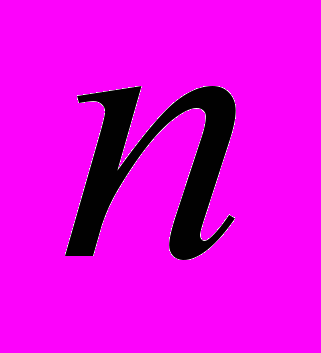нечётных чисел.
  2. Подберите коэффициенты так, чтобы сумма квадратов первых 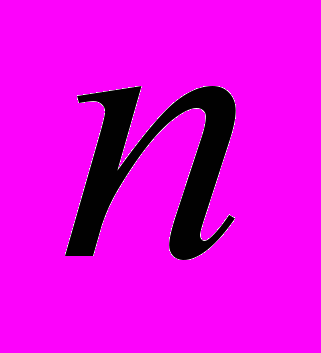натуральных чисел равнялась 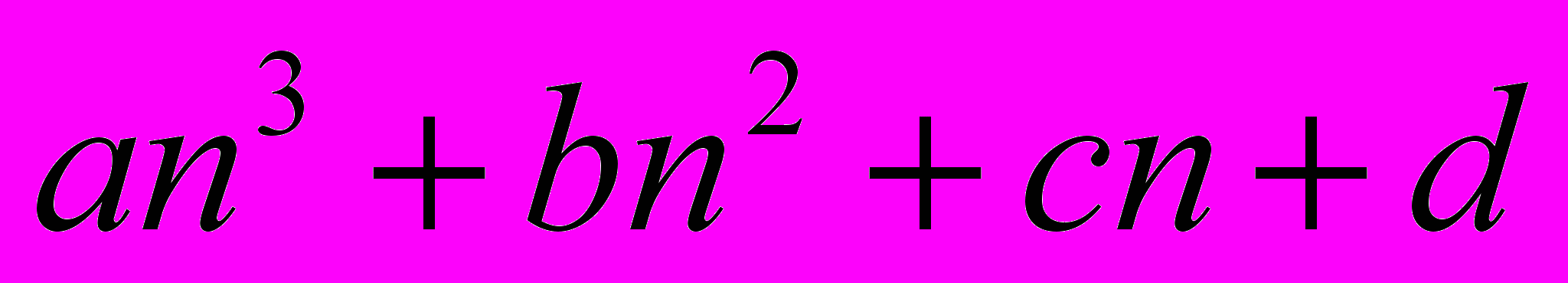(при любом 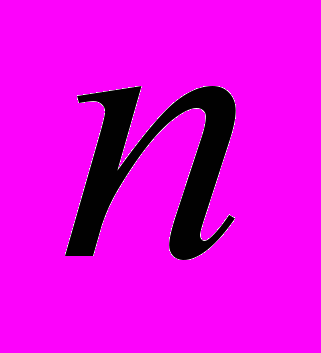) и докажите полученную формулу.
  3. Сформулируйте и докажите аналогичное утверждение про сумму .
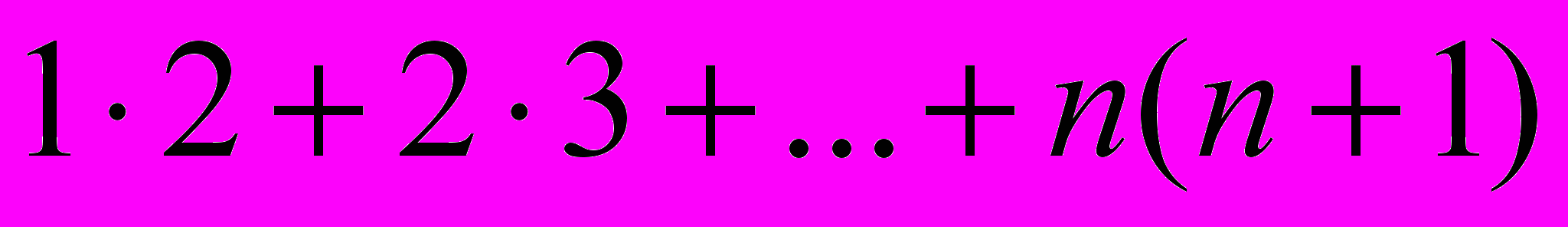  4. Сформулируйте и решите задачу, аналогичную предыдущей, для суммы кубов первых 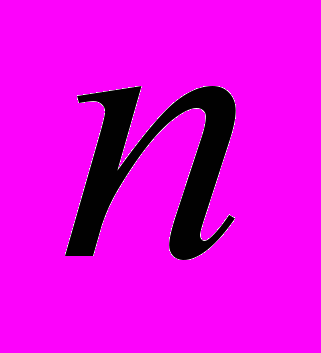натуральных чисел. Подсказка 1. Можно решать аналогично задаче 2. Какой степени многочлен надо брать? Подсказка 2. Можно посчитать несколько первых сумм и найти закономерность.
  5. Найдите и докажите формулу для суммы знакопеременной суммы (чётные числа с минусом, нечётные с плюсом).
  6. Сформулируйте и решите задачу, аналогичную предыдущей, для знакопеременной суммы квадратов. Предложите общую гипотезу.1
  7. Найдите и докажите формулу для суммы (она имеет вид для некоторых чисел ).
  8. Найдите и докажите формулу для суммы .
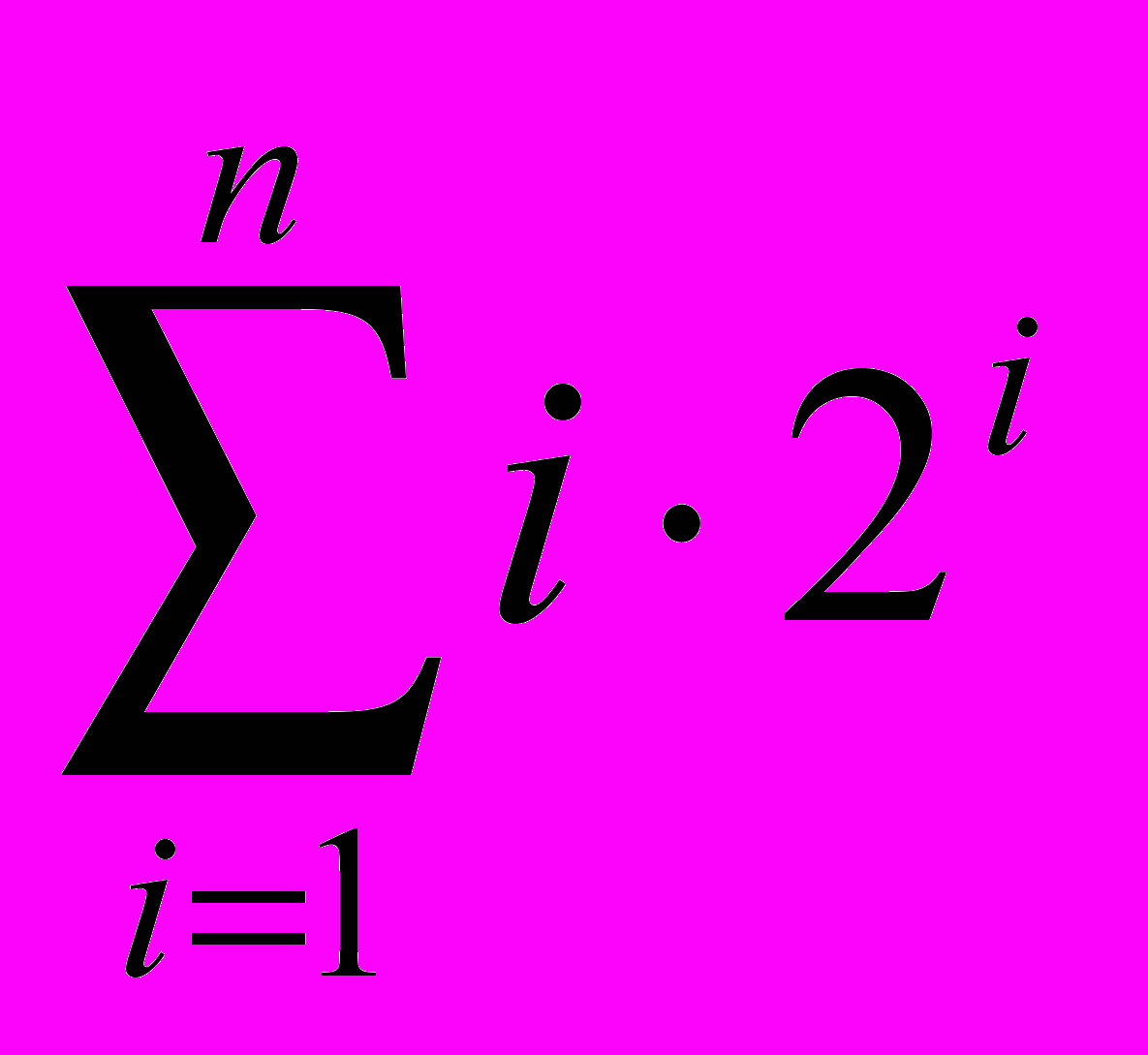  9. Найдите и докажите формулу для (обобщение квадрата суммы).
  10. Рассмотрим два числа и 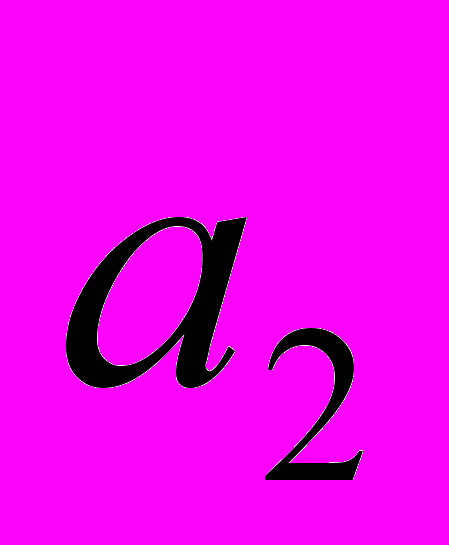, удовлетворяющие неравенствам 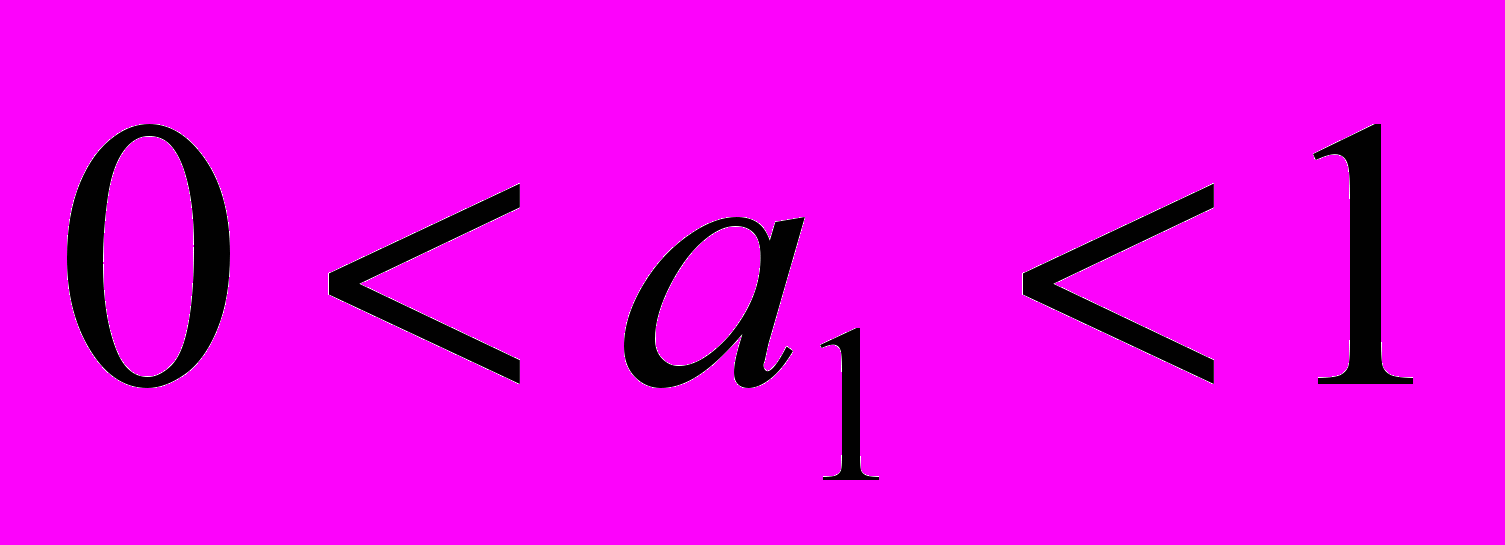, 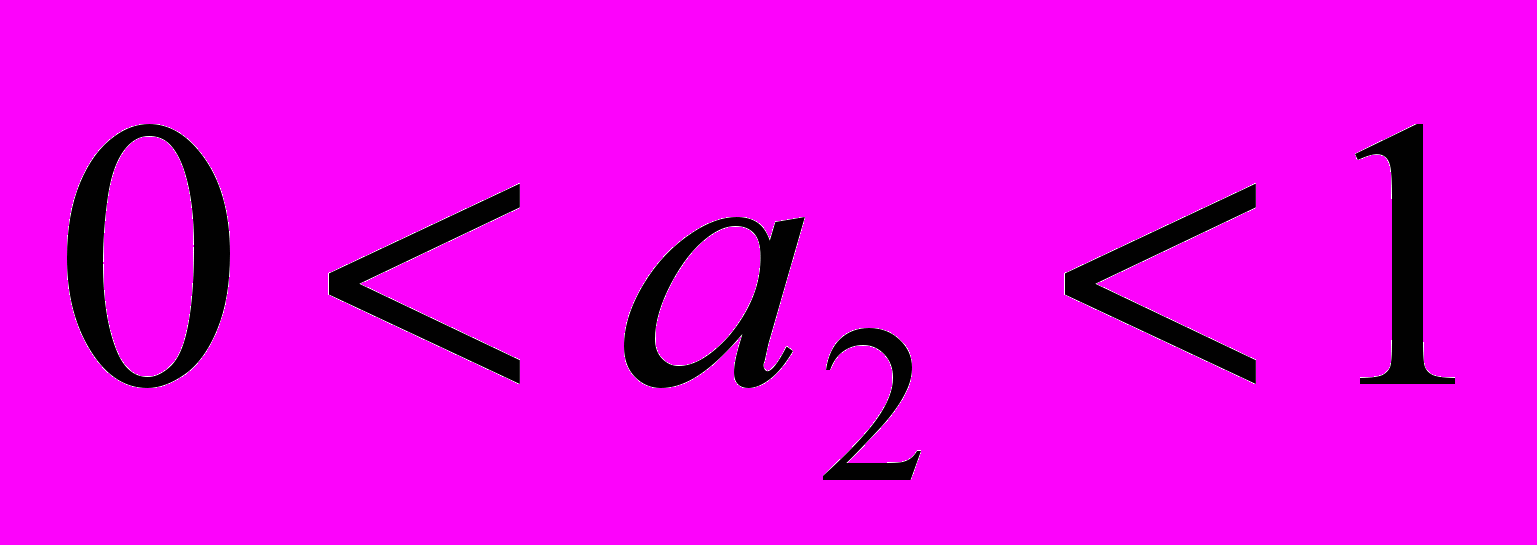. Тогда, очевидно, . Обобщите это утверждение на 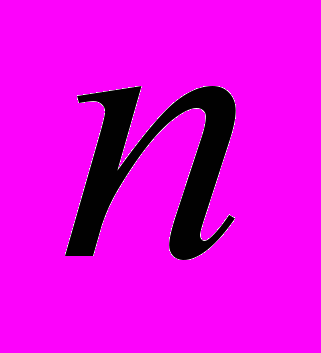чисел и докажите своё обобщение.
  11. Последовательность задана рекуррентно: . Докажите, что Найдите и докажите формулу 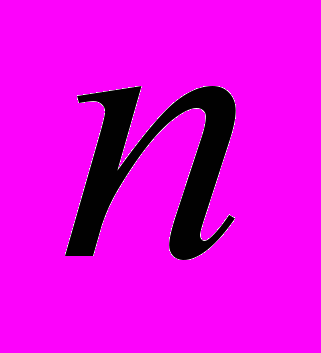-го члена для последовательности :




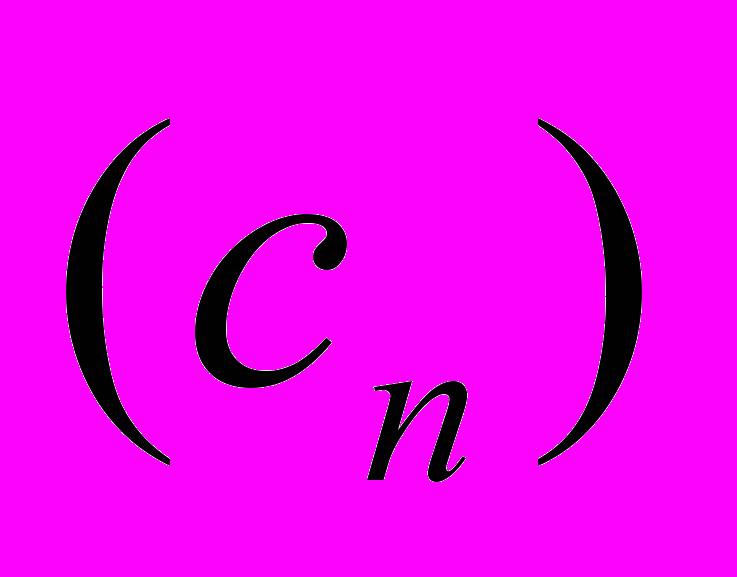1 Знакопеременная сумма k-х степеней выражается многочленом степени k.