Методы вычислительной физики Программа курса лекций
| Вид материала | Программа курса |
- Курс лекций по экологической мелиорации птс план лекций, 534.92kb.
- Программа курса физики для студентов геологического факультета (вечернее отделение)., 128.6kb.
- Программа курса лекций Введение. Физика полупроводников раздел физики конденсированного, 109.27kb.
- Рабочая программа учебной дисциплины численные методы Направление подготовки 210400, 273.35kb.
- Зайцева Евдокия Ивановна учитель физики высшей квалификационной категории элективный, 847.73kb.
- Учебно-методический комплекс по дисциплине Линейные и нелинейные уравнения физики (Методы, 325.5kb.
- Физика, 200.62kb.
- Физика, 212.85kb.
- Программа специального курса лекций для магистрантов направления "Прикладные физика, 41.55kb.
- Программа курса лекций «Методы исследования макромолекул», 15.25kb.
Методы вычислительной физики
Программа курса лекций
(4 курс, 7 сем., 36 ч., экзамен)
1. Введение:
- история и основные этапы развития вычислительной гидродинамики; прикладные пакеты программ решения уравнений гидродинамики и теплопереноса (CFD-коды), области применения;
2. Методы дискретизации краевых задач математической физики:
- метод конечных разностей: приближения производных и дифференциальных выражений; аппроксимации дифференциальных уравнений; методы аппроксимации граничных условий;
- метод конечных объёмов: интегро-интерполяционный метод построения разностных схем;
- устойчивость, согласованность и сходимость конечно-разностных схем: теорема Лакса, метод Неймана;
3. Прямые и итерационные методы решения сеточных уравнений:
- системы уравнений с трёхдиагональными матрицами, методы прогонки;
- быстрое дискретное преобразование Фурье;
- итерационные методы решения нелинейного уравнения: методы бисекции, простой итерации, Ньютона; критерии сходимости и оптимальные параметры;
- итерационные методы решения систем линейных уравнений: метод Якоби, Зейделя и последовательной верхней релаксации; критерии и оценки скорости сходимости для модельной задачи уравнения Пуассона; методы неполной факторизации;
4. Применение методов конечных разностей для решения модельных уравнений:
- линейное уравнение переноса (уравнение гиперболического типа): явные методы Эйлера, метод разностей против потока, схема Лакса, метод с перешагиванием, одношаговый и двухшаговый методы Лакса-Вендроффа, метод Мак-Кормака, схема Кабаре, метод Кранка-Николсона;
- нелинейное уравнение переноса (уравнения Римана и Бюргерса): схемы Куранта-Изаксона-Риса (противопоточная) и Годунова, Лакса-Вендроффа, Мак-Кормака, Кранка-Николсона; понятие монотонности конечно-разностных схем; TVD-схемы с ограничителями потока;
- уравнение теплопроводности (уравнение параболического типа): простой явный метод, простой неявный метод, метод Кранка-Николсона, комбинированные методы, методы переменных направлений, методы дробных шагов (методы расщепления);
- нелинейное уравнение в дисперсионной среде (уравнение Кортевега-де Вриза): трёхслойные явные схемы, схема Лакса-Вендроффа;
5. Численные методы решения уравнений пограничного слоя:
- уравнения аэрогидродинамики и теплопереноса в приближении пограничного слоя;
- решение уравнений пограничного слоя: простая явная схема, метод Кранка-Николсона и полностью неявный метод, линеаризация уравнений;
6. Численные методы решения уравнений Навье-Стокса несжимаемой жидкости:
- особенности численного решения уравнений Навье Стокса: дискретизация уравнений с помощью метода конечных объёмов; особенности дискретизации конвективных членов (противопоточная схема, схема QUICK Леонарда, схемы с ограничителями потока); выбор совмещённой и разнесённой сеток.
- Итерационные алгоритмы совместного решения уравнений переноса импульса и неразрывности: методы проекции: методы SIMPLE, SIMPLEС.
Литература
1. Флетчер К. Вычислительные методы в динамике жидкостей. - М.: Мир, 1991.- Т.1,2.
2. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. - М.: Мир, 1990.- Т.1,2.
3. Самарский А.А., Гулин А.В. Численные методы. М., Наука, 1989. 432с.
4. Ильин В.П. Методы конечных разностей и конечных объёмов для эллиптических уравнений. – Новосибирск, Изд-во Ин-та математики, 2000. - 345 с.
5. Ferziger J.H., Peric M. Computational Methods for Fluid Dynamics. Berlin: Springer, 1996.
Задачи к курсу «Методы вычислительной физики»
1. Найти условие устойчивости методом Неймана и получить дифференциальное приближение для конечно-разностной схемы Кабаре решения линейного уравнения переноса
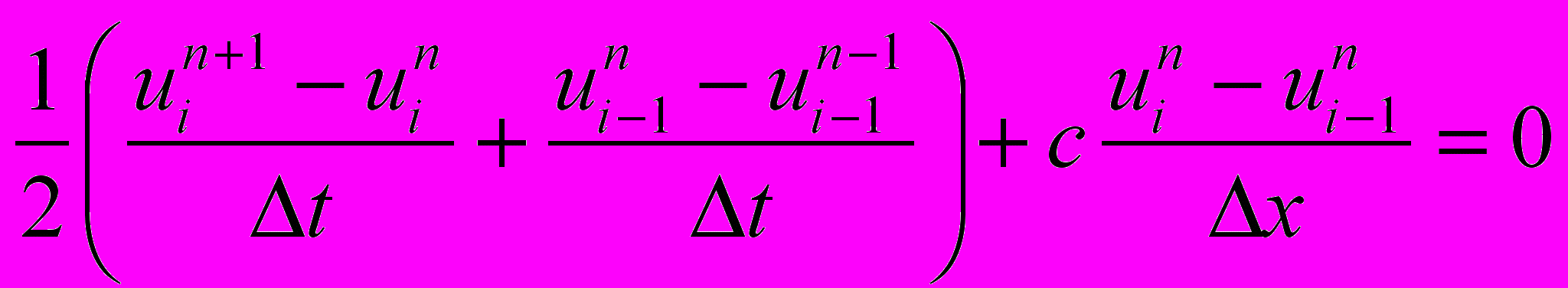
2. Показать выполнение TVD-свойства для решения уравнения Бюргерса
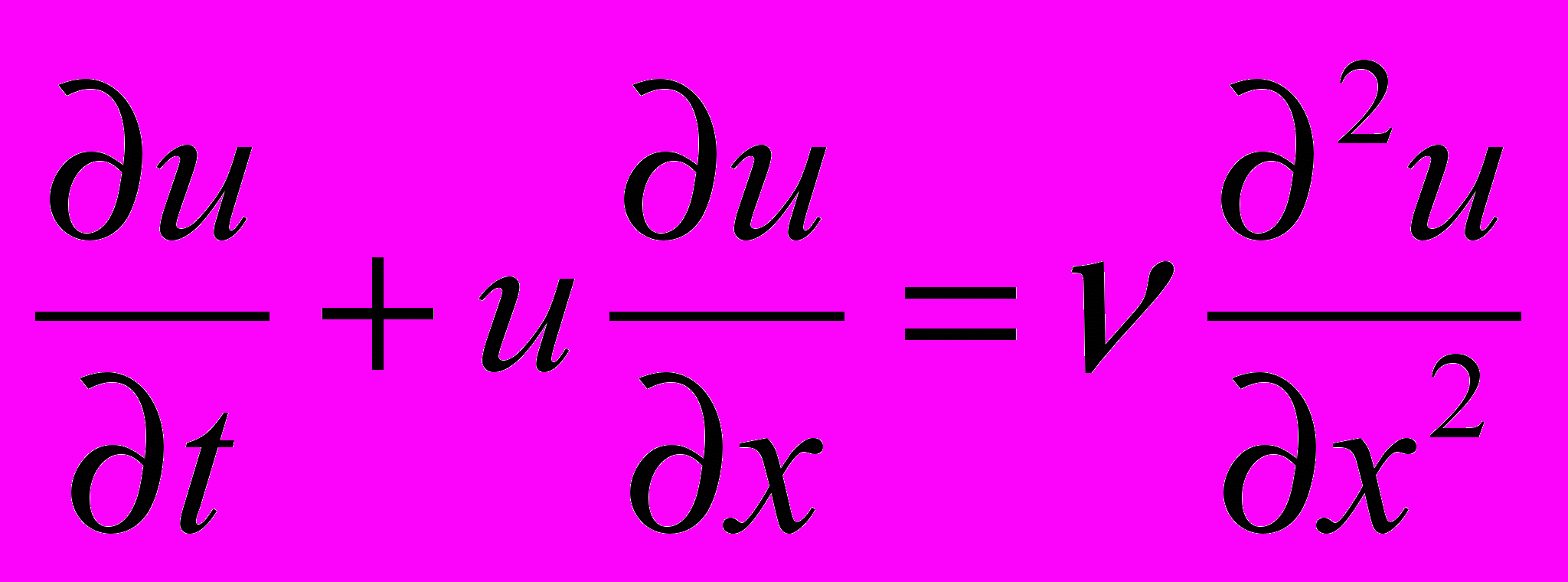
3. Получить аналитическое решение уравнения Бюргерса
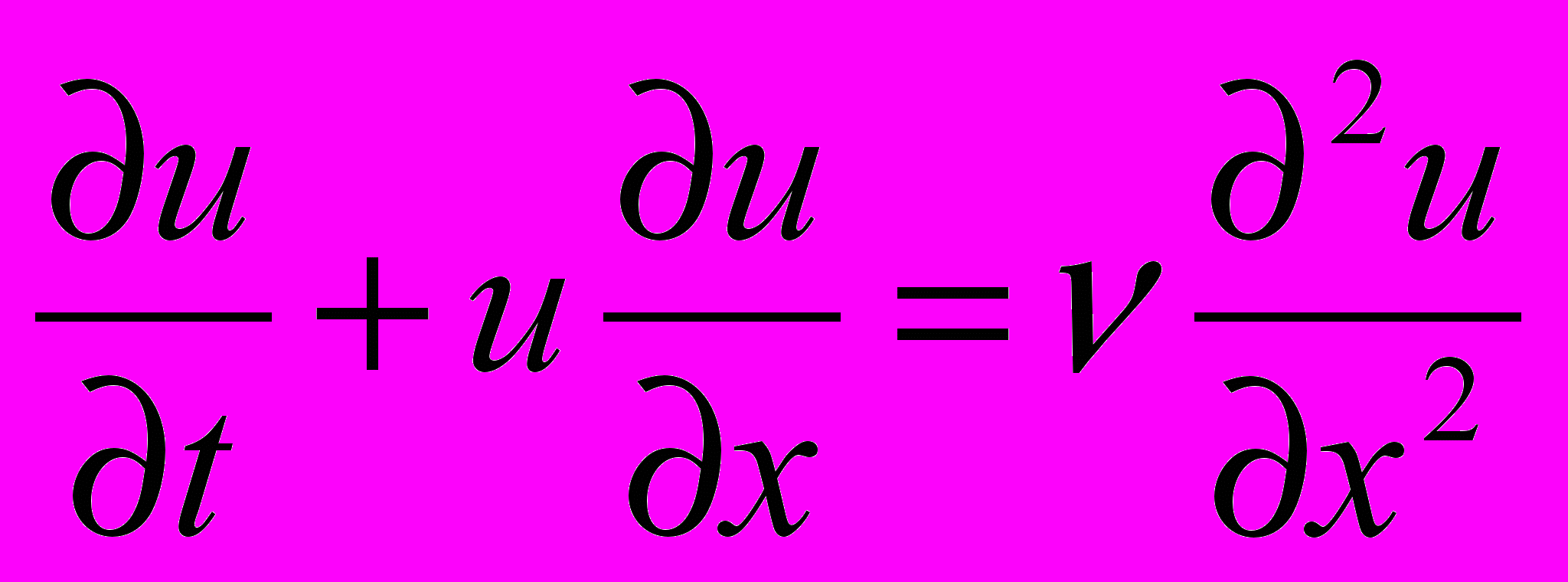
в интервале
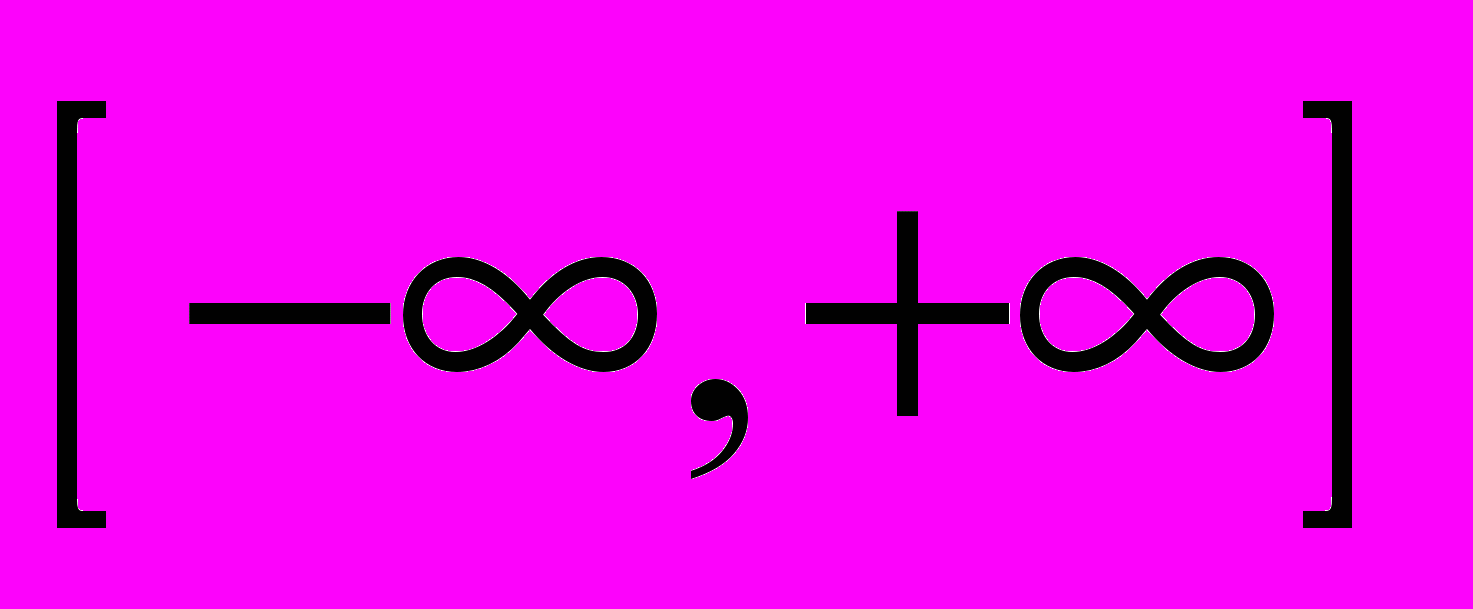с начальным условием 
, 
,
, 
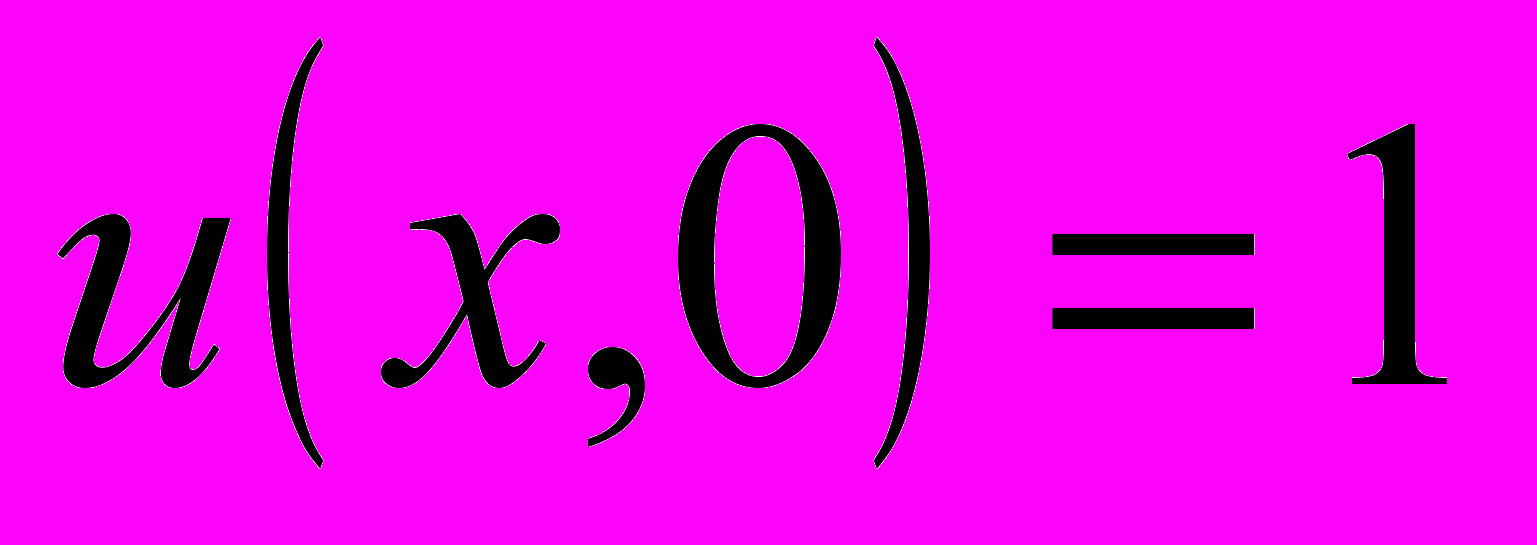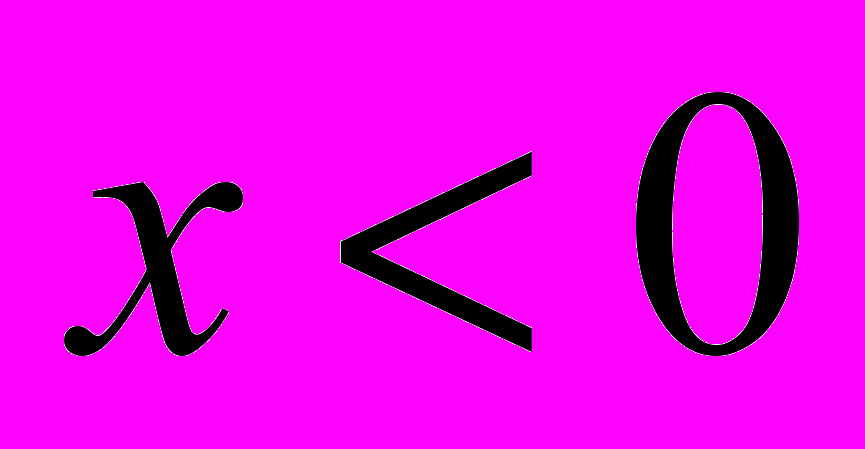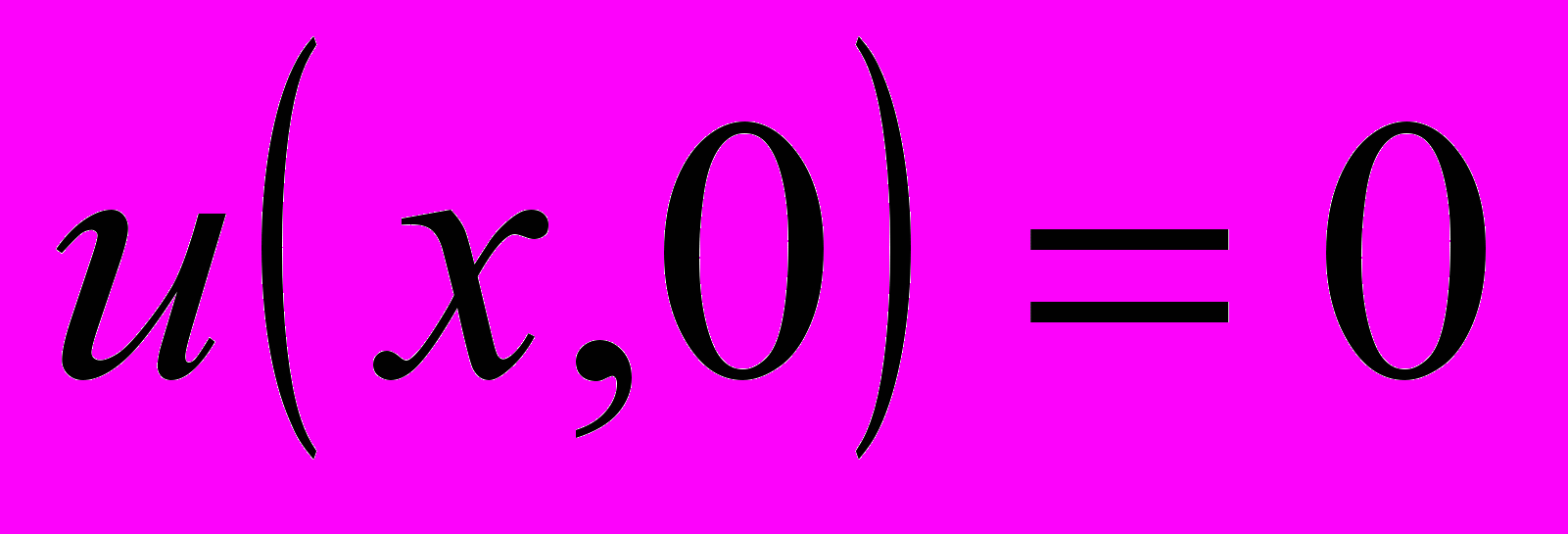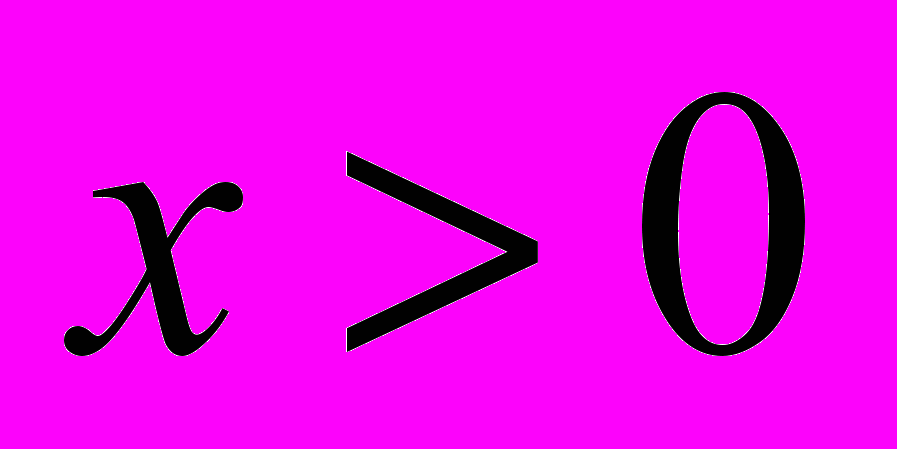
4. Сравнить с полученным в предыдущем пункте точным решением численное решение уравнения Бюргерса на отрезке
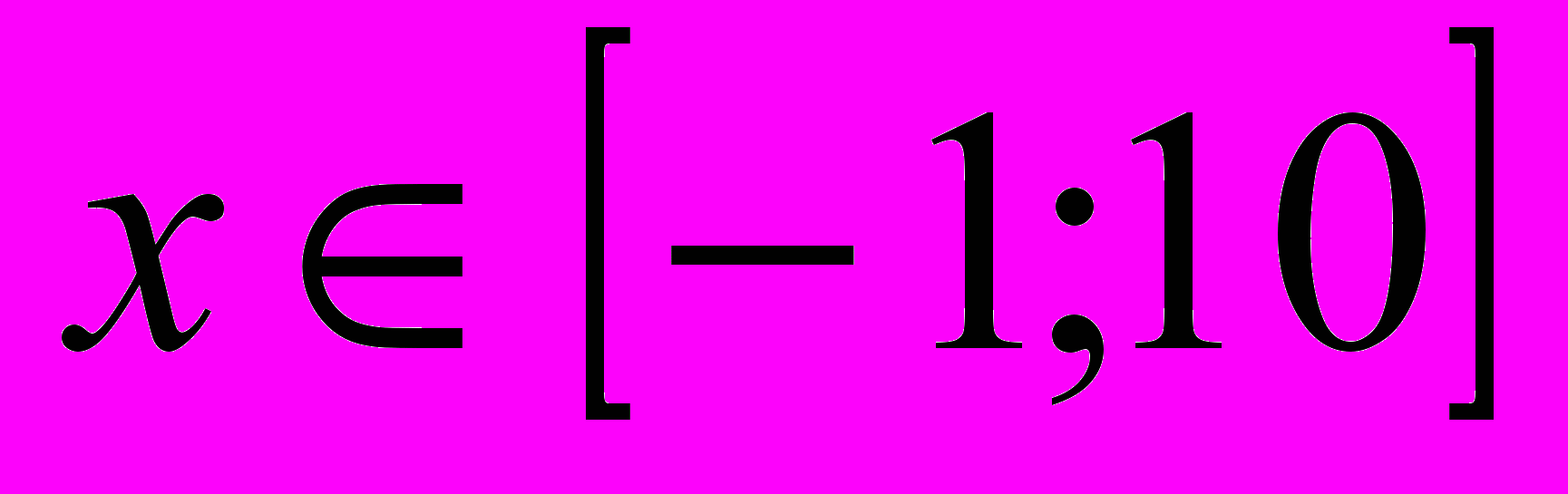при двух значениях вязкости 
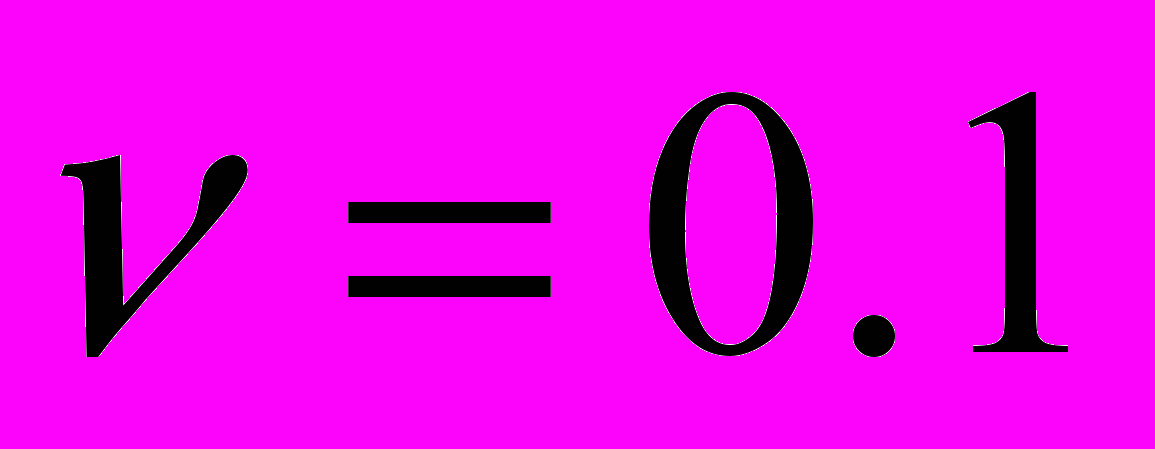и 
и 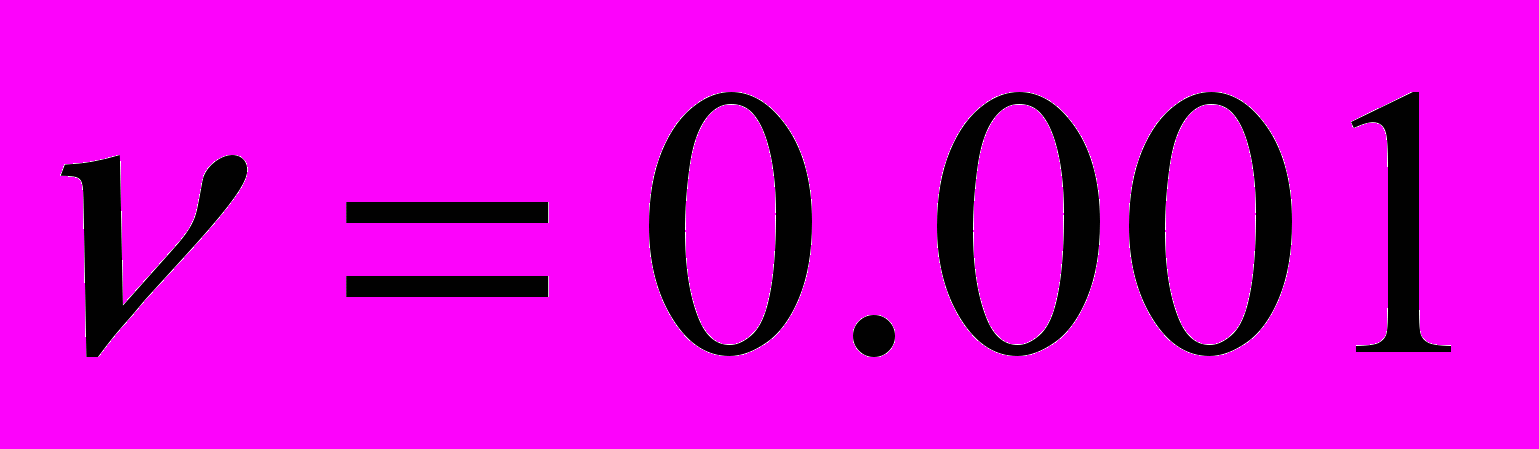граничных условиях:
, 
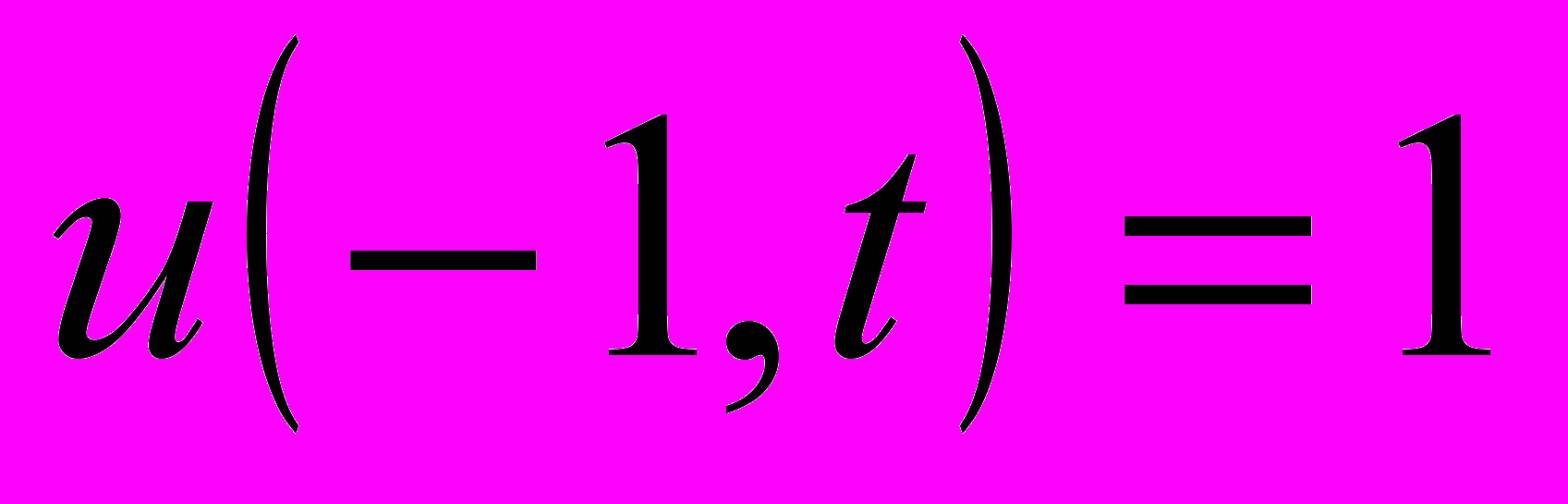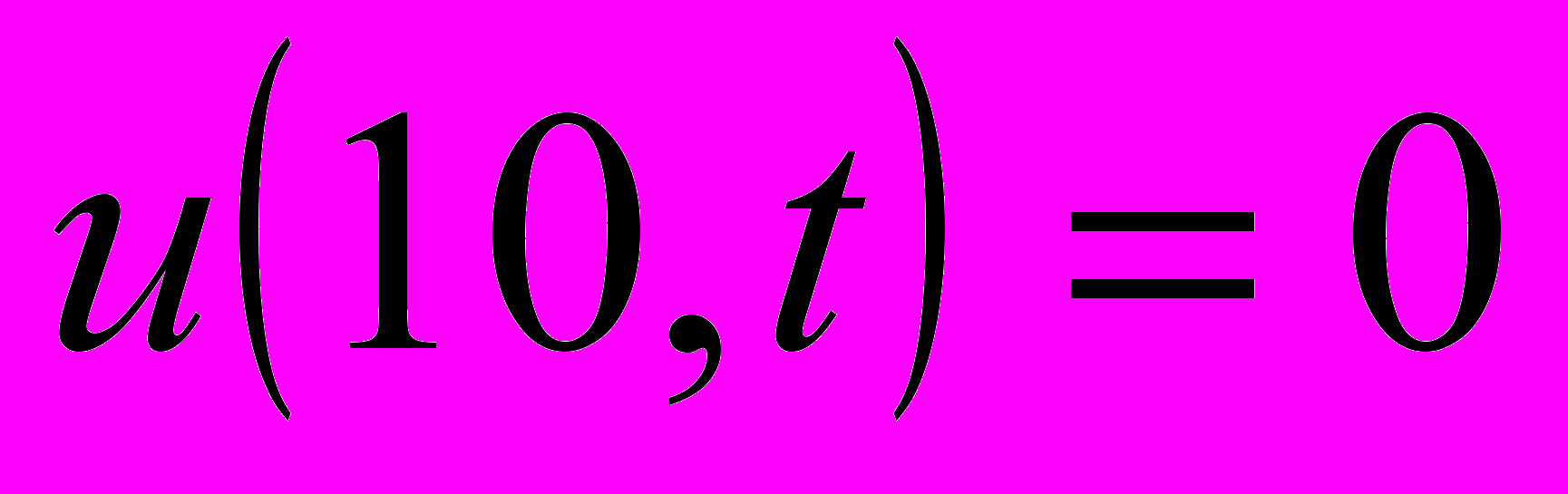,полученное с помощью противопоточной схемы Куранта-Изаксона-Риса
, 
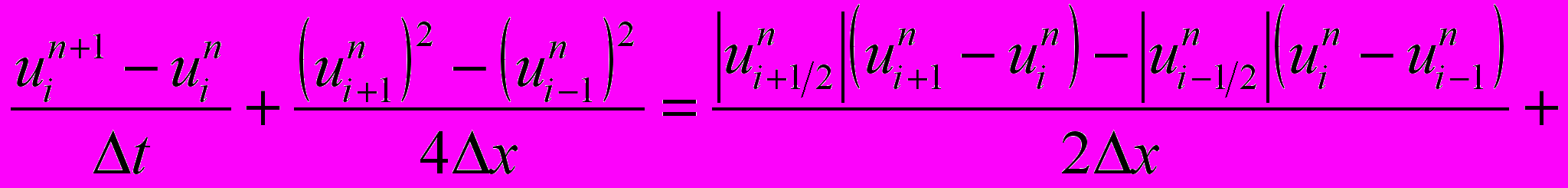
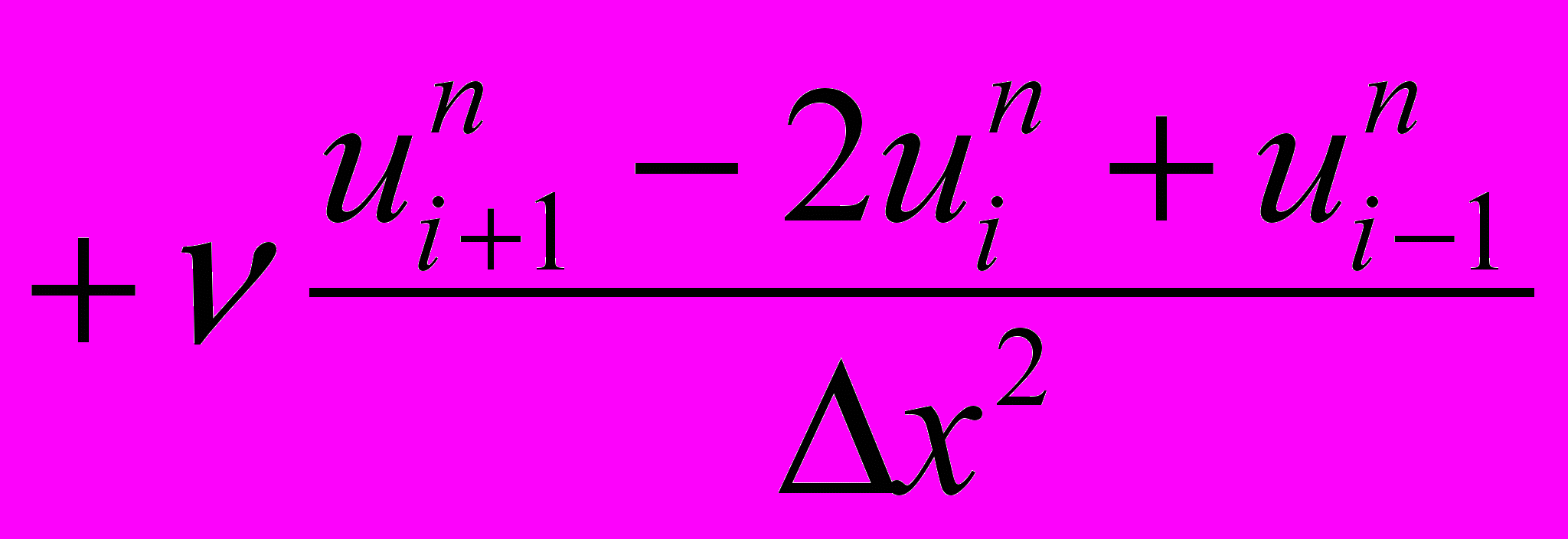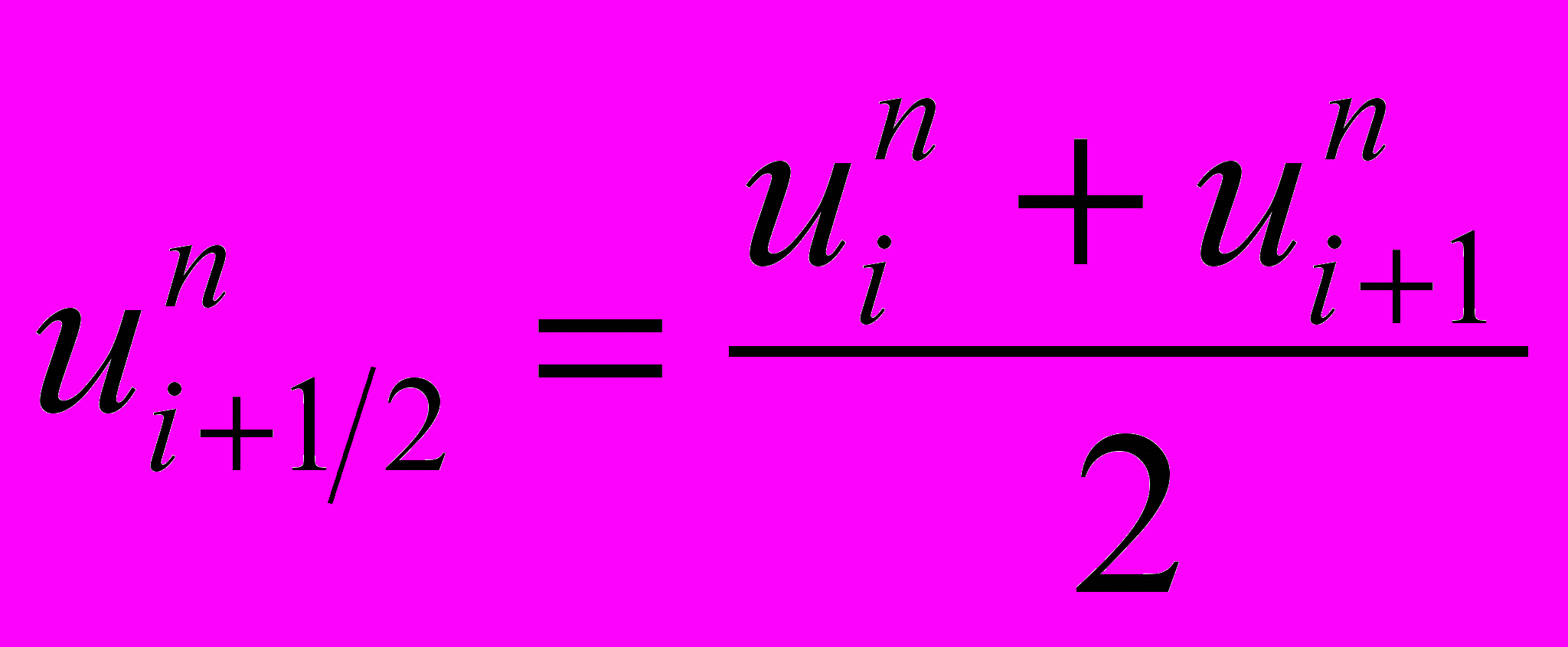
и одного из перечисленных ниже методов:
1) Лакса-Вендроффа
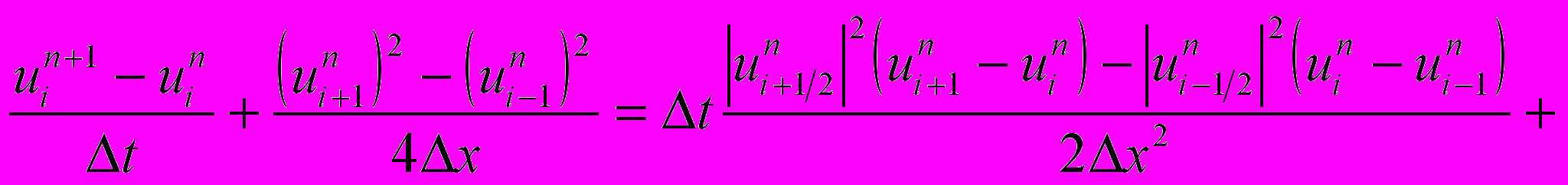
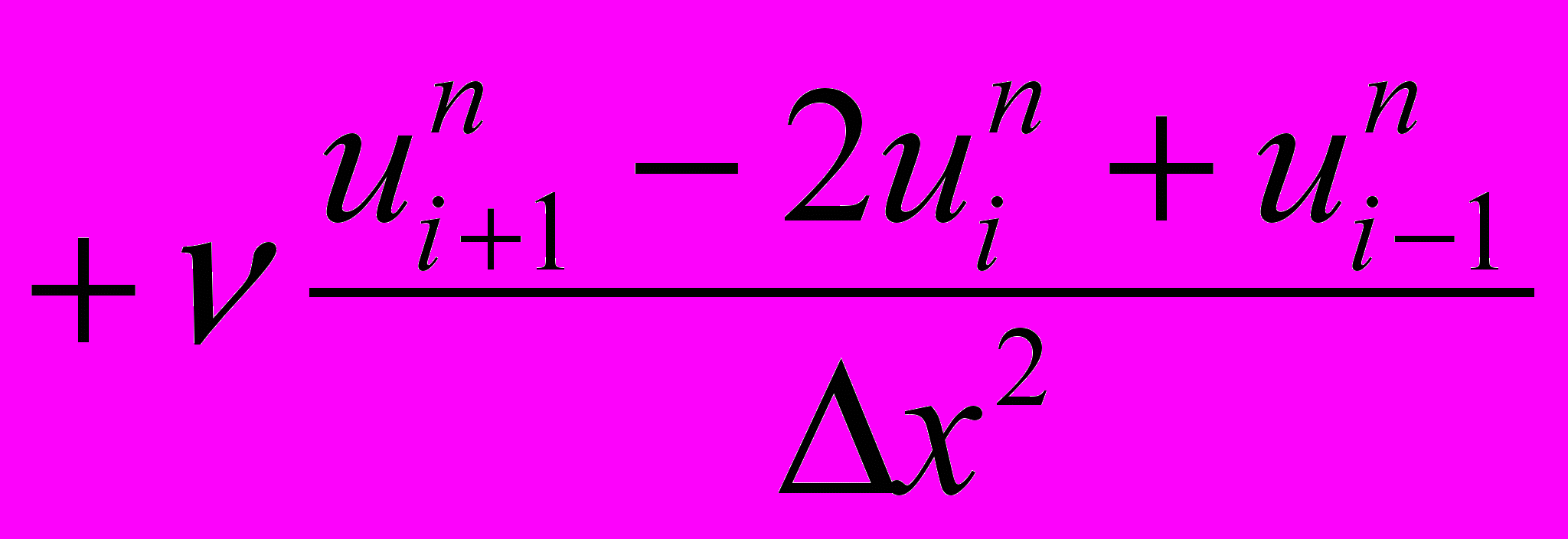
2)Мак-Кормака
, 
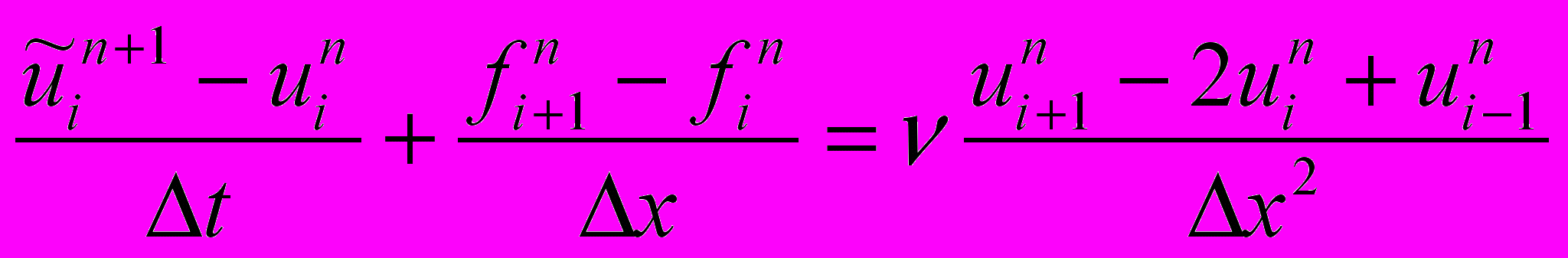
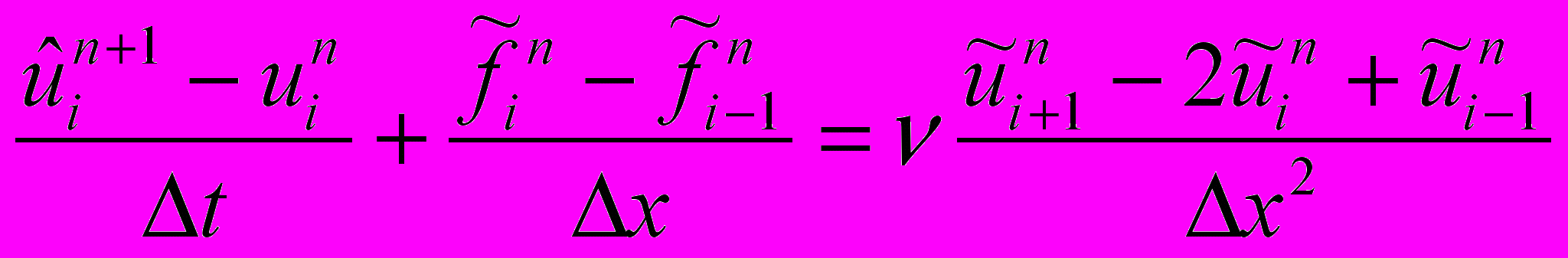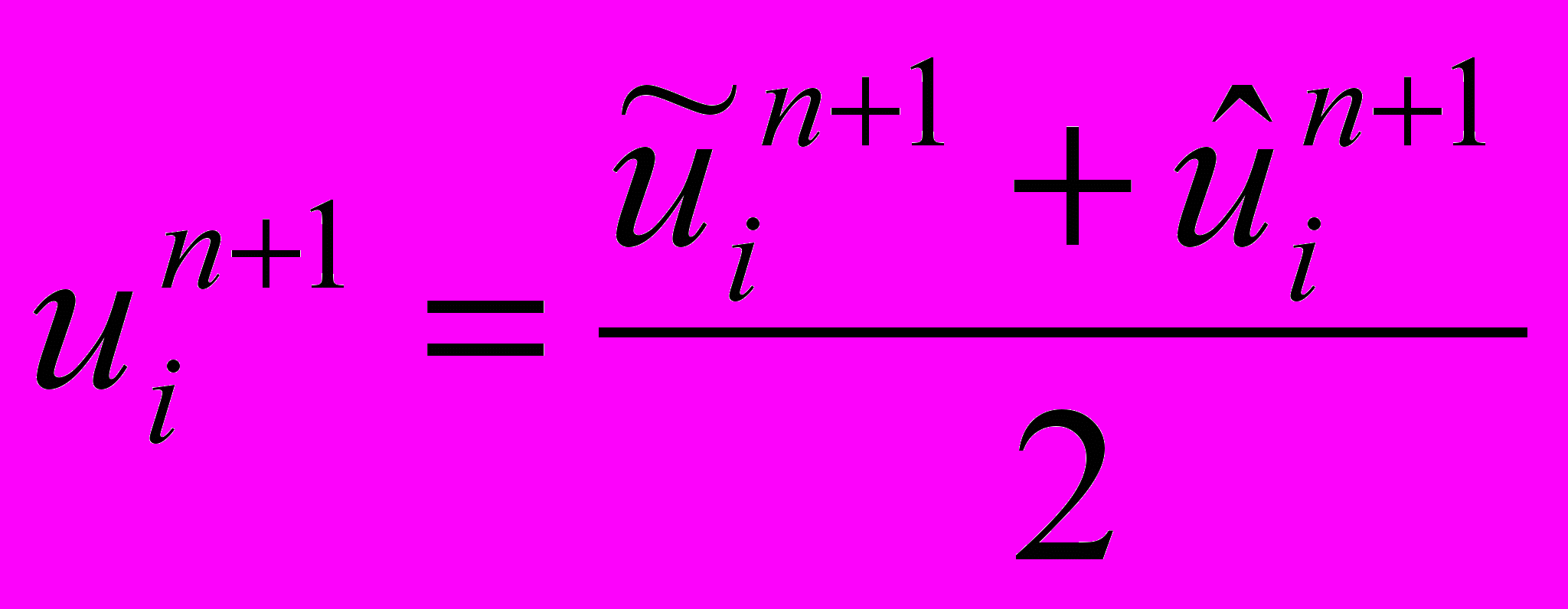, где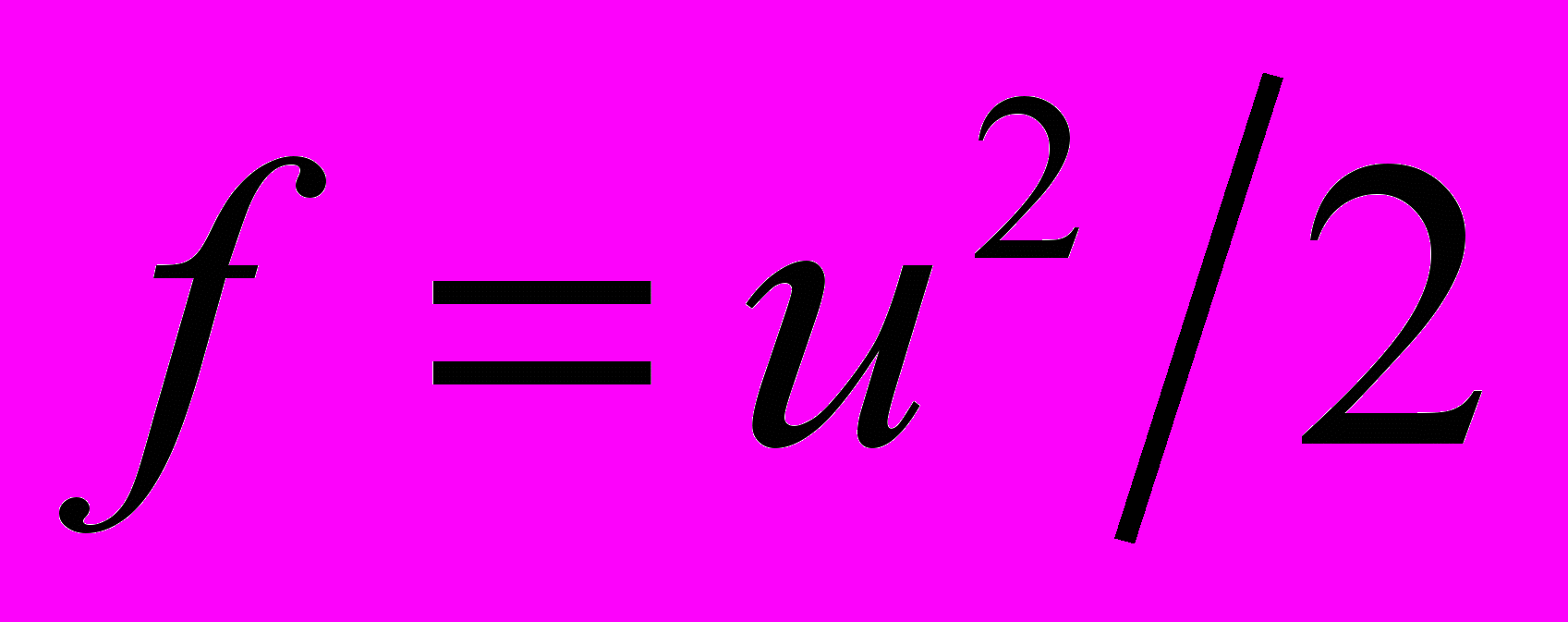 
3) двухшагового метода Кабаре
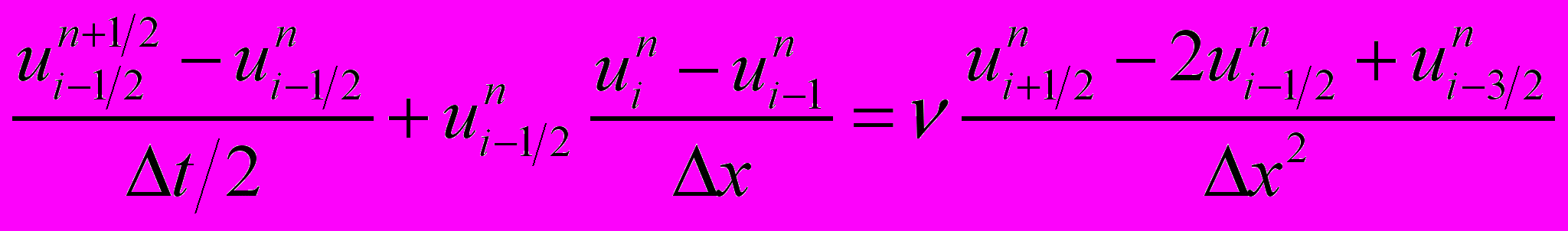
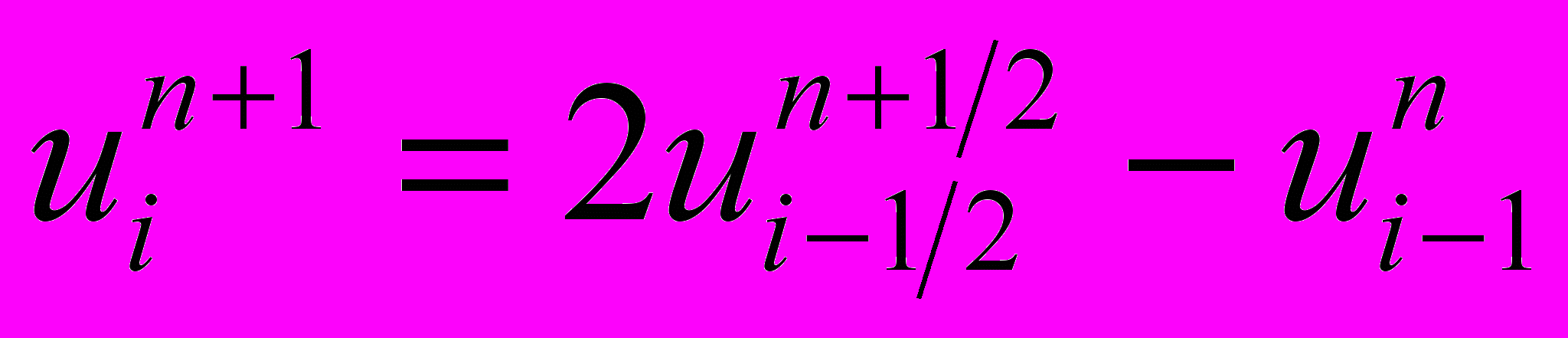
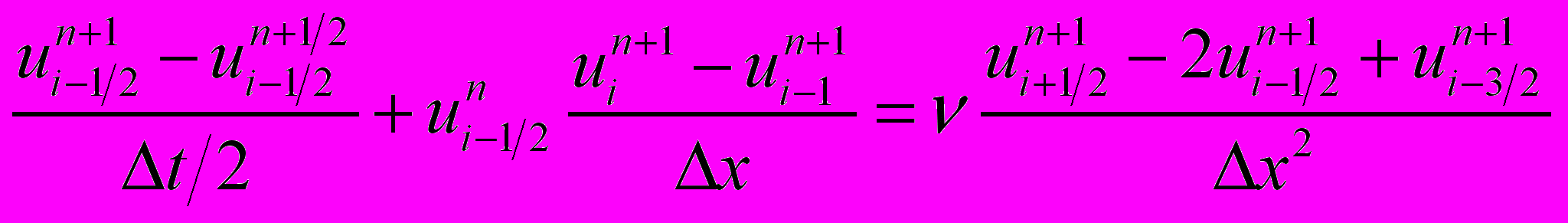
4) Кранка-Николсона с центральными разностями
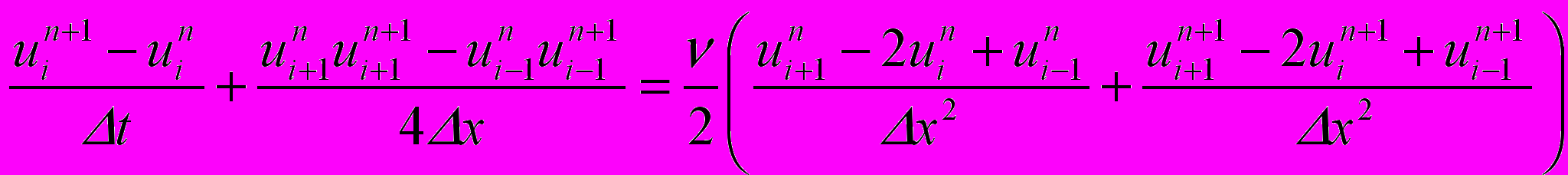
и той же схемой с демпфером в правой части (схема Бима-Уорминга)
, 
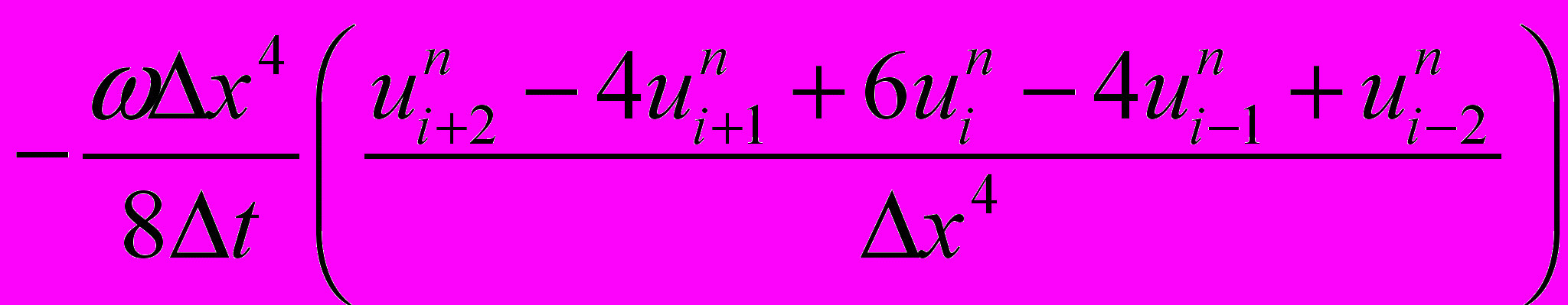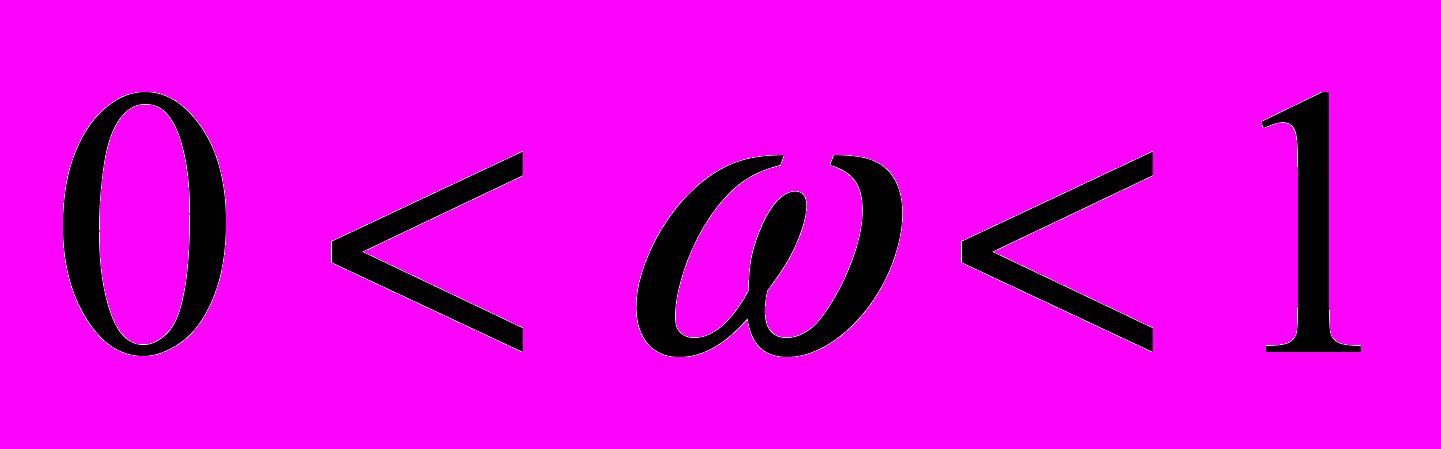
5) Кранка-Николсона-Самарского
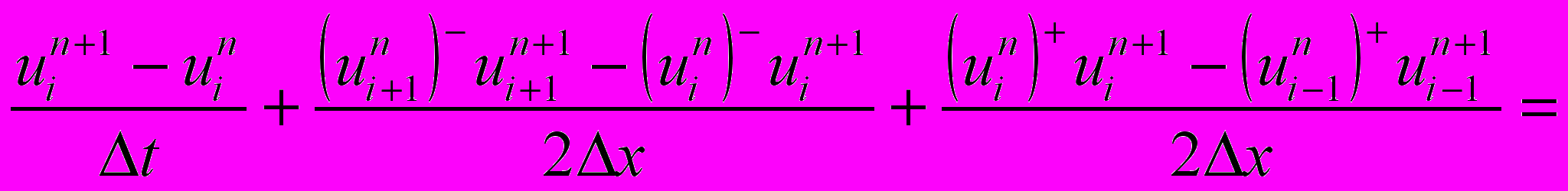
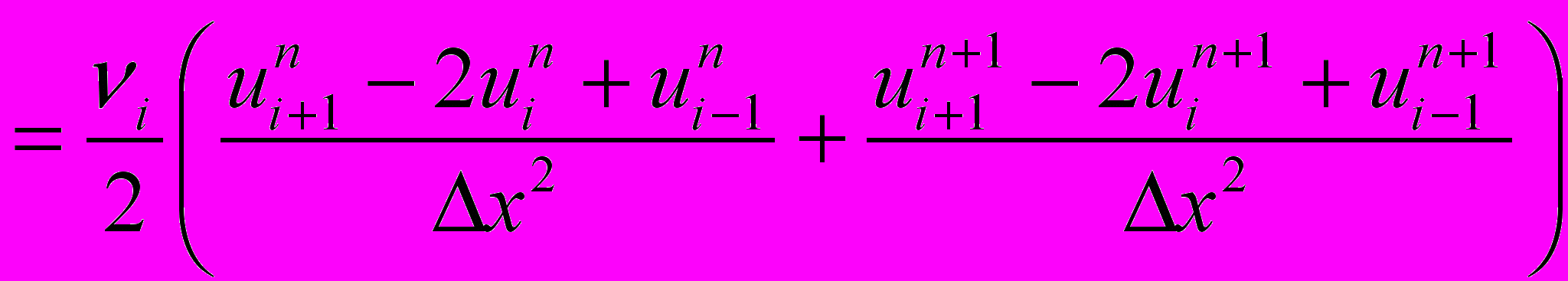
где
, 
, 
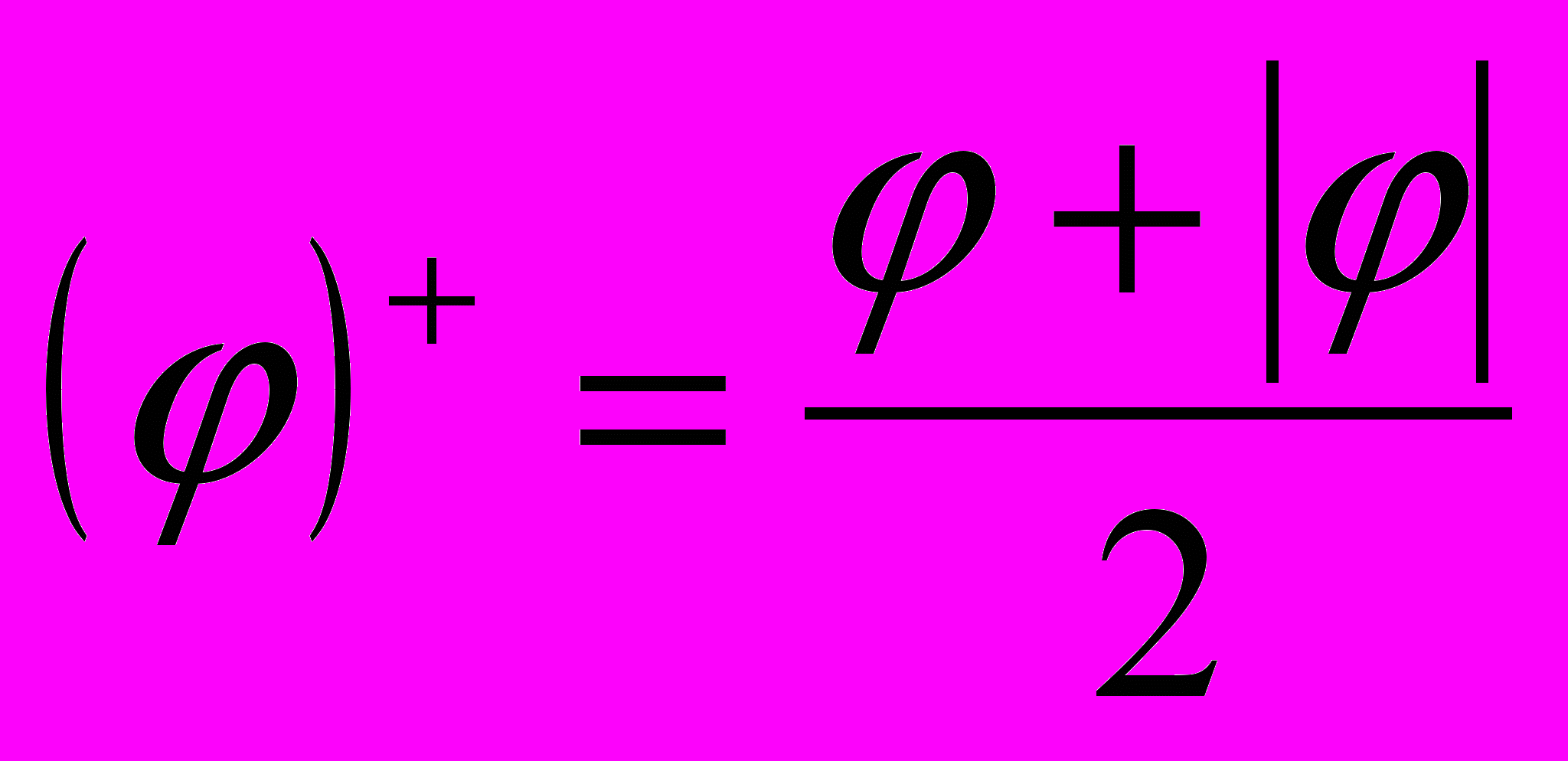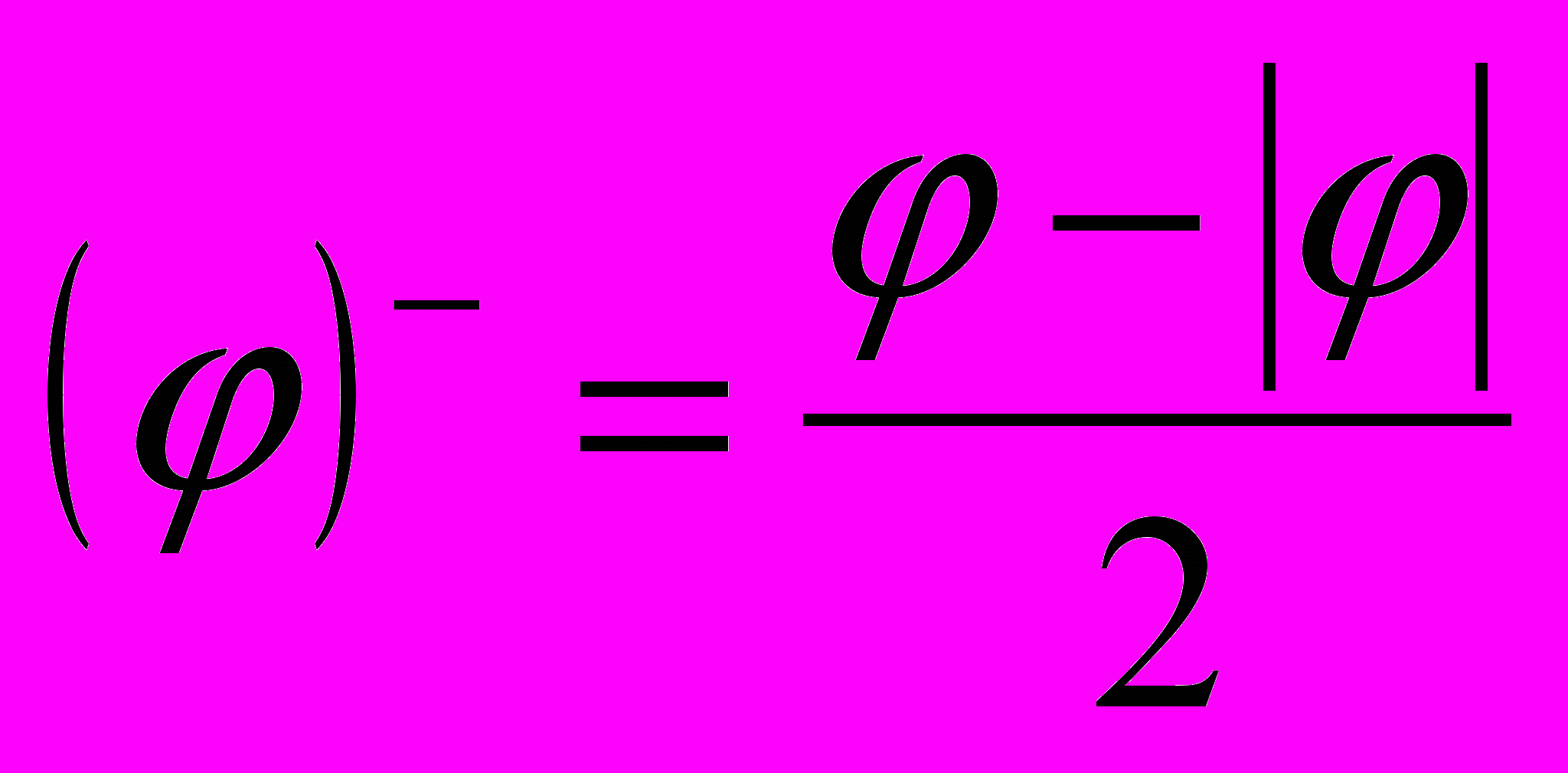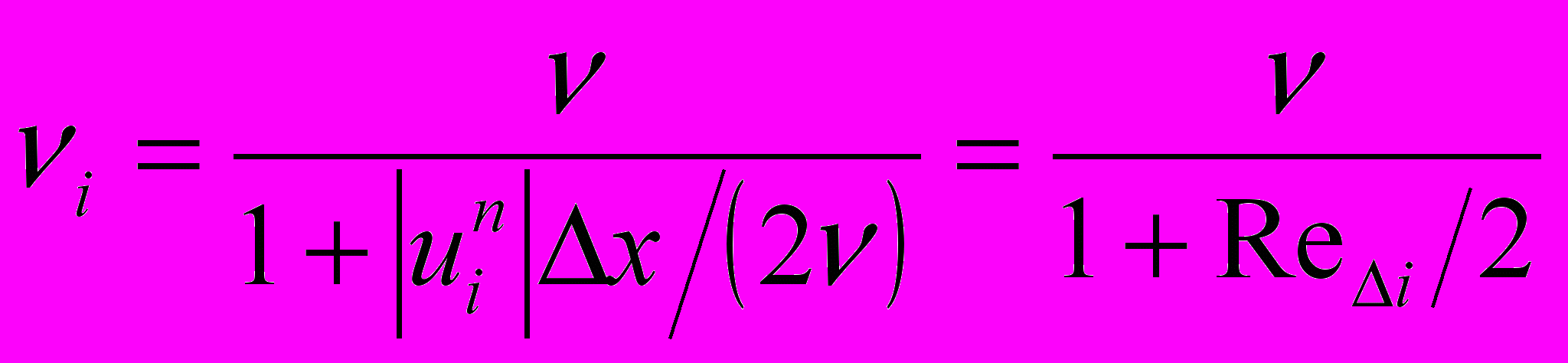
6) Лакса-Вендроффа с ограничителем minmod
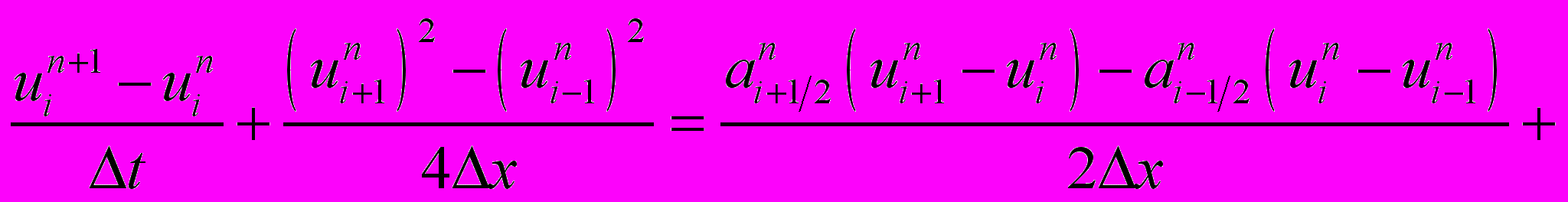
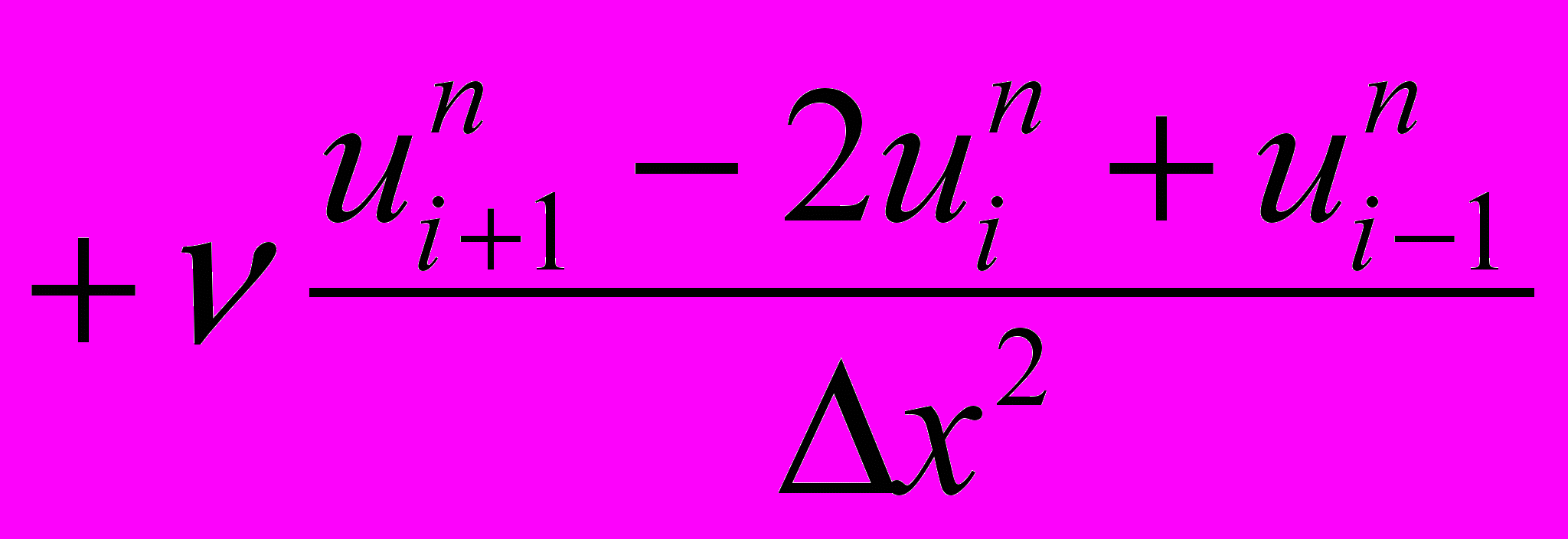,где
,
, 
, 
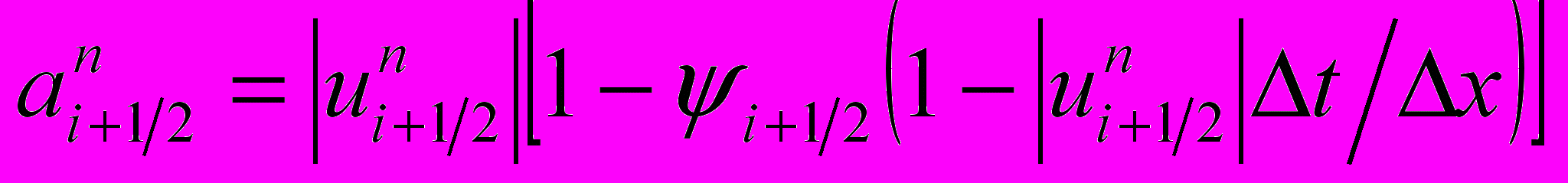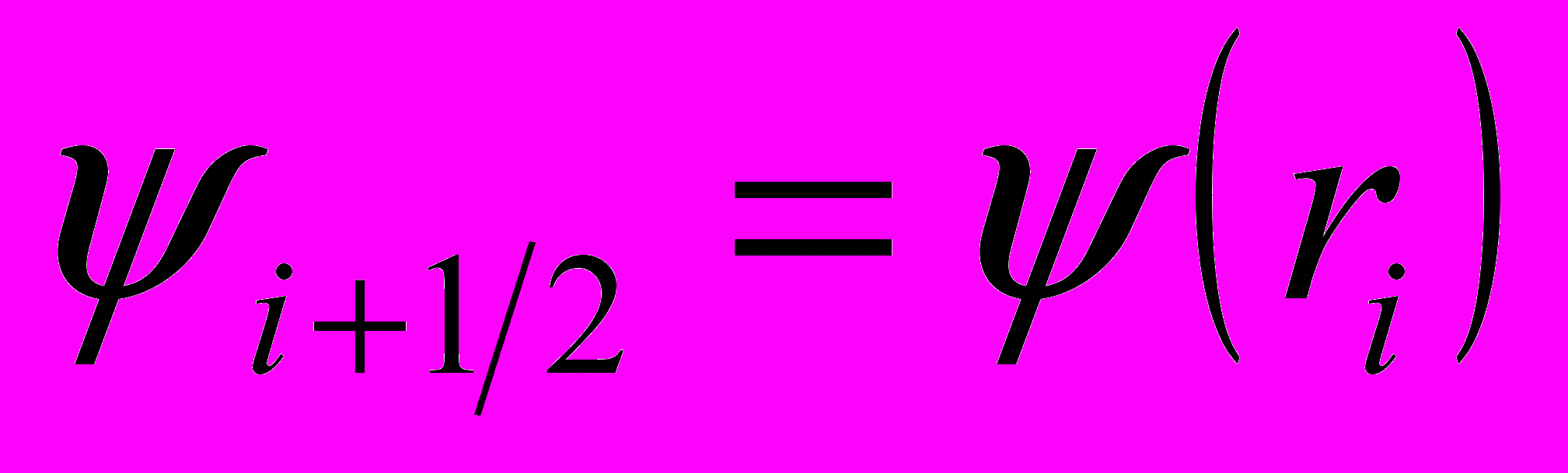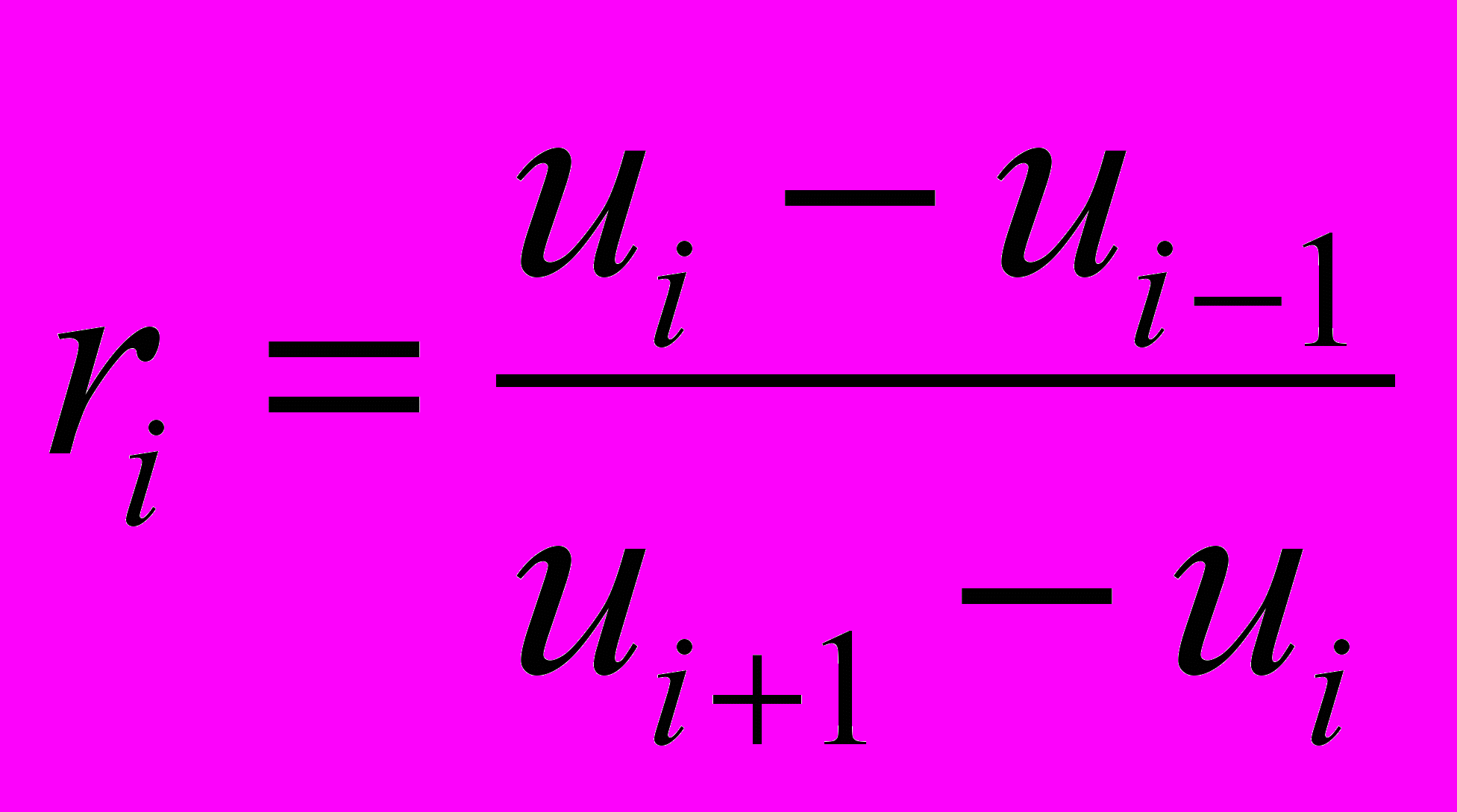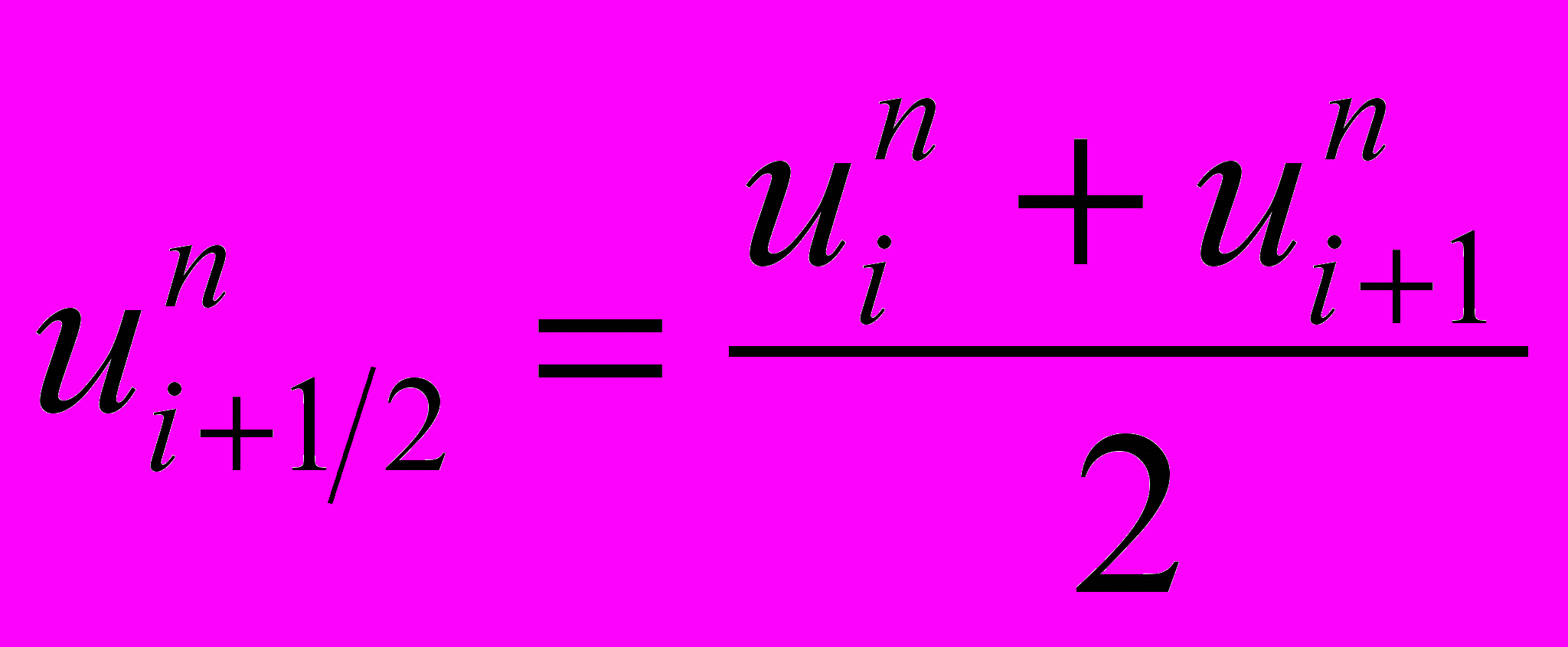
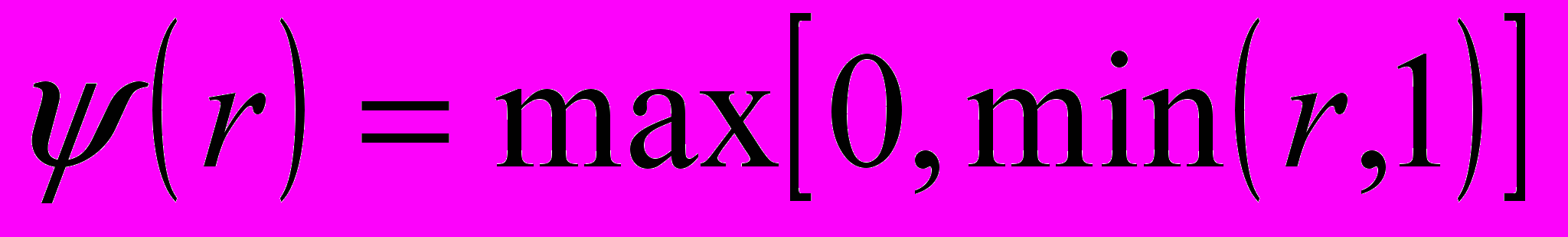
7) Лакса-Вендроффа с ограничителем superbee
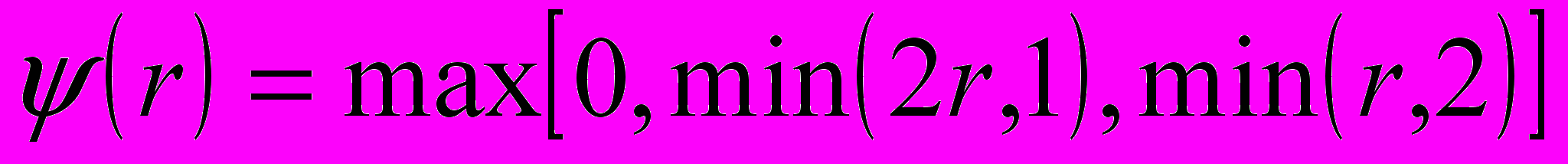
8) Лакса-Вендроффа с ограничителем Van Leer
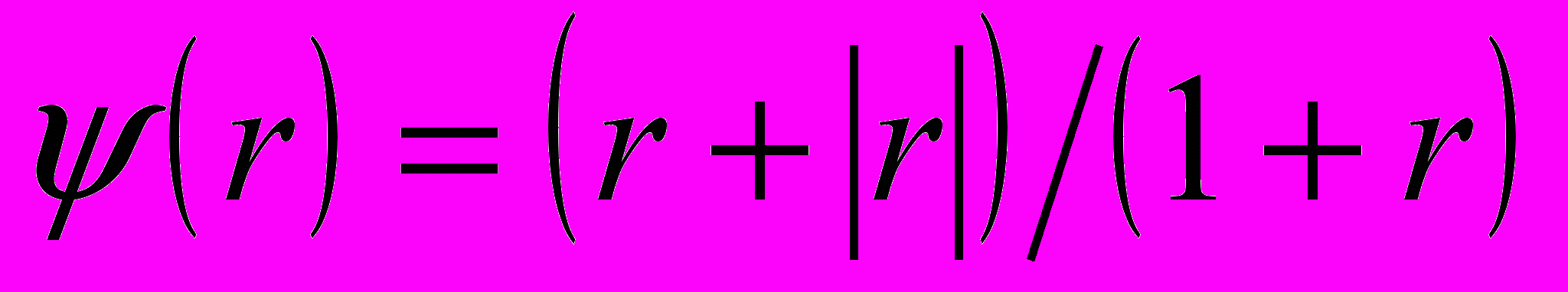
9) Лакса-Вендроффа с ограничителем VanAlbada
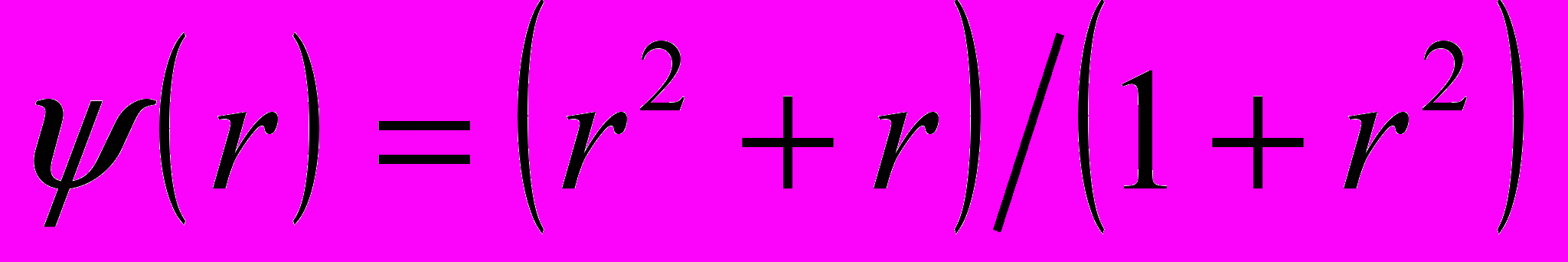
Провести расчёты на грубой и на мелкой сетках. Сравнить поведение двух схем. Для каждой схемы привести условие устойчивости и показать его применимость в численных расчётах.
5. Получить аналитическое решение нелинейного уравнения теплопроводности
, 
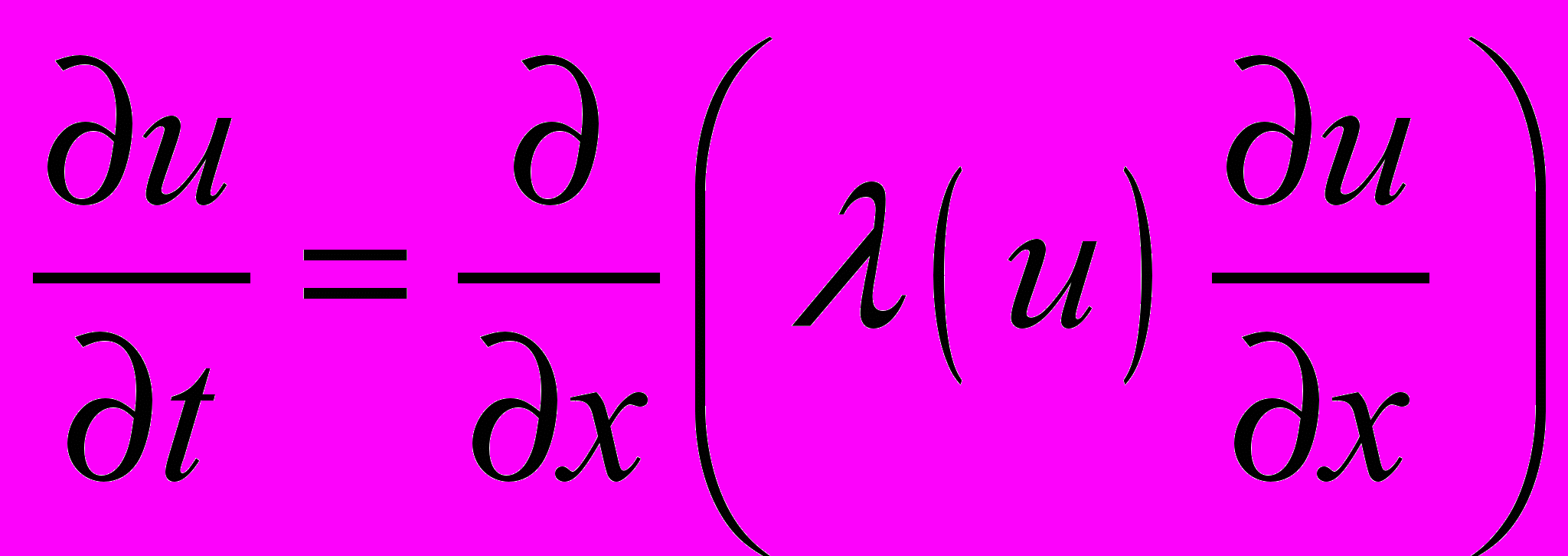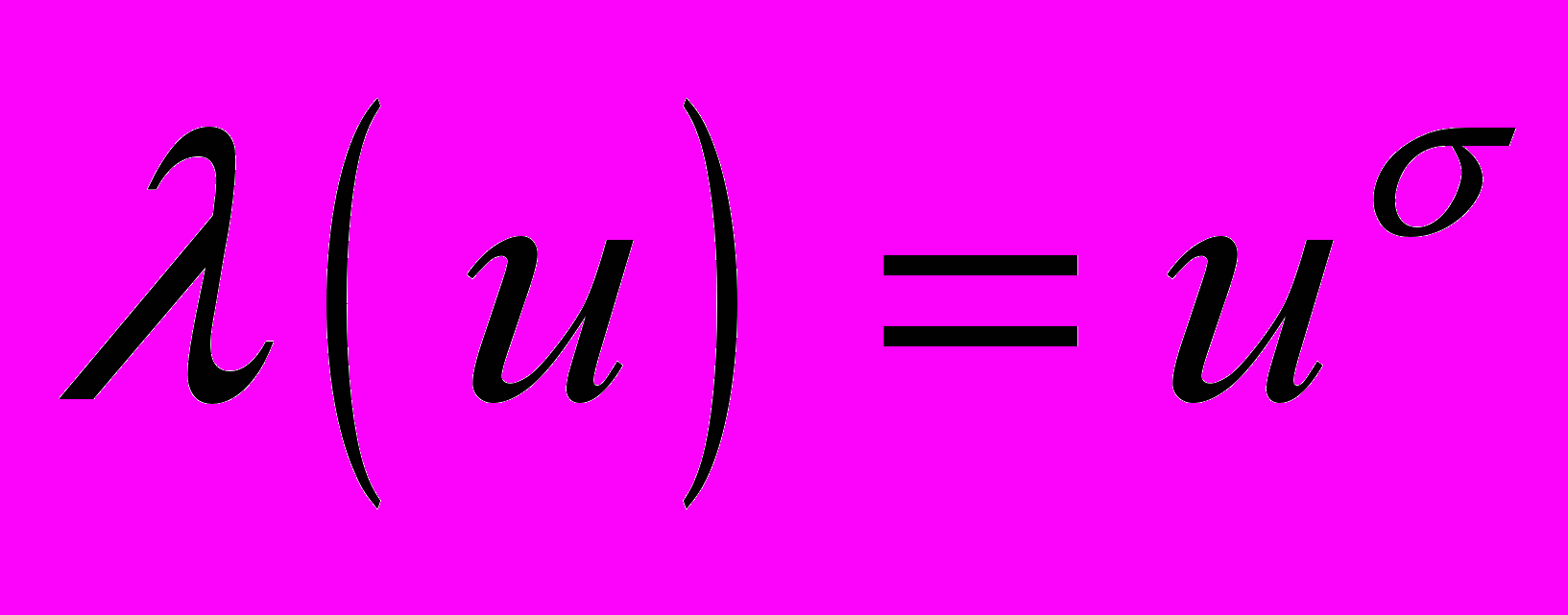на вещественной полуоси 
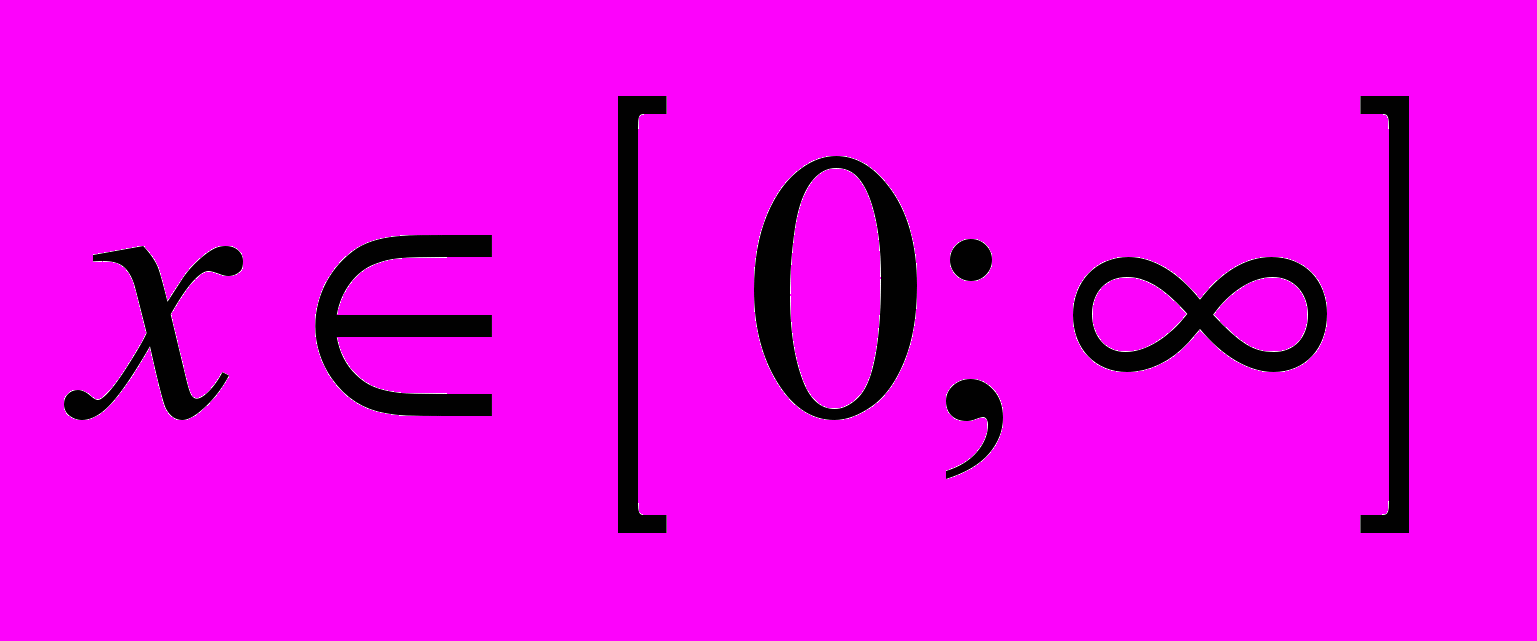с начальным условием 
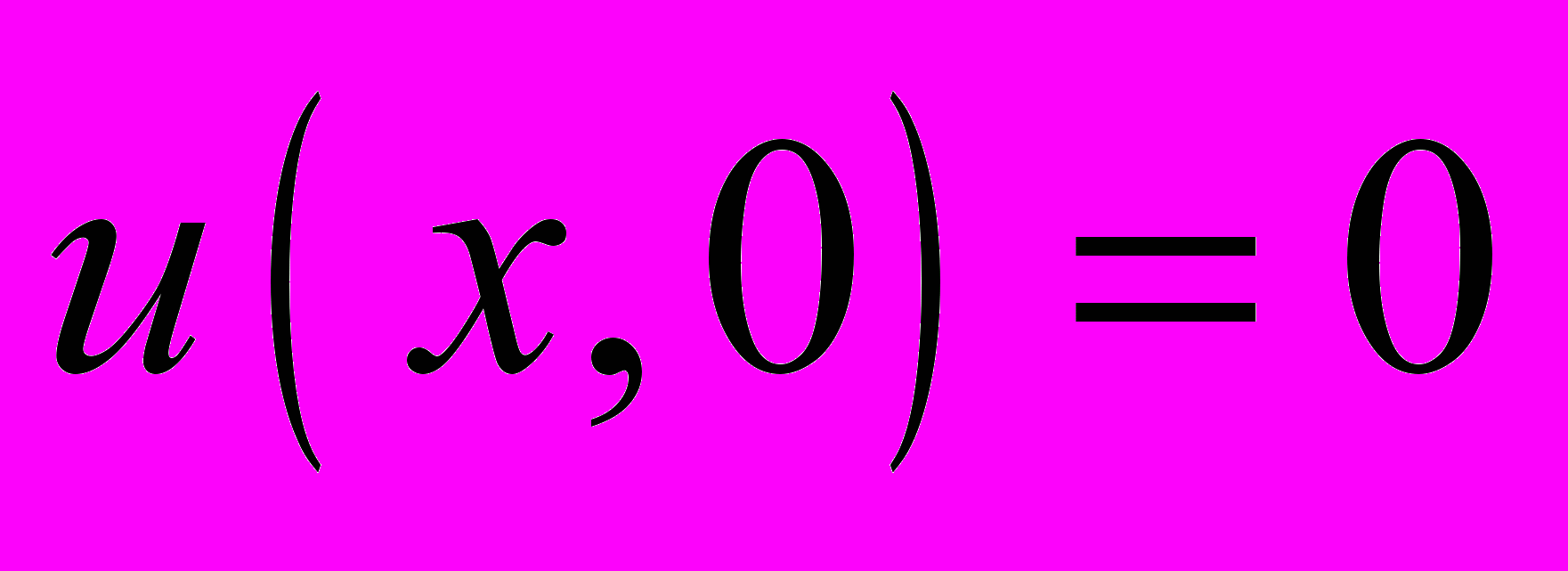и граничными условиями 
, 
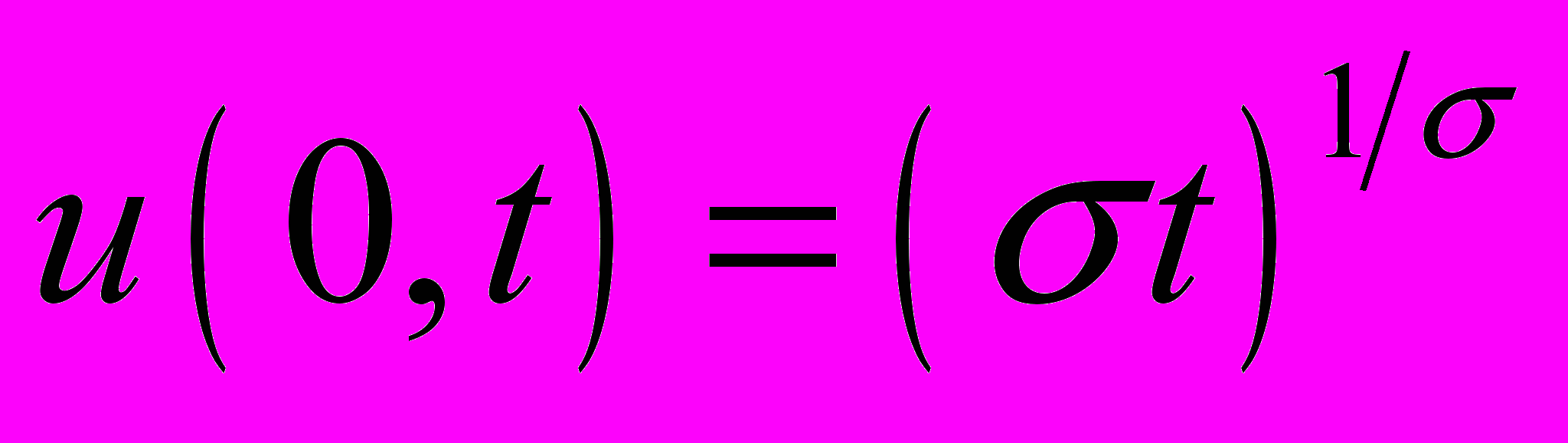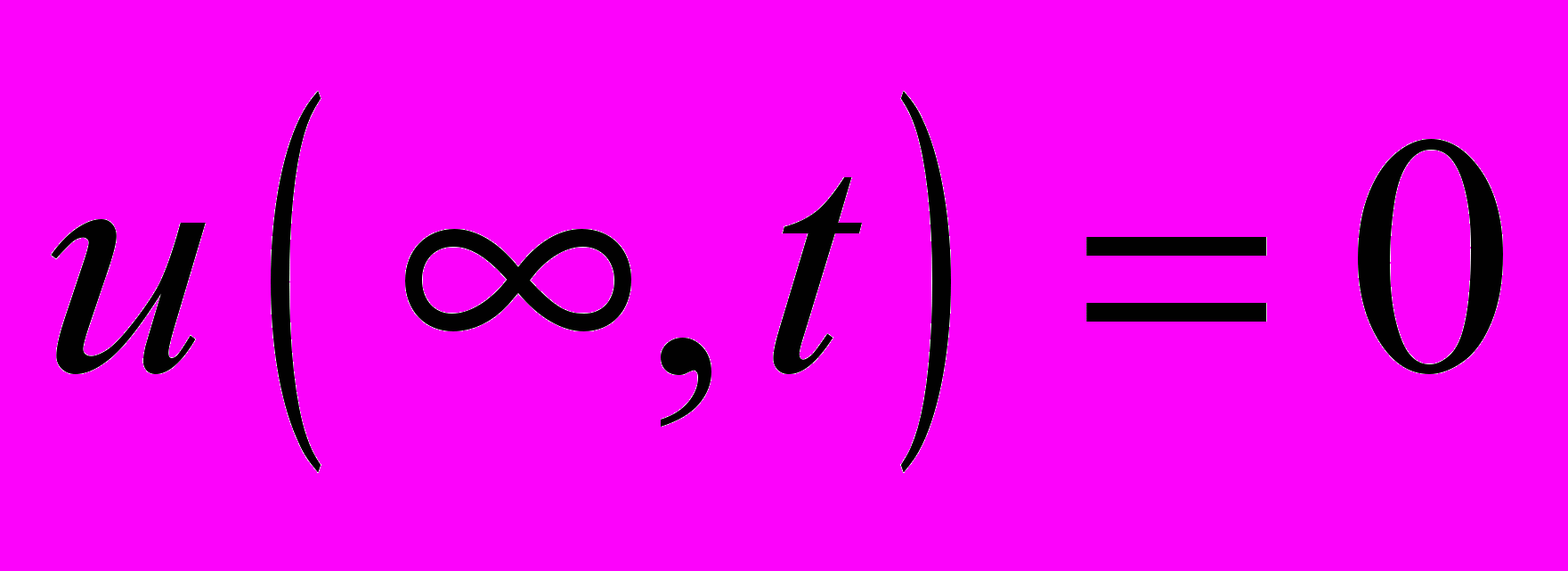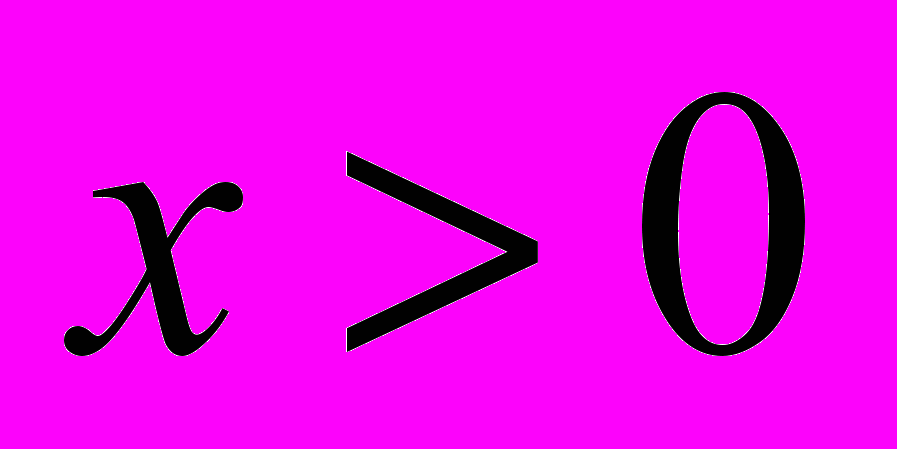, . Численно решить это уравнение с помощью неявной схемы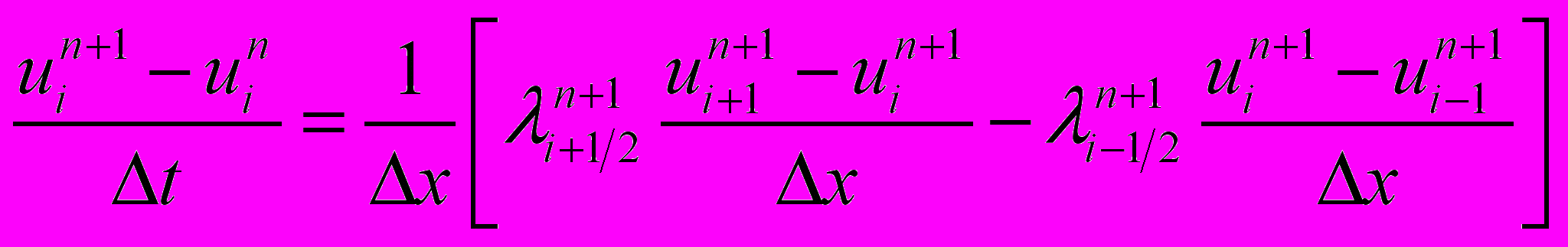
Для линеаризации уравнения использовать метод итерационной замены коэффициентов
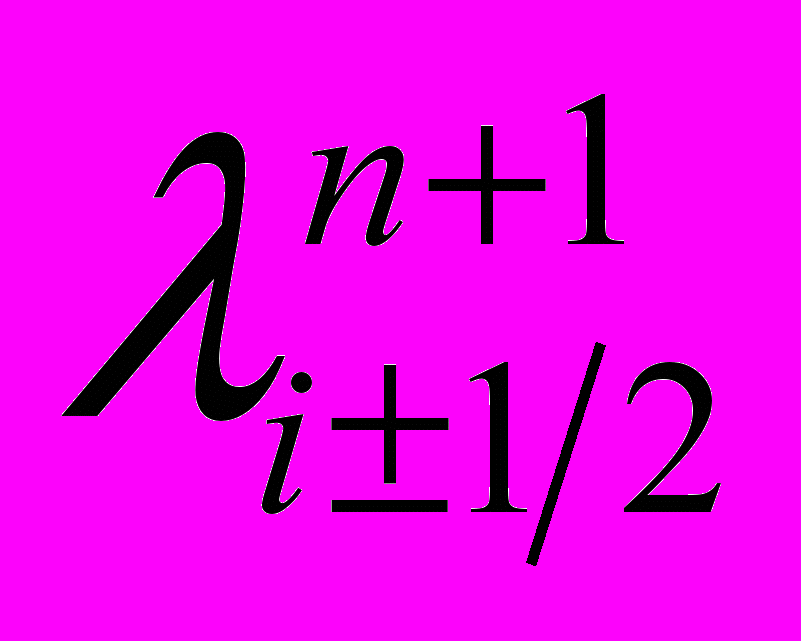. Коэффициенты 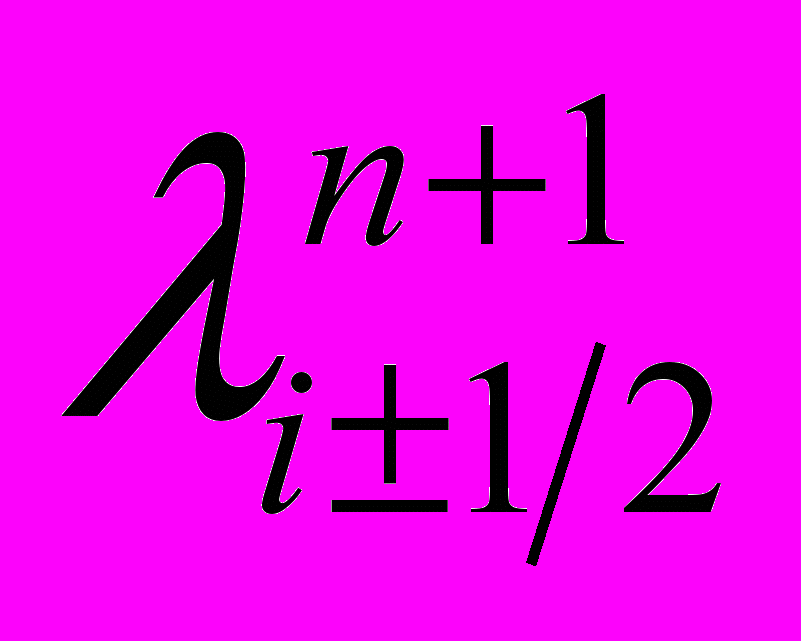вычислять по выражениям:1)
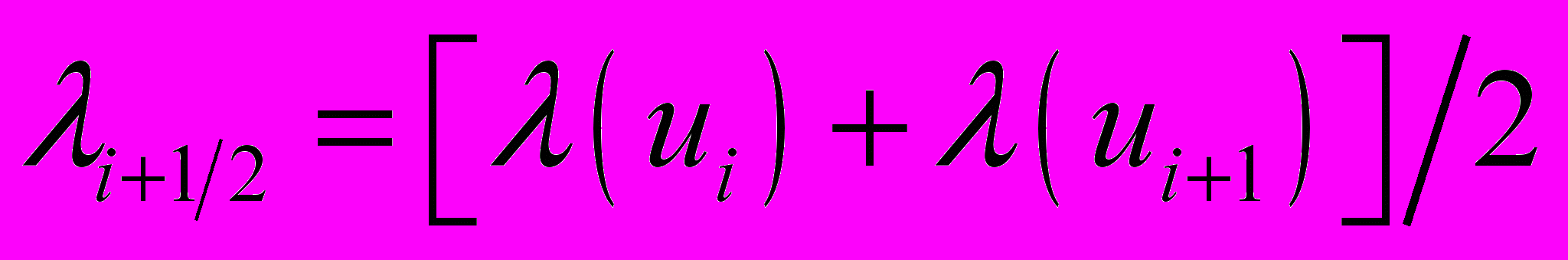
2)
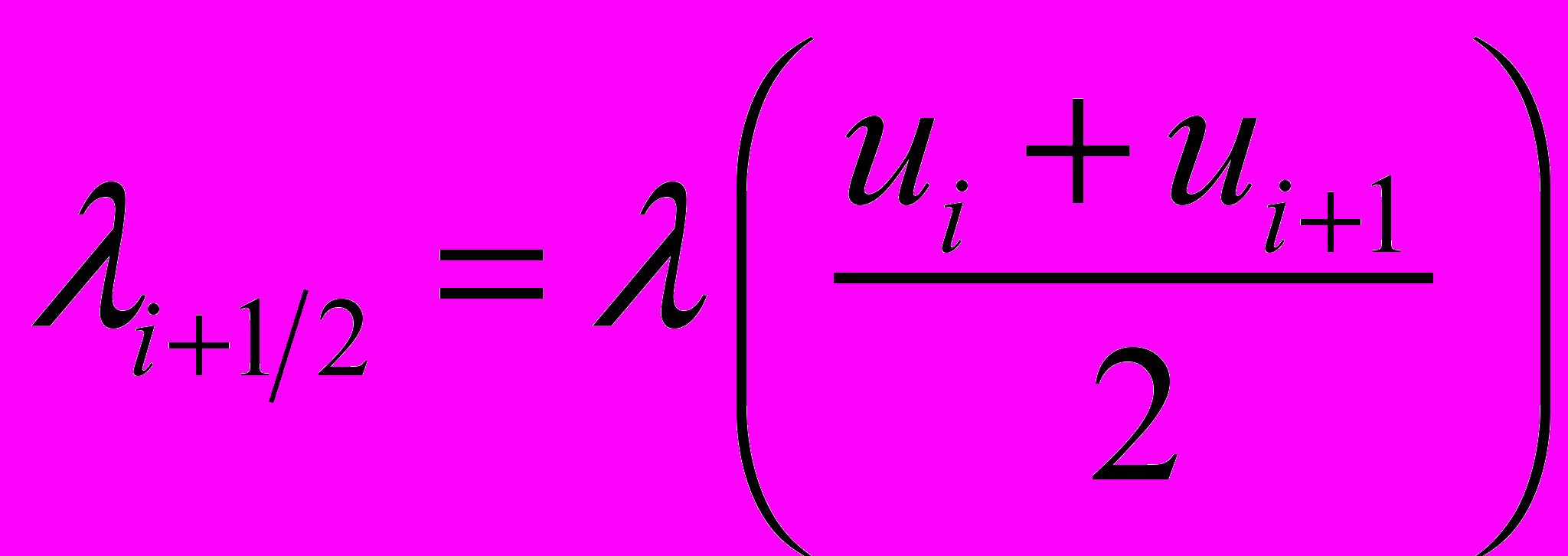
3)
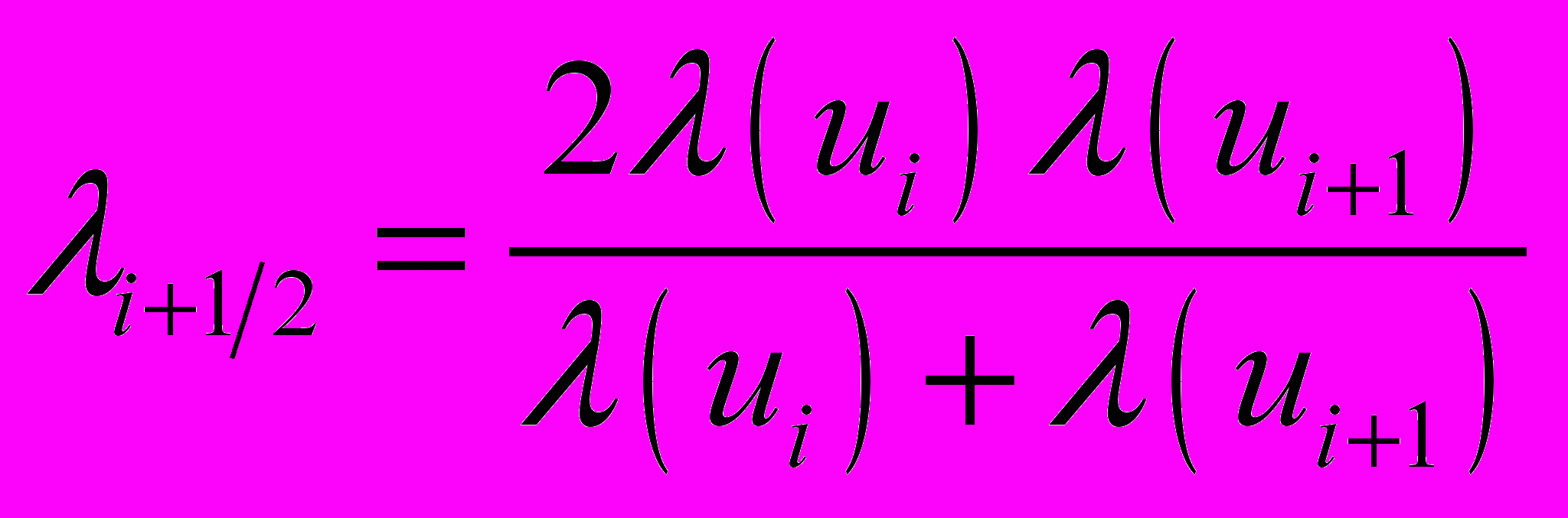
При необходимости задавать в начальную температуру отличной от нуля малой величиной. Сравнить с точным решением.