Geum.ru

Лабораторная работа n 1

Вид материалаЛабораторная работа

Содержание


Алгоритмы методов и примеры их реализации в электронной таблице
Метод простой итерации
Метод Ньютона
Метод хорд
Метод секущих
Подобный материал:


ЛАБОРАТОРНАЯ РАБОТА N 1

Итерационные методы решения нелинейного уравнения

Задание

Решить уравнение F(x)=0 c точностью  одним из методов:

  • половинного деления, =10-3;
  • простой итерации, =10-6;
  • Ньютона (касательных), =10-9;
  • секущих, =10-9;
  • хорд, =10-9.



Вариант

Уравнение
Вариант

Уравнение

1

2

3

4

5

6

7

8
x2+ex = 2

3sin(x+0,7)-0,5x = 0

cos x – (x-1)2 = 0

5 sin x = x+ln(x)

x2+cos (2+x) = 1

x ln(x+1) = 1

ln (x+1)-(x-2)2 = 0

2 ln x – 0,5 x +1 = 0
9

10

11

12

13

14

15

16
(x-2) ln(x) = 1

sin (x-0,5)-2x+0,5 = 0

cos (x+0,3) = x2

x2-3 sin x = 0

x ln(x+2) = 2

x3-0,5-sin x = 0

sin (x+1) = 0,2x

0,3 e0,6 x - x = 0


Примечание: для того, чтобы организовать в Excel’е итерационный процесс, необходимо:
  1. настроить Excel на выполнение итераций, для чего выполнить следующие действия Сервис – Параметры – Вычисления – вычисления производить вручную, итерации разрешить, предельное число итераций = 1;
  2. организовать в таблице циклическую ссылку, для чего в ячейке, где хранилось старое значение корня поставить ссылку на ячейку, где рассчитано новое, более точное значение корня;
  3. нажимать клавишу F9, наблюдая за поведением погрешности.



Алгоритмы методов

и примеры их реализации в электронной таблице

Метод деления отрезка пополам


1. Отделить интересующий нас корень уравнения – найти отрезок [a0,b0], на котором F(x) меняет знак: F(a0)* F(b0)<0.

2. Выбрать .

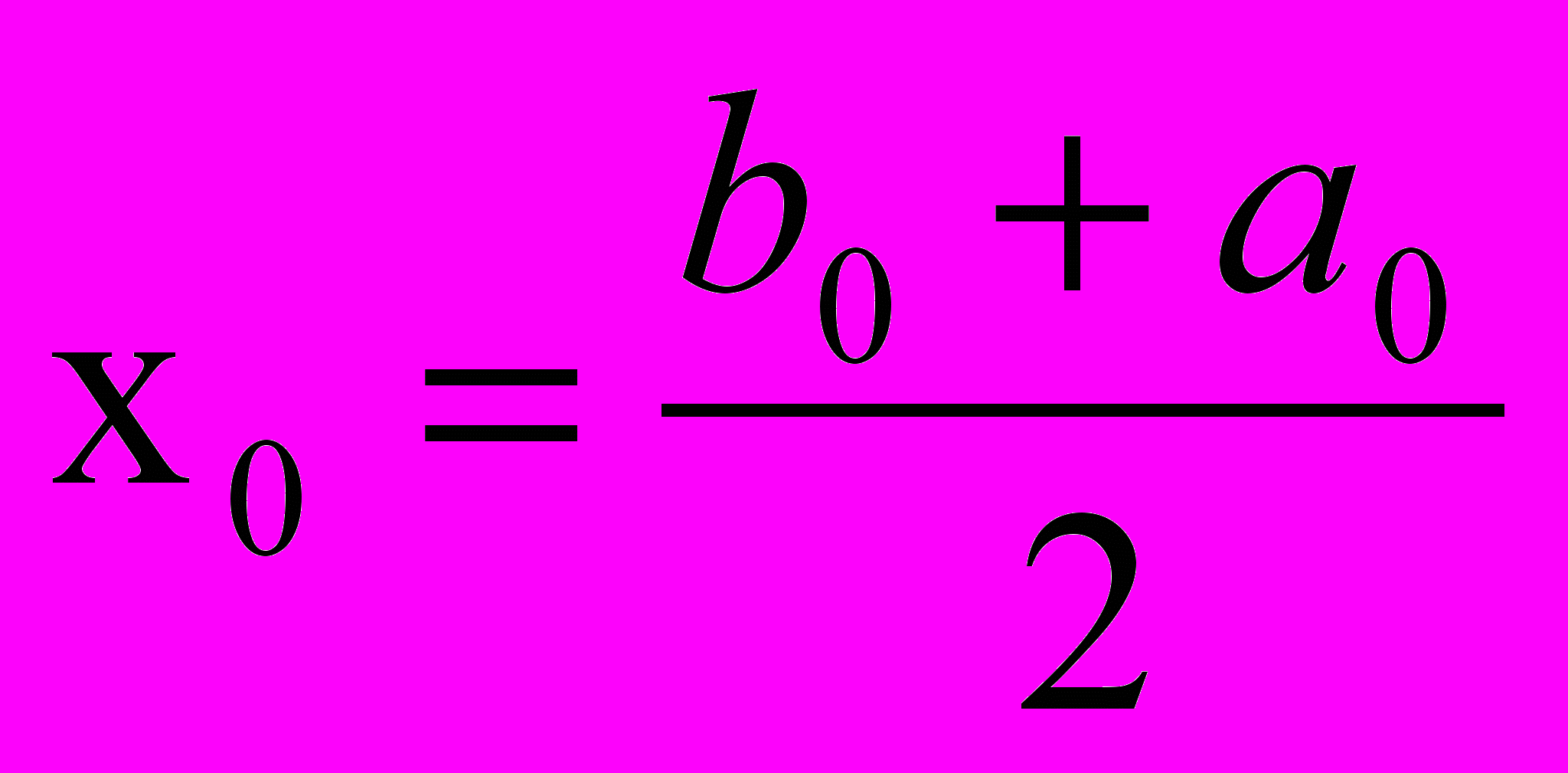3. Вычислить значение функции F(x0).

4. В зависимости от знака F(x0) определить новые границы отрезка [ai,bi], i=1,2…. следующим образом:

если F(a0)* F(x0)<0, то ai= ai-1, bi=xi-1, i=1,2….;

если F(a0)* F(x0)>0, то ai= xi-1, bi= bi-1, i=1,2….

5. Вычислить .

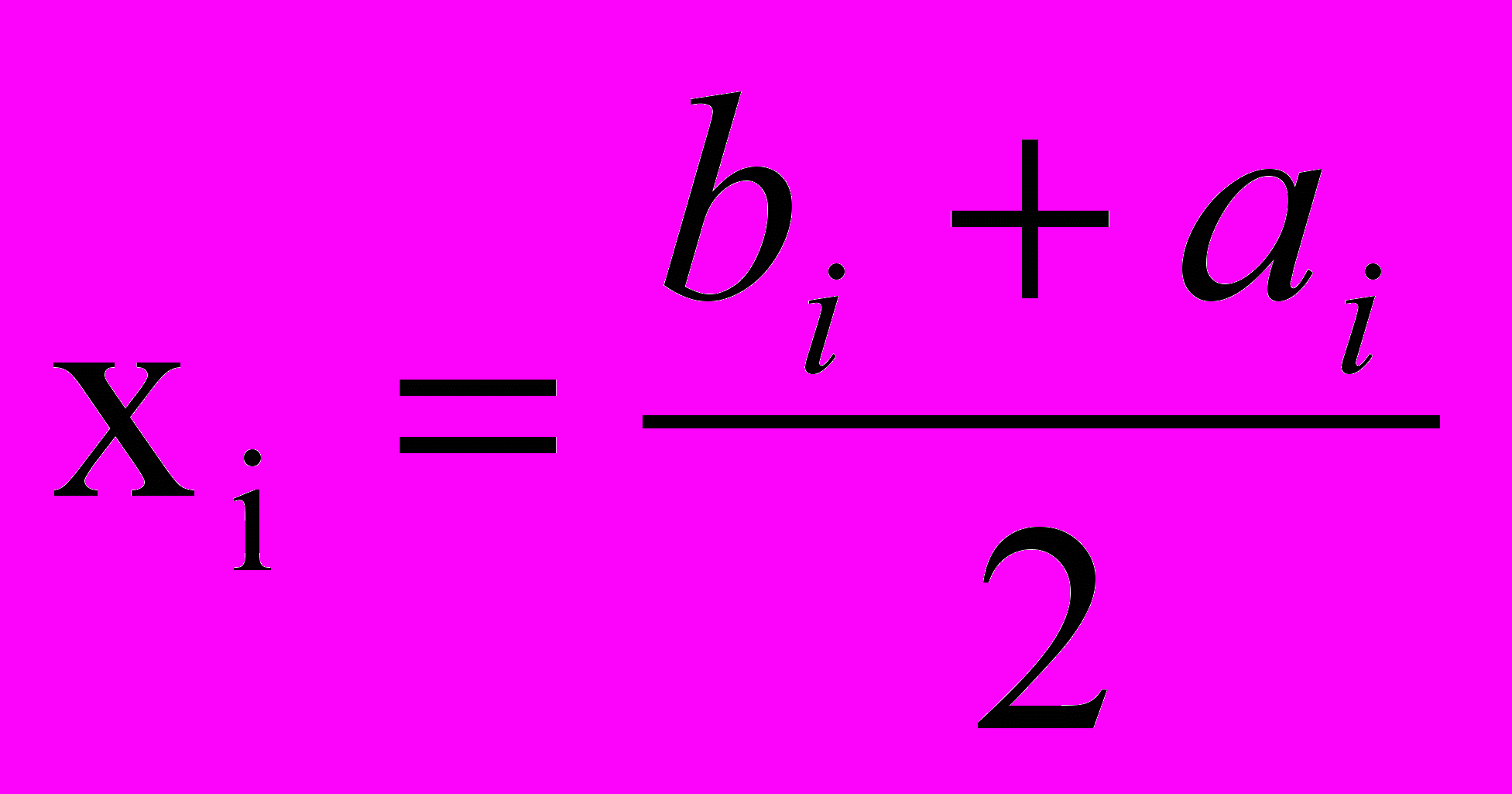6. Вычислить погрешность по формуле ri= bi- ai,

7. Итерационный процесс заканчивается как только ri<.
A
B
C
D
E
F
G
H

1
Решение уравнения x2-2=0 методом деления отрезка пополам

2



x
F(x)



Определение новых границ отрезка

3
a
1
-1



1









4
(a+b)/2
1,5
0,25















5
b
2
2



1,5









6
























7
Погрешность















8
r
1



















Примечание: для определения новых границ отрезка целесообразно использовать логическую функцию ЕСЛИ; циклическими ссылками будут связаны ячейки, в которых хранятся старые и новые значения границ отрезков

Метод простой итерации




  1. Отделить интересующий нас корень уравнения – найти отрезок [a,b], на котором F(x) меняет знак: F(a)* F(b)<0.
  2. Исследовать первую производную F’(x) на отрезке [a,b] (найти ее минимум и максимум, константы m = min |F’ (x)| x[a,b] и M = max |F’ (x)| x[a,b]).
  3. Рассчитать  = 1/М, sign  = - sign F’(x).
  4. Выбрать x0 – любую точку из отрезка [a,b], для определенности можно взять .
  5. Следующие приближения к корню рассчитываются по итерационной формуле xi = xi-1 +  * F(xi), i=1,2…
  6. Погрешность найденного приближения к корню оценивается по формуле
  7. Итерационный процесс заканчивается как только ri<.

A
B
C
D
E
F
G
H
I
J
K
L

1
Решение уравнения x2-2=0 методом простой итерации

2
Шаг
































3
h.
0,1






























4
Отрезок [a,b], разбитый c шагом h















5
x.
1
1,1
1,2
1,3
1,4
1,5
1,.6
1,.7
1,8
1,9
2

6
Значения функции на отрезке [a,b]















7
F(x)
-1
-0,79
-0,56
-0,31
-0,04
0,25
0,56
0,89
1,24
1,61
2

8
Значения первой производной на отрезке [a,b]















9
F’(x)
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4

10
m
2






























11
M
4






























12


-0,25






























13
(i-1)-ое приближение к корню















14
X(i-1)
1,5






























15
(i)-ое приближение к корню















16
X(i)
1,4






























17
Погрешность



























18
r(x)
-0,02
































Метод Ньютона




  1. Отделить интересующий нас корень уравнения – найти отрезок [a,b], на котором F(x) меняет знак: F(a)* F(b)<0.
  2. Исследовать первую производную F’(x) на отрезке [a,b] (найти ее минимум m = min |F’ (x)| x[a,b] ).
  3. Исследовать вторую производную F’’(x) на отрезке [a,b].
  4. Убедиться, что ни F’(x), ни F’’(x) не обращаются в 0 и не меняют знак на [a,b], в противном случае уменьшить шаг.
  5. Выбрать x0 =a, если F(a)*F’’(a)>0 или x0 =b, если F(b)*F’’(b)>0.
  6. Следующие приближения к корню рассчитываются по итерационной формуле xi = xi-1 - F(xi)/F' (xi), i=1,2….
  7. Погрешность найденного приближения к корню оценивается по формуле .
  8. Итерационный процесс заканчивается как только ri<.

A
B
C
D
E
F
G
H
I
J
K
L

1
Решение уравнения x2-2=0 методом Ньютона

2
Шаг
































3
h.
0,1






























4
Отрезок [a,b], разбитый c шагом h















5
x.
1
1,1
1,2
1,3
1,4
1,5
1,.6
1,.7
1,8
1,9
2

6
Значения функции на отрезке [a,b]















7
F(x)
-1
-0,79
-0,56
-0,31
-0,04
0,25
0,56
0,89
1,24
1,61
2

8
Значения первой производной на отрезке [a,b]















9
F’(x)
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4

10
Значения второй производной на отрезке [a,b]















11
F’’
2
2
2
2
2
2
2
2
2
2
2

12
(i-1)-ое приближение к корню















13
X(i-1)
2






























14
(i)-ое приближение к корню















15
X(i)
1,5






























16
Погрешность



























17
r(x)
0,125
































Метод хорд

  1. Отделить интересующий нас корень уравнения – найти отрезок [a,b], на котором F(x) меняет знак: F(a)* F(b)<0.
  2. Исследовать первую производную F’(x) на отрезке [a,b] (найти ее минимум m = min |F’ (x)| x[a,b] ).
  3. Исследовать вторую производную F’’(x) на отрезке [a,b].
  4. Убедиться, что ни F’(x), ни F’’(x) не обращаются в 0 и не меняют знак на [a,b], в противном случае уменьшить шаг.
  5. Выбрать x0 =a, если F’(x)*F’’(x)>0, x[a,b]; или

x0 =b, если F’(x)*F’’(x)<0, x[a,b].
  1. С
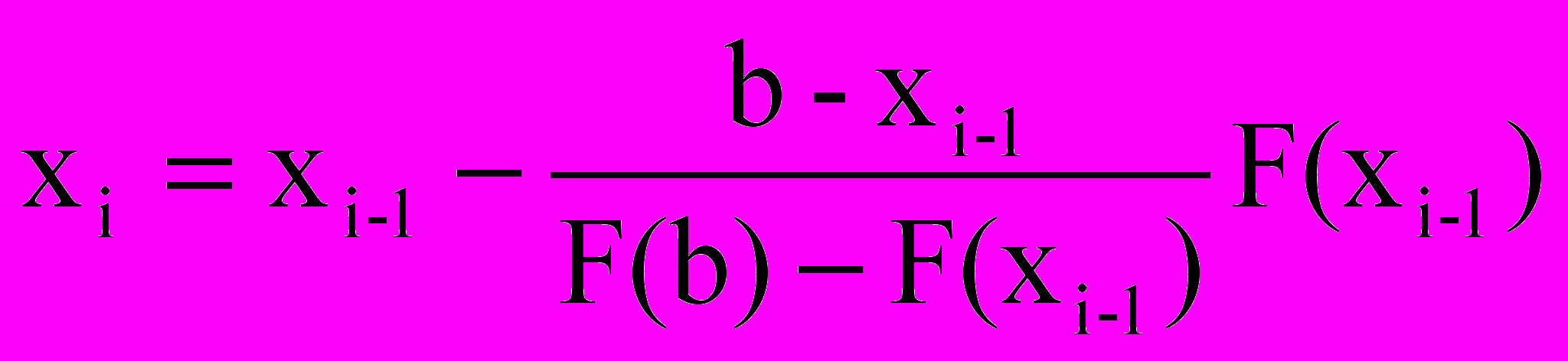
    ледующие приближения к корню рассчитываются по итерационной формуле


где i=1,2…., если F’(x)*F’’(x)>0, x[a,b]; или





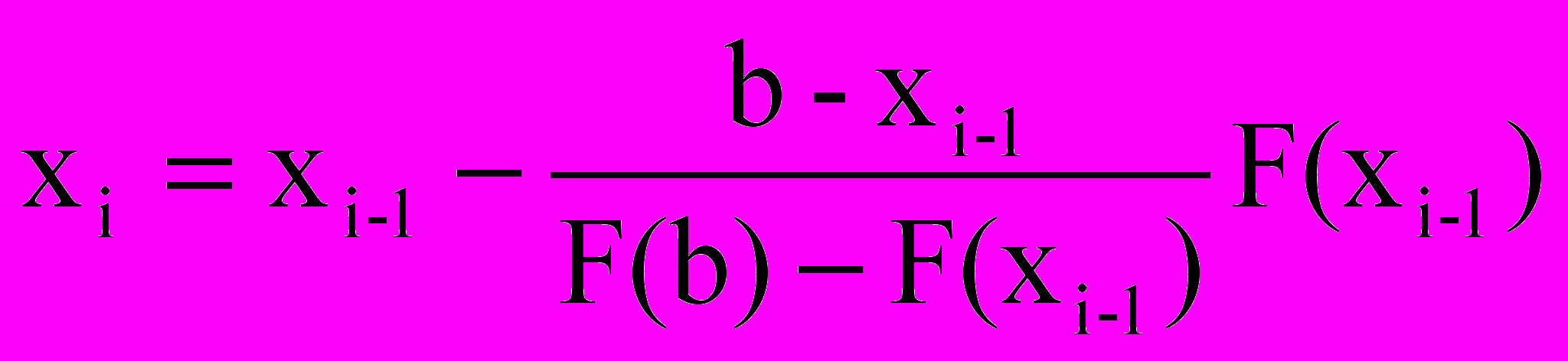
где i=1,2…., если F’(x)*F’’(x)<0, x[a,b].
  1. Погрешность найденного приближения к корню оценивается по формуле .
  2. Итерационный процесс заканчивается как только ri<.

A
B
C
D
E
F
G
H
I
J
K
L

1
Решение уравнения x2-2=0 методом Ньютона

2
Шаг
































3
h.
0,1






























4
Отрезок [a,b], разбитый c шагом h















5
x.
1
1,1
1,2
1,3
1,4
1,5
1,.6
1,.7
1,8
1,9
2

6
Значения функции на отрезке [a,b]















7
F(x)
-1
-0,79
-0,56
-0,31
-0,04
0,25
0,56
0,89
1,24
1,61
2

8
Значения первой производной на отрезке [a,b]















9
F’(x)
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4

10
Значения второй производной на отрезке [a,b]















11
F’’
2
2
2
2
2
2
2
2
2
2
2

12
(i-1)-ое приближение к корню















13
X(i-1)
2






























14
(i)-ое приближение к корню















15
X(i)
1,5






























16
Погрешность



























17
r(x)
0,125





























Метод секущих

  1. Отделить интересующий нас корень уравнения – найти отрезок [a,b], на котором F(x) меняет знак: F(a)* F(b)<0.
  2. Исследовать первую производную F’(x) на отрезке [a,b] (найти ее минимум m = min |F’ (x)| x[a,b] ).
  3. Исследовать вторую производную F’’(x) на отрезке [a,b].
  4. Убедиться, что ни F’(x), ни F’’(x) не обращаются в 0 и не меняют знак на [a,b], в противном случае уменьшить шаг.
  5. Выбрать x0 =a, если F(a)*F’’(a)>0 или x0 =b, если F(b)*F’’(b)>0.
  6. Вычислить x1 = x0+.
  7. Следующие приближения к корню рассчитываются по итерационной формуле




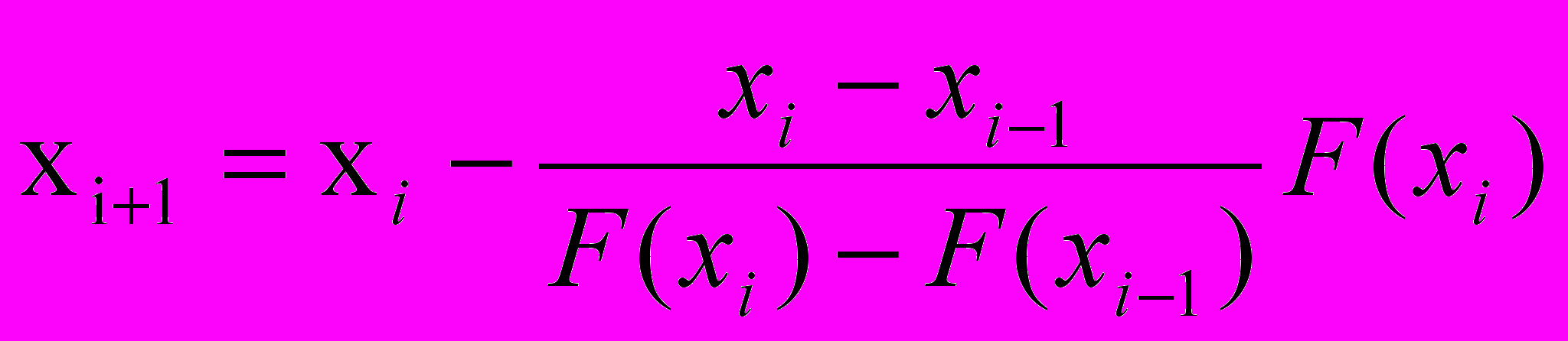
где, i=1,2….
  1. Погрешность найденного приближения к корню оценивается по формуле .
  2. Итерационный процесс заканчивается как только ri<.

A
B
C
D
E
F
G
H
I
J
K
L

1
Решение уравнения x2-2=0 методом секущих

2
Шаг
































3
h.
0,1






























4
Отрезок [a,b], разбитый c шагом h















5
x.
1
1,1
1,2
1,3
1,4
1,5
1,.6
1,.7
1,8
1,9
2

6
Значения функции на отрезке [a,b]















7
F(x)
-1
-0,79
-0,56
-0,31
-0,04
0,25
0,56
0,89
1,24
1,61
2

8
Значения первой производной на отрезке [a,b]















9
F’(x)
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4

10
Значения второй производной на отрезке [a,b]















11
F’’
2
2
2
2
2
2
2
2
2
2
2

12
(i-1)-ое приближение к корню















13
X(i-1)
2






























14
(i)-ое приближение к корню















15
X(i)
1,499






























16
Погрешность



























17
r(x)
0,124