А*. в противном случае будем рассматривать задачу с оператором при решении вариационной задачи. Будем также считать, что А

Вид материала

Лекция

Содержание А — положительный оператор, т.е. A 2.7 О спектральных задачах A эквивалентно отысканию такой ортогональной матрицы T

Подобный материал:

• Об управлении наукой, 121.64kb.
• История роботов, написанная роботом, 101.24kb.
• Задача примет вид, 48.6kb.
• Моя тема называется: «Медальный ряд России XVIII первой половины XIX в.». Мы будем, 77.89kb.
• Решение задач на «сплавы», 60.59kb.
• Ву и комнаты, где проходит урок, 474.67kb.
• «экологическая ниша», 206.75kb.
• Подпрограмма последовательность инструкций, которой можно дать произвольное имя и использовать, 222.35kb.
• Н. И. Афанасьев, 33.15kb.
• А. А. Борисенкова "Львиные ворота" из собрания Государственного музея-заповедника "Коломенское":, 262.74kb.

Лекция 7

23 октября 2006 года.

5. Вариационные итерационные методы
   
   1. Связь между вариационной задачей и задачей решения СЛАУ.
      

Пусть , где Lⁿ есть n-мерное евклидово пространство. Рассмотрим квадратичный функционал от u, называемый функционалом энергии:



где А — линейный оператор, 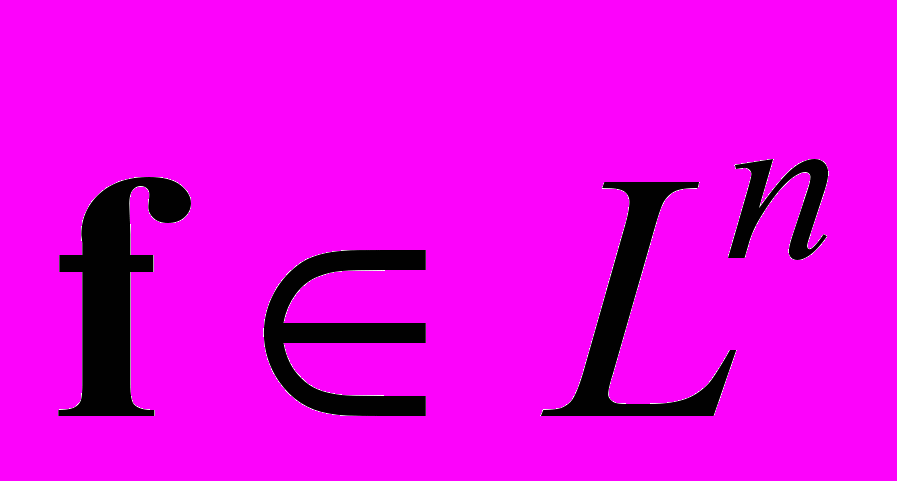, с — константа. Этот функционал совпадает с квадратичным функционалом 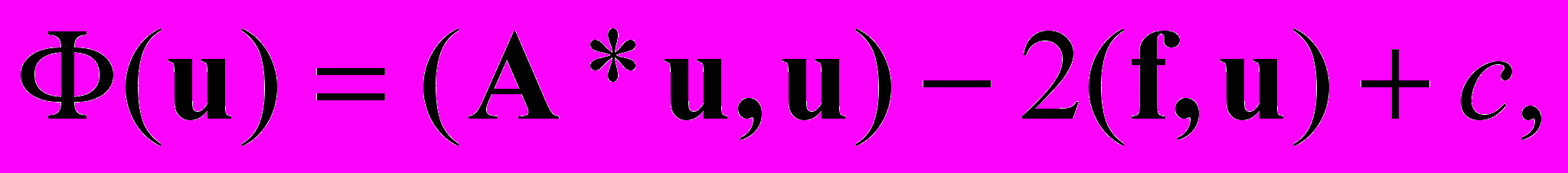где А* — сопряженный к А оператор. Действительно, 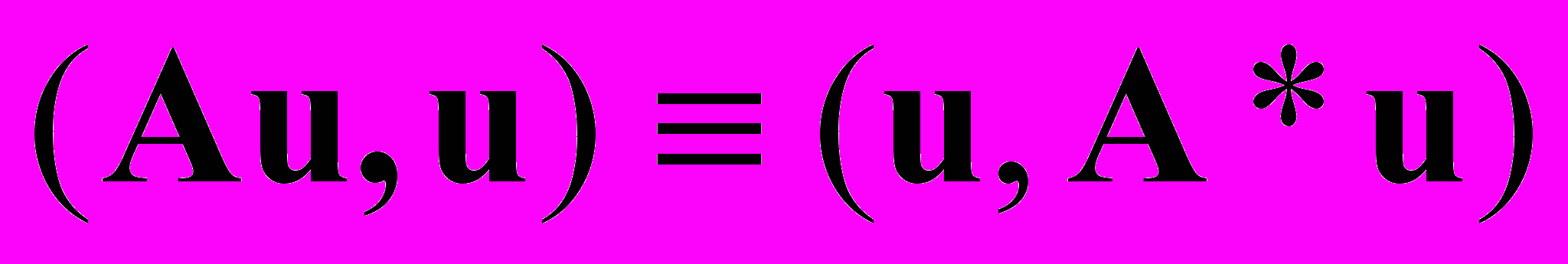по определению сопряженного оператора и (u, A*u) = (A*u, u) в силу коммутативности скалярного произведения. Тогда

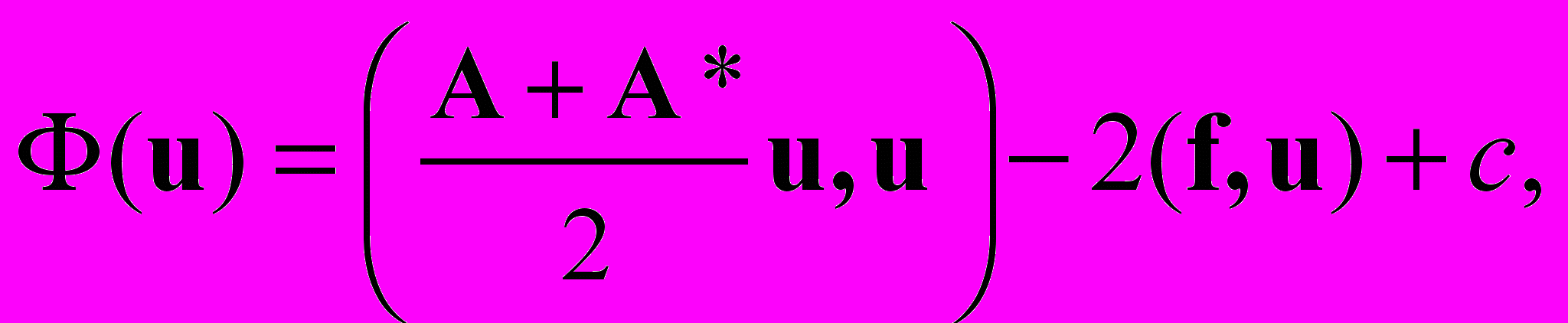так как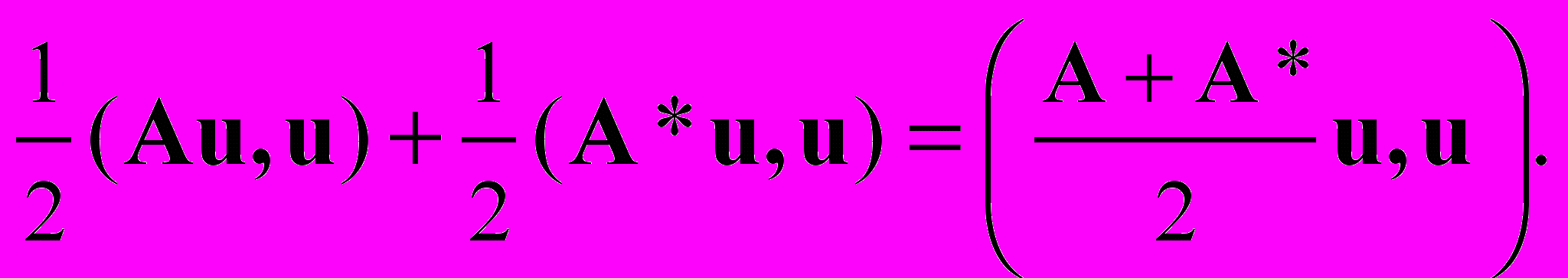

Без ограничения общности предположим, что оператор А самосопряженный, А = А*. В противном случае будем рассматривать задачу с оператором 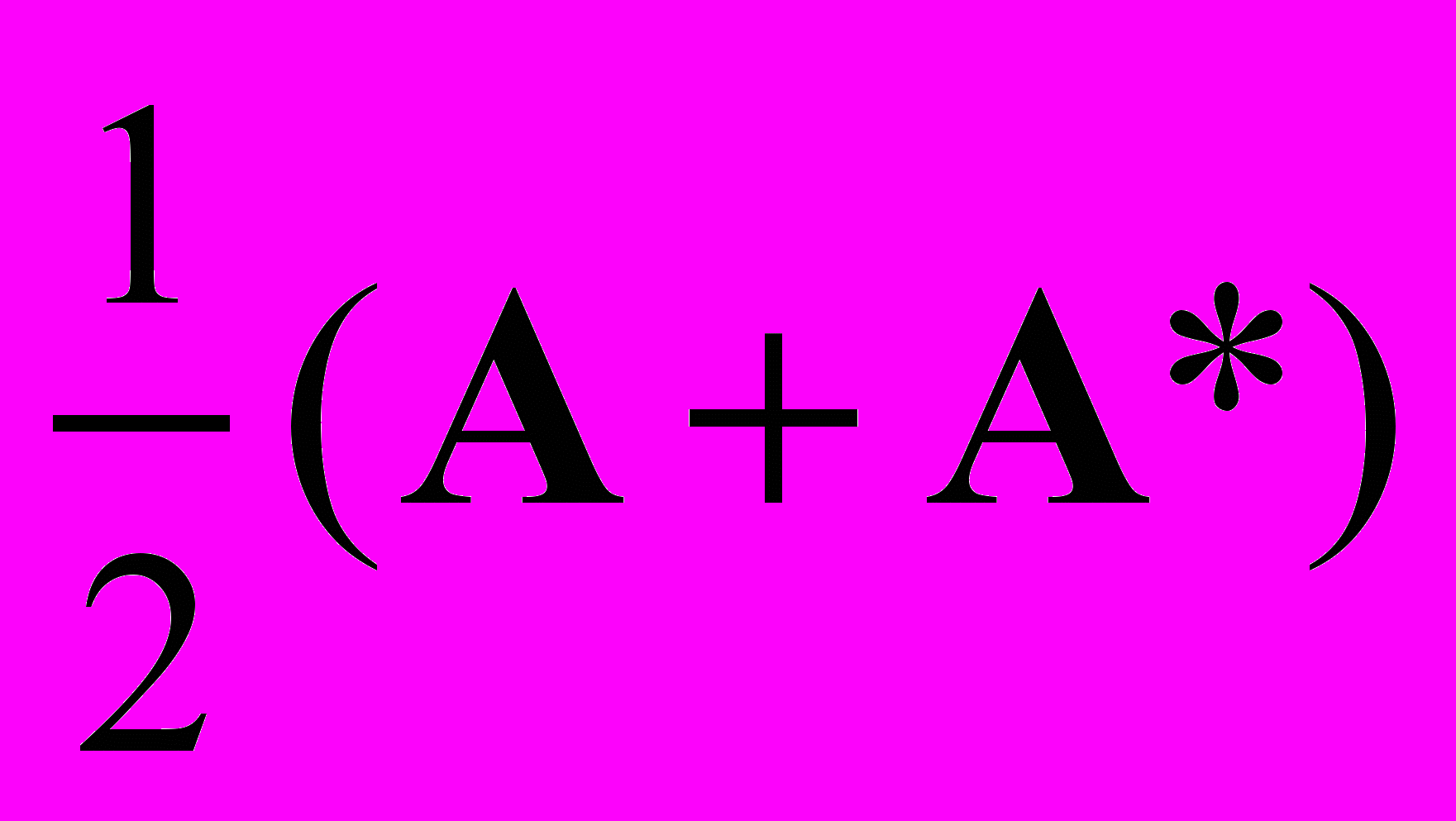при решении вариационной задачи.

Будем также считать, что А — положительный оператор, т.е. A > 0, это означает, что для любого ненулевого вектора u выполнено (Au, u) > 0. Поставим задачу об отыскании элемента v, придающего наименьшее значение функционалу Ф(u):

.

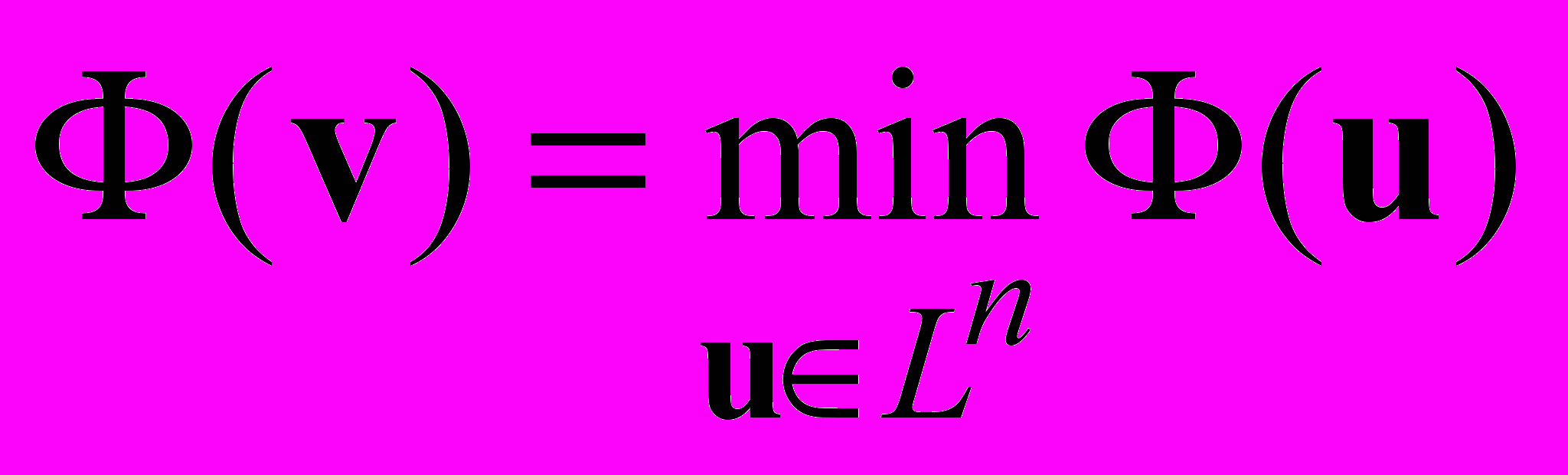Теорема Пусть А = А* > 0. В этом случае существует единственный элемент 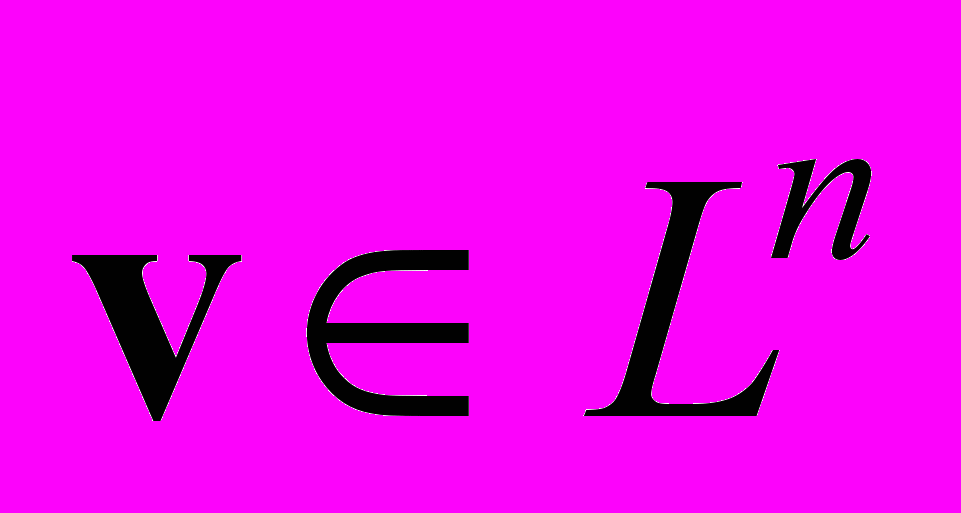, придающий наименьшее значение квадратичному функционалу 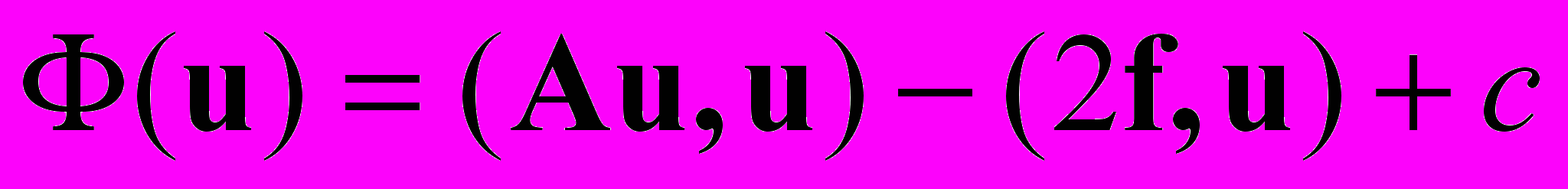, являющийся решением СЛАУ Аu = f.

Доказательство. СЛАУ Au = f имеет единственное решение v, поскольку А является невырожденным оператором в силу его положительной определенности. Покажем, что в этом случае при для любого вектора Δ имеет место: т.е. при 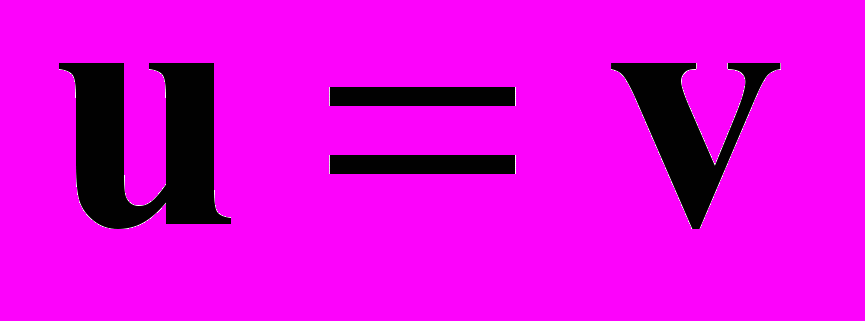достигается минимум квадратичного функционала .

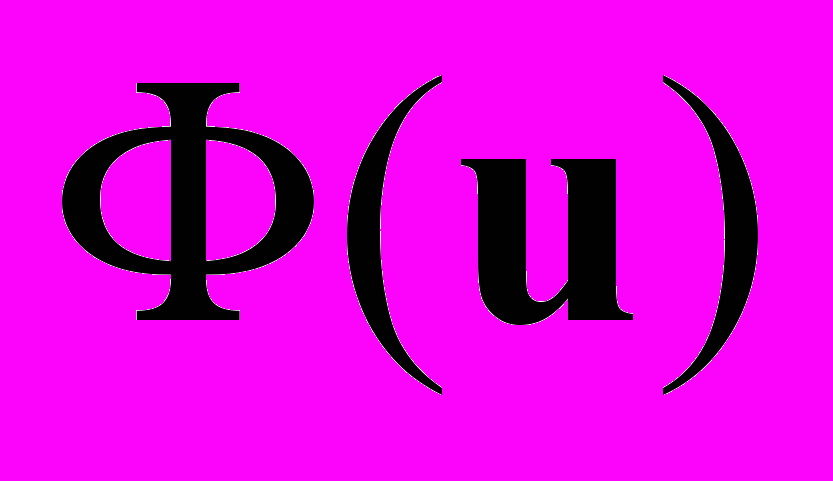Действительно,











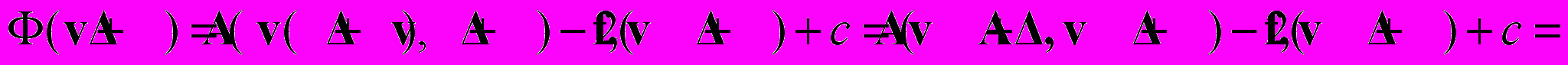
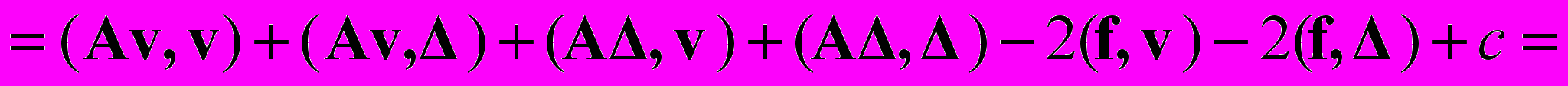
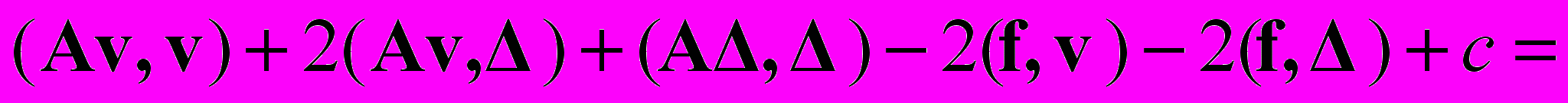
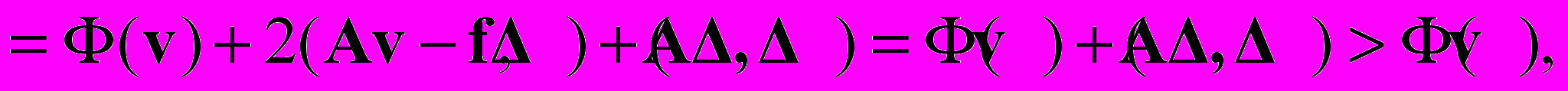
т.е. при 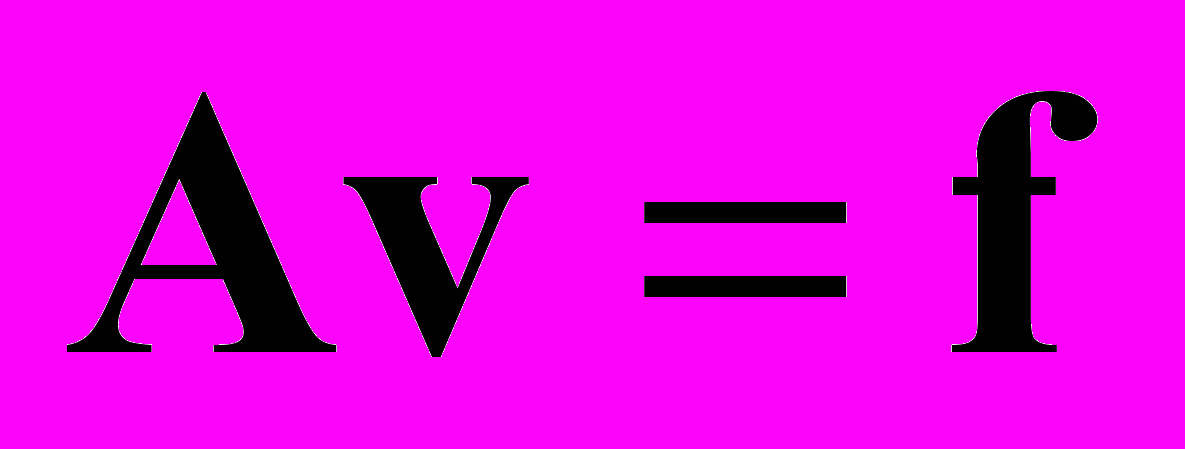и любом имеет место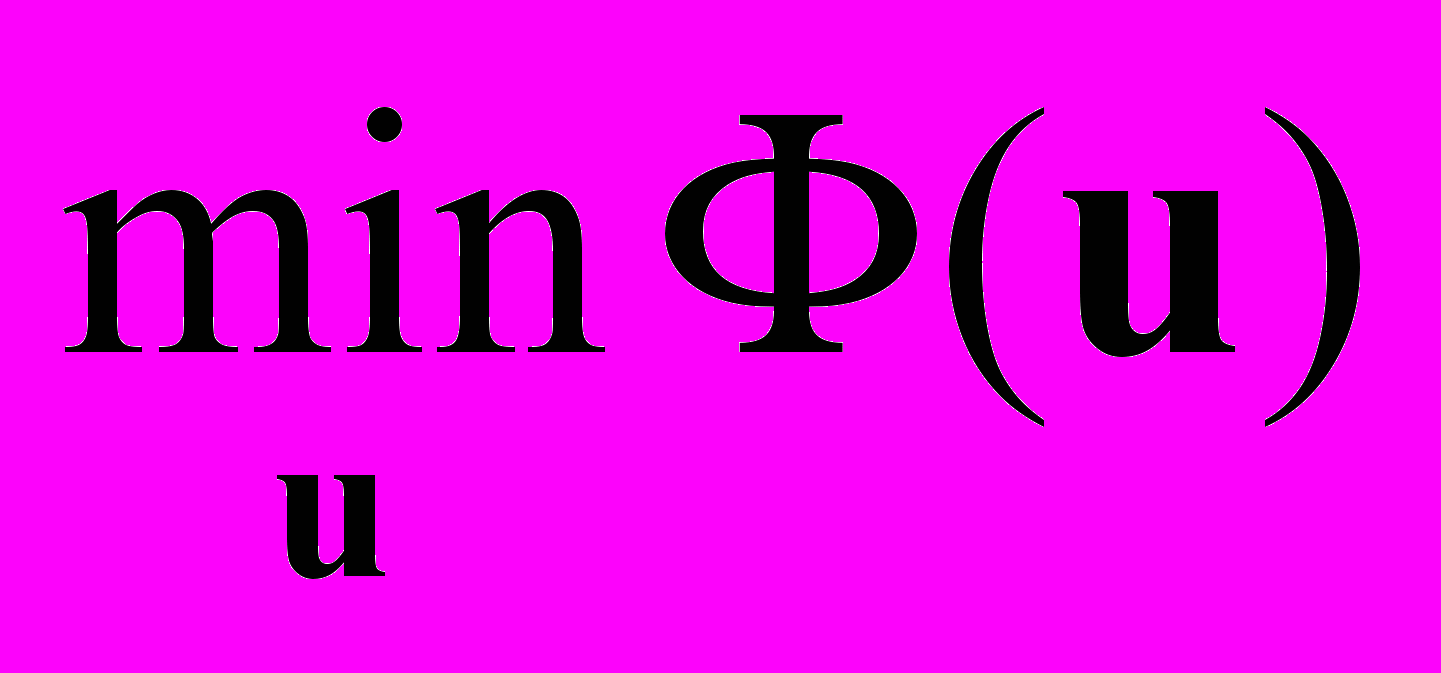. Докажем, что верно и обратное утверждение. Если элемент доставляет минимальное значение функционалу энергии, то он является решением системы линейных уравнений 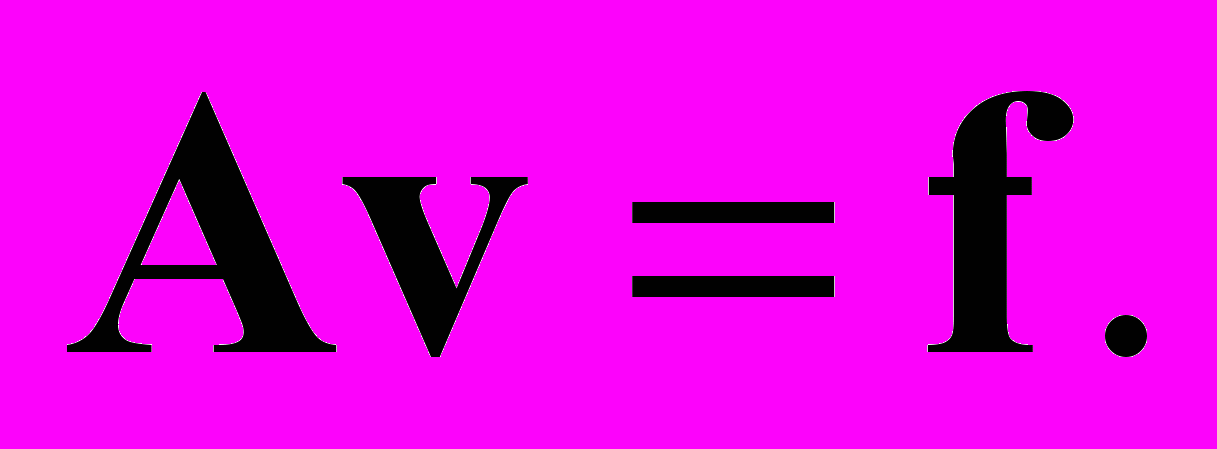Из курса математического анализа известно, что в точке минимума должно выполняться условие 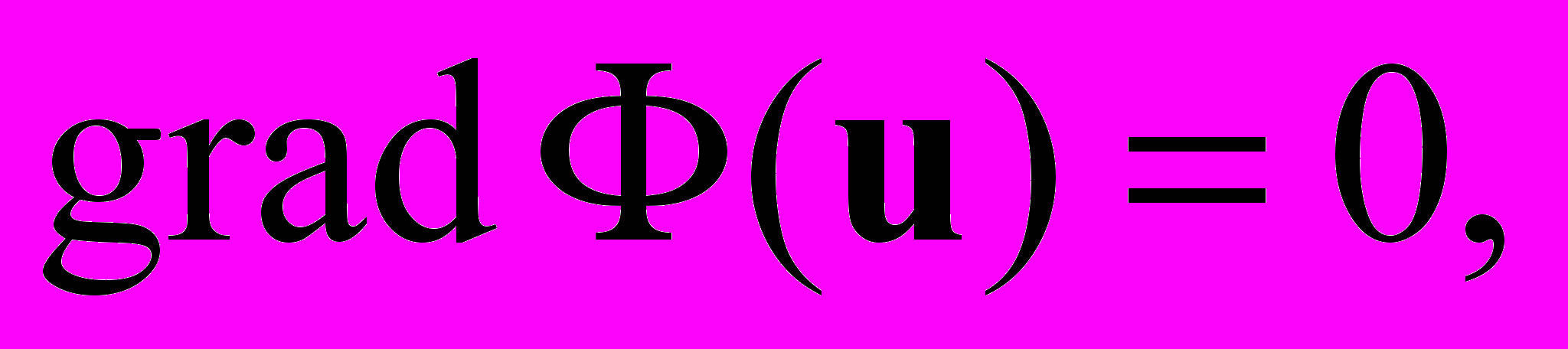A > 0. Вычисляя градиент, приходим к условию минимума функционала 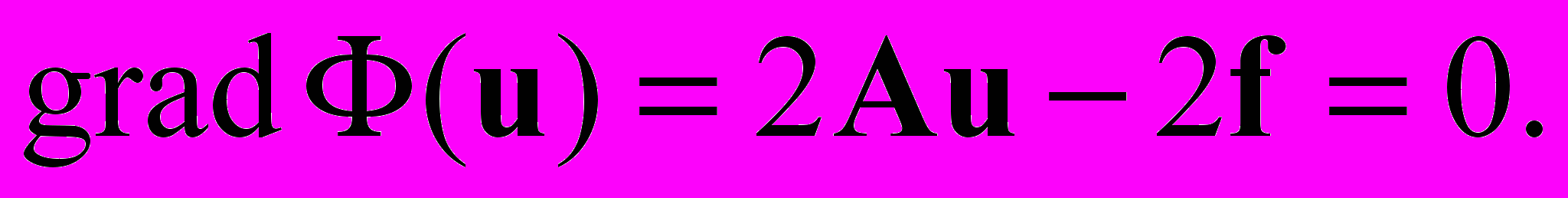Таким образом установлена эквивалентность вариационной задачи (отыскание элемента, придающего минимум Ф(u)) и задачи о нахождении решения СЛАУ.

Заметим, что СЛАУ с самосопряженным и положительно определенным оператором А представляют собой важный класс задач в математической физике, в частности, они возникают при решении краевых задач для эллиптических уравнений. При необходимости можно произвести симметризацию по Гауссу исходной системы.

2. Методы градиентного и наискорейшего спуска
   

Метод градиентного спуска состоит в нахождении следующего приближения в итерационном процессе из предыдущего, путем смещения в направлении градиента функционала

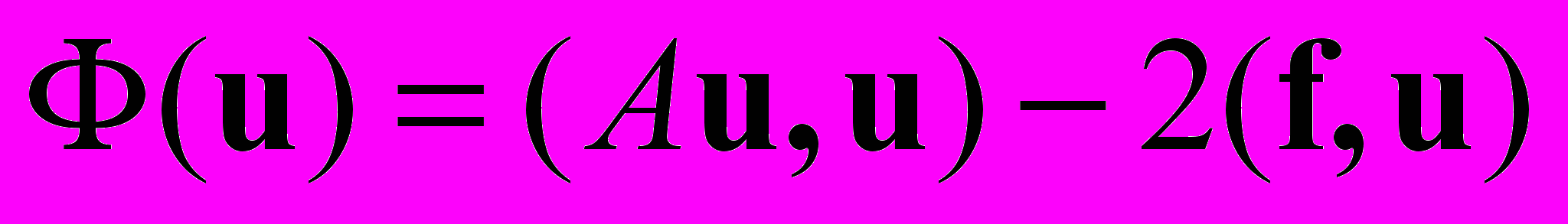(2.25)

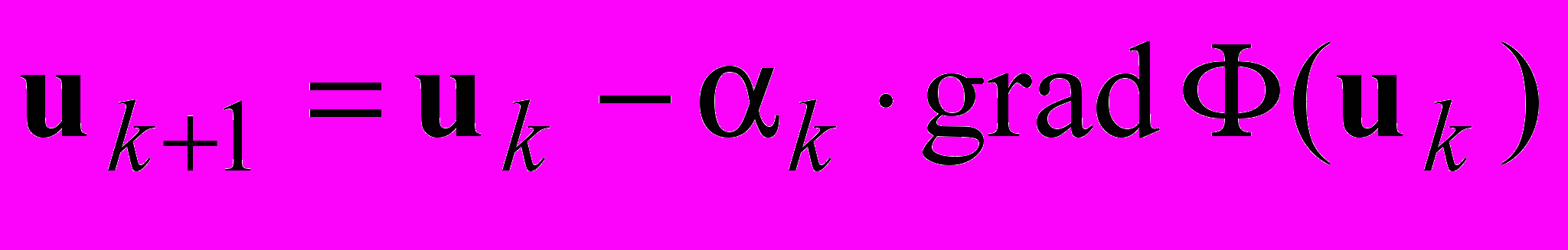, (2.26)

где А — положительно определенная симметричная матрица; α_k — параметр, определяемый из заданных условий; например, из условия минимума величины



В этом случае итерационный метод называется методом наискорейшего спуска.

Так как 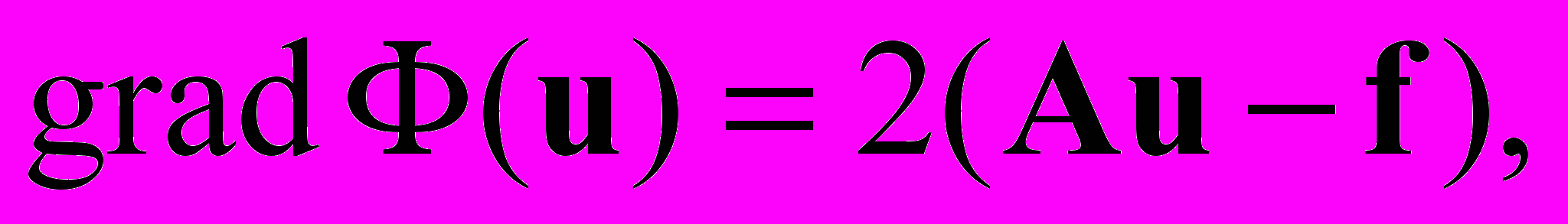то (2.26) приобретает вид

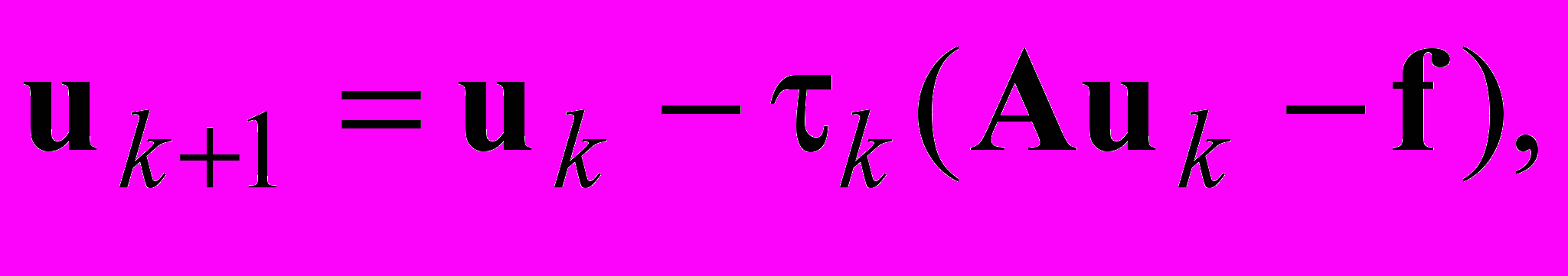где 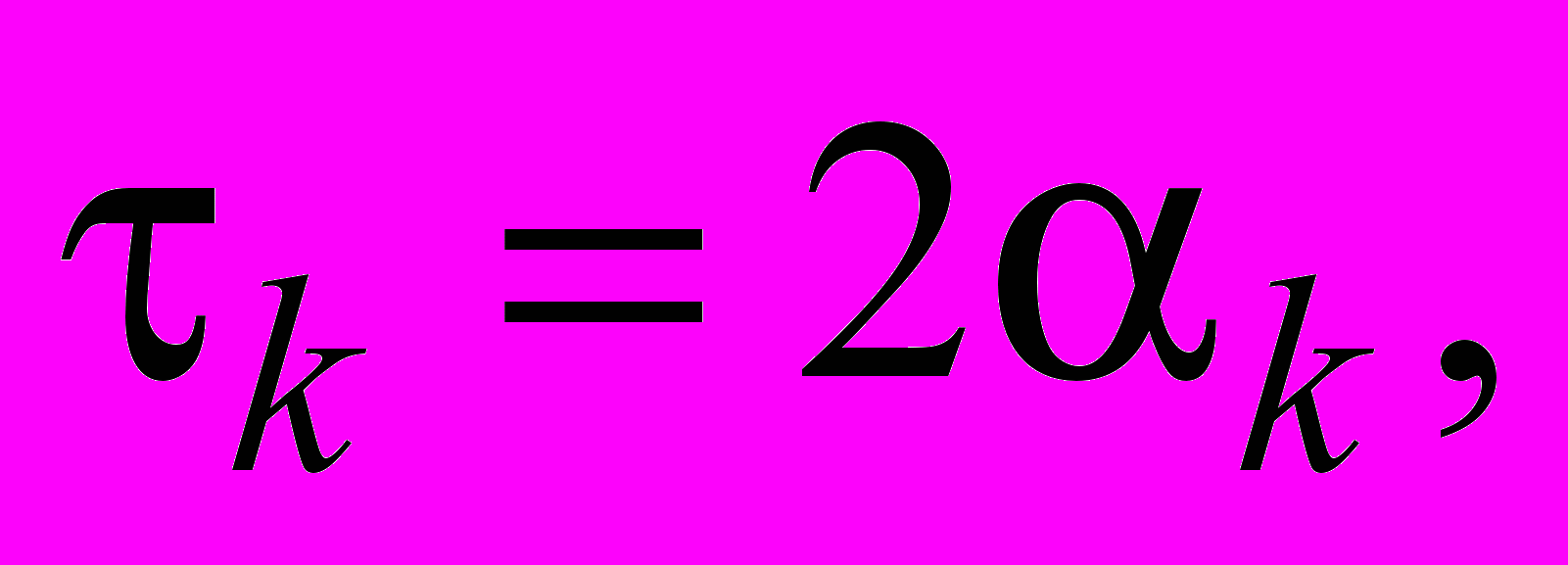(2.27)

что соответствует записи итерационного метода в форме (2.17). Здесь τ_k является итерационным параметром, который в методе наискорейшего спуска определяется из условия минимума функции 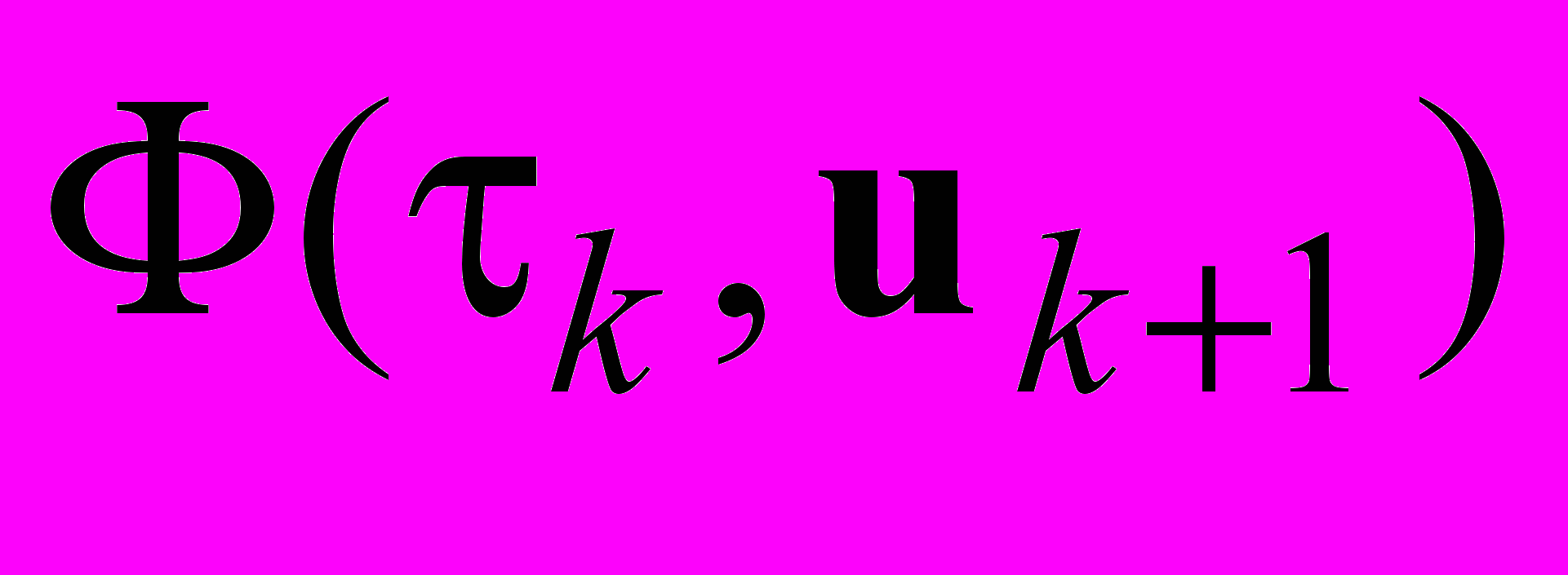по τ_k. Найдем условие этого минимума.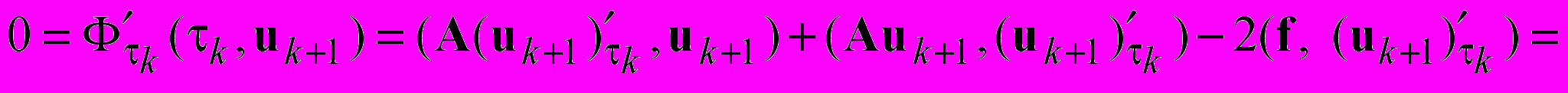





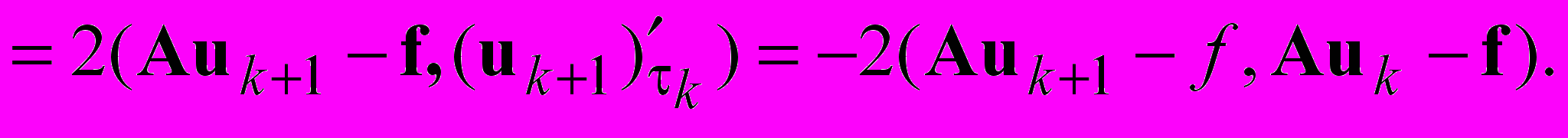
Здесь учтено соотношение: , поскольку и 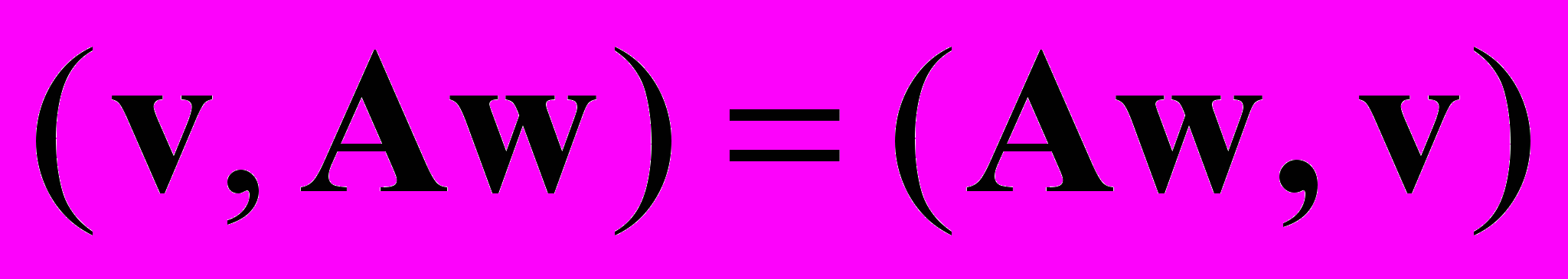в силу коммутативности оператора А. Подставим в последние равенства 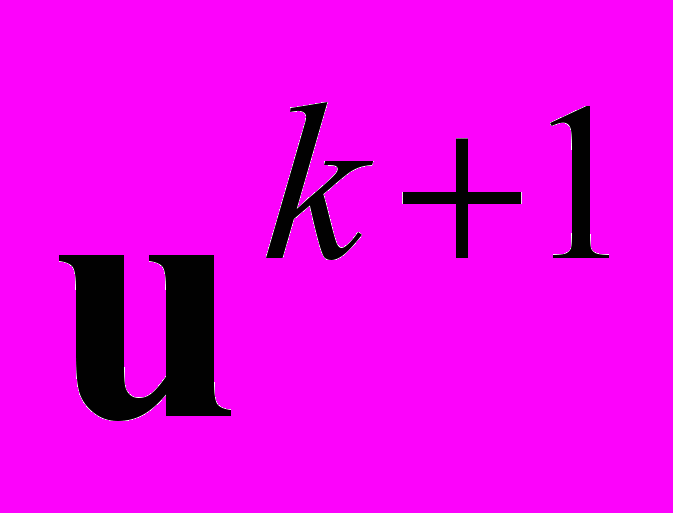из (2.27), получим 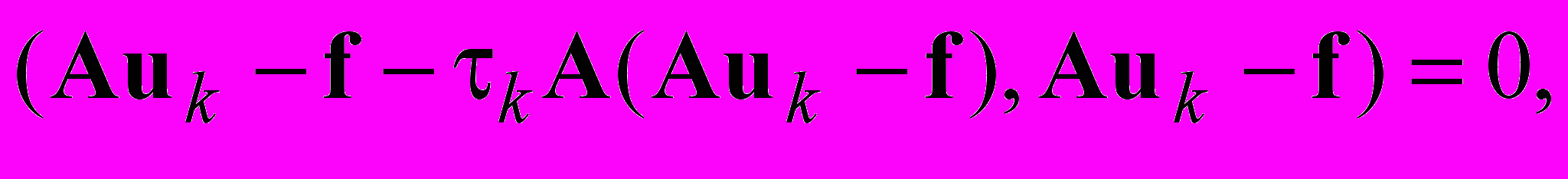откуда следует



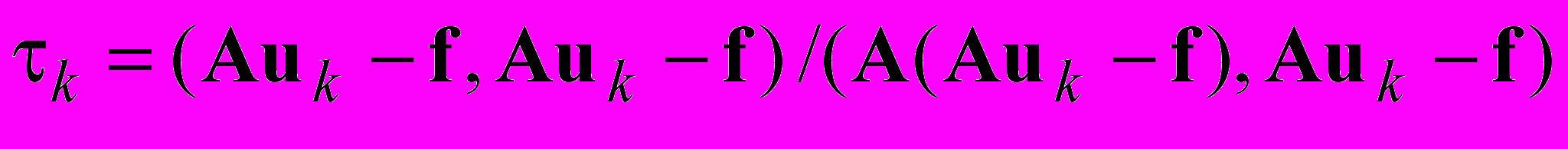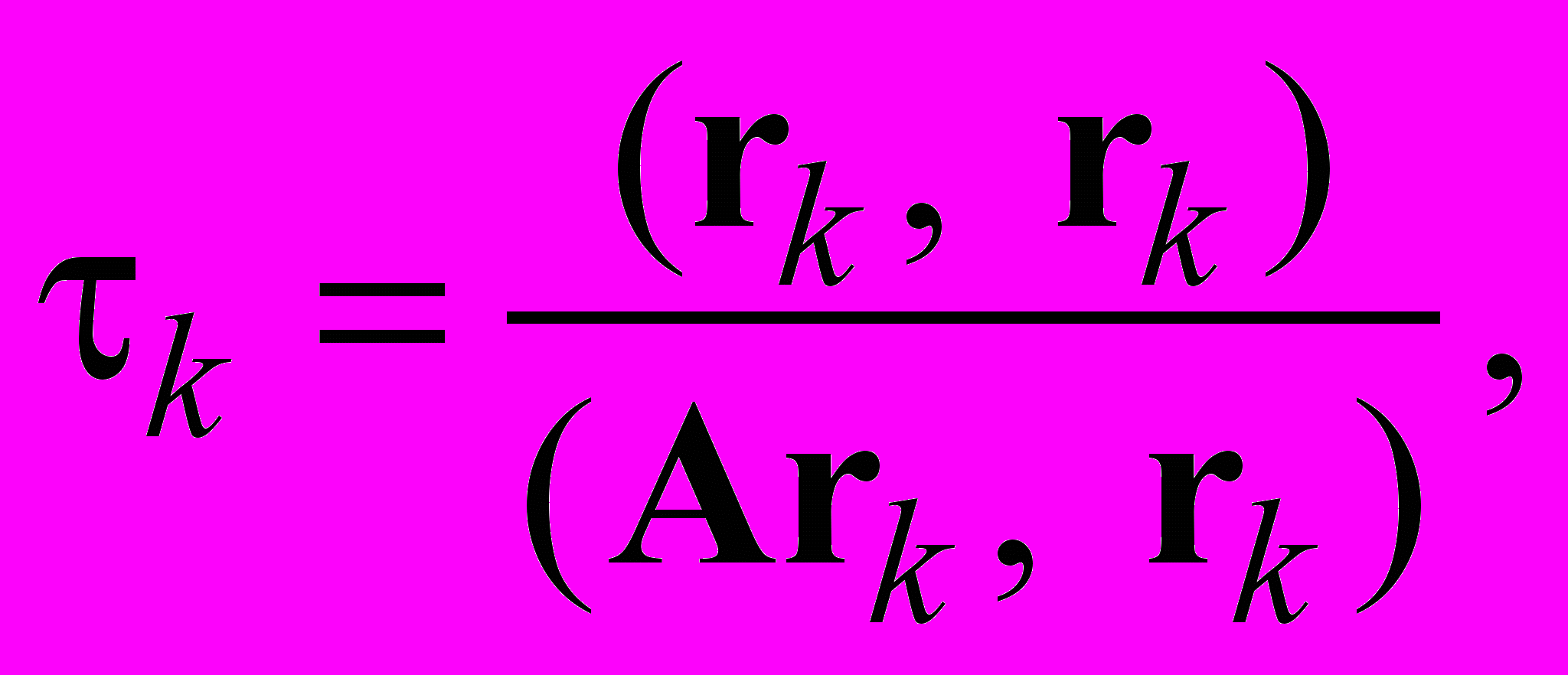, или где

Вектор r_k называют вектором невязки.

2.6.3. Метод минимальных невязок

Этот итерационный метод определяется следующим образом. Пусть

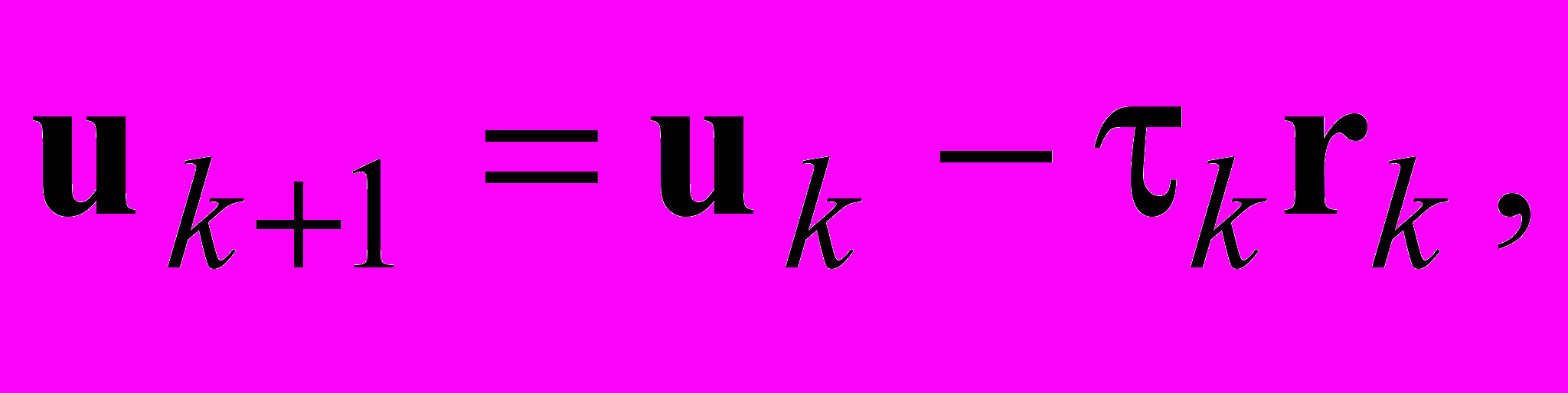как и ранее, 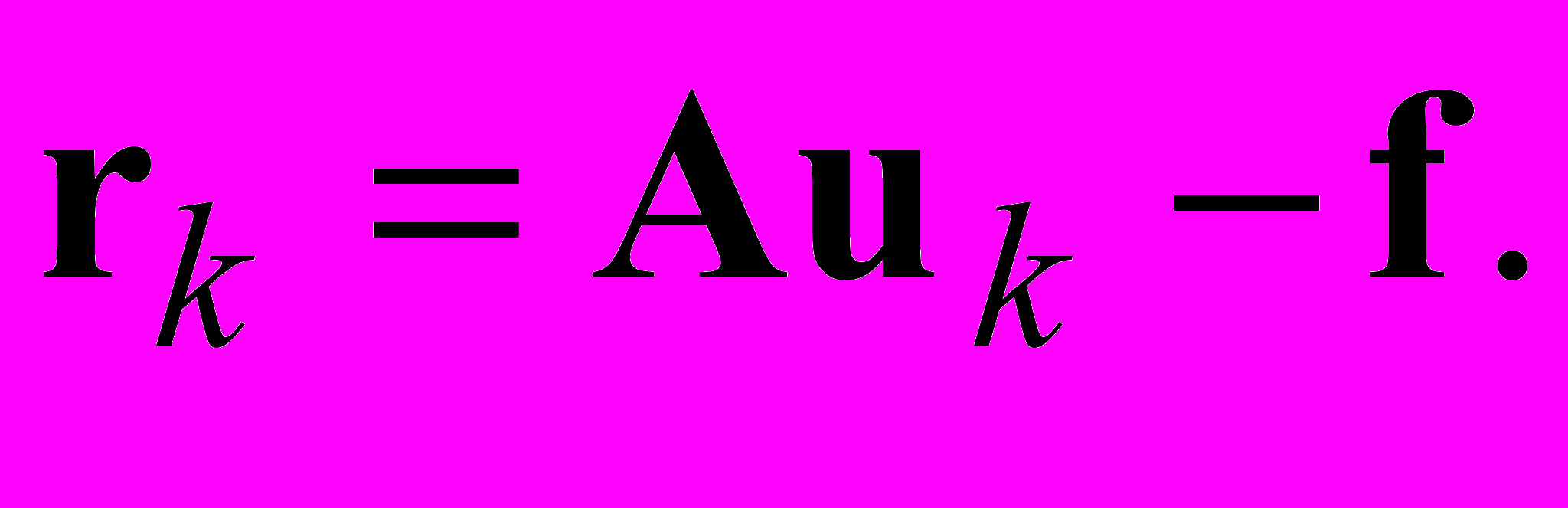Итерационный параметр τ_k на каждой итерации выбирается так, чтобы минимизировать, евклидову норму невязки 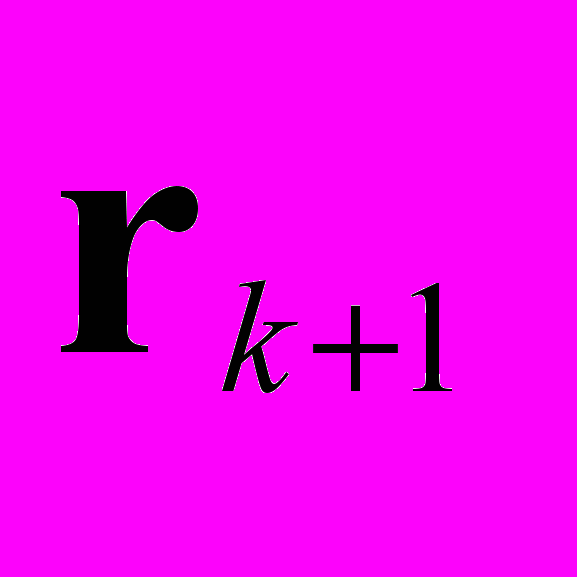. Заметим, что итерационный процесс может быть представлен в равносильном виде в терминах невязки 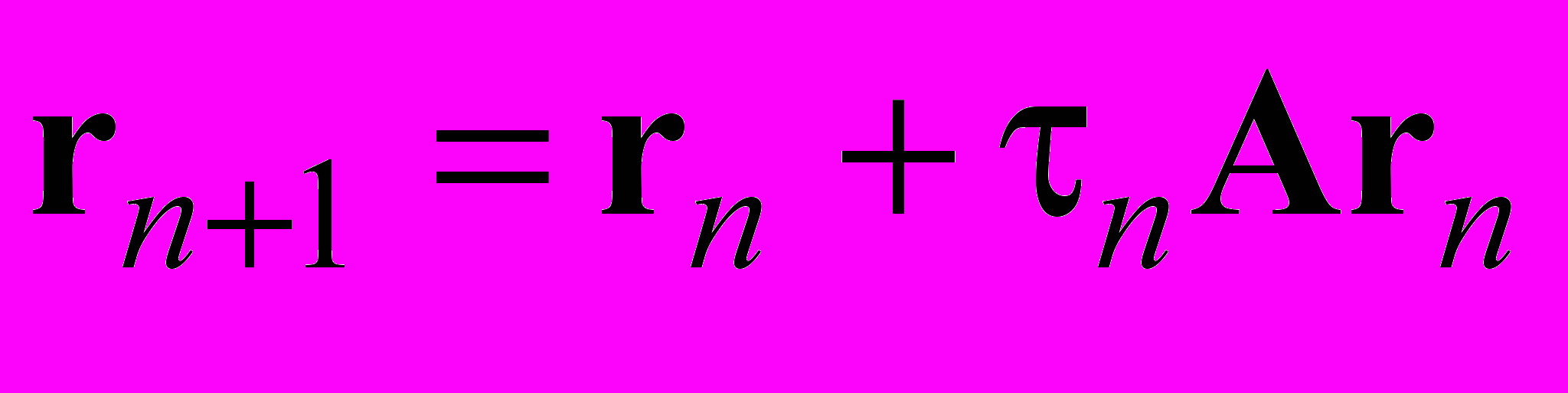. Тогда для квадрата евклидовой (третьей) нормы невязки получаем условие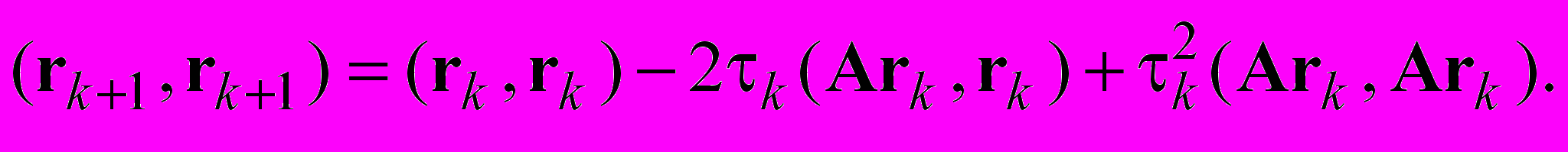



Для отыскания минимума невязки на следующей итерации приравняем нулю производную последнего выражения по итерационному параметру τ_k. Получим равенство

.

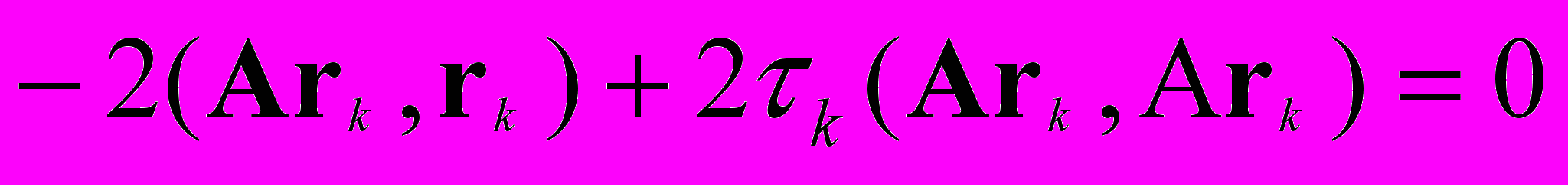Из последнего соотношения находим значение итерационного параметра

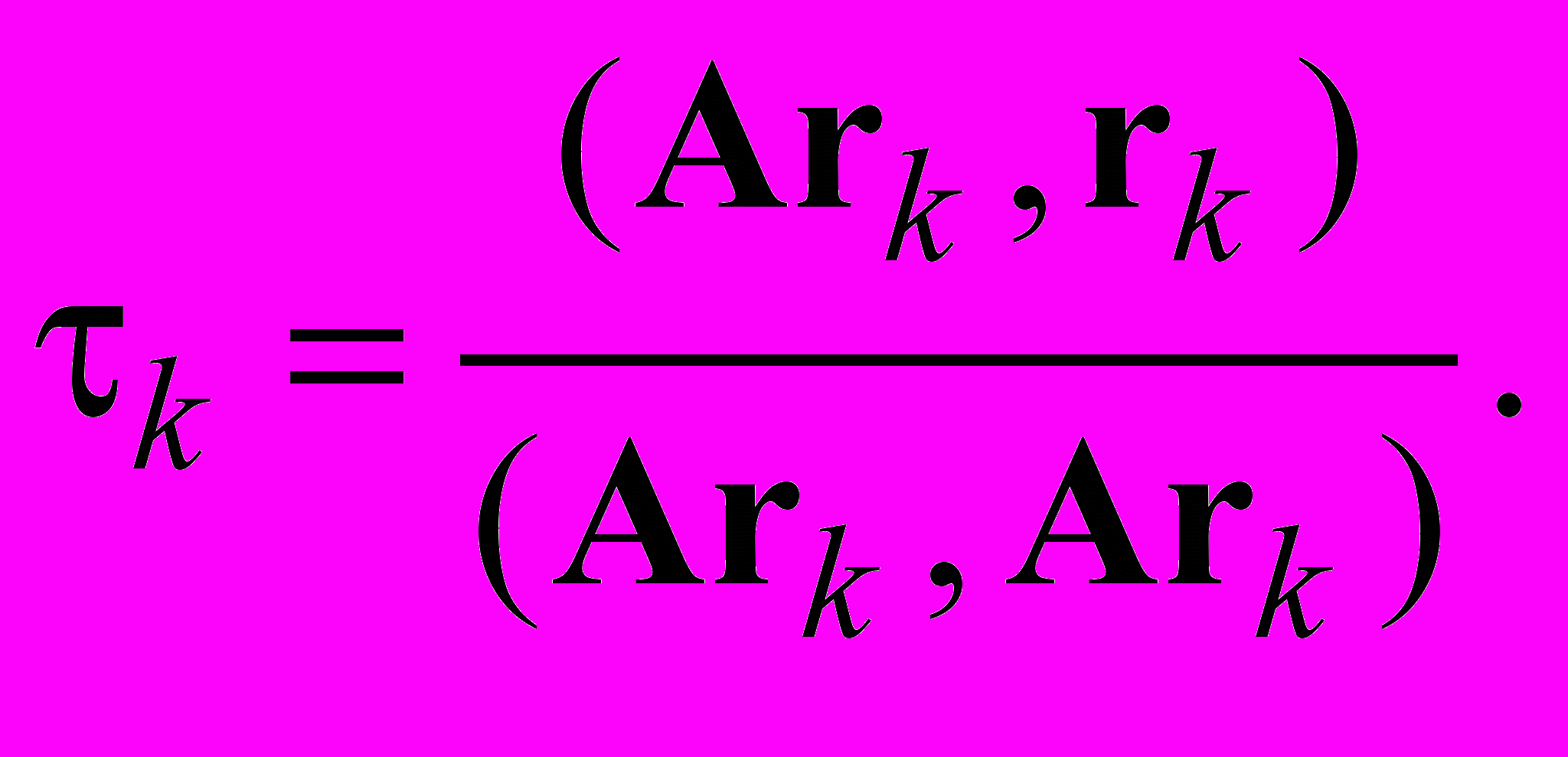
2.6.4 Метод сопряженных градиентов

Этот метод применяется для решения систем уравнений с самосопряженной положительной матрицей А = А* > 0.

Оптимизируем градиентный метод, выбирая параметры τ таким образом, чтобы на последующем шаге невязка была ортогональна всем предыдущим. На первом шаге ищем аналогично методу наискорейшего спуска. Получим невязки, образующие ортогональный базис. На последнем шаге невязка становится равна нулю, так как пространство конечномерно, и единственный элемент, ортогональный всем базисным векторам конечномерного пространства — нулевой. Получаем точное решение за конечное число шагов (прямой метод). Однако этот метод работает не всегда, так как при плохой обусловленности матрицы он становится вычислительно неустойчивым.

Идея метода состоит в следующем. Выбираем произвольное начальное приближение и вычисляем по нему вектор невязки 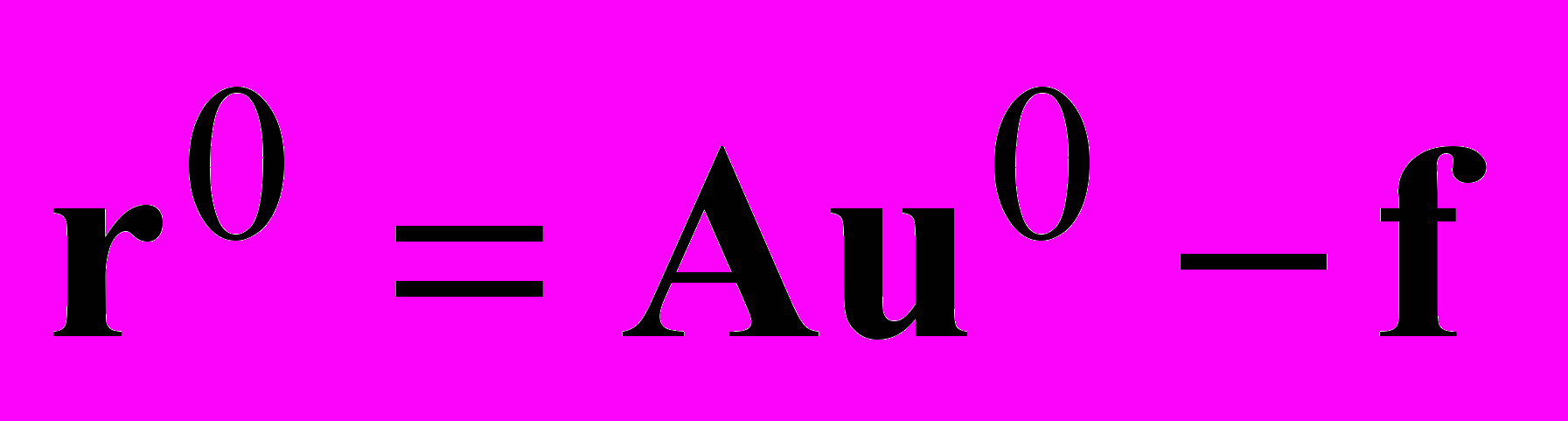, тогда первое приближение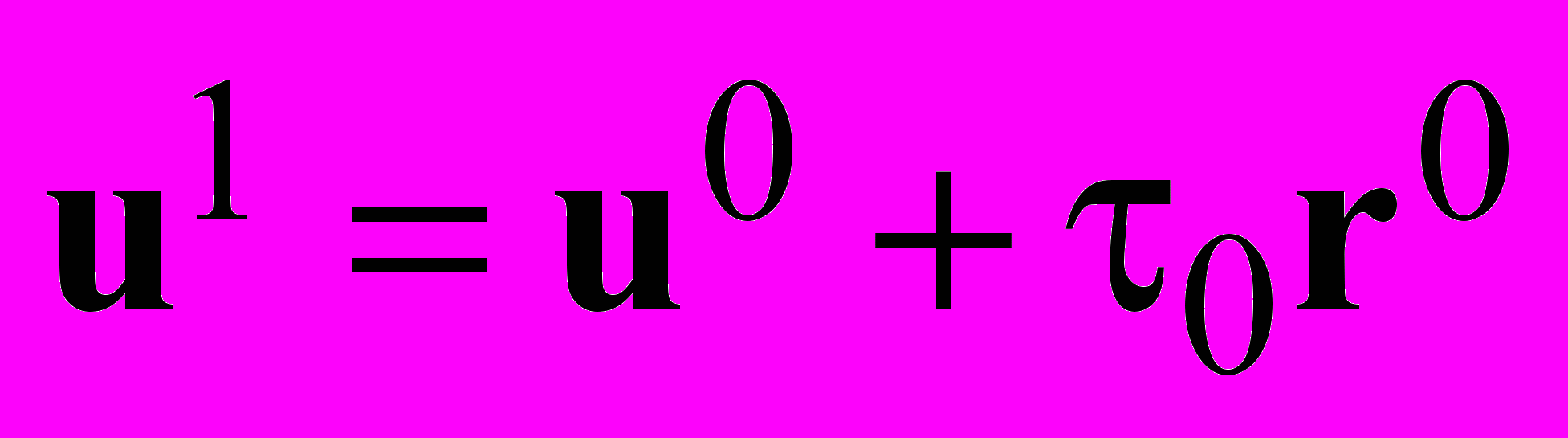

Из условия ортогональности невязок на двух первых шагах находим значение итерационного параметра

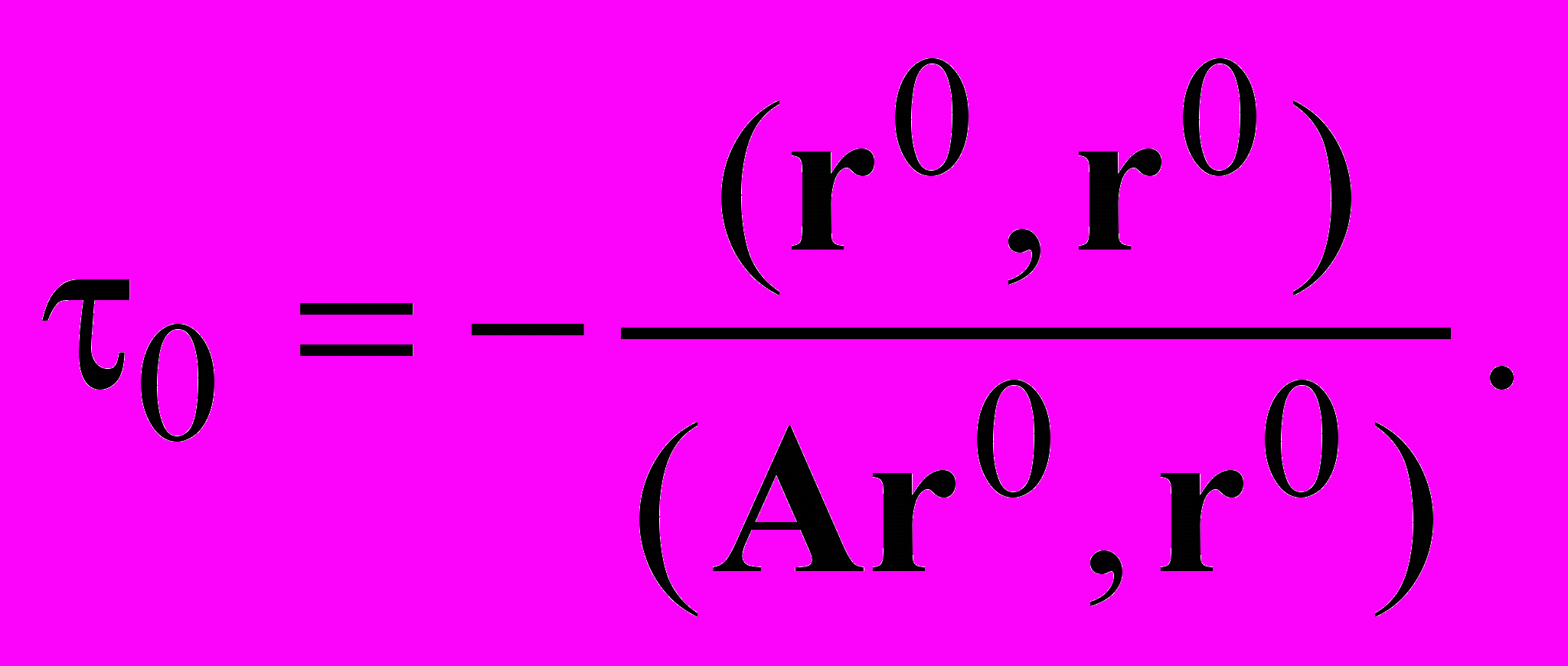
Построим такое приближение, чтобы учитывались две предыдущие — трехслойный итерационный метод. Фактически, при построении его применяется процесс ортогонализации Грамма – Шмидта.

Если 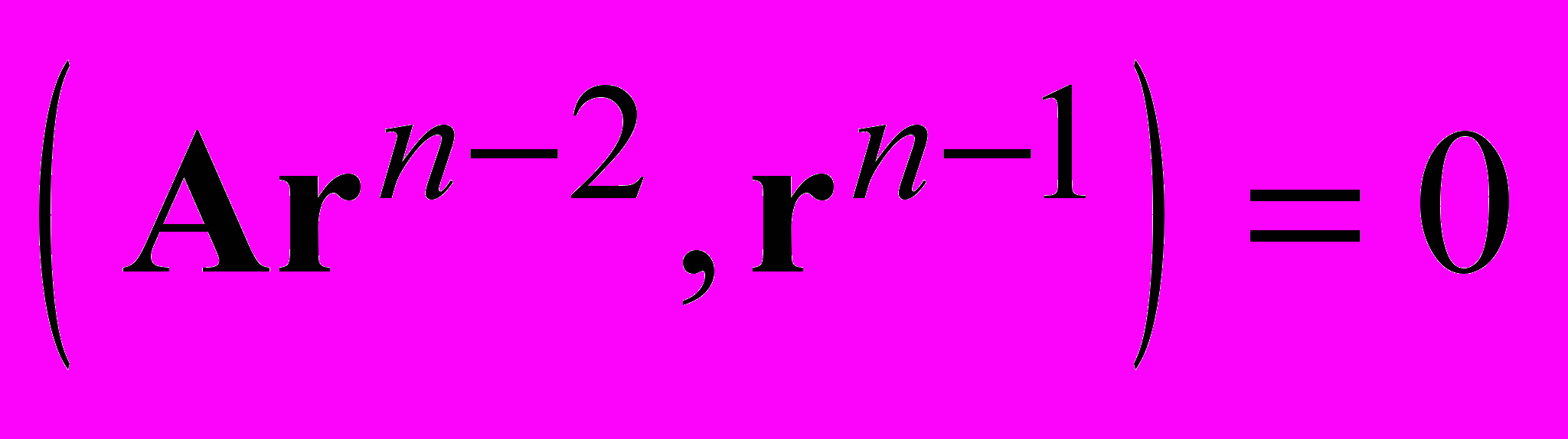, то 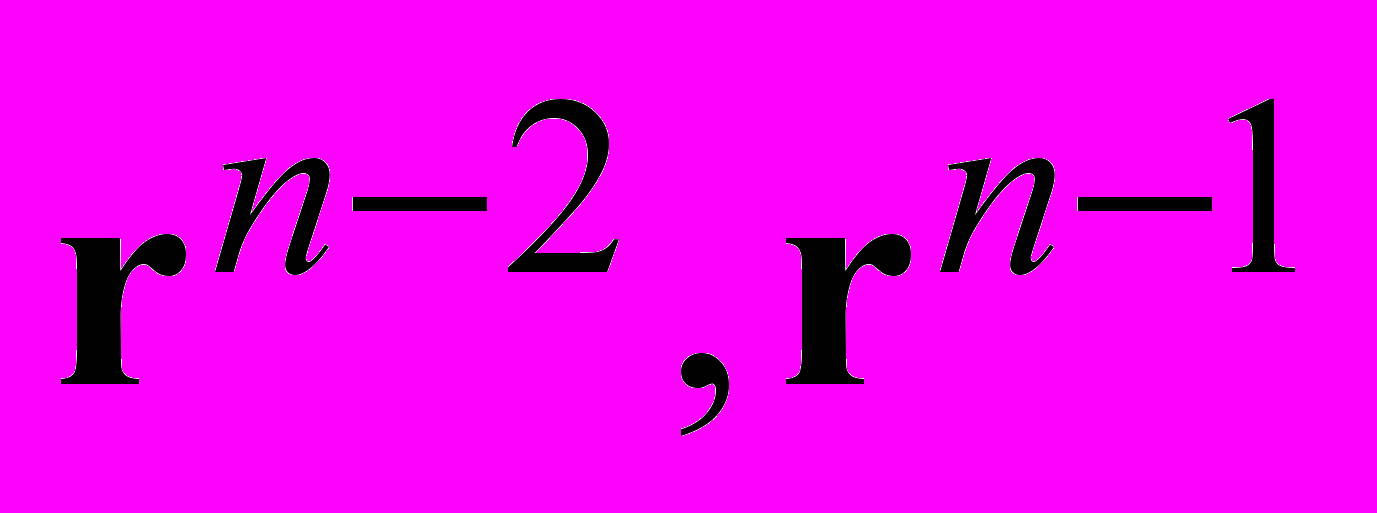— A-сопряженные невязки.

Имеем метод сопряженных градиентов.

Все невязки уменьшаются по норме, поэтому данный метод эффективен даже для плохо обусловленных задач, т.к. на определенном шаге можно оборвать вычисления и получить приближение к решению с заданной точностью. Тогда этот метод становится итерационным.

Приведем последовательность расчетных формул одного из вариантов метода сопряженных градиентов.



…

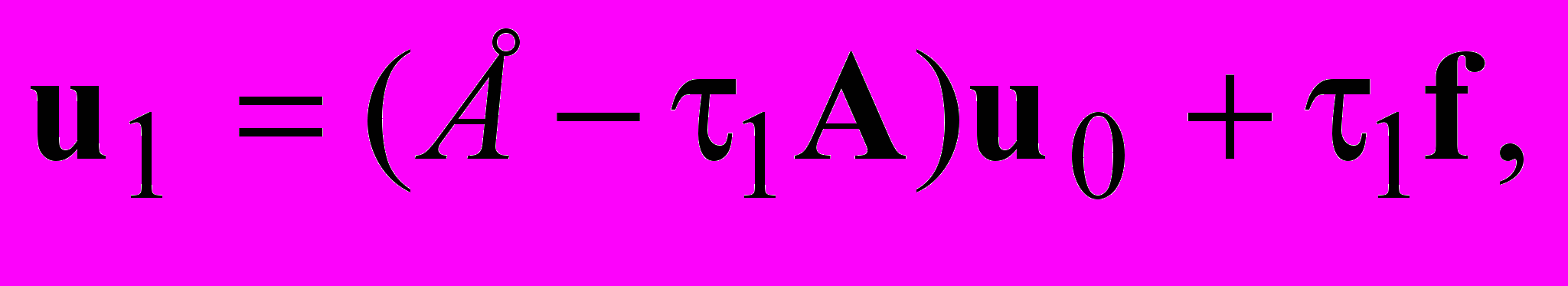
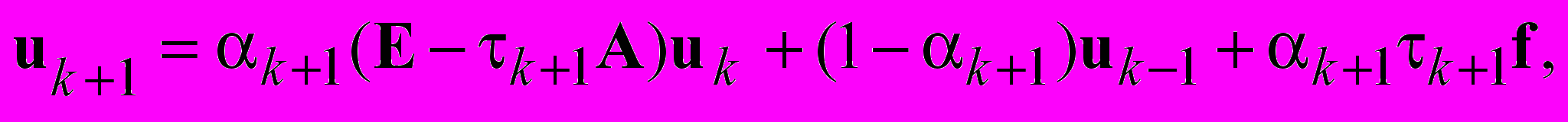(2.29)

где





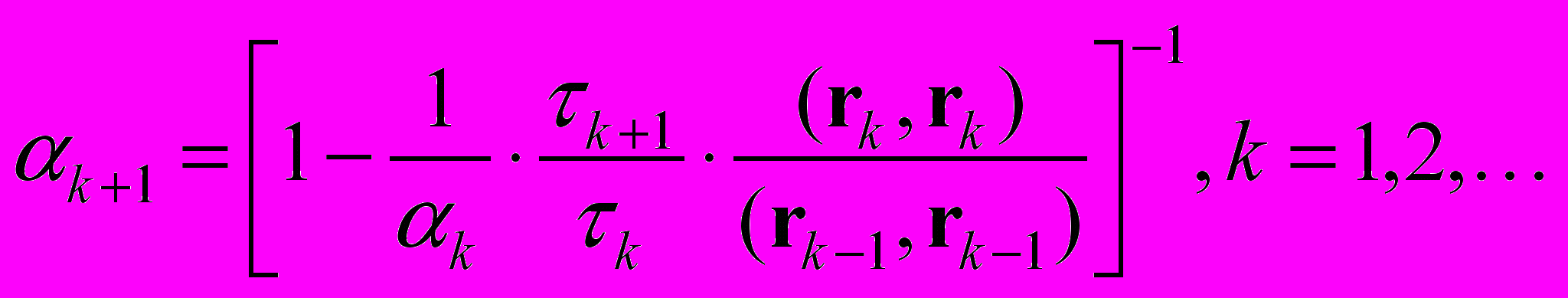
В вычислительной практике этот метод используется при умеренном числе обусловленности, больших n и неизвестных границах спектра матрицы А, как итерационный метод, поскольку k₀ обычно достаточно большое число. Подробнее о методах сопряженных градиентов можно прочитать в [2].

2.7 О спектральных задачах

Спектральные задачи — вычислительно наиболее трудоемкие задачи в прикладной линейной алгебре. Различают полную и частичную проблемы собственных значений. В первом случае необходимо отыскать ВСЕ собственные числа матрицы, во втором – лишь максимальное по абсолютной величине собственное число. Различают также самосопряженную спектральную задачу и задачу для произвольной матрицы. Очевидно, самосопряженная проблема решается проще — спектр самосопряженной матрицы всегда действительный.

Рассмотрим два алгоритма для самосопряженных матриц. Первый — степенной алгоритм, для вычисления наибольшего по абсолютной величине собственного числа. Выбираем произвольный ненулевой вектор u₀ и строим последовательность векторов



Легко показать, что выражение



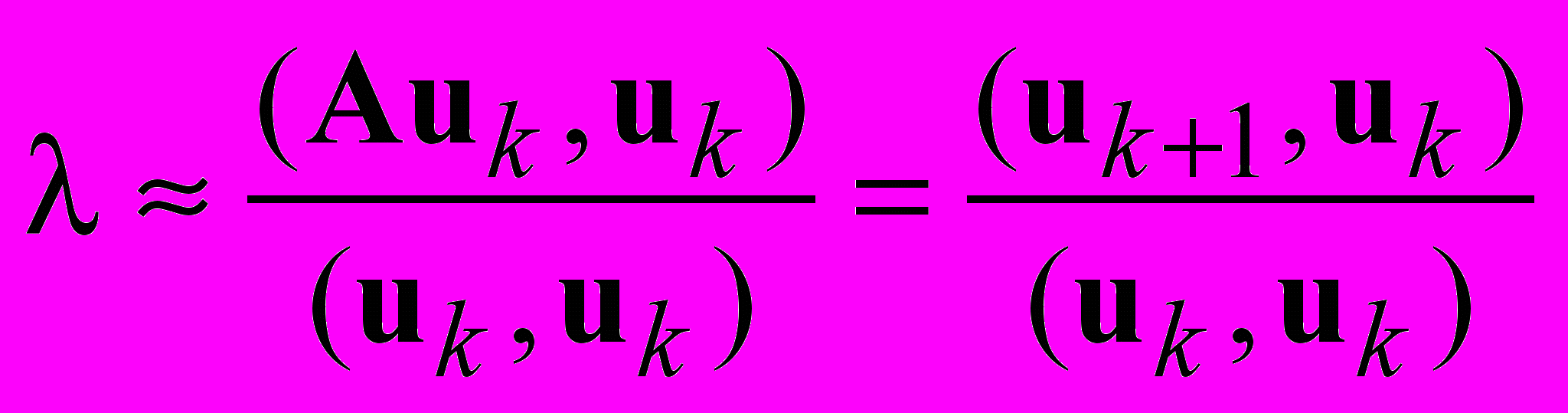
приближает максимальное по абсолютной величине собственное значение с точностью . Здесь 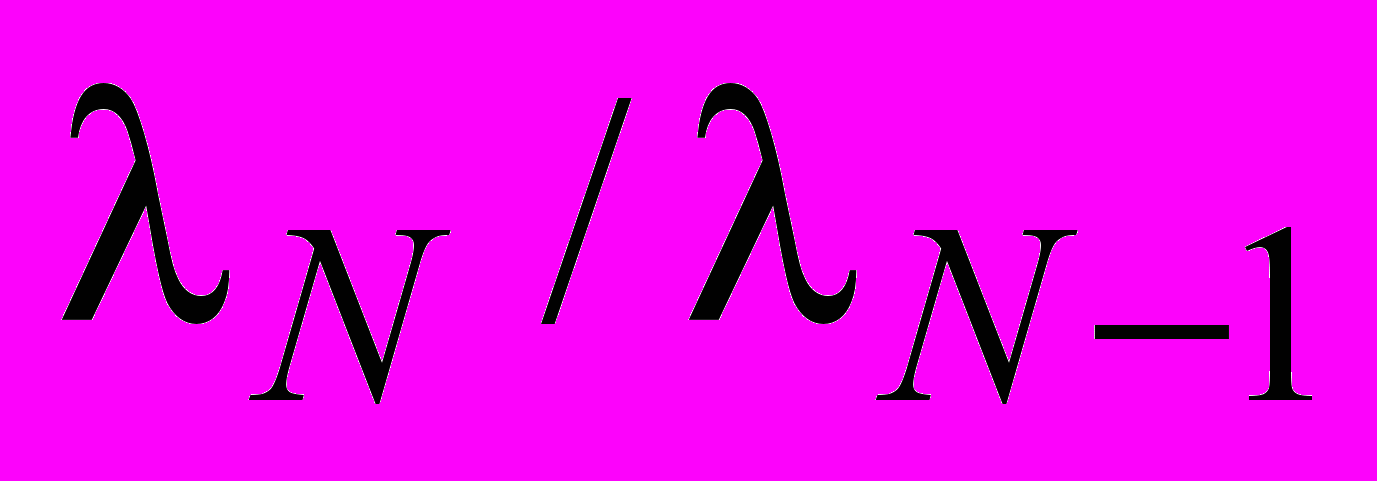— отношение самого большого по модулю собственного числа матрицы к следующему по абсолютной величине.

Для решения полной самосопряженной проблемы собственных значений применяется метод вращений.

Определение собственных значений самосопряженной матрицы A эквивалентно отысканию такой ортогональной матрицы T, что



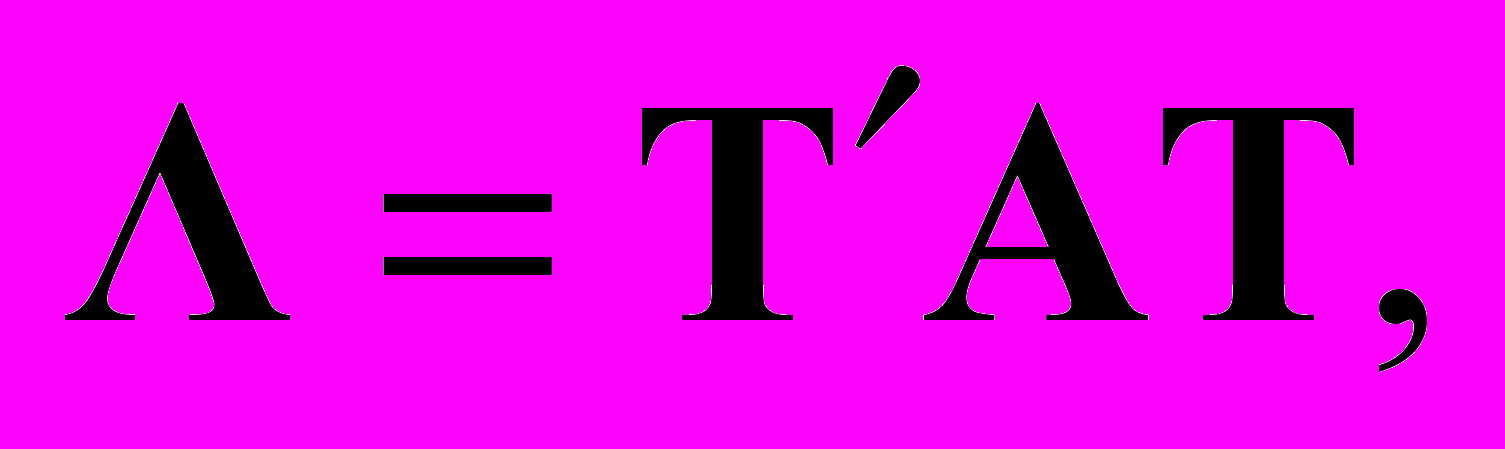
матрица Λ — диагональная.

Среди всех ортогональных преобразований данное минимизирует сумму квадратов внедиагональных элементов исходной матрицы. Построим итерационный метод, минимизирующий эту сумму на каждой итерации. Пусть каждое преобразование подобия на каждой итерации содержит лишь одну матрицу вращения

где матрица T_ij есть матрица поворота в плоскости u_i u_j на угол α. Эта матрица отличается от матрицы A только двумя строками и двумя столбцами (с номерами i и j). Так как евклидова норма матрицы не изменяется при ортогональных преобразованиях, то легко получить соотношение между суммами квадратов внедиагональных элементов старой и новой матриц: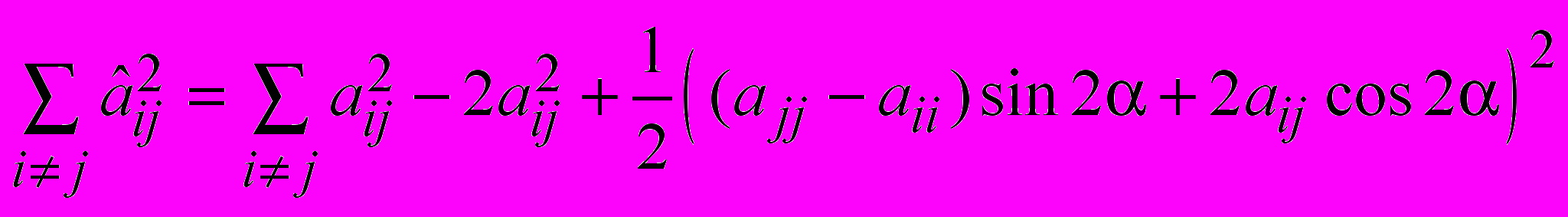



Очевидны условия минимизации суммы в левой части последнего равенства. Следует на текущей итерации выбирать индексы так, чтобы выполнялось условие 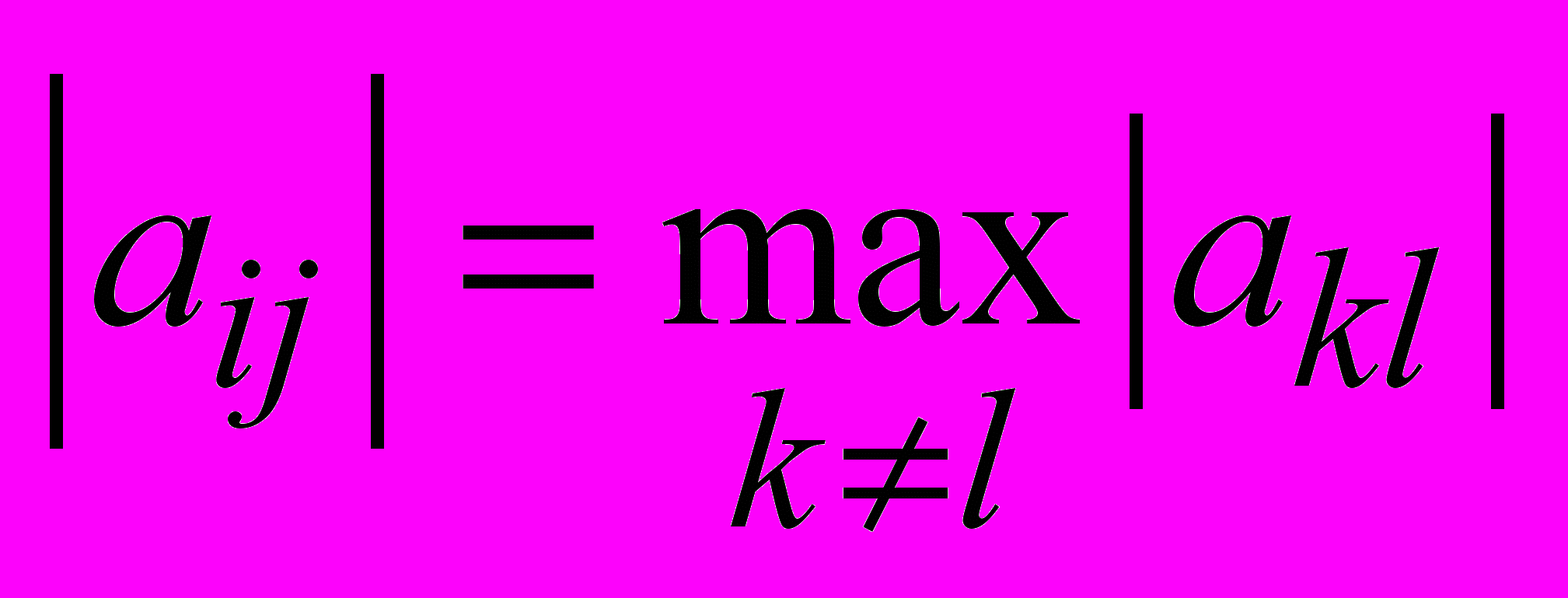, а угол поворота выбирается из условия 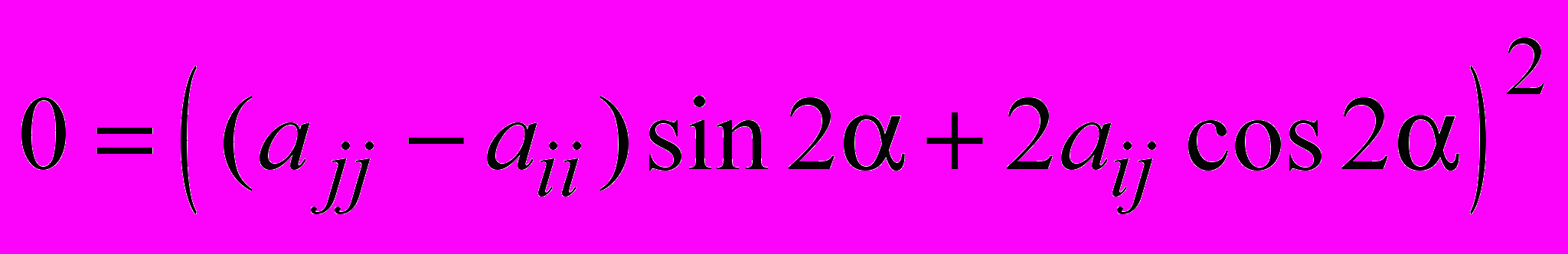. Тогда он удовлетворяет условию

Независимо от наличия кратных собственных значений метод вращений обладает квадратичной сходимостью.

Выбор максимального по модулю внедиагонального элемента — затратная операция, поэтому часто реализуется метод вращений с барьерами. Его идея состоит в следующем. При переборе внедиагональных значений вращение производится тогда, когда значение элемента по абсолютной величине превосходит некоторую величину (барьер). Если все элементы меньше барьера, его значение уменьшается, например, на порядок, и снова начинается циклический перебор внедиагональных элементов