Прогнозирование методом линейной статистической экстраполяции

Вид материала

Документы

Подобный материал:

• Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
• Методические указания к выполнению курсового расчёта на тему: «Анализ и моделирование, 58.09kb.
• Алгоритм решения системы n линейных уравнений методом Гаусса- зейделя представлен, 111.8kb.
• Официальные статистические издания, 2008 к читателям статистической информации, 2774.64kb.
• Задача 1 посвящена анализу линейной электрической цепи однофазного синусоидального, 157.7kb.
• Урок по теме «Линейная функция», 121.46kb.
• Контрольная работа выполняется на тему «Основные законы теории цепей, анализ установившегося, 35.6kb.
• Прогнозирование, 282.54kb.
• Учебно-методический комплекс для специальностей 080504 Государственное и муниципальное, 821.84kb.
• Порядка представления статистической информации, а равно представление недостоверной, 92.89kb.

Прогнозирование методом линейной статистической экстраполяции

Одним из наиболее распространенных методов прогнозирования является статистическая экстраполяция, в том числе линейная, т.е. распространение закономерностей, связей и соотношений, проявляющихся в изучаемом объекте (явлении) и действующих в наблюдаемом периоде за его пределы.

Экстраполяция базируется на следующих допущениях:

1) развитие явления может быть с достаточным основанием охарактеризовано плавной (эволюторной) траекторией — трендом;

2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем [20], т.е. предполагается определенная консервативность поведения явления.

Для экстраполяции характерно нахождение плавной линии, отражающей закономерности развития во времени или линии теоретического тренда. Тренд- это длительная тенденция изменения экономических показателей [21]. Под трендом обычно понимается основная составляющая динамического временного ряда, на которую накладываются другие составляющие, например сезонные колебания.

Экстраполяция на основе тренда включает:

• сбор информации по динамическому ряду показателя, характеризующего изучаемое явление, за прошлые периоды;
  
• выбор оптимального вида функции, описывающей указанный ряд путем его сглаживания и выравнивания (аппроксимация);
  
• расчёт параметров выбранной аппроксимационной функции;
  
• расчёт прогноза на будущее по выбранной функции путем ее экстраполяции.
  

Для прогнозирования была собрана статистическая информация о динамике численности приема аспирантов и докторантов по Брянской области за 2003-2007 годы. В процессе анализа статистических данных была выявлена монотонная тенденция изменения тренда в рассматриваемый период времени. В качестве тренда была принята линейная функция вида x_t = a + bt, где x_t –значение исследуемого параметра в t-ом году, t – порядковый номер года из рассматриваемого периода, a и b - коэффициенты регрессии прогнозной модели.

Для нахождения коэффициентов регрессии a и b были использованы следующие формулы (получены на основе имеющихся статистических данных методом наименьших квадратов):


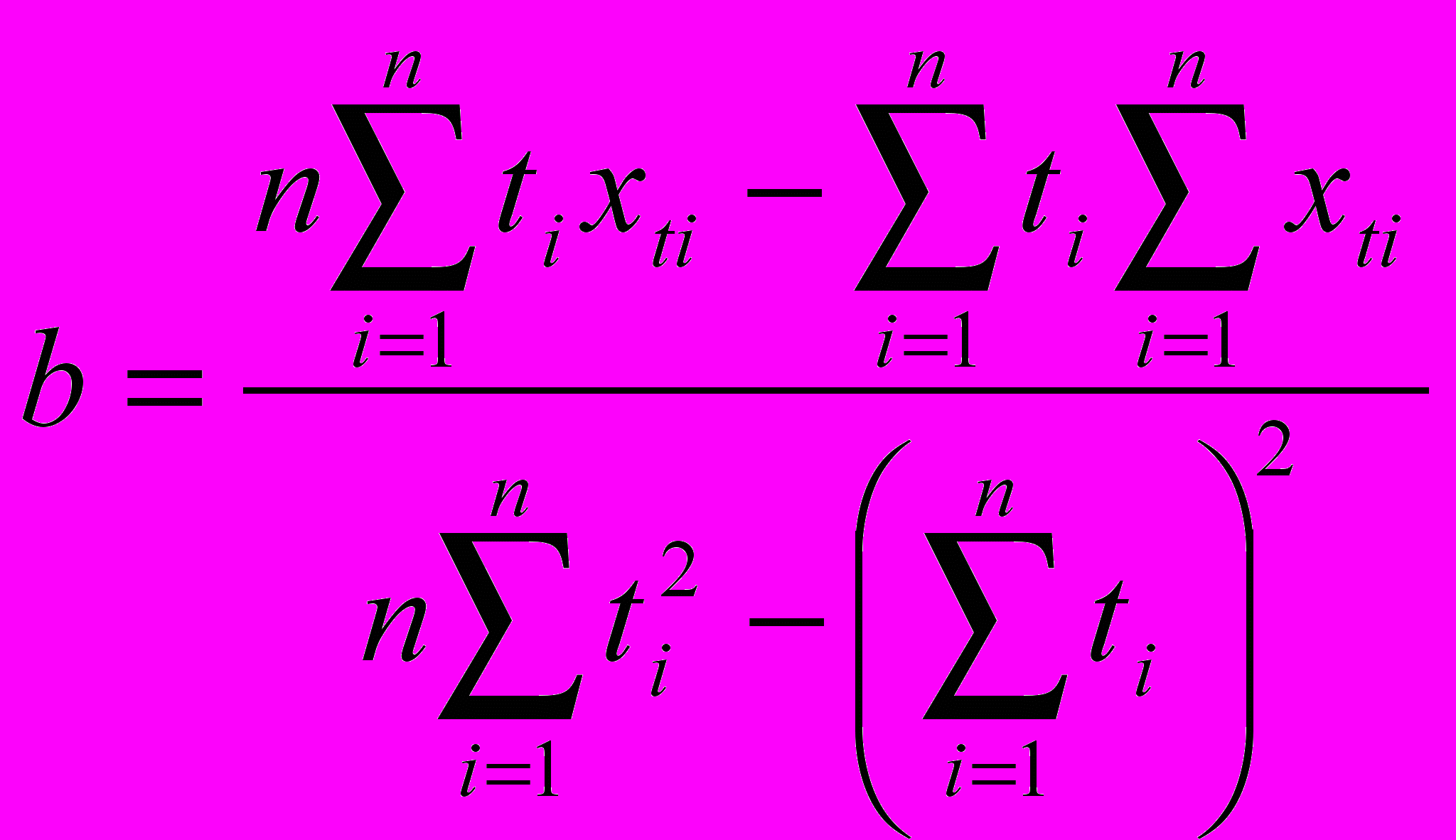, (4.2.1)

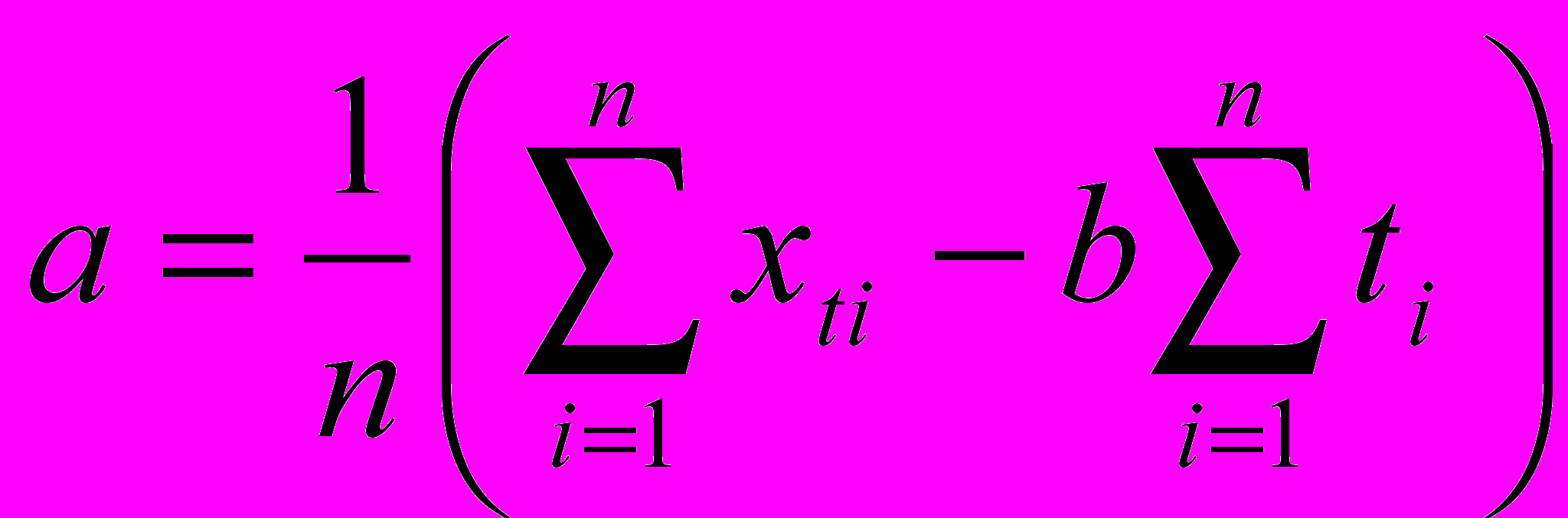, (4.2.2)

где n – число наблюдений, i – порядковый номер наблюдения [22].

Для вычисления расчетных (сглаженных) и прогнозных значений в полученное уравнение тренда следует подставить порядковый номер прогнозного года, начиная с первого года базисного периода.

Метод экстраполяции не дает однозначного прогнозного показателя, а представляется в виде интервала значений, называемого доверительным [23].

Доверительные границы для наиболее вероятного прогнозного значения при небольшом числе наблюдений определяются следующим образом:

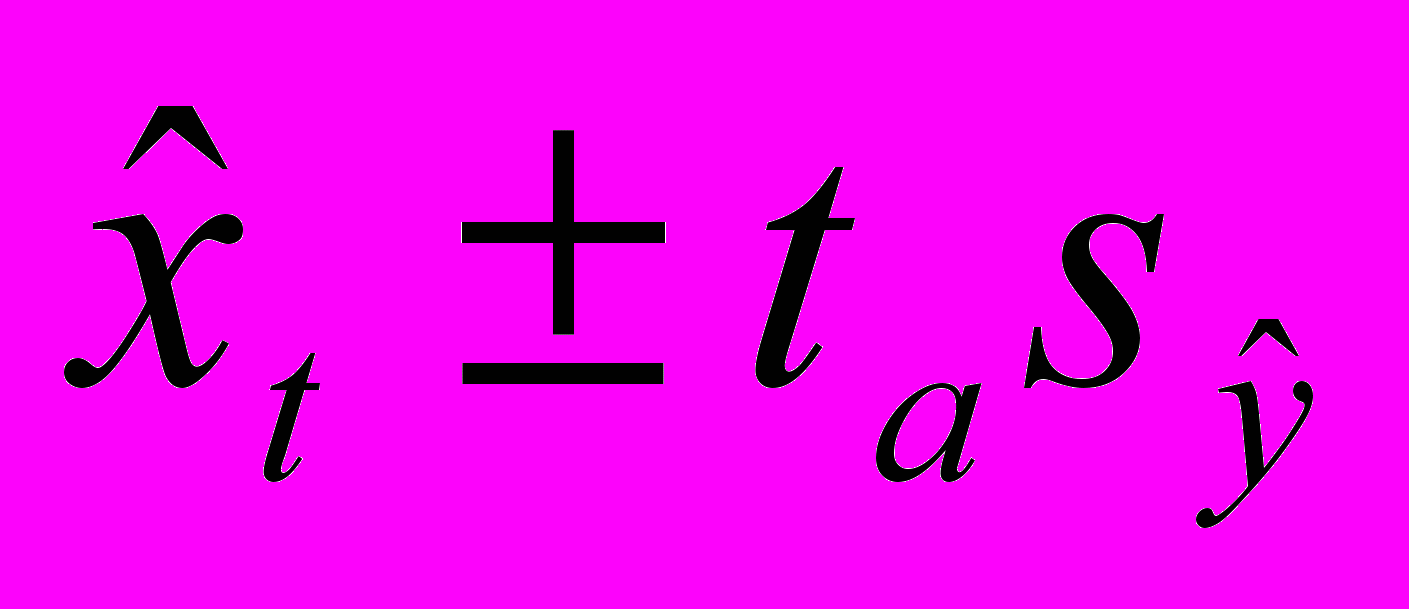, (4.2.3)

где t_a – табличное значение t – статистики Стьюдента с n-1 степенями и уровнем вероятности p; s_y - средняя квадратическая ошибка выборки. Значение ее определяется по формуле:

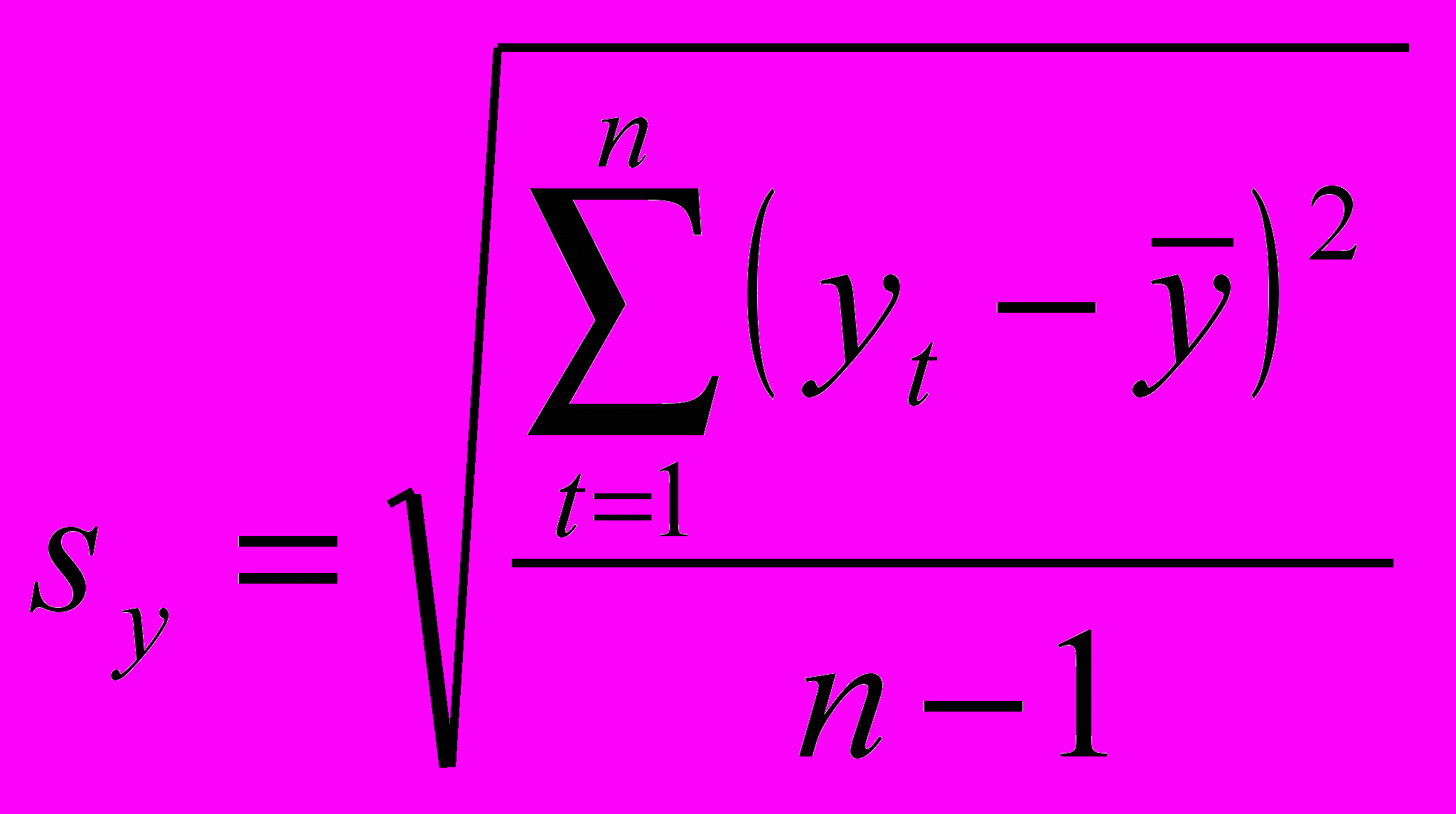, (4.2.4)

где y_t – фактические значения показателя.

Доверительный интервал, полученный как t_as_y, учитывает вероятность, которая связана с оценкой средней величины [21].

Данный подход был применен для расчета прогнозных значений численности приема аспирантов и докторантов по Брянской области. Исходные данные для моделирования приведены в прил.Г. В качестве первого года (i=1) рассматривался 2003 год. Во всех нижеприведенных моделях t_i – расчетный год.

Прогнозная модель зависимости численности приема аспирантов по Брянской области

(по статистическим данные Росгосстата)¹

x_ti=142,7 + 6,43t_i, (4.2.5)

где x_ti – численность приема аспирантов по Брянской области.

Таблица 4.2.1 - Характеристика модели

Наименование показателя	Значение
Объем исходной выборки	7 наблюдений
Коэффициент множественной корреляции	0,49
Коэффициент множественной детерминации	0,24
t-критерий для переменной, входящей в модель:	1.13<2.01 1,13
Табличное значение t-критерия	2,01

Несмотря на то, что некоторые из полученных моделей недостаточно надежны (см. значение t-критерия), они, тем не менее, за неимением других, до накопления значений более продолжительных динамических рядов, использованы для прогнозирования с целью сопоставления.

На основе приведенной модели получена следующая прогнозная информация.

Таблица 4.2.2 - Результаты прогнозирования численности приема аспирантов по Брянской области

Прогнозный год2	Нижняя граница доверительного интервала	Прогнозное значение численности приема аспирантов	Верхняя граница доверительного интервала
2011	160	200	239
2012	167	206	245
2013	173	212	252
2014	179	219	258

Справочно приводятся данные по моделированию численности приема аспирантов в области по данным Минобразования. Так как статистические сборники Минобразования не содержат информации о приеме в аспирантуру, был выполнен расчет общей численности аспирантов по Брянской области, прогнозные значения набора в аспирантуру были получены путем корректирования на коэффициент K_ПА,I, равный 0,37.


Прогнозная модель зависимости общей численности аспирантов Брянской области

(по статистическим данным Минобразования)³

x_ti=335,2 + 10,8t_i , (4.2.6)

где x_ti – общая численность аспирантов по Брянской области по статистическим данным Минобразования РФ.


Таблица 4.2.3 - Характеристика модели

Наименование показателя	Значение
Объем исходной выборки	5 наблюдений
Коэффициент множественной корреляции	0,56
Коэффициент множественной детерминации	0,32
t-критерий для переменной, входящей в модель:	1 1.19<2.01 ,19
Табличное значение t-критерия	2,01

Таблица 4.2.4 – Прогнозные значения общей численности и численности набора аспирантов

Прогнозный год	Нижняя граница доверительного интервала	Прогнозное значение общей численности аспирантов	Верхняя граница доверительного интервала	Прогнозное значение набора аспирантов
2011	386	432	479	160
2012	396	443	490	164
2013	407	454	501	168
2014	418	465	512	172

Статистические данные Минобразования РФ содержат преимущественно информацию о количестве научных работников, сосредоточенных в государственных вузах регионов, в то время как статистические данные Росгосстата включают в себя также численность работников научных организаций, численность научных и педагогических работников отраслевой напрвленности. Из сопоставления показателей табл.4.2.2 и 4.2.4 предположительно видно, что основной контингент научных работников сосредоточен в вузах и составляет примерно 75% от общей численности научных работников в области (см. также прил.П.2 и П.4). Остальные примерно 25% относятся к работникам других (преимущественно отраслевых) научных организаций, не входящих в ведомство Минобразования РФ. Представляется очевидным, что преподаватели-ученые, основным делом которых является учебный процесс, ведут научную деятельность попутно.

Прогнозная модель зависимости численности приема докторантов в Брянской области

(по статистическим данным Росстата)

x_ti=8,26 – 0,6t_i , (4.2.7)

где x_ti –численность приема докторантов по Брянской области по статистическим данным Росгосстата РФ.

Таблица 4.2.5 - Характеристика модели

Наименование показателя	Значение
Объем исходной выборки	6 наблюдений
Коэффициент множественной корреляции	0,50
Коэффициент множественной детерминации	0,25
t-критерий для переменной, входящей в модель:	- 1,16<1,94 1,16
Табличное значение t-критерия	1,94

Таблица 4.2.6 - Прогнозные значения численности приема докторантов

Прогнозный год	Нижняя граница доверительного интервала	Прогнозное значение	Верхняя граница доверительного интервала
2011	0	3	7
ё2012	0	2	6
2013	0	2	5
2014	0	1	5

Так как статистические сборники Минобразования не содержат информации о приеме в докторантуру, был выполнен расчет общей численности докторантов по Брянской области, прогнозные значения набора в докторантуру были получены путем корректирования на коэффициент K_ПА,I, равный 0,38.

Прогнозная модель зависимости общей численности докторантов в Брянской области

(по статистическим данным Минобразования)

x_ti=22,3 – 1,5t_i , (4.2.8)

где x_ti – общая численность докторантов по Брянской области по статистическим данным Минобразования РФ.

Таблица 4.2.7 - Характеристика модели

Наименование показателя	Значение
Объем исходной выборки	5 наблюдений
Коэффициент множественной корреляции	0,91
Коэффициент множественной детерминации	0,83
t-критерий для переменной, входящей в модель:	-3,96
Табличное значение t-критерия	2,01

Таблица 4.2.8 - Прогнозные значения общей численности и численности набора докторантов

Прогнозный год	Нижняя граница доверительного интервала	Прогнозное значение общей численности докторантов	Верхняя граница доверительного интервала	Прогнозное значение набора докторантов
2011	7	9	11	3
2012	5	7	9	3
2013	4	6	8	2
2014	2	4	6	2

Поскольку общие данные по прогнозируемой численности аспирантов и докторантов недостаточно конкретны для учета приоритетности научных проблем и критических технологий, представилось целесообразным уточнить их и перепроверить путем прогнозирования по отраслям наук. Статистические сборники Росгосстата по Брянской области не содержат информации о приеме в аспирантуру по отраслям наук, поэтому был выполнен расчет общей численности аспирантов отраслям наук по Брянской области, прогнозные значения набора в аспирантуру были получены путем корректирования на коэффициент K_ПА,I, равный 0,37.

Алгоритм определения прогнозной численности аспирантов в регионе с учетом приоритетных направлений развития науки и критических технологий РФ методом линейной экстраполяции приведен на рис.4.2.1.



















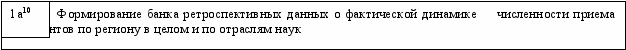
qqqqq⁴

















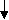
Продолжение рис.4.2.1

Рисунок 4.2.1 – Блок-схема алгоритма рассмотренного метода

Достоинства метода линейной статистической экстраполяции является отражение и использование показателей по реально протекающему процессу, «как он есть». В связи реально наблюдаемыми и отраженными статистикой процессами совместительства, штатного и внештатного, он представляет заниженные прогнозные данные.