Лекция 10
| Вид материала | Лекция |
- «Социальная стратификация и социальная мобильность», 46.19kb.
- Первая лекция. Введение 6 Вторая лекция, 30.95kb.
- Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
- Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
- Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
- Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
- Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
- Тема Лекция, 34.13kb.
- Лекция посвящена определению термина «транскриптом», 219.05kb.
- А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.
Лекция 10.
1. Роль и значение статистических методов в управлении качеством. Причины, сдерживающие применение статистических методов в практике отечественных предприятий
1.1 Введение
Необходимость использования статистических методов обоснована изменчивостью, наблюдаемой в процессе работы и влияющей на результаты производственной и коммерческой деятельности, даже при условии кажущейся стабильности. Такая изменчивость может проявляться в измерении характеристик продукции и процессов на различных этапах их жизненного цикла (начиная от исследования рынка и заканчивая реализацией готовой продукции).
Статистические методы помогают измерить, описать, проанализировать и смоделировать подобную изменчивость даже при наличии ограниченного объема данных. Статистический анализ данных может помочь при формировании лучшего понимания природы, сроков и причин изменчивости, а в дальнейшем - при решении и даже предупреждении проблем, связанных с такого рода изменчивостью.
Таким образом, статистические методы позволяют наилучшим образом использовать имеющиеся в распоряжении данные при принятии решений и улучшить качество продукции и процессов на стадиях проектирования, разработки, производства, поставки и технического обслуживания.
В настоящее время на отечественных предприятиях использование прикладной статистики инженерно-техническим персоналом, а тем более рабочими, встречается сравнительно редко. На это есть три основные причины.
Во-первых, традиционное понимание технологии приводит к тому, что большинство инженеров занимаются преобразованием материалов и энергии. Они не понимают важности преобразования, осмысления и использования информации.
Во-вторых, традиционное техническое образование построено на принципе “точности”. Со студенческих лет точность расчета конструкции, точность обработки, измерения в сознании специалиста становится главным фактором. Отклонения признаются нежелательными, а поскольку они нежелательны, то срабатывает ортодоксальный принцип: отклонений не должно быть, значит их быть не должно. Это тем более удивительно, что все же производственники прекрасно видят и понимают, что бездефектных технологий и производств нет и быть не может.
Неопределенность всегда присутствует в производственных процессах, действиях людей, функционировании машин, станков, приспособлений и инструмента, качества материалов и комплектующих изделий и т.п. “Вскрыть”, выявить, обнаружить закономерность этой неопределенности может только статистика, при условии корректного и осмысленного се применения. Статистика помогает различать случайные н систематические отклонения, а также выявить их причины. При этом на первый план выходит умение находить, контролировать отклонения (дефекты, брак) выявлять те причины брака, которые подлежат устранению, Только в этом случае с браком (отклонениями, несоответствиями) можно бороться осмысленно н приближаться к концепции точности. (Можно четко проследить полную аналогию с медициной. При лечении любого недуга его степень определяется именно величиной отклонения от нормы, а сам метод лечения целиком н полностью определяется причиной недуга.)
В-третьих, большинство специалистов не имеют опыта обработки эмпирических данных н не могут на основании конкретных наблюдений сделать общие выводы. Стереотип производственного мышления на сегодняшний день сложился так, что фактор интеллекта сведен практически к нулю. Производственные проблемы зачастую решаются с ориентацией только на данный момент времени, что приводит к тяжелым, порой непоправимым, последствиям. Традиции такой работы нужно ломать “с позиции силы” и это, прежде всего, должны понимать руководители.
Статистика существенно помогает решать традиционные инженерные и производственные проблемы. Она облегчает обработку, анализ и использование информации. Семь статистических методов анализа (схема Исикава, диаграмма Парето, гистограмма и др. — см. тему 6 в таблице) помогают представить данные в удобном для обобщения и анализа виде. Применение этих методов позволяет сделать достоверные и корректные выводы, получить большую определенность в поиске причин выявления неполадок н, следовательно, большую конкретность и эффективность разрабатываемых мероприятии по устранению этих причин.
Неоценимым преимуществом применения статистики и производственной практике является быстрое снижение издержек. Например, в компании “Хьюлетт Паккард” с помощью статистических методов были установлены оптимальные характеристики работы оборудования в различных условиях. Была получена информация для использования этого оборудования. Результатом десяти месяцев работы, основанной на анализе процесса с помощью статистических методов, явилось резкое снижение брака: с 9 тыс. дефектов на миллион изделий до 45 дефектов на миллион. В этой же компании, но в другом случае, были достигнуты еще более впечатляющие результаты: всего лишь после семи недель статистических исследований и реализации корректирующих мер брак снизился с 36 тыс. Дефектов на миллион изделий до 1 500. Поэтому широкое распространение статистических методов в деятельности зарубежных фирм (идеолог – Э. Деминг), а также широкое использование этих методов в стандартах ИСО серии 9000 вполне закономерны и не вызывают удивления.
В настоящее время нам необходимо переосмыслить узаконенные, рутинные методы работы, ориентированные нередко на стихийное решение сиюминутных проблем. В качестве альтернативы следует наращивать широкое применение статистических методов всеми специалистами, включая рабочих, направленное на профессиональное выявление и последовательное устранение узких мест. А для этого необходимо выполнить, по крайней мере, три условия:
- провести обучение методам прикладной статистики (семь методов анализа и выборочный контроль) всех работающих;
- создать поддерживаемые руководством предприятия официальные установки, требующие применения этих методов;
- морально и материально поощрять работников, применяющих методы прикладной статистики для решения производственных проблем, высказывать официальное одобрение их деятельности.
Применение семи методов анализа способствует повышению качества, снижению брака, а следовательно, резкому упорядочению производства, снижению издержек и себестоимости. Применение методов статистического (выборочного) контроля также даст ощутимые экономические и организационные преимущества.
К. Исикава утверждает, что “95 % всех проблем фирмы могут быть решены с помощью этих семи принципов. Они просты, однако без них невозможно владеть более сложными методами. В Японии применение этих методов имеет большое значение. Ими пользуются без всякого труда даже выпускники средних школ”. Американский ученый А. Фейгенбаум также считает обязательным применение на производстве статистических методов анализа и выборочного контроля.
1.2 Характеристика статистических методов
| № | вид метода | содержание, цель |
| | ведомость сбора данных | систематический учет ситуации в виде конкретных данных |
| | гистограмма | упорядочение данных в соответствии с периодичностью появления (например, во временном выражении) |
| | Парето-анализ | упорядочение фактов по значимости |
| | стратификация | расслоение данных различного происхождения |
| | диаграмма «причины-действия» | анализ источников возникновения основных проблем (человек, машина, материал, метод...) со ссылкой на воздействие проблемы |
| | диаграмма корреляции | вывод закономерностей и связей из информационного материала |
| | карточка регулирования качества | постоянный контроль, работает ли процесс в пределах заданного допуска |
| | описательная статистика | Цель – количественная оценка характеристик полученных данных, метод основывается на аналитических процедурах, связанных с обработкой и предоставлением количественных данных |
| | анализ измерений | Набор процедур для оценки точности измерительной системы в условиях ее работы |
| | построение доверительных интервалов | Процедура определения допусков, основанная на достоверность действий, совершенных с помощью статистического распределения измерений |
| | анализ возможностей процесса | Возможности процесса являются оценкой изменчивости процесса, находящегося в состоянии статистической устойчивости (оценкой являются индексы воспроизводимости) |
| | проверка гипотез | Статистическая процедура проверки обоснованности гипотезы, рассматривающей параметры одной или нескольких выборок с определенными уровнями доверия |
| | регрессионный анализ | Связывает поведение изучаемой характеристики с потенциальными причинами |
| | анализ надежности | Использование инженерных и аналитических методов для решения проблем надежности. Это касается оценки, прогноза и предупреждения случайных отказов с течением времени |
| | выборочный контроль | Систематических статистический метод для получения информации о характеристиках совокупностей путем изучения представительной выборки (статистический приемочный контроль, выборочное обследование) |
| | моделирование | Совокупность процедур, помощью которых теоретическая или эмпирическая система может быть представлена математически в виде компьютерной программы для поиска решения проблем |
| | анализ временных рядов | Анализ временных трендов представляет набор методов для изучения последовательных во времени групп наблюдений |
| | планирование экспериментов | Используются преднамеренные измерения в исследуемой системе, включается статистическая оценка этих изменений в данной системе. В результате появляется возможность определить основные характеристики системы или исследовать влияние одного или нескольких факторов на эти характеристики системы. |
1.3. Простые неформализованные методы системного анализа и методы японских групп качества
Группы качества, естественно, предполагают использование таких методов решения возникающих проблем, которые основаны в первую очередь на коллективных усилиях. Во многих фирмах, к примеру, практикуют метод “мозгового штурма” и его разновидности.
1.3.1 “Мозговой штурм”.
Цель: получение максимального количества предложений
Алгоритм проведения:
-
1. стадия формирования идей
- анализ критериев деловой игры
- составление перечней вопросов
- анализ критериев деловой игры
-
2. стадия разъяснения
- изучение перечня проблем для лучшего понимания
- изучение перечня проблем для лучшего понимания
-
3. стадия проведения оценки
- анализ перечня для исключения повторов и несоответствий
- анализ перечня для исключения повторов и несоответствий
Правила проведения деловой игры:
- Четко устанавливать цель
- Каждый может выступать по очереди или идеи могут выражаться спонтанно
- Предлагать по одной идее
- Не обсуждать идеи
- Учитывать идеи остальных
- Регистрировать все идеи, ..... для членов группы
1.3.2 Метод Делфи.
Цель: выбрать из серии альтернатив лучшую.
Алгоритм проведения:
-
1. ранжирование проблемы
- на первое место каждый ставит ту альтернативу, которую считает самой главной, на пятое – самую второстепенную
- на первое место каждый ставит ту альтернативу, которую считает самой главной, на пятое – самую второстепенную
-
2. оценка альтернатив
- каждая альтернатива оценивается по 10-балльной шкале в зависимости от издержек, связанных с той или иной причиной дефекта; высший балл здесь – единица, низший — десять
- составляется таблица расчетов (см. ниже пример таблицы)
- каждая альтернатива оценивается по 10-балльной шкале в зависимости от издержек, связанных с той или иной причиной дефекта; высший балл здесь – единица, низший — десять
-
3. получение результатов
- результаты по каждой альтернативе перемножаются и находится сумма их произведений
- наименьшая сумма указывает на причину, которую надо устранить в первую очередь
- результаты по каждой альтернативе перемножаются и находится сумма их произведений
Таблица расчетов.
| Фамилии участников обсуждения | Альтернативы | ||||||||||||||
| | 1 | 2 | 3 | 4 | 5 | ||||||||||
| | Р | Б | П | Р | Б | П | Р | Б | П | Р | Б | П | Р | Б | П |
| А | 4 | 7 | 28 | 3 | 4 | 12 | 1 | 1 | 1 | 2 | 3 | 6 | 5 | 10 | 50 |
| Б | 5 | 2 | 10 | 3 | 6 | 18 | 2 | 7 | 14 | 1 | 10 | 10 | 4 | 4 | 16 |
| В | 2 | 8 | 16 | 1 | 1 | 1 | 4 | 3 | 12 | 3 | 4 | 12 | 5 | 2 | 10 |
| Г | 5 | 10 | 50 | 4 | 5 | 20 | 3 | 4 | 12 | 2 | 3 | 6 | 1 | 1 | 1 |
| Сумма произведений | | | 104 | | | 51 | | | 39 | | | 34 | | | 77 |
Р – ранговая оценка (от 1 до 5); Б – оценка в баллах (от 1 до 10); П – произведение Р*Б.
Согласно расчетам, четвертая альтернатива – с суммой 34 – оказалась той самой причиной, которую надо устранить в первую очередь. Результаты подсчета безоговорочно принимаются всей группой.
1.3.3 Методы групп качества
Метод “черного ящика”. Решение проблем на основе данного метода осуществляется посредством анализа конкретных ситуаций, которые подбираются таким образом, что при их анализе участники дискуссии невольно затрагивают вопросы возникновения дефектов. К этому участников побуждают специальными, целенаправленными вопросами, например: “К чему может привести данная ситуация?” или: “Насколько устойчива в данном случае работа механизмов?” и т. д. Сущность метода “черного ящика” состоит в том, что причины дефектов выявляются как бы косвенным путем. Здесь развязывается творческая инициатива людей.
Синектика. Метод применяется как для выявления проблемных ситуаций, так и для решения возникающих проблем. Процедура состоит из трех этапов. На первом этапе анализируются проблемы, сформулированные лидером группы. Затем каждый участник обсуждения выдвигает свои проблемы, и они также тщательно обсуждаются. По завершении этих двух этапов выявляется какая-то общая модель решения. На третьем этапе все обобщения, а также выявленная модель подвергаются интенсивному исследованию. В обсуждении принимают участие не только члены группы, защищающие свою коллективную идею, но и приглашенные эксперты. Задача экспертов состоит в том, чтобы помочь членам группы качества принять правильное решение.
Метод дневников. Каждому члену группы качества раздаются карманные записные книжки. Туда в течение, скажем, недели вписываются все возникающие по обсуждаемой проблеме идеи. Нередко записи всех участников анализируются лидером группы с последующим обсуждением подготовленного материала на очередном заседании. Как считают японцы, данный метод ценен тем, что, во-первых, появившаяся идея или конкретное рационализаторское предложение обретает коллективную групповую окраску, а во-вторых, все неувязки и различные точки зрения выявляются до заседания группы, категоричные точки зрения сглаживаются. На заседание выносится обычно “усредненное” мнение.
Метод 6-6. Не менее шести членов группы качества в течение шести минут стараются сформулировать конкретные идеи, которые должны способствовать. решению стоящей перед группой проблемы (отсюда — название метода). Каждый участник на отдельном листе записывает свои соображения. Это делается в лаконичной форме. Например: нарушение герметизации, разрушение материала, нарушение технологии и т. д. После этого в группе организуется обсуждение всех подготовленных списков. В процессе обсуждения отсеиваются явно ошибочные мнения, уточняются спорные, группируются по определенным признакам все оставшиеся. Задача—отобрать несколько наиболее важных альтернатив, причем их количество должно быть меньше числа участников дискуссии.
Перечисленные методы решения возникающих проблем объединяет общая ориентация на выработку единого мнения. Ориентация эта определяет и саму тональность обсуждения группой качества даже наиболее острых вопросов. Доброжелательный стиль дискуссии, при котором невозможны взаимные обвинения, личные выпады, 'наклеивание ярлыков, выявление “правых” и “виноватых”, рассматривается как важное условие быстрого обнаружения оптимальных решений.
В ориентации на единое мнение, вне всякого сомнения, проявляются элементы национального культурного наследия японцев. Известный японский биофизик проф. Сэцуро Эбаси говорит, что японцы исторически приучены вчувствоваться в других людей. В Японии считается хорошим тоном, подчеркивает он, когда собеседники не навязывают друг другу своей точки зрения, когда делают все возможное, чтобы избежать излишней напряженности при рассмотрении каких-либо спорных моментов. В практике деятельности групп качества эти поведенческие установки прослеживаются с предельной ясностью.
2.4 Законы распределения
В разделе 1.1 мы рассматривали элементарные примеры случайных величин. В случаях с монетой и кубиком говорили о том, что все возможные значения равновероятны.
Так вот, если случайная величина Х принимает значения X1,X2,...,Xn с одинаковой вероятностью р, то говорят, что случайная величина Х имеет равномерное распределение или равномерно распределена. Вероятность p появления каждого значения Xn одинакова, то есть p=1/n. Нужно отметить то, что значения равномерно распределенной величины всегда находятся в замкнутом или конечном интервале числовой оси.
Однако, когда мы рассматривали пример с двумя кубиками, и как можно видеть из таблицы, значения случайной величины имеют различную вероятность, то в этом случае, мы имеем закон распределения случайной величины отличающийся от равномерного. Из всего многообразия законов распределения существующих в природе, одним из наиболее изученных есть закон нормального распределения.
2.4.1 Условия «нормальности»
Известна шутка: практики широко используют нормальное распределение, т.к. его применимость доказана теоретиками; теоретики же многие свои выводы делают для нормального распределения, т.к. его очень часто применяют практики.
На самом же деле нормальное распределение - не более, чем удобная модель, широкое применение которой однако можно обосновать.
В теории вероятностей существует центральная предельная теорема, которая утверждает:
если случайная величина есть результат совместного действия очень многих факторов, причем:
• ни один из факторов по " силе своего действия" не превосходит многократно остальные факторы;
• факторы действуют независимо друг от друга и не подчиняются какой-то общей тенденции;
• количество факторов достаточно велико,
то независимо от того, какие воздействия производят отдельные факторы, результатом их совместного действия будет нормальное распределение.
Заметим в качестве примера, что если взять несколько, например, 10 случайных величин, имеющих равномерное распределение в интервале [0,1] и вычислить среднее арифметическое от этих равномерно распределенных величин, то это среднее будет иметь почти нормальное распределение, и притом, с очень высокой точностью. То есть центральная предельная теорема здесь срабатывает уже при количестве факторов (случайных чисел), равном всего 10, но все они входят в результат "с равной силой". Такой метод и применяется в ЭВМ для моделирования нормально распределенной случайной величины.
На практике с достаточно хорошей точностью нормальное распределение получается при усреднении всего 4-х равномерно-распределенных случайных величин. Это значит, что средние арифметические значения от выборок объема п=4 или более можно считать нормально распределенными величинами, даже если исходные выборочные данные достаточно далеки от нормального распределения.
В очень многих производственных процессах разброс как раз и является результатом действия очень многих факторов, действующих совместно. Иногда кажется, что факторов немного, но бывает, что каждый из них есть уже результат множества других факторов.
В практических ситуациях предположение о нормальности распределения чаще всего основывается на ситуациях-аналогах, где нормальность распределения подтверждена продолжительной практикой его использования и достаточной точностью результатов. Если же ситуаций-аналогов нет или они сомнительны, то не остается ничего другого, кроме проверки гипотезы о нормальности по одному из критериев согласия, которые имеются во многих учебниках по статистике. Но в этом случае потребуется взятие выборки из десятков или даже сотен деталей, причем процесс за это время не должен изменять своих статистических свойств, т.е. распределение должно сохраняться "неподвижным".
Мы же сейчас будем предполагать, что нормальность распределения выполняется. Рассмотрим основные важные для практики свойства нормального закона.
На рис. 3 изображен график плотности нормального распределения диаметров поршневых пальцев, который мы уже рассматривали ранее на гистограмме, под ним изображена функция соответствующего распределения.
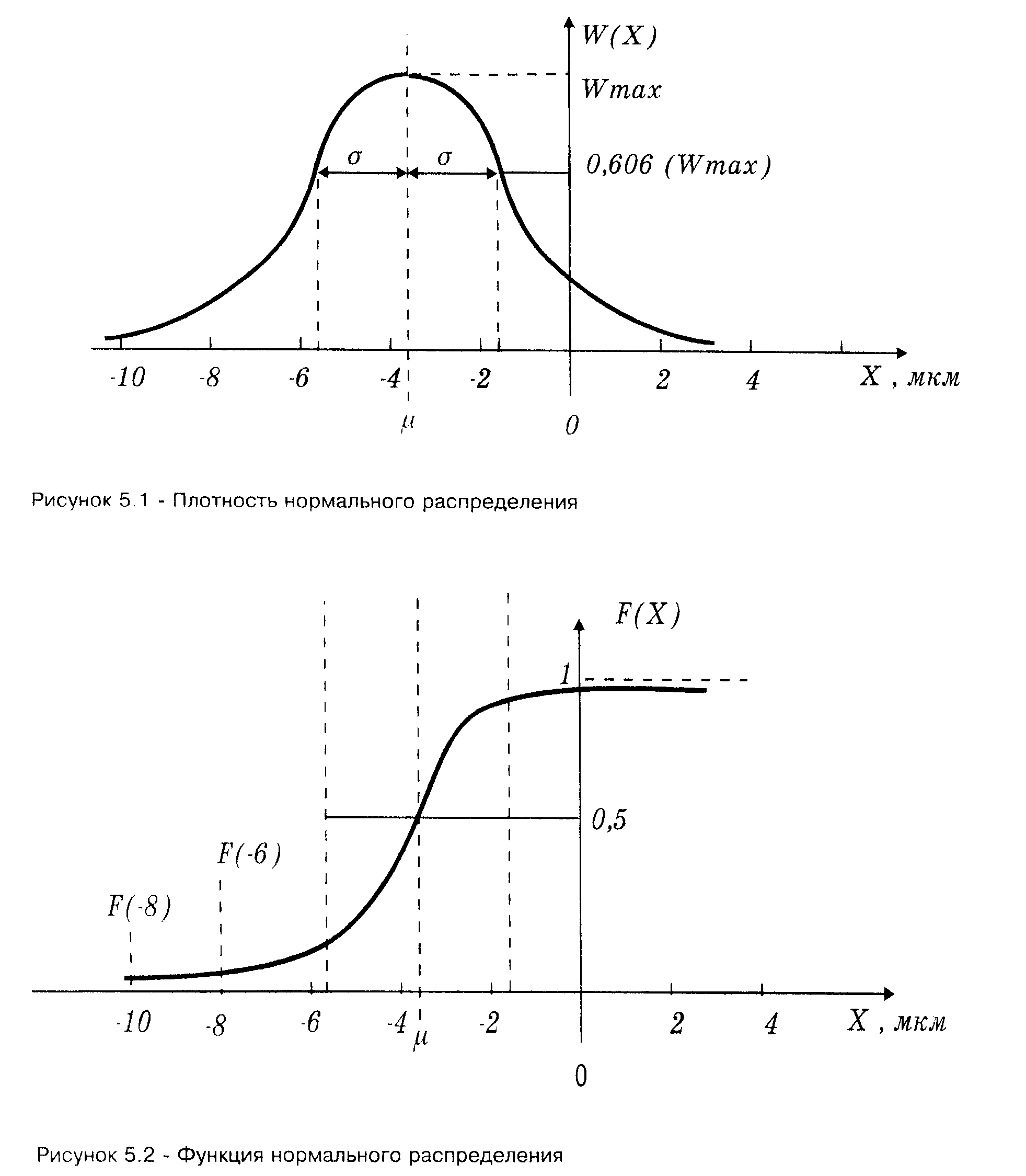
Рис.3 График плотности нормального распределения и график функции нормального распределения
2.4.2 Свойства нормального распределения
Перечислим основные свойства нормального распределения:
1) Плотность W(x) описывается формулой:
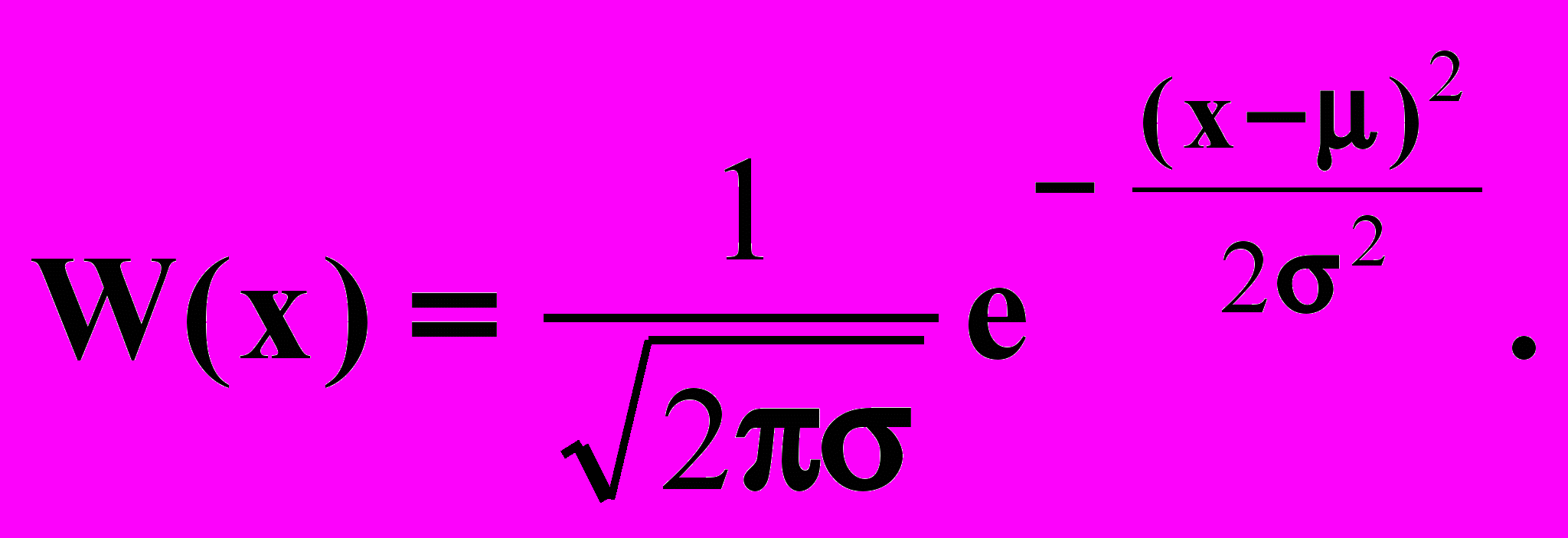
(4.1)
где
- математическое ожидание,
- среднее квадратическое отклонение.Параметры распределения присутствуют в формуле плотности в явном виде. Если мы формально попробуем вычислить математическое ожидание и среднее квадратическое отклонение для (4.1), то получим соответственно
и .Плотность распределения для приведенного в разделе 1.2 примера с диаметрами поршневых пальцев приведена на рисунке 3.
1.а) Плотность симметрична относительно
, т.е. отклонения х вправо и влево относительно центра равновероятны.1.б) Как видно из (4.1), формально плотность распределения существует для значений X в пределах от (
) до (+
), однако с удалением значений от влево или вправо плотность быстро падает. При удалении от на расстояние влево или вправо плотность убывает до величины 0.6065 от максимального значения в точке . При удалении от на 2 плотность убывает до величины 0.1353, а при удалении на 3 - до величины 0.01111 от максимального значения. С достаточной, для практики, точностью можно считать, что плотность равна нулю при отклонении от . на расстояние более 4-5 значений .2) Функция нормального распределения F(Х) (как впрочем, и любого другого) является определенным интегралом от плотности распределения по всей области левее заданного значения X, те. F(X) равняется площади под кривой W(х) левее заданного значения X. Например, для Х=-6 мкм значение F(X) равно площади под кривой W(х) левее значения Х=-6 мкм. Интеграл от плотности (4.1) в явном виде не берется, поэтому F(X) в формульном виде остается в виде интеграла
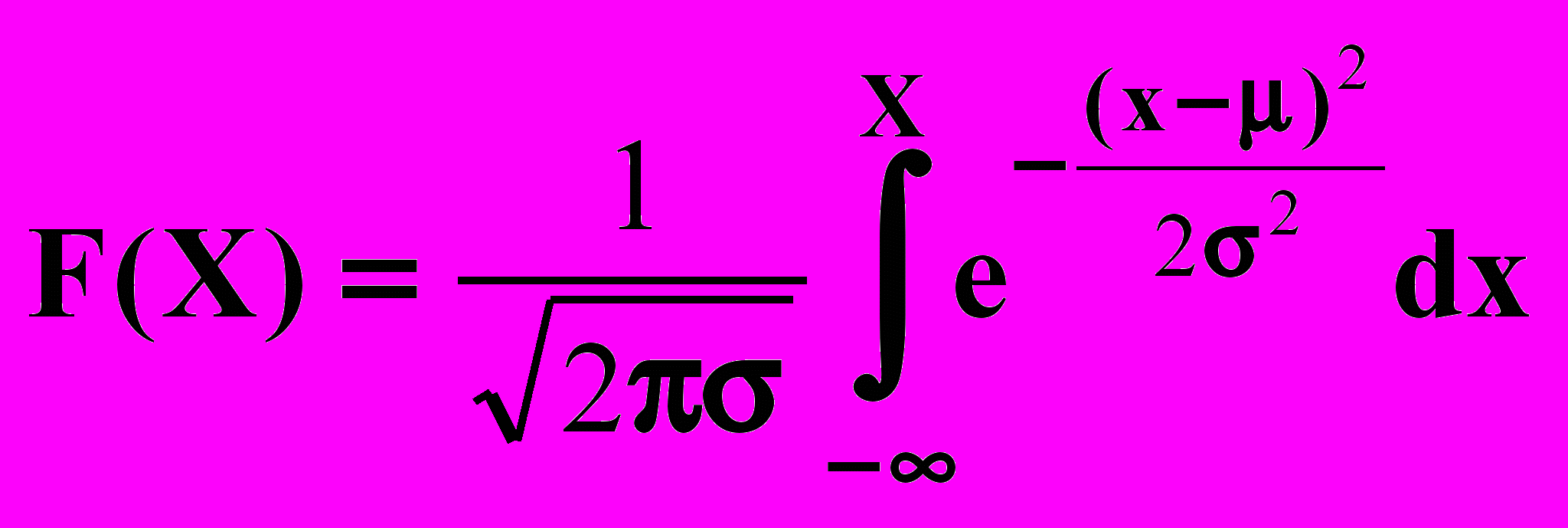
(4.2)
Значение F(X) или интеграл (4.2) численно равны вероятности того, что случайная величина не превосходит определенного заданного значения: х < X Иногда эту вероятность называют долей распределения, лежащей левее заданного значения X. Методика вычисления этой вероятности описана ниже.
3) Вероятность попадания случайной величины Х- в любой заданный интервал:
А < х < В
численно равна площади под кривой W(х) между значениями х = А и х = В (рис. 4) и определяется как разность между F(B) и F(A).
P{A
В самом деле, согласно свойству 2:
(Вероятность попасть левее В) = (Площадь под кривой плотности левее В) = F(B)
(Вероятность попасть левее А) = (Площадь под кривой плотности левее А) = F(A)
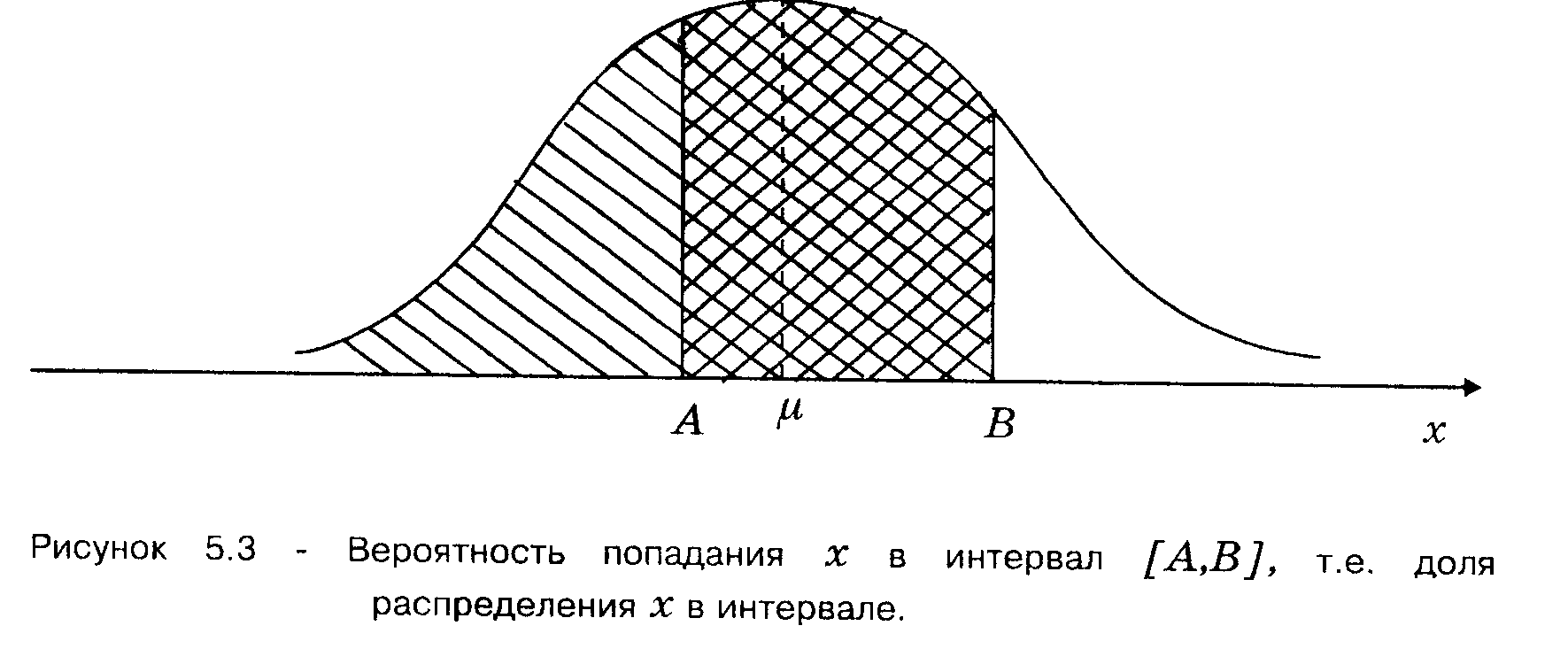
(Вероятность попасть между А и В) = (Площадь под кривой плотности между А и В) = (Площадь под кривой плотности левее В) - (Площадь под кривой плотности левее А) = F(B)-F(A).
Рисунок 4.
Иногда эту вероятность называют долей распределения, лежащей между А и В. В частности, доля распределения, лежащая в заданном допуске с нижней границей Тн и верхней границей Тв. P{Tн
3а) Доля распределения в интервале, как функция от ширины интервала, изображена на рисунке 5. Ширина интервала задана в определенном количестве значений
при этом находится в центре интервала.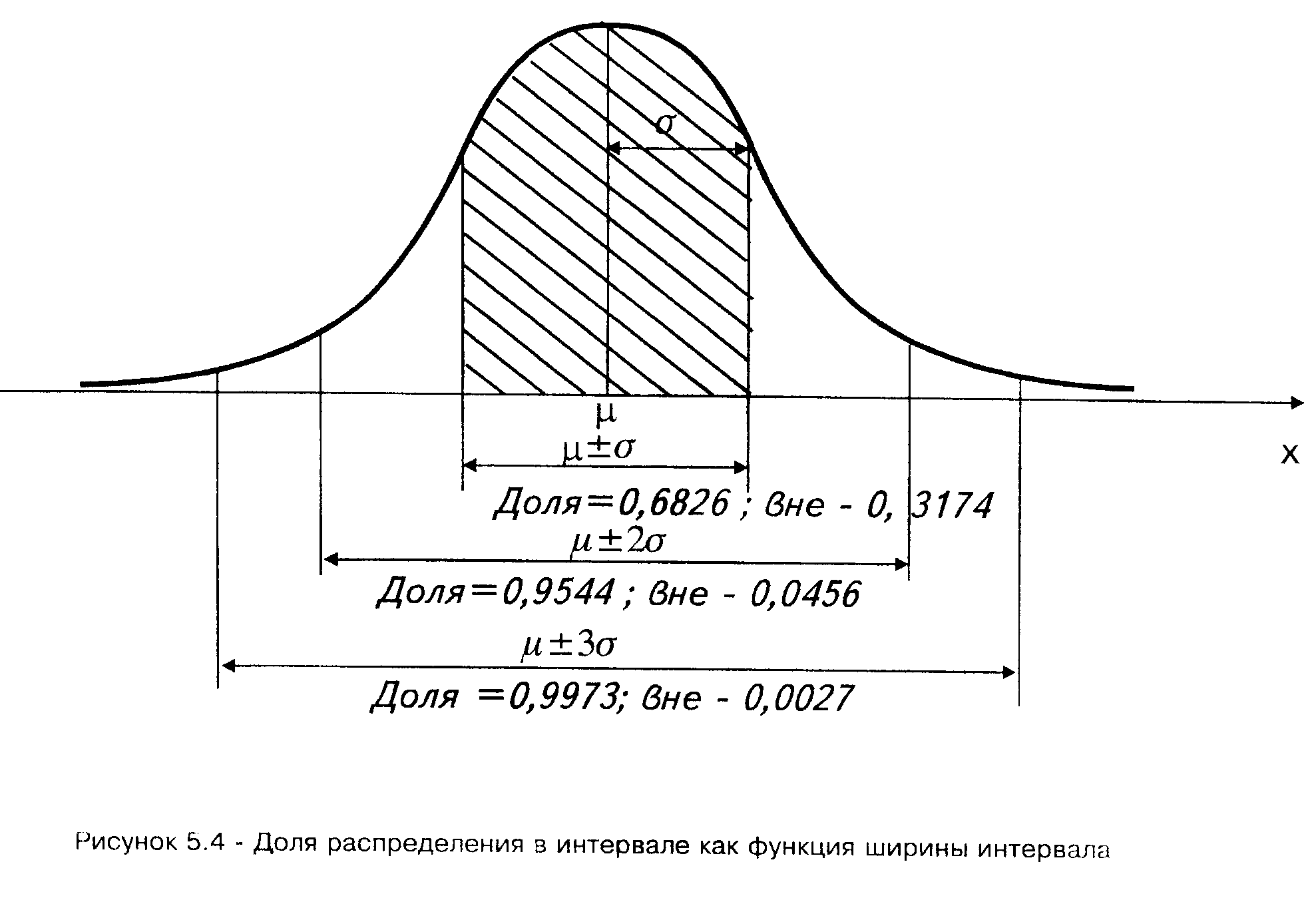
Рисунок 5
3б) Из определения вероятности как определенного интеграла от плотности распределения, т.е. площади под кривой (4.1), следует, что вероятность для строгих и нестрогих неравенств по х равны между собой:
P{A
х B2} = P{A1 < х B2} = P{A1 х < B2} = P{A1 < х < B2).Это справедливо для любых заданных значений А и В, причем А<В.
3в) Максимум вероятности попадания в допуск соответствует значению
в центре допуска.Это является следствием симметрии плотности распределения (4.1) и ее монотонного убывания при удалении значений x от
.На практике этот случай соответствует минимальному уровню несоответствий (уровню дефектности), который может дать технологический процесс или станок. Поэтому, если нет каких-то веских оснований, настройку станка или технологического процесса стремятся вести по центру допуска.
4) Все кривые плотностей нормальных законов распределения геометрически подобны. Изменяя значение
, т.е. осуществляя "сдвиг" плотности по оси х, и изменяя , т.е. ширину колоколообразной кривой (рис.5), всегда можно плотность одного нормального распределения привести к плотности другого нормального распределения.Это важнейшее свойство позволяет любое нормальное распределение преобразовать к стандартному нормальному распределению и наоборот. Стандартное нормальное распределение имеет параметры:
соответствующая стандартная нормально-распределенная случайная величина обычно обозначаетcя z и имеет плотность распределения вида:
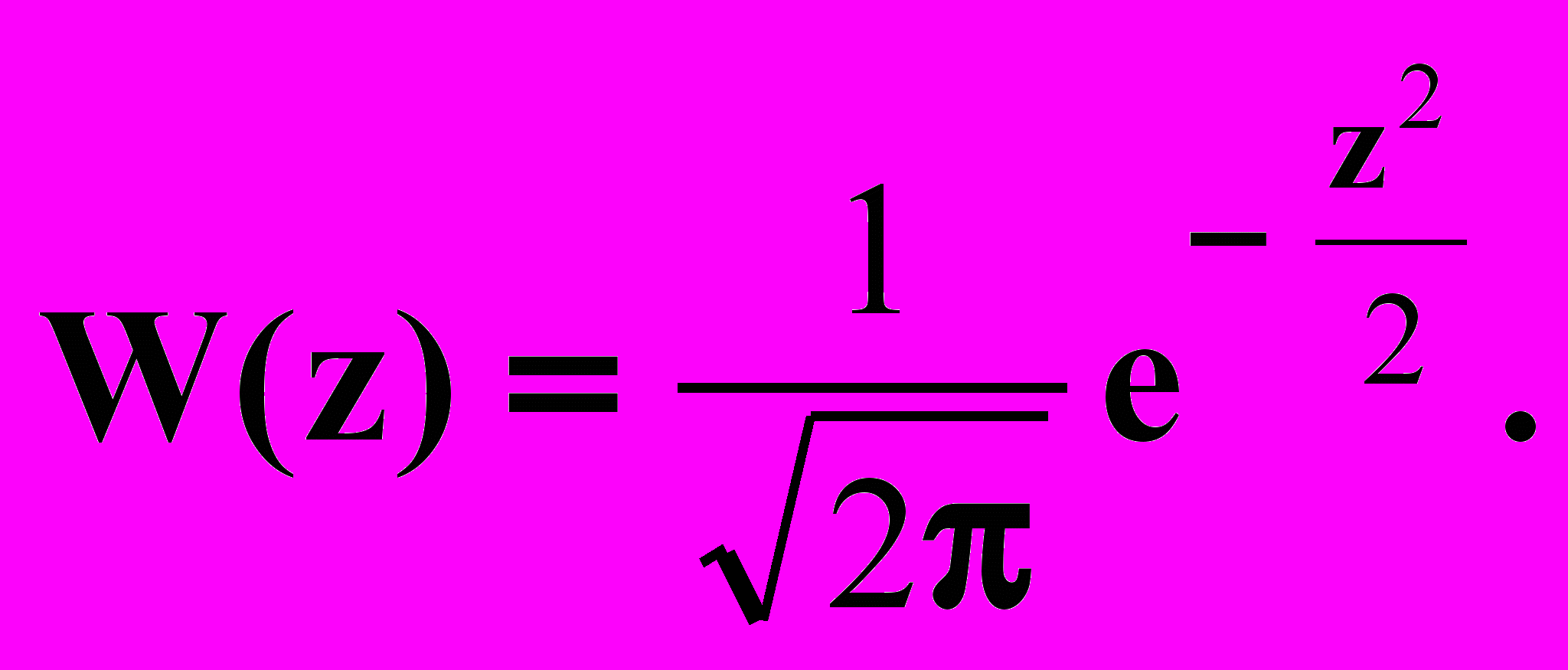
(4.3)
и функцию стандартного нормального закона распределения вида:
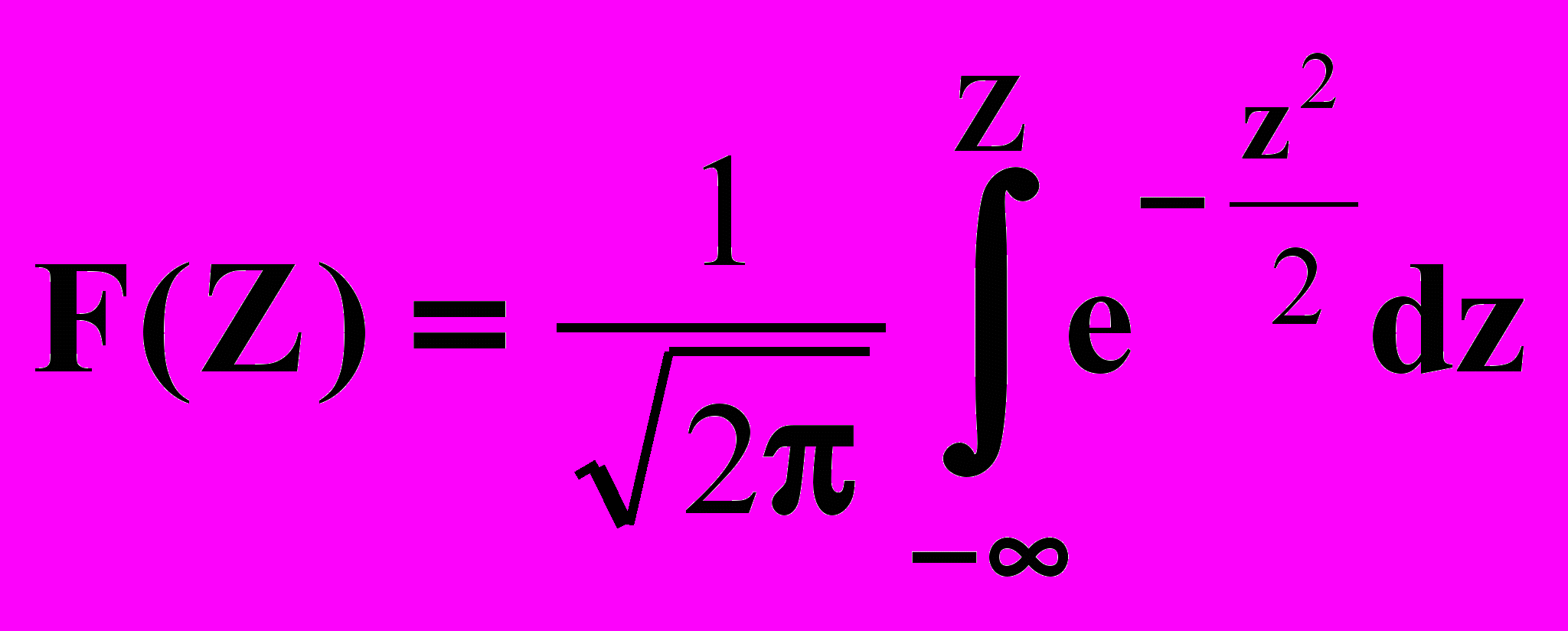
(4.4)
Функция распределения (1.18) рассчитана для различных значений Z и представлена в виде таблиц (табл.2). По этой таблице для любого заданного Z можно определить F(Z) и наоборот.
5) Для отрицательных значений нормально-распределенной величины (4.3)- (4.4) функция распределения обладает свойством:
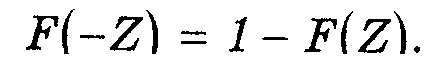
6) Преобразования подобия для нормальных случайных величин
Любое определенное значение Х для случайной величины может быть преобразовано в эквивалентное определенное значение Z для стандартной случайной величины z:
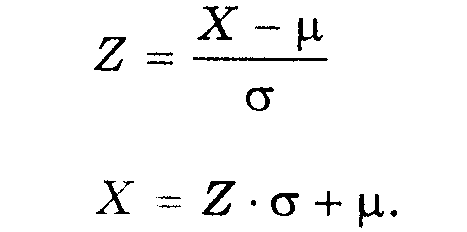
Эти преобразования сохраняют значение функции распределения F, т.е. значения вероятностей для Х и Z совпадают:
P(x
Приведенные преобразования широко используются при любых вероятностных расчетах, в частности при расчетах вероятности попадания в допуск. Они позволяют, вместо вычисления вероятностей для исходной случайной величины Х методом взятия интегралов, приводить их для стандартной случайной величины Z, для которой эти интегралы уже посчитаны и приведены в табл.2.
Для более наглядного представления метод преобразования нормальной случайной величины к стандартной и наоборот изображен на рис. 6, а ниже приведены методики ряда типовых расчетов.
При незначительном практическом навыке оператор проводит такие расчеты за несколько минут. Для приобретения навыка достаточно 3-4 раза решить практические задачи. При этом, особенно на первых порах, рекомендуется рисовать картинки с плотностями распределения, аналогичные приведенным на рис. 6, но с соблюдением реальных масштабов, т.е. с сохранением соотношения между величиной интервала [А,В] и величиной
, а также с соблюдением местоположения параметра относительно границ А и В.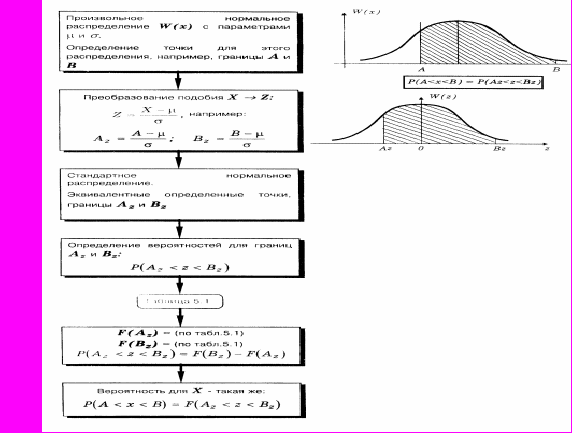
Рисунок 6 - Проведение вероятностных расчетов для нормально-распределенных величин
2.4..3 Правила пользования таблицей значений функции стандартного нормального закона распределения
В таблице 6 даны значения функции стандартного нормального закона распределения
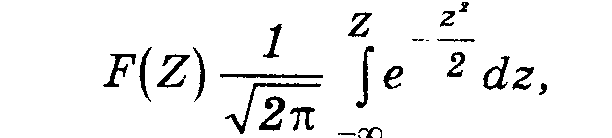
т.е. значения площади под кривой плотности стандартного нормального закона распределения:
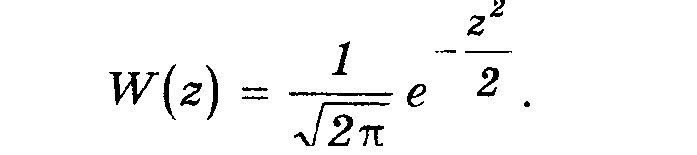
Площадь F(Z) под кривой W(z) определяется левее заданной точки Z, эта площадь численно равна вероятности того, что стандартная нормальная случайная величина z не превосходит заданного значения Z.
Значения F(Z) для различных положительных значений аргумента Z с шагом 0,01 приведены в таблице 6. При этом F(Z) для Z=0,50 и т.д. до Z=0,99 приведены в третьей колонке таблицы, озаглавленной: F(0,5+Z); для Z=l,00 и т.д. до Z=l,49 - в четвертой колонке таблицы, озаглавленной F(1,0+Z) и т.д.
Пример - Для Z = 1,86 =(1,5 + 0,36); F(l,86) = 0,96856.
С достаточной для практики точностью можно считать, что для Z =3,5 и более выполняется: F(Z)= 1,000.
Значения функции F(Z) для отрицательных Z рассчитывают по формуле:
F(-Z)=1-F{Z).
например, F(-l,56) = I- F( 1,56) == 1-0,94062 = 0,05938.
Обратное действие - по значению функции F найти значение аргумента Z: значение квантили Z, уровня у находится как значение аргумента Z. соответствующего значению функции F(Z)= у. Пример - для у= 0.99 (ближайшее табличное значение - 0.99010):
Z = 2.0+ 0.33 = 2.33.
2.4.4 Примеры вероятностных расчетов для нормальных случайных величин.
Расчет вероятностей попадания случайной величины в допуск [А,В], ниже допуска и выше допуска.
Имеется выборка значений показателя качества X: {Xi,...,Xк} и границы поля допуска А и В. Требуется определить оценку трех вероятностей: "в допуске", "ниже допуска", "выше допуска".
Проводим оценку параметров
, и по формулам (3.5) и (3.8). Считаем, что полученные оценки равны истинным значениям параметров нормального распределения.Проводим пересчет границ допуска А и В для масштаба переменной Z:
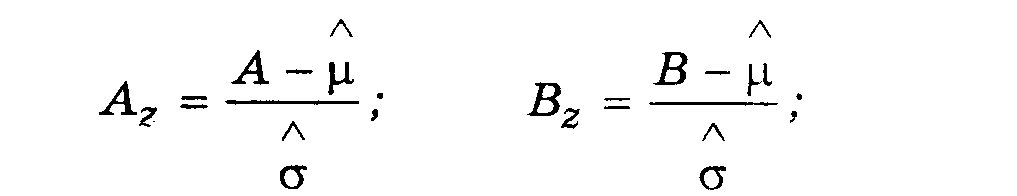
Желательно изобразить плотности W(x) и W(z) в масштабе с соответствующими границами допусков, как это сделано на рис. 4.
Находим F(Az) по табл. 2(5.1). Имеем:
Р{х < A} = P{z < Az}= F{Az},
т.e. определили вероятность попадания "ниже допуска" или уровень несоответствий с заниженными значениями X.
Находим F(Bz) по табл.2(5.1). Имеем:
Р{х < В} = P{z < Вz} = F(Bz),
Р{х > В} = 1 - P{z < Вz} = 1 - F(Bz),
т.е. определили долю распределения ниже значения В, остальное - доля распределения (уровень несоответствий) с завышенными значениями х (выше В):
Доля распределения в допуске: P{A < x < B}=P{Az < Z < Bz}=F(Bz) - F(Az).
Таблица 2 - Значения функции стандартного нормального закона распределения
| Z | F(Z) | F(0,5+Z) | F(1,0+Z) | F(1,5+Z) | F(2,0+Z) | F(2,5+Z) | F(3,0+Z) |
| 0,00 0,01 0,02 0.03 0,04 0,05 0,03 0,07 0,08 0,09 | 0,50000 0,50399 0,50798 0,51197 0,51595 0,51994 0.52392 0,52790 0,53188 0,53586 | 0,69146 0,69497 0,69847 0,70194 0,70540 0,70884 0,71226 0,71566 0,71904 0,72240 | 0,84134 0,84375 0,84614 0,84850 0,85083 0,85314 0,85543 0,85769 0,85993 0,86214 | 0,93319 0,93448 0,93574 0,93699 0,93822 0,93943 0,94062 0,94179 0,94295 0,94408 | 0,97725 0,97778 0,97831 0,97882 0,97932 0,97982 0,98030 0,98077 0,98124 0,98169 | 0,99379 0,99396 0,99413 0,99430 0,99446 0,99461 0,99477 0,99492 0,99506 0,99520 | 0,99865 0,99869 0,99874 0,99878 0,99882 0,99886 0,99889 0,99893 0,99896 0,99900 |
| 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 | 0,53983 0,54380 0,54776 0,55172 0,55567 0,55962 0,56356 0,56750 0,57142 0,57535 | 0,72575 0,72907 0,73237 0,73565 0,73891 0,74215 0,74537 0,74857 0,75175 0,75490 | 0,86433 0,86650 0,86864 0,87076 0,87286 0,87493 0,87698 0,87900 0,88100 0,88298 | 0,94520 0,94630 0,94738 0,94845 0,94950 0,95053 0,95154 0,95254 0,95352 0,95449 | 0,98214 0,98257 0,98300 0,98341 0,98382 0,98422 0,98461 0,98500 0,98537 0,98574 | 0,99534 0,99547 0,99560 0,99573 0,99585 0,99598 0,99609 0,99621 0,99632 0,99643 | 0,99903 0,99906 0,99910 0,99913 0,99916 0,99918 0,99921 0,99924 0,99926 0,99929 |
| 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 | 0,57926 0.58317 0,58706 0,59095 0,59483 0,59871 0,60257 0,60642 0,61026 0,61409 | 0,75804 0,76115 0,76424 0.76731 0,77035 0.77337 0,77637 0,77935 0,78230 0,78524 | 0,88493 0,88686 0,88877 0,89065 0,89251 0,89435 0,89617 0,89796 0,89973 0,90147 | 0,95543 0,95637 0,95728 0,95818 0,95907 0,95994 0,96080 0,96164 0,96246 0,96327 | 0,98610 0,98645 0,98679 0,98713 0,98745 0,98778 0,98809 0,98840 0,98870 0,98899 | 0,99653 0.99664 0,99674 0,99683 0,99693 0,99702 0,99711 0,99720 0,99728 0,99736 | 0,99931 0,99934 0,99936 0,99938 0,99940 0,99942 0,99944 0,99946 0,99948 0,99950 |
| 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 | 0,61791 0,62172 0,62552 0,62930 0,63307 0,63683 0,64058 0,64431 0,64803 0,65173 | 0,78814 0,79103 0,79389 0.79673 0,79955 0,80234 0,80511 0,80785 0,81057 0,81327 | 0,90320 0,90490 0,90658 0,90824 0,90988 0,91149 0,91308 0,91466 0,91621 0,91774 | 0,96407 0,96485 0,96562 0,96638 0,96712 0,96784 0,96856 0,96926 0,96995 0,97062 | 0,98928 0,98956 0,98983 0,99010 0,99036 0,99061 0,99086 0,99111 0,99134 0,99158 | 0,99744 0,99752 0,99760 0,99767 0,99774 0,99781 0,99788 0,99795 0,99801 0,99807 | 0,99952 0,99953 0,99955 0,99957 0,99958 0,99960 0,99961 0,99962 0,99964 0,99965 |
| 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 | 0,65542 0,65910 0,66276 0,66640 0,67003 0,67364 0,67724 0,68082 0,68439 0,68793 | 0,81594 0,81859 0,82121 0,82381 0,82639 0,82894 0,83147 0,83398 0,83646 0,83891 | 0,91924 0,92073 0,92220 0,92364 0,92507 0,92647 0,92785 0,92922 0,93056 0,93189 | 0,97128 0,97193 0,97257 0,97320 0,97381 0,97441 0,97500 0,97558 0,97615 0,97670 | 0,99180 0,99202 0,99224 0,99245 0,99266 0,99286 0,99305 0,99324 0,99343 0,99361 | 0,99813 0,99819 0,99825 0,99831 0,99836 0,99841 0,99846 0,99851 0,99856 0,99861 | 0,99966 0,99968 0,99969 0,99970 0,99971 0,99972 0,99973 0,99974 0,99975 0,99976 |