Частично редактированный машинный перевод

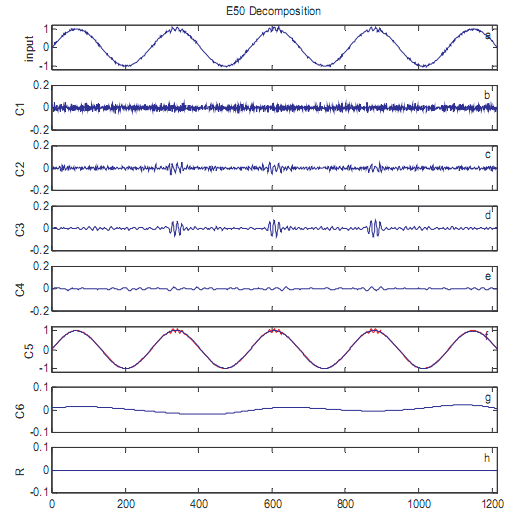
Иллюстрация 4: подобные IMF точки декомпозиции первоначального ввода в иллюстрации 1a, используя EEMD. В EEMD используется элемент множества 50, и у добавленного белого шума в каждом элементе множества есть среднеквадратичное отклонение 0.1. В панели a, среднее значение искажения составлен график измененный ввод. В панели 5 первоначальный ввод (красная линия) также отображен для сравнения.

Нужно указать, что эффект добавленного белого шума должен уменьшиться после известного статистического правила:



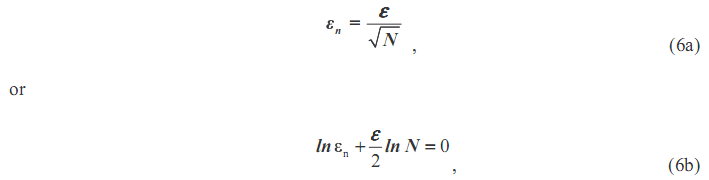
где N - количество элементов множества, является амплитудой добавленного шума, и n - конечное среднеквадратичное отклонение погрешности, которая определена как разность между входным сигналом и соответствующим IMF. Такое соотношение ясно в иллюстрации 5, в которой среднеквадратичное отклонение погрешности составлено как график функции количества элементов множества. Вообще, результаты хорошо соглашаются с теоретическим прогнозом. Относительно большая девиация для фундаментального сигнала от теоретической пригонки линии понятна: распространение погрешности для низкочастотных сигналов является большим, как указано Wu и Huang (2004).

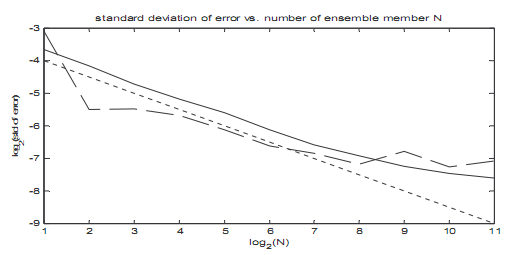
Иллюстрация 5: среднеквадратичное отклонение погрешности как функция количества элементов множества. Сплошная линия для высокочастотных прерывистых сигналов, и пунктирная линия для низкочастотных сигналов основной составляющей. Пунктир - теоретическая линия, предсказанная уравнением (6) с произвольным вертикальным расположением, используемым как справочная информация.


Фактически, если добавленная шумовая амплитуда является слишком небольшой, то она, возможно, не представляет изменения extrema, на который полагается EMD. Однако, увеличивая элементы множества, эффект добавленного белого шума всегда будет приведенным к небольшому уровню. Продемонстрировав основной подход, дополнительные примеры будут даны добавлением шума с конечным (или даже большими) амплитуда в следующем разделе, имея дело со сложными действительными данными.

4. Больше Примеров

Предыдущий пример представлял понятие анализа данных с помощью шума, используя метод EEMD. Вопрос теперь - помогает ли EEMD действительно в достижении окончательной цели анализа данных: изолировать и извлечь истину в данных, и таким образом понять свойства данных и ее основной физики. Самый простой способ продемонстрировать мощность EEMD и его полноценность состоит в том, чтобы рассмотреть данные естественных явлений. В этом разделе EEMD применен к двум действительным случаям: первый - данные климата, которые определяют взаимодействие между атмосферой и океаном; и второй - раздел digitalized фонограммы с высоким разрешением. Оба случая сложны и имеют богатые свойства в данных. Эти данные считают достаточно общими, чтобы быть представителями действительных случаев.

4.1 Пример 1: Анализ Данных Климата

Первое множество данных, которые будут исследованы вот, является представителем взаимодействующей воздушно-морской системы в тропиках, известных как эль Niño-южное Колебание (ENSO) явление. Южное Колебание (SO) - возвратно-поступательное движение глобального масштаба на атмосферном давлении между западным и юго-восточным тропическим Tихим океаном, и эль Niño обращается к изменениям в температуре и циркуляции в тропическом Тихом океане. Эти две системы близко соединены (Philander, 1990, National Research Council 1996), и вместе они производят важные флуктуации климата, которые оказывают существенное влияние на погоду и климат по глобусу так же как социально-экономическим следствиям (см., например, Glantz и al.1991). Основная физика ENSO была объяснена в многочисленных работах (см., например, Suarez и 1988 Schopf, Battisti и 1989 Hirst, Jin 1996).

Южное Колебание часто представляется Южным Индексом Колебания (SOI), нормализованный ежемесячный индекс давления уровня моря, основанный на прижимных отчетах, собранных в Дарвине, Австралии и Острове Острова Tаити в восточном тропическом Tихом океане (Trenberth 1984). Должно быть замечено здесь, что отчет Острова Tаити, используемый для вычисления SOI, менее достоверен и содержит данные отсутствия до 1935. Холодный Индекс Языка (CTI), определенный как среднее число, большое год от года флуктуации аномалии синхронного прерывания по 6°N-6°S, 180-90°W, является хорошим представлением эль Niño (Deser и Уоллис 1990). Большое максимальное отрицательное значение SOI, которая часто происходит с периодом двух - семи лет, соответствует сильному эль Niño (теплое) явление. С ее богатыми статистическими свойствами и научной значимостью, SOI - один из самых выпуклых временных рядов в геофизическом исследовательском семействе и была хорошо изучена. Много инструментальных средств анализа временных рядов использовались на этом временные ряды, чтобы отобразить их возможность раскрытия полезной научной информации (например, Wu и др. 2001, Ghil и др. 2002, Wu и 2004 Huang). Отдельный вопрос, который будет исследован, какие масштабы времени - эль Niño и Южное соединенное Колебание?

SOI, используемая на этом изучении, описана в Ropelewski и Джонсе (1987) и Аллан и др. (1991). CTI основан на синхронном прерывании с января 1870 до декабря 2002, снабженного Hadley Center для Прогноза Климата и Исследования (Rayner и др., 1996), который усовершенствован от непосредственных наблюдений. Разреженные и низкие качественные наблюдения в ранних стадиях периода делают эти два индекса в ранних стадиях менее непротиворечивыми и их взаимосвязь менее достоверный, как отражено фактом, что полные корреляции между этими двумя временными рядами-0.57 для целой длины данных, но только-0.45 для первой половины, и-0.68 для второй половины. График этих двух индексов в иллюстрации. 6.



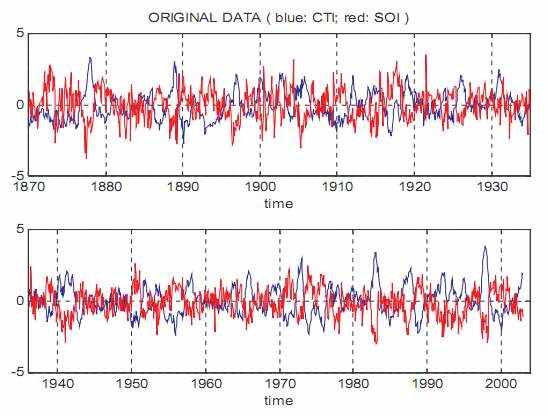
Иллюстрация 6: Южный Индекс Колебания (синяя линия) и Холодный Индекс Языка (красная линия).

Декомпозиции этих двух индексов, используя первоначальный EMD составлены график в иллюстрации 7. Хотя у SOI и CTI есть весьма большая корреляция (-0.57), IMFs, однако, показывают небольшую синхронизацию. Для целой длины данных наибольшая отрицательная корреляция среди IMFs - только-0.43 (см. иллюстрацию 8), намного меньшее значение чем та из корреляции между целыми данными SOI и CTI. Так как основные материальные процессы, которые диктуют крупномасштабное взаимодействие между атмосферой и океаном, расходятся в различной шкале времени, хороший метод декомпозиции, как ожидают, идентифицирует такие изменения. Однако, низкие корреляции между передачей IMFs, кажется, указывают, что декомпозиции, используя первоначальный EMD на SOI и CTI помогают немного идентифицировать и понимать, какие времена для связи между атмосферой и океаном в системе климата в тропиках более выпуклы.

Это отсутствие корреляции ясно представляет типичную задачу модовых функций, смешивающегося в первоначальном EMD. От визуального осмотра легко замечено, что в почти любом высоком или среднем IMF масштаба SOI или CTI, части колебаний, имеющих приблизительные периоды тех, появляются также в его соседнем IMFs. Смешивание является также инфекционным: если это случится в одном IMF, то это случится в следующем IMFs в том же самом временном сетевом окружении. Следовательно, смешивание модовых функций приводит возможность EMD в идентификации истинных масштабов времени непротиворечивых двойных колебаний в индивидуальном узле IMF в системе ENSO. Этому ясно показывают в иллюстрации 8, в которой никакой IMF не соединяется с рангом от 1 до 7, имеют более высокую корреляцию чем полный набор данных.



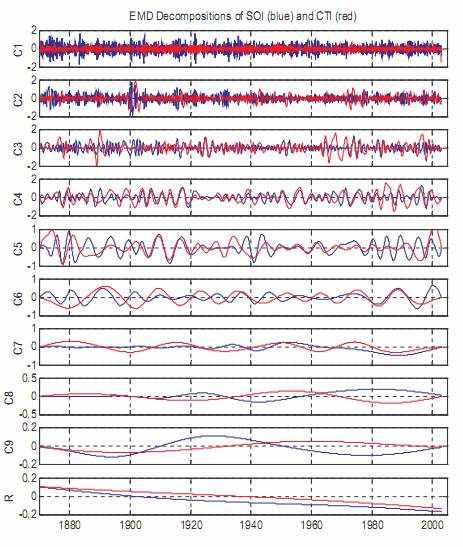
Иллюстрация 7: модовые функции и тенденции Южного Индекса Колебания (синие линии) и Холодного Индекса Языка (синие линии). Для удобства идентификации их синхронизации щелкают CTI и его точками.



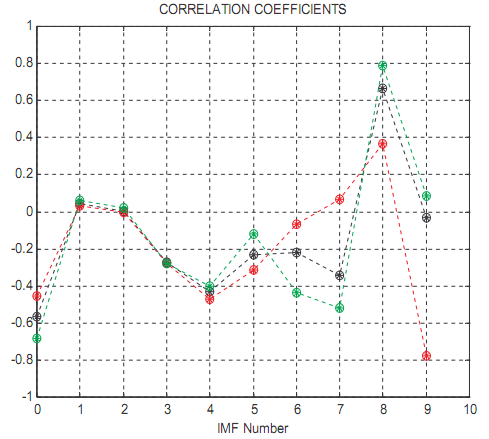
Иллюстрация 8: коэффициенты корреляции (круг звездочки) SOI и CTI и их передачи IMFs. IMF 0 здесь первоначальный сигнал. Черное для целой длины данных; красный цвет для первой половины; и зеленый для второй половины.

Чтобы решить эту задачу и идентифицировать масштаб времени, в котором действительно происходит взаимодействие, оба временных ряда были повторно разложены, используя EEMD. Результаты отображены в иллюстрации 9. Это ясно, что синхронизации между передачей пар IMFs очень улучшены, специально для узлов IMF 4-7 в более поздней половине отчета. Как упомянуто ранее, и SOI и CTI не столь же достоверны в первой половине отчета как те во второй половине сбора к разреженным или пропускающим наблюдениям. Поэтому, более низкая степень синхронизации соответствующих узлов IMF SOI и CTI в более ранней половине вряд ли вызвана EEMD, но менее непротиворечивыми данными SOI и CTI в тот период. Чтобы определить количество этого требования, детализированные значения корреляции соответствующих пар IMF будут обсуждаться затем.



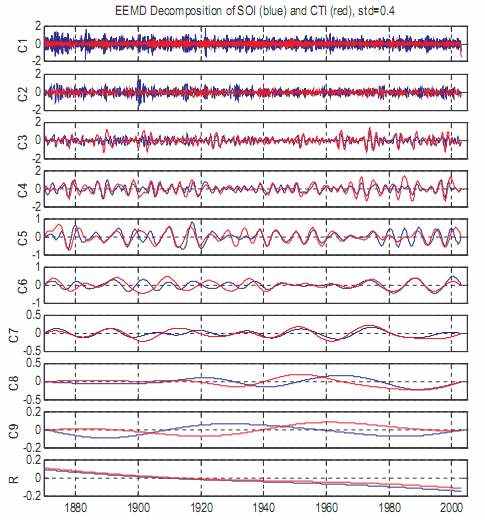
Иллюстрация 9: Подобные IMF точки декомпозиции SOI (синие линии) и (красные линии) CTI с использованием EEMD. В EEMD используется размер множества 100, и у добавленного белого шума в каждом элементе множества есть среднеквадратичное отклонение 0.4. Для удобства идентификации их синхронизации щелкают CTI и его точками.


Детализированная корреляция между соответствующими узлами IMF SOI и CTI отображена в иллюстрации 10. Ясно, декомпозиции, используя EEMD улучшают значения корреляции значительно. EEMD следует справка очень изоляцией сигналов различных масштабов, которые отражают связь между атмосферой и океаном в системе ENSO. Последовательно высокие корреляции между IMFs из SOI и CTI на различной шкале времени были получены, особенно таковые межежегодного (Точки 4 и 5 со средними периодами 2.83 и 5.23 лет соответственно) и межпроисходящее каждые десять лет короткое замыкание (точки 6 и 7 со средними периодами 10.50 и 20.0 лет соответственно) шкала времени. Увеличение коэффициентов корреляции от только под 0.68 для более поздней половины целых данных к значительно более чем 0.8 для этих пар IMF замечательно. Еще не было никакого другого метода фильтрации, используемого, чтобы изучить эти два временных ряда, который привел к таким высоким корреляциям между фильтрованными полосой следствиями изданной литературы по всей этой шкале времени. (Для длинных межпроисходящих каждые десять лет масштабов времени, специально для C8 и C9, так как количество степени свободы узлов IMF - очень небольшой сбор к отсутствию изменений колебания, коэффициенты корреляции, соответствующие им, могут очень вводить в заблуждение; поэтому, они должны игнорироваться). Эти результаты ясно указывают, что самая важная связь между атмосферой и океаном происходит на широком диапазоне шкалы времени, покрывая межежегодные и межпроисходящие каждые десять лет масштабы с 2 до 20 лет.



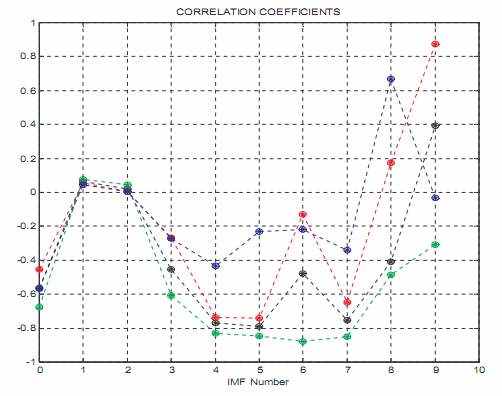
Иллюстрация 10: коэффициенты корреляции (круг звездочки) SOI и CTI и их соответствующих IMF узлов. IMF 0 здесь первоначальный сигнал. Черное для целой длины данных; красный цвет для первой половины; и зеленый для второй половины. Синий цвет - то же самое как черное в иллюстрации 8, то есть, коэффициенты корреляции SOI и CTI и их передачи IMFs для целой длины данных.


Высокие корреляции на межежегодной и короткой межпроисходящей каждые десять лет шкале времени между IMFs SOI и CTI, особенно в последней половине отчета, совместимы с материальными объяснениями, снабженными свежими изучениями. Эти IMFs статистически существенны на 95%-ом доверительном уровне, основанном на методе испытания, предложенном в Wu и Huang (2004, 2005) против основной гипотезы белого шума. Два межежегодных модовых функций (C4 и C5) также статистически существенны на 95%-ом доверительном уровне против традиционной красной шумовой основной гипотезы. Действительно, Jin и др. (персональная связь, их рукопись, являющаяся в процессе подготовки), решил нелинейную двойную океанскую атмосферой систему и показал аналитически, что у межежегодной изменчивости ENSO есть две отдельных модовых функции с периодами в согласии с результатами, полученными здесь. Относительно двойных коротких межпроисходящих каждые десять лет модовых функций они находятся также в хорошем соглашении со свежим изучением моделирования Yeh и Kirtman (2004), который продемонстрировал, что такие модовые функции могут быть результатом связанной системы в ответ на стохастическое форсирование. Поэтому, метод EEMD действительно дает более точный инструмент, чтобы изолировать сигналы с отдельными масштабами времени в наблюдательных данных, произведенных различной основной физикой.

Чувствительность декомпозиции данных будет исследована с использованиемя EEMD для амплитуды шума. В Рис. 11 и 12 добавлен шум со среднеквадратичным отклонением 0.1, 0.2, и 0.4. Размер множества для каждого случая 100. Ясно, синхронизация между случаями различных уровней добавленного шума замечательно хороша, кроме случая никакого добавленного шума, когда смешивание модовых функций производило неустойчивую декомпозицию. В последнем случае любое возмущение может поместить результат в различное состояние, как изучено Gledhill (2003). Дополнительно, уточнение декомпозиции для CTI, кажется, больше чем это для SOI. Причина проста: SOI является намного более шумной чем CTI, так как основано на шумных наблюдениях за данными уровня моря только от двух расположений (Дарвин и давления Острова Tаити), в то время как CTI основано на усредненной наблюдаемой морской температуре поверхности в сотнях расположений вдоль экватора. Это действительно указывает, что EMD - шум - дружественный метод: шум, содержавшийся в данных, делает декомпозицию EMD действительно бинарной.



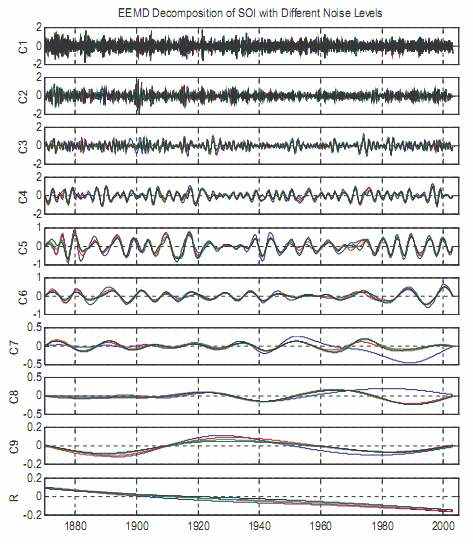
Иллюстрация 11: декомпозиции EEMD SOI с добавленным шумом. Синяя линия переписывается, стандартная декомпозиция, используя EMD без любого добавленного искажения. Красный цвет, зеленый, и черный соответствует декомпозициям EEMD с добавленным искажением среднеквадратичного отклонения 0.1, 0.2, и 0.4, соответственно. Номер множества для каждого случая 100.




Иллюстрация 12: То же самое как иллюстрация 11, но для CTI.


Больше декомпозиции SOI и CTI с различными уровнями помех и элементами множества было выполнено. Результаты (не показанные здесь) указывают, что увеличение шумовых амплитуд и количество множества изменяет декомпозицию немного, пока у добавленного шума есть умеренная амплитуда, и у множества есть достаточно большое количество испытаний. Нужно заметить, что количество множества должен увеличиться когда амплитуда шумовых увеличений, чтобы привести содействие добавленного шума в анализируемых результатах. Выводы, сделанные для декомпозиций SOI и CTI здесь, также истинны для других данных, которые попробовали методом EEMD. Поэтому, EEMD снабжает своего рода результат "единственности" и надежности, что первоначальный EMD обычно не мог, и это также увеличивает уверенность декомпозиции.

4.2 Пример 2: Анализ Переговорных Данных

В предыдущем примере доказательство мощности и подтверждение полноценности EEMD были сделаны через анализ двух различных, но физически близко взаимодействующих подсистем (соответствующий двум различным наборам данных) системы климата. Такая пара высоко связанных наборов данных редка в большем количестве общих случаев обработки сигналов. Поэтому, чтобы далее пояснять EEMD как эффективный метод анализа данных в частотно-временном домене для универсального, мы анализируем часть речевых данных, используя EEMD. Первоначальные данные, данные в иллюстрации 13, показывают звук digitalized слова, 'Привет', при преобразовании в цифровую форму на 22 050 Гц (Huang 2003).



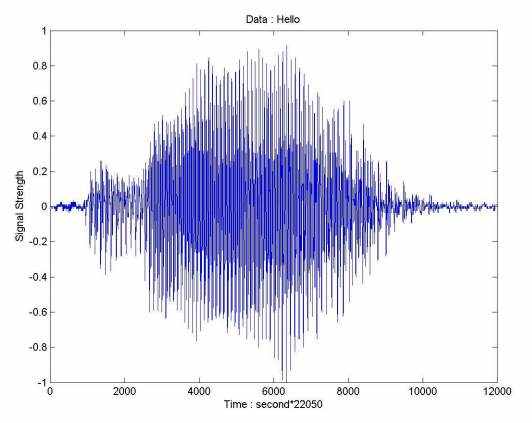
Иллюстрация 13: звук Digitalized слова, 'Привет', в 22 050 Гц.

Точки EMD, полученные из первоначального EMD без добавленного шума, даны в иллюстрации 14, которые составляют график с равномерной шкалой. Здесь мы можем видеть, что очень ясные модовые функции смешивается от второго узла и вниз, где высоко несоизмеримые амплитуды и масштабы очевидны. Модовых функций, смешивающих влияние четности масштаба во всех точках IMF, хотя некоторые не столь очевидны.



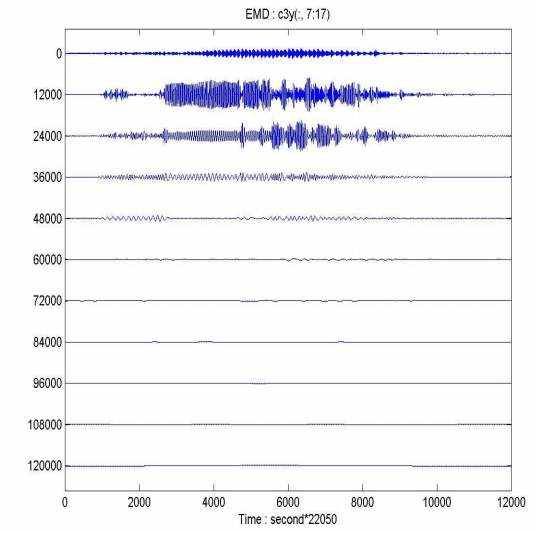
Иллюстрация 14: IMFs (C1 к C11, от максимальной синей кривой до основы синяя кривая, соответственно) digitalized зондируют "Привет" от EMD без добавленного искажения. Смешивание функций заставило вторые и третьи узлы вкраплять разделами данных, имеющих очень несоизмеримые амплитуды и масштабы.

Те же самые данные были тогда обработаны с EEMD с шумом, выбранным в амплитуде в 0.2 раза больше чем то из RMS данных, и 1000 испытаний. Результат - решительное уточнение как показано в иллюстрации 15. Здесь все точки IMF непрерывны и без очевидной фрагментации. Третий IMF - почти полный сигнал, который может произвести звук, который ясен и с почти первоначальным звуковым качеством. Все другие точки также регулярны и имеют сопоставимые и равномерные шкалы и амплитуды для каждого соответствующего узла IMF, но звуки, произведенные ими, не понятны: они главным образом состоят или из высокочастотного шипения или низкочастотного стенания. Результаты еще раз ясно демонстрируют, что у EEMD есть возможность захвата сущности данных, которая проявляет основную физику.



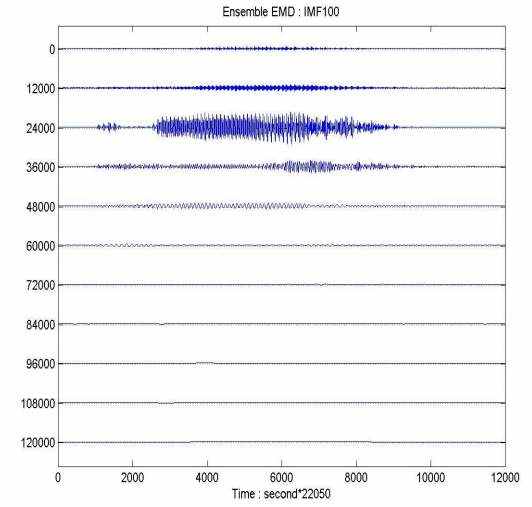
Иллюстрация 15: IMFs (C1 к C11, от максимальной синей кривой до основы синяя кривая, соответственно) digitalized зондируют "Привет" от Множества EMD с добавленным шумом. Смешивание функций почти исчезло. У каждого узла IMF есть непротиворечивые амплитуды и масштабы.


Уточнения на качестве IMFs также имеют решительные эффекты на время - гистограмма данных в Гильбертовом формате спектров как показано в двух различных Гильбертовых спектрах, данных в иллюстрациях 16 и 17. В первоначальном EMD модовых функций mixings заставил гистограмму времени быть фрагментированной в иллюстрации 16. Предполагается что в точках перехода от одного масштаба до другого ясно видим. Хотя Гильбертовы спектры этого качества могли использоваться для некоторых общих целей, таких как идентификация основных частот и их диапазонов изменения, количественные меры будут чрезвычайно трудными. Гильбертов спектр от EEMD, данный в иллюстрации 17, однако, показывает большие уточнения. Все основные частоты непрерывны без транзитных промежутков.



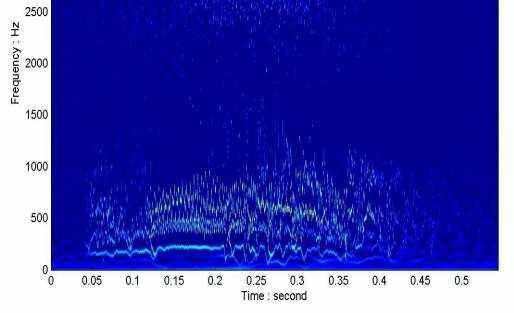
Иллюстрация 16: Гильбертов спектр от первоначального EMD без добавленного шума. Смешивание функций вызвало многочисленные переходные промежутки, и отдало время - частотные проекции прямой фрагментированный.

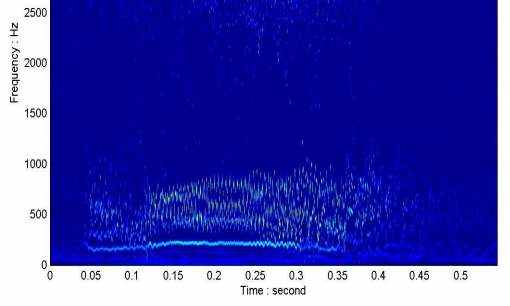
Иллюстрация 17: Гильбертов спектр от множества EMD с добавленным шумом. Смешивание функций исчезло. Нет никаких переходных промежутков, и все основные частотные проекции прямой непрерывны в частотно-временном месте.


5. Обсуждение и Заключения

Основной принцип множественной эмпирической модовой декомпозиция (EEMD) прост, мощность нового подхода очевидна из примеров. Новый метод действительно может отделить сигналы различных масштабов без чрезмерного смешивания модовых функций. Добавление белого шума помогает устанавливать бинарную прикладную рамку в частотно-временной шкале. Действительные данные с сопоставимым масштабом могут обнаружить естественное расположение, где постоянно находятся. EEMD использует всю статистическую характеристику шума: Это помогает тревожить сигнал и давать возможность алгоритму EMD посетить все возможные решения в конечном (не бесконечно малая величина) окружении истинного конечного ответа; это также использует в своих интересах нулевое среднее значение шума, чтобы уравновесить этот шумовой фон, как только это обслужило свою функцию обеспечения равномерно распределенной рамки масштабов, подвиг, только возможный в анализе данных временного интервала. В некотором смысле, этот новый подход - по существу повторенный эксперимент, которым управляют, чтобы произвести среднее значение множества для неустановившихся данных как конечный ответ. Так как роль добавленного шума в EEMD должна облегчить разделение различных масштабов введенных данных без действительного содействия IMFs данных, EEMD - действительно метод анализа данных с помощью шума (NADA), который эффективен в распаковке сигналов от данных.

Хотя анализ с добавлением шума попробовали пионеры, такие как Flandrin и др. (2004) и Gledhill (2003), есть решающие разности между нашим подходом и их. Во-первых, и Flandrin и Gledhill определяют правду или как результаты без добавленного шума, или как дано в Уравнении (2), который является пределом, когда представленное шумовое возмущение приближается к нулю. Правда, определенная EEMD, дана количеством во множестве приближающуюся бесконечность, то есть:

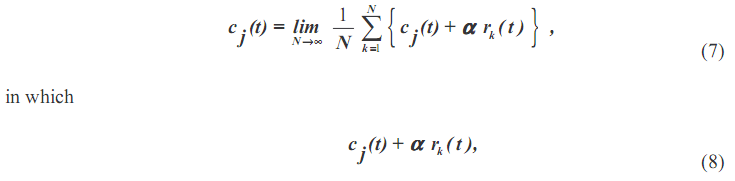где k^th испытаний над j^th IMF с добавленным к сигналу шумом, и величина добавленного шума, является не обязательно небольшой. Но количество испытаний во множестве N, должен быть большим. Разностью между правдой и результатом множества управляют по известному статистическому правилу: это уменьшается как один по квадратному корню N, как дано в Уравнении (6).

С определенной правдой несоответствие, вместо один данный в Уравнении (3), должно быть

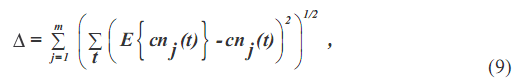
в котором E {} является ожидаемым значением как дано в Уравнении (7).

Предложено здесь, чтобы EEMD действительно представил большое уточнение по первоначальному EMD. Поскольку уровень добавленного шума не имеет критической значимости, пока это имеет конечную амплитуду, чтобы допустить справедливому множеству всех возможностей, EEMD может использоваться без любого субъективного вмешательства; таким образом, это действительно адаптивный метод анализа данных. Устраняя задачу смешивания модовых функций, это производит ряд IMFs, которые имеют полное материальное значение, и гистограмму времени без транзитных промежутков. EMD, с подходом множества, стал более зрелым инструментом для анализа нелинейных и неустановившихся временных рядов (и данных другой размерности).

В то время как EEMD предлагает большое уточнение по первоначальному EMD, есть все еще некоторые нерешенные задачи. Первый недостаток EEMD: результаты EEMD, к которым приходят, не удовлетворяют строгому определению IMF. Хотя каждое испытание во множестве производит ряд узлов IMF, сумма IMF - не обязательно IMF. Девиации от строгого IMFs, однако, являются небольшими для примеров, представленных на этом изучении, и не интерферировали заметно в вычисление мгновенной частоты, используя Гильбертову Трансформанту или любые другие методы как обсуждается Huang и др. (2005). Однако, эти недостатки должны быть устранены. Одно возможное решение состоит в том, чтобы провести другую окружность отсеивания на IMFs, произведенном EEMD. Поскольку IMFs следует из EEMD, имеют сопоставимые масштабы, смешивание модовых функций не было бы критической задачей здесь; и простое просеивание могло отделить стоячие волны для любой задачи. Эта тема будет обсуждена и сообщена в другом месте.

Вторая задача, присоединенная с EEMD, как обработать много модовых функций распределения IMFs. Как обсуждается Gledhill (2003), несоответствие между испытанием и его справочной информацией имеет тенденцию к бимодальному (если не многомодальному) распределению. Всякий раз, когда бимодальное распределение происходит, значения несоответствия могли быть весьма большими, и значение дисперсии больше не будет следовать за формулой, данной Уравнением (6). Хотя часть большого несоответствия могла быть возможно приписана выбору справочной информации как невозмущенное состояние, выбор одной только справочной информации не может объяснить всю дисперсию и ее распределение. Истинная причина задачи может быть объяснена легко на основанная изучении белого шума, используя EMD Wu и Huang (2004), в котором бинарный банк фильтра показывает небольшое количество перекрытия в масштабах. У сигналов, определяющих местонахождение масштаба в накладывающейся области, была бы конечная вероятность, появляющаяся в двух различных модовых функций. Хотя задача не была полностью решена безусловно, некоторые переменные реализации процедур отсеивания могут облегчить его серьезность. Первый вариант должен настроить уровень помех и использовать больше испытаний, чтобы привести корневую среднеквадратическую девиацию. Результаты Gledhill’s ясно показывают эту возможность, поскольку 'бимодальное' распределение действительно имеет тенденцию объединять в единственное, хотя более широкое, унимодальное распределение. Второй вариант - тот, используемый в случаях большой части на этом изучении: просейте низкое, но установленное число раз (10 на этом изучении) для того, чтобы получить каждые точки IMF. Сдержанный двухместным свойством группы фильтра EMD, этот метод почти гарантировал бы тот же самый номер IMFs, просеиваемого из каждого испытания во множестве, хотя копии добавленного шума в различных испытаниях являются различными. Оба подхода попробовали на этом изучении, но ни один не избегает много модовых функций задачи полностью. Истинному решению, вероятно, придется комбинировать много модовых функций в единственные модовые функции, и просеять это снова, чтобы произвести присущий единственный IMF. Третий подход должен использовать строгую проверку каждого узла против определения, и разделить результат в различные группы согласно общему количеству IMF. Наш ограниченный опыт состоит в том, что распределение количества IMF является весьма узким даже с умеренным количеством шумового возмущения. Тогда пик распределения принят как ответ. Мы нашли все подходы приемлемыми, и их разности небольшой. Дальнейшие изучения будут выполнены по этой проблеме.

Наконец, наш опыт в использовании EEMD поднял две других ранее сохраненных задачи для EMD: концевой эффект и критерии остановки. Обе из задач были долго существующими и не решили все же. Доверительный предел EMD приводил к результатам, и его зависимость от критериев остановки были обращены до некоторой степени Huang и др. (2003). Здесь EEMD снабжает вариант, но лучше, мера доверительного предела, так как произведенные декомпозиции EEMD намного менее чувствительны к используемым критериям остановки. Однако, оптимальный диапазон критериев остановки как дано Huang в al. (2003) может все еще использоваться как справочник здесь. Что касается концевого эффекта, искажение прибавило, что процессы помогают повышать качество трудности, поскольку с добавленным шумом конечное падение будет более равномерно распространено. Таким образом конечные результаты могли избежать детерминированного дрейфа в одном направлении или другом. Однако, больше через изучение концевого эффекта срочно необходим.