Частично редактированный машинный перевод

  1   2   3

Аннотация

Представлено новое множество эмпирической модовой декомпозиции (EEMD). Новый подход к процессу отсеивания заключается во многократном добавлении к сигналу белого шума и вычислении среднего значения модовых функций как конечного истинного результата. Конечный, не бесконечно малый, амплитудный белый шум необходим, чтобы вынудить множество получить все возможные решения в процессе отсеивания, таким образом делая сигналы различного масштаба сопоставимыми в модовых функциях (IMF), продиктованных бинарными банками фильтра. Поскольку EMD – метод временного анализа, белый шум с достаточным количеством испытаний действует усредняюще; единственная устойчивая часть выживает, результат усреднения - сигнал, который можно считать истинным и физически значимым. Эффект добавленного белого шума должен создать равномерную прикладную рамку в частотно-временном масштабе; поэтому, добавленный шум сопоставляет часть сигнала сопоставимого масштаба в одном IMF. С этим средним значением множества можно разделить масштабы естественно без любого априорного субъективного выбора критерия, как в испытании нестационарности на первоначальный алгоритм EMD. Этот новый подход использует полное преимущество статистических характеристик белого шума, чтобы встревожить сигнал в районе его истинного решения, и уничтожить себя после достижения цели; поэтому, это представляет существенное уточнение по первоначальному EMD и является действительно анализом данных, которому помогает шумовой метод (NADA).

1. Введение

Эмпирическая модовая декомпозиция (EMD) была предложена (Huang, и др. 1998, 1999) как адаптивный частотно-временной метод анализа данных. Она применяется в широком диапазоне приложений для того, чтобы выделить сигналы из данных, сгенерированных в шумных нелинейных и неустановившихся процессах (см., например, Huang и Shen, 2005, Huang и Attoh-Okine, 2005). Но есть и трудности.

Один из больших недостатков первоначального EMD - частое появление смешивания модовых функций, которое определено как единственная модовая функция (IMF), или строение сигналов широко несоизмеримых масштабов, или сигнал подобного масштаба, постоянно находящегося в различных точках IMF. Смешивание модовых функций - следствие нестационарности сигнала. Как обсуждается Huang и др. (1998 и 1999), нестационарность могла не только вызвать серьезную ступенчатость в гистограмме времени, но также сделать индивидуальный IMF лишенным материального значения. Чтобы облегчить это от появления, Huang и др. (1999) предложил испытание нестационарности, которое может действительно повысить качество некоторых из трудностей. Однако, у самого подхода есть свои собственные задачи: Во-первых, испытание нестационарности основано в субъективно выбранном масштабе. С этим субъективным вмешательством EMD прекращает быть полностью адаптивным. Во-вторых, субъективный выбор масштабов работает, если есть ясно отделимые и определимые масштабы времени в данных. В случае, если масштабы не ясно отделимы, но не смешаны более чем диапазон непрерывно, поскольку в большой части естественных или искусственных сигналов, алгоритм испытания нестационарности с субъективно определенными масштабами времени часто не работает очень хорошо.

Чтобы преодолеть задачу о разделении масштаба, не используя субъективное испытание нестационарности, предложен новый метод анализ данных с помощью шума (NADA), , Множество EMD (EEMD), который определяет истинные точки IMF как среднее значение множества испытаний, каждого строения сигнала плюс белого шума конечной амплитуды. С этим подходом множества мы можем ясно разделить масштабы естественно без априорного субъективного выбора критерия. Этот новый подход основан на проникновении, собранном колосья от свежих изучений статистических свойств белого шума (Flandrin, и др., 2004, и Wu и Huang, 2004), который показывал этому, EMD - эффективно адаптивный двухместный фильтр bank1, когда относился к белому шуму. Более критически, новый подход вдохновлен методами анализа данных с помощью шума, инициализированными Flandrin и др. (2005) и Gledhill (2003). Их результаты продемонстрировали, что шум может помочь анализу данных в EMD.

Правило EEMD просто: добавленный белый шум заполнил бы частотно-временное место равномерно точками образования различных масштабов, отделенных группой фильтра. Когда сигнал добавлен к этому равномерно распределенному белому фону, биты сигнала различных масштабов автоматически спроектированы на присущие масштабы справочной информации, установленной белым шумом на заднем плане. Конечно, каждое индивидуальное испытание может привести к очень шумным результатам, для каждого из добавленных к шуму составов декомпозиций сигнала и добавленного белого шума. Так как шум в каждом испытании является различным в отдельных испытаниях, это уравновешено в среднем значении множества достаточно многих следов. Среднее значение множества обработано как истинный ответ, поскольку, в конец, единственная устойчивая часть сигнал как все больше испытаний добавлен во множестве.


¹ бинаоный банк фильтра - коллекция фильтров прохода полосы, у которых есть постоянная форма прохода полосы (например, гауссово распределение), но с соседними фильтрами, покрывающими половину или двойное количество частотного диапазона любого, выбирают, просачиваются группа. На частотные диапазоны фильтров можно наложиться. Например, простая бинарный банк фильтра может включать фильтры, покрывающие частотный windows, такие как 50 - 120 Гц, 100 к 240 Гц,

200 - 480 Гц, и и др.

Критическое понятие, продвинутое здесь, основано на следующих наблюдениях:

1. Коллекция белого шума уравновешивает друг друга в среднем значении временного множества; поэтому, только сигнал может выжить и сохраниться в конечном значении среднего множества сигналов с добавленным шумом.

2. Конечный, не бесконечно малый, амплитудный белый шум необходим, чтобы вынудить множество, чтобы получить все возможные решения; конечное искажение величины заставляет различные сигналы масштаба постоянно находиться в соответствующем IMF, продиктованном двухместными группами фильтра, и делать следующее среднее значение множества более значимым.

3. Истинный и физически значимый ответ EMD не тот без шума; это определяется, чтобы быть средним значением множества большого количества испытаний сигнала с добавленным шумом.

Этот EEMD, предложенный здесь, использовал все эти важные статистические характеристики шума. Мы покажем, что EEMD использует правило разделения масштаба EMD, и дает возможность методу EMD быть действительно двухместной группой фильтра любых данных. Прибавляя конечный шум, EEMD устраняет модовые функции, смешивающиеся во всех случаях автоматически. Поэтому, EEMD представляет большое уточнение метода EMD.

В следующем будет представлено систематическое исследование соотношения между шумом и сигналом в данных. Изучения Flandrin и др. (2004) и Wu и Huang (2004) открыли, что EMD служит двухместным фильтром для различных типов шума. Это подразумевает, что сигнал подобного масштаба в шумном наборе данных мог возможно содержаться в одном узле IMF. Этому покажут, что добавление шума с конечной, а не бесконечно малой амплитудой к данным действительно создает такой шумный набор данных; поэтому, добавленный шум, заполнив все места масштаба равномерно, может помочь устранять раздражение модовых функций, смешивающих задачу, сначала замеченную в Huang и др. (1999). Основанный на этих результатах, мы предложим формально понятия анализа данных с помощью шума (NADA) и извлечения сигнала с помощью (NASE), и разработаем метод, названный множественная эмпирическая модовая декомпозиция, которая основана на первоначальном эмпирическом методе декомпозиции модовых функций, сделать NADA и NASE возможным.

Работа размещена следующим образом. Раздел 2 будет суммировать предыдущие попытки использования шума как инструмента в анализе данных. Раздел 3 будет представлять метод EEMD, пояснять больше деталей недостатков, присоединенных со смешиванием модовых функций, существующими понятиями метод анализ данных с помощью шума и извлечения сигнала с помощью шума, и представлять EEMD подробно. Раздел 4 отобразит полноценность и возможность EEMD через примеры. Резюме и обсуждение будут представлены в конечном разделе.

2. Краткий обзор шумов, помогающих анализу данных

Слово " шум" может быть прослежено назад к его латинскому корню "тошноты", означая "морскую болезнь". Только на среднеанглийском и старом французском языке оно начинает получать значение “шумного спора и ссоры”, как индикации чего-то нежелательного. Сегодня определение шума изменяется при различных обстоятельствах. В науке и технике шум определен как возмущение, имеющее случайный и устойчивый вид, которое затемняет ясность сигнала. В естественных явлениях шум мог быть стимулирован непосредственно процессом, таким как локальная и прерывистая нестабильность, неразрешимые явления подархитектуры, или некоторые сходящиеся процессы в среде, в которой проведены исследования. Это могло быть также сгенерировано чувствительными элементами и системами регистрации, когда выполняются наблюдения. Когда предприняты усилия, чтобы понять данные, нужно рассмотреть важные разности между чистыми сигналами, которые являются прямыми результатами основных фундаментальных материальных процессов нашего интереса ("правда") и шум, стимулированный различными другими процессами, которые так или иначе должны быть удалены. Вообще, все данные - объединение сигнала и шума, то есть:

x(t) = s(t) + n(t), (1)

в котором x(t) является зарегистрированными данными, а s(t) и n(t) являются истинным сигналом и шумом, соответственно. Поскольку шум является повсеместным и представляет очень нежелательную часть любых данных, много методов анализа данных были проектированы определенно, чтобы удалить шум и извлечь истинные сигналы в данных, хотя часто не успешно.

Начиная с разделения сигнала и шума в данных необходимо обратиться к трем важным проблемам:

1) зависимость результатов от используемых методов анализа и предположений, сделанных для данных. (Например, линейная регрессия данных неявно предполагает, что основная физика данных линейна, в то время как спектральный анализ данных подразумевает, что процесс является стационарным).

2) уровень помех, который будет допущен в извлеченных "сигналах", ни для какого метода анализа не совершенен, и почти во всех случаях извлеченные "сигналы" все еще содержат немного шума.

3) часть действительного сигнала, стертого или деформированного через анализ, обработанного как часть шума. (Например, фильтрующий Фурье может удалить гармонику при низкочастотной фильтрации и таким образом деформировать форму волны основного сигнала).

Все эти проблемы вызывают неверное истолкование данных, и последние две проблемы определенно связаны с существованием и удалением шума. Поскольку шум является повсеместным, должны быть сделаны шаги, чтобы обеспечить, чтобы любое значимое следствие анализа не было загрязнено шумом. Чтобы избежать возможной иллюзии, испытание основной гипотезы против шума часто используется с известными шумовыми характеристиками, присоединенными с методом анализа (Wu и 2004 Huang, 2005, Flandrin и др. 2005). Хотя большинство методик анализа данных определенно, чтобы удалить шум, есть, однако, случаи, когда шум добавляется, чтобы помочь анализу данных, помочь обнаружению слабых сигналов, и очертить основные процессы. Намерение здесь состоит в том, чтобы дать краткий обзор выгодного использования шума в анализе данных.

Самое раннее известное использование шума в помощь анализу данных было предпринято Press и Tukey (1956), известное как предбеление, где белый шум был добавлен, чтобы сгладить узкие спектральные пики, чтобы получить лучшую спектральную оценку. С тех пор предбеление стало общей методикой в анализе данных. Например, Fuenzalida и Rosenbluth (1990) добавляли шум, чтобы обработать данные климата; Link и Buckley (1993) и Zala и др. (1995) использовали шум, чтобы улучшить акустический сигнал. Strickland и Il Hahn (1997) использовали вейвлет и добавленный шум, чтобы обнаружить объекты вообще, и Trucco (2001) использовал шум, чтобы помочь проектировать специальные фильтры для того, чтобы обнаружить внедренные объекты на океанском дне экспериментально. Некоторые общие задачи с этим подходом, могут быть найдены в Priestley (1992), Kao и др. (1992), Politis (1993), и Douglas и др. (1999).

Другая категория популярного использования шума в анализе данных связана с методом анализа, чтобы помочь выделению сигнала из данных. Добавление шума к данным помогает повышать чувствительность метода анализа к шуму и надежность полученных результатов. Этот подход добавленное шум к различным данным используется широко, например, Cichocki и Amari (2002), чтобы проверить надежность алгоритма независимого факторного анализа (МСА), а De Lathauwer и др. (2005) используют шум, чтобы идентифицировать погрешность в МСА.

Добавление шума к вводу на определенно проектированные нелинейные детекторы может также быть выгодным для обнаруживания слабых периодических или квазипериодических сигналов, основанных на материальном процессе, названном стохастическим резонансом. Изучение стохастического резонанса велось Benzi и его коллегами в начале 1980-ых. Детали разработки теории стохастического резонанса и его приложений могут быть найдены в длинном обзоре Gammaitoni и др. (1998). Здесь должно быть замечено, что большинство прошлых приложений (включая их ранние упоминания) не использовало эффекты компенсации, присоединенные ко множествам добавленных к шум случаев, чтобы улучшить их результаты.

Используя эмпирическую декомпозицию модовых функций, Huang и др. (2001) добавлял бесконечно малый шум к данным землетрясения в попытке препятствовать низкочастотным модовым функциям расшириться в статическую область. Но они были не в состоянии понимать полностью значения добавленного шум в методе EMD. Истинные усовершенствования, связанные с методом EMD, должны были ждать до двух работ Gledhill (2003) и Flandrin и др. (2005).

Flandrin и др. (2005) использовали добавление шума, чтобы преодолеть одну из трудностей первоначального метода EMD. Поскольку EMD основан исключительно на существовании extrema (или в амплитуде или в кривизне), метод прекращает работать, если в данных отсутствуют необходимые extrema. Критический пример - в декомпозиции импульса Дирака (треугольная функция), где есть только один extrema в целом наборе данных. Чтобы преодолеть трудность, Flandrin и др. (2005) предложил прибавить шум с бесконечно малой амплитудой к импульсу Дирака, чтобы сделать алгоритм EMD действующим. Так как результаты декомпозиции чувствительны к добавленному шуму, Flandrin и др. (2005) выполнил множество 5000 декомпозиций, с различными версиями шума, все бесконечно малой амплитудой. Он использовал среднее значение, как конечную декомпозицию импульса Дирака, и определил истинный ответ как



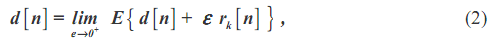
в котором, [n] представляет энную точку на графике, d[n] - функция Dirac, r_k[n] - случайное число, бесконечно малый параметр, и E {} является ожидаемым значением. Новое использование Flandrin’s добавленного шума сделало алгоритм EMD действующим для набора данных, который не мог быть ранее разложен.

Другое новое использование шума в анализе данных у Gledhill (2003), он использовал шум, чтобы проверить надежность алгоритма EMD. Хотя использовалось множество шума, он никогда не использовал правило отмены, чтобы определить среднее значение множества как истинный ответ. Основанное на его открытии, что шум может заставить EMD производить немного различные результаты, он предполагал, что следствие достоверных данных без шума было истинным ответом, и таким образом определял это как справочную информацию. Он определил несоответствие, как

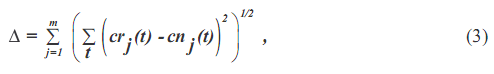
в котором cr_j и cn_j - j^th точка IMF без и с добавленным шумом, а m является общим количеством IMFs, сгенерированного от данных. На его обширном изучении детализированного распределения, вызванного шумом 'несоответствия' он заключил, что алгоритм EMD разумно устойчив для небольших возмущений. Это заключение находится в тонком конфликте с его наблюдениями, что возмущенный ответ с бесконечно малым шум показывал бимодальное распределение несоответствия.

Gledhill также поместил добавленный шум в другое направление анализа: Он предложил использовать среднее значение множества с добавленным шумом, чтобы сформировать ‘Составной Гильбертов спектр’. Поскольку спектр неотрицателен, добавленный шум не может уравновеситься. Он тогда предложил сохранить шум в спектре и вычесть его из полного спектра с добавленным шумом в конце. Эта неотмена шума в спектре, однако, вынуждала Gledhill (2003), чтобы ограничить используемый шум до небольшой величины, так, чтобы он мог убедиться, что не будет слишком большого взаимодействия между добавленным шумом и первоначальным чистым сигналом, и чтобы содействие шума к конечной энергетической плотности в спектре было бы незначительно.

Хотя бесконечно малый шум, используемый Gledhill (2003), не улучшил доверительный предел конечного спектра, эта работа не полностью зондировала свойство отмены шума, ни мощность конечного возмущения зондировать все возможные решения. Кроме того, известно, что всякий раз, когда есть нестационарность, сигнал без шума может произвести IMFs со смешиванием модовых функций. Нет никакого выравнивания, чтобы предположить, что результат без добавленного шума - правда или опорный сигнал. Это резервирование несмотря на это, все эти изучения Flandrin и др. (2005) и Gledhill (2003) очень продвинули понимание эффектов шума в методе EMD, хотя решающие эффекты шума должны были все же быть ясно сочленены и полностью зондироваться.

В следующем разделе будет объяснен новый подход к добавлению шума в EMD, в котором правило отмены будет полностью использоваться, даже с конечным амплитудным шумом. Также подчеркнуто, что истинное решение метода EMD должно быть средним значением множества, а не достоверными данными. Эта полная индикация нового метода будет темой следующего раздела.

3. Множественная эмпирическая модовая декомпозиция

3.1 Эмпирическая модовая декомпозиция

Этот раздел начинается с краткого обзора первоначального метода EMD. Детализированный метод может быть найден в Huang и др. (1998, 1999). Различный к почти всем предыдущим методам анализа данных, метод EMD адаптивен, с базисом декомпозиции, основанным и выведенным из данных. В подходе EMD данные X(t) анализируются в терминах IMFs, c_j, то есть,

где r_n - остаток данных x(t), после того, как n количество IMFs извлечены. IMFs - простые колебательные функции с переменной амплитудой и частотой, и следовательно имеют следующие свойства:

1. всюду по целой длине единственного IMF количество extrema и количество нулевых пересечений должны или быть равными или отличаться самое большее одним (хотя эти количества могли отличаться значительно для первоначального набора данных);

2. в любом расположении данных среднее значение огибающих, определенных локальными максимумами и локальными минимумами, является нулем.

Практически, EMD осуществляется через процесс отсеивания, который использует только локальные extrema. От любых данных r_j-1, процедура следующая:

1) идентифицируйте все локальные extrema (комбинация и максимумов и минимумов) и аппроксимируйте все эти локальные максимумы (минимумы) кубическим сплайном, как верхняя и нижняя огибающие;

2) получите первые точки h, беря разность между данными и локальным средним значением этих двух огибающих;

3) обработайте h, повторяя шаги 1 и 2 так много раз, как потребуются, пока огибающие не симметричны относительно нулевого среднего значения согласно определенным критериям. Конечный h определяется как c_j . Отсеивание закончивается, когда остаток, r_n, становится монотонной функцией, из которой не может быть больше извлечено IMF.

Основанный на этом простом описании EMD, Flandrin и другие (2004) и Wu и Huang (2004) показали, что если данные состояли из белого шума, у которого есть масштабы, заполненные равномерно через целую шкалу времени или частотно-временное место, EMD ведет себя как бинаоный банк фильтра: спектры Фурье различных IMFs разрушаются к единственной форме вдоль оси логарифма периода или частоты. Тогда общее количество IMFs набора данных - близко к log₂ N с N полных точек на графике. Когда данные не чистый шум; некоторые масштабы могут пропускаться, и это - то, когда происходит смешивающее явление модовых функций.

3.2 Смешивание модовых функций

‘Смешивание модовых функций” определено как любое строение IMF колебаний драматично несоизмеримых масштабов, главным образом вызванных нестационарностью механизмов запуска. Когда происходит смешивание модовых функций, IMF может прекратить иметь материальное значение отдельно, предполагая ложно, что могут быть различные материальные процессы, представленные в модовых функциях. Даже при том, что конечная частотно-временная проекция могла выпрямить смешение модовых функций до некоторой степени, предполагается что на каждом перемещении от одного масштаба до другого будет повреждать чистое разделение масштабов. Такой недостаток сначала пояснялся в Huang и др. (1999), в котором смоделированные данные была смесь прерывистых высокочастотных колебаний, стоячих синусоидальных сигналов на непрерывной низкой частоте. Почти идентичный пример, используемый Huang и др. (1999), представлен здесь подробно как иллюстрация.

Данные и его процесс отсеивания поясняются в иллюстрации 1. У данных есть его фундаментальная часть как низкочастотная синусоида с амплитудой модуля. В трех средних гребнях низкочастотной волны высокочастотные прерывистые стоячие колебания с амплитудой 0.1, как показано на панели в иллюстрации 1. Процесс отсеивания начинается с идентификации максимумов и минимумов в данных. В этом случае, 15 локальных максимумов идентифицированы, с первым и последним исхожением из основной гармоники, и других 13, вызванных главным образом прерывистыми колебаниями (панель b). В результате верхняя огибающая не напоминает верхней огибающей основной гармоники (который является плоской линией в одном), ни верхней огибающей из прерывистых колебаний (которая, как предполагается, является основным правилом вне прерывистых областей). Скорее огибающая - строго искаженная комбинация обоих (красная линия в панели c). Следовательно, начальное предположение IMF (панель d) является смесью и низкочастотного основного правила и высокочастотных прерывистых волн, как показано в иллюстрации 2, делая это более трудный интерпретировать и идентифицировать основные материальные процессы.



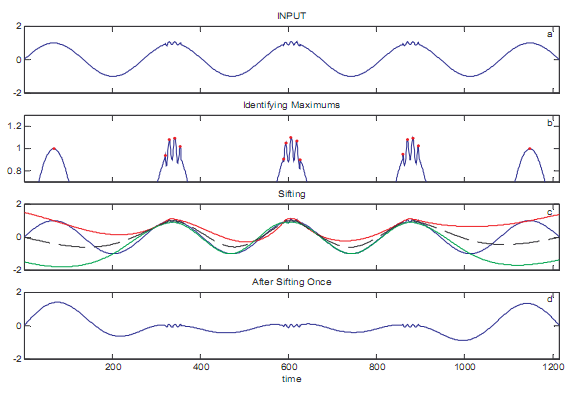
Иллюстрация 1: Самый первый процесс отсеивания. а - панель ввода; панель b идентифицирует локальные максимумы (красные точки); панель c составляет график верхней огибающей (красная) и нижней (синяя) огибающей и их среднее значение (серная); и панель d является разностью между вводом и средним значением оболочек.



Иллюстрация 2: модовые функции ввода, отображенного в иллюстрации 1a.

Чтобы облегчить этот недостаток, Huang и др. (1999) предложил испытание нестационарности, которое субъективно извлекает колебания с периодами, значительно меньшими чем предвыбранное значение во время процесса отсеивания. Метод работает весьма хорошо на этот пример. Однако, для сложных данных с переменной масштабов, но непрерывно распространенный, никакой единственный критерий испытания нестационарности не может быть выбран. Кроме того, самый неприятный аспект этого субъективно предвыбранного критерия - то, что он отсутствия материального выравнивания отдает неадаптивное EMD. Дополнительно, смешивание модовых функций - также главная причина, которая делает алгоритм EMD неустойчивым: Любое небольшое возмущение может отображаться новым множеством IMFs как сообщено Gledhill (2003). Очевидно, нестационарность препятствует тому, чтобы EMD распаковал любой сигнал с подобными масштабами. Чтобы решить эти задачи, предложен EEMD, который будет описан в следующем.

3.3 Множественная эмпирическая модовая декомпозиция

Как дано в Уравнении (1), все данные – объединения сигнала и шума. Чтобы улучшить точность измерений, среднее значение множества - сильный подход, где данные собраны отдельными наблюдениями, каждое из которых содержит различный шум. Чтобы обобщить эту идею множества, шум представлен единственному набору данных, x(t), как будто отдельные наблюдения действительно делались как аналоговое к материальному эксперименту, который мог быть повторен много раз. Добавленный белый шум обработан как возможный белый шум, с которым столкнулись бы в процессе измерения. При таких условиях i^th 'искусственное' наблюдение будет



В случае только одного наблюдения одному из множеств множественного наблюдения подражают, добавляясь не произвольные но различные копии белого шума, w_i(t), к тому единственному наблюдению как дано в Уравнении (5). Хотя добавление шума может следовать меньшим сигналом - к относительной шумовая мощности, добавленный белый шум снабдит, равномерная справочная информация масштабируют распределение, чтобы облегчить EMD; поэтому, низкая относительная шумовая мощность сигнала не воздействует на метод декомпозиции, но фактически увеличивает его, чтобы избежать смешивания модовых функций. Основанный на этом параметре, дополнительный шаг сделан, утверждая, что добавление белого шума может помочь извлекать истинные сигналы в данных. Метод, который называют множественной эмпирической декомпозицией модовых функций (EEMD), метод анализа данных с помощью шума noise-assisted data analysis (NADA).

Перед смотрением на детали нового EEMD представлен обзор нескольких свойств первоначального EMD:

1. EMD - адаптивный метод анализа данных, который основан на локальных характеристиках данных, и следовательно, он захватывает нелинейные, неустановившиеся колебания более эффективно;

2. EMD - бинарный банк фильтра любого белого цвета (или дробный гауссиан) прогрессия только для шума.

3. когда данные являются прерывистыми, бинарное свойство часто ставится под угрозу в первоначальном EMD как пример в иллюстрации 2;

4. добавление шума к данным могло снабдить равномерно распределенный масштаб справочной информации, который дает возможность EMD исправить поставившее под угрозу бинарное свойство;

5. у передачи IMFs различной прогрессии шума нет никакой корреляции друг с другом. Поэтому, средства передачи IMFs различной прогрессии белого шума, вероятно, отменят друг друга.

С этими свойствами EMD в памяти, предложенная множественная эмпирическая модовая декомпозиция разработана следующим образом:

1. прибавьте прогрессию белого шума к целенаправленным данным;

2. анализируйте данные с добавленным белым шумом в IMFs;

3. шаг 1 повторения и шаг 2 снова и снова, но с различной прогрессией белого шума каждый раз;

4. получите среднее множества декомпозиций IMFs как конечный результат.

Эффекты декомпозиции, используя EEMD - то, что добавленные ряды белого шума компенсируют друг друга, и средние опоры IMFs в пределах естественного бинарного оконного фильтра, значительно приводя шанс смешивания модовых функций и сохранения бинарного свойства.

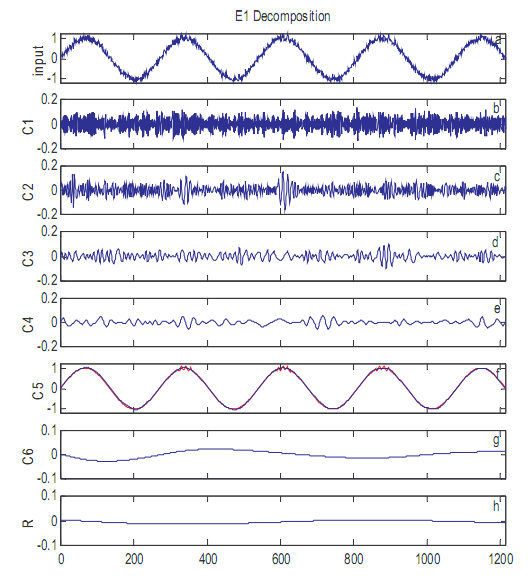
Чтобы пояснять процедуру, данные в иллюстрации 1 используются как пример. Если EEMD осуществлен с добавленным шума, имеющим амплитуду 0.1 среднеквадратичных отклонений первоначальных данных только для одного испытания, результат дан в иллюстрации 3. Здесь низкая частотная составляющая уже извлечена почти отлично. Высокие частотные составляющие, однако, похоронены в шуме. Заметьте это, когда количество увеличений элементов множества, высокочастотный прерывистый сигнал появляется, как дисплеи иллюстрации 4. Ясно, фундаментальный сигнал (C5) представлен почти совершенный, так же как прерывистые сигналы, если C2 и C3 добавлены вместе. Это снабжает первый пример, чтобы продемонстрировать, что помогавший шум анализ данных, используя EEMD значительно улучшает возможность распаковки сигналов в данных, и представляет большое уточнение метода EMD.