Geum.ru

Развитие научных основ и разработка совмещенных методов обработки металлов давлением, обеспечивающих экономию материальных и энергетических ресурсов

Вид материалаАвтореферат

Содержание


Основное содержание работы
2 Научные основы использования возможностей сил трения в
Подобный материал:
1   2   3   4

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ


1 Анализ современного уровня развития

совмещенных методов обработки металлов давлением

В данном разделе проведен анализ имеющихся в информационных источниках материалов по совмещенным методам ОМД, использующим продольную силу, обеспеченную переводом реактивных сил трения в активное состояние для повышения эффективности формоизменения за счет экономии материальных и энергетических ресурсов.

В результате проведенного анализа литературных и патентных материалов установлено следующее:

– в настоящее время у нас в стране и за рубежом активно разрабатываются совмещенные методы ОМД. Наиболее известны работы В. Aвитцур, Р. Грцуб, Я.М. Охрименко, В.Н. Щербы, Н.Н. Довженко, С.Б. Сидельникова, В.Н. Корнилова, С.М. Жучкова, Ю.В. Горохова, С.В. Беляева и др., в которых заложены основы новых технологий;

– аналитический обзор состояния работ по использованию сил трения в очаге деформации позволил классифицировать известные совмещенные методы ОМД и выявить наиболее перспективные направления исследований. Перспективность изучения совмещения методов ОМД обусловлена, с одной стороны, весьма широкими возможностями применения и высоким ожидаемым эффектом, с другой стороны малой изученностью вопроса в практическом и теоретическом плане;

– обзор области использования совмещенных методов ОМД показал, что они находятся на начальном этапе разработки и далеко не все возможности в техническом и технологическом плане исследованы и применены на практике;

– анализ литературы позволил установить, что в теоретическом плане совмещенные методы ОМД мало изучены, а немногочисленные материалы затрудняют их промышленное использование. Определены наиболее перспективные в плане развития и возможной экономии материальных и энергетических ресурсов совмещенные методы: прокатка в приводной–неприводной клети, прокатка – разделение неприводным инструментом, прокатка – прессование, работа системы очаг деформации – валковая арматура.

Выводы литературного анализа позволили определить основные направления исследований и сформулировать задачи диссертационной работы.

2 Научные основы использования возможностей сил трения в

очаге деформации при прокатке для реализации совмещенных

методов обработки металлов давлением

Процесс прокатки реализуется благодаря использованию сил трения на контакте металла с вращающимися валками, которые втягивают полосу в сужающееся пространство, обеспечивая формоизменение. Согласно классическим представлениям теории прокатки на установившейся стадии процесса в очаге деформации присутствуют зона отставания, где силы трения со стороны валков направлены по ходу прокатки, являясь активными, и зона опережения, где силы трения направлены в противоположную сторону движения металла, создавая реактивное действие и снижая эффективность процесса прокатки (рисунок 1). Момент прокатки складывается из момента активных сил трения (Макт) и момента реактивных сил (Мреак):

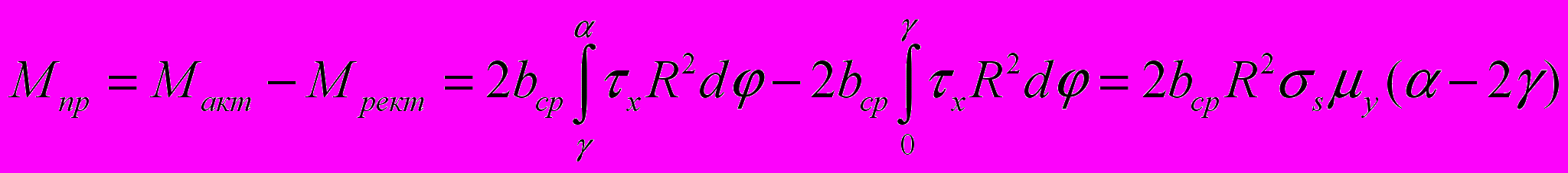, (1)

где bср – средняя ширина, мм; α – угол захвата, рад; R – радиус валков, мм; σs – сопротивление деформации, МПа; γ – нейтральный угол, рад; μу – коэффициент трения на установившейся стадии процесса.



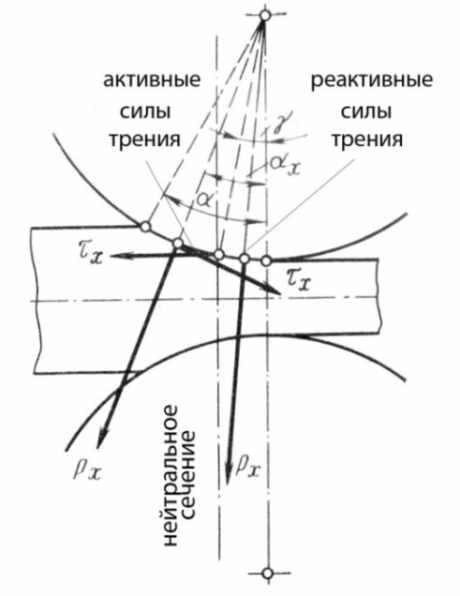
Рисунок 1 – Схема сил, действующих в двухзонном очаге деформации при

прокатке

При постоянных ширине, радиусе валков, сопротивлении деформации, коэффициенте трения, угле захвата момент прокатки будет зависеть от нейтрального угла, изменение которого при прочих равных условиях возможно только при реализации совмещенных методов ОМД. При изменении нейтрального угла от γ до 0 (реактивные силы трения переходят в активные) момент прокатки увеличивается, достигая максимального значения, что позволяет подвести в очаг деформации большую мощность, использовав ее для дополнительной обработки заготовки. Разностью между максимальным значением момента (γ=0) и моментом, соответствующим нейтральному углу при установившейся стадии процесса, является дополнительный момент (Мдоп), который, в свою очередь, находится как произведение продольной силы (Q1) на радиус валка:

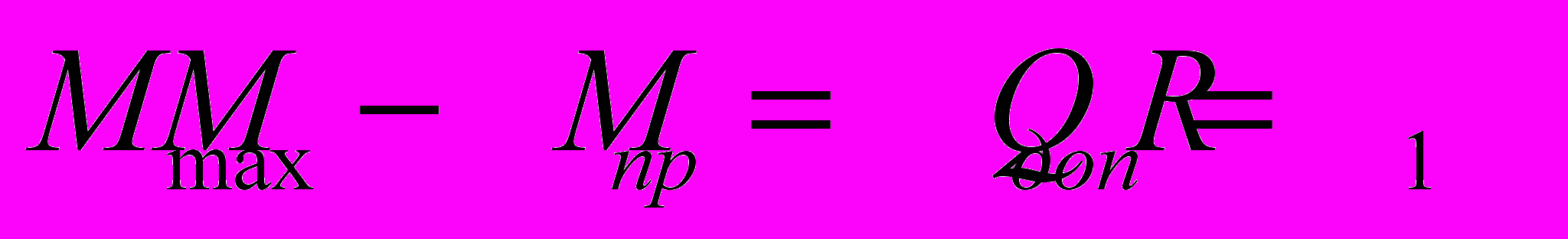, (2)

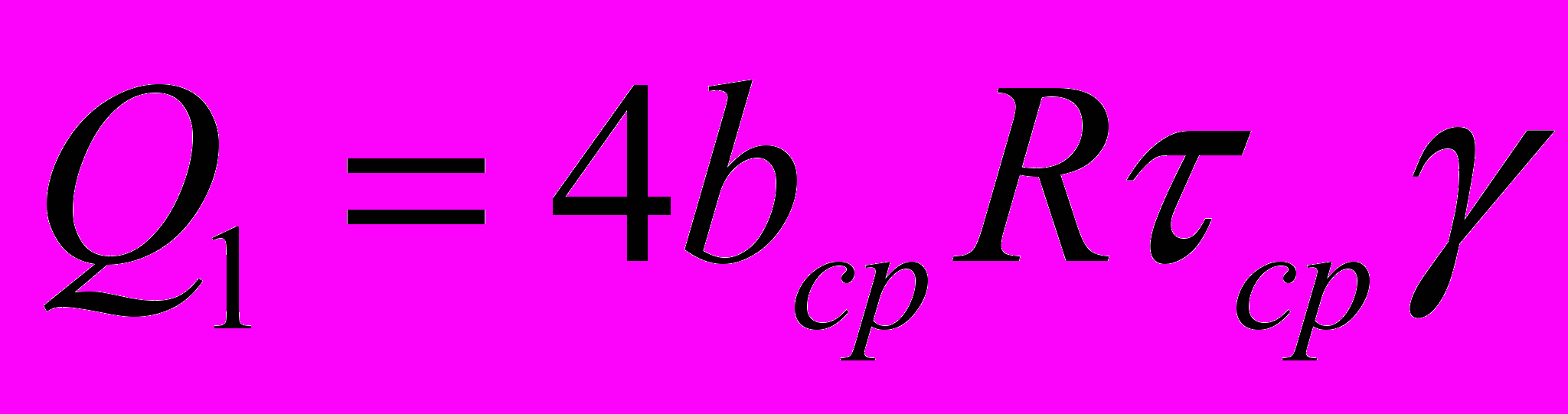. (3)

Возможности и перспективы совмещенных методов ОМД зависят от величины продольной силы, обеспеченной переводом реактивных сил трения в активное состояние. Поэтому для успешной реализации совмещенных методов ОМД в первую очередь необходимо оценить перспективность использования продольной силы, найти зависимости для ее определения, учитывающие не только условия деформирования, но и форму калибров, изучить влияние использования продольной силы при совмещении методов ОМД на протяженность зон на контактной поверхности в очаге деформации и получить отсутствующие в литературе зависимости для их определения. Изменение протяженности зон скольжения и прилипания при использовании продольной силы приводит к изменению энергосиловых параметров процесса прокатки, что требует дополнительного изучения. Решение поставленных вопросов позволяет заложить научные основы, необходимые для практической реализации совмещенных методов ОМД.

Для оценки перспективности применения продольной силы при совмещении методов ОМД предложен показатель возможностей очага деформации (КN):

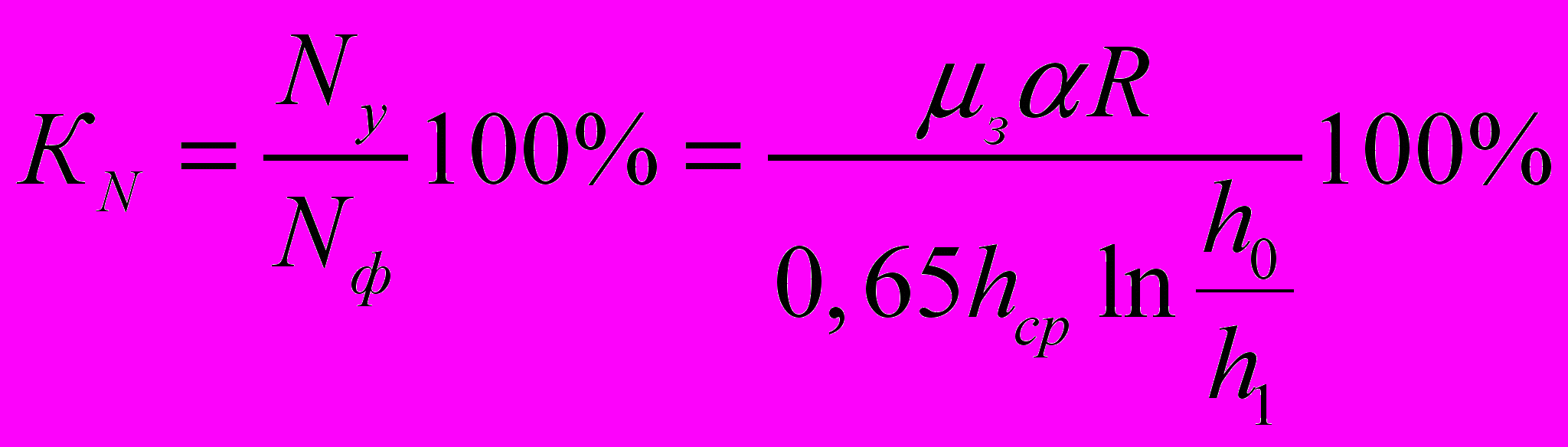, (4)

где Nф – мощность формоизменения, Вт; Nу – мощность, которую могут обеспечить силы трения, Вт; μз – коэффициент трения при захвате; h0, h1, hср –начальная, конечная и средняя толщина полосы соответственно, мм.

В результате проведенных аналитических исследований (рисунок 2) установлено, что наиболее полно силы трения на контакте используются при α/μз=1, однако и в этих условиях КN=170 – 200 %, то есть переводя реактивные силы трения в активное состояние, можно обеспечить полезный момент прокатки (полезную мощность) в 1,7–2,0 раза больше, чем необходимо на деформирование, и использовать его для совмещения методов ОМД. С уменьшением α/μз значение показателя КN увеличивается, достигая в исследуемом диапазоне величины 280%. При прокатке в прямоугольном калибре показатель КN в 1,2 – 1,35 раза больше, чем при прокатке в гладких валках в сопоставимых условиях, что объясняется увеличением активной площади очага деформации за счет боковых стенок калибра. Такой большой невостребованный потенциал процесса прокатки дает основание считать совмещенные методы ОМД перспективными.

На следующем этапе изучения вопроса была поставлена и решена задача по определению продольной силы при начальных условиях: 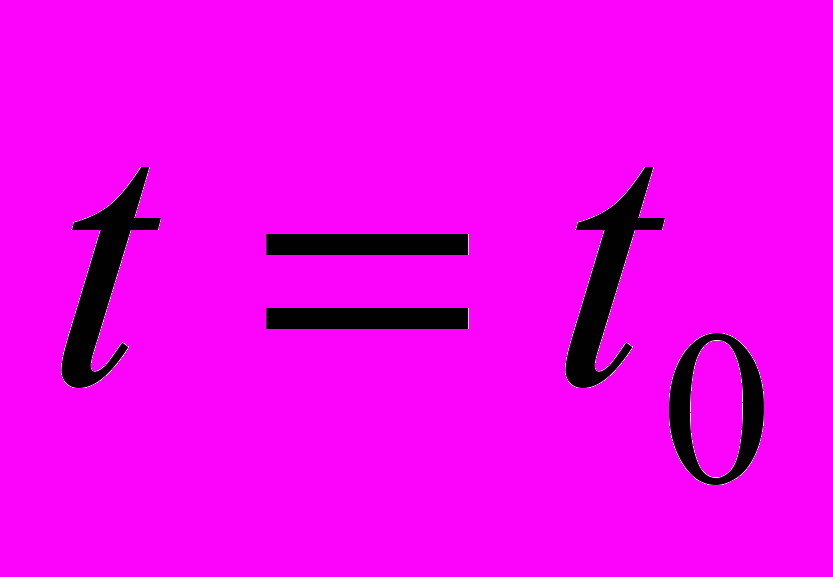, , 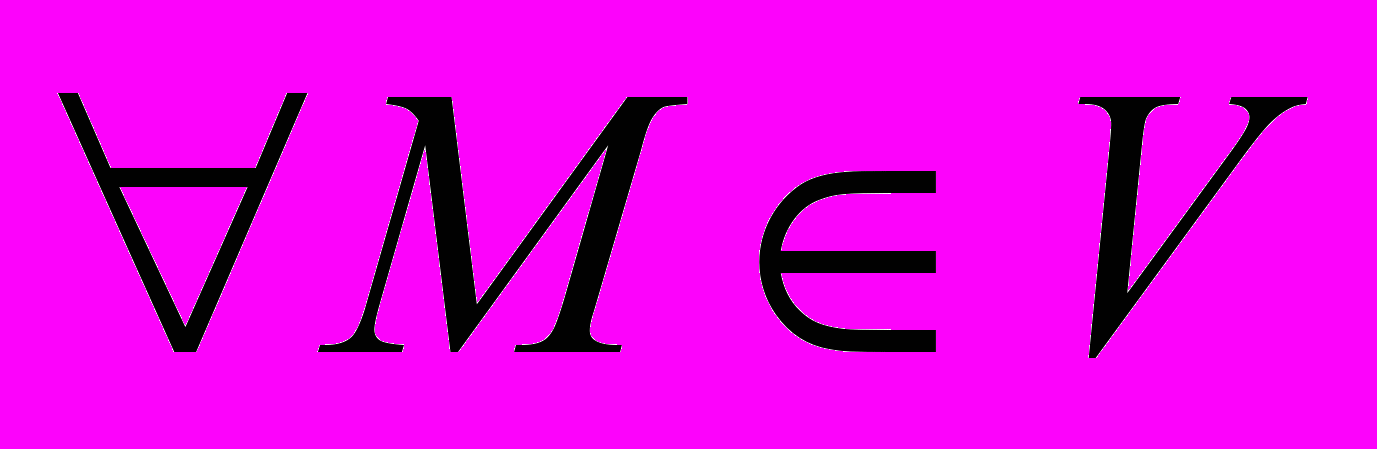, , 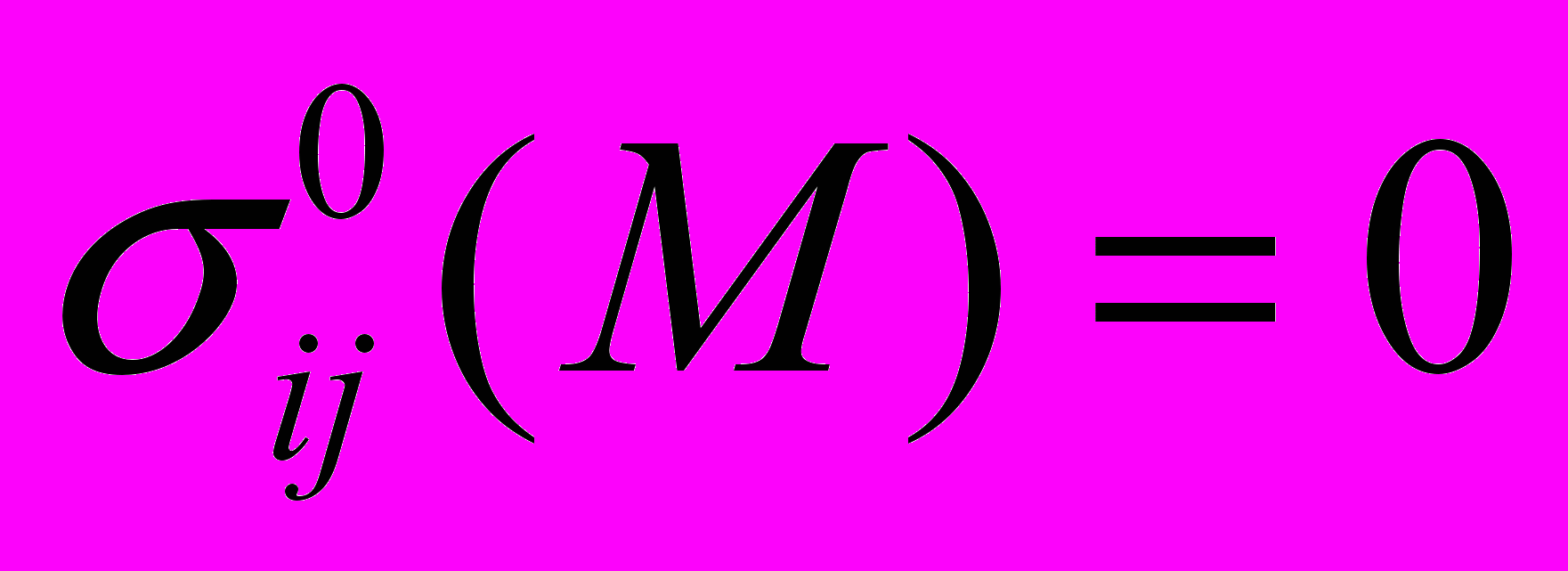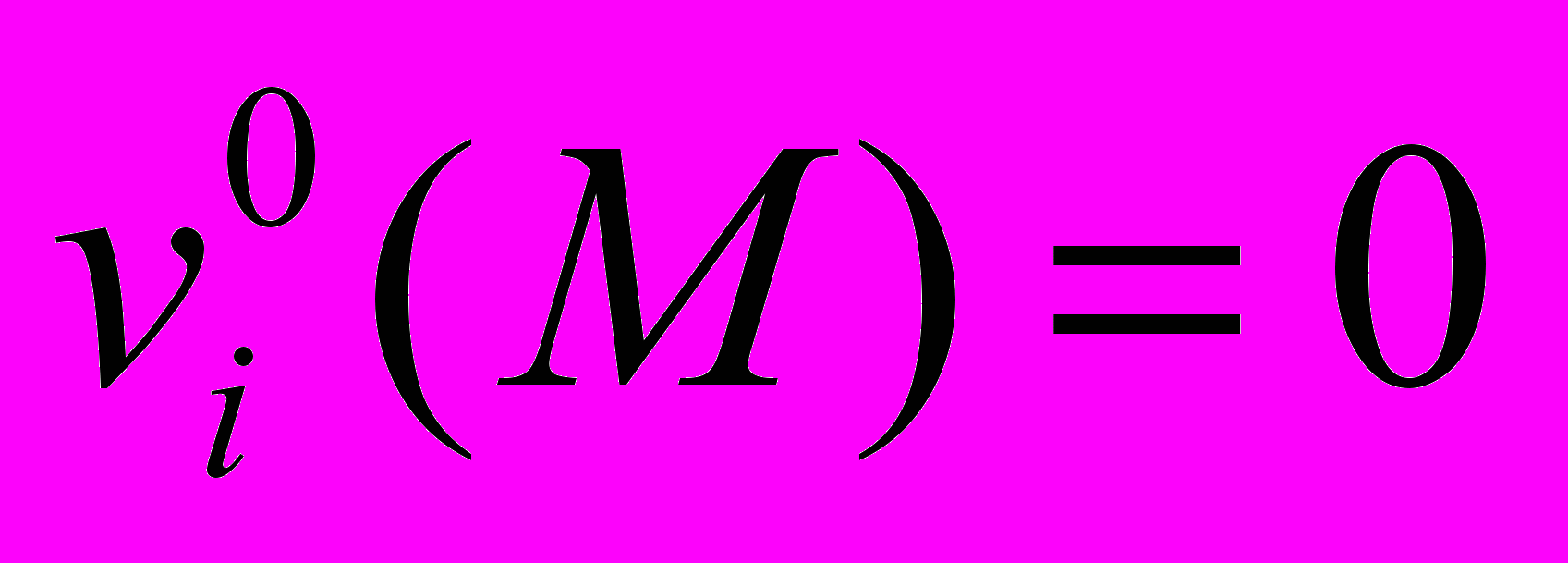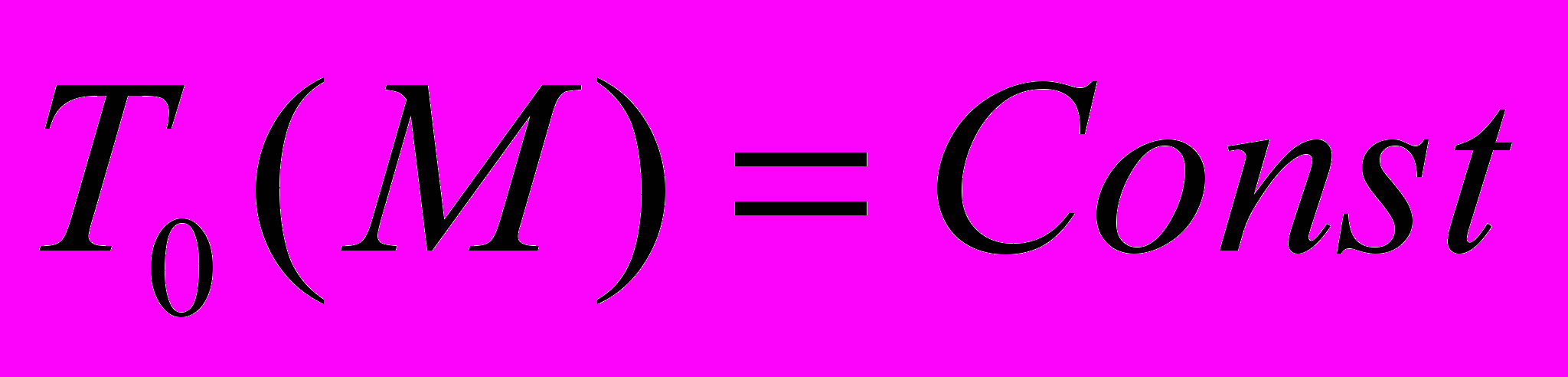. Граничные условия, отображающие взаимодействие деформируемого тела с окружающей средой, оговариваются следующими допущениями: на установившейся стадии процесса прокатки на полосу действуют внешние силы заднего натяжения (подпора) (Q0) и переднего подпора, результирующая внешних сил полностью уравновешивается продольной силой (Q1), в очаге деформации действуют средние нормальные (рср) и касательные (τср) давления, на участке скольжения действует закон трения Кулона-Амонтона .



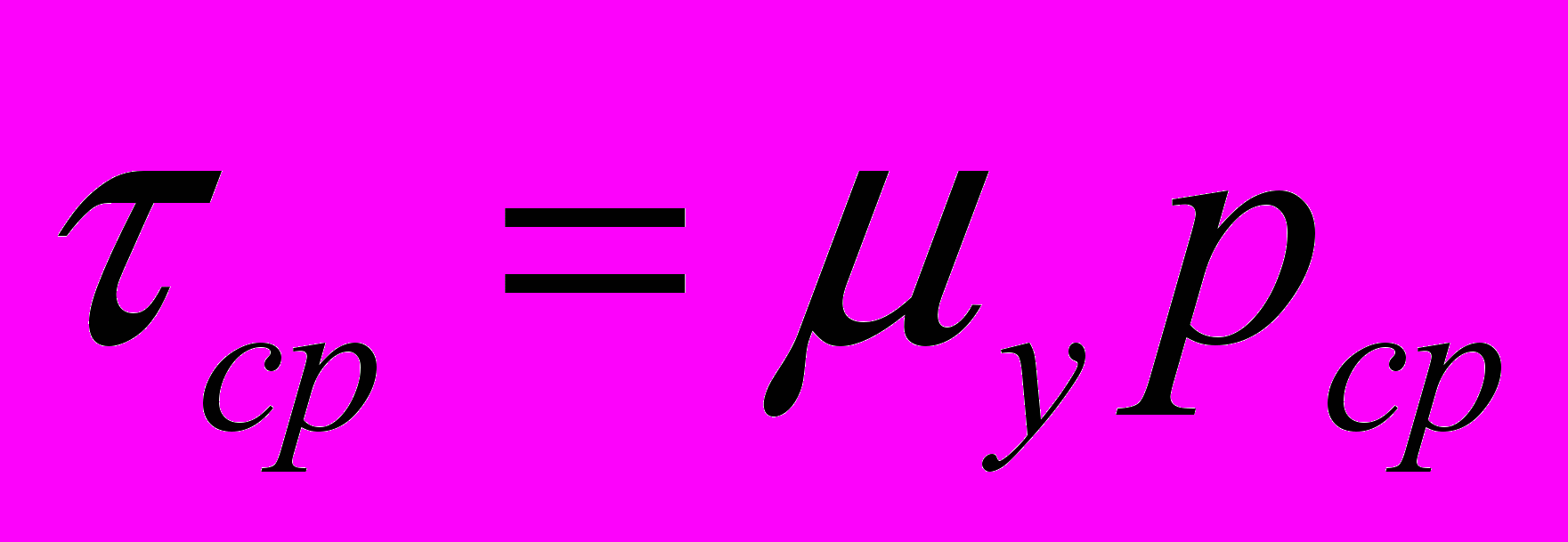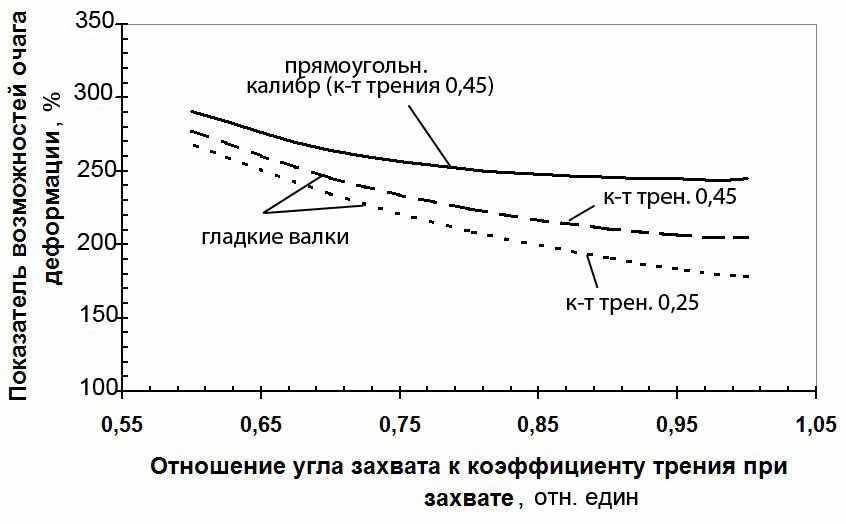
Рисунок 2 – Зависимость показателя возможностей очага деформации от отношения α/μз и коэффициента трения при прокатке в гладких валках и

прямоугольном калибре

Ввиду важности рассматриваемого вопроса для большей объективности с целью выбора метода решения, максимально учитывающего влияние различных факторов, задача по определению продольной силы при прокатке полосы прямоугольного сечения в гладких валках была решена тремя независимыми методами:

– методом баланса мощностей:

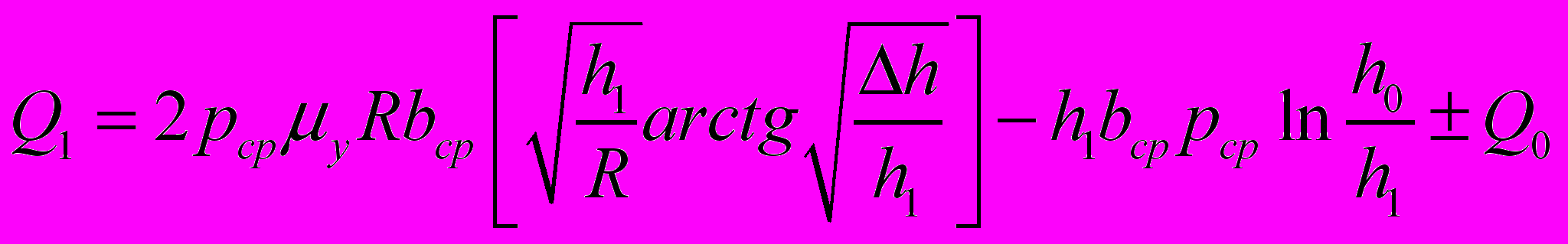; (5)

– решением дифференциального уравнения равновесия элементарного объема в симметричном очаге деформации:

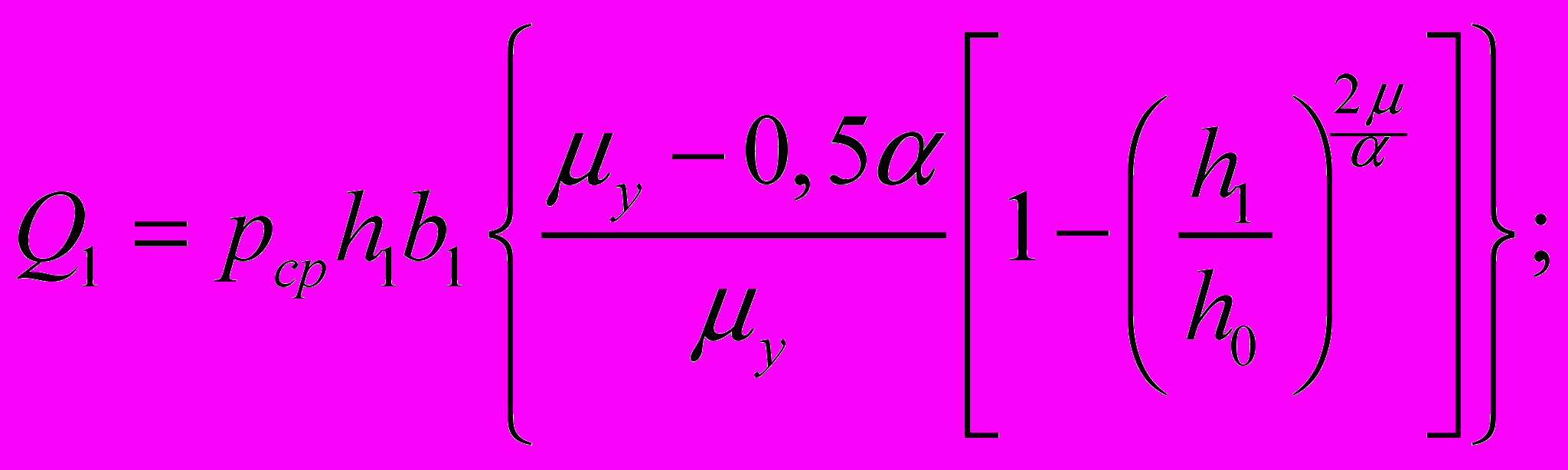(6)

– решением уравнения равновесия сил в очаге деформации:

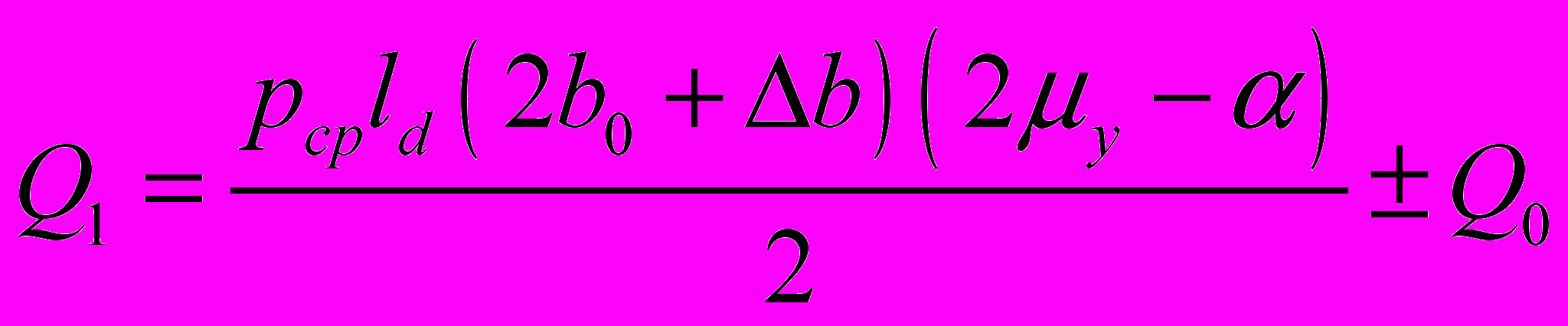, (7)

где ld – длина дуги захвата, мм; b0, b1 – начальная и конечная ширина, мм; ∆b – уширение, мм; ∆h – абсолютное обжатие, мм.

Графический анализ полученных зависимостей (рисунок 3) показал, что все решения дают близкие результаты, а следовательно, они верны, и выбор того или иного метода обусловлен простотой решения и возможностью учета максимального количества факторов. Данным критериям лучше всего подходит метод решения уравнения равновесия сил в очаге деформации, используя который, были получены зависимости для случаев прокатки в вытяжных калибрах:

а) в прямоугольном калибре:

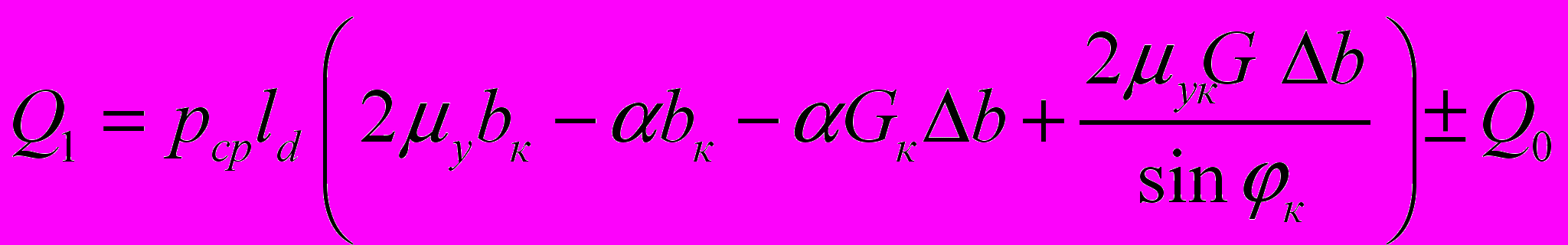, (8)

где bк – ширина дна калибра, мм; Gк – коэффициент заполнения калибра при прокатке; к – угол наклона стенки калибра (выпуск), град;

б) в ромбическом и квадратном калибрах:

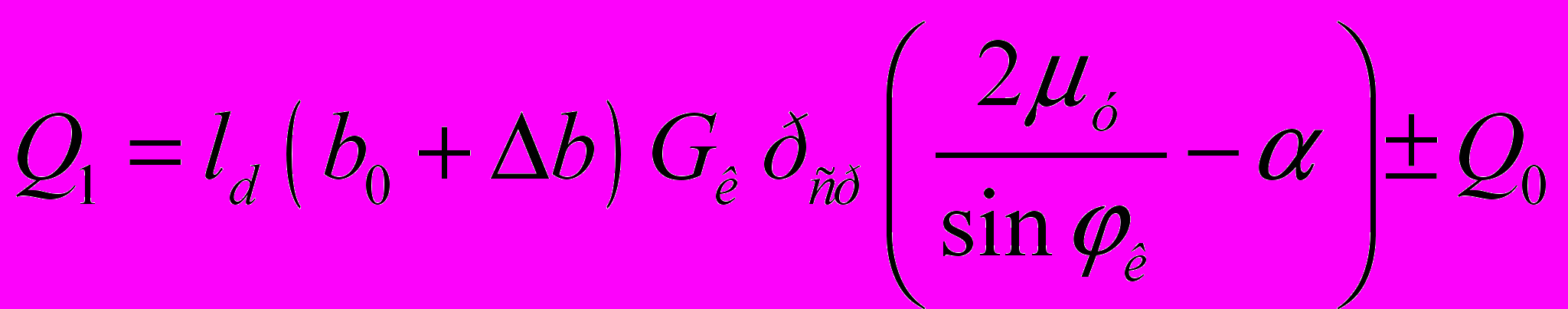, (9)

в) в овальном и круглом калибрах:

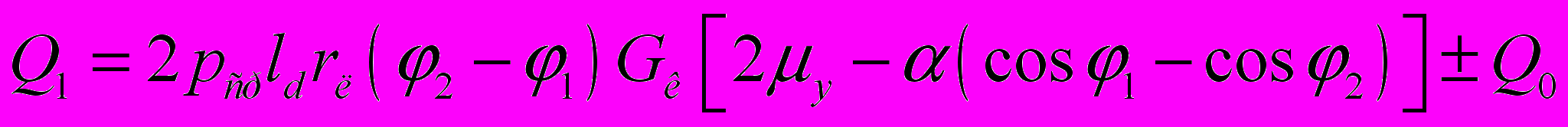, (10)

где rл – радиус овала, мм; φ1, φ2 – углы, описывающие овал (для круга φ1=0о, φ2=90о).

в) в закрытом полосовом калибре:

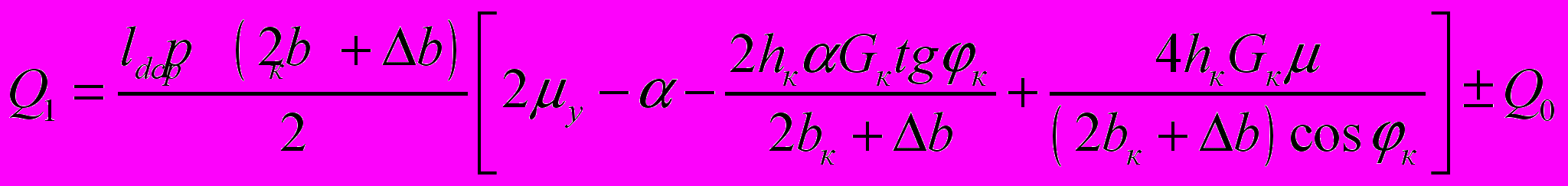, (11)

где hк – высота калибра, мм.



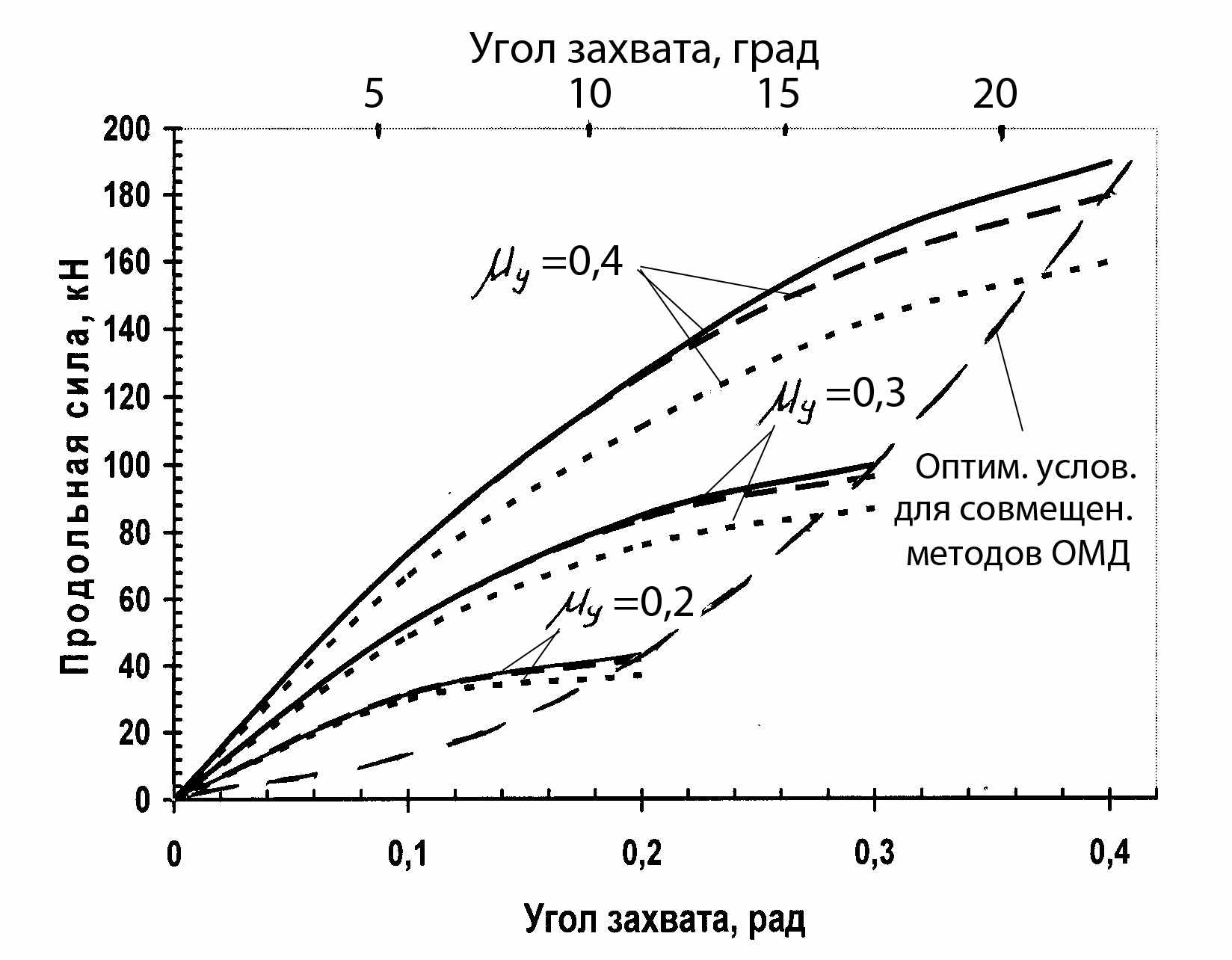
Рисунок 3 – Зависимости продольной силы от угла захвата и коэффициента

трения, рассчитанные ( ̶ ̶ ̶ ) - по формуле 5;( ̶ ̶ ̶ ) - по формуле 7;

(----) - по формуле 6)

Отдельно необходимо остановиться на определении продольной силы при деформировании в калибрах, формирующих сочлененный профиль для последующего продольного разделения неприводным инструментом. Рассмотрены наиболее часто применяемые при формировании сочлененного профиля калибры (начальные и граничные условия те же, что в случае вывода зависимостей 2 – 8), полученные зависимости величины продольной силы, учитывающие условия деформирования и геометрические параметры калибров, имеют вид:

для гладких валков с гребнями:

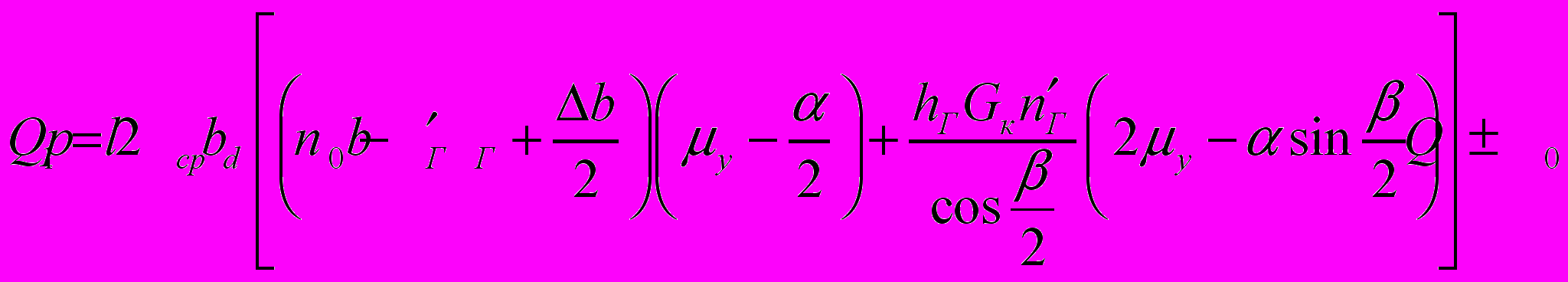, (12)

где hГ, bГ – соответственно высота и ширина гребня, мм; – угол при вершине гребня, град; nʹГ – число гребней;

для сочлененного прямоугольного калибра:

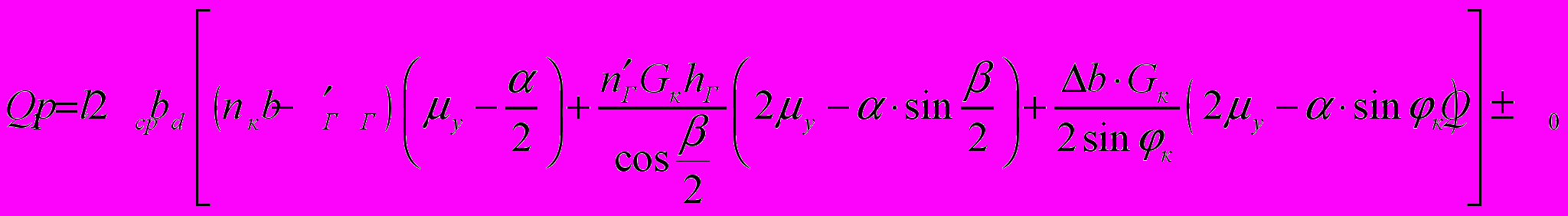; (13)

для сочлененного ромбического (квадратного) калибра:

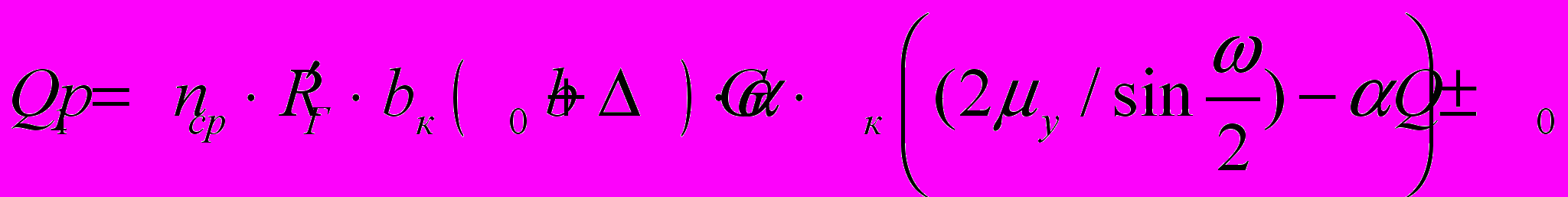, (14)

где – угол при вершине ромба, град;

для сочлененных круглых или овальных калибров:

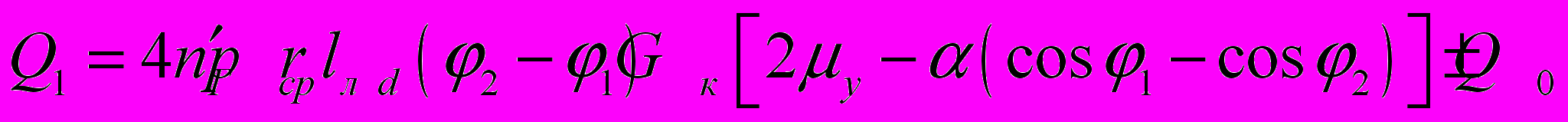. (15)

Практическая реализация совмещенных методов ОМД невозможна без всестороннего экспериментального изучения факторов, влияющих на величину продольной силы и оценки достоверности полученных теоретических зависимостей. С этой целью была создана установка на базе лабораторного стана 150, с помощью которой экспериментально изучено влияние факторов h0/D, степени деформации, коэффициента трения (μу), угла захвата (α) на величину продольной силы (Q1) при прокатке полосы прямоугольного сечения в гладких валках. Значения изучаемых факторов выбирали с учетом моделирования условий сортовой прокатки. Полученные результаты по влиянию величины h0/D, степень деформации (ε) обработаны с использованием метода математического планирования эксперимента и приведены в виде уравнения регрессии (16), данные по влиянию μу и α графически показаны на рисунке 4. Установлено, что из рассмотренных



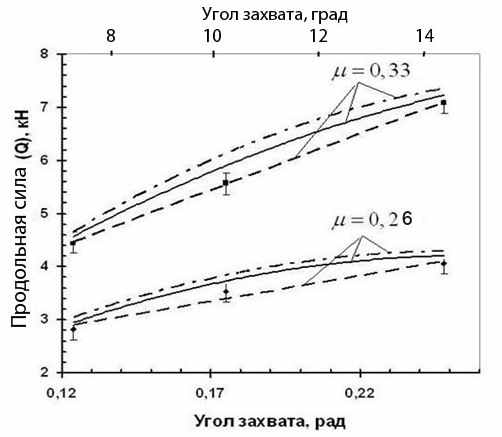
Рисунок 4 – Экспериментальные и теоретические зависимости продольной силы от коэффициента трения и угла захвата

(− - по формуле (7); − · − - по формуле (5); − − - экспериментальные данные)

факторов наиболее существенно на продольную силу влияет коэффициент трения, с ростом которого изучаемый параметр увеличивается:

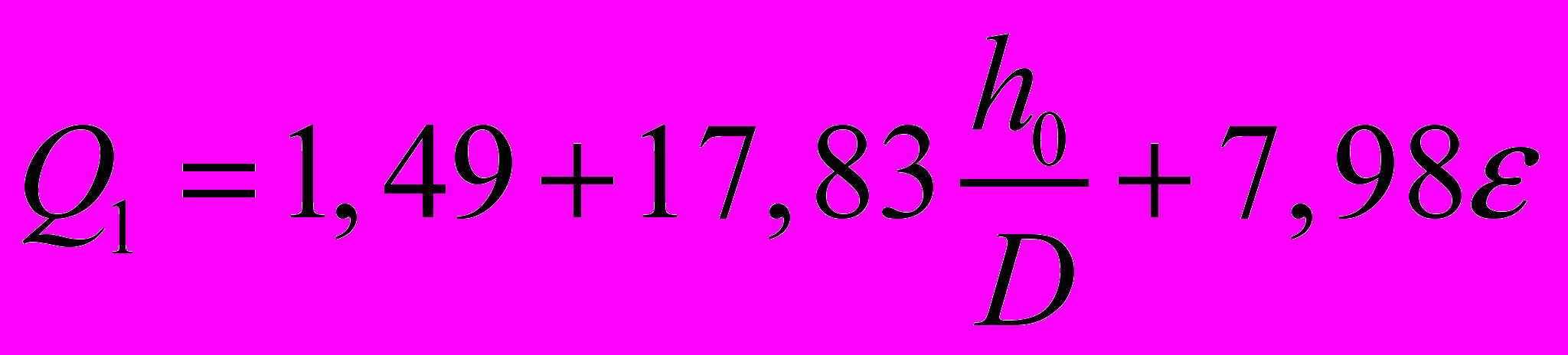. (16)

Изучено влияние прокатки в вытяжных калибрах на величину продольной силы. Результаты исследований приведены на рисунке 5. Установлено, что при прокатке в сопоставимых условиях продольная сила в калибрах больше, чем при прокатке полосы прямоугольного сечения в гладких валках за счет большей активной площади калибра. Экспериментально изучено влияние формы калибра, формирующего сочлененный профиль, и угла захвата на величину продольной силы, а также оценена достоверность теоретических зависимостей (рисунок 6). Установлено, что при формировании сочлененного профиля в калибре величина продольной силы на 23 % больше, чем при использовании гладких валков с выступом. Сопоставление экспериментальных результатов, полученных при прокатке на гладких валках в прямоугольном калибре и в системе квадрат–ромб (рисунок 7), показало, что в прямоугольном калибре с выпуском 20о показатель величины активных сил трения (σ1 /σs), а следовательно, и продольная сила больше ввиду большей площади контакта.



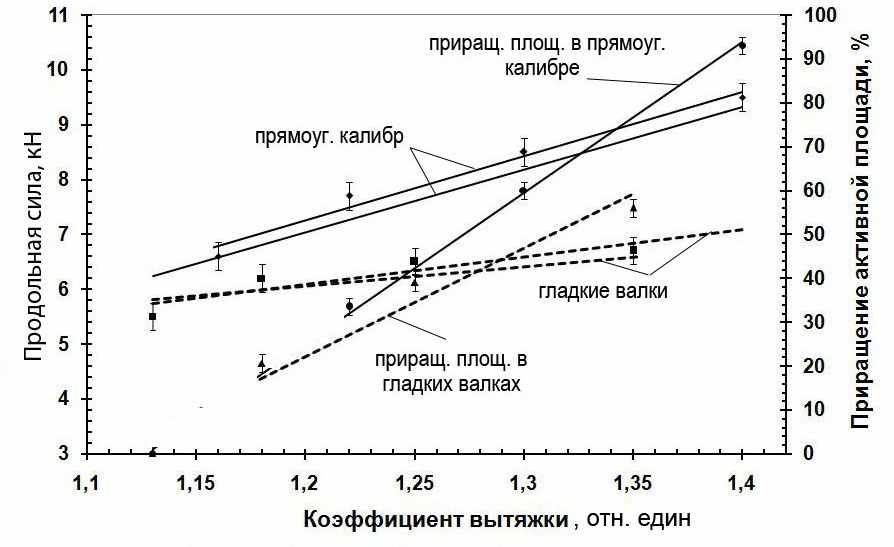
Рисунок 5 – Экспериментальные результаты по изучению прокатки

в прямоугольном калибре и в гладких валках на величину продольной силы

Экспериментальный материал использовался для проверки точности полученных теоретических зависимостей, оценивающих величину продольной силы. В результате проверки установлено, что расчетные величины продольной силы хорошо согласуются с данными экспериментов (ошибка аппроксимации 6 – 8 %).

Рассмотрение вопроса использования совмещенных методов ОМД было бы не полным без изучения протяженности зон на контактной поверхности в очаге деформации. Несмотря на важность вопроса в теоретическом и практическом планах, большое внимание к проблеме со стороны таких видных ученых, как А.И. Целиков, А.П. Чекмарев, В.С. Смирнов, И.М. Павлов, О.Г. Музалевский, И.Я. Тарновский, Д.И. Пирязев, В.П. Северденко, Н.М. Санько и др., в литературе отсутствует теоретическое решение данной задачи, позволяющее определить протяженность зон скольжения и прилипания на контактной поверхности в очаге деформации при прокатке. Решая совместно уравнения равновесия сил и моментов в очаге деформации на установившейся стадии процесса при допущении,



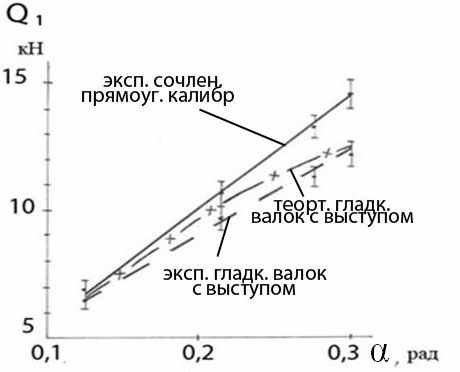
Рисунок 6 – Экспериментальные и теоретические данные по величине

продольной силы, создаваемой клетью, формирующей сочлененный профиль



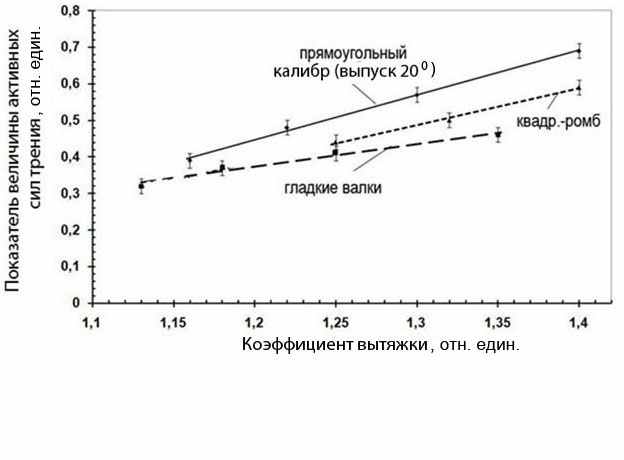
Рисунок 7 – Экспериментальные зависимости показателя активных сил трения от формы калибра и коэффициента вытяжки

что в очаге деформации действуют средние контактные силы трения и нормальные напряжения, 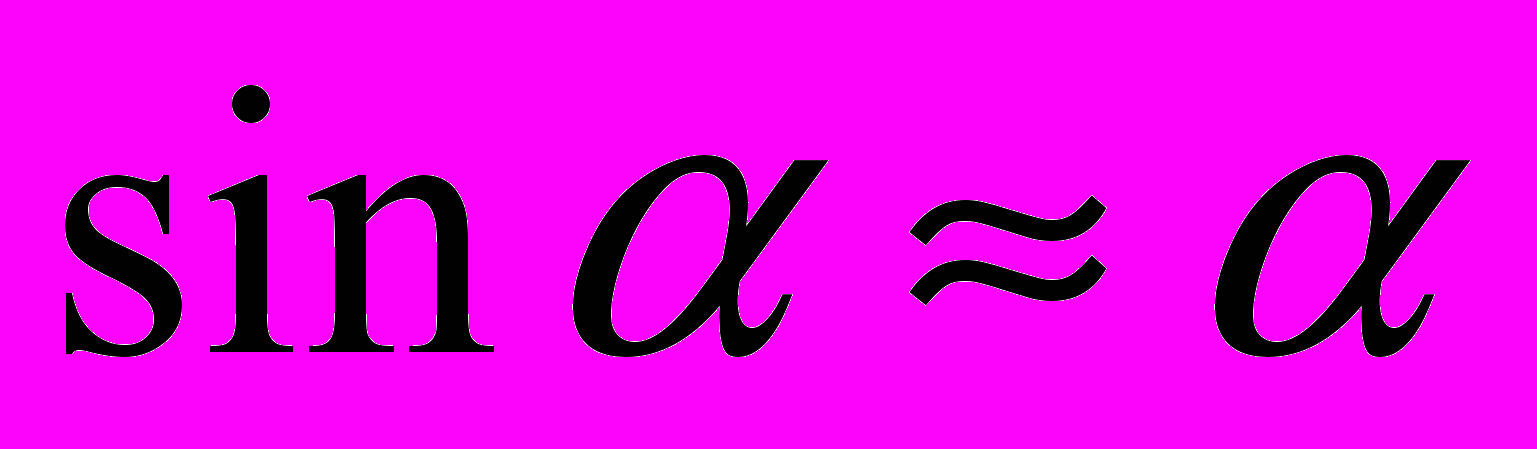, , 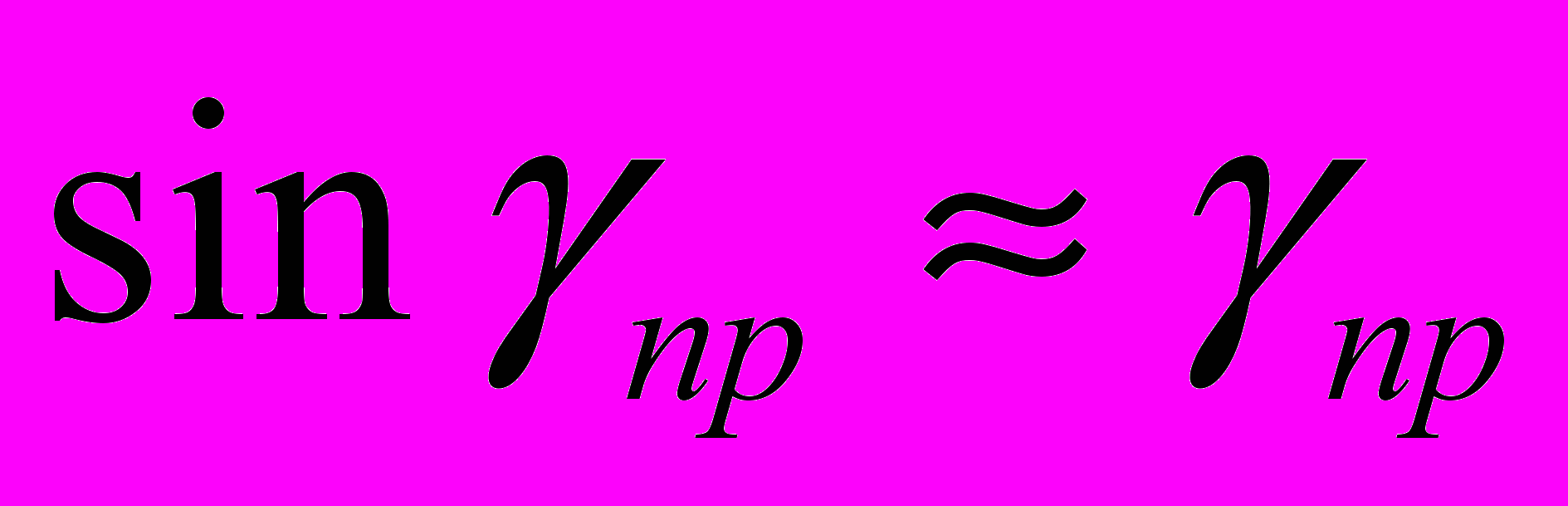, , 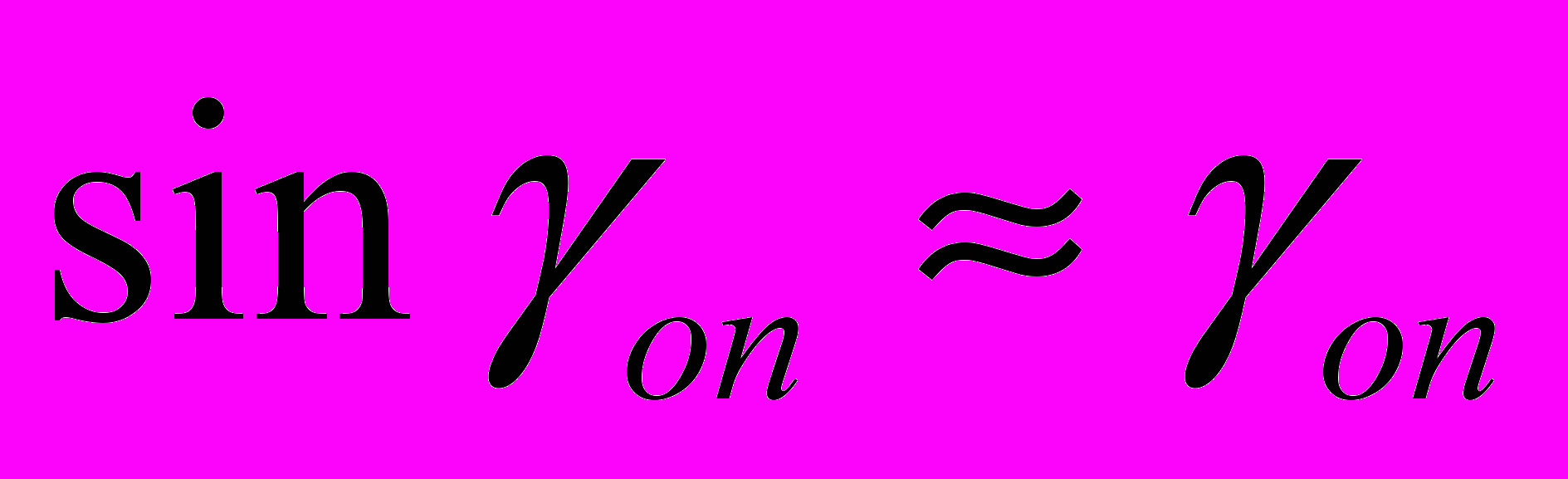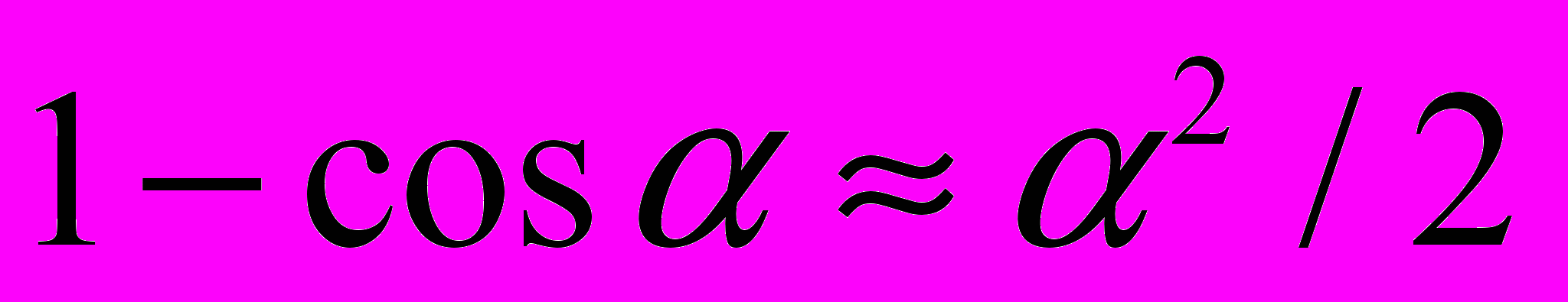уширение в основном происходит в зоне отставания, а в зоне опережения – отсутствует, получены зависимости, позволяющие определить углы, характеризующие протяженность зон опережения (оп), прилипания (пр), отставания (от) на контактной поверхности в очаге деформации применительно как к классической прокатке, так и к совмещенным методам ОМД:

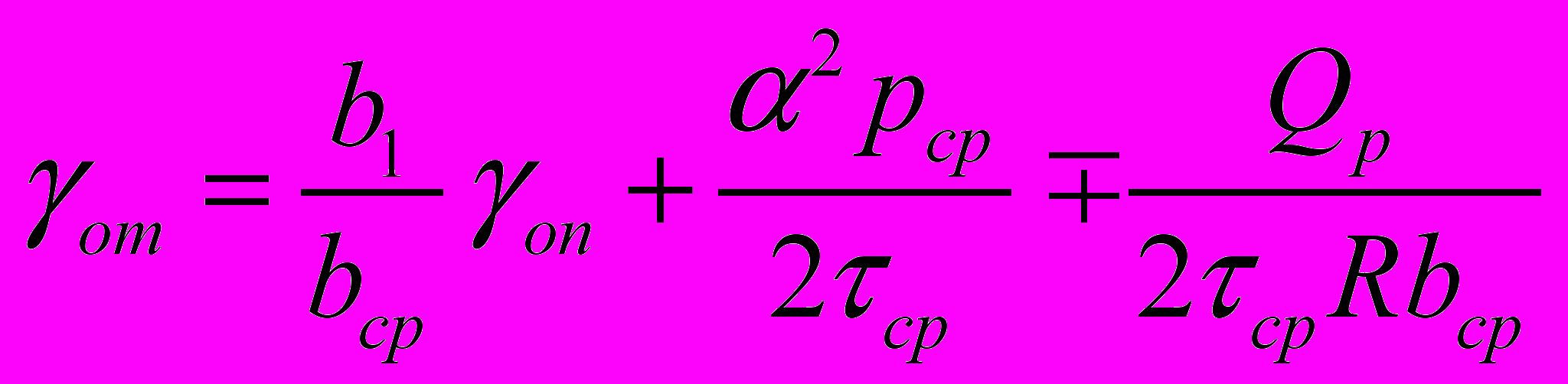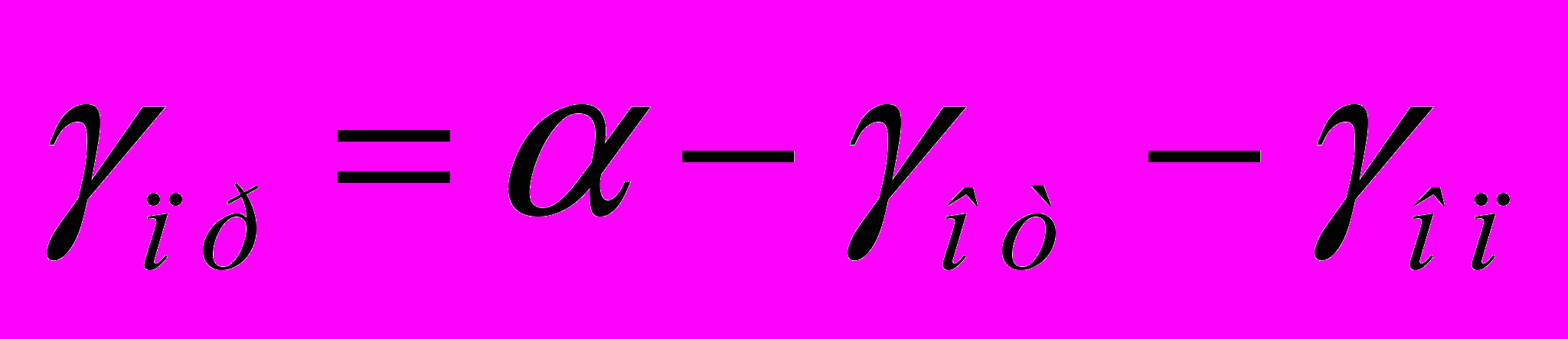; ; (17)

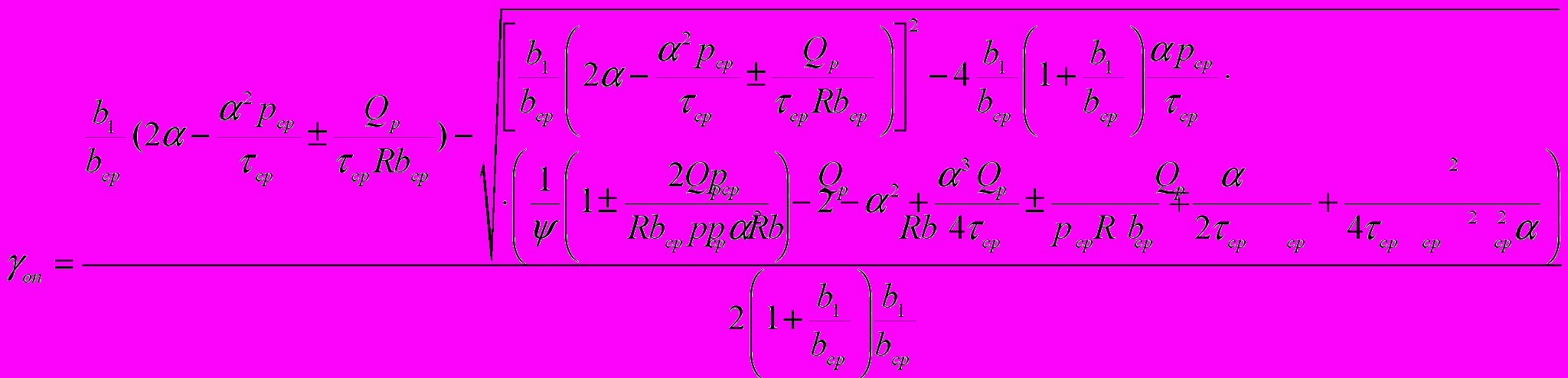; (18)

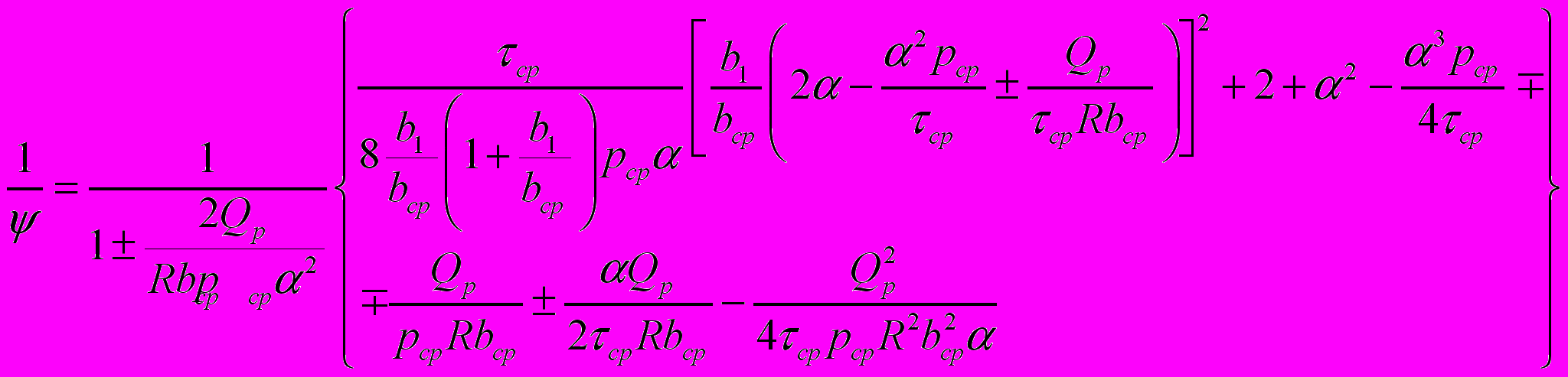, (19)

где Qр – результирующая внешних сил, н; ψ – коэффициент положения плеча равнодействующей.

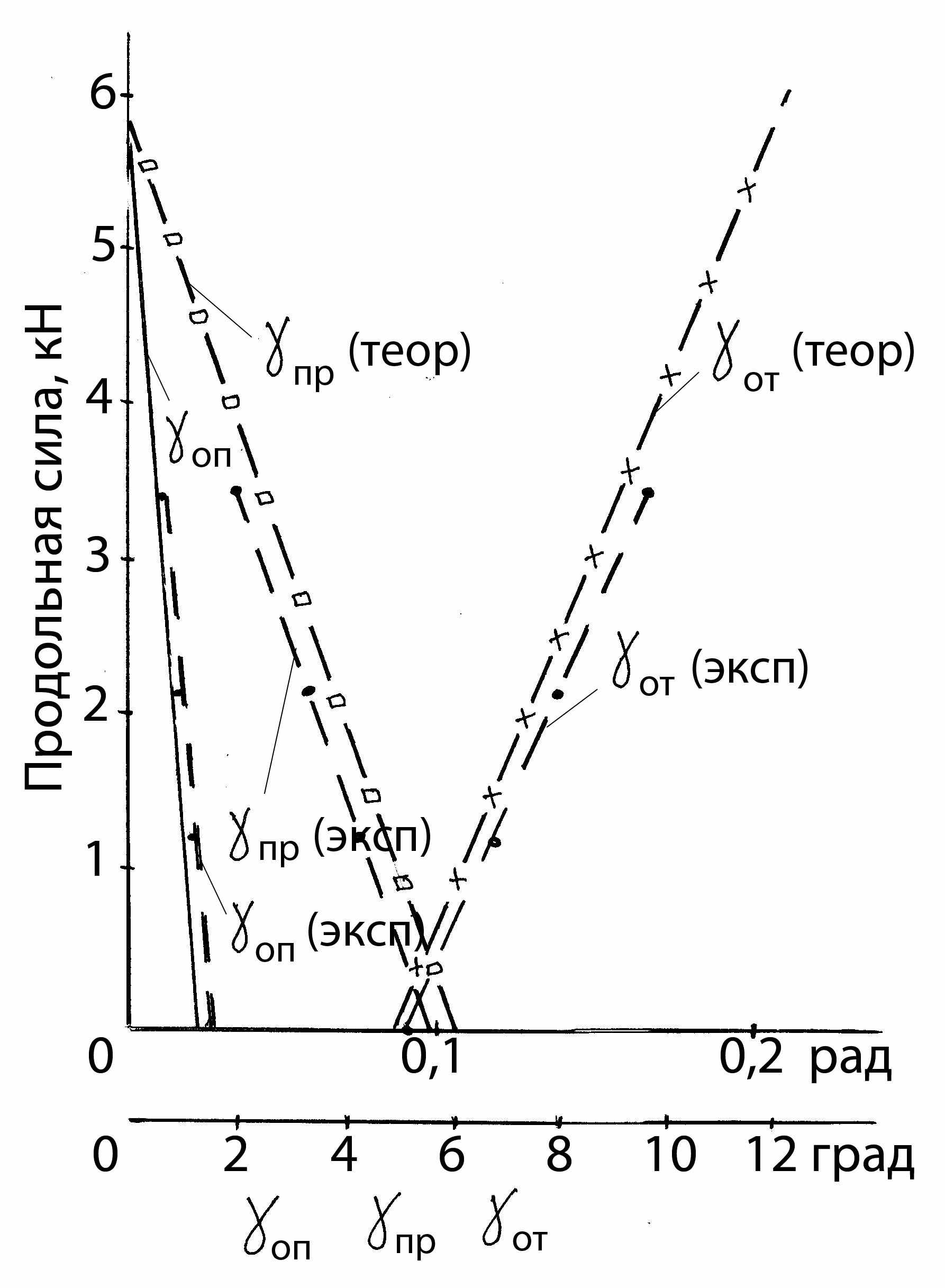
Для проверки достоверности полученных теоретических зависимостей, определения связи сил трения с расположением зон скольжения и прилипания создана оригинальная установка (а.с. № 1233971), позволяющая регистрировать в динамике при помощи скоростной киносъемки смещения металла на контактной поверхности в очаге деформации при прокатке (рисунок 8, а). Используя разработанную методику и установку с привлечением аппарата математического планирования эксперимента, получены статистически достоверные зависимости, показывающие влияние параметров h0/D, b0/ld, степени деформации (ε), моделирующих условия сортовой прокатки на углы, характеризующие протяженность зон скольжения и прилипания на контактной поверхности в очаге деформации:




а б

Рисунок 8 – Установка для регистрации перемещений на контактной

поверхности очага деформации при прокатке и кадры кинограммы (а), а также график зависимости продольной силы от протяженности зон (б)

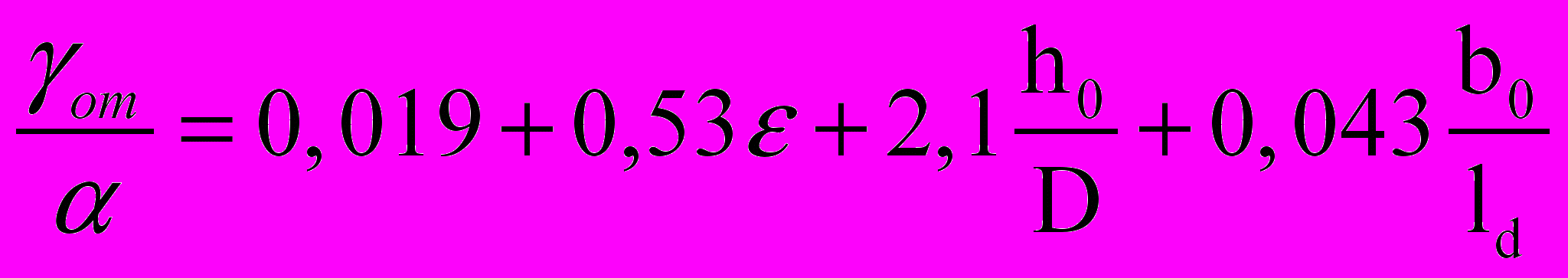; (20)

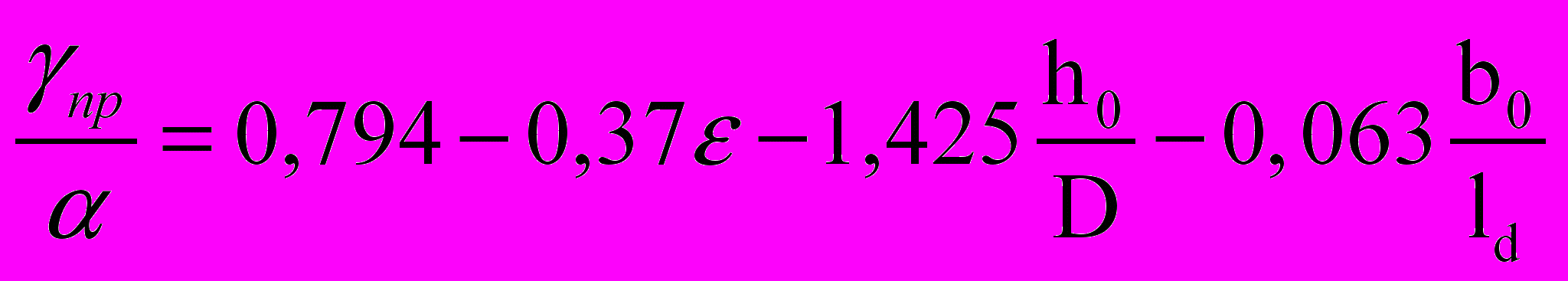; (21)

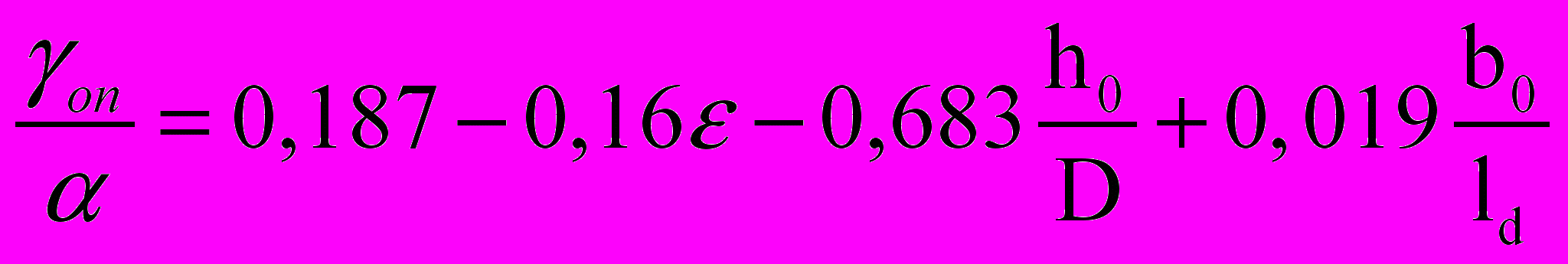, (22)

где D – диаметр валков, мм.

Изучено изменение продольной силы от углов, характеризующих протяженность зон скольжения и прилипания (рисунок 8, б). Установлено, что с уменьшением протяженности зон опережения и прилипания продольная сила увеличивается, достигая максимального значения, когда в очаге деформации остается только зона отставания. Экспериментальные данные согласуются с предложенными теоретическими зависимостями (17 – 19).

Полученная информация по протяженности зон скольжения и прилипания представляет большой практический интерес и является научной основой для разработки методики расчета энергосиловых параметров классических процессов прокатки и совмещенных методов ОМД.

Изучением энергосиловых параметров процесса прокатки занимались многие видные ученые, из которых следует особо отметить Т. Кармана, Е. Орована, А.И. Целикова, С. Экелунда, А.П. Чекмарева, В.С. Смирнова, А.А. Королева, Г. Валквиста, Э.А. Гарбера, Б.В. Кучеряева и др. Однако, несмотря на большое количество материала по данному вопросу, практически неизученным остается процесс прокатки с подпором. Развитие совмещенных методов ОМД вызывает необходимость изучения этого вопроса в теоретическом и практическом плане. По мнению большинства исследователей из всего многообразия известных теоретических моделей для определения усилия прокатки наилучшие результаты дает модель, предложенная А.И. Целиковым. Однако отсутствие в литературе зависимостей для определения протяженности зон скольжения и прилипания на контактной поверхности в очаге деформации при прокатке не позволило использовать все возможности модели. Как известно, при нахождении усилия прокатки по методике А.И. Целикова условия трения на контакте описываются коэффициентом n,, который изменяется в широких пределах (от 1 до 6) и определяет точность расчетов энергосиловых параметров. Предложено решение для уточненного определения коэффициента n с учетом протяженности зон скольжения и прилипания на контакте при классическом процессе прокатки, развивающее теорию А.И. Целикова в виде:

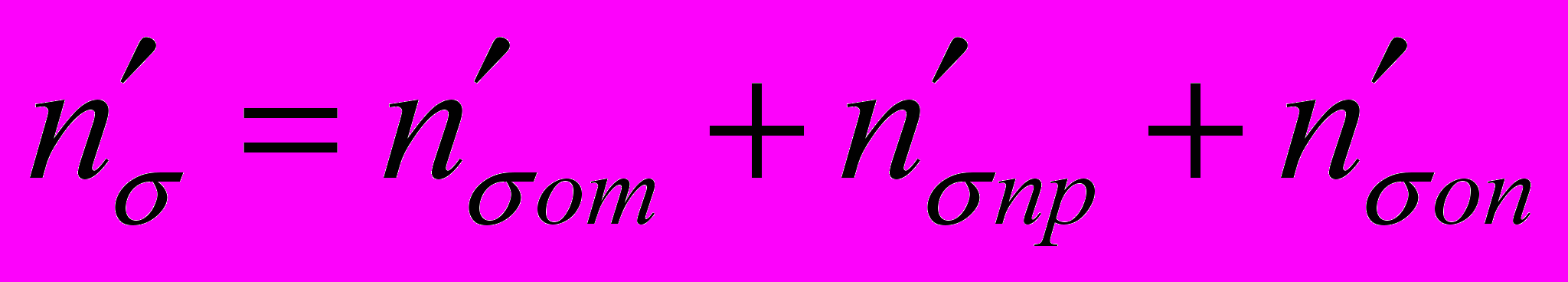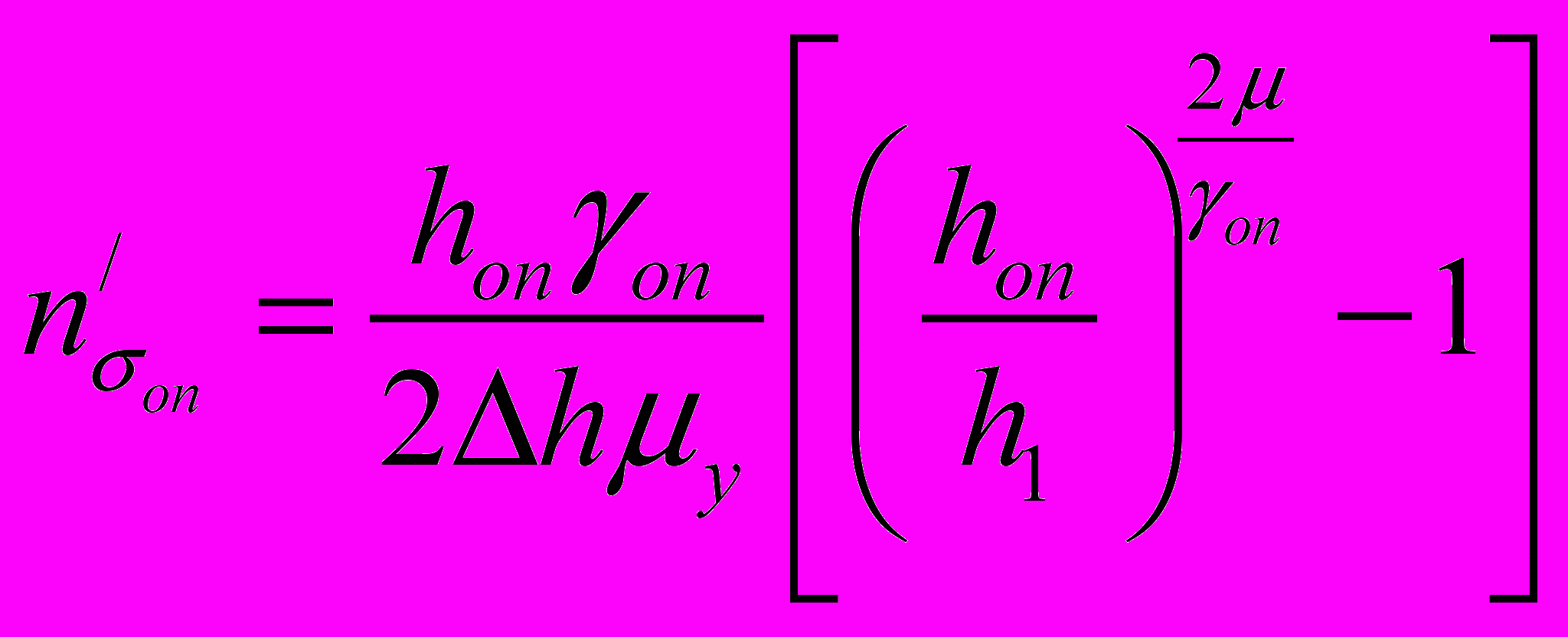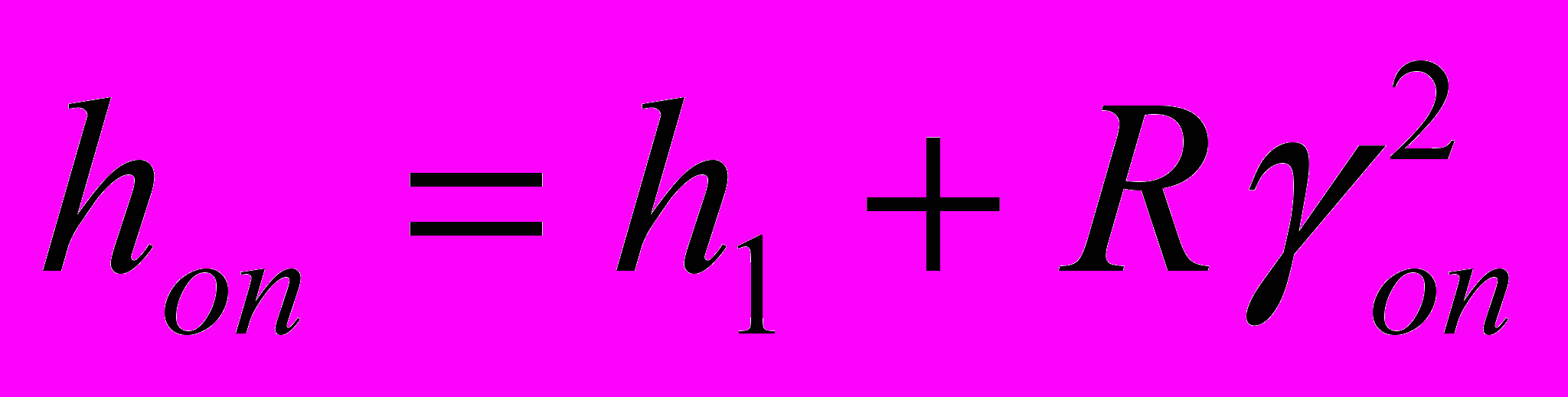; ; ; (23)

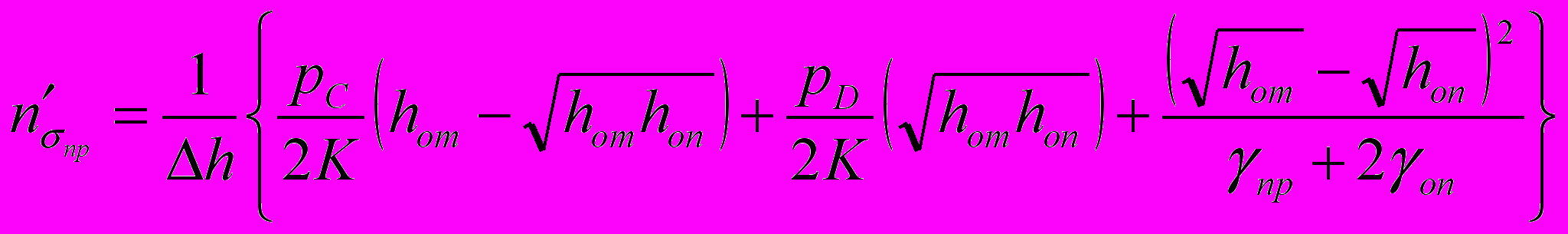; (24)

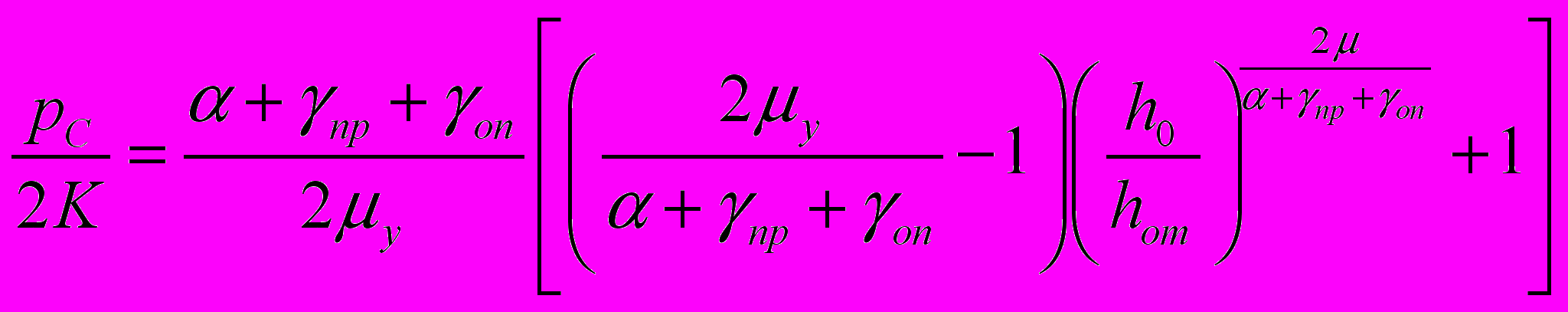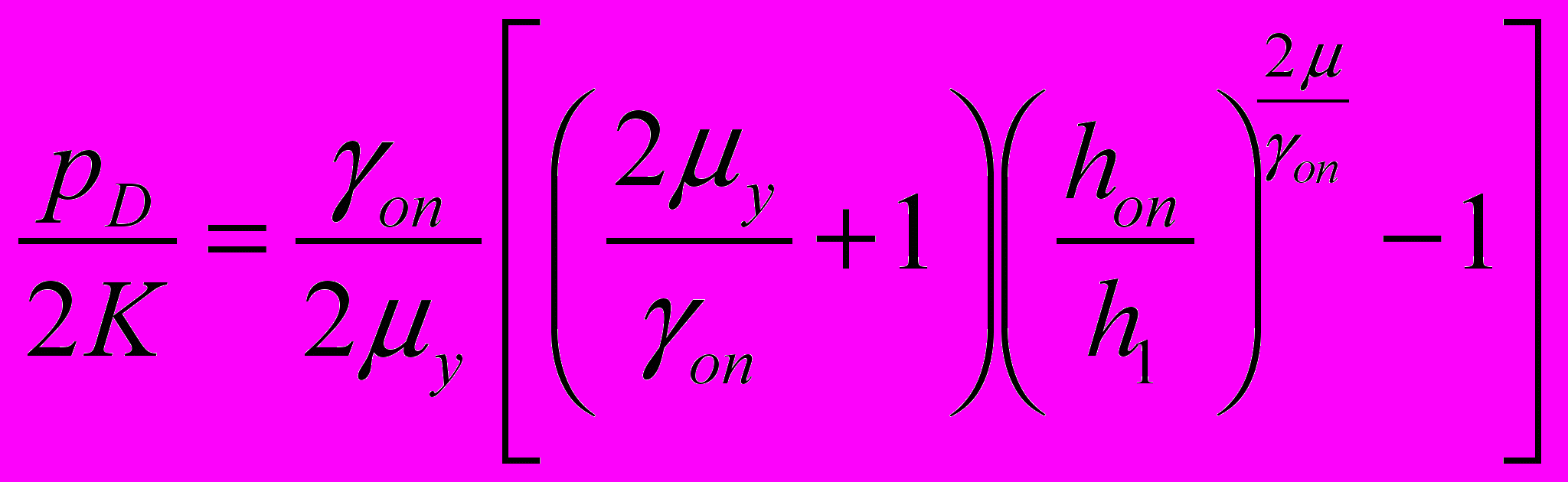; ; (25)

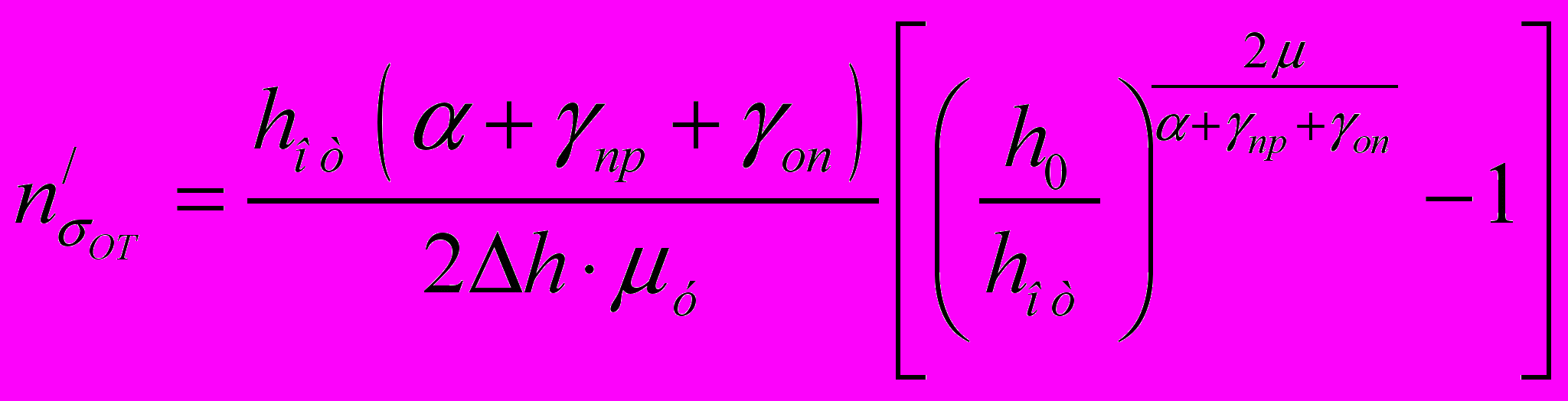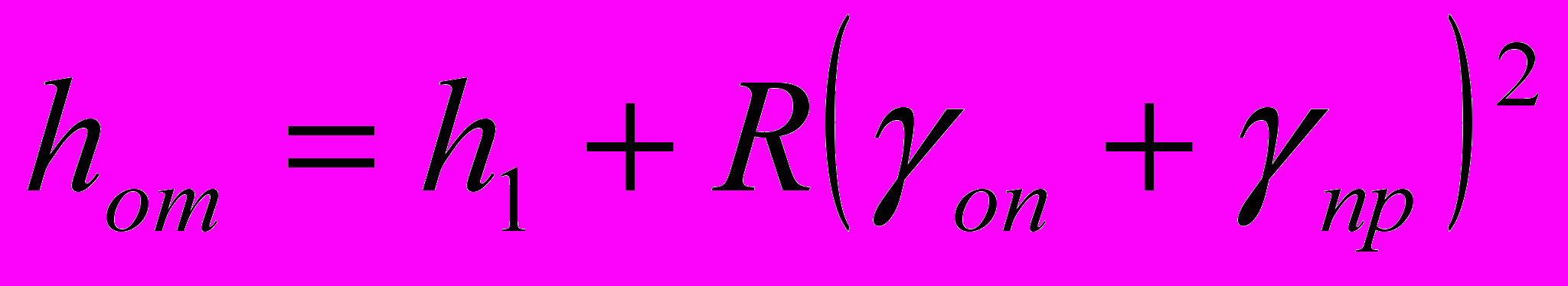; , (26)

где hоп, hот – высота полосы на границе между зонами опережения и прилипания, отставания и прилипания, мм.

Знание протяженности зон на контакте позволяет обоснованно определить момент прокатки (Мпр) и мощность, затраченную на деформирование (Nпр), для различных условий, в том числе и для совмещенных методов ОМД. Расчетные формулы имеют вид:

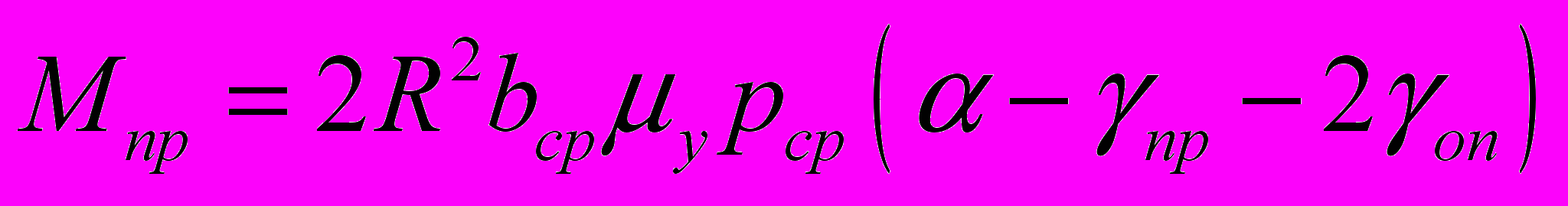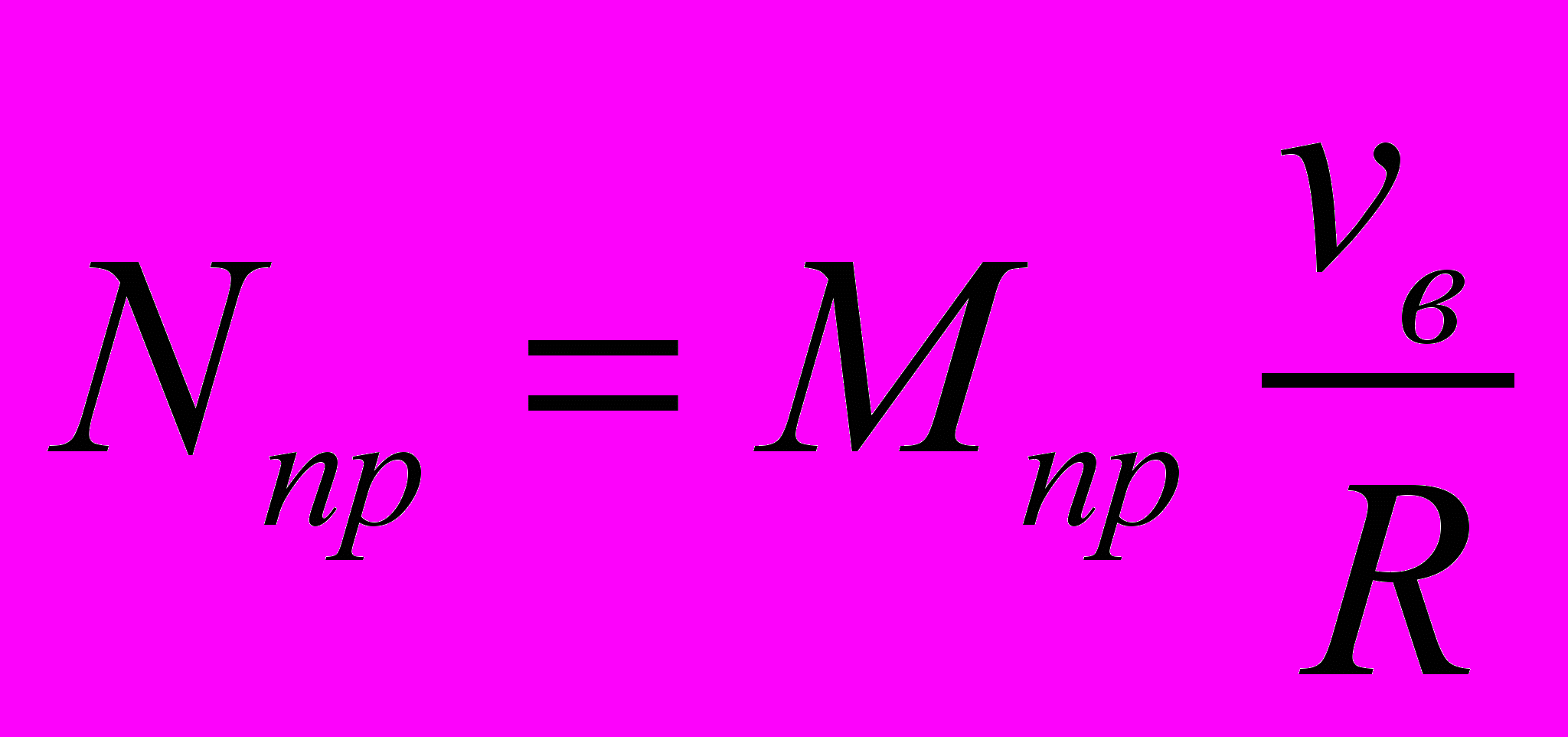, , (27)

где vв – скорость прокатки, м/с.

При реализации совмещенных методов ОМД изменяется соотношение протяженности зон на контакте, что влияет на величину коэффициента n, изменяя зависимости (23 – 26) до вида:

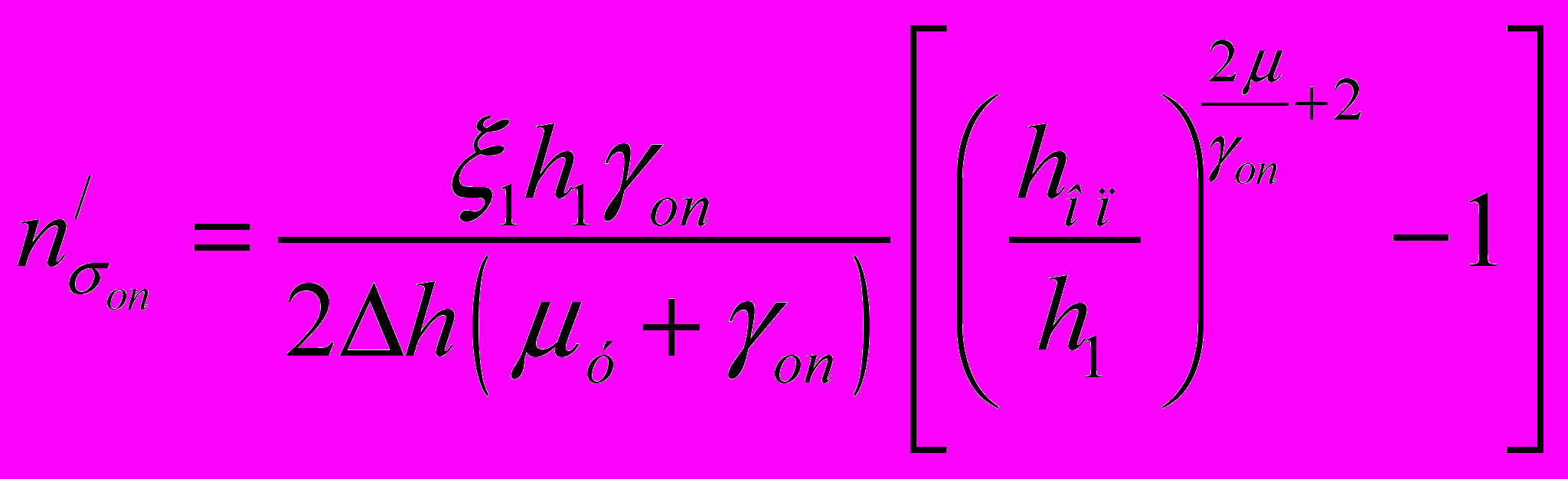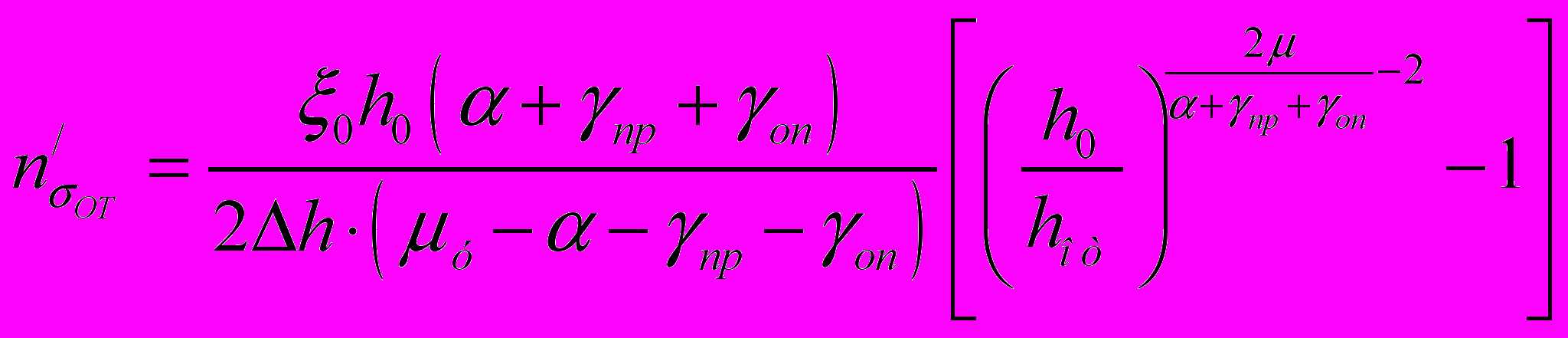; ; (28)

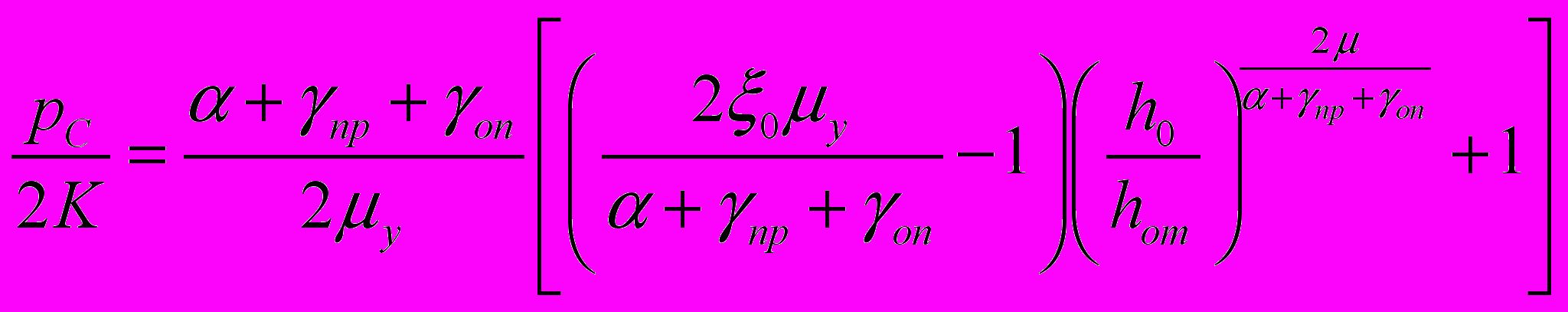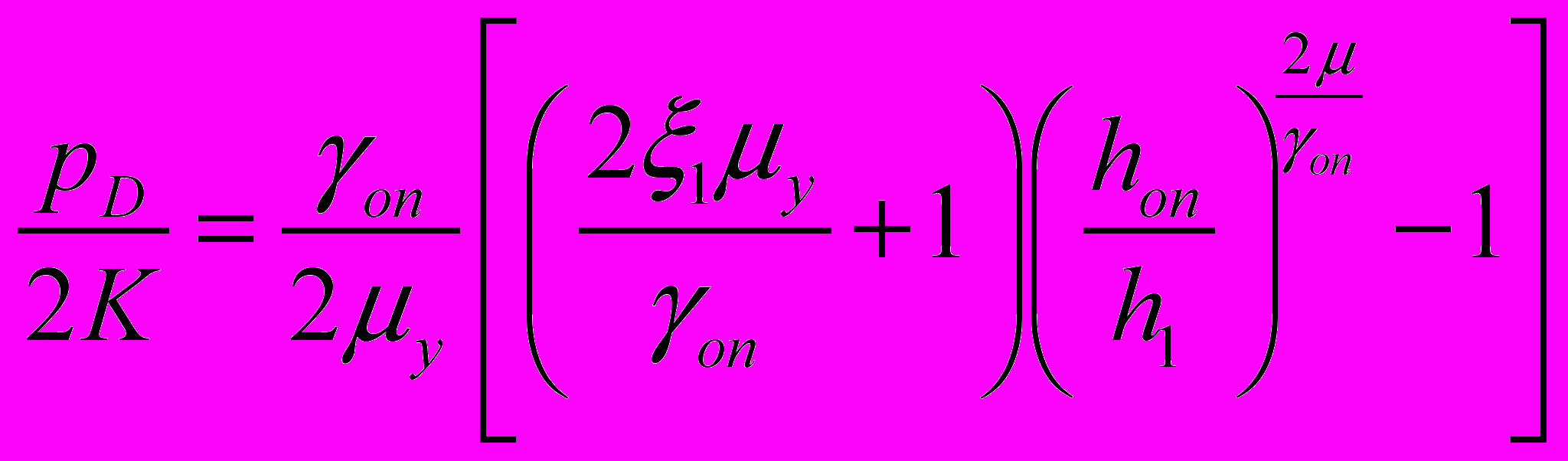;, (29)

где 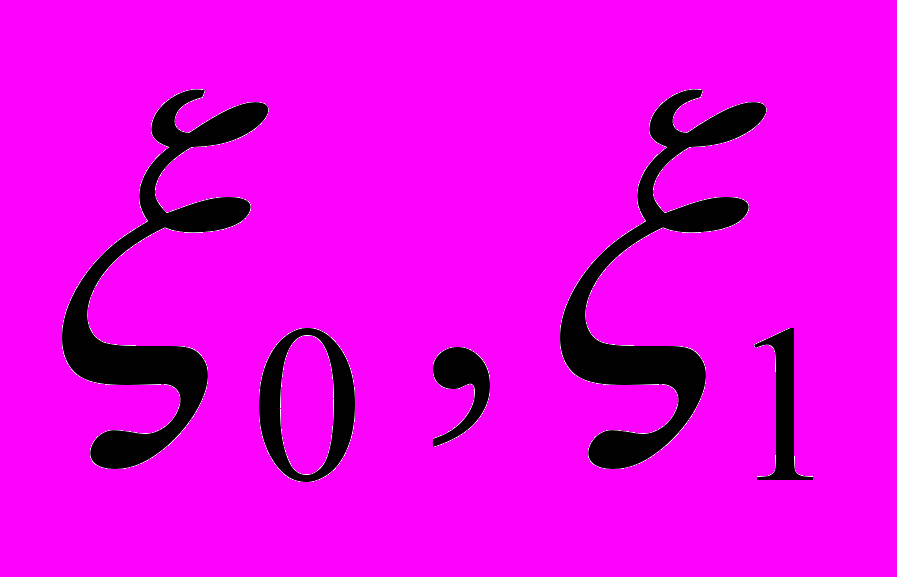– коэффициенты, учитывающие соответственно заднее и переднее натяжение (подпор); K – сопротивление чистому сдвигу, МПа.

Разработанная уточненная методика для расчета энергосиловых параметров прошла всестороннюю проверку в лабораторных условиях, а также при сопоставлении расчетных данных с экспериментальным материалом, имеющемся в литературе, и в сравнении с известными, наиболее часто используемыми на практике, методиками. На рисунке 9 приведены результаты сопоставления экспериментального материала, полученного в промышленных условиях при замере усилия прокатки в черновой группе клетей непрерывного широкополосного стана 2000 ОАО “Северсталь” (*) (рисунок 9). Как следует из приведенного материала, наиболее близкие расчетные значения получены с использованием предлагаемой методики (ошибка не превысила 6 – 8 %). Разработанная методика оформлена в компьютерную модель, выполненную в среде Borland Delphi 7, объемом 3,5 Мбайт дополнительно снабженную базой данных из 73 аналитических зависимостей для определения сопротивления деформации, из которых 39 получены автором (свидетельство на программу для ЭВМ № 2007610475) и позволяет проводить расчеты энергосиловых параметров обычных процессов и совмещенных методов ОМД.

Экспериментально изучено влияние степени использования продольной силы при реализации совмещенного метода прокатки в приводной – непри- водной клети на энергосиловые параметры приводной клети. Установлено, что при увеличении загрузки неприводной клети (увеличении степени использования продольной силы) увеличивается усилие прокатки и необходимая мощность в


* Коновалов, Ю.В. Расчет параметров листовой прокатки: Справочник/ Ю.В. Коновалов, А.Л. Остапенко, В.И. Пономарев. – М.: Металлургия, 1986. – 428.

приводной клети, но изменение данных характеристик неравнозначно. При таком же обжатии в неприводной клети, как в приводной, усилие в приводной клети увеличивается на 15 %, мощность на 87 %, таким образом, энергозатраты сокращаются на 13 %.



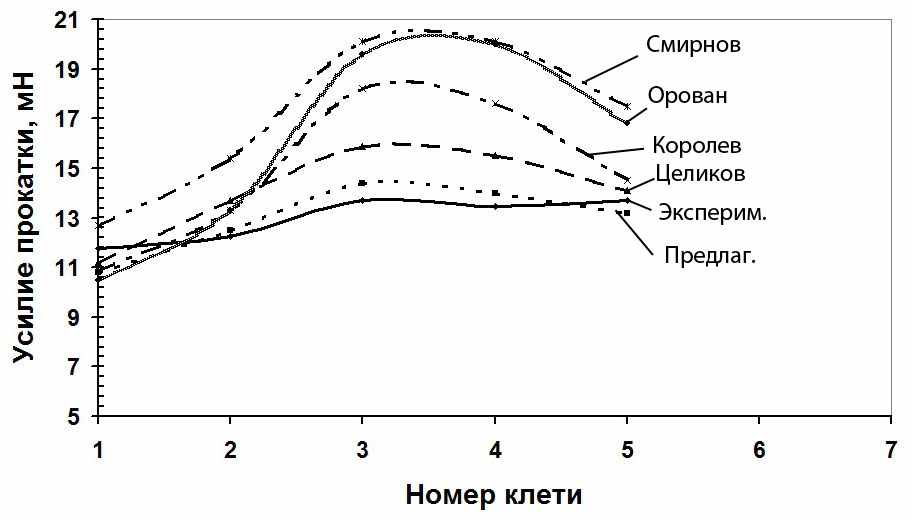
Рисунок 9 – Оценка точности предлагаемой методики для определения

усилия прокатки в сопоставлении с результатами промышленного

эксперимента, приведенного в литературе (*), и другими известными

методиками

Выполненная теоретическая часть работы позволила разработать научные основы совмещенных методов ОМД и показала, что величина продольной силы на установившейся стадии процесса прокатки велика, использование ее для совмещения методов ОМД перспективно и позволит повысить эффективность производства за счет экономии материальных и энергетических ресурсов. Разработка совмещенных методов ОМД, основанных на использовании продольной силы, открывает новые перспективы для обработки металлов давлением, так как совмещение в данном случае не является аддитивной суммой составляющих методов. Совмещение позволяет снять ограничения, свойственные каждому методу в отдельности, и получить дополнительные преимущества, и поэтому вызывает необходимость изучения и поиска новых технических и технологических решений. Определены наиболее удачные варианты совмещения методов ОМД: прокатка в системе приводная-неприводная клеть, прокатка-разделение неприводным делительным инструментом, прокатка-прессование, работа системы очаг деформации – валковая арматура.