Секция “Краевые задачи в физике и химии твердого тела”
| Вид материала | Документы |
- Секция “Краевые задачи в физике и химии твердого тела”, 192.16kb.
- Ix международная научная конференция «химия твердого тела: монокристаллы, наноматериалы,, 81.75kb.
- Рабочая программа дисциплины «теория представлений групп в физике твердого тела», 52.74kb.
- Рабочая программа дисциплины «Физика твердого тела», 72.99kb.
- Отчет за 2008-2009 гг по гранту ведущих научных школ № нш-2405. 2008 «Методы механики, 20.7kb.
- Интеркалаты оксидов ванадия и нанотубулены на их основе: синтез, строение, свойства, 829.32kb.
- Учебно-методический комплекс дисциплина «физика твёрдого тела» Челябинск, 194.36kb.
- Программа курса «квантовая химия твердого тела», 18.91kb.
- Программа курса общей физики для I курса этф осенний семестр 2011, 58.04kb.
- А. черникова, 342.71kb.
Секция “Краевые задачи в физике и химии твердого тела”
УДК 621.771.252:669.15-194
Казырский Е.О.
ОАО "Запсибметкомбинат", г. Новокузнецк
Использование генетических алгоритмов для решения задач обработки металлов давлением
В работе предложено использовать генетические алгоритмы для решения задач обработки металлов давлением.
В настоящее время задачи обработки металлов давлением, как правило, сводятся к вариационной задаче - нахождению минимума функционала работы или мощности деформации. Известен метод приближенного решения вариационной задачи – метод локальных вариаций [1]. Он обладает рядом преимуществ по сравнения с такими методами минимизации функционала как методы Ритца и Галеркина, так как не связан с выбором базисной системы функций и поэтому применим для областей произвольной формы, кроме того он легко учитывает краевые условия, которые представляют трудности при применении ряда других методов. В этом методе решение задачи о нахождении функции доставляющей минимум функционалу заменяется дискретной задачей в которой искомая функция заменяется ломаной с вершинами в выбранных точках, которая находится итеративным методом последовательного приближения.
Однако применение метода локальных вариаций в задачах пластического деформирования не всегда возможно. При использовании жесткопластической среды метод дает множество несовпадающих решений, то есть фактически задача не имеет решения. Иными словами имеем многоэкстремальную задачу.
Классические методы нахождения экстремума (максимума или минимума) для многоэкстремальных задач не дают возможности нахождения глобального экстремума. Пример такой многоэкстремальной задачи показан на рисунке.
В настоящее время для решения подобных многоэкстремальных задач используются градиентные методы и методы прямого перебора. Однако они недостаточно эффективны. Градиентные методы работают быстро, но не гарантируют нахождение глобального экстремума. Они оптимальны для унимодальных задач, где функция имеет единственный экстремум. Методы прямого перебора легко программируются, но требуют для своей реализации очень большого количества вычислений, что неприемлемо для сложных задач большой размерности.
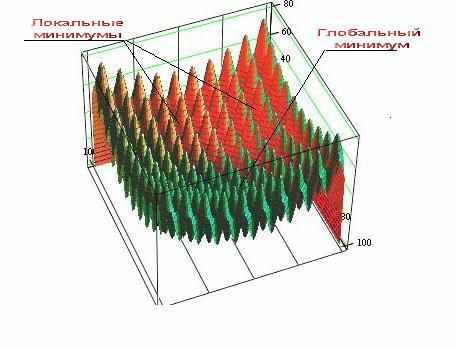
Рисунок - Многоэкстремальная функция
В качестве комбинации переборного и градиентного метода был предложен генетический алгоритм. Сразу после своего появления, генетические алгоритмы и их модификации как следствие, были использованы в целом ряде случаев для решения многих реальных мировых проблем в таких областях как экология, машинное обучение, проектирование и управление. Это одно из немногих эволюционных направлений в области компьютерной техники, включая стратегии эволюции, генетическое программирование и развивающееся программирование, которые основываются на принципах эволюции, связанных с наследованием и борьбой за выживание индивидов. Это эвристическая технология поиска, которая поддерживает популяцию индивидов P(t)={X1….XN} в итерациях от t к следующей t+1. Каждый индивид может быть рассмотрен как представление потенциального решения поставленной проблемы. Хотя в исходной формулировке структура каждого индивида была двоично-кодированной, современное представление структуры включает, например, целочисленную и реальную кодировку. Каждому индивиду соответствует своя мера пригодности к выживанию. Новая популяция P(t+1) получается из старой использованием генетических операторов, таких как создание пересекающихся потомков путем обмена частей, обычно более чем одного родителя, через процесс выбора для спаривания родителей, и мутации – создании новых индивидов, внося мутацию в их индивидуальную структуру.
В настоящее время генетические алгоритмы реализованы в виде готовых программных модулей и включены в состав такого известного математического пакета, как MATLAB.
Опыт использования генетических алгоритмов для нахождения глобального минимума функционала работы деформации пластического формоизменения жесткопластической среды показали возможность его нахождения и хорошего совпадения ряда решенных тестовых задач с известным точным решением.
СПИСОК ЛИТЕРАТУРЫ
1. Черноусько Ф.Л. Вариационные задачи механики управления / Ф.Л. Черноусько, Н.В. Баничук.– М:Наука, 1973. – 237 с.
