Секция “Краевые задачи в физике и химии твердого тела”
| Вид материала | Документы |
СодержаниеАтомистическое моделирование. Метод молекулярной динамики Мезоструктурное и континуальное моделирование материалов |
- Секция “Краевые задачи в физике и химии твердого тела”, 31.36kb.
- Ix международная научная конференция «химия твердого тела: монокристаллы, наноматериалы,, 81.75kb.
- Рабочая программа дисциплины «теория представлений групп в физике твердого тела», 52.74kb.
- Рабочая программа дисциплины «Физика твердого тела», 72.99kb.
- Отчет за 2008-2009 гг по гранту ведущих научных школ № нш-2405. 2008 «Методы механики, 20.7kb.
- Интеркалаты оксидов ванадия и нанотубулены на их основе: синтез, строение, свойства, 829.32kb.
- Учебно-методический комплекс дисциплина «физика твёрдого тела» Челябинск, 194.36kb.
- Программа курса «квантовая химия твердого тела», 18.91kb.
- Программа курса общей физики для I курса этф осенний семестр 2011, 58.04kb.
- А. черникова, 342.71kb.
Секция “Краевые задачи в физике и химии твердого тела”
УДК 538.9: 539.2…8: 548.4
Огородников В.В.
Институт проблем материаловедения НАН Украины, г. Киев, Украина
КОМПЬЮТЕРНЫЕ МОДЕЛИ В МАТЕРИАЛОВЕДЕНИИ
Рассмотрено новое, интенсивно развивающееся направление в материаловедении – компьютерное моделирование. Дана иерархическая классификация компьютерных моделей, очерчены области их применения. Особое внимание уделено атомистическому моделированию методом молекулярной динамики и проведению компьютерных экспериментов на виртуальных моделях, играющих важную роль при исследовании свойств наноразмерных частиц материалов как объектов нанотехнологии. Рассмотрены динамика и механизмы атомноструктурных превращений в нанокристаллах. Приведены примеры мультимасштабного моделирования на суперкомпьютерах объектов с числом частиц до сотен миллиардов, что позволяет охватить весь диапазон размеров от нанокристаллов до микрокристаллического уровня и проложить мостик между атомными моделями и экспериментально изучаемыми реальными структурами. Даны также примеры моделирования гетерогенных материалов, композитов на мезоструктурном уровне. Показаны перспективы использования компьютерной технологии, виртуальных моделей и экспериментов для развития новой отрасли - наноинженерии.
Введение
Материаловеды всегда создавали умозрительные модели будущих материалов и старались тщательно просчитать их всеми доступными средствами. Роль моделирования и вычислительных методов в материаловедении резко возросла благодаря происшедшему в последнее время революционному развитию компьютерной техники, глубоко проникшей во все области человеческой деятельности. Компьютерное материаловедение стало самостоятельным разделом общего материаловедения, неотъемлемой частью технологии и инженерии новых материалов.
Поскольку материал как макроскопическая система представляет собой сложную иерархическую конфигурацию подсистем, обычно невозможно в рамках одной модели учесть все детали каждой подсистемы. Поэтому модели также строят по принципу иерархии, подразделяя их в соответствии с масштабным фактором на модели макро-, мезо-, микро-, нано- и электронного уровней. Каждая модель более высокого масштабного уровня учитывает свойства более глубоких подсистем обобщенно, в интегральной форме.
Модели самого глубокого уровня, электронного, являются первопринципными (ab initio), поскольку связаны с решением фундаментальных уравнений квантовой механики. В моделях наноуровня, или атомистических, рассматриваются взаимодействия между отдельными атомами по законам классической механики. Для моделей более высоких масштабных уровней "строительными кирпичиками" являются соответственно элементы микро-, мезо- и макроструктуры.
Наиболее трудоемких вычислений в расчете на одну частицу требуют первопринципные модели. Поэтому даже на современных суперкомпьютерах не удается просчитать из первых принципов системы, содержащие более десятков - сотен атомов. Атомистические модели более высоких масштабных уровней сталкиваются с ограниченными возможностями компьютерной техники, когда число частиц слишком велико или необходимы слишком длительные итерационные процедуры. Поэтому компьютерное моделирование применяется на том или ином иерархическом уровне в соответствии с поставленными задачами и возможностями компьютерной техники.

| Рисунок 1 – Распространение трещины в модели двумерного кристалла Леннарда-Джонса с числом атомов 2 027 776 (F. F. Abraham at al, 1994) |
Пример мультимасштабного моделирования процесса зарождения и развития трещины для двумерного кристалла с числом атомов более двух миллионов дан на рисунке 1.
Рекордным достижением в настоящее время является моделирование кубического кристалла с длиной ребра ~ 1мкм, содержащего 160 миллиардов атомов (1,6∙1011, IBM Corporation, суперкомпьютер Blue Gene, 2006).
Чтобы в одном эксперименте охватить несколько масштабных уровней применяют комбинированные, или гибридные модели. Таким способом можно соединить континуальное, атомистическое и квантовое описание материала (F. F. Abraham, H. Van Swygenhoven, S. J. Zhou, J. Roth и др.). Мультимасштабное моделирование с применением современных многопроцессорных компьютеров и новой методики параллельного программирования позволяет создавать реалистические модели широкого диапазона размеров и назначения. Тем не менее, моделирование с менее масштабными моделями не утрачивает своего значения, так как многие детали атомных и молекулярных процессов в твердых телах, наночастицах с успехом решаются на компьютерах меньшей мощности, включая современные персональные компьютеры. Благодаря насыщенности исследовательских центров такой техникой и ее постоянному совершенствованию, работы по моделированию идут широким фронтом. И далее они будут расширяться, так как круг явлений, которые они помогают решать, неисчерпаем, как сама природа.
Представляется, что современная вычислительная техника, опирающаяся на математические действия с дискретными величинами и большими массивами чисел, является идеальным инструментом для описания и исследования физических явлений в дискретном мире ансамблей частиц любых размеров.
До создания современной вычислительной техники основным математическим инструментом для этой цели было дифференциальное и интегральное исчисление. Был создан мощный математический аппарат, который позволил описать многие физические явления с помощью абстрактной концепции непрерывной среды. В результате в нашем распоряжении оказался большой набор дифференциальных уравнений, многие из которых вообще не были решены, и часто даже не до конца поняты.
Современные компьютеры дают возможность, с одной стороны, исследовать напрямую большие ансамбли частиц, а с другой – решить неразрешимые дифференциальные уравнения методами вычислительной физики. В последнем случае дискретную среду вначале заменяют непрерывной, а затем применяют обратный переход от непрерывности к дискретности. Например, теория упругости построена на концепции непрерывной среды, а константы теории упругости используются для расчета параметров потенциалов межатомных взаимодействий. Сочетание методов вычислительной и аналитической физики часто бывает необходимо, так как возможности вычислительной техники, хотя и велики и постоянно растут, но на каждом этапе развития имеют свои пределы.
Модель разрабатывается таким образом, чтобы на ней можно было виртуально воспроизводить разнообразные изменения в элементном составе и начальной структуре материала, в строении композита, задавая различные термодинамические параметры (температуру, давление) и подвергая материал или конструкцию разнообразным внешним воздействиям (физическим, химическим, механическим). Иначе говоря, виртуальная модель должна быть такова, чтобы с ней можно было экспериментировать в компьютерном пространстве, как с натуральным образцом. Естественно, что возможности компьютерного эксперимента в создании разнообразных условий испытания, в том числе запредельных, намного шире, чем в реальности. Это позволяет всесторонне исследовать поведение материала в заданных условиях и критических ситуациях до проведения натурных испытаний, решая вопрос о наибольшей целесообразности их применения. Однако требования к такой модели чрезвычайно велики, но все они сводятся к самому главному: она должна быть максимально адекватна проектируемому материалу. Для этого виртуальная модель, прежде чем применяться, должна пройти тщательный тест на существующих аналогичных объектах.
Большую роль компьютерные модели играют также при решении многих научных вопросов, таких как выяснение механизма явления, который не поддается экспериментальному исследованию, изучение атомного строения границ зерен, дислокаций и других дефектов, их роли в процессах деформации, разрушения, сверхпластического течения, спекания порошков, диффузионной ползучести и т. д.
Наряду с моделями, опирающимися на реальные структуры материала, как на прообраз, который хотят воспроизвести в некотором приближении, существуют и бесструктурные, формально-математические (эвристические) модели, например формальная теория диффузии, описывающая случайные блуждания атомов методом Монте-Карло. Связь с материалом в этом случае осуществляется через параметры, соответствующие его свойствам, и набор некоторых экспериментальных закономерностей.
Атомистическое моделирование. Метод молекулярной динамики
Объекты моделирования.
Впервые метод молекулярной динамики (МД) с применением вычислительных машин был применен в работе Олдера и Уэйнрайта (B. О. Alder, T. E. Wainwright, 1959) для описания свойств жидкостей в модели жестких сфер и в работе Гибсона, Голанда, Милгрэма и Виньярда (J. B. Gibson, A. N. Goland, M. Milgram, G. H. Vineyard, 1960) для исследования процесса радиационного повреждения металлов при облучении в ядерном реакторе. В СССР инициаторами молекулярно-динамического моделирования атомных процессов в материалах стали А. Н. Орлов, А. Г. Гривцов, В. В. Кирсанов и ряд других исследователей в разных научных центрах страны, в том числе в Харьковском физико-техническом институте (В. В. Ганн), в Институте проблем материаловедения АН УССР (В. В. Огородников, В. В. Покропивный), в Институте металлофизики АН УССР (С. А. Котречко, А. В. Филатов, А. В. Овсянников). С развитием атомной энергетики фронт работ в этом направлении быстро расширялся. Новый импульс МД метод получил с увеличивающимся интересом к нанокристаллам и нанотехнологии.
МД метод обычно применяется к системам, содержащим несколько тысяч или десятков тысяч атомов, хотя в последнее время проведены расчеты на системах, включающих миллионы и даже миллиарды частиц (до 1,6∙1011). Уникальные расчеты для суперсистем требуют применения особо мощной техники (параллельных суперкомпьютеров) и специального программирования, что делает их недоступными для широкого применения. При обычном моделировании структурных дефектов внутри кристалла влияние поверхности может быть исключено введением трехмерных периодических граничных условий. Двумерные периодические условия позволяют исследовать свободные поверхности в третьем направлении, а одномерные – моделировать цилиндры и стержни бесконечной длины. Ячейка, которая дает начало периодическому воспроизведению, называется расчетной или первичной ячейкой. Пристраиваемые к ней воспроизводимые ячейки называются ячейками изображения. Они полностью повторяют размеры, форму, состав и структуру расчетной ячейки. Процессы, протекающие в них, также идентичны.
Однако периодическая трансляция расчетной ячейки не всегда приемлема, например, при моделировании процессов неоднородной деформации и разрушения образца в целом. В этом случае приходится проводить эксперименты на образцах, доступных для моделирования, то есть на нанообъектах. При этом, естественно, чем больше размеры нанообразца, тем представительней результаты.
В зависимости от поставленной задачи выбирается начальная конфигурация, то есть распределение всех атомов по узлам периодической или непериодической решетки, а также размеры и форма нанообразца. Начальные скорости всех атомов задаются в соответствии с распределением Максвелла для назначенной температуры. Затем эти случайные скорости должны быть вновь подрегулированы так, чтобы центр масс системы был неподвижным, то есть скорость центра масс должна равняться нулю, и чтобы соблюдался закон сохранения полной энергии, потенциальной плюс кинетической.
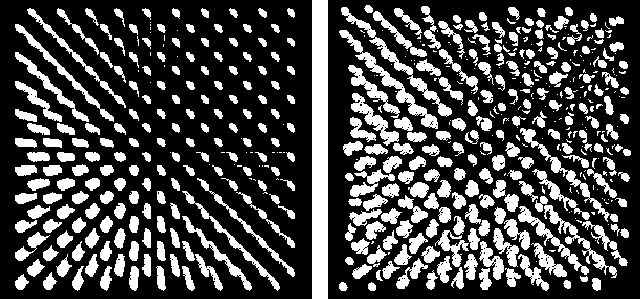
В трехмерной молекулярной динамике, кроме математических аспектов, важным элементом является визуализация атомных структур и процессов, так как наглядное изображение на плоскости трехмерных объектов с внутренней архитектурой представляет непростую задачу. Поэтому разрабатываются специальные программы визуализации результатов молекулярно-динамического моделирования. Для получения рисунков типа 2 была разработана специальная методика визуализации структурных данных, позволяющая усиливать трехмерное восприятие путем проникновения взгляда "внутрь". Это достигается специальным подбором точки наблюдения (С. Соркин).
а б
Рисунок 2 – Визуализация структурных данных:
а – совершенная ОЦК-решетка ванадия при T = 0 К; б – атомное строение нанообразца ванадия при T = 2100 K. Число атомов – 2000. Программа визуализации AViz
Метод МД является естественным математическим инструментом для моделирования нанообъектов и процессов, протекающих на наноуровне. К таким объектам относятся на
нокристаллы, неорганические и органические наномолекулы, нанокластеры, фуллерены, наностержни, нанотрубки, нанослойные материалы, наноэлементы композиционных материалов, нанодефекты структуры и другие наноструктурные элементы. Создаются также комбинированные модели, сочетающие наноструктурные и микроструктурные элементы, сопрягаемые между собой, и т. п. Исследуются процессы релаксации неравновесных структур, фазовые переходы, атомная структура дефектов и их энергетика, равновесная структура молекул, кластеров, эволюция структур и свойств нанообъектов под действием внешних сил. Чтобы проследить динамику этих процессов методом МД, необходимо уметь рассчитывать силы, действующие на атомы. В МД их находят из потенциалов межатомных взаимодействий (ПМВ) или комбинированным способом, привлекая ПМВ и первопринципные приближенные методы.
Динамика и механизмы превращений.
В настоящее время нет практически ни одной области структурного материаловедения, куда бы ни проникла молекулярная динамика. Можно дать лишь некоторые примеры в этой области.
Спекание дисперсных частиц. Работ по молекулярно-динамическому моделированию спекания немного. Это обусловлено медлительностью диффузионных и криповых процессов по атомным масштабам. Требуются очень длительные итерационные процедуры, чтобы получить заметный эффект.
Х. Жу и Р. С. Авербак (H. Zhu, R. S. Averback, 1996) спекали два медных монокристаллических наношара, содержащих по 4688 атомов каждый и имеющих диаметр 4,8 нм. Температура изотермического спекания составляла 700 К. Использовался потенциал погруженного атома. Сферы радиуса R со случайной плоскостной ориентацией друг относительно друга приводились в контакт на расстояние действия потенциала
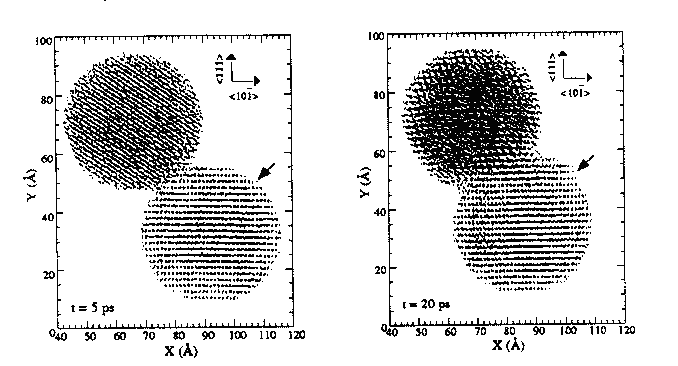
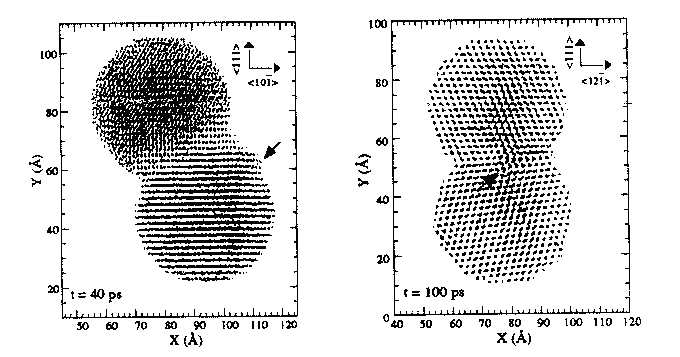
а (5 пс) б (10 пс) в (20 пс) г (40 пс)
Рисунок 3 – Спекание двух медных монокристаллических наношара:
а – в – атомы спроецированы на плоскость
 , стрелки – плоскость скольжения;
, стрелки – плоскость скольжения; г – то же на плоскость
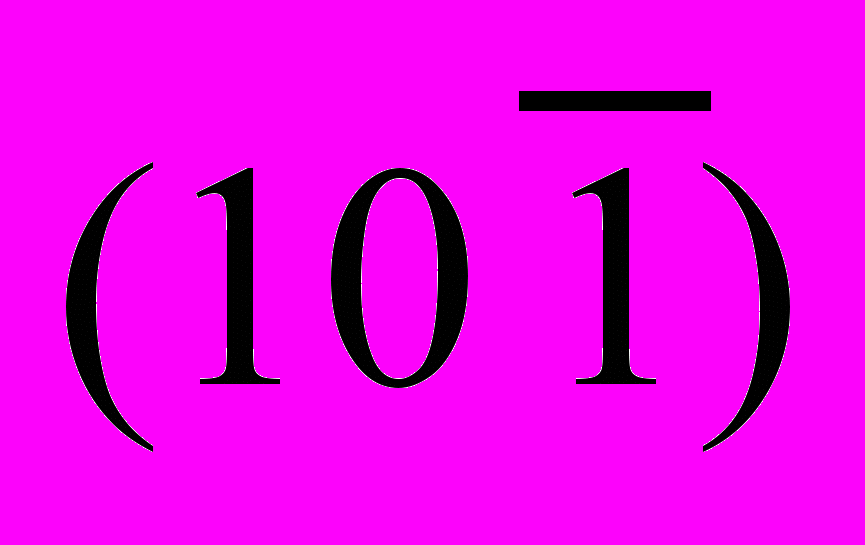 , стрелка – расположение зернограничной дислокации
, стрелка – расположение зернограничной дислокацииНаблюдался отчетливый эффект увеличения площади контакта и усадки (рисунок 3), который нельзя было объяснить механизмом решеточной диффузии, так как в модельных образцах меди отсутствовали вакансии и другие дефекты. Поверхностная диффузия могла бы объяснить увеличение площади контакта, но не изменение расстояния между центрами шаров, то есть усадку. Можно было бы предположить, что оба явления обязаны механизму зернограничной диффузии, однако расчеты показали, что и этот механизм нереален, так как коэффициент з/г диффузии должен быть в 200 раз выше коэффициента диффузии в жидкой меди, чтобы обеспечить наблюдаемую скорость спекания.
Был также проведен расчет возможных локальных сдвиговых напряжений. Оказалось, что при диаметре частиц порядка 30 нм они достигают сдвиговой прочности материала, а при диаметре 2,4 нм превышают его в несколько раз. На основании этого был сделан вывод о сдвиговом механизме деформации при спекании за пределами начальной упругой области. Получено также прямое атомноструктурное подтверждение этого механизма. На рисунке 3,в стрелкой указана явная выпуклость на поверхности наносферы, появившаяся в результате сдвиговых деформаций по плоскости скольжения (стрелки на рисунках 3,а–в). О высоких напряжениях, возникающих на границе сфер, свидетельствует также отмеченный разворот их относительно друг друга вокруг направления <111>, составившее к концу спекания 1800, и возникновение з/г дислокации (рисунок 3,г, стрелка).
Атомный механизм деформации и разрушения нанокристаллов ОЦК металлов. Молекулярно-динамическое моделирование деформации и разрушения нанокристаллов хрома, ниобия и бикристаллов Cr – Nb (В. В. Огородников и К. В. Малишевский, 2003) проведено с использованием парных потенциалов, совпадающих по форме с энергетическим уравнением Роуза. Параметры потенциалов Cr – Cr, Nb – Nb и Cr – Nb определялись из эмпирических свойств хрома и ниобия: теплоты испарения, периода решетки, модуля объемной упругости и постоянной Грюнайзена, с учетом двух координационных сфер. Моделируемые образцы представляли собой цилиндры (с точностью до кристаллографической огранки) длиной 4–5 нм, поперечником 2–2,5 нм и числом атомов 1350 – 1400. Образцы подвергали линейному растяжению (испытанию на разрыв) вдоль направлений <100>, <110> и <111>. Растягивающие усилия прикладывали к атомам двух крайних плоскостей, скорость растяжения была постоянной и составляла 2∙10-4 нм/фс (200 м/с). Температура поддерживалась равной 300 К.
Атомные перестройки, представленные на рисунках 4-7, показывают четкую зависимость механизма деформации и разрушения от ориентации кристалла относительно действующей нагрузки (ориентационный эффект).
При растяжении хрома вдоль направления <100> (рисунок 4) основным механизмом деформации является переориентация плоскостей (100) → (110). Наблюдается также разворот поперечного сечения на 450 (рисунок 4,б, поперечное сечение). Разрушающая трещина возникает на границе двух ориентаций, в месте наибольшей концентрации напряжений.
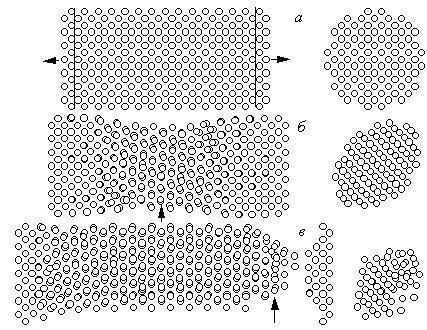
Рисунок 5 - Структурные изменения в нанокристалле хрома при растяжении вдоль направления <100>. Деформации (%): 0 (а), 16 (б) и 58 (в). Проекции слева – продольные сечения, справа - поперечные (место разреза соответствует стрелкам). Эти обозначения справедливы и для следующиих рисунков
Иной механизм имеет место при растяжении вдоль направления <110>. Рост напряжений приводит к пластическим сдвигам по разным направлениям, в результате чего возникают межзеренные границы с последующей их перестройкой (эффект фрагментации).

Рисунок 6 – Структурные изменения в нанокристалле хрома при растяжении вдоль направления <110>. Деформации (%): 0 (а), 19 (б) и 60 (в)
Напряжения концентрируются на стыке зерен, где и возникает разрушающая трещина.
Наиболее неблагоприятной для формоизменения оказывается растяжение вдоль направления <110> (рисунок 7). Разрушение происходит хрупко путем накопления нарушений кристаллической структуры в локализованной области. В зоне трещины образуются значительные пустоты, что наглядно показывает затрудненность пластических деформаций. За пределами этой зоны структура сохраняется неизменной.
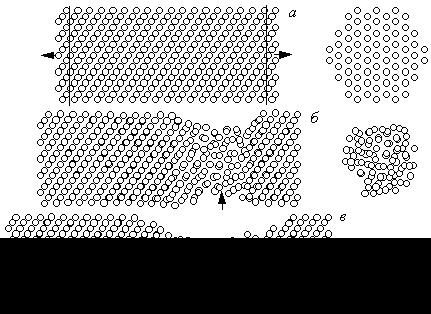
Рисунок 7 – Структурные изменения в нанокристалле хрома при растяжении вдоль направления <111>. Деформации (%): 0 (а), 18,4 (б) и 49 (в)
Аналогичные процессы наблюдались и в случае растяжения нанокристаллов ниобия.
Для бикристаллов важно проследить поведение атомов на межфазной границе. На рисунке 8 видно, как при растяжении вдоль <100> деформация сначала охватывает кристаллит ниобия, а затем переносится на кристаллит хрома (эстафетная передача деформации). Формоизменение происходит за счет перестройки плоскостей (100) ® (110) в обоих кристаллитах.

Рисунок 8 – Структурные изменения в бикристалле Cr-Nb. Величины и направления деформации растяжения указаны на рисунке
При растяжении вдоль <110> ниобий испытывает только упругую деформацию, а пластическая деформация целиком обеспечивается хромом. Разрушение идет, в основном, по межфазной границе, хотя небольшая часть атомов хрома «прилипает» к стенке ниобия. В случае растяжения вдоль <111> атомные перестройки в обоих кристаллитах затруднены, что приводит к хрупкому разрушению сколом и образованию атомных ступенек.
Сравнение свойств исследованных металлов в нано- и макросостояниях показывает, что нанообразцы обладают намного большей пластичностью и прочностью. Массивный поликристаллический хром при комнатной температуре разрушается хрупко. Даже у более пластичного массивного ниобия предел текучести оказался в 20 раз ниже, чем у нанообразца. Предел прочности модельных нанообразцов на 2-3 порядка превысил обычную прочность металлов. Полученные механические характеристики наносостояний более соответствуют свойствам нитевидных кристаллов – усов и являются естественными для бездислокационных кристаллов.
Данные для бикристалла Cr - Nb имеют практическое значение в связи с разработкой композитных материалов на основе тугоплавких металлов. Они свидетельствуют о высокой вероятности транскристаллитного разрушения композита Cr – Nb и необходимости введения в него барьерного слоя между хромом и ниобием, что отмечалось также в экспериментальных исследованиях.
Всестороннее растяжение сферических нанокристаллов молибдена. Чтобы лучше изучить деформационные свойства кристаллической решетки ОЦК металлов на атомном уровне, необходимо исследовать их поведение в разных условиях нагружения и при разных температурах. В данном эксперименте растягивающие усилия были приложены к поверхностным атомам шара, смещаемым только в радиальном направлении. В этих условиях напряженное состояние характеризуется значительным преобладанием нормальных напряжений над касательными вплоть до появления трещин. Касательные напряжения появляются из-за кристаллографической анизотропии. Для уменьшения влияния поверхности на зарождение трещины в объеме было взято достаточно большое число атомов – 34621, диаметр шара составил D0 = 10,09 нм.
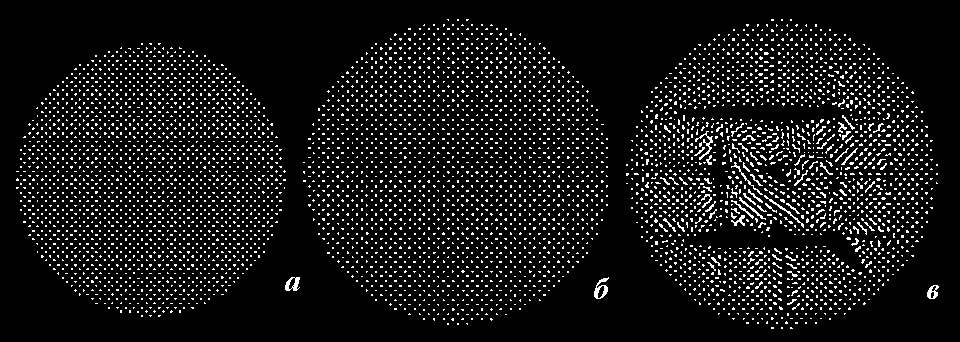
Рисунок 9 – Растяжение наношара молибдена при температуре 30 K. Скорость растяжения – 200 м/с. Деформация (ΔD/D0, %): а) 0; б) 15,25; в) 16,07
Первая стадия растяжения характеризуется длительным упругим расширением решетки (до ~15 %, рисунок 9,б). Это критическая деформация, при которой растягивающие напряжения достигают предела прочности межатомных связей. В этот момент образец быстро растрескивается (рисунок 9,в). Одновременно между трещинами возникают области интенсивной пластической деформации. Трещины образуются за счет разрывов по плоскостям спайности (100).
Исследование влияния температуры показало, что критическая деформация с ее увеличением изменяется не очень существенно. Растрескивание происходит не менее интенсивно, но трещины становятся более округлыми и не привязаны к определенным кристаллографическим направлениям. При высоких температурах проявляются процессы диффузионной ползучести и диффузионновязкого течения.
Мультимасштабное моделирование
Нанотехнология имеет дело с объектами, имеющими линейный размер до 1000 нм = 1 мкм. Это условная граница, отделяющая ее от микротехнологии. Именно в области наноразмеров роль компьютерного моделирования резко возрастает как важного инструмента исследования. Приведенные выше примеры ограничены размером кристаллов до 10 нм и числом атомов до 35000. Для моделирования кристаллов диаметром свыше 100 нм и числом частиц свыше 35000000 нужны особо мощные многопроцессорные компьютеры, а микрокристаллит в 1мкм с числом частиц порядка 1010 – 1011, можно обсчитать лишь на самых последних компьютерных комплексах с векторно-параллельным программированием. Несмотря на чрезвычайную дороговизну, такие исследования проводятся, но пока в очень ограниченном объеме (Абрахам, Рапапорт, Германн, Кадау, Калья, Рот).
Абрахам с сотрудниками соединили континуальное, атомистическое и квантовое описание материала в мультимасштабном моделировании динамического разрушения кремния. Они разработали схемы согласования метода конечных элементов, молекулярной динамики и квантовомеханической модели сильной связи и реализовали их для хрупкого распространения трещины в кремнии (11 093 376 атомов) и двумерном кристалле Леннарда – Джонса (2 027 776 атомов).

Рисунок 10 – Распространение трещины:
а – трещина в кремнии, увеличение шероховатости краев с увеличением длины.
б – динамика трещины в двумерном кристалле Леннарда – Джонса, стадии: I – равномерное продвижение, зеркальные края, II – легкая неравномерность, шероховатость краев, III – нестабильность, рубленые края
Ими детально изучена динамика распространения трещины, возникновение волн напряжений и нестабильности при движении (рисунок 10). Согласно континуальной теории, скорость продвижения трещины Гриффитса должна увеличиваться от нуля до предельной скорости, равной скорости распространения звука по поверхности трещины (скорости Релея). При этом поверхности остаются гладкими, зеркально симметричными. Компьютерный эксперимент показал, что это соблюдается только до скорости, равной одной трети скорости Релея. Далее, как и в случае кремния (рисунок 4,а), появляется и затем увеличивается шероховатость на поверхностях трещины (рисунок 4,б). А при скорости, равной двум третям скорости Релея, трещина теряет устойчивость, начинает осциллировать, двигаясь то назад, то вперед, зигзагообразно, оставляя после себя рваные края. При некоторых условиях нагружения скорость трещины в области динамической неустойчивости может даже превысить скорость Релея.
Мезоструктурное и континуальное моделирование материалов
В настоящем докладе основное внимание уделено атомистическим компьютерным моделям как объектам нанотехнологии. Не менее интенсивно разрабатываются также модели более крупных масштабных уровней: микро-, мезо- и макроуровней. В качестве примера можно упомянуть многоуровневую модель (от микро- до макро-) керамического материала для описания структурной эволюции дисперсной системы в процессе спекания (В.В. Скороход, В. В. Картузов и др.), компьютерное моделирование проводимости композитов типа проводник-изолятор (В.В. Скороход, М. Б. Штерн), процессов деформации и разрушения композиционных материалов (В. В. Огордников, Н. Н. Роженко). Создание все более совершенных компьютеров и широкое внедрение их в повседневную практику открывает большие возможности развития компьютерных моделей и применение их в материаловедении и технологии материалов.
Заключение
К важнейшим направлениям развития мировой науки в ХХI веке, академик Велихов отнес, в частности, нанотехнологии и высокопроизводительные вычислительные технологии, которые он назвал «ключом к конкурентоспособности». Как отметил Евгений Велихов, компьютерное моделирование, наконец, позволило получать точные предсказания, ценность которых намного выше, чем у модных сейчас форсайт-исследований. Заметим, что в нанотехнологии компьютерное моделирование, или компьютерный эксперимент, играет настолько органичную роль, что часто они образуют единую технологическую цепочку. Компьютерная технология становится важным звеном в новой отрасли - наноинженерии. В настоящее время созданы мощные комплексы программ для решения задач на всех уровнях иерархической системы моделей для однопроцессорных и многопроцессорных компьютеров. Компьютерные технологии потребуются вскоре также для управления наномеханизмами и наносистемами (K. E. Drexler). Уже накоплено большое количество лабораторных разработок разнообразных необычных наноустройств и еще больше предложено умозрительных проектов. Недавно американские физики из университета Райса (James M. Tour et al.) создали автомобиль размером с молекулу, передвигающийся по микроскопической «трассе» из золота. Он может двигаться под действием света и перевозить молекулярные грузы.
При рассмотрении этих проблем не обойтись без системы математических моделей. Выдающийся английский физик 19 века Вильям Томсон, он же лорд Кельвин, как-то сказал: "Мне кажется, что настоящий смысл вопроса – понимаете ли вы то или иное физическое положение? – будет такой: можете ли вы сделать соответствующую механическую модель?.. Я никогда не чувствую себя удовлетворенным, если не могу представить себе модель явления. Если я могу представить себе такую модель - значит, понимаю вопрос; если не могу - значит, я не понимаю его…" Живи лорд Кельвин в наше время, он, возможно, использовал бы в своем высказывании термин компьютерная модель. Профессор Г. Г. Еленин (МГУ) перефразировал высказывание Томсона на современный лад: "Если, вы можете предложить математическую модель, алгоритм, компьютерную программу позволяющую воспроизвести с достаточной точностью наблюдаемое в эксперименте явление в достаточно широком диапазоне внешних параметров и эта модель не будет противоречить установленным физико-химическим законам, то вы понимаете это явление. Если вы не в состоянии построить удовлетворительную модель, то это означает, что у вас нет понимания явления".
СПИСОК ЛИТЕРАТУРЫ
1. Огородников В.В. Компьютерное моделирование в материаловедении. Неорганическое материаловедение. Основы науки о материалах. Том 1 / В.В. Огородников, В.В. Покропивный, М.Б. Штерн.-Киев, Наукова думка, НАН Украины, 2008, с. 1092 – 1145.
2. Покропивный В.В. Атомистическое моделирование материалов / В.В. Покропивный, Ю.И. Роговой, В.В. Огородников, А.А. Лисенко.- Киев, ИПМ НАН Украины, 2008, 462 с.
