Конспект лекций по информатике для специальностей 2102, 2103 Автор доц., к т. н. Каширская Е. Н

Вид материала

Содержание

1.3. Линейные алгоритмы
1.4. Разветвляющиеся алгоритмы
1.5. Циклические алгоритмы

Подобный материал:

Конспект лекций бурлачков в. К., д э. н., проф. Москва, 1213.67kb.
Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
Конспект лекций по дисциплине «Маркетинг», 487.79kb.
Конспект лекций для студентов всех специальностей дневной и заочной формы обучения, 1439.07kb.
Конспект лекций для студентов, магистров и аспирантов всех специальностей, 373.35kb.
Конспект лекций для студентов по специальности i-25 01 08 «Бухгалтерский учет, анализ, 2183.7kb.
Конспект лекций организация производства и маркетинг для студентов 3 курса специальностей, 2989.73kb.
Конспект лекций по дисциплине «психология и педагогика» омск 2005, 2020.42kb.
Конспект лекций по курсу «Организация производства», 2034.84kb.
Конспект лекций по курсу «Организация производства», 2032.47kb.

1 2 3 4 5 6 7 8 9 ... 25

1.3. Линейные алгоритмы

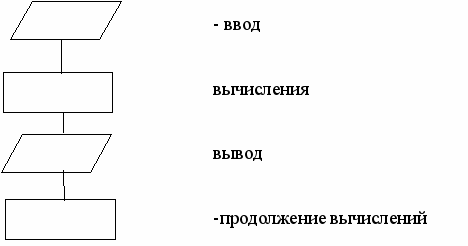
Линейным называется алгоритм, выполнение шагов которого происходит последовательно в порядке возрастания их номеров. В схеме он изображается последовательностью вычислительных блоков и блоков ввода-вывода.

Общий вид линейного участка:

1.4. Разветвляющиеся алгоритмы

Разветвляющимся называется алгоритм, в котором предусмотрено прохождение различных вариантов работы в зависимости от выполнения или не выполнения некоторого условия. В блок-схеме это условие записывается в ромб-блок сравнения.

Общая структура ветвления:

да

ет

Вар «да»

Вар. «нет»

1.5. Циклические алгоритмы

Алгоритм циклической структуры – алгоритм, в котором предусмотрено выполнение одной и той же последовательности действий.

Циклом называется участок алгоритма, реализующий многократно повторяющееся при различных значениях параметров однотипные вычисления (например, расчеты по одной и той же формуле), Алгоритм, содержащий цикл, называется циклическим.

Циклический алгоритм позволяет существенно сократить объем программы.

Для организации цикла необходимо предусмотреть:

- задание начального значения параметра цикла – переменной, которая будет изменяться при повторениях цикла;

- изменение значения этой переменной перед каждым новым повторением цикла;

- проверку условия окончания повторений по значению параметра и переход к началу цикла, если повторения не закончены.

Пример. Вычислить сумму: S=1²+2²+3²+…+n²=∑i²,

где n – заданное число.

Предлагается следующий алгоритм решения задачи.

Шаг 1. Ввести n.

Шаг 2. Положить S=0 (обнуление ячейки суммы).

Шаг 3. Положить i = 1.

Шаг 4. Вычислить i² и прибавит к текущему значению S: обозначение: S=S+i² .

Шаг 5. Увеличить i на 1; обозначение: i = i + 1.

Шаг 6. Сравнить i с n; если i < n, вернуться к шагу 4, иначе перейти к шагу 7.

Шаг 7. Вывести S.

Шаг 8. Останов.

Основная повторяющаяся операция: S=S+i² выполняется при различных значениях i. Величина i называется параметром цикла. В рассмотренном примере параметр цикла изменяется от начального значения i = 1 до конечного i = n с шагом 1.

Варианты: 1) S=1²+3²+5²+…

2) S=1*2*3*…*n

Задача. Задача табулирование функции. Требуется построить таблицу значений функции y=f(x) на отрезке [a, b] с шагом h, т.е. вычислить значения функции в точках x=a, a+h, a+2h, … , b вывести их на печать.

Задача. Составить схему алгоритма вычисления 100 значений функции y=sin(ax)/x при x_i=1,2,3,…,100. Очевидно, что для определения всех значений функции y необходимо 100 раз вычислять по этой формуле значения y и печатать их, изменяя каждый раз аргумент x на единицу. Цикл должен повторяться, пока x<100. Если х станет больше 100, то будет осуществлен выход из цикла, т.е. переход к следующему по порядку действию.

П
Вкл.
ример алгоритма.