Карельский Государственный Педагогический Университет

Вид материала

Документы

Подобный материал:

• «Карельский государственный педагогический университет», 4000.17kb.
• А. Общая информация о курсе Наименование вуза (разработчика материалов), 881.24kb.
• Концепция семейственности и средства ее художественного воплощения в прозе Л. Улицкой, 254.83kb.
• А. Общая информация о модуле Наименование вуза (разработчика материалов), 252.12kb.
• Ум «Использование цор при обучении школьников русскому языку», 88.51kb.
• Методические рекомендации по истории россии для слушателей курсов по подготовке, 467.23kb.
• "Философские науки", 789.13kb.
• Карельский Государственный Педагогический Университет, 65.92kb.
• Карельский государственный педагогический университет факультет начального образования, 312.33kb.
• Положение о порядке образования и использования Фонда материальной помощи и поощрения, 45.32kb.

Карельский Государственный Педагогический Университет


Синергетика – наука о самоорганизации структур


Выполнила: Смирнова О.

553 гр. (2007 г.)


Введение


Наука зародилась очень давно, на Древнем Востоке, и затем интенсивно развивалась в Европе. В научных традициях долгое время оставался недостаточно изученным вопрос о взаимоотношениях целого и части. Как стало ясно в середине 20 века, часть может преобразовать целое радикальным и неожиданным образом.

Из классической термодинамики известно, что изолированные термодинамические системы в соответствии со вторым началом термодинамики для необратимых процессов энтропия системы S возрастает до тех пор, пока не достигнет своего максимального значения в состоянии термодинамического равновесия. Возрастание энтропии сопровождается потерей информации о системе.

Со временем открытия второго закона термодинамики встал вопрос о том, как можно согласовать возрастание со временем энтропии в замкнутых системах с процессами самоорганизации в живой и не живой природе. Долгое время казалось, что существует противоречие между выводом второго закона термодинамики и выводами эволюционной теории Дарвина, согласно которой в живой природе благодаря принципу отбора непрерывно происходит процесс самоорганизации.

Противоречие между вторым началом термодинамики и примерами высокоорганизованного окружающего нас мира было разрешено с появлением более пятидесяти лет назад и последующим естественным развитием нелинейной

неравновесной термодинамики. Ее еще называют термодинамикой открытых систем. Большой вклад в становление этой новой науки внесли И.Р.Пригожин, П.Гленсдорф, Г.Хакен. Бельгийский физик русского происхождения Илья Романович Пригожин за работы в этой области в 1977 году был удостоен Нобелевской премии.

Как итог развития нелинейной неравновесной термодинамики появилась совершенно новая научная дисциплина синергетика - наука о самоорганизации и устойчивости структур различных сложных открытых неравновесных систем: физических, химических, биологических и социальных. Синергетика занимается изучением систем, состоящих из многих подсистем самой различной природы, таких, как электроны, атомы, молекулы, клетки, нейтроны, механические элементы, фотоны, органы, животные и даже люди.


Глава 1 «Основные понятия и положения синергетики»


1.1 Общая характеристика открытых систем


Открытые системы - это термодинамические системы, которые обмениваются с окружающими телами (средой), веществом, энергией и импульсом. Если отклонение открытой системы от состояния равновесия невелико, то неравновесное состояние можно описать теми же параметрами (температура, химический потенциал и другие), что и равновесное. Однако отклонение параметров от равновесных значений вызывают потоки вещества и энергии в системе. Такие процессы переноса приводят к производству энтропии. Примерами открытых систем являются: биологические системы, включая клетку, системы обработки информации в кибернетике, системы энергоснабжения и другие. Для поддержания жизни в системах от клетки до человека необходим постоянный обмен энергией и веществом с окружающей средой. Следовательно, живые организмы являются системами открытыми, аналогично и с другими приведенными параметрами. Пригожиным в 1945 году был сформулирован расширенный вариант термодинамики.

В открытой системе изменение энтропии можно разбить на сумму двух

вкладов:

d S = d S_e + d S_i

Здесь d S_e - поток энтропии, обусловленный обменом энергией и веществом с окружающей средой , d S_i - производство энтропии внутри системы.

Итак, открытая система отличается от изолированной наличием члена в

выражении для изменения энтропии, соответствующего обмену. При этом знак

члена d S_e может быть любым в отличие от d S_i . Для неравновесного состояния:

S < Smax Неравновесное состояние более высокоорганизованно, чем равновесное, для которого S = Smax. Таким образом, эволюцию к более высокому порядку можно представить как процесс, в котором система достигает состояния с более низкой энтропией по сравнению с начальной.

Фундаментальная теорема о производстве энтропии в открытой системе с независимыми от времени краевыми условиями была сформулирована Пригожиным: в линейной области система эволюционирует к стационарному состоянию, характеризуемому минимальным производством энтропии, совместимым с наложенными граничными условиями. Итак, состояние всякой линейной открытой системы с независящими от времени краевыми условиями всегда изменяется в направлении уменьшения производства энтропии P = d S / d t, пока не будет достигнуто состояние текущего равновесия, при котором производство энтропии минимально:

d P < 0 (условие эволюции)

P = min , d P = 0 (условие текущего равновесия)

d P/ d t < 0


1.2. Диссипативные структуры


Каждая система состоит из элементов (подсистем). Эти элементы находятся в определенном порядке и связаны определенными отношениями. Структурой системы можно назвать организацию элементов и характер связи между ними. В реальных физических системах имеются пространственные и временные структуры. Формирование структуры - это возникновение новых свойств и отношений в множестве элементов системы. В процессах формирования структур играют важную роль понятия и принципы:
1.Постоянный отрицательный поток энтропии.
2.Состояние системы в дали от равновесия.
3.Нелинейность уравнений описывающих процессы.
4.Коллективное (кооперативное) поведение подсистем.
5.Универсальный критерий эволюции Пригожина - Гленсдорфа.

Формирование структур при необратимых процессах должно сопровождаться качественным скачком (фазовым переходом) при достижении в системе критических значений параметров. В открытых системах внешний вклад в энтропию d S в принципе можно выбрать произвольно, изменяя соответствующим образом параметры системы и свойства окружающей среды. В частности энтропия может уменьшаться за счет отдачи энтропии во внешнюю среду, т.е. когда d S < 0 . Это может происходить, если изъятие из системы в единицу времени превышает производство энтропии внутри системы.

Чтобы начать формирование структуры, отдача энтропии должна превысить некоторое критическое значение. В сильно неравновесном состоянии переменные системы удовлетворяют нелинейным уравнениям. Таким образом , можно выделить два основных класса необратимых процессов:
1. Уничтожение структуры вблизи положения равновесия. Это универсальное
свойство систем при произвольных условиях .
2. Рождение структуры вдали от равновесия в открытой системе при особых
критических внешних условиях и при нелинейной внутренней динамики. Это
свойство не универсально .

Пространственные, временные или пространственно-временные структуры, которые могут возникать вдали от равновесия в нелинейной области при критических значениях параметров системы, называются диссипативными структурами. В этих структурах взаимосвязаны три аспекта:
1. Функция состояния, выражаемая уравнениями .
2. Пространственно - временная структура, возникающая из-за
неустойчивости .
3. Флуктуации, ответственные за неустойчивости.

Взаимодействия между этими аспектами приводит к неожиданным явлениям – к возникновению порядка через флуктуации, формированию высокоорганизованной структуры из хаоса. Таким образом, в диссипативных структурах происходит становление из бытия, формируется возникающее из существующего.


1.3. Самоорганизация различных систем


Переход от хаоса к порядку, происходящий при изменении значений параметров до критических, изменяет симметрию системы. Поэтому такой переход аналогичен термодинамическим фазовым переходам. Переходы в неравновесных процессах называются кинетическими фазовыми переходами. В близи неравновесных фазовых переходов не существует непротиворечивого макроскопического описания. Флуктуации столь же важны, как и среднее значение. Например, макроскопические флуктуации могут приводить к новым типам не устойчивостей. Итак, вдали от равновесия между химической, кинетической и пространственно-временной структурой реагирующих систем существует неожиданная связь. Взаимодействия между константами скоростей и коэффициентами переноса обусловлены короткодействующими силами (силами валентности, водородными связями и силами Ван-Дер-Вальса). Однако решения соответствующих уравнений зависят, кроме того, от глобальных характеристик. Для возникновения диссипативных структур обычно требуется, чтобы размеры системы превышали некоторое критическое значение - сложную функцию параметров, описывающих реакционно-диффузионные процессы. Поэтому можем утверждать , что химические неустойчивости задают дальнейший порядок, посредством которого система действует как целое. Если учесть диффузию, то математическая формулировка проблем,

связанных с диссипативными структурами, потребует изучении дифференциальных уравнений в частных производных. Основное решение уравнений соответствует термодинамической ветви. Неустойчивости такого типа удобно изучать методами теории бифуркации. Бифуркация есть нечто иное , как возникновение при некотором критическом значении параметра нового решения уравнений. При этом развитее системы в дальнейшем непредсказуемо, оно может происходить как по восходящей ветви, так и по нисходящей пока не будет достигнута следующая точка бифуркации и не появится новое решение.





Рис. 1. Бифуркационная диаграмма.

(Сплошная линия соответствует устойчивой ветви, точки – неустойчивой ветви)

В общем случаи при возрастании некоторого характеристического параметра р происходят последовательные бифуркации.

На рисунке 1 показано единственное решение при р = р1 , но при р = р2 единственность уступает место множественным решения. А и А1 - точки первичных бифуркаций из термодинамической ветви , В и В1 - точки вторичной бифуркации . Известно , что при изменении управляющих параметров в системе наблюдаются разнообразные переходные явления . Таким образом в критической области развитие системы происходит по следующей схеме: флуктуация – бифуркация – неравновесный фазовый переход – рождение новой структуры.

Бифуркация в широком понимании - приобретении нового качества движениями

динамической системы при малом изменении ее параметров (возникновение при некотором критическом значении параметра нового решения уравнений). Отметим, что при бифуркации выбор следующего состояния носит сугубо случайный характер, так что переход от одного необходимого устойчивого состояния к другому необходимому устойчивому состоянию проходит через случайное (диалектика необходимого и случайного). Любое описание системы , претерпевающей бифуркацию , включает как детерминистический , так и вероятностный элементы , от бифуркации до бифуркации поведении системы детерминировано , а в окрестности точек бифуркации выбор последующего пути случаен .

Общая теория процессов самоорганизации в открытых сильно не равновесных системах развивается на основе универсального критерия эволюции Пригожина - Гленсдорфа. Этот критерий является обобщением теоремы Пригожина о минимальном производстве энтропии.

Упорядоченные структуры, которые рождаются вдали от равновесия, в соответствии с критерием и есть диссипативные структуры. Эволюция бифуркации и последующей самоорганизации обусловлено, таким образом, соответствующими не равновесными ограничениями.


Глава 2 «Примеры самоорганизации различных систем»


2.1 Ячейки Бенара


Классическим примером возникновения структуры из полностью хаотической
фазы являются конвективные ячейки Бенара. В 1900 году была опубликована
статья Х.Бенара с фотографией структуры, по виду напоминавшей пчелиные
соты.




Эта структура образовалась в ртути, налитой в плоский широкий сосуд , подогреваемый снизу, после того как температурный градиент превысил
некоторое критическое значение. Весь слой ртути (или другой вязкой
жидкости) распадался на одинаковые вертикальные шестигранные призмы с
определенным соотношением между стороной и высотой (ячейки Бенара). В центральной области призмы жидкость поднимается, а вблизи вертикальных граней - опускается. Возникает разность температур Т между нижней и верхней поверхностью (Т = Т2 - Т1) . Для малых до критических разностей (Т<Тkp) жидкость остается в покое , тепло снизу вверх передается путем теплопроводности. При достижении температуры подогрева критического значения Т2 = Тkp начинается конвекция. При достижении критического значения параметра Т, рождается, таким образом, пространственная диссипативная структура. При равновесии температуры равны Т2 =Т1. При кратковременном подогреве (подводе тепла) нижней плоскости, то есть при кратковременном внешнем возмущении температура быстро станет однородной и равной ее первоначальному значению. Возмущение затухает, а состояние - асимптотически устойчиво. При длительном, но до критическом подогреве (Т < Тkp) в системе снова установится простое и единственное состояние, в котором происходит перенос к верхней поверхности и передачи его во внешнюю среду (теплопроводность). Отличие этого состояния от равновесного состояния состоит в том , что температура , плотность , давление станут неоднородными. Они будут приблизительно линейно изменяться от теплой области к холодной .


Увеличение разности температур, то есть дальнейшее отклонение
системы от равновесия, приводит к тому, что состояние неподвижной
теплопроводящей жидкости становится неустойчивым, возникают конвективные потоки. Это состояние сменяется устойчивым состоянием, характеризующимся образованием ячее. При больших разностях температур покоящаяся жидкость не обеспечивает большой перенос тепла, жидкость вынуждена двигаться, причем кооперативным коллективным,
согласованном образом.


2.2 Вихри Тейлора

Рассмотрим в качестве примера неустойчивость Тейлора и следующие за ней неустойчивости. В этих экспериментах (рис. 1.2.1) изучается движение жидкости между коаксильными цилиндрами. Обычно внутренний цилиндр заставляют вращаться, а наружный закрепляют неподвижно, но производились и такие эксперименты, в которых вращались оба цилиндра. Мы опишем явления, наблюдаемые в том случае, когда наружный цилиндр закреплен неподвижно, а внутренний вращается с различными скоростями. При малых скоростях вращения жидкость образует коаксильные линии тока. Это вполне понятно, так как внутренний цилиндр пытается увлечь за собой жидкость за счет трения между поверхностью цилиндра и жидкостью. При возрастании скорости (обычно измеряемой в безразмерных числах Тейлора) возникает движение нового типа. Движение жидкости организуется в так называемые вихри Тейлора, в которых жидкость периодически движется то наружу, то внутрь в горизональных слоях (рис. 1.2.2, а, б).




Когда числа Тейлора, продолжая нарастать, достигают второго критического значения, вихри Тейлора начинают осциллировать с одной основной частотой, а при еще более высоких числах Тейлора - с двумя основными частотами. Иногда наблюдаются еще более сложные структуры. Наконец, при дальнейшем увеличении числа Тейлора наступает хаотическое движение. Как видно из рис. 1.2.3, возникающие структуры можно наблюдать непосредственно. Кроме того, по рассеянию излучения лазера измерялись распределение скоростей и его спектр Фурье... В отдельных случаях при увеличении числа Тейлора наблюдалось появление серии новых частот, составляющих 1/2, 1/4, 1/8, 1/16 от основной частоты. Поскольку половинная частота соответствует удвоенному периоду, это явление получило название удвоения периода. Некоторые особенности, присущие образованию вихрей Тейлора, характерны для самоорганизующихся систем. Когда мы изменяем внешний параметр (в случае вихрей Тейлора - скорость вращения), система может образовывать иерархию структур, не обусловленную внешними воздействиями. Кроме того, структуры могут усложняться во времени и в пространстве.




2.3 Реакция Белоусова-Жаботинского


Самый знаменитый и наиболее впечатляющий процесс, коренным образом изменивший наши представления о реакционных системах, получил название реакции Белоусова–Жаботинского (реакция Б–Ж). Военный химик Борис Павлович Белоусов открыл эту реакцию в 1950 г., а Анатолий Маркович Жаботинский, в то время аспирант физического факультета МГУ, усовершенствовал методики проведения этой реакции и открыл новые эффекты (автоволны), которые могут иметь место в специфических условиях протекания реакции. Что же изменилось в наших представлениях о поведении веществ в химических реакциях благодаря открытию реакции Б–Ж? За прошедшие века химики привыкли к тому, что исходные вещества с той или иной скоростью реагируют друг с другом и дают продукты реакции, концентрации которых в состоянии равновесия постоянны. Такой ход реакции предсказуем и совместим с законом постепенного возрастания энтропии до максимального значения в состоянии равновесия, как изложено выше.

При проведении реакции Б–Ж в колбе смешивают растворы бромида NaBr и бромата натрия NaBrO₃, добавляют малоновую CH₂(COOH)₂ и серную кислоты H₂SO₄, а в качестве катализатора используют соли церия. При определенном соотношении ингредиентов можно наблюдать эффектную картину: через равные интервалы времени жидкость изменяет цвет, как бы отсчитывая неумолимый ход времени. Понятно, что механизм действия этих «химических часов» основан исключительно на межмолекулярных взаимодействиях.

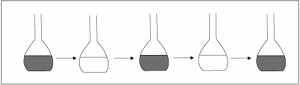«Химические часы». Реакционная смесь с большой точностью периодически изменяет окраску

В других условиях та же реакция приводит к расслоению среды с появлением горизонтальных красных и синих полосок, организуя таким образом систему в пространственно-временную структуру, что противоречит стремлению молекулярных систем к установлению максимального беспорядка. В чашке Петри тонкий слой реакционной смеси превращается в замечательное динамическое произведение искусства. Красные и синие концентрические дуги постепенно раскручиваются вокруг нескольких центров, образуя абстрактные движущиеся узоры. Это так называемые автоволны.

Проводя реакцию Б–Ж в тонком слое (в чашке Петри), можно увидеть динамические кольцевые структуры

Их открыл А.М.Жаботинский, а термин предложил академик Р.В.Хохлов во время защиты Жаботинским докторской диссертации. В упрощенном виде механизм реакции Б–Ж можно представить в следующем виде. Окислительно-восстановительная реакция

BrO₃^– + 4Ce³⁺ + CH₂(COOH)₂ + 5H⁺   BrCH(COOH)₂ + 4Ce⁴⁺ + 3H₂O

идет только в отсутствии Br^–, являющегося ингибитором процесса. Ингибитор удаляется за счет реакции:

BrO₃^– + 2B^– + 3CH₂(COOH)₂ + 3H⁺ 3BrCH(COOH)₂ + 3H₂O.

Но продукты первой и второй реакции могут реагировать с образованием ингибитора:

4Ce⁴⁺ + BrCH(COOH)₂ + 2H₂O Br^–  + 4Ce³⁺ + HCOOH + 2CO₂ + 5H⁺.

Таким образом, имеет место периодическое появление и исчезновение бромид-иона, Ce³⁺ и Ce⁴⁺. Соединения, содержащие окисленную и восстановленную формы катализатора, имеют разную окраску, отсюда и возникает эффект работы «химических часов».

При осторожном блокировании кольцевых волн можно наблюдать образование спиралей

2.3 Образование ячеистой структуры в твердых телах


Исследование твердого тела занимает особое место в физике, потому что это наука о строении материи живой и неживой природы, наука о материалах окружающего нас технического мира. Внимание к самоорганизованным состояниям в твердом теле привлечено не так давно, хотя некоторые исследования показывают, что такие структуры, возможно, представляют не только научный, но и первостепенный практический интерес, поскольку открывают пути создания материалов с принципиально новыми свойствами. При сильном воздействии на твердое тело часто наблюдается сложное переплетение процессов возбуждения и релаксации, кроме того, иногда одна часть системы может подвергаться воздействию со стороны другой. Тем не менее, по-видимому, и здесь действуют закономерности, общие для неравновесной термодинамики.

Наиболее простыми случаями, при котором формируются сильно неравновесные состояния твердого тела, являются процессы, происходящие при взаимодействии излучения с веществом. В некоторых новейших технологиях, в том числе в атомной технике или при радиационном модифицировании материалов (в этом случае поверхность материалов обрабатывают пучками электронов или ионов), вещество находится в радиационном поле. Очевидно, что во всех этих случаях мы имеем дело с открытой системой, подвергающейся притоку энергии извне. Кроме того, часто оказывается, что имеется и приток вещества (например, при облучении материалов в ускорителе мы вводим - имплантируем - чужие ионы).

Что же происходит при взаимодействии излученияс твердым телом? Напомним, что в большинстве твердых тел атомы (или ионы) составляют так называемую кристаллическую решетку - трехмерную периодическую структуру. Сами атомы расположены в ее узлах, но достаточно плотно, так что по некоторым направлениям они касаются, а межатомные промежутки малы - не более 0,4 размера атома. Кроме кристаллов бывают также аморфные материалы, в которых нет трехмерной периодичности, однако атомы упакованы так же плотно. При облучении быстрая частица (например, ион) сталкивается с атомом вещества, выбивает его из узла в межузельный промежуток. При этом узел решетки остается пустым, и образуются сразу два дефекта: вакансия и межузельный атом (такая пара дефектов называется парой Френкеля). Если частица тяжелая, то есть не электрон, а существенно превосходящие ее по массе нейтрон или ион, и если энергия частицы достаточно велика, то, выбив из узла один атом (и потеряв при этом часть энергии), она может продолжать соударения, пока ее энергия не иссякнет. В свою очередь, выбитый из узла атом тоже может обладать энергией, достаточной для того, чтобы производить дефекты. В результате образуется каскад, в котором может быть несколько сот дефектов: вакансий и межузельных атомов.

Теперь рассмотрим, как изменяется состояние облучаемого твердого тела во времени. Источник облучения (это может быть атомный реактор, в котором образуются нейтроны, или ускоритель, электронный или ионный) непрерывно генерирует дефекты в твердом теле. Одновременно в веществе идут процессы, при которых эти дефекты уничтожаются. Во-первых, это процесс аннигиляции, когда два разноименных дефекта Р вакансия и межузельный атом - встречаются и взаимно уничтожают друг друга. Во-вторых, дефект может «погибнуть на стоках». Дефекты распределены по объему приблизительно равномерно, если не учитывать области каскадов, которые играют роль флуктуаций концентрации дефектов. За счет градиента концентрации диффектов могут образовываться пространственно-организованные стуктуры. В качестве примера можно рассмотреть облучение металлического ионами аргона энергией 20 кэВ.


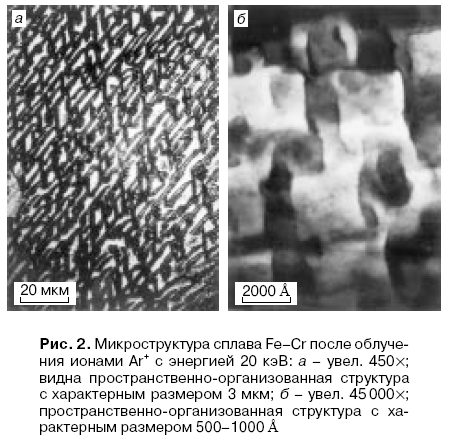Ячеистая структура может образовываться при кристализации металлов из расплавов. Если расплав нечистый (присутствуют примесные атомы - грязь), то формирование ячеек аналогично образованию ячеек Бенара ( за счет градиента концентрации).




Заключение


Изучение явлений самоорганизации и в более широком смысле сильно неравновесных состояний в системах только начинается. Очевидно, что оно может дать сильный толчок развитию физики открытых систем. Современная наука избавляется от иллюзии, что мир устроен просто, что все процессы могут быть описаны простыми и ясными закономерностями. В научный обиход входят понятия нелинейности, неустойчивости, флуктуаций, они становятся лейтмотивом во многих областях знания. Становится более понятным, как, исходя из химии, из науки о материалах, можно построить сложные структуры и формы, в том числе тe, которые стали предшественниками живой природы. Нелинейные неравновесные состояния весьма чувствительны к внешним условиям. В равновесии материя слепа и мертва, она безразлична к внешним условиям и неспособна к изменению. В сильно неравновесных условиях система готова к восприятию различий во внешнем мире.

Все более очевидным становится, что изучение сильно неравновесных состояний сулит большие практические выгоды. На основе таких состояний может быть совершен прорыв в создании материалов с новыми свойствами.

Уже сейчас некоторые достижения в этой области используются в микротехнологиии микроэлектронике. Завтра эти необычные увлекательные структуры, возможно, лягут в основу новых, ныне неизвестных технологий.


Литература

1. Пригожий И., Стенгерс И. Порядок из хаоса. - М., 1986. Те же. Время, хаос, квант. - М., 1994.
   
2. Алексеев Д.М. — Энциклопедия физики . - М., 2005.
   
3. А. С. Малков. Фазы исторического процесса и социальная самоорганизация — М.: «КомКнига», 2006. — С. 80—115.
   
4. Хакен, Г. Информация и самоорганизация: Макроскопический подход к сложным системам. М. М.: Мир 1991г. 240с.
   
5. ссылка скрыта
   
6. ссылка скрыта
   
7. ссылка скрытассылка скрытассылка скрыта
   
8. ссылка скрыта