Программа, методические указания и контрольные задания Для студентов-заочников Казань, 2009 г

Вид материала

Содержание

Подобный материал:

1 2 3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ

ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ»

ЕДИНАЯ ТРАНСПОРТНАЯ СИСТЕМА

РЕСПУБЛИКИ ТАТАРСТАН

Программа, методические указания

и контрольные задания

Для студентов-заочников

Казань, 2009 г.

ПРЕДИСЛОВИЕ

В соответствие с требованиями Государственного образовательного стандарта высшего профессионального образования к уровню подготовки лиц, обучающихся по специальности «Электрический транспорт», изучение дисциплины «Единая транспортная система Республики Татарстан» является важным и обязательным компонентом цикла общих гуманитарных и социально-экономических дисциплин.

Без знаний основополагающих принципов формирования, функционирования и развития транспортных процессов, транспортных систем и транспортного комплекса РТ, критериев эффективности функционирования и технико-экономические параметров современного транспорта невозможно эффективное и качественное транспортное обслуживание народного хозяйства и населения Республики Татарстан.

Под единой транспортной системой подразумевают совокупность всех видов транспорта, связанных экономическими, технологическими, техническими и нормативно-правовыми взаимоотношениями.

В состав транспортной системы РТ входит железнодорожный, автомобильный, внутренний водный, или речной, воздушный, трубопроводный, промышленный, городской, транспорт энергии и информации.

В задачу дисциплины «Единая транспортная система РТ» входит формирование у студентов комплексного представления о транспорте, системности, значении и роли транспорта в современном обществе, в экономики РТ и удовлетворении потребителей в перевозках.

Хорошее усвоение этой дисциплины создает благоприятную базу для изучения и творческого осмысливания студентами дисциплин учебного плана специальности «Электрический транспорт».

Общие рекомендации по работе над дисциплиной

«Единая транспортная система РТ»

Работа студентов над дисциплиной «Единая транспортная система РТ» слагается из следующих элементов: самостотельное изучение разделов и тем дисциплины по учебникам и учебным пособиям с последующей самопроверкой; индивидуальные консультации (очные и письменные); посещение лекций; выполнение контрольной работы; сдача зачетов по дисциплине.

Самостоятельная работа

Начинать изучение дисциплины необходимо с рассмотрения её содержания по программе, затем приступить к рассмотрению отдельных тем. При первом прочтении необходимо получить общее представление об излагаемых вопросах. При повторном прочтении необходимо параллельно вести конспект, в который необходимо заносить основные представления и понятия, краткий вывод полученных закономерностей, а также рисунки , поясняющие сущность рассматриваемого вопроса.

Переходить к изучению новой темы следует только после полного изучения теоретических вопросов, выполнения самопроверки по предыдущей теме.

Самопроверка

Закончив изучение темы, проверьте, хорошо ли вы запомнили и поняли основные представлении и понятия, отражающие сущность рассматриваемых вопросов. Частое обращение к конспекту показывает недостаточное усвоение материала.

Контрольная работа

В процессе изучения дисциплины студент должен выполнить одну контрольную работу, в которой необходимо по заданной матрице пропускных способностей построить транспортную сеть. Определить на ней максимальный поток и найти величину минимального разреза.

Контрольная работа должна выполняться самостоятельно, поскольку она является формой отчетности, и показывает, насколько студент овладел теоретическим знаниями, а также умениями применить их на практике.

Консультации

В период установочной или экзаменационной сессии студентам читаются лекции, на которых проводится обзор наиболее важных тем и разделов дисциплины, а также рассматриваются вопросы, недостаточно полно или мало освещенные в учебной литературе или вызывающие затруднения у большого числа студентов.

Дифференцированный зачет

По дисциплине «Единая транспортная система РТ» по окончании 8 семестра предусмотрен дифференцированный зачет. Студенты, успешно выполнившие контрольную работу и Сдавшие зачет по практическим занятиям, допускаются к сдаче дифференцированного зачета. Контрольная работа, зачтенная преподавателем, предъявляется экзаменатору. При сдаче зачета необходимо показать знание дисциплины «Единая транспортная система» в объеме программы, а также дать пояснение по существу к вопросам, касающимся контрольной работы.

ПРОГРАММА ДИСЦИПЛИНЫ

«ЕДИНАЯ ТРАНСПОРТНАЯ СИСТЕМА РЕСПУБЛИКИ ТАТАРСТАН»

ЦИКЛА ОБЩИХ ГУМАНИТАРНЫХ И СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ДИСЦИПЛИН ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ФАКУЛЬТЕТА КГЭУ

1. УЧЕБНЫЙ ПЛАН ПО ДИСЦИПЛИНЕ

Семестр	Зачеты	Контрольные работы	Часы учебных занятий
Семестр	Зачеты	Контрольные работы	Всего	Лекции	Практика	Самостоятельная работ
8	1	1	135	6	2	126

2. САМОСТОЯТЕЛНОЕ ИЗУЧЕНИЕ

8 семестр

Тема 1. Роль единой транспортной системы в развитии экономики РТ

Транспорт, его значение в жизни общества и экономике Республики Татарстан. Производственный процесс, продукция транспорта и ее особенности. Особенности управления транспортом. Единая транспортная система и сферы деятельности различных видов транспорта.

Тема 2. Технико-экономическая характеристика видов транспорта

Железнодорожный транспорт. Автомобильный транспорт. Внутренний водный (речной) транспорт. Воздушный транспорт. Трубопроводный транспорт. Промышленный транспорт. Транспорт энергии. Специализированные и нетрадиционные виды транспорта. Принципы выбора транспорта для перевозки грузов. Организация транспортного процесса в единой транспортной системе РТ.

Тема 3. Наука, экология и безопасность на транспорте

Научные проблемы транспорта. Проблемы экологии на транспорте. Проблемы безопасности на транспорте. Организации, контролирующие вопросы безопасности на транспорте.

3. СОДЕРЖАНИЕ ЛЕКЦИЯ

8 семестр

Лекция 1. Обзорная лекция по теме «Роль единой транспортной системы в развитии экономики РТ» (2 часа).

Лекция 2. Обзорная лекция по теме «Технико-экономическая характеристика видов транспорта» (2 часа).

Лекция 3. Обзорная лекция по теме «Наука, экология и безопасность на транспорте» (2 часа).

4. СОДЕРЖАНИЕ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

8 семестр

Практическое занятие 1. Элементы теории графов и транспортные сети (2 часа).

5. ЛИТЕРАТУРА

Основная:

Троицкая Н.А., Чубуков А.Б. Единая транспортная система. - М.: Академия, 2004. – 240с.
Ульяницкий Е.М., Филоленков А.И., Ломаш Д.А. Информационные системы взаимодействия видов транспорта: Учебное пос. для вузов ж.д. транспорта. – М.: Маршрут, 2005. – 264с.
Экономика железнодорожного транспорта. – М.: УМК МПС России, 2001. – 600с.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ

«ЕДИНАЯ ТРАНСПОРТНАЯ СИСТЕМА РТ»

Программа дисциплины состоит из 5 лекций и 5 тем. Ниже приводятся ссылки на литературу по каждой теме с указанием страниц.

Лекция 1. Обзорная лекция по теме «Роль единой транспортной системы в развитии экономики РТ» (2 часа).

Литература: [1], с.

Лекция 2. Обзорная лекция по теме «Технико-экономическая характеристика видов транспорта» (2 часа).

Литература: [1], с.

Лекция 3. Обзорная лекция по теме «Наука, экология и безопасность на транспорте» (2 часа).

Литература: [1], с.

Тема 1. Роль единой транспортной системы в развитии экономики РТ

Транспорт, его значение в жизни общества и экономике Республики Татарстан. Производственный процесс, продукция транспорта и ее особенности. Особенности управления транспортом. Единая транспортная система и сферы деятельности различных видов транспорта.

Литература: [1], с.

Вопросы для самопроверки:

Что такое единая транспортная система РТ?
Принципы построения системы управления транспортным процессом?
Перспективы развития единой транспортной системы РТ?

Тема 2. Технико-экономическая характеристика видов транспорта

Железнодорожный транспорт. Автомобильный транспорт. Внутренний водный (речной) транспорт. Воздушный транспорт. Трубопроводный транспорт. Промышленный транспорт. Транспорт энергии. Специализированные и нетрадиционные виды транспорта. Принципы выбора транспорта для перевозки грузов. Организация транспортного процесса в единой транспортной системе РТ.

Литература: [1], с.

Вопросы для самопроверки:

Классификация подвижного состава различных видов транспорта ?
Основные технико-эксплуатационные особенности и достоинства различных видов транспорта?
Проблемы и тенденции развития различных видов транспорта?

Тема 3. Наука, экология и безопасность на транспорте

Научные проблемы транспорта. Проблемы экологии на транспорте. Проблемы безопасности на транспорте. Организации, контролирующие вопросы безопасности на транспорте.

Литература: [1], с.

Вопросы для самопроверки:

Классификация научных проблемы различных видов транспорта ?
Проблемы экологии для различных видов транспорта?
Проблемы безопасности для различных видов транспорта?

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

ПРАКТИЧЕСКОГО ЗАНЯТИЯ №1

«Элементы теории графов и транспортные сети»

Теория графов является разделом дискретной математики. В дискретной математике важное место занимают задачи, связанные с упорядочением тех или иных объектов, а также задачи, в которых изучаются отношения между различного рода объектами. Приведем в качестве примера некоторые задачи.

1. Указать для водителя такой маршрут, чтобы пройденное им расстояние было минимальным.

2. Для имеющейся сети шоссейных дорог, соединяющих данные населенные пункты, указать маршрут между двумя любыми заданными пунктами, который обеспечил бы максимальный транспортный поток между ними.

Задачи такого рода удобно формулировать и решать, пользуясь рисунком, состоящим из точек (вершин) и отрезков (ребер или дуг), соединяющих эти вершины. Структуры такого типа объединяются названием - графы, а изучающий их раздел дискретной математики носит название теории графов. Приведем ряд определений и понятий, связанных с графами.

Определение графа

Пусть задано некоторое конечное множество X = {x₁, x₂, ..., x_n}, элементы которого будем называть вершинами. Образуем из него новое множество U = {u₁, u₂, ..., u_m}, состоящее из пар элементов (x_i, x_j) множества X . Будем при этом различать два случая :

а) когда безразлично, в каком порядке берутся вершины при образовании из них пар; в этом случае пара (x_i, x_j) (или (x_j, x_i) - все равно) называется ребром, соединяющим вершины x_i и x_j ;

б) когда существенно, в каком порядке выбираются вершины, т.е. когда пары (x_i, x_j) и (x_j, x_i) считаются различными; в этом случае пару (x_i, x_j) будем называть дугой.

Пара множеств G= (X, U) называется конечным графом, если имеет место случай “ а “. В случае “ б “ пара G= (X, U) называется конечным ориентированным графом или орграфом. В случае графа говорят, что ребро (x_i, x_j) инцидентно вершинам x_i, x_j . В свою очередь вершины x_i, x_j инцидентны ребру (x_i, x_j). Если граф ориентированный, то говорят, что дуга (x_i, x_j) исходит из вершины x_i и заходит в вершину x_j. Вершину x_i называют при этом предшественником вершины x_j, а вершину x_j последователем вершины x_i.

Подграфом графа G=(X,U) называется граф G′ = (X′,U′) такой, что X′ является подмножеством множества X, а U′ - подмножеством множества U. Если при этом X′ совпадает с X, то G′ называется остовным подграфом графа G. Граф называется полным, если для любых двух его вершин существует соединяющее их ребро.

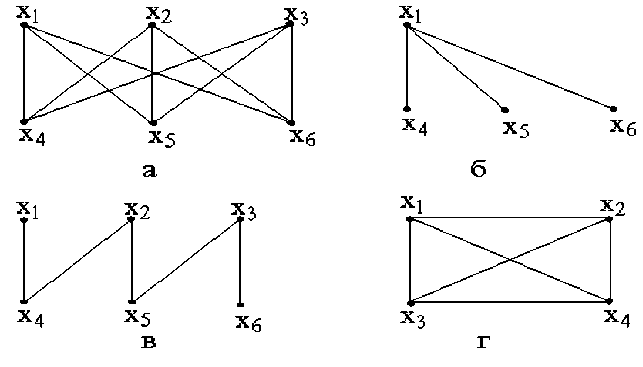
Рис. 1

На рис. 1,а изображен граф, на рис. 1,б - один из его подграфов, на рис. 1,в основной подграф этого графа. На рис. 1,г приведен пример полного графа с четырьмя вершинами.

Матричный способ задания графа

Кроме представления графа в виде рисунка, существуют и другие способы задания графа, одним из которых является задание графа с помощью матрицы смежностей. Этот способ, изложение которого приведено ниже, очень удобен для “введения” графа в память ЭВМ. Построение матрицы смежностей производится следующим образом.

Пусть G=(X,U) граф, где X={x₁, x₂, ...,x_n} - множество его вершин. Любая пара взятых вершин соединена или нет ребром. Нарисуем квадратную таблицу (матрицу) размером nхn, элементы которой формируются по следующему правилу. Если в графе G вершины x_i и x_j соединены ребром, в таблице на пересечении i- й строки и j- го столбца поставим единицу, в противном случае на соответствующем месте поставим нуль. Заполненная таким образом таблица и носит название матрицы смежности. Нетрудно убедиться, что матрица смежности симметрична относительно главной диагонали, элементами которой будут нули. Если граф имеет петли, т.е. ребра вида (x_i, x_i) или дуги, выходящие из некоторой вершины и в нее же заходящие, то на главной диагонали в соответствующих местах будут стоять единицы.

Для графа, изображенного на рис.1, а, например, матрица смежностей имеет вид (см. табл. 1).

Таблица 1

	x₁	x₂	x₃	x₄	x₅	x₆
x₁	0	0	0	1	1	1
x₂	0	0	0	1	1	1
x₃	0	0	0	1	1	1
x₄	1	1	1	0	0	0
x₅	1	1	1	0	0	0
x₆	1	1	1	0	0	0

Для ряда практических задач удобно использовать понятие взвешенного графа. Граф называется взвешенным, если каждому его ребру (дуге) (x_i, x_j) поставлено в соответствие вещественное число p_ij, называемое весом этого ребра (дуги). Для взвешенного графа аналогичным образом определяется матрица весов. В зависимости от конкретной задачи веса несуществующих ребер считаются равными нулю или бесконечности.

Простой путь, цикл графа. Дерево

Приведем еще ряд понятий и определений, которые нам потребуются в дальнейшем.

Простой путь в графе - это последовательность смежных ребер, у которой все вершины, за исключением, может быть, последней и первой, различны. Простой путь можно задавать последовательностью смежных вершин в виде x_i₁, x_i₂, ..., x_ip. Если G - орграф, то путь в нем называется ориентированным. Если в пути первая и последняя вершины совпадают, то такой путь называется циклом. Так, для графа на рис.1, а из вершины x₁ в x₄ можно попасть, например, путями: x₁, x₄; x₁, x₅, x₂, x₄. На этом же графе путь x₁, x₅, x₂, x₄, x₁ является циклом.

Если для любой пары вершин существует хотя бы один путь между ними, то граф называется связным. Так, все графы, изображенные на рис.1(а-г), являются связными.

Деревом называется связный граф, не содержащий циклов. Если у дерева выделена одна вершина, то она называется корнем дерева, а сам граф -корневым деревом. Так, легко видеть, что графы 1,б, 1,в являются деревьями, причем 1,б - корневым деревом (корень x₁); графы же 1,а, 1,г не являются деревьями, как содержащие циклы.

Классификация задач теории графов

Задачи, возникающие в теории графов, условно можно разбить на два класса:

1. Собственные задачи теории графов, в частности задачи подсчета числа объектов с заданными свойствами.

2. Задачи, связанные с построением того или иного объекта на графе, явного задания некоторой “наилучшей” конфигурации на графе. Это так называемые алгоритмы на графах.

Приведем постановку некоторых задач, имеющих отношение к организации транспортного процесса, на одной из которых - задаче о кратчайшем пути - остановимся более подробно.

Алгоритмы на графах

В задачах этого класса производится поиск такой конфигурации ребер (дуг) и вершин заданного графа, которая обладала бы некоторым оптимальным свойством. Говоря иными словами, на графе выбирается подграф, обладающий этим свойством. Как правило, для конечных графов эта задача принципиально всегда разрешима. Для этого достаточно перебрать все возможные варианты и выбрать из них наилучший в соответствующем оптимальном смысле. Однако в подавляющем большинстве случаев подобный перебор практически не осуществим за любое реальное мыслимое время ввиду обилия имеющихся возможных вариантов. Поэтому приходится изобретать алгоритмы, уменьшающие количество перебираемых вариантов.

Приведем теперь несколько задач, связанных с практическими проблемами, возникающими в организации транспортных (в широком смысле) процессов.

Задача о минимальном остовном дереве

На практике очень часто решается задача о построении сетей шоссейных или железных дорог (водных путей, газопроводов, линий электропередач) с минимальной “стоимостью “, причем, под “стоимостью“ соответствующих объектов можно понимать не только финансовые затраты, но также и количество материала, требующееся для построения объекта. На языке теории графов эта задача формулируется, следующим образом:

Дан взвешенный граф с n вершинами. Построить для него остовное дерево с минимальным суммарным весом ребер. Здесь в качестве вершин графа выступают пункты, к которым следует проводить элементы соответствующей сети, а в качестве ребер - участки этой сети. Вес p_ij ребра (x_i, x_j) в зависимости от конкретной задачи может интерпретироваться как количество материала, используемого на изготовление ребра (x_i, x_j), или его денежную стоимость.

Опишем в общих чертах одну из процедур решения задачи о минимальном остовном дереве - так называемый алгоритм ближайшего соседа.

Выбираем произвольную вершину, скажем x₁, и сравниваем веса всех ребер, инцидентных этой вершине. Ребро с минимальным весом включаем в искомое дерево. Другую вершину выбранного ребра обозначим через x₂.
Просматриваем все ребра, отличные от (x₁, x₂), инцидентные вершинам x₁ и x₂, выбираем из них ребро с минимальным весом и включаем его в будущее дерево. Другую вершину, инцидентную этому ребру, обозначим через x₃.
На каждом из следующих шагов добавляем самое дешевое из звеньев, при присоединении которого к уже построенным ребрам не образуется никакого цикла. Если имеется несколько звеньев одной и той же стоимости, выбираем любое из них.

Дальнейшая процедура ясна: алгоритм прекращает работу после того, как будут пройдены все n вершины графа. Мы оставляем без доказательства два следующих утверждения:

а). В процессе построения мы никогда не получим циклов,

б). Описанная выше процедура действительно порождает минимальное остовное дерево.

Задача о кратчайшем пути

Многие прикладные задачи на языке теории графов могут быть сформулированы следующим образом.

Пусть дан граф такой, что для любых двух его вершин из одной исходит, а в другую заходит не более одного ребра (иначе говоря, граф не имеет параллельных ребер). Пусть, кроме того, каждому ребру (x_i, x_j) приписано неотрицательное число R_ij - его вес (здесь удобно интерпретировать веса ребер как их длины). Веса несуществующих ребер будем считать как угодно большими и обозначать их символом ∞. Для любых двух выделенных вершин графа требуется найти длину кратчайшего пути между ними и указать этот путь.

Для решения поставленной задачи используем алгоритм Дейкстры. Он состоит в присваивании вершинам графа временных меток, которые по определенному правилу заменяются постоянными. В общем виде рассматриваемый алгоритм выглядит следующим образом.

Первой из двух выделенных вершин, скажем x₁, присваиваем постоянную метку 0 (расстояние вершины до самой себя), а всем остальным вершинам присваиваем временные метки ∞. Дальнейшая процедура состоит в том, чтобы определенным образом изменять метки вершин, присваивая некоторым из них постоянные метки. Делается это так.

Шаг 1. Если вершины x_j не имеют окончательных меток и они являются последователями вершины x_i, которой на предыдущем шаге была присвоена постоянная метка L^*(x_i), то для каждой из вершин x_j вычисляется новая временная метка, равная

min {L(x_j), R_ij + L^* (x_i)}, (1)

где L(x_j) - старая временная метка вершины x_j,

R_ij - расстояние от вершины xi до вершины x_j, т. е. вес ребра (x_i_, x_j).

Шаг 2. Из всех имеющихся временных меток (сюда входят не только метки вершин x_j, последователей вершины x_i) выбирается наименьшая, которая становится постоянной для своей вершины.

Процедура заканчивается после того, как второй из выделенных вершин, до которой ищется кратчайший путь, будет присвоена постоянная метка. Затем по имеющимся постоянным меткам восстанавливается кратчайший путь.

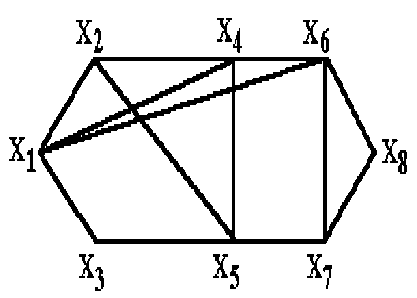
Пример. Пусть требуется найти кратчайший путь между вершинами в графе, приведенном на рис. 2. Расстояния между вершинами графа даны в табл. 2 (для простоты знак ∞ в таблице опущен).

Таблица 2

	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈
x₁		2	1	6		9
x₂	2			3	5
x₃	1				1
x₄	6	3			2	2
x₅		5	1	2			3
x₆	9			2			2	2
x₇					3	2		1
x₈						2	1

Blog

Программа, методические указания и контрольные задания Для студентов-заочников Казань, 2009 г

Содержание