В. Г. Будашевский инновационный менеджмент (Практические основы технологии) Учебное пособие

Вид материала

Учебное пособие

Содержание 6.2.Функционально – стоимостный анализ (ФСА): задачи, модели

Подобный материал:

• Программа дисциплины «Инновационный менеджмент» для слушателей подготовительного отделения, 80.58kb.
• Н. Ю. Каменская основы финансового менеджмента учебное пособие, 1952.65kb.
• Н. Ю. Каменская основы стратегического менеджмента учебное пособие, 2151.46kb.
• Учебное пособие Житомир 2001 удк 33: 007. Основы экономической кибернетики. Учебное, 3745.06kb.
• Учебное пособие «управление персоналом» для студентов заочного обучения специальности, 1516.37kb.
• З. Е. Алексеева > О. В. Крутеева управление качеством учебное пособие, 2122.76kb.
• М. И. Ковальская Корпоративный менеджмент на железнодорожном транспорте Учебное пособие, 2787.11kb.
• Сибирский Энерго Парк Федосеев В. И. Инновационный менеджмент учебное пособие, 674.08kb.
• К. Д. Ушинского Институт педагогики и психологии Кафедра управления образованием Основы, 1895.05kb.
• М. Н. Машкин Информационные технологии Учебное пособие, 2701.91kb.

Рис. 6

Таким образом, имея для конкретного варианта системы численные значения каждого из критериев, фиксируя их на радиусах – шкалах, а затем соединяя эти точки, получают «паутину». Два варианта системы сравнивают по картине их паутин: чем оптимальнее система, тем более паутина стянута к центру. Однако диаграмма «паутина» не позволяет формализовать учет различной значимости критериев, их больший или меньший вклад в результат выбора варианта системы.

В научно – методической литературе рассмотрено немало методов «свертки» критериев – переходу от группы частных, разнородных критериев к одному, обобщенному. В последние годы значительный интерес специалистов – практиков в различных областях привлек метод обобщенной функции Харрингтона, логика и процедура применения которого вкратце следующие.

Вначале шкалы измерения каждого критерия преобразуют – переходя к безразмерной, с диапазоном от 0 до 1 (1 соответствует предельно благоприятной величине критерия, 0 – предельно неблагоприятной).

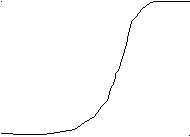
Такой переход можно осуществить или с помощью специально разработанных таблиц, или графически (последний вариант как наиболее наглядный, легче пояснить):


f₁ f₂
















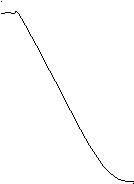
O К₁ O К₂

Рис. 7

Пусть, например, критерий К₁ - прогнозируемый срок разработки, а К₂ - ожидаемая прибыль, f₁ и f₂ – частные функции полезности, соответственно для К₁ и К₂. Очевидно стремление К₁ – min, К₂ – max, чему соответствует характер зависимостей f₁(К₁) и f₂(К₂), выбираемых экспертно с учетом относительного вклада каждого критерия в комплексную эффективность системы: при К₁→ min f₁→ 1, при К₂→ max f₂→ 1. Таким образом, в идеале желательно одновременно достичь f₁= f₂ =1. Так как все частные функции полезности fi безразмерны и измеряются по одной и той же шкале [0,1], то логично перейти к обощенной функции полезности F, построив ее в виде среднего геометрического от fi


F= ,

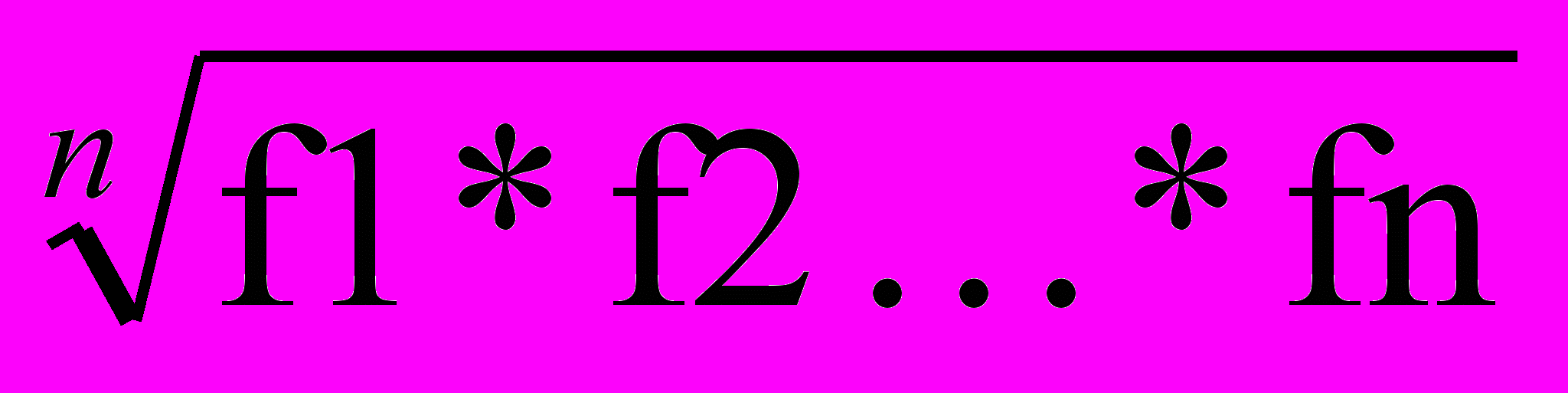при этом величина F, как и f_i; безразмерна и измеряется в интервале [0,1]. Имея вариант системы А с численными значениями критериев 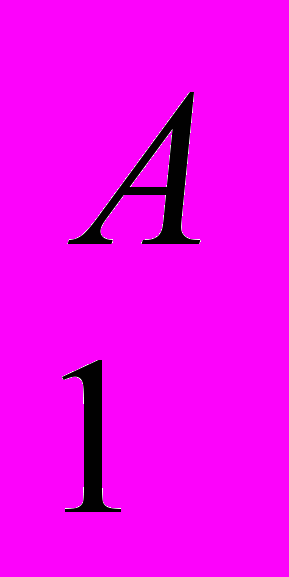(К, К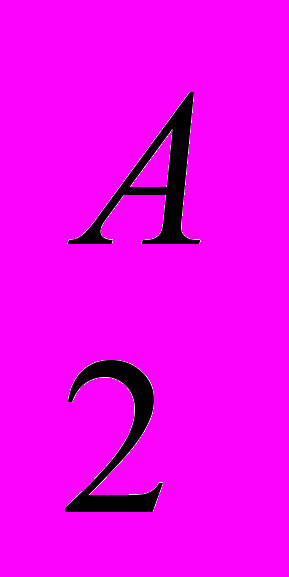) и вариант Б с 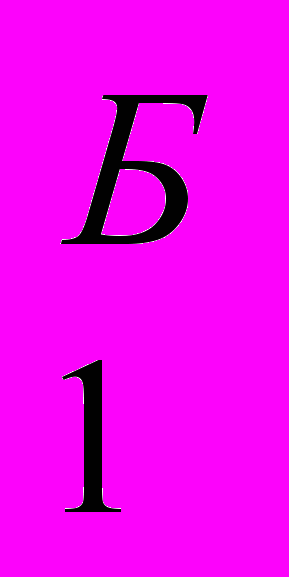К, К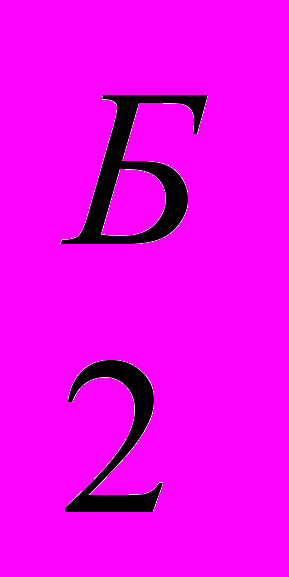 …, а затем переходя от частных критериев к их частным функциям полезности (т.е. K_i→f_i), а далее к обобщенной функции полезности F для каждого из сравниваемых вариантов системы, получаем F и F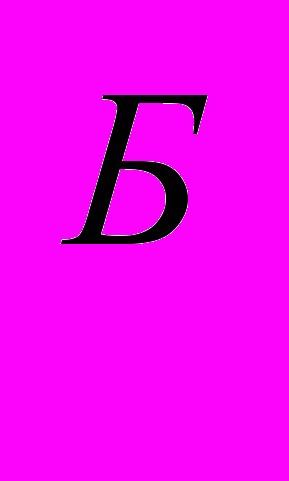; этот метод позволяет сопоставить варианты не только по величине обобщенного критерия F, но и проследить относительный вклад каждого частного критерия.


6.2.Функционально – стоимостный анализ (ФСА): задачи, модели

ФСА объединяет технико – экономический анализ, творческий поиск новых решений и организационно – управленческое обеспечение всех стадий анализа, включая реализацию его результатов. Область возможного применения ФСА неограниченна: различная продукция, процессы материальные и информационные на разных стадиях их жизненного цикла. В отличие от традиционного, объектно ориентированного аналогового проектирования (которое начинается с выбора конкретного аналога, уже реализованного на практике или лишь проектируемого ), ФСА открывает путь безаналогового проектирования, при котором существенно увеличиваются шансы выйти на нетрадиционные решения, позволяющие оптимально разрешать противоречие «цена - качество» (другими словами, «эффективность - стоимость»).

Суть ФСА проста. Любой объект – это прежде всего совокупность выполняемых им функций («что он делает?»). Но функции следует разделить на полезные (Ф+), вредные (Ф-) и нейтральные, остальные (Ф0).

Чтобы реализовать функции, необходимо затратить средства, в частности это – стоимость материалов и комплектующих, а также изготовления объекта.

Чтобы создание объекта было максимально эффективным, необходимо, по – возможности, избавиться от вредных функций и свести к минимуму нейтральные, т.к. они создают избыточные затраты. А полезные функции, подразделяемые на основные (непосредственно удовлетворяющие потребности) и вспомогательные, необходимо увеличить. Таким образом, ФСА начинается с выявления всех функций объекта. Далее проводится структурно – функциональный анализ, при котором оценивается конкретный вклад каждого элемента системы в выполнение каждой из ее функций. После чего сравнивают значимость каждой функции (для объекта в целом) и затраты на ее реализацию. Такой поэтапный анализ вскрывает источники непроизводительных затрат, открывает способы повышения конкурентоспособности объекта.

Для указанного анализа используют рабочие модели 4-х видов:

структурную, функциональную, функционально – структурную и функционально – стоимостную.

Все эти модели проще всего проиллюстрировать на конкретном примере, для простоты выбрана элементарная шариковая ручка.

Структурная модель («анатомия» объекта) – элементы объекта и их взаимосвязи, в виде ярусной схемы «целое – его главные части – элементы каждой части»: