Введение

Вид материала

Методические рекомендации

Содержание Общие принципы разработки заданий Процедура проведения муниципального этапа. Процедура оценивания решений и подведения итогов Дополнительные вопросы по математике Дополнительные вопросы по физике Дополнительные вопросы по математике Дополнительные вопросы по математике Задачи муниципального этапа всероссийской олимпиады по астрономии и физике космоса Задачи муниципального этапа всероссийской олимпиады по астрономии и физике космоса 29 марта 2006 г. произошло солнечное затмение, в каком созвездии в этот момент находилась Луна? Туманность Ориона Задачи муниципального этапа всероссийской олимпиады по астрономии и физике космоса Задачи муниципального этапа всероссийской олимпиады по астрономии и физике космоса В какой четверти Луна лучше освещает Землю – в первой или в третьей? Если полное лунное затмение произойдёт сегодня, то можно ли будет наблюдать его с Южного полюса Земли? Дайте развёрнутый ответ. 2 = 4GR/3. Отсюда средняя плотность планеты Вторая космическая скорость Задачи муниципального этапа всероссийской олимпиады по астрономии и физике космоса Задачи муниципального этапа всероссийской олимпиады по астрономии и физике космоса Как называется такое расположение планет? Сколько больших планет сейчас находится над горизонтом? Сколько карликовых планет сейч ... Полное содержание

Подобный материал:

• Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
• Введение глава психологизм как особенность характерологии в рассказах Всеволода Иванова, 12.47kb.
• Лабунец Ольга Юрьевна мытищи 2009 г. Оглавление Введение 3 Использование видеофильмов, 263.17kb.
• Анализ и планирование трудовых показателей Аудит и контроллинг персонала Введение, 12.45kb.
• Программа курса. План семинарских занятий Методические рекомендации Новосибирск 1999, 340.75kb.
• Учебной дисциплины (модуля) Наименование дисциплины (модуля) Введение в спецфилологию:, 83.08kb.
• 1. Целеполагание в процессе менеджмента Введение, 49.78kb.
• Пояснительная записка. Особенностью курса «Введение в языкознание» является высокая, 305.75kb.
• Курносов Владимир Анатольевич Волжск 2007 Оглавление Введение 3-5 Глава I. Юродство, 355.39kb.
• Целевые программы и непрограммная деятельность Распределение расходов по целям, задачам, 396.48kb.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по разработке заданий для

муниципального этапа

Всероссийской олимпиады школьников по астрономии

в 2009/2010 учебном году


Воронеж 2009

ВВЕДЕНИЕ

Настоящие методические рекомендации подготовлены предметно-методической комиссией по астрономии и направлены на помощь соответствующим методическим комиссиям и жюри в составлении заданий для школьного этапа Всероссийской олимпиады школьников по астрономии в субъектах Российской Федерации.

Данный материал содержит рекомендации по структуре и тематике заданий муниципального этапа олимпиады по астрономии, условиям проведения этих этапов, материально-техническому обеспечению, а также системе оценивания и процедуре определения победителей и призеров соответствующих этапов.

Предметно-методическая комиссия по астрономии желает организаторам успехов в проведении школьного этапа олимпиады. По любым вопросам, связанным с данным этапом можно обратиться по электронной почте tba2000@mail.ru, Татьянкин Борис Александрович.

1. ОБЩИЕ ПРИНЦИПЫ РАЗРАБОТКИ ЗАДАНИЙ

Муниципальный этап Всероссийской олимпиады школьников является ее вторым этапом (первый этап – школьный). Ее целью является поощрение у школьников интереса к изучению того или иного предмета и выделение талантливых ребят для участия в последующих этапах Всероссийских олимпиад.

Основные принципы, в соответствии с которыми формируются задания того или иного этапа Всероссийской олимпиады школьников по астрономии, описаны в книге «Всероссийская олимпиада школьников по астрономии в 2006 году» (автор-составитель О.С. Угольников, Федеральное Агентство по образованию РФ, АПКиППРО, 2006). В 2009-2010 году методические рекомендации по составлению заданий олимпиады составлены в соответствии с Положением о Всероссийской олимпиаде школьников, утвержденного Министерством Образования и науки Российской Федерации в 2007 году.

В соответствии с данным Положением, муниципальный этап Всероссийской олимпиады школьников проводится в ноябре – декабре, разработку заданий формирует методическая комиссия субъекта Российской Федерации. Муниципальный этап олимпиады по астрономии проводится среди школьников 7-11 классов, которые целесообразно разделить на четыре возрастные параллели: 7-8, 9, 10 и 11 классы. На данном этапе из 6 предлагаемых заданий 2- 3 должны иметь односложную структуру решения, связанную с применением одного–двух астрономических фактов или физических законов (задания первой категории) и 2-3 должны быть многоступенчатыми задачами второй категории сложности. Так как муниципальный этап проводится в ноябре-декабре, то в задания можно включать большее количество вопросов программы текущего года обучения (для 10-11 классов).

2. ПРОЦЕДУРА ПРОВЕДЕНИЯ МУНИЦИПАЛЬНОГО ЭТАПА.

Муниципальный этап Всероссийской олимпиады школьников по астрономии проводятся в один тур.

Для проведения олимпиады Организационный комитет предоставляет аудитории в количестве, определяемом числом участников олимпиады. В каждой аудитории должны находиться не более 15 участников, каждый из которых должен сидеть за отдельной партой. Вне зависимости от их количества, участники олимпиады по каждой возрастной группе должны находиться в разных аудиториях. Каждому участнику олимпиады Оргкомитет должен предоставить ручку, карандаш, линейку, резинку для стирания и пустую тетрадь со штампом Организационного комитета. В каждой аудитории должны быть также запасные канцелярские принадлежности и калькулятор. В течение всего тура олимпиады в каждой аудитории находится наблюдатель, назначаемый Организационным комитетом. Перед началом работы участники олимпиады пишут на обложке тетради свою фамилию, имя и отчество, номер класса и школы, район и населенный пункт.

По окончании организационной части участникам выдаются листы с заданиями, соответствующими их возрастной параллели. Наблюдатель отмечает время выдачи заданий. На решение заданий муниципального этапа олимпиады по астрономии школьникам 9 класса и моложе отводится 3 часа, школьникам 10 и 11 классов – 4 часа. Участники начинают выполнять задания со второй страницы тетради, оставляя первую страницу чистой. По желанию участника он может использовать несколько последних страниц тетради под черновик, сделав на них соответствующую пометку. При нехватке места в тетради наблюдатель выдает участнику дополнительную тетрадь. По окончании работы вторая тетрадь вкладывается в первую.


Во время работы над заданиями участник олимпиады имеет право:

1. Пользоваться любыми своими канцелярскими принадлежностями наряду с выданными оргкомитетом.
   
2. Пользоваться собственным непрограммируемым калькулятором, а также просить наблюдателя временно предоставить ему калькулятор.
   
3. Обращаться с вопросами по поводу условий задач, приглашая к себе наблюдателя поднятием руки.
   
4. Принимать продукты питания.
   
5. Временно покидать аудиторию, оставляя у наблюдателя свою тетрадь.
   

Во время работы над заданиями участнику запрещается:

1. Пользоваться мобильным телефоном (в любой его функции).
   
2. Пользоваться программируемым калькулятором или переносным компьютером.
   
3. Пользоваться какими-либо источниками информации, за исключением листов со справочной информацией, раздаваемых Оргкомитетом перед туром.
   
4. Обращаться с вопросами к кому-либо, кроме наблюдателя, членов Оргкомитета и жюри.
   
5. Производить записи на собственную бумагу, не выданную оргкомитетом.
   
6. Запрещается одновременный выход из аудитории двух и более участников.
   

После завершения работы участников они переходят в конференц-зал или большую аудиторию, где проводится заключительное собрание. Перед ними может выступить член оргкомитета и жюри с кратким разбором заданий.

Отдельное помещение для жюри должно быть предоставлено Оргкомитетом на весь день проведения олимпиады, при надобности – и на следующий день. Члены жюри должны прибыть на место проведения олимпиады не позднее, чем через 2 часа после начала работы участников. Председатель жюри (или его заместитель) и 1-2 члена жюри должны прибыть к началу этапа и периодически обходить аудитории, отвечая на вопросы участников по условию задач.

3. ПРОЦЕДУРА ОЦЕНИВАНИЯ РЕШЕНИЙ И ПОДВЕДЕНИЯ ИТОГОВ

Решение каждого задания оценивается по 8-балльной системе с возможностью выставления оценки в 9 баллов. Большая часть из этих 8 баллов (не менее 4-5) выставляется за правильное понимание участником олимпиады сути предоставленного вопроса и выбор пути решения. Оставшиеся баллы выставляются за правильность расчетов, аккуратную и полную подачу ответа.

Максимальная оценка за каждое задание одинакова и не зависит от темы, освещаемой в задании, и категории сложности. Таким образом, достигается максимальная независимость результатов школьного и муниципального этапов олимпиады от конкретных предпочтений каждого школьника по темам в курсе астрономии и смежных дисциплин.

Суммарная оценка за весь этап (школьный или муниципальный) составляет 48 баллов. Победителем этапа становится участник, набравший максимальное количество баллов (не менее 24 баллов) в своей возрастной параллели. Призерами олимпиады становятся участники, идущие в итоговом протоколе за победителем и имеющие результат не ниже 15-20 баллов. Число призеров олимпиады ограничивается квотой, установленной организаторами школьного и муниципального этапа Всероссийской олимпиады по астрономии.


Приложение

Вопросы по астрономии,

рекомендуемые методической комиссией Всероссийской Олимпиады по астрономии для подготовки школьников к решению задач этапов Олимпиады


§ 1. 9 класс.


1.1. Звездное небо.

Созвездия и ярчайшие звезды неба: названия, условия видимости в различные сезоны года.


1.2. Небесная сфера.

Суточное движение небесных светил на различных широтах. Восход, заход, кульминация. Горизонтальная и экваториальная система координат, основные круги и линии на небесной сфере. Высота над горизонтом небесных светил в кульминации. Высота полюса Мира. Изменение вида звездного неба в течение суток. Подвижная карта звездного неба. Рефракция (качественно). Сумерки: гражданские, навигационные, астрономические. Понятия углового расстояния на небесной сфере и угловых размеров объектов.


1.3. Движение Земли по орбите.

Видимый путь Солнца по небесной сфере. Изменение вида звездного неба в течение года. Эклиптика, понятие полюса эклиптики и эклиптической системы координат. Зодиакальные созвездия. Прецессия, изменение экваториальных координат светил из-за прецессии.


1.4. Измерение времени.

Тропический год. Солнечные и звездные сутки, связь между ними. Солнечные часы. Местное, поясное время. Истинное и среднее солнечное время, уравнение времени. Звездное время. Часовые пояса и исчисление времени в нашей стране; декретное время, летнее время. Летоисчисление. Календарь, солнечная и лунная система календаря. Новый и старый стиль.


1.5. Движение небесных тел под действием силы всемирного тяготения.

Форма орбит: эллипс, парабола, гипербола. Эллипс, его основные точки, большая и малая полуоси, эксцентриситет. Закон всемирного тяготения. Законы Кеплера (включая обобщенный третий закон Кеплера). Первая и вторая космические скорости. Круговая скорость, скорость движения в точках перицентра и апоцентра. Определение масс небесных тел на основе закона всемирного тяготения. Расчеты времени межпланетных перелетов по касательной траектории.


1.6. Солнечная система.

Строение, состав, общие характеристики. Размеры, форма, масса тел Солнечной системы, плотность их вещества. Отражающая способность (альбедо). Определение расстояний до тел Солнечной системы (методы радиолокации и суточного параллакса). Астрономическая единица. Угловые размеры планет. Сидерический, синодический периоды планет, связь между ними. Видимые движения и конфигурации планет. Наклонение орбиты, линия узлов. Прохождения планет по диску Солнца, условия наступления. Малые тела Солнечной системы. Метеороиды, метеоры и метеорные потоки. Метеориты. Орбиты планет, астероидов, комет и метеороидов. Возмущения в движении планет. Третья космическая скорость для Земли и других тел Солнечной системы.


1.7. Система Солнце - Земля - Луна.

Движение Луны вокруг Земли, фазы Луны. Либрации Луны. Движение узлов орбиты Луны, периоды «низкой» и «высокой» Луны. Синодический, сидерический, аномалистический и драконический месяцы. Солнечные и лунные затмения, их типы, условия наступления. Сарос. Покрытия звезд и планет Луной, условия их наступления. Понятие о приливах.


1.8. Оптические приборы.

Глаз как оптический прибор. Устройство простейших оптических приборов для астрономических наблюдений (бинокль, фотоаппарат, линзовые, зеркальные и зеркально-линзовые телескопы). Построение изображений протяженных объектов в фокальной плоскости. Угловое увеличение, масштаб изображения. Крупнейшие телескопы нашей страны и мира.


1.9. Шкала звездных величин.

Представление о видимых звездных величинах различных астрономических объектов. Решение задач на звездные величины в целых числах. Зависимость яркости от расстояния до объекта.


1.10. Электромагнитные волны.

Скорость света. Различные диапазоны электромагнитных волн. Видимый свет, длины волн и частоты видимого света. Радиоволны.


1.11. Общие представления о структуре Вселенной.

Пространственно-временные масштабы Вселенной. Наша Галактика и другие галактики, общее представление о размерах, составе и строении.


1.12. Измерения расстояний в астрономии.

Внесистемные единицы в астрономии (астрономическая единица, световой год, парсек, килопарсек, мегапарсек). Методы радиолокации, суточного и годичного параллакса. Аберрация света.


1.13. Дополнительные вопросы.

Дополнительные вопросы по математике: Запись больших чисел, математические операции со степенями. Приближенные вычисления. Число значащих цифр. Пользование инженерным калькулятором. Единицы измерения углов: градус и его части, радиан, часовая мера. Понятие сферы, большие и малые круги. Формулы для синуса и тангенса малого угла. Решение треугольников, теоремы синусов и косинусов. Элементарные формулы тригонометрии.


Дополнительные вопросы по физике: Законы сохранения механической энергии, импульса и момента импульса. Понятие об инерциальных и неинерциальных системах отсчета. Потенциальная энергия взаимодействия точечных масс. Геометрическая оптика, ход лучей через линзу.


§ 2. 10 класс.


2.1. Шкала звездных величин.

Звездная величина, ее связь с освещенностью. Формула Погсона. Связь видимого блеска с расстоянием. Абсолютная звездная величина. Изменение видимой яркости планет и комет при их движении по орбите.


2.2. Звезды, общие понятия.

Основные характеристики звезд: температура, радиус, масса и светимость. Законы излучения абсолютно черного тела: закон Стефана-Больцмана, закон смещения Вина. Понятие эффективной температуры.


2.3. Классификация звезд.

Представление о фотометрической системе UBVR, показатели цвета. Диаграмма «цвет-светимость» (Герцшпрунга-Рассела). Звезды главной последовательности, гиганты, сверхгиганты. Соотношение «масса-светимость» для звезд главной последовательности.


2.4. Движение звезд в пространстве.

Эффект Доплера. Лучевая скорость звезд и принципы ее измерения. Тангенциальная скорость и собственное движение звезд. Апекс.


2.5. Двойные и переменные звезды.

Затменные переменные звезды. Спектрально-двойные звезды. Определение масс и размеров звезд в двойных системах. Внесолнечные планеты. Пульсирующие переменные звезды, их типы, кривые блеска. Зависимость «период-светимость» для цефеид. Долгопериодические переменные звезды. Новые звезды.

2.6. Рассеянные и шаровые звездные скопления.

Возраст, физические свойства скоплений и особенности входящих в них звезд. Основные различия между рассеянными и шаровыми скоплениями. Диаграммы «цвет-светимость» для звезд скоплений. Движения звезд, входящих в скопление. Метод «группового параллакса» определения расстояния до скопления.


2.7. Солнце.

Основные характеристики, общее представление о внутреннем строении и строении атмосферы. Характеристики Солнца как звезды, солнечная постоянная. Солнечная активность, циклы солнечной активности. Магнитные поля на Солнце. Солнечно-земные связи.


2.8. Ионизованное состояние вещества.

Понятие об ионизованном газе. Процессы ионизации и рекомбинации. Общие представление об ионах в атмосфере Земли и межпланетной среде. Магнитное поле Земли. Полярные сияния.


2.9. Межзвездная среда.

Представление о распределении газа и пыли в пространстве. Плотность, температура и химический состав межзвездной среды. Межзвездное поглощение света, его зависимость от длины волны и влияние на звездные величины и цвет звезд. Газовые и диффузные туманности. Звездообразование. Межзвездное магнитное поле.


2.10. Телескопы, разрешающая и проницающая способность.

Предельное угловое разрешение и проницающая способность. Размеры дифракционного изображения, ограничения со стороны земной атмосферы на разрешающую способность. Аберрации оптики. Оптические схемы современных телескопов.


2.11. Дополнительные вопросы.

Дополнительные вопросы по математике: площадь поверхности и сферы, объем шара.

Дополнительные вопросы по физике: Газовые законы. Понятие температуры, тепловой энергии газа, концентрации частиц и давления. Основы понятия спектра, дифракции света.


§ 3. 11 класс.


3.1. Основы теории приливов.

Приливное воздействие. Понятие о радиусе сферы Хилла, полости Роша. Точки либрации.


3.2. Оптические свойства атмосфер планет и межзвездной среды.

Рассеяние и поглощение света в атмосфере Земли, в межпланетной и межзвездной среде, зависимость поглощения от длины волны. Атмосферная рефракция, зависимость от высоты объекта, длины волны света.


3.3. Законы излучения.

Интенсивность излучения. Понятие спектра. Излучение абсолютно черного тела. Формула Планка. Приближения Релея-Джинса и Вина, области их применения. Распределение энергии в спектрах различных астрономических объектов.


3.4. Спектры звезд.

Основы спектрального анализа. Линии поглощения в спектрах звезд, спектральная классификация. Атмосферы Солнца и звезд. Фотосфера и хромосфера Солнца.


3.5. Спектры излучения разреженного газа.

Представление о спектрах солнечной короны, планетарных и диффузных туманностей, полярных сияний.


3.6. Представление о внутреннем строении и источниках энергии Солнца и звезд.

Ядерные источники энергии звезд, запасы ядерной энергии. Выделение энергии при термоядерных реакциях. Образование химических элементов в недрах звезд различных типов, в сверхновых звездах (качественно).


3.7. Эволюция Солнца и звезд.

Стадия гравитационного сжатия при образовании звезды. Время жизни звезд различной массы. Сверхновые звезды. Поздние стадии эволюции звезд: белые карлики, нейтронные звезды, черные дыры. Гравитационный радиус. Пульсары.


3.8. Строение и типы галактик.

Наша Галактика. Ближайшие галактики. Расстояние до ближайших галактик. Наблюдательные особенности галактик. Состав галактик и их физические характеристики. Вращение галактических дисков. Морфологические типы галактик. Активные ядра галактик, радиогалактики, квазары.

3.9. Основы космологии.

Определение расстояний до галактик. Сверхновые I типа. Красное смещение в спектрах галактик. Закон Хаббла. Скопления галактик. Представление о гравитационных линзах (качественно). Крупномасштабная структура Вселенной. Реликтовое излучение и его спектр.


3.10. Приемники излучения и методы наблюдений.

Элементарные сведения о современных методах фотометрии и спектроскопии. Фотоумножители, ПЗС-матрицы. Использование светофильтров. Прием радиоволн. Угловое разрешение радиотелескопов и радиоинтерферометров.


3.11. Дополнительные вопросы.

Дополнительные вопросы по математике: основы метода приближенных вычислений и разложений в ряд. Приближенные формулы для cos x, (1+x)ⁿ, ln (1+x), e^x в случае малых х.


Дополнительные вопросы по физике: Элементы специальной теории относительности. Релятивистская формула для эффекта Доплера. Гравитационное красное смещение. Связь массы и энергии. Основные свойства элементарных частиц (электрон, протон, нейтрон, фотон). Квантовые и волновые свойства света. Энергия квантов, связь с частотой и длиной волны. Давление света. Спектр атома водорода. Космические лучи. Понятие об интерференции и дифракции.


ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

7- 8 класс.

1. Какая из перечисленных звёзд - Арктур, Вега, Капелла, Полярная, Сириус - является самой яркой звездой северного полушария неба? В каком созвездии она расположена и какую примерно имеет видимую звёздную величину?
   

2. "После захода Солнца стало быстро темнеть. Ещё не зажглись на тёмно-синем небе первые звёзды, а на востоке уже ослепительно сияла Венера". Все ли верно в этом описании?
   

3. 29 марта 2006 г. произошло солнечное затмение, в каком созвездии в этот момент находилась Луна?
   

4. Что представляют собой две самые яркие, видимые даже невооруженным глазом, туманности земного неба Туманность Андромеды и Туманность Ориона, из чего они состоят, и за счёт чего они светят?
   

5. В 2004 году весеннее равноденствие состоялось не 21 марта, как обычно, а 20 марта в 06 ч 49 м UT (всемирное время) Поскольку к этому моменту на летнее время мы еще не перешли, то в Москве было 09 ч 49 м. Почему это произошло 20 марта? Когда будет весеннее равноденствие в последующие годы? Какова продолжительность дня и ночи в этот день? С момента весеннего равноденствия начинается астрономическая весна. До какого дня она будет продолжаться в 2005 году?
   

6. В настоящее время космический аппарат Кассини исследует и фотографирует планету Сатурн и его спутники. Расстояние от Сатурна до Солнца 29,46 астрономические единицы (1а.е.=150 млн. км). За какое минимальное время информация, полученная аппаратом, достигает Земли? (Скорость света в вакууме 300000км/с).
   

ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

7- 8 класс (решения).

1. Какая из перечисленных звёзд - Арктур, Вега, Капелла, Полярная, Сириус - является самой яркой звездой северного полушария неба? В каком созвездии она расположена и какую примерно имеет видимую звёздную величину?
   

Решение:

Самая яркая звезда на небе – Сириус. Но эта звезда не северного небесного полушария, а южного. Поэтому самая яркая звезда – Вега ( Лиры). У нее примерно нулевая видимая звёздная величина..

2. "После захода Солнца стало быстро темнеть. Ещё не зажглись на тёмно-синем небе первые звёзды, а на востоке уже ослепительно сияла Венера". Все ли верно в этом описании?
   

Решение:

Венера на нашем небе никогда не удаляется от Солнца более чем на 46, следовательно, она не может быть на востоке, когда Солнце на западе.

3. 29 марта 2006 г. произошло солнечное затмение, в каком созвездии в этот момент находилась Луна?
   

Решение.

29 марта Солнце находилось в созвездии Рыб недалеко от точки весеннего равноденствия. Во время затмения Луна закрыла Солнце, поэтому располагалась в том же созвездии Рыб.

4. Что представляют собой две самые яркие, видимые даже невооруженным глазом, туманности земного неба Туманность Андромеды и Туманность Ориона, из чего они состоят, и за счёт чего они светят?
   

Решение.

Туманность Андромеда - ближайшая спиральная галактика из крупных галактик в созвездии Андромеды. Расстояние до Туманности Андромеды - около 2 млн св. лет. Галактику можно увидеть невооружённым глазом в созвездии Андромеда. Её свечение обусловлено совокупным свечением всех звезд.

Галактику Туманность Андромеды также называют Великой спиральной галактикой. Известна под номером М31 (по каталогу Мессье) и под номером NGC224 по Новому общему каталогу. Туманность Андромеды имеет восемь спутников, из которых два самых известных – эллиптическая галактика М 32 (NGC221) рядом с центром М 31 и эллиптическая галактика NGC205. Другие спутники галактики Туманность Андромеды М31 менее яркие, например карликовая галактика, названная Андромеда VIII, расположена на небе вблизи карликовой эллиптической галактики M32.

Угловой диаметр галактики М31 - 100 (16 кпк), расстояние – 670 кпк (около 2 млн св. лет.). Абсолютная звездная величина М= 21,1^m. Видимая звездная величина m=3,4^m.

Туманность Ориона (или М 42) – это газовая туманность, состоящая в основном из водорода (из газа). Она находится в нашей Галактике на расстоянии около 1000 св. лет, ее диаметр около 16 св. лет. Её свечение объясняется свечением горячего газа. Туманность Ориона видна невооружённым глазом в созвездии Ориона. Иногда эту туманность, чтобы отличить от других туманностей в созвездии Ориона, называют Большой туманностью Ориона. Большую туманность Ориона можно наблюдать невооруженным глазом в созвездии Ориона, ниже и левее так называемого пояса Ориона, состоящего из трёх легко узнаваемых звезд. Газовая туманность Большая туманность Ориона светится за счет молодых горячих звёзд спектрального класса О. Эти звезды имеют мощное ультрафиолетовое излучение, которое ионизирует газ туманности Ориона. Большая туманность Ориона представляет собой огромную область звёздообразования и является одной из самых известных астрономических туманностей. Она расположена сравнительно недалеко от нас. Расстояние до туманности Ориона 460 пк. Диаметр туманности 35 или 5 пк. Масса 300 М _Солнца.


Учащиеся могут ответить лишь частично, но главное, что они обязаны написать в ответе – это принципиальное отличие в этих объектах: галактика, её свечение обусловлено свечением звёзд, и газовая туманность, её свечение объясняется свечением горячего газа.

5. В 2004 году весеннее равноденствие состоялось не 21 марта, как обычно, а 20 марта в 06 ч 49 м UT (всемирное время) Поскольку к этому моменту на летнее время мы ещё не перешли, то в Москве было 09 ч 49 м. Почему это произошло 20 марта? Когда будет весеннее равноденствие в последующие годы? Какова продолжительность дня и ночи в этот день? С момента весеннего равноденствия начинается астрономическая весна. До какого дня она будет продолжаться в 2005 году?
   

Решение:

Раннее наступление равноденствия связано с тем, что 2004 год – високосный и «лишний день» 29 февраля сдвинул дату равноденствия. В следующие три года всё вернётся на свои места, а потом повторится. В эти дни по всей Земле Солнце перемещается по небу от восхода до заката почти ровно за 12 часов (без учёта рефракции) и, следовательно, везде продолжительность дня и ночи одинакова. С момента весеннего равноденствия начинается астрономическая весна, которая продлится до дня летнего солнцестояния, которое в 2005 году наступит 21 июня.

6. В настоящее время космический аппарат Кассини исследует и фотографирует планету Сатурн и его спутники. Расстояние от Сатурна до Солнца 29,46 астрономические единицы (1а.е.=150 млн. км). За какое минимальное время информация, полученная аппаратом, достигает Земли? (Скорость света в вакууме 300000 км/с).
   

Решение.

Минимальное расстояние от Земли до Сатурна 29,46 – 1 = 28,46 а.е. = 28,46·150000000 = 4,27·10⁹ км. Свет имеет скорость с = 300000 км/с, поэтому информация достигнет Земли за время 4,27·10⁹км/300000 км/с =1,42·10⁴с = 3ч 57м.


ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

9 класс.

1. Во время полёта самолёта штурман отмечает, что высота Полярной звезды остаётся неизменной. Как в этом случае изобразить на географической карте путь самолёта?
   

2. В индейской сказке «О белой кувшинке» говорится: «Ваби приподнял кожаный полог, и глаза его от удивления стали круглыми, как у совы. Звёзды – голубоватые, зелёные, крохотные и чуть крупнее – весело шевелили лучами почти у самого его носа!». Что неверно в данном описании?
   

3. Период обращения вокруг Солнца самой короткопериодической кометы Энке  составляет 3.3 года. Почему же условия её видимости повторяются с  характерным периодом в 10 лет?
   

4. В какой четверти Луна лучше освещает Землю – в первой или в третьей?
   

5. Если полное лунное затмение произойдёт сегодня, то можно ли будет наблюдать его с Южного полюса Земли? Дайте развёрнутый ответ.
   

6. Роберт Хайнлайн в романе «Дорога доблести» описывает планету - Центр галактической империи. Планета эта «размером с Марс», сила тяжести на ней «почти земная». Что можно сказать о плотности этой планеты? Каковы для этой планеты первая и вторая космическая скорости? Каков период обращения спутника на низкой орбите? Радиус Марса - 3400 км, гравитационная постоянная G = 6,6710^-11 Нм²/кг², g = 9,8 н/кг.
   

ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

9 класс (решения).

1. Во время полёта самолёта штурман отмечает, что высота Полярной звезды остаётся неизменной. Как в этом случае изобразить на географической карте путь самолёта?
   

Решение:

Географическая широта остаётся неизменной, - следовательно, самолёт летит вдоль экватора или параллели.

2. В индейской сказке «О белой кувшинке» говорится: «Ваби приподнял кожаный полог, и глаза его от удивления стали круглыми, как у совы. Звёзды – голубоватые, зелёные, крохотные и чуть крупнее – весело шевелили лучами почти у самого его носа!». Что неверно данном описании?
   

Решение.

Цвет звезды зависит от температуры звезды. Голубоватые звезды имеют высокую температуру, большую 12000К. Зеленых звезд не бывает. Видимые размеры звезд соответствуют разным видимым звездным величинам.

«Шевеление лучей» - дрожание атмосферы.

Таким образом, неверно – зеленый цвет звезд.

3. Период обращения вокруг Солнца самой короткопериодической кометы Энке  составляет 3.3 года. Почему же условия её видимости повторяются с  характерным периодом в 10 лет?
   

Решение:

Через 10 лет комета сделает ровно 3 оборота по своей орбите, а  Земля - ровно 10. Значит, оба небесных тела окажутся почти в тех же точках пространства, а значит, такими же будут условия видимости кометы  на Земле.

4. В какой четверти Луна лучше освещает Землю – в первой или в третьей?
   

Решение:

Правая часть видимой нам поверхности Луны, где меньше морей отражает солнечные свет лучше, чем левая – это видно. Поэтому в первой четверти, когда освещена правая часть Луны, она освещает Землю лучше, чем в третьей.

5. Если полное лунное затмение произойдёт сегодня, то можно ли будет наблюдать его с Южного полюса Земли? Дайте развёрнутый ответ.
   

Решение:

Полярная ночь на Южном полюсе, когда можно наблюдать лунное затмение, продолжается с 21 марта по 23 сентября. Если дата приходится на этот период, то затмение наблюдать можно.

6. Роберт Хайнлайн в романе «Дорога доблести» описывает планету - Центр галактической империи. Планета эта «размером с Марс», сила тяжести на ней «почти земная». Что можно сказать о плотности этой планеты? Каковы для этой планеты первая и вторая космическая скорости? Каков период обращения спутника на низкой орбите? Радиус Марса - 3400 км, гравитационная постоянная G = 6,6710^-11 Нм²/кг², g = 9,8 н/кг.
   

Решение.

Из закона всемирного тяготения выразим ускорение свободного падения вблизи поверхности планеты: g = GM/R ² = 4GR/3.

Отсюда средняя плотность планеты = 3g/4GR = 10322 кг/м³ - значительно больше плотности железа.

Первая космическая скорость υ₁ = 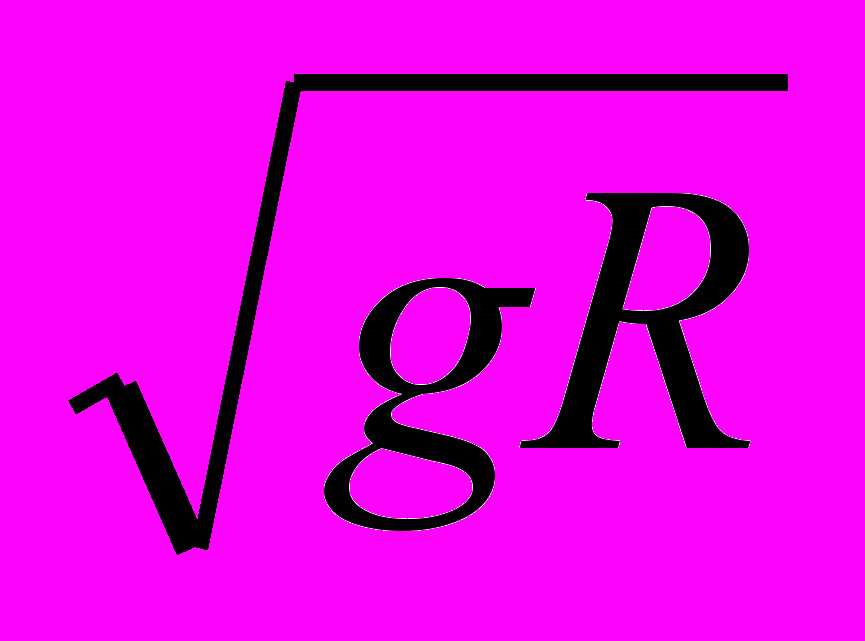= 5,83 км/с.

Вторая космическая скорость в корень из 2 раз больше первой: v₂ = 8,14 км/с.

Период обращения спутника на низкой орбите Т = 2R/υ₁ = 3661,8 с - чуть больше часа.


ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

10 класс.

1. 20 января Солнце перешло из созвездия Стрельца в созвездие Козерога. Сейчас (днем 27 января 2007 года) Меркурий и Венера находятся в созвездии Козерога, Марс – в созвездии Стрельца, Нептун в созвездии Козерога, карликовая планета Плутон находится на границе созвездий Стрельца и Змееносца, карликовая планета Церера находится в созвездии Рыбы, Юпитер – на границе созвездий Змееносца и Скорпиона. Уран находится в созвездии Водолея, граничащим с созвездием Козерога. Сатурн находится в созвездии Льва.
   

Как называется такое расположение планет? Сколько больших планет сейчас находится над горизонтом? Сколько карликовых планет сейчас находится над горизонтом? Сколько больших планет можно будет наблюдать всю ночь?

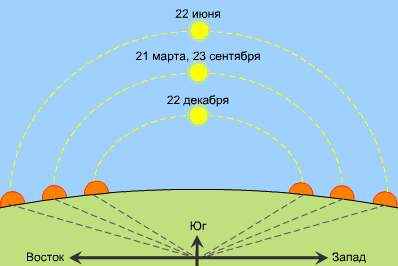
2. На рисунке изображены восходы и заходы Солнца в северном полушарии. Укажите, в чем ошибка художника и нарисуйте верный рисунок.
   

3. Температура в центре Солнца 15млн.К, и там протекают термоядерные реакции. Почему же у белого карлика Сириус В, температура внутри которого оценивается в 40 млн.К, эти реакции не протекают?
   

4. Удаление Венеры от Солнца составляет 45˚. Нарисуйте взаимное расположение Венеры, Земли и Солнца в момент наибольшего удаления Венеры от Солнца и определите расстояние Венеры от Солнца в астрономических единицах и километрах.
   

5. Исследователи решили совершить поездку на вездеходе вокруг небольшого астероида по его экватору. Определите минимальное время такого путешествия, учитывая, что вездеход не должен отрываться от поверхности астероида, иначе он рискует оказаться выброшенным на орбиту. Средняя плотность вещества астероида ρ=3500кг/м³, форма – сферическая. Астероид не вращается относительно звёзд,. Гравитационная постоянная в системе «СИ» G = 6,67∙10^-11(н∙м²/кг²).
   

6. В XIX веке вопрос об источнике энергии Солнца Дж. Гершель назвал «великой тайной». Среди первых научных гипотез было предположение, что наше дневное светило является раскаленным остывающим телом или представляет собой химически горящее тело. Юлиус Роберт Майер в середине XIX века показал, что даже если Солнце состояло бы из чистого каменного угля, оно сгорело бы за исторически короткий промежуток времени. Сделайте оценку этого времени.
   

Подсказка. Масса Солнца М = 210³⁰ кг, светимость Солнца L=3,810²⁶ Вт, удельная теплота сгорания каменного угля q=2,710⁷ Дж/кг.




ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

10 класс (решения).

1. 20 января Солнце перешло из созвездия Стрельца в созвездие Козерога. Сейчас (днём 27 января 2007 года) Меркурий и Венера находятся в созвездии Козерога, Марс – в созвездии Стрельца, Нептун в созвездии Козерога, карликовая планета Плутон находится на границе созвездий Стрельца и Змееносца, карликовая планета Церера находится в созвездии Рыбы, Юпитер – на границе созвездий Змееносца и Скорпиона. Уран находится в созвездии Водолея, граничащим с созвездием Козерога. Сатурн находится в созвездии Льва.
   

Как называется такое расположение планет? Сколько больших планет сейчас находится над горизонтом? Сколько карликовых планет сейчас находится над горизонтом?

Сколько больших планет можно будет наблюдать всю ночь?

Решение.

Это расположение планет называется парадом планет. Сегодня днём над горизонтом находится 6 больших планет: Меркурий, Венера, Марс, Юпитер, Уран, Нептун. Сегодня днём над горизонтом находится 2 карликовых планеты: Церера и Плутон. К сожалению, сегодня парад планет не виден вечером и ночью, так как планеты находятся над горизонтом днем.

Всю ночь будет виден Сатурн, следовательно одну планету.

2. На рисунке изображены восходы и заходы Солнца в северном полушарии. Укажите, в чем ошибка художника и нарисуйте верный рисунок.
   

Решение.

Только в дни равноденствий 21 марта и 23 сентября Солнце восходит в точке востока и заходит в точке запада (везде).

Например, для Москвы, =56, в день летнего солнцестояния Солнце восходит на северо-востоке, а в день зимнего солнцестояния – на юго-востоке.


Поэтому надо по-другому нарисовать направления сторон горизонта: стрелку востока направить на точку восхода Солнца 21 марта, а стрелку запада – на точку захода 21 марта.

3. Температура в центре Солнца 15млн.К, и там протекают термоядерные реакции. Почему же у белого карлика Сириус В, температура внутри которого оценивается в 40 млн.К, эти реакции не протекают?
   

Решение:

В недрах Солнца много водорода, для горения которого температуры в 15млн.К вполне достаточно. А в недрах Сириуса В водород уже выгорел в процессе эволюции этой звезды, и там только гелий с примесью более тяжёлых элементов. Для горения гелия температуры в 40 млн.К недостаточно.

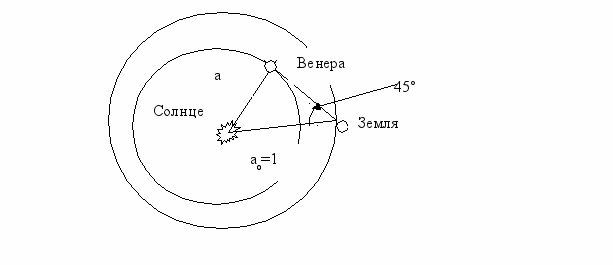
4. Удаление Венеры от Солнца составляет 45˚. Нарисуйте взаимное расположение Венеры, Земли и Солнца в момент наибольшего удаления Венеры от Солнца и определите расстояние Венеры от Солнца в астрономических единицах и километрах.
   

Решение.

Из рисунка видно, что в равнобедренном прямоугольном треугольнике расстояние Венеры до Солнца равно катету а = а₀sin 45˚ = 0,71 а.е. = 106 млн.км.

5. Исследователи решили совершить поездку на вездеходе вокруг небольшого астероида по его экватору. Определите минимальное время такого путешествия, учитывая, что вездеход не должен отрываться от поверхности астероида, иначе он рискует оказаться выброшенным на орбиту. Средняя плотность вещества астероида ρ=3500кг/м³, форма – сферическая. Астероид не вращается относительно звёзд,. Гравитационная постоянная в системе «СИ» G = 6,67∙10^-11(н∙м²/кг²).
   

Решение:

Скорость движения не может превышать первой космической: 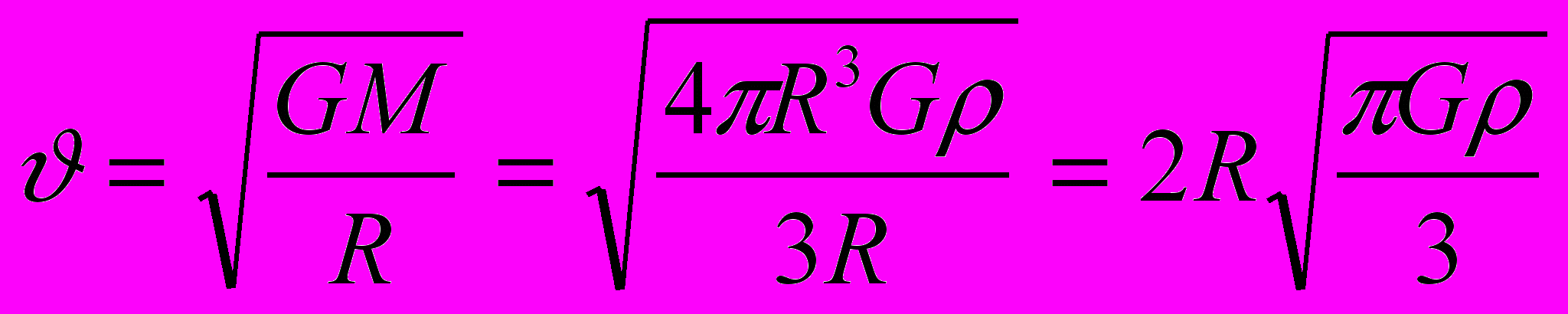. Время путешествия:

6. В XIX веке вопрос об источнике энергии Солнца Дж. Гершель назвал «великой тайной». Среди первых научных гипотез было предположение, что наше дневное светило является раскаленным остывающим телом или представляет собой химически горящее тело. Юлиус Роберт Майер в середине XIX века показал, что даже если Солнце состояло бы из чистого каменного угля, оно сгорело бы за исторически короткий промежуток времени. Сделайте оценку этого времени.
   

Подсказка. Масса Солнца М=210³⁰ кг, светимость Солнца L=3,810²⁶Вт, удельная теплота сгорания каменного угля q=2,710⁷Дж/кг.


Решение:

Время сгорания каменного угля с массой, равной массе Солнца, при мощности горения равной светимости Солнца, легко найти по формуле:

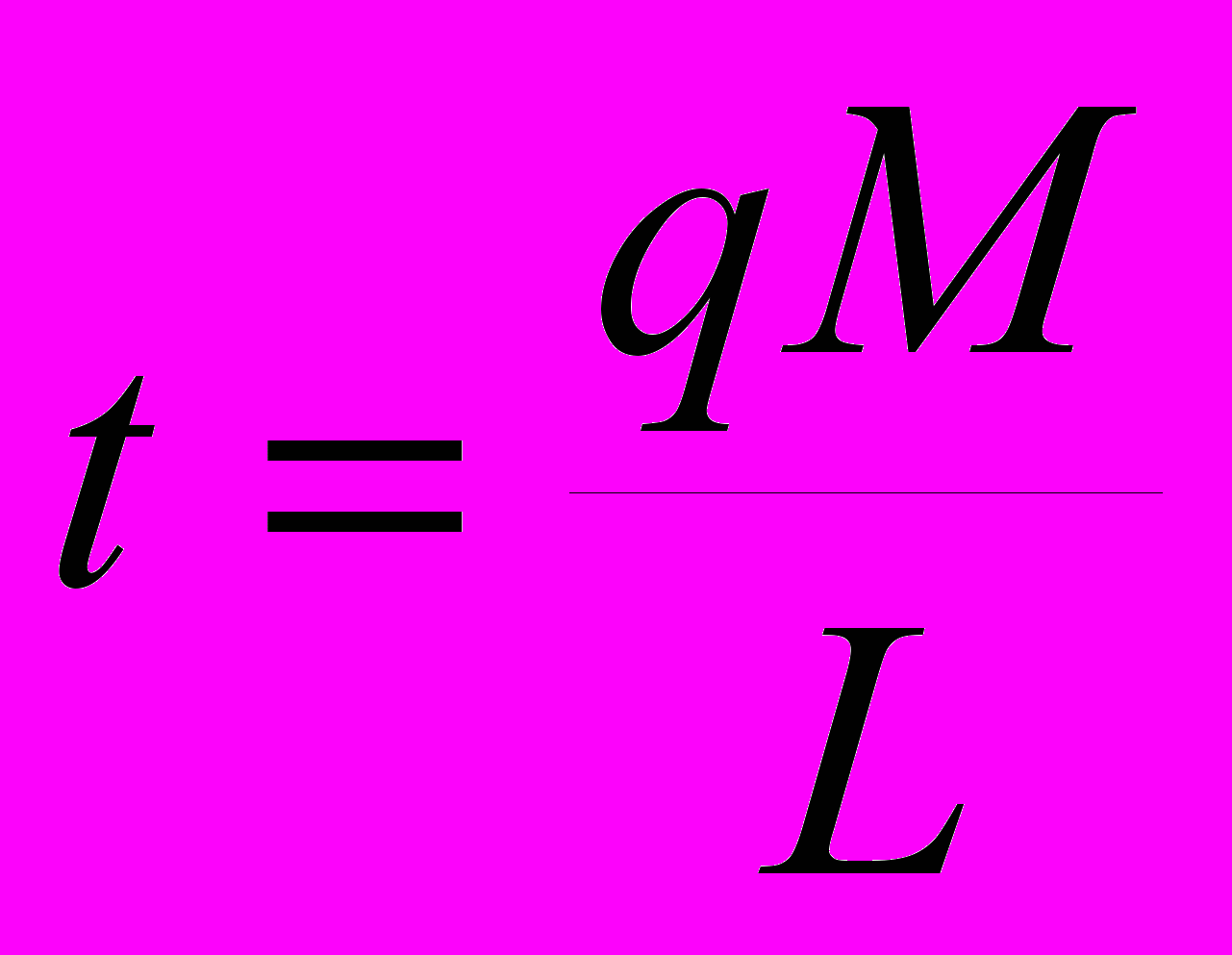. Отсюда время сгорания «каменного угля» Солнца примерно 1,42∙10¹¹ = 4500 лет. Кроме того, для сгорания потребовалось бы большое количество кислорода, которого нет в таких количествах в Солнечной системе.


ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

11 класс.

1. Какие характеристики Солнца связаны с действием гравитационных сил? Какие явления, происходящие на нём, обусловлены наличием магнитного поля?
   

2. Почему днём небо синее, а ночью – чёрное?
   

2. Звезда отстоит от полюса мира на 45⁰. Всегда ли её можно видеть над горизонтом Ялты (φ=44,5⁰), Санкт-Петербурга (φ=60⁰), Архангельска (φ=64,6⁰) и Ташкента (φ=41,3⁰)?
   

2. Взрыв Тунгусского метеорита наблюдался на горизонте в городе Киренске (на реке Лене) в 350 км от взрыва. Определите, на какой высоте произошёл взрыв? (Радиус Земли равен 6371км).
   

2. На какой планете Меркурии или Марсе тело в свободном падении пролетит дальше за 10сек? Масса Меркурия 0,055 М_з, радиус 0,38R_з. Масса Марса 0,107М_з, радиус 0,53 R_з.
   

2. Белый карлик, имеющий радиус 6000км, температуру поверхности 10000К и массу, равную массе Солнца, пролетает через звёздное скопление кометных ядер, каждое, из которых имеет радиус 1км и плотность 1 г/см³. Сколько комет должно ежедневно падать на белый карлик, чтобы его средняя светимость удвоилась? (Постоянная Стефана-Больцмана σ = 5,67 ∙ 10^-8 кг∙с^-3∙ К^-4).
   

ЗАДАЧИ МУНИЦИПАЛЬНОГО ЭТАПА ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО АСТРОНОМИИ И ФИЗИКЕ КОСМОСА

2009 – 2010 уч. год

11 класс (решения).

1. Какие характеристики Солнца связаны с действием гравитационных сил? Какие явления, происходящие на нём, обусловлены наличием магнитного поля?
   

Решение:

С действием гравитационных сил связана шаровая форма и стационарность Солнца (стабильность размеров). Наличие магнитного поля обуславливает возникновение пятен, вспышек, характер движения протуберанцев.

2. Почему днём небо синее, а ночью – чёрное?
   

Решение:

Цвет неба полностью определяется процессами рассеяния солнечного излучения в атмосфере Земли. Днём солнечное излучение рассеивается в атмосфере, причём коротковолновое излучение (синяя часть спектра) рассеивается сильнее длинноволнового (красная часть спектра). Поэтому днём с разных направлений от небесной сферы в глаз наблюдателя попадает много коротковолнового (фиолетового, синего, голубого) излучения и гораздо меньше длинноволнового (красного, оранжевого, жёлтого), которое рассеиваясь в меньшей степени, проходит через атмосферу Земли (видимый нами солнечный диск на небе – это и есть пришедшие от Солнца не рассеянные лучи). В результате небо имеет голубой цвет (а солнечный диск – жёлтый). А ночью, когда солнечный свет не попадает в атмосферу на стороне наблюдателя, рассеянное излучение отсутствует – небо становится чёрным (атмосфера – бесцветной).

Иногда днём небо имеет белёсый цвет, особенно вблизи горизонта. Это связано с наличием большого количества аэрозольных и пылевых частиц в атмосфере, которые из-за своих относительно больших размеров хорошо рассеивают свет не только в синей части спектра.

2. Звезда отстоит от полюса мира на 45⁰. Всегда ли её можно видеть над горизонтом Ялты (φ=44,5⁰), Санкт-Петербурга (φ=60⁰), Архангельска (φ=64,6⁰) и Ташкента (φ=41,3⁰)?
   

Решение:

Если, речь идёт о Северном полюсе мира, то звезда будет восходящей там, где высота полюса (равна широте места) больше, чем 45⁰. Это Санкт – Петербург и Архангельск. Если речь идёт о Южном полюсе мира, то звезда не будет восходящей в Санкт – Петербурге и Архангельске, но появится у горизонта Ялты и Ташкента.

2. Взрыв Тунгусского метеорита наблюдался на горизонте в городе Киренске (на реке Лене) в 350 км от взрыва. Определите, на какой высоте произошёл взрыв? (Радиус Земли равен 6371км).
   

Решение:

Т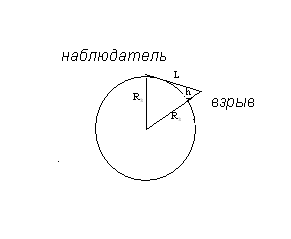реугольник со сторонами L, R_з и (R_з + h) – прямоугольный, поскольку взрыв был виден, то атмосферной рефракцией мы пренебрегаем. Следовательно L²+R²= (R_з+h)², откуда 2R_зh + h² = L². Поскольку радиус Земли R_з = 6371км и расстояние до точки взрыва L = 350км известны, то это квадратное уравнение решаем относительно высоты взрыва h.

Но можно поступить проще. Поскольку h << R_з, можно упростить уравнение: 2R₃h ≈ L² h = = 9,6км.

2. На какой планете Меркурии или Марсе тело в свободном падении пролетит дальше за 10сек? Масса Меркурия 0,055М_з, радиус 0,38R_з. Масса Марса 0,107М_з, радиус 0,53R_з.
   

Решение:

При свободном падении тело проходит путь, равный , где g – ускорение свободного падения. Ускорение свободного падения находим по формуле 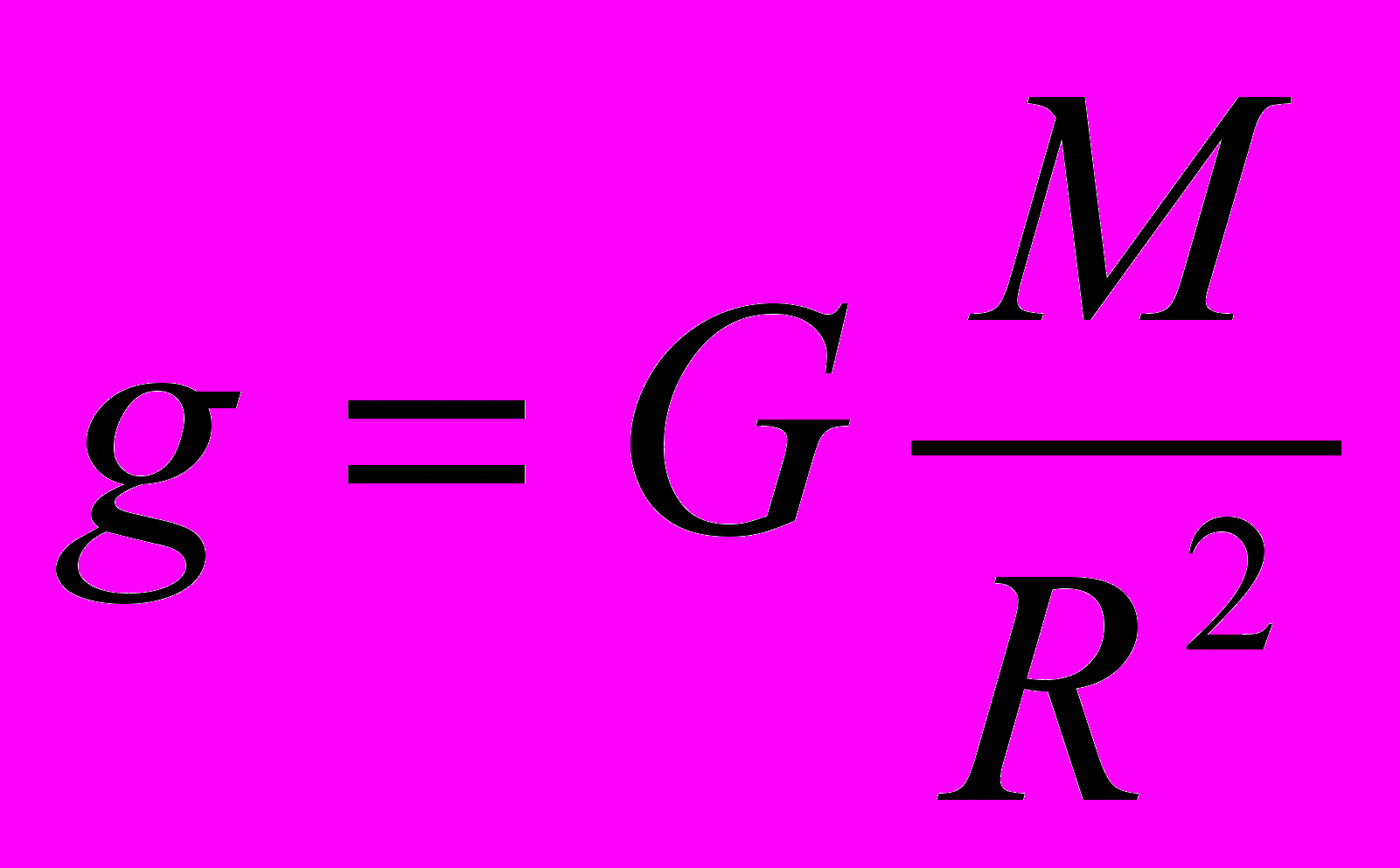. Подставляя значения массы и радиусов, получим, что g_{Меркурия}=g _Марса = 3,8 м/с², следовательно тело в свободном падении на обоих планетах пролетит одно и то же расстояние без учета трения атмосферы.

2. Белый карлик, имеющий радиус 6000км, температуру поверхности 10000К и массу, равную массе Солнца, пролетает через звёздное скопление кометных ядер, каждое, из которых имеет радиус 1км и плотность 1 г/см³. Сколько комет должно ежедневно падать на белый карлик, чтобы его средняя светимость удвоилась? (Постоянная Стефана-Больцмана σ = 5,67 ∙ 10^-8 кг∙с^-3∙ К^-4).
   

Решение:

Количество энергии, излучаемой карликом за одну секунду (светимость): L= 4πσR²T⁴ =2,56∙10²³ Вт или 6,6∙10^-4 светимости Солнца. За сутки (86400с) белый карлик излучает количество энергии Е₀, равное 2,21∙10²⁸ Дж. Масса одного кометного ядра: m = 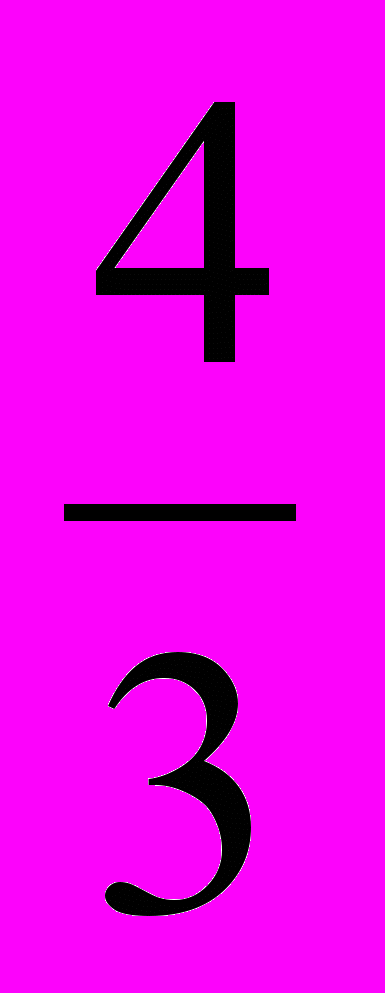πρr³ = 4,19∙10¹²кг.

При падении такого ядра на поверхность белого карлика освобождается энергия Е = = 9,2∙10²⁵ Дж. Чтобы кометы обеспечивали энерговыделение, равное светимости белого карлика, они должны ежедневно падать в количестве (Е₀/Е)~240 штук. На светимость белого карлика будут влиять также два противоположных фактора: 1) не вся энергия падающего ядра кометы будет переходить в видимое излучение, 2) обильное выпадение вещества на поверхность белого карлика будет вызывать его дальнейшее сжатие и дополнительное выделение энергии. При достижении массы 1,4 массы Солнца белый карлик взорвётся как сверхновая звезда I типа.