Общая программа высшая математика для экономических специальностей высших учебных заведений Гродно 2004

Вид материала

Общая программа

Содержание При участии Теории функций, функционального анализа, вероятностей и прикладной математики 1.2. Векторы и матрицы 1.3. Линейные операторы и квадратичные формы 1.4. Элементы аналитической геометрии в пространстве 1.5. Системы линейных уравнений и неравенств Часть 2. Введение в математический анализ 2.2. Числовые ряды 3.1. Функции одной переменной 3.2. Непрерывные функции одной переменной 3.3. Дифференцирование функции одной переменной 3.4. Основные теоремы о функции одной переменной 3.5. Исследование функции с помощью производной. Экстремумы 3.6. Функциональные ряды Часть 4. Интегральное исчисление 4.2. Определенный интеграл Часть 5. Функции нескольких переменных 5.2. Дифференцирование функции нескольких переменных Часть 6. Дифференциальные и разностные уравнения 6.2. Разностные уравнения ... Полное содержание

Подобный материал:

• Учебное пособие для студентов высших медицинских учебных заведений Издание 2-е, дополненное, 955.76kb.
• Учебник Третье издание, 10532.1kb.
• В. В. Москвин Экономическая география России, 9279.48kb.
• Типовая учебная программа для высших учебных заведений по специальности: 1-23, 794.76kb.
• Курс высшей алгебры: Учебник. 17-е изд. Рекомендовано Министерством образования, 177.3kb.
• Типовая учебная программа для высших учебных заведений по специальности: 1-21, 290.18kb.
• Типовая учебная программа для высших учебных заведений по специальности 1-33, 400.17kb.
• Учебная программа для студентов высших учебных заведений, обучающихся по специальностям, 438.29kb.
• Типовая учебная программа для высших учебных заведений по специальности: 1-23, 987.19kb.
• Типовая учебная программа для высших учебных заведений по специальностям: 1-21, 1015.06kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

ОБЩАЯ ПРОГРАММА

ВЫСШАЯ МАТЕМАТИКА

для экономических специальностей

высших учебных заведений


Гродно 2004


Программа разработана

Гродненским государственным университетом им. Я. Купалы

и

Белорусским государственным экономическим университетом


Авторы:

Альсевич В.В. – кандидат физико-математических наук, профессор БГУ;

Вувуникян Ю.М.  кандидат физико-математических наук, доцент ГрГУ:

Денисенко Н.В.  кандидат физико-математических наук, доцент БГЭУ;

Косьянчук В.В.  кандидат физико-математических наук, доцент БГЭУ;

Минюк С.А.  доктор физико-математических наук, профессор, ГрГУ;

Ровба Е. А.  доктор физико-математических наук, первый проректор ГрГУ;

Самаль С.А.  кандидат физико-математических наук, доцент БГЭУ;

Свирид Г.П. – доктор физико-математических наук, профессор БГЭУ;

Сенько В.В.  кандидат физико-математических наук, проректор по научной

работе ГрГУ;

Шевченко Л.И.  кандидат физико-математических наук, доцент БГЭУ;

Янчук Л.Ф.  кандидат физико-математических наук, доцент БГЭУ.


При участии :

Федосенко В.С. – профессора БГУ, заведующего кафедрой общей математики;

Корзникова А.Д. – доцента БГПА, заведующего кафедрой высшей математики №2.


Рецензенты:

Калинин А.Н. – доктор физико-математических наук, профессор БГУ;

Кафедра высшей математики Белорусского государственного экономического университета.


Рекомендована в качестве типовой МО РБ


Рассмотрена и рекомендована для утверждения кафедрой

Теории функций, функционального анализа, вероятностей и прикладной математики

Протокол № 10 от «26 » мая 2004 г.


Утверждена Советом математического факультета

Протокол № 9 от « 29 » июня 2004 г.


Предисловие


Математические дисциплины занимают особое место в образовании экономиста. Поступив же в высшее учебное заведение на экономическую специальность, студенты стремятся к получению специального экономического образования, и многие из них недооценивают важность изучения математики. А именно, основная цель изучения математики на экономических факультетах и экономических высших учебных заведениях состоит в необходимом математическом обеспечении фундаментальных и специальных экономических дисциплин. В связи с этим перед преподавателями математических дисциплин ставятся следующие задачи:

• с помощью математики, как части общечеловеческой культуры, способствовать формированию высоко нравственного гражданина общества;
  
• суметь развить у студентов убеждённость, что без глубокого изучения математики они не смогут овладеть специальными дисциплинами необходимыми им в их будущей деятельности;
  
• научить пользоваться математическими методами, увлечь их красотой;
  
• научить применять математические знания к исследованию реальных экономических процессов и решению профессиональных задач;
  
• помочь развить студентам их способности к абстрактному мышлению, превращая математику в орудие познания окружающего мира.
  

• дать представление:
  

а). о месте математики в системе естественных и экономических наук;

б). об отличии прикладной математики от фундаментальной;

в). о математическом моделировании и его применении в экономике;

Математическое образование современного экономиста включает изучение курса высшей математики, курса теории вероятностей и математической статистики и курса математического программирования. Курс высшей математики, читаемый на первом курсе, является фундаментом математической подготовки специалиста. Однако, уже в рамках этого курса, должно проводится ориентирование на приложение математических методов в профессиональной деятельности. Преподавание курсов «Теории вероятностей и математическая статистика» и «Математическое программирование» ориентированно, главным образом, на применение математических методов к решению практических задач. Выбор специальных разделов математики, которые должны изучать студенты, а также методики их преподавания, осуществляется с учётом характера их будущей профессиональной деятельности и согласуется с выпускающими кафедрами. Все вопросы преподавания этих разделов профилирующими кафедрами должны быть согласованы с кафедрами высшей математики.

Программа определяет основное содержание тем и разделов курсов, подлежащих изучению. Последовательность их изложения и расположения по семестрам разрабатывается кафедрами высшей математики. При разработке следует учитывать необходимость своевременного математического обеспечения фундаментальных и специальных дисциплин; сохранения логической стройности и завершённости самих математических курсов. Кафедрам высшей математики высших учебных заведений рекомендуется всестороннее внедрение компьютеров в учебный процесс, так как это даёт качественно новые возможности в математических дисциплин.

Введение

Роль и место математики и математических методов в решении экономических задач. Лауреаты Нобелевской премии в области экономики Л. В. Канторович и В. Леонтьев.

Элементы теории множеств множества и операции над ними, соответствия и отображения и математической логики логические операции, пропозициональные формулы, булевы функции, кванторы. Аксиоматический подход, математические доказательства, примеры неправильных логических выводов.

Часть 1. Аналитическая геометрия и линейная алгебра


1.1. Аналитическая геометрия на плоскости

Прямоугольная система координат на плоскости. Простейшие задачи аналитической геометрии на плоскости. Прямая на плоскости. Общее уравнение прямой. Уравнение прямой с данным угловым коэффициентом, проходящей через заданную точку. Уравнение прямой, проходящей через две заданные точки. Уравнение прямой в отрезках. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой. Взаимное расположение двух прямых на плоскости.

Кривые второго порядка на плоскости. Примеры кривых второго порядка: окружность, эллипс, парабола, гипербола.


1.2. Векторы и матрицы

Понятие вектора на плоскости. Декартова прямоугольная система координат в трехмерном пространстве и понятия вектора в трехмерном пространстве. Векторы в пространстве 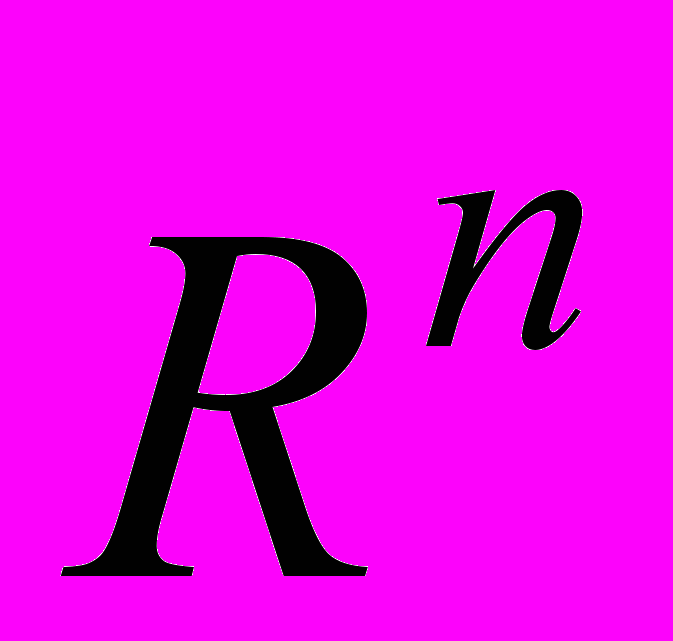и основные операции над ними. Скалярное произведение векторов. Векторное произведение и смешанное произведение векторов, и их свойства.

Линейные комбинации векторов. Линейно независимые системы векторов. Ортогональные системы векторов. Базис и ранг системы векторов. Разложение вектора по базису.

Понятие матрицы. Операции над матрицами. Понятия определителя второго и третьего порядков. Определители n-го порядка. Разложение определителя по строке или столбцу. Свойства определителей. Ранг матрицы. Обратная матрица. Задача межотраслевого баланса (модель Леонтьева) и ее решение с помощью обратной матрицы. Транспонирование матриц. Блочные матрицы. Положительные матрицы. Теорема Перрона – Фробениуса. Матрица Минковского – Леонтьева.


1.3. Линейные операторы и квадратичные формы

Линейные отображения пространства 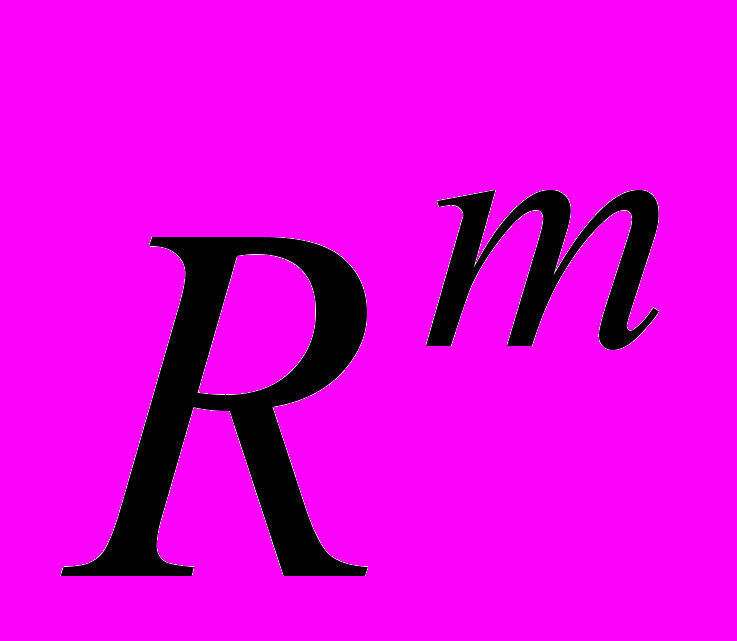в пространство 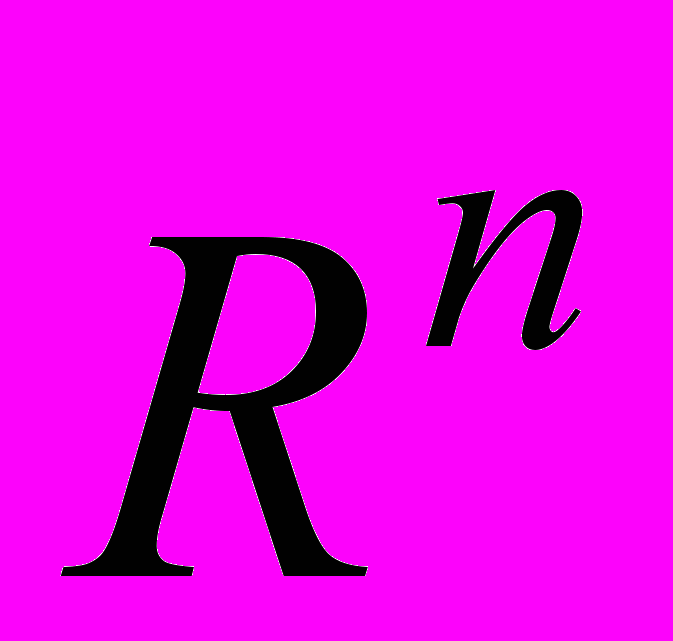. Представление линейного отображения в виде матрицы. Собственные числа и собственные векторы матрицы. Характеристическое уравнение. Приведение матрицы к диагональному виду. Квадратичные формы и преобразование кривых второго порядка к каноническому виду.


1.4. Элементы аналитической геометрии в пространстве

Простейшие задачи аналитической геометрии в пространстве Плоскость в пространстве. Общее уравнение плоскости. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Уравнение плоскости, проходящей через три заданные точки. Расстояние от точки до плоскости. Угол между плоскостями.

Прямая в пространстве. Общее уравнение прямой в пространстве. Параметрическое и каноническое уравнение прямой. Угол между двумя прямыми. Угол между прямой и плоскостью.


1.5. Системы линейных уравнений и неравенств

Экономические задачи, приводящие к системам линейных уравнений и неравенств. Системы линейных уравнений. Правило Крамера. Метод Гаусса. Базисные и опорные решения системы линейных уравнений. Системы линейных неравенств. Смешанные системы линейных уравнений и неравенств. Эквивалентные преобразования систем линейных уравнений и неравенств. Графический метод решения системы линейных неравенств с двумя переменными.

Часть 2. Введение в математический анализ

2.1. Числа и числовые последовательности

Действительные числа. Числовые множества. Числовые последовательности. Бесконечно малые последовательности. Сходящиеся последовательности и их свойства. Монотонные последовательности. Экономическая интерпретация числа e. Фундаментальные последовательности и критерий Коши. Бесконечно большие последовательности.

2.2. Числовые ряды

Понятие числового ряда. Геометрическая прогрессия. Сходимость числового ряда. Простейшие свойства сходящихся числовых рядов с положительными членами. Необходимый и достаточные признаки сходимости положительных рядов.

Знакопеременные ряды. Теорема Коши. Абсолютная и условная сходимость. Признак Лейбница сходимости знакочередующегося ряда.


Часть 3. Дифференциальное исчисление функций одной переменной


3.1. Функции одной переменной

Понятие функции. Область определения и область значений функций. Способы задания функций. Графики функций. Примеры функций. Сложные функции. Предел функции в точке. Основные теоремы о пределах функций. Замечательные пределы. Односторонние пределы. Бесконечные пределы и пределы на бесконечности.


3.2. Непрерывные функции одной переменной

Непрерывность функции в точке. Односторонняя непрерывность. Классификация точек разрыва. Непрерывность монотонной функции. Непрерывность сложной функции и обратной функции. Непрерывность элементарных функций. Функции, непрерывные на множестве и их свойства.


3.3. Дифференцирование функции одной переменной

Производная функции. Геометрический, механический и экономический смысл производной. Правила дифференцирования. Производная сложной и обратной функции. Производные основных элементарных функций. Таблица производных элементарных функций. Логарифмическая производная. Дифференциал, его геометрический и экономический смысл. Применение дифференциала в приближенных вычислениях. Примеры применения производной в экономике (эластичность спроса относительно цены, предельные издержки производства). Производные высших порядков. Формула Лейбница. Неявные функции. Теорема о неявной функции.


3.4. Основные теоремы о функции одной переменной

Стационарные точки. Теоремы Ферма и Ролля. Теорема Лагранжа и формула конечных приращений. Теорема Коши. Правило Лопиталя.


3.5. Исследование функции с помощью производной. Экстремумы

Условие постоянства функций. Условия монотонности функций. Экстремум функции. Необходимое условие экстремума дифференцируемой функции. Наибольшее и наименьшее значение функции. Достаточные условия экстремума. Условия выпуклости и вогнутости. Точки перегиба. Асимптоты. Общая схема исследования функции. Построение графика функции.


3.6. Функциональные ряды

Функциональные ряды. Степенной ряд. Теорема Абеля. Область сходимости степенного ряда.

Разложение функций в степенные ряды. Ряды Тейлора и Маклорена. Необходимый и достаточный признаки разложения функции в ряд Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа.

Разложение элементарных функций в степенные ряды. Биномиальный ряд. Формула бинома Ньютона. Применение рядов к приближенным вычислениям.

Часть 4. Интегральное исчисление

4.1. Первообразная и неопределенный интеграл

Первообразная функции и неопределенный интеграл. Свойства неопределенного интеграла. Метод замены переменной. Формула интегрирования по частям. Таблица неопределенных интегралов. Интегрирование простейших рациональных дробей. Интегрирование рациональных функций. Интегрирование иррациональных функций. Интегрирование рациональных выражений, содержащих тригонометрические функции.


4.2. Определенный интеграл

Определенный интеграл. Формула Ньютона – Лейбница. Основные свойства определенного интеграла. Замена переменной в верхнем интеграле. Формула интегрирования по частям для определенного интеграла. Методы вычисления определенного интеграла. Необходимые условия интегрируемости функций. Достаточные условия интегрируемости функций. Применение определенного интеграла в экономике. Применение определенного интеграла для вычисления площадей фигур, длин дуг плоских кривых и объемов тел вращения. Приближенные методы для вычисления определенных интегралов. Несобственные интегралы.

Часть 5. Функции нескольких переменных

5.1. Функции нескольких переменных

Сходящиеся последовательности в пространстве 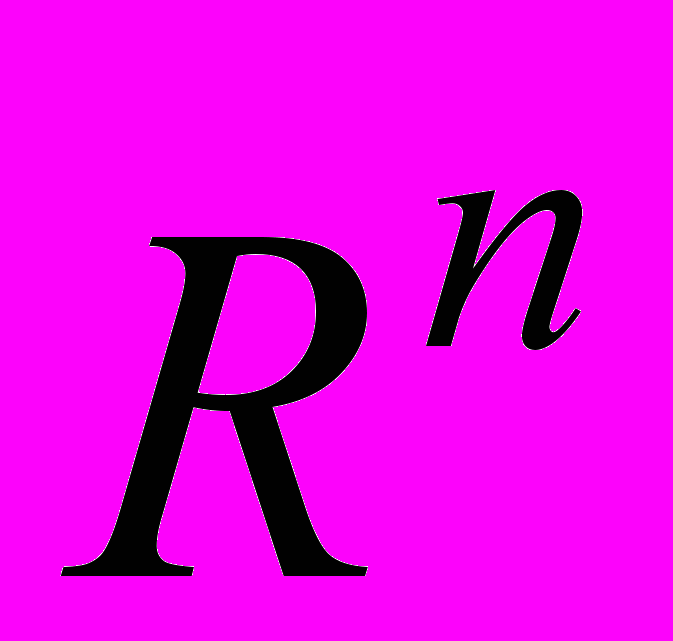и их свойства. Функции нескольких переменных. Однородные функции. Выпуклые и вогнутые функции. Предел функции в точке. Непрерывность. Свойства непрерывных функций.


5.2. Дифференцирование функции нескольких переменных

Частные производные. Примеры применения частных производных в экономике. Дифференцируемость функции. Дифференцирование композиции функций нескольких переменных. Дифференцирование обратной функции. Градиент функции и его свойства. Производная функции по направлению. Неявные функции нескольких переменных. Экстремумы функции. Необходимое условие экстремума. Достаточные условия экстремума. Определение условного экстремума. Условный экстремум в экономике. Наибольшее и наименьшее значение..

Понятие об эмпирических формулах. Подбор параметров по методу наименьших квадратов. Выравнивание по прямой и параболе.

Часть 6. Дифференциальные и разностные уравнения

6.1. Обыкновенные дифференциальные уравнения

Основные понятия теории обыкновенных дифференциальных уравнений. Дифференциальные уравнения первого порядка. Составление дифференциального уравнения первого порядка. Макромодель Домара. Методы интегрирования дифференциальных уравнений первого порядка.

Задача Коши. Теорема существования и единственности решения. Линейные дифференциальные уравнения первого порядка.

Комплексные числа и действия над ними. Комплексная экспонента.

Линейные дифференциальные уравнения высших порядков. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Устойчивость линейных систем второго порядка.


6.2. Разностные уравнения

Конечные разности и обыкновенные разностные уравнения. Линейные стационарные разностные уравнения. Линейные разностные уравнения с постоянными коэффициентами. Линейные нестационарные разностные уравнения.

Часть 7. Теория вероятностей и математическая статистика

7.1. Случайные события и вероятность

Случайные события и соотношения между ними. Частота и вероятность. Геометрическая вероятность. Теоремы сложения и умножения вероятностей. Условная вероятность. Независимость событий. Формула Бернулли. Наивероятнейшее число наступления события. Формула полной вероятности. Формула Байеса. Элементы теории нечетких множеств. Понятие инциденции, нечеткой матрицы, матрицы инциденций. Примеры использования матриц инциденций при исследовании скрытых воздействий в финансовой и производственной областях.


7.2. Случайные величины и законы их распределения

Случайные величины и законы их распределения. Математическое ожидание и дисперсия случайной величины. Мода и медиана. Равномерное распределение. Биномиальный закон распределения. Закон Пуассона. Показательное распределение. Функция надежности.


7.3. Нормальный закон распределения

Нормальный закон распределения. Функция Лапласа. Моменты, асимметрия и эксцесс случайной величины. Закон больших чисел и его частные случаи. Усиленный закон больших чисел. Теорема Колмогорова. Предельные теоремы. Центральная предельная теорема. Определение характеристик и нахождение законов распределения случайных величин на основе опытных данных.


7.4. Основы математической статистики

Предмет математической статистики. Генеральная и выборочная совокупности. Вариационный ряд и его характеристики. Теория оценивания. Интервальные оценки. Предельная ошибка и необходимый объем выборки.

Статистическая гипотеза. Уровень значимости и мощность критерия. Проверка гипотезы о среднем значении при известной и неизвестной дисперсиях. Критерии согласия Пирсона и Колмогорова.

Основные понятия дисперсионного анализа. Однофакторный и двухфакторный дисперсионный анализ.

Модели и основные понятия корреляционного и регрессионного анализа. Линейная корреляционная зависимость и прямые регрессии. Нелинейная регрессия. Множественная линейная регрессия и корреляция. Проверка значимости уравнения и коэффициентов уравнения регрессии.

Модели временных рядов и их составляющие. Анализ случайных процессов. Оценки составляющих временного ряда и автокорреляционной функции.


7.5. Непараметрические методы математической статистики

Основные понятия. Критерии знаков, Вилкоксона, Манна и Уитни. Проверка гипотезы о равенстве дисперсией двух генеральных совокупностей. Критерий серий.

Ранговая корреляция в экономике. Коэффициент ранговой корреляции Спирмена. Коэффициент конкордации Кендэла.

Часть 8. Математическое программирование

8.1. Линейное программирование

Основные постановки задач линейного программирования. Геометрический метод решения. Симплекс-метод. Теория двойственности. Двойственный симплекс-метод. Транспортная задача. Метод потенциалов для решения транспортной задачи. Задача планирования технологий. Задача планирования уровней производства.


8.2. Выпуклое программирование

Выпуклые множества и функции и их свойства. Задачи выпуклого программирования. Теорема Куна-Таккера. Теория двойственности. Приложения к квадратичному программированию. Численные методы решения задач выпуклого программирования. Проблема инвестирования с минимальным риском.


8.3. Нелинейное программирование

Общая задача нелинейного программирования. Необходимое условие минимума первого порядка (правило множителей Лагранжа). Необходимое условие минимума второго порядка. Достаточное условие минимума.


8.4. Целочисленное программирование

Постановки задач целочисленного программирования: общая задача о расписании, задача коммивояжера, задачи о разбиении, покрытии и упаковке, задача о размещении оборудования, задача раскроя. Методы ветвей и границ. Методы отсечений.


8.5. Динамическое программирование

Изложение принципов динамического программирования на примерах задач о распределении ресурсов, обработки деталей на станках, сетевого планирования, построения кратчайшего пути. Методы динамического программирования для решения задач оптимального управления дискретного типа. Задача управления запасами.

ЛИТЕРАТУРА

Основная литература

1. Карасев А.И., Аксютин З.М., Савельев Т.И. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982.
   
2. Самаль С.А. и др. Высшая математика: Общий курс. Учебник для студентов экономических специальностей ВУЗов. Минск, Беларусь, 2000.
   
3. Минюк С.А., Ровба Е.А. Лекции по высшей математике. Учебное пособие для студентов экономических специальностей ВУЗов. Гродно: ГрГУ, 1999. – 389 с.
   
4. Математические методы решения экономических задач. /Под ред. Федоренко Н.П. М.: Наука, 1980. – 184 с.
   
5. Габасов Р., Кириллова Ф.М. Методы оптимизации. Минск: БГУ, 1981. – 350 с.
   
6. Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высш. школа, 1986. – 317 с.
   
7. Кузнецов А.В., Холод Н.И. Математическое программирование. Рекомендовано научно-методическим центром к изданию в 2000 году.
   
8. Мацкевич И.П., Свирид Г.П. Высшая математика: Теория вероятностей и математическая статистика. – Минск: Выш. шк., 1993. – 269 с.
   
9. Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике: Теория вероятностей и математическая статистика. – Минск: Выш. шк., 1996. – 318 с.
   

Дополнительная литература

1. Мороз А. Математические основы менеджмента. М.: Academia, 1997, 256 с.
   
2. Беллман Р. Введение в теорию матриц. М.: 1969. – 368 с.
   
3. Высшая математика для экономистов: учебник /Под ред. Н.Ш. Кремера. – 2-е изд., перераб. И доп. М., Банки и биржи: Юнити, 1998. – 471 с.
   
4. Волков В.А. Элементы теории множеств и развитие понятия числа: Учебное пособие. Мн.: Полымя, 1978. – 83 с.
   
5. Альсевич В.В., Габасов Р.Ф., Глушенков В.С. Оптимизация линейных экономических моделей. Ч. 1. Статистические задачи. Рекомендовано научно-методическим центром к изданию в 2000 году.
   
6. Габасов Р. Методы линейного программирования. Ч. 1. Общие задачи. Мн.: БГУ, 1977. – 173 с.
   
7. Габасов Р., Кириллова Ф.М. Методы линейного программирования. Ч.2. Транспортные задачи. Мн.: БГУ, 1977. – 237 с.
   
8. Габасов Р., Кириллова Ф.М. Методы линейного программирования.
   

Ч. 3. Специальные задачи. Мн.: БГУ, 1980. – 368 с.

9. Беллман Р. Динамическое программирование. /Под ред. Воробьева Н.Н. М.: Иностр. лит., 1960. – 400 с.
   
10. Гейл Д. Теория линейных экономических моделей. /Под ред. Воробьева Н.Н. М.: Иностр. лит., 1963. – 418 с.
    
11. Гольштейн Е.Г. Теория двойственности в математическом программировании и ее приложения. М.: Наука, 1971. – 349 с.
    
12. Капустин В.Ф. Практические занятия по курсу математического программирования. Л.: ЛГУ, 1976. – 192 с.
    
13. Холод Н.И. Пособие по решению задач по линейной алгебре и линейному программированию. /Под ред. Комлика В.И. Мн.: БГУ, 1971. – 176 с.
    
14. Виславский М.Н. Линейная алгебра и линейное программирование. Мн.: Выш. шк., 1966. – 222 с.
    
15. Гольштейн Е.Г., Юдин Д.Б. Задачи линейного программирования транспортного типа. М.: Наука, 1969. – 382 с.
    
16. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. М.: Высш. шк., 1979. – 128 с.
    
17. Калихман И.Л. Сборник задач по математическому программированию. М.: Высш. шк., 1975. – 270 с.
    
18. Кузнецов А.В. Руководство по решению задач по математическому программированию. Минск: Выш. шк., 1978. – 256 с.
    
19. Еремин И.И. Введение в теорию линейного и выпуклого программирования. М.: Наука, 1976. – 189 с.
    
20. Нечеткие множества и теория возможностей: последние достижения. Мн.: Легпромбытиздат, 1986. – 405 с.
    
21. Кофман А., Хил Алуха Х. Модели для исследования скрытых воздействий. Мн.: Выш. шк., 1993.
    
22. Кендэл М. Ранговые корреляции. М.: Статистика, 1975.