Лекции 12-13 по преобразованию Гильберта-Хуанга
| Вид материала | Лекции |
- Sherman Riemenschneider, Bao Liu, Yuesheng Xu and Norden, 1550.08kb.
- Тема 24. Преобразование гильберта-хуанга судьба новой истины такова: в начале своего, 912.36kb.
- Обучающая программа школы предусматривает: Установочные, аналитические и экспертные, 17.82kb.
- Указом Президента Республики Татарстан «Омерах по преобразованию государственных предприятий,, 402.3kb.
- Критерии оценки качества лекции, 33.79kb.
- 1. Записать решение неоднородной системы дифференциальных уравнений с постоянными коэффициентами,, 33.23kb.
- Методическая разработка лекции для преподавателя тема лекции, 39.55kb.
- Московский Государственный Университет им. Ломоносова, 235.89kb.
- План лекций порядковый номер лекции Наименование лекции Перечень учебных вопросов лекции, 36.49kb.
- Методические рекомендации по подготовке и проведению лекции Лекции, 73.92kb.
Лекции 12-13 по преобразованию Гильберта-Хуанга
Сокращенный и частично редактированный машинный перевод.
Преобразование Гильберта-Хуанга: ссылка скрыта
Фон:
• Экспертиза анализа Fourier
• Существующие методы обработки нестационарных данных
• Мгновенная частота
• Внутренние модовые функции (IMF)
• Эмпирическая модовая декомпозиция (EMD)
• Математические вопросы
Оригинал : Huang, и др. "Эмпирическая модовая декомпозиция и спектр Hilbert для анализа нелинейного и нестационарного временного ряда.
"Proc. R. Soc. Lond. (1998) 454, 903–995.
НАСА: ссылка скрыта
Книга: HILBERT-HUANG ПРЕОБРАЗОВАНИЕ И ЕГО ПРИМЕНЕНИЯ. Ред. Norden E. Huang и Сэмюэль S. P. Shen
Коды EMD: ссылка скрытаemd.php
Другое полезное: ссылка скрыта
HHT-базовые коды идентификации: ссылка скрыта
Почему не анализ Fourier (FA)?
• FA хорош, когда система линейна;
Измерьте по крайней мере два выхода: y1 (t) и y2 (t), соответствующие входам x1 (t) и x2 (t).
Теперь примените вход: x (t) = x1 (t) + b x2 (t) + c x3 (t) + …
Если выход: y (t) = y1 (t) + b y2 (t) + c y3 (t) + …, тогда систему считают линейной.
• И когда данные являются периодическими или постоянными:
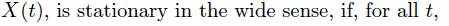
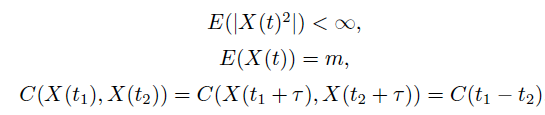
А когда FA – не лучший способ?
• когда данные являются нестационарными;
• функции основания (базиса) FA глобальны, следовательно они не могут рассматривать локальную нелинейность без существенной дисперсии (расширения);
• вышеупомянутое особенно верно, когда форма волны значительно отклоняется от синусоидальной формы;
• для дельта-подобных функций требуется чрезмерное большое число гармонических составляющих,
не говоря о явлениях Гиббса.
Методы обработки нестационарных данных.
• Спектрограмма
• Вейвлетный анализ
• Распределение Wigner-Ville
• Эволюционный спектр
• Эмпирическое ортогональное расширение функции (EOF)
• Приглаженное скользящее среднее значение
• Оценка наименьших квадратов
Мгновенная Частота
Определение преобразования Hilbert:
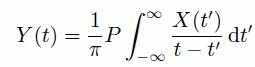
Комплексная форма:
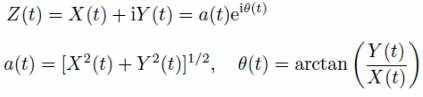
Частота:
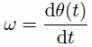
Мгновенная частота - cont’d
Определенная мгновенная частота является скаляром. Это означает, что это монокомпонент. В действительности, сигнал возможно, не представляет монокомпоненту. Поэтому, нужно интерпретировать это как ограниченную частоту в пределах узкой группы. Поскольку понятие полосы пропускания играет решающую роль, мы заимствуем ее определение из обработки сигналов:
Если число пересечения нулей в единицу времени определить как
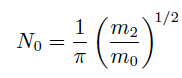 , в то время как ожидаемое число extrema (экстремумов) в единицу времени
, в то время как ожидаемое число extrema (экстремумов) в единицу времени 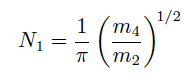 , где mi i-й момент спектра.
, где mi i-й момент спектра.То, стандартной мерой по полосе пропускания можно считать
 .
.Отметьте что если v=0, ожидаемые числа extrema и пересечений ноля равны. Это наблюдение мы будем эксплуатировать в эмпирическом разложении способа позже.
Тем не менее, мгновенная частота, определенная выше, приводит к глобальной мере. Следовательно, когда сигнал разделяется на мультикомпоненты, ключевой критерий должен гарантировать, что связанная частота в локальном масштабе действительна. Это обсуждено в следующем.
Эмпирическая модовая декомпозиция.
Внутренние модовые функции (IMF) (колебания, вложенные в данные),
Предположим, что функция является симметрической относительно локального нуля, и имеет одинаковые числа extrema и нулевого пересечения. Тогда функция может иметь физически значимую локальную мгновенную частоту. Эксплуатируя это понятие, модовая функция удовлетворяет следующим двум условиям:
1. В целом наборе данных число extrema и число нулевых пересечений должны или быть равными или отличаться самое большее на 1 (адаптация узкого понятия группы)
2. В любой текущий момент сумма верхней и нижней огибающих, определенных локальными максимумами и локальными минимумами, является нолем (новый - принятие местных свойств).
Модификация свойства локальности: свойство двух огибающих, определенных местными максимумами и местными минимумами - это местная симметрия. Это действительно порождает псевдоним в мгновенной частоте для нелинейно деформированных волн.
Свойства IMF:
• каждый IMF вовлекает только один способ колебания;
• каждый IMF характеризует не только узкую группу, но и и модуляции амплитуды и частоты;
• IMF может таким образом быть нестационарным.
Утверждение Huang и других о том, почему основанная на IMF мгновенная частота имеет смысл (Proc. R. Soc. Lond. (1998), p.916):

Метод эмпирической модовой декомпозиции (EMD)
EMD идентифицирует внутренние колебательные процессы их характерными временными рамками в данных опытным путем, затем анализирует данные в передачу IMFs через процесс просеивания.
Это - алгоритм, чтобы назначить мгновенную частоту на каждый IMF, чтобы анализировать произвольный набор данных; это означает, для сложных данных, мы можем позволить больше чем одна мгновенная частота за один раз в локальном масштабе.
Другими словами, EMD разлагает произвольный набор данных, являются ли они линейными, нелинейными или нестационарными, в ряд IMFs.
Введенные предположения (Huang и другие, 1998):
1. У сигнала есть по крайней мере один максимум и один минимум;
2. Характерные временные рамки определены к этому времени ошибка между extrema;
3. Если данные были полностью лишены extrema, но содержали только пункты перегибов, то он может быть дифференцирован однажды или больше раз, чтобы показать extrema; и, заключительные результаты могут быть получены интеграцией компонентов.
В дополнение к вышеупомянутым предположениям они вводили ограничение на то, что получающиеся модовые функции (IMF) должны быть симметрическими в местном масштабе относительно ноля. Это ограничение подразумевает, что у IMFs есть те же самые числа нулевых пересечений и extrema. Это ограничение тогда позволяет определять мгновенную частоту для каждого из анализируемых IMFs. Другими словами, IMF удовлетворяет:
(1) в наборе данных, число extrema и нулевых пересечений должно быть или то же самое или отличаться самое большее на 1;
(2) в любом пункте сумма верхней и нижней огибающих экстремумов должна быть нулевой.
Первое условие подобно узкому требованию группы для постоянного Гауссовского процесса. Второй, однако, изменяет классическое требование глобального нулевого среднего к локальному. Именно эта вторая особенность согласуется с понятием мгновенной частоты, которая действительна для нестационарного процесса и нелинейных сигналов.
Применяя вышеупомянутые предположения и ограничения, Huang и другие показали, что их эмпирическое модовое разложение (EMD) может идентифицировать внутренние колебательные процессы их характерными временными рамками в данных.
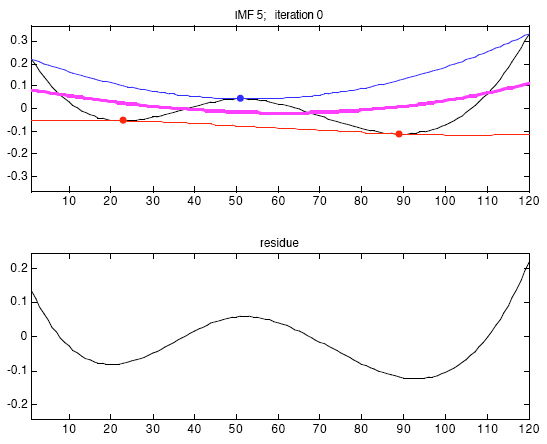
Алгоритм процесса выделения функций IMF.
1. Для данных X(t) отмечаем местные максимумы и местные минимумы, и интерполируем пункты extrema через, например, сплайны, чтобы получить верхнюю и нижнюю огибающие.
2. Получаем среднее из этих двух огибающих, m1.
3. Получаем h1 = X(t) - m1 и проверяем число extrema и число нулевых перекрестков (должны быть равными или отличаться самое большее на 1). Проверяем положительны ли все местные максимумы, и отрицательны ли все местные минимумы.
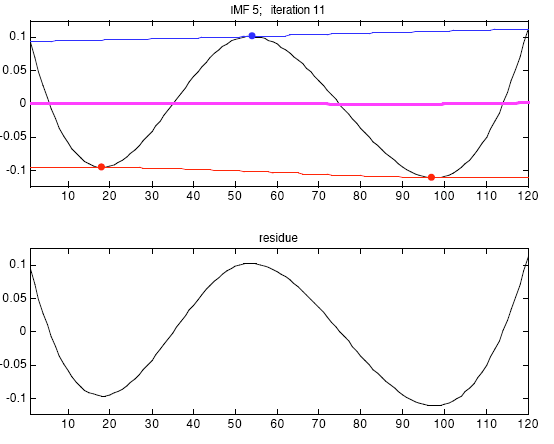
3. В противном случае повторяем просеивание и получаем h1 - m11 = h11. Процесс продолжаем с получением h1(k-1) - m1k = h1k.
Если h1k составляет IMF, то назовите его c1 = h1k . Теперь мы получаем первый остаточный r1 через r1 = X(t) - c1.
Рассматривайте r1 как новый набор данных, и выполните процесс просеивания, чтобы получить c2.
Продолжение просеивания обрабатывает, мы получаем r2 = r1 - c2, …, rn-1 - cn = rn .
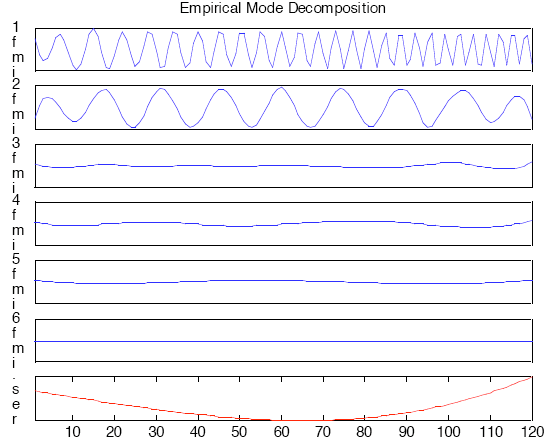
Наконец, оригинальный сигнал анализируется в терминах IMFs.




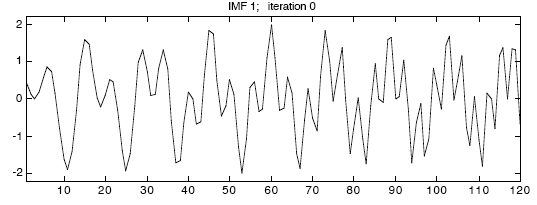
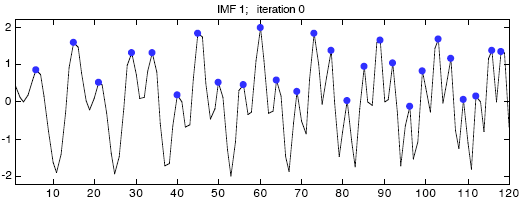
Отметьте максимумы
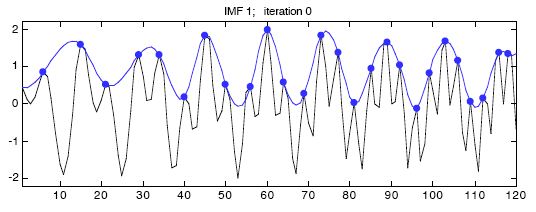
Интерполируйте максимумы кубическими сплайнами
Повторите минимумы кубическими сплайнами
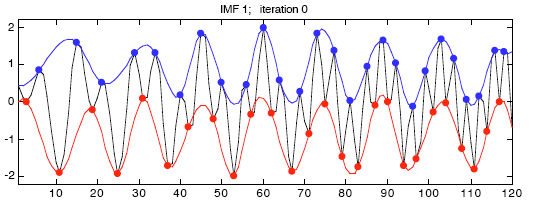
Получите местную среднюю кривую, m1
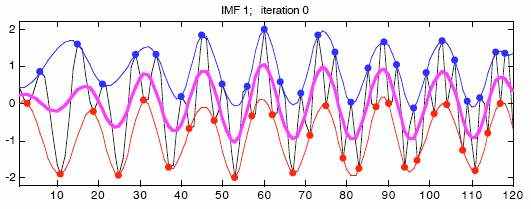
Получите остаток, r1 = x - m1
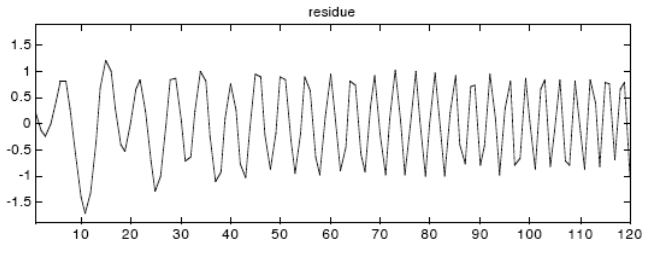
Повторите на h1, если он нарушает предположения и ограничения
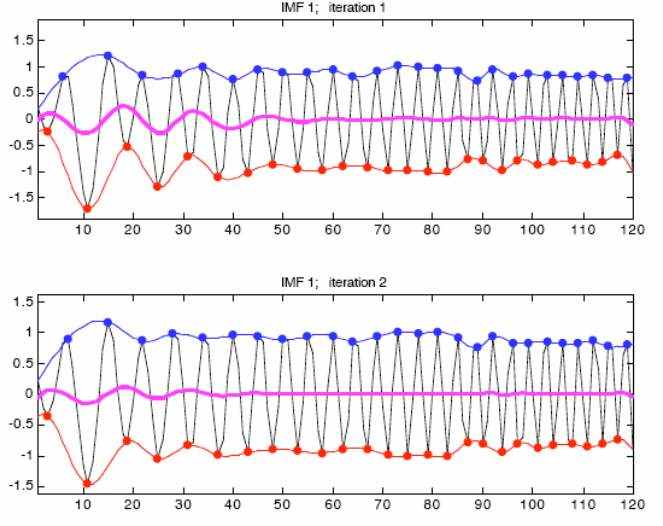
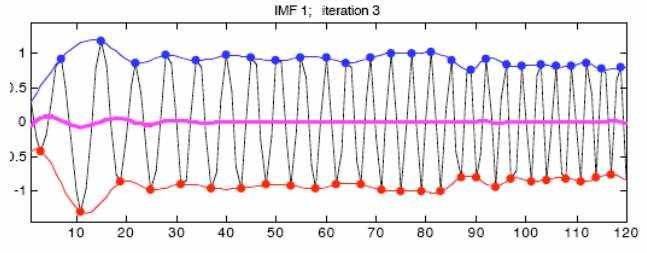
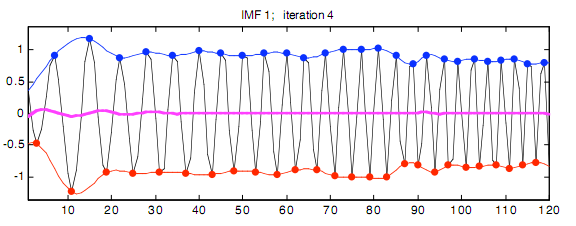
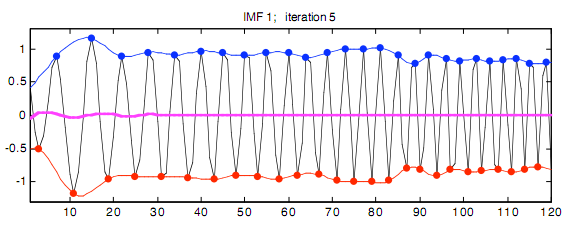
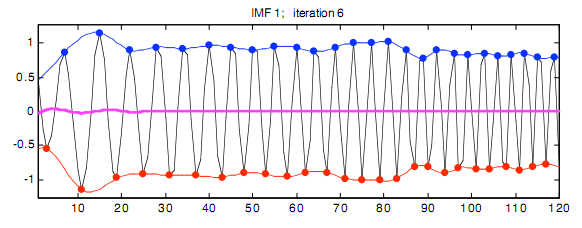
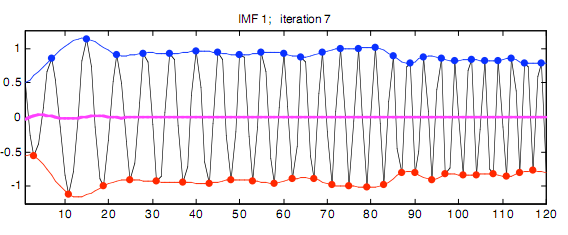
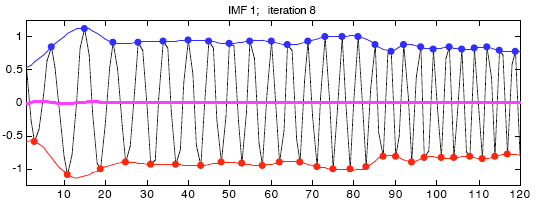
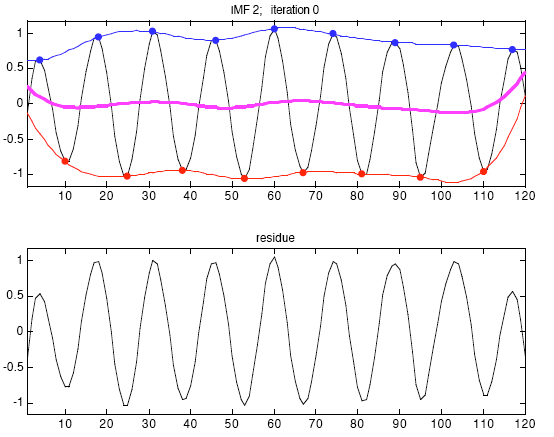
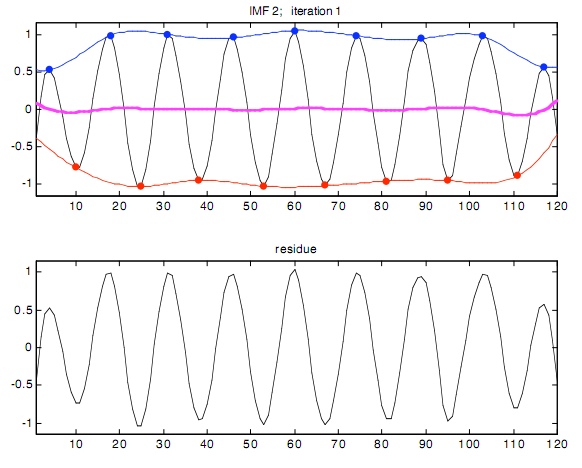
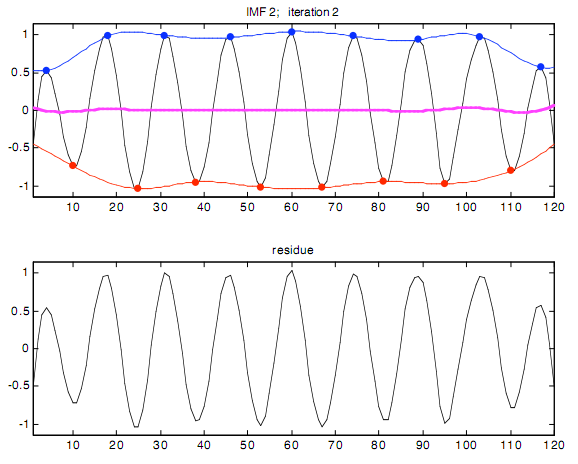
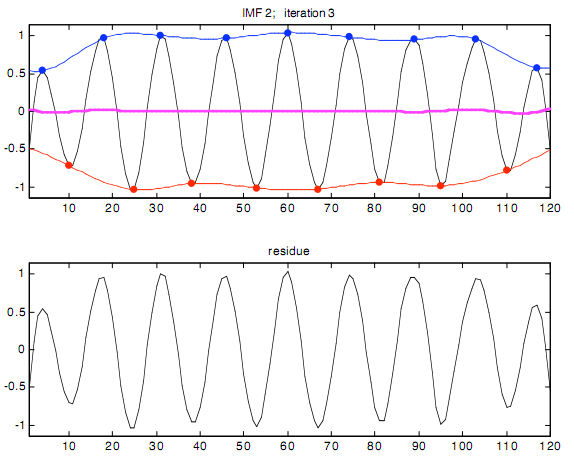
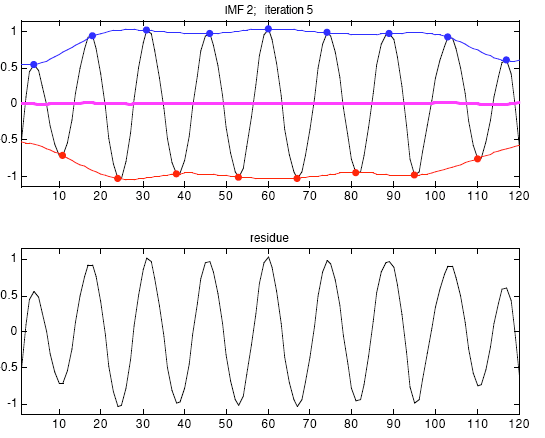
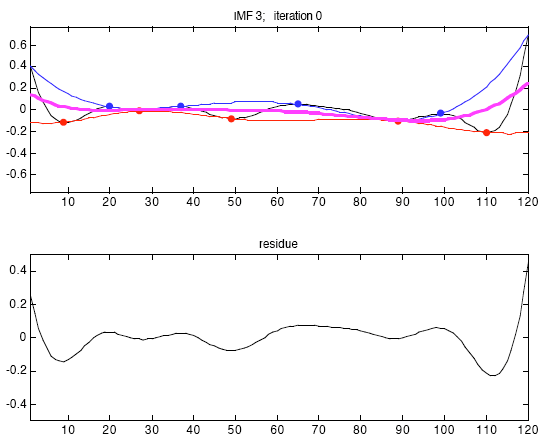
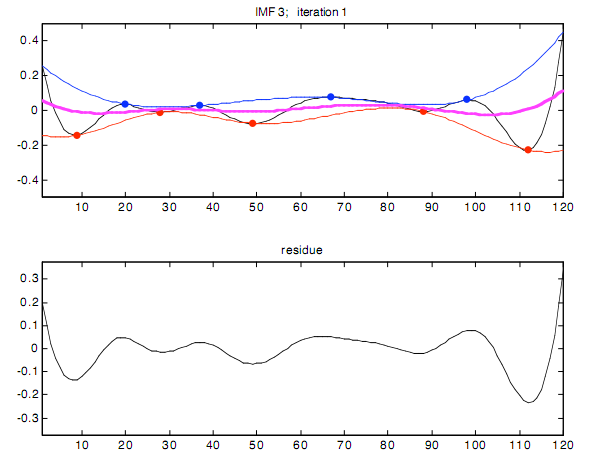
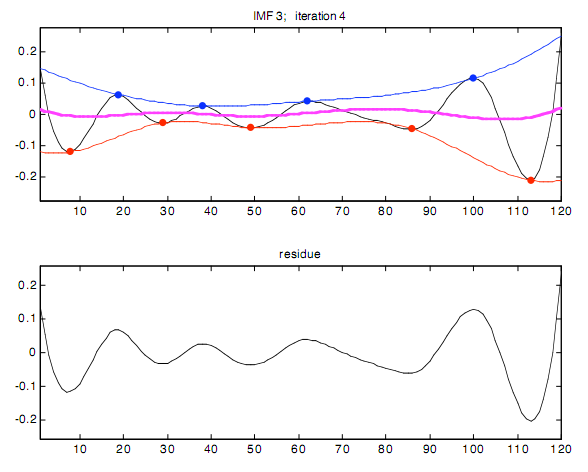
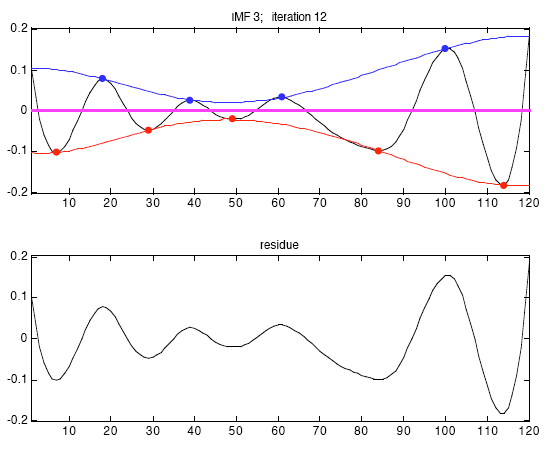
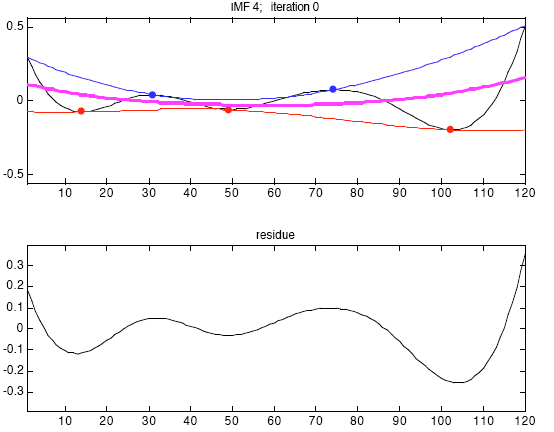
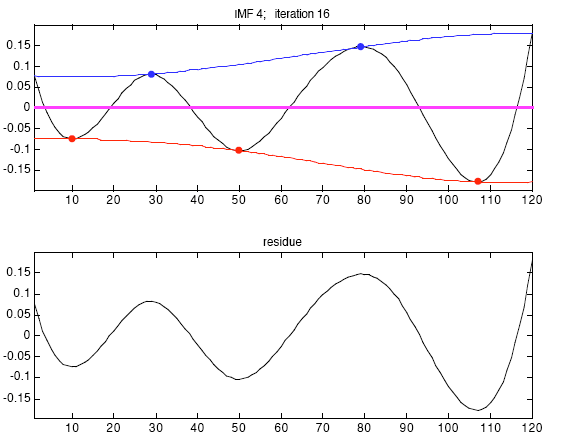
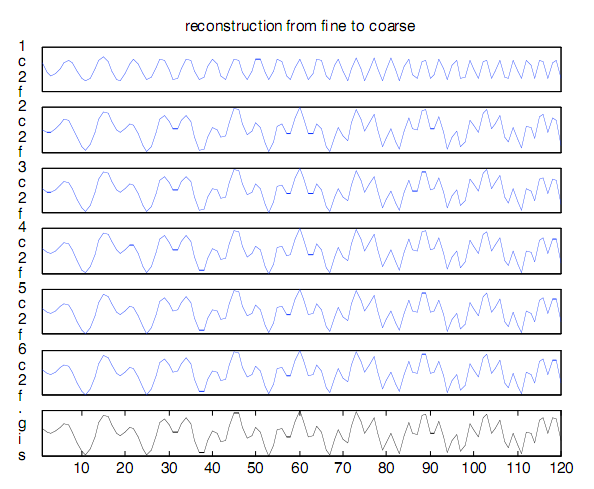
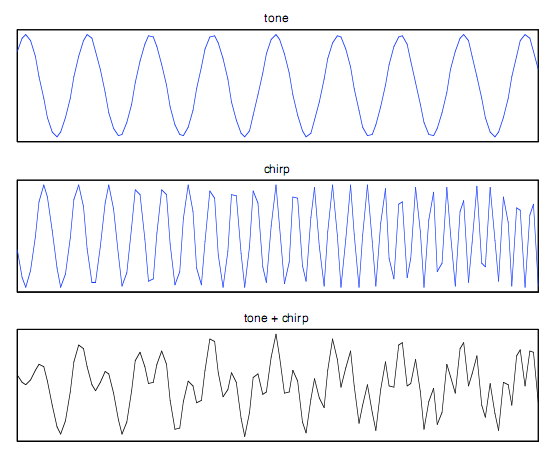
Способность Фильтрования
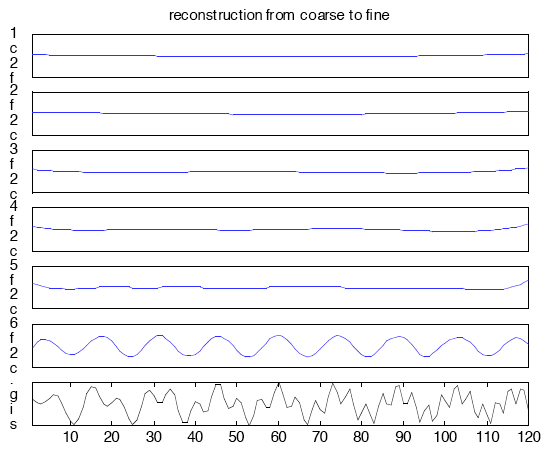
Демонстрация Законченности
Применение спектра Гильберта
Смотреть в подлиннике.
rod.ru\arhiv\hht\Lecture12-13.pdf