Sherman Riemenschneider, Bao Liu, Yuesheng Xu and Norden E
| Вид материала | Документы |
Sherman Riemenschneider, Bao Liu, Yuesheng Xu and Norden E. Huang
ГЛАВА 2.
B-СПЛАЙН - БАЗА ЭМПИРИЧЕСКОГО МЕТОДА ДЕКОМПОЗИЦИИ СИГНАЛОВ
Машинный перевод.
Эта работа рассматривает некоторые математические проблемы, связанные с эмпирической модовой декомпозицией сигналов. B-сплайновый алгоритм EMD представляется и разрабатывается для удобства математического изучения. Численный анализ, используя и моделируемые, и практические сигналы, и прикладные примеры анализа вибрации, указывает, что алгоритм B-сплайна сопоставим по производительности с первоначальным алгоритмом EMD. Также демонстрируется, что для белого шума алгоритм B-сплайна действует как двоичный банк фильтра. Математические результаты на EMD включают Эйлеровы сплайны, как встроенные функции режима, преобразование Гильберта B-сплайнов, и необходимые и достаточные условия, которые гарантируют справедливость тождественности Бедрозиэн преобразованию Гильберта функций произведения.
2.1. Введение
Обработка информации важна и в чистом исследовании, и в практических применениях. Информация, содержащаяся в данных, как правило, осложнена искажениями. С быстрой разработкой науки и техники мы каждый день получаем огромное количество данных. Данные должны быть обработаны, чтобы извлечь значимую информацию для различных применений. Преобразование Фурье - наиболее используемый и сильный традиционный метод анализа данных. Однако, этот метод не эффективен в обработке нестационарных и нелинейных сигналов, потому что функции базиса, которые он использует, не локализуются и не могут должным образом характеризовать изменение спектра во времени. Частотно-временной анализ считают лучшим подходом для того, чтобы преодолеть ограничения традиционных методов. Это стремление представить сигнал функцией и времени и частоты, отображая частотную информацию во временной области, позволяет выполнять исследования нестационарных и нелинейных характеристик сигнала.
Больше пятидесяти лет исследователи затрачивали существенные усилия в поиске эффективных путей частотно-временного представления. Кратковременное преобразование Фурье (Гэбор 1946; Коэн 1995; 1996 Киэн), представляющее достижение этого усилия, сильно в различных применениях. К сожалению, у него есть трудности в обработке некоторых типов сигналов, таких как составленные из небольших пакетов квазистационарных компонент, потому что его время и частотная разрешающая способность задаются. Хотя многие улучшенные методы были разработаны при приспосабливании размера окна к локальной композиции сигнала (сравни, Джонс и Парк 1990), эти методы или в вычислительном отношении дороги или эффективны только для определенных применений. Распределение Вигнер-Вилл (Коэн 1995; 1996 Киэн) другой классический метод. Он может хорошо сохранить время и частотную концентрацию сигнала, но имеет недостаток перекрестной интерференции, которая часто затемняет полезные образцы частотно-временной плоскости. Для преодоления этой задачи были разработаны различные методы (Choi и 1989 Виллиэмс; Жэо и др. 1990), основанные на общей структуре Коэна, (Коэн 1966) с целью сокращения перекрестной интерференции при сохранении желательных свойств распределения Вигнер-Вилл. Свежие построения вейвлет-анализа открыли новый путь для частотно-временного анализа. Существенным прорывом вейвлет-анализа было использование мультимасштабов, чтобы характеризовать явления сигнала. Этот метод привел к разработке нескольких основанных на вейвлетах методик определения частотно-временных характеристик (Добечис 1992; Маллэт 1998). Некоторые из них адаптивны, таковы как вейвлет-пакеты (Койфман и др. 1992), соответствуя преследованию (Маллэт и 1993 Жэнг), и преследованию базиса (Чен и др. 2001). Несмотря на большой успех многочисленных применений всех вышеупомянутых методов, однако, у каждого есть их собственные ограничения, и почти все они неэффективны для того, чтобы характеризовать детальную частотно-временную композицию нелинейных сигналов. С другой стороны, большинство существующих нелинейных методов анализа временного ряда (Дикс 1999) предназначается только для стационарных систем.
По прошлым нескольким десятилетиям исследователи пытались эксплуатировать понятие мгновенной частоты, создать частотно-временное представление, выведенное из аналитических сигналов, Ожидается, что у такого представления не может быть фундаментальных препятствий в вышеупомянутых методах. Однако, сбор к существованию небольшого количества парадоксов, включающих мгновенную частоту, выводил этот путь и понятие частоты в анализе Фурье или в нашей интуиции (Коэн 1995), это усилие не имело большого количества успеха, пока Хуанг и др. (1998, 1999) не разработал эмпирическую модовую декомпозицию (EMD). Этот метод теперь известен в литературе как Преобразование Гильберта-Huangа (HHT). Оно дает сильный инструмент для того, чтобы улучшить частотно-временную технологию. Основной подход метода - EMD должен расчленить сигнал в коллекцию встроенных функций мод (IMF), которые позволяют хорошие преобразования Гильберта для вычисления физически значимых мгновенных частот. Это позволяет создать частотно-временное представление, известное как "Гильбертов спектр," при использовании мгновенной частоты. Другой прорыв состоит в том, что, в отличие от вейвлет-анализа, который характеризует масштаб явления сигнала с предуказанными функциями базиса, HHT расчленяет сигнал прямым извлечением локальной энергии, соединенной с масштабами собственного времени сигнала непосредственно. Гильбертов спектр, поэтому, может изобразить не только меж - но также и внутриволновые частотные характеристики времени локального явления. Таким образом, HHT применим и к неустановившимся и к нелинейным сигналам.
HHT доказал свою эффективность в различных применениях (Эчеверрия и др. 2001; Сосны и 2002 Сэльвино; Жэнг и др. 2003). Однако, большинство основных математических задач все еще не было отработано. Поскольку HHT находит все более широкие применения, потребность в строгой математической основе становится более срочной. Недавно, в попытке обойти математические трудности, Чен и др. (2004) разработал разновидность первоначального EMD, которая кажется потенциально более удобной для аналитической формулировки EMD и для изучения определенных связанных математических проблем. Этот метод представляет локальное среднее значение сигнала при использовании скользящих средних значений экстремумов как комбинации B-сплайнов и избегает использования огибающих, для которых присущее математическое определение - все еще нерешенная проблема. Кроме того, этот метод преодолевает задачу, которую в реализации первоначального EMD могут пересечь верхние и нижние огибающие. Недавно, мы применяли этот метод в анализе сигналов вибрации для обнаружения ошибок оборудования (Лиу и др. 2004). Результаты показали, что у этого метода была сопоставимая производительность к тому из первоначальных EMD.
Данная работа делает обзор работы над B-сплайном EMD , основанный на Чен и др. (2004), Лиу и др. (2004), и Ксу и Ян (2004). В следующем разделе делается обзор алгоритам BS-EMD. Тогда в разделе 2.3, некоторые связанные математические результаты представляются, включая Эйлеровы сплайны как формирующие прототип примеры B-сплайна IMFs, свойства преобразования Гильберта B-сплайнов, и необходимые и достаточные условия, которые гарантируют справедливость тождественности Бедрозиэн преобразования Гильберта функций произведения. Раздел 2.4 - части свойств BS-EMD как банк фильтра, и исследует производительность BS-EMD через сравнение с первоначальным EMD. В разделе 2.5, мы представляем некоторые прикладные примеры метода BS-EMD и его соответствующего Гильбертова спектра в анализе сигнала вибрации. Наконец, в разделе 2.6, представляется заключение, и будущие задачи об исследовании выделяются.
2.2. Алгоритм B-сплайна для эмпирической модовой декомпозиции
Эмпирический метод декомпозиции расчленяет сигнал в конечную сумму встроенных функций, которые позволяют вычисление физически значимой мгновенной частоты, определенной в терминах преобразования Гильберта. Чтобы описать алгоритм B-сплайна для эмпирической декомпозиции, сначала повторим определение преобразования Гильберта. Для действительного сигнала s(t),преобразование Гильберта определяется главным значением (PV) интеграла
(2.1)Это приводит к аналитическому сигналу
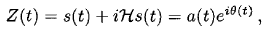(2.2)
(2.3)где a(t) и t)- соответственно, амплитуда и фаза сигнала во время t. Мгновенная частота может быть вычислена
(t) = d(t)/dt. (2.4)
Заметим, что вышеприведенные и амплитуда и мгновенная частота - функции времени. Мы естественно надеемся создать частотно-временное представление сигнала с использованием преобразования Гильберта. Если бы это представление было правильно для какого-нибудь произвольного сигнала, то у нас было бы частотно-временное представление с более высокой энергетической концентрацией, чем на кратковременном преобразовании Фурье и вейвлет-преобразовании, и более чистое представлениие, чем на распределении Вигнер-Вилл. К сожалению, существенная трудность состоит в том, что у мгновенной частоты, полученной таким образом, могут быть частотные величины, которые бессмысленны в физике. Эта задача досаждала исследователям много лет, потому что попытки преодолеть ее были основаны на классических методах Фурье и теории фильтров.
Разработка EMD - метод для того, чтобы решить вышеупомянутую задачу. Хуанг и др. (1998) нашел, что, чтобы определить значимую функцию мгновенной частоты при использовании преобразования Гильберта, эта функция должна удовлетворить следующим двум условиям:
- Число экстремумов и число нулевых пересечений функции должны быть равными или отличаться самое большее на 1.
- В любой точке функции среднее значение огибающих, определенных локальным экстремумами, должно быть нулем.
Такую функцию называют "встроенной функцией моды" (IMF). Так как IMFs, определенные таким образом, допускают вычисление значимых мгновенных частот, это становится возможным, чтобы создать частотное временем представление, основанное на Гильбертовой трансформанте.
Алгоритм EMD снабжает метод, чтобы получить IMFs с основной идеей удалениия локального среднего значения от сигнала при использовании процесса отсеивания. В первоначальном EMD локальное среднее значение вычисляется как среднее значение верхних и нижних огибающих. Сами огибающие аппроксимируются как кубический сплайн интерполяции локальных максимумов и локальных минимумов, соответственно. Можно заметить, что "огибающие" имеют решающую роль в этом алгоритме. Однако, хорошее математическое описание огибающих остается нерешенной проблемой. Для удобства изучения математической основы метода EMD желательна более прямая связь от локального экстремума до среднего значения в процессе отсеивания. Эта потребность привела к разработке алгоритма B-сплайна EMD (Чен и др. 2004). Эн использует скользящее среднее значение экстремума как комбинации B-сплайнов и является очень удобным для математического изучения. Мы представляем основную идею BS-EMD от Чен и др. (2004) в следующем.
Мы сначала определяем B-сплайны порядка k для произвольной последовательности узлов (Хам Де 1978). Для данной увеличивающейся последовательности j, j∈ Z, jth B-сплайн порядка k определяется kth, заказывает разностное отношение, j..., j+k], в к + 1 точка j..., j+k относитя к обрезанной степени как к функции x
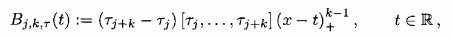(2.5)где (x — t)+k-1 нуль, если x
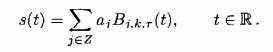(2.6)B-сплайны удовлетворяют следующей рекурсивной формуле
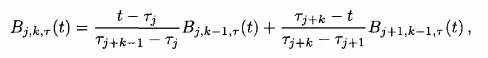(2-7)
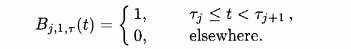(2-8)Они нормализуются так, чтобы
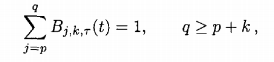(2.9)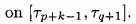
Для использования в EMD мы определяем оператор на данном сигнале s следующим образом: РТС узлов:
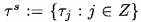берутся как экстремальные точки s. Узлы в поддержку B-сплайна 
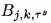, тс порядка, 
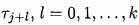с 
, обращающаяся в нуль снаружи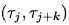 
и строго позитивны в том интервале (следовательно, в 
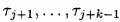) - В этих экстремальных точках строго в основании 
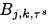, следующий линейный оператор, определяются: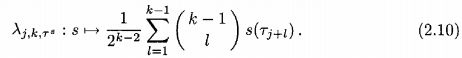
Это определение - биномиальное среднее число экстремума, содержавшего в поддержку
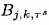, где больше веса дается к центру основания. Мы берем
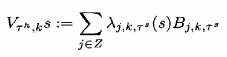(2.11)как оператор, чтобы заменить среднюю оболочку(огибающую) в первоначальном алгоритме EMD.
Как специфические примеры, когда к = 3, у нас есть квадратное приближение B-сплайна
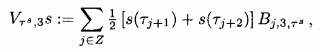(2.12)и когда к = 4, у нас есть кубическое приближение B-сплайна
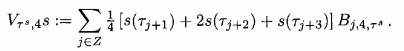(2.13)Используя оператор, определенный выше, мы получаем алгоритм B-сплайна для эмпирической модовой декомпозиции. Этот алгоритм извлекает первый IMF сигнала s при использовании следующего процесса отсеивания:
- Обнаружьте локальный экстремум s.
- Примените оператор
.
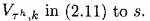- Вычислите
.
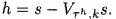- Если h - IMF, остановка. Иначе, обработайте h как сигнал и выполните итерации на h через Шаги 1 - 4.
Обозначьте c1 первый IMF и установите r1=s-c1, первый остаток (вычет). Алгоритм переходит выбирать следующий IMF, применяя вышеупомянутую процедуру к первому остатку (вычету) r1. Этот процесс повторяется, пока последний остаток rn имеет самое большее один экстремум (исключая концы) или становится постоянным. Первоначальный сигнал тогда может быть представлен как
Останов задается параметром SD:
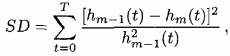(2.15)где T - длина сигнала, и hm, результат отсеивания на m итерации. Типичное значение (величина) остановки СД устанавливается между 0.2 и 0.3.
Наши численные изучения показывают, что после конечного числа итераций, результат отсеивания BS-EMD будет IMF. После применения Гильбертовой трансформанты на каждом IMF мы получаем аналитический сигнал, соответствующий сигналу s(t)
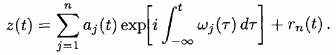(2.16)Как в Хуэнг и др. (1998), условие остановки синхронно 4 состоит в том, чтобы ограничить следующее стандартное отклонение от двух консекутивных результатов в процессе отсеивания:
Первый член на правой стороне (2.16) можно рассмотреть как обобщение разложения Фурье. Это отличается от последнего тем, у компонентов в (2.16) есть переменная амплитуда и частота. Это позволяет амплитуде и частотной модуляции быть отделенной и делает возможным преобразование сигнала к совместной функции времени и частоты. Остаток rn характеризует тенденцию сигнала и может быть обработан отдельно.
2.3. Некоторые связанные математические результаты
В этом разделе мы делаем обзор некоторых математических результатов, связанных с IMFs, Гильбертовыми Преобразованиями и тождественностью Бедрозиэн в контексте EMD. Большинство результатов, обсужденных в этом разделе, исходит из Чен и др. (2004) и Ксу и Ян (2004).
IMFs, полученные из алгоритма EMD, допускают физически значимую мгновенную частоту. Однако, математическое определение и характеристики IMFs остаются нерешенными. Мы представляем разъясняющий математический пример IMFs, который очень проницателен для дальнейшей разработки в математических характеристиках IMFs. Интересное наблюдение состоит в том, что Эйлеровы сплайны Шеенберга - важный класс сплайновых функций режима встроенных средств типа, которые имеют тенденцию к самому простому IMF, гармоническому сигналу, когда их степень имеет тенденцию к бесконечности.
Мы теперь повторно вызываем определение Эйлеровых многочленов и Эйлеровых сплайнов. Эйлеров многочлен нулевой степени определяется p0=1, и Эйлеровы многочлены более высокой степени определяются рекурсивно
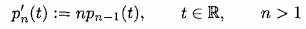(2.17)при условиях(состояниях) ограничения
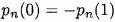. Определенно, Эйлеровы многочлены более низкого порядка
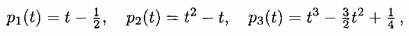(2.18)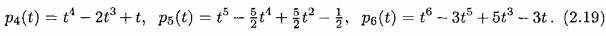
Самый простой Эйлеров сплайн - кусочная постоянная периодическая функция
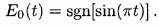(2.20)Вообще, при использовании Эйлеровых многочленов, Эйлеровы сплайны сгенерируются следующим образом: Определите сплайны En на R. как растяжения(выступы) Эйлеровых многочленов
ко всем R. через функциональное уравнение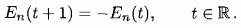
(2.21)Таким образом,
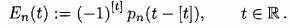(2.22)Эйлеровы сплайны Шеенберга n определяются, чтобы быть
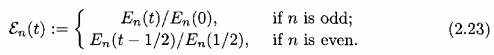
Заметьте, что Эйлеровы сплайны - 2-периодические кусочные многочлены.
Иллюстрация 2.1 показывает, что Эйлеровы сплайны - неустановившиеся сигналы, так как их частоты меняются в зависимости от времени. Однако, мгновенные частоты Эйлеровых сплайнов имейте тенденцию скорее быстро к этому, когда порядок сплайнов имеет тенденцию к бесконечности. Это наблюдение может быть объяснено интересными результатами Шеенберга (1964, 1972, 1976, 1983) и Голичек (1972), которые формулируют это,
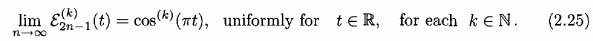
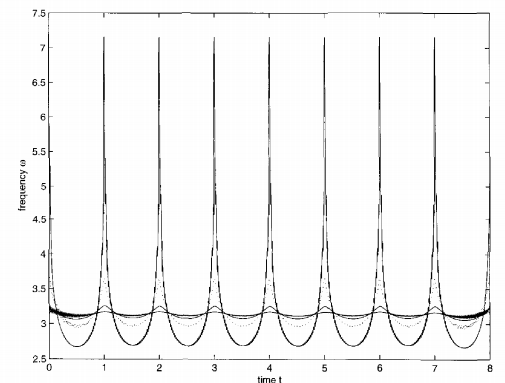
Иллюстрация 2.1: сравнения мгновенной частоты Эйлеровых сплайнов: кривая с самым высоким изменением - мгновенная частота 2-, кривая пунктира обозначает кривую 3. Сохранение двух кривых сплошных линий является мгновенной частотой 4 и 5. Изменение мгновенных частотных уменьшений от 2 до5, и мгновенной частоты 5 уже очень близко к .
Фактически, от (6.10) в Шеенберге (1976), первый из них может быть определен количественно как
Абсолютной сходимостью прогрессии в (2.26), это также следует легко за этим
с той же самой связанной(обязанной) погрешностью. Таким образом,
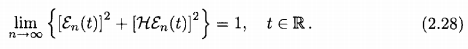
B-сплайны запускают решающую роль в алгоритме BS-EMD с тех пор за исключением первого IMF, все, что другие - линейные комбинации B-сплайнов. Кроме того, кубические сплайны, используемые для интерполяции огибающих в первоначальном EMD, могут также быть написаны как линейные комбинации B-сплайнов. Так как частотное временем представление получается из Гильбертовой трансформанты каждого IMF, желательно рассмотреть Гильбертову трансформанту B-сплайнов. Рекурсивные формулы Гильбертовой трансформанты B-сплайнов были установлены в Чен и др. (2004). Мы теперь делаем обзор главных результатов той бумаги относительно рекурсивных формул.
Мы повторно вызываем определение одинаково раздельных количественных B-сплайнов. Пустите
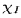обозначать характеристическую функцию интервала I. Мы устанавливаем 
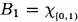, и количественные B-сплайны высших порядков определяются рекурсивно сверткой с B1, то есть,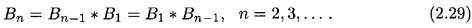
Можно заметить, что Bn является сплайном порядка n с узлами в целых числах j = 0,1..., n. Количественные B-сплайны обладают многими хорошими свойствами (сравни, Хам Де 1978). Если мы пускаем ∇ обозначать обратный оператор разности, определенный рекурсивно
у производной B-сплайнов есть форма
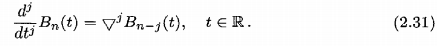
B-сплайны удовлетворяют рекурсивную формулу
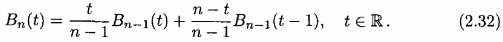
Такая рекурсивная формула делает B-сплайны очень удобными, чтобы использовать в применениях. Мы также знаем, что количественные B-сплайны симметричны в центре их основания; то есть,
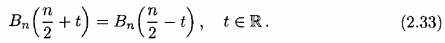
Мы будем видеть, что эти свойства переносятся на Гильбертову трансформанту B-сплайнов. Используя рекурсивное определение количественных B-сплайнов и свойства Гильбертовой трансформанты, у нас есть это
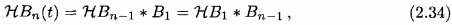
где HBn дали удельное выражение
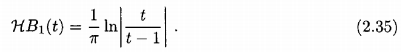
Для производной НВ, мы получаем формулу
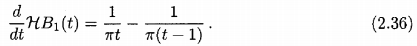
Эта формула может быть обобщена к производной старшего разряда Гильбертовой трансформанты B-сплайнов высшего порядка. В следующей теореме мы показываем, что j-th производная Гильбертовой трансформанты Bn является j-th обратная разность HBn-j.