Краткое содержание: Прямая задача динамики машин. Понятие о динамической модели машины при

Вид материала

Краткое содержание

Подобный материал:

• Краткое содержание: Классификация кинематических пар. Модели машин. Методы исследования, 258.21kb.
• Задача об остановке произвольной машины Тпри обработке произвольного слова t алгорифмически, 97kb.
• Г. Р. Серебряков опыт построения динамической межотраслевой равновесной модели российской, 330.44kb.
• Наименование и краткое содержание лекций № Тема лекций. Краткое содержание. Количество, 67.09kb.
• Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
• Волгоградская Государственная Сельскохозяйственная Академия Описание проекта Название, 116.08kb.
• Комплекс машин для заготовки прессованного сена. Марки машин и их технические характеристики, 8.88kb.
• Конструирование модели транспортных машин, 664.04kb.
• Темы лекционных занятий Принципы и методы математического моделирования. Базовые модели., 42.45kb.
• Курсовая работа по дисциплине «Статистика» на тему "Аналитические показатели рядов, 396.09kb.

Лекция 6.


Краткое содержание: Прямая задача динамики машин. Понятие о динамической модели машины при W=1. Уравнения движения динамической модели. Параметры динамической модели: I^пр_ - приведенный суммарный момент инерции механизма и М^пр_ - приведенный суммарный момент внешних сил. Механические характеристики машин. Пример на определение параметров динамической модели. Режимы движения машины. Режим движения пуск-останов. Определение управляющих сил по параметрам движения при пуске и останове. Алгоритм решения прямой задачи динамики при неустановившемся режиме движения машины.

Прямая задача динамики машин.

Прямая задача динамики машины, как отмечалось и ранее, является задачей анализа, задачей по определению закона движения механической системы под действием заданных внешних сил. При решении этой задачи параметры машинного агрегата и действующие на него внешние силы известны, необходимо определить закон движения: скорости и ускорения в функции времени или обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы управляющие силы и силы внешнего сопротивления, определить обеспечиваемый ими закон движения машины. Обратная задача - это задача синтеза управления, когда задан требуемый закон движения машины и внешние силы сопротивления, а определяются управляющие силы. При решении задач динамики используются либо уравнения силового равновесия системы - метод кинетостатики, либо уравнения энергетического равновесия - закон сохранения энергии. Для идеальной механической системы, в которой не потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы о изменении кинетической энергии. Согласно этой теореме работа всех внешних сил действующих на систему расходуется только на изменение ее кинетической энергии. При этом потенциальные силы - силы веса рассматриваются как внешние силы.

_f+m

T = T - T_нач =  А_i ,

ⁱ⁼¹

где T - изменение кинетической энергии системы,

T - текущее значение кинетической энергии системы,

T_нач - начальное значение кинетической энергии системы,

_n

 А_i - суммарная работа внешних сил, действующих на систему.

ⁱ⁼¹

Рассмотрим сложную механическую систему (рис.6.1), состоящую из n подвижных звеньев из которых r - звеньев совершают вращательное движение, j - плоское, k - поступательное. Основная подвижность системы равна W=1. На систему действуют: f - внешних сил и m - внешних моментов. Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные - суммарным приведенным моментом инерции I^пр_ , силовые - суммарным приведенным моментом М^пр_ . Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.

_{f+m n}

 А_i = A_Мпр  T_i = T_м

^{i=1 i=1}




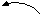
2 С i 1

M_i I^пр_

1

B D _i

_i j

L M^пр_

M_д1 ₁ E,K F_k ₁

A x A x




0 k 0


Механическая система с W_o=1 Динамическая модель



Рис. 6.1


где

_f+m

 А_i - сумма работ всех внешних сил, действующих на систему,

ⁱ⁼¹

A_Мпр - работа суммарного приведенного момента,

_n

 T_i - сумма кинетических энергий звеньев системы,

ⁱ⁼¹

T_м - кинетическая энергия динамической модели.


Уравнения движения динамической модели

1. Уравнение движения динамической модели в интегральной форме.
   

Запишем для динамической модели теорему о изменении кинетической энергии


T = T - T_нач = A_Мпр ,

_1

где T = I^пр_²₁/2 ; T_нач = I^пр_нач²_1нач/2 ; A_Мпр =  М^пр_d₁ ;

^1нач

и уравнение движения динамической модели в интегральной или энергетической форме





I^пр_²₁/2 - T_нач = A_Мпр.


Из этого уравнения после преобразований

__________________

₁ =  2 (A_Мпр + T_нач)/ I^пр_ ,


получим формулу для расчета угловой скорости звена приведения.

Для машин работающих в режиме пуск-останов

_1нач = 0 и T_нач = 0,


формула принимает вид

___________

₁ =  2 A_Мпр / I^пр_ .

2. Уравнение движения динамической модели в дифференциальной форме.
   

Продифференцируем полученное выше уравнение по обобщенной координате


I^пр_d(₁²)/(2d₁) + (d I^пр_ /d₁)(₁²/2) = d(A_Мпр)/ d₁,


где 0.5 (d(₁²)/ dt ) (dt/d₁) = 0.52₁ d₁/ dt (1/₁) = d₁/ dt = ₁ ,


d(A_Мпр)/ d₁ = М ^пр_ .


После подстановки получим




I^пр_  d₁/dt + (₁²/2)  (d I^пр_ /d₁) = М ^пр_ ,


уравнение движения динамической модели в дифференциальной форме.

Из этого уравнения после преобразований



₁ = d₁/dt = М ^пр_/ I^пр_ - ₁²/(2 I^пр_)  (d I^пр_ /d₁),


получим формулу для расчета углового ускорения звена приведения.

Для механических систем в которых приведенный момент не зависит от положения звеньев механизма (I^пр_ = const )




₁ = d₁/dt = М ^пр_/ I^пр_ .


Определение параметров динамической модели машины

(приведение сил и масс).


Рассмотрим изображенную на рис. 6.1 механическую систему и ее динамическую модель. Запишем для них уравнение изменения кинетической энергии. Кинетическая энергия: _{r+k r+j}

для механической системы Т_с =  m_i V_Si²/2 +  I_si  _i²/2 ,

^{i=1 i=1}


для модели T_м = I^пр_²₁/2 ;


Суммарная работа внешних сил:

_{f _  _ m}

для механической системы A_c =   F_i  dS_icos (F_i , dS_i) +   M_i d_i ,

^{i=1 i=1}

для модели A_м =  М^пр_d₁ .

Модель будет с энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть для левых частей выполняется условие Т_с = Т_м , а для правых - A_c = A_м. Для того чтобы второе равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений dA_c =dA_м . Подставляя в равенства, записанные ранее выражения для кинетических энергий и работ получим:

для левых частей

_{r+k r+j}

I^пр_²₁/2 =  m_i V_Si²/2 +  I_si  _i²/2 ,

^{i=1 i=1}

для правых частей

_{f _  _ m}

М^пр_d₁ =  F_i  dS_icos (F_i , dS_i) +  M_i d_i .

^{i=1 i=1}

Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели

_{r+k r+j}

I^пр_=  m_i (V_Si/₁)² +  I_si  (_i/₁)² ,

^{i=1 i=1}

_{r+k r+j}

I^пр_=  m_i (V_qSi)² +  I_si  (_qi)² .

^{i=1 i=1}


Из уравнения для правых частей получаем формулу для определения приведенного суммарного момента динамической модели




_{f _  _ m}

М^пр_ =  F_i (dS_i /d₁)