Краткое содержание: Прямая задача динамики машин. Понятие о динамической модели машины при

Вид материала

Краткое содержание

Подобный материал:

• Краткое содержание: Классификация кинематических пар. Модели машин. Методы исследования, 258.21kb.
• Задача об остановке произвольной машины Тпри обработке произвольного слова t алгорифмически, 97kb.
• Г. Р. Серебряков опыт построения динамической межотраслевой равновесной модели российской, 330.44kb.
• Наименование и краткое содержание лекций № Тема лекций. Краткое содержание. Количество, 67.09kb.
• Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
• Волгоградская Государственная Сельскохозяйственная Академия Описание проекта Название, 116.08kb.
• Комплекс машин для заготовки прессованного сена. Марки машин и их технические характеристики, 8.88kb.
• Конструирование модели транспортных машин, 664.04kb.
• Темы лекционных занятий Принципы и методы математического моделирования. Базовые модели., 42.45kb.
• Курсовая работа по дисциплине «Статистика» на тему "Аналитические показатели рядов, 396.09kb.

 cos (F_i , dS_i) +  M_i(d_i/ d₁).

^{i=1 i=1}

_{f _  _ m}

М^пр_ =  F_i V_qSi  cos (F_i , dS_i) +  M_i _qi.

^{i=1 i=1}


Механические характеристики машин.


Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.

Рассмотрим примеры механических характеристик различных машин.

1. Двигатели внутреннего сгорания (ДВС):
   

• четырехтактный ДВС
  

р,МПа



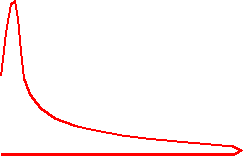
ab - расширение

(рабочий ход);

bc - выхлоп;

a p_max

cd - всасывание;


b da - сжатие.

c

0 d S_C,м

H_C




Рис. 6.2


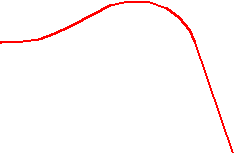
Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.

• двухтактный ДВС
  

р,МПа



ab - расширение

(рабочий ход);

bc - продувка;

a p_max

b ca - сжатие.




c

c

0 d S_C,м

H_C




Рис. 6.3

2. Электродвигатели
   

• асинхронный электродвигатель переменного тока
  

На диаграмме: М_дп - пусковой момент; М_дн - номинальный крутящий момент; М_дк или М_дmax - критический или максимальный момент; _дн - номинальная круговая частота вращения вала двигателя; _дхх или _дс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части


М_д = b₁ + k₁_д ,


где М_д - движущий момент на валу двигателя,

_д - круговая частота вала двигателя ,

b₁ = М_дн  _д /(_дс - _дн ) , k₁ = - М_дн / (_дс - _дн ).

Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса


М_д = 2 М_дк  (S/S_к + S_к/S ), где S = 1 - _д /_дс , S_к = 1 - _дк /_дс , _д >=_дс .





М_д ,Н м

b ab - неустойчивый

a участок характеристики;

с bd -устойчивый

М_дн М_дmax участок характеристики.

М_дп.


d

0 _дк _дн _дс _д , рад/с

Рис. 6.3

• двигатель постоянного тока с независимым возбуждением
  

М_д ,Н м

a ac - внешняя

регулировочные характеристика

характеристики



М_дп М_дн b


c

0 _дн _дхх _д , рад/с

Рис. 6.4


Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением


М_д = M_дн + k (_дн - _д ) ,


где k = М_дн /(_дхх - _дн ).

В электрических параметрах характеристика записывается в следующем виде


М_д = k_M  (U_я - k_ _д)/ R_я ,


где

k_M = M_дн/I_ян - коэффициент момента, k_ = (U_ян - R_я I_ян ) / _дн - коэффициент противоэлектродвижущей силы, U_я - напряжение в цепи якоря, R_я - сопротивление цепи якоря

3. Рабочие машины
   

• поршневой насос
  

р,МПа



ab - нагнетание;

a b

cd - всасывание.

p_max

линия атмосферного давления

p_min

0

d c S_C,м

H_C




Рис. 6.5

• поршневой компрессор
  

р,МПа



a ba - нагнетание;

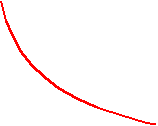
b cb - сжатие;

dc - всасывание;

ad - расширение

p_max остаточного воздуха.

линия атмосферного давления

p_min



0 d c S_C,м

H_C




Рис. 6.6


Линии bc и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p Vⁿ = const , где n - показатель политропы ( 1 n  0 ).

• строгальный станок
  

F_c,Н м

F_сmin

0 ab,ef - перебег;

S_C,м

a b e f cd - резание;

F_cmax fa - холостой ход.




c d

l_п l_р l_п




H_C




Рис. 6.7


Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.


Пример на определение параметров динамической модели

( на приведение сил и масс ).


Дано: Кинематическая схема механизма поршневого насоса( l_i, _i ),

М_д , F_c , m_i , I_Si ;

__________________________________________________


Определить: М^пр_ , I^пр_ - ?


1. Определение сил веса G_i = m_i  g .

2. Определение кинематических передаточных функций.
   

Простой и наглядный метод определения передаточных функций - графоаналитический метод планов возможных скоростей. При этом в произвольном масштабе строятся планы скоростей для рада положений цикла движения механизма. По отрезкам плана скоростей рассчитываются соответствующие передаточные функции по следующим формулам ( для машины, схема которой изображена на рис.6.8 ):


Векторное уравнение скоростей: V_C = V_B + V_CB ;

<sup>----- === -------

гориз. АВ СВ</sup>