Краткое содержание: Прямая задача динамики машин. Понятие о динамической модели машины при

Вид материала

Краткое содержание

Подобный материал:

• Краткое содержание: Классификация кинематических пар. Модели машин. Методы исследования, 258.21kb.
• Задача об остановке произвольной машины Тпри обработке произвольного слова t алгорифмически, 97kb.
• Г. Р. Серебряков опыт построения динамической межотраслевой равновесной модели российской, 330.44kb.
• Наименование и краткое содержание лекций № Тема лекций. Краткое содержание. Количество, 67.09kb.
• Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие, 294.78kb.
• Волгоградская Государственная Сельскохозяйственная Академия Описание проекта Название, 116.08kb.
• Комплекс машин для заготовки прессованного сена. Марки машин и их технические характеристики, 8.88kb.
• Конструирование модели транспортных машин, 664.04kb.
• Темы лекционных занятий Принципы и методы математического моделирования. Базовые модели., 42.45kb.
• Курсовая работа по дисциплине «Статистика» на тему "Аналитические показатели рядов, 396.09kb.

2 _l , мм/м 3

М_д1

3 B S₂

1 C,D,S₃

₁ F_c

A,S₁

6 0,12 G₂ C C

F_c,Нм

G₁ _F, мм/Н

₁ 0 S_C, м

9 _S, мм/м





Маховик Н_С



I_доп

m₂,I_S2 C,D,S₃

A,S₁ B S₂









I₀₁ m₃

Планы скоростей

I^пр_ред V_C Поз.0

p_v c p_v c

u_д1 = _д /₁ V_S2 V_CB V_C

Редуктор s₂

V_B V_S2 s₂

Поз.9 b

I_д _д V_B b

Двига- V_C=V_B=V_CB

тель p_v c,b,s₂




М_д

M_д, Н м; _М , мм/Н м








0  2 ₁,рад; _М , мм/рад


Рис. 6.8


Передаточные функции:

точки С V_qC = dS_C /d₁ = V_C /₁ = (V_C / V_B ) l_AB = ( p_vc / p_vb)  l_AB ;


точки S₂ V_qS2 = dS_S2 /d₁ = V_S2 /₁ = (V_S2 / V_B ) l_AB = ( p_vs₂ / p_vb)  l_AB ;


звена 2 _q2 = u₂₁ = d₂ /d₁ = ₂ /₁ = (V_CB /V_B ) ( l_AB / l_BC ) =

= (cb / p_vb)  ( l_AB/ l_BC );


По этим формулам строятся цикловые диаграммы передаточных функций для рассматриваемого механизма ( см. рис. 6.9 ).





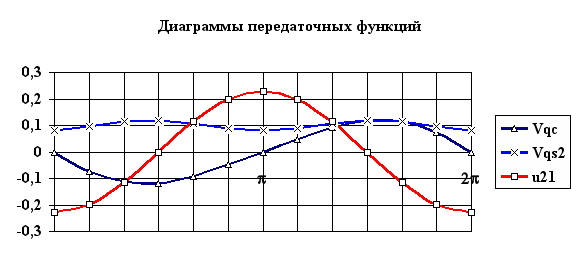
Рис. 6.9


3. Определение суммарного приведенного момента М^пр_ .

Для определения суммарного приведенного момента необходимо просуммировать приведенные моменты от всех внешних сил, действующих на рассматриваемую систему. Приведенный момент от силы равен скалярному произведению вектора силы на вектор передаточной функции точки ее приложения, от момента - произведению момента на передаточное отношение от звена приложения момента к звену приведения. На рассматриваемую систему действуют силы веса звеньев G_i , сила сопротивления F_с и движущий момент М_д . Приведенный момент от этих сил рассчитывается по формуле:

_{__  __}

М^пр_ = М^пр_д + М^пр_G2 + М^пр_G3 + М^пр_Fc = М_д u_д1 + G₂ V_qS2  cos (G₂ ,V_qS2 ) + G₃ V_qC 

_{__  __ __  __}

 cos (G₃ ,V_qC ) + F_c V_qC  cos (F_c ,V_qC ) = М_д u_д1 + G₂ V_qS2y + G₃ V_qCy +

_{__  __}

+ F_c V_qC  cos (F_c ,V_qC ).




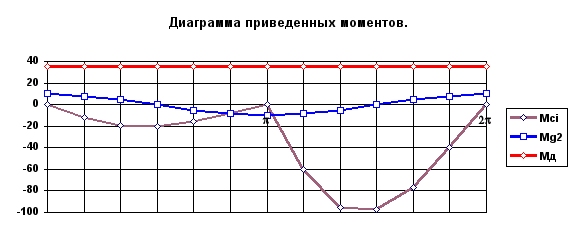
Рис. 6.10




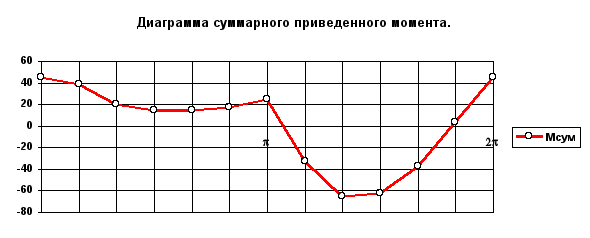
Рис. 6.11

4. Определение суммарного приведенного момента инерции I^пр_ . Для определения суммарного приведенного момента инерции необходимо просуммировать приведенные моменты инерции от всех масс и моментов инерции подвижных звеньев рассматриваемой системы. Приведенный момент инерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инерции - произведению момента инерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2 и 3 и моментами инерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2. В суммарный приведенный момент инерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инерции и относятся к первой группе звеньев, момент инерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:
   

I^пр_ = I^пр_I + I^пр_II = I^пр_C + I^пр_V =

= I_д (_qд1)² + I^пр_ред + I₀₁ + I_М + m₂ (V_qS2)² + + I_S2  (_q2)² + m₃ (V_qC)² ,

где I^пр_I = I^пр_C = I_д (_qд1)² + I^пр_ред + I₀₁ + I_М = const,


I^пр_II = I^пр_V = m₂ (V_qS2)² + I_S2  (_q2)² + m₃ (V_qC)² = I^пр_2П + I^пр_2В + I^пр₃ = var.


I^пр_II = I^пр_V



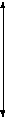
I^пр_I = I^пр_C


Рис. 6.12


Таким образом выполнена поставленная задача - определены параметры динамической модели поршневого насоса: приведенный суммарный момент М^пр_ и приведенный суммарный момент инерции I^пр_ .