Geum.ru

Программа дисциплины теория алгоритмов специальность 050201. 65 «Математика» с дополнительной специальностью «Информатика» Согласовано

Вид материалаПрограмма дисциплины

Содержание


Содержание и тематика
Введение. Уточнение поня­тия ал­горитма
II. Рекурсивные функции
Машины Тьюринга
IV. Нормальные алгоритмы Мар­кова
V. Дополнительные главы
4. Содержание разделов дисциплины
II. Рекурсивные функции.
III. Машины Тьюринга
IV. Нормальные алгоритмы Маркова
V. Дополнительные главы
5. Темы практических занятий
6. Примерные контрольные работы
7. Тематика рефератов по теории алгоритмов
8. Учебно-методическое обеспечение дисциплины
Подобный материал:
1   2   3



3.2 Распределение часов по видам и темам деятельности

Содержание и тематика
Аудиторные занятия
Самостоятель­ная работа (часы)
Всего часов по плану

Лекции

(часы)
Практика

(часы)

I. Введение. Уточнение поня­тия ал­горитма
6
3
4
13

  1. Интуитивное понятие алго­ритма.
  2. Свойства алгоритмов.
  3. Различные подходы к уточне­нию понятия алго­ритма.
1


2

3
1


1

1
1


2

1
3


5

4

II. Рекурсивные функции
6
5
9
20

  1. Основные функции и опе­рации.
  2. Рекурсивность различ­ных функ­ций.
  3. Тезис Черча.

4. Ре­кур­сив­но-пе­ре­чис­ли­мое мно­же­ст­во. Кри­те­рий ре­кур­сив­но­сти мно­же­ст­ва.
2

2


1


1
2

1


1


1
2

2


3


2
6

5


5


4

III. Машины Тьюринга
5
5
9
19

  1. Опе­ра­ции над ма­ши­на­ми Тью­рин­га .Ба­зис эле­мен­тар­ных ма­шин Тью­рин­га. Гё­де­ле­ва ну­ме­ра­ция ма­шин Тью­рин­га
  2. Фун­кция, вы­чис­ли­мая по Тью­рин­гу. Фун­кция, пра­ви­ль­но-вы­чис­ли­мая по Тью­рин­гу. До­ка­за­те­ль­ст­во су­ще­ст­во­ва­ния фун­к­ций, не­вы­чис­ли­мых по Тью­рин­гу. При­мер не­вы­чис­ли­мой по Тью­рин­гу фун­кции.
  3. При­ме­ры ал­го­рит­ми­че­с­ки не­раз­ре­ши­мых про­блем (про­бле­ма рас­по­зна­ва­ния са­мо­при­ме­ни­мо­сти, про­бле­ма при­ме­ни­мо­сти).
1


2


2
1


2


2
3


3


3
5


7


7

IV. Нормальные алгоритмы Мар­кова
2
2
6
10

  1. Нор­ма­ль­ный ал­го­ритм Мар­ко­ва в ал­фа­ви­те и над ал­фа­ви­том.
  2. Нор­ма­ль­но-вы­чис­ли­мые фун­к­ции. При­ме­ры нор­ма­ль­ных ал­го­ритмов
1


1
1


1
3


3
5


5

V. Дополнительные главы
5
5
18
28

1. "Ма­ши­на" По­ста. Ма­ши­на По­ста-Успен­ско­го. Ма­ши­на с не­огра­ни­чен­ны­ми ре­ги­стра­ми (МНР).

2. Эк­ви­ва­ле­нт­ность ма­те­ма­ти­че­с­ких мо­де­лей по­ня­тия "ал­го­ритм".

Сов­па­де­ние клас­са фун­к­ций, пра­ви­ль­но-вы­чис­ли­мых по Тью­рин­гу, и клас­са час­тич­но ре­кур­сив­ных фун­кций.

3. Те­зи­сы те­ории ал­го­рит­мов. Те­зис Чёр­ча-Кли­ни. При­нцип нор­ма­ли­за­ции Мар­ко­ва. Те­зис Тью­рин­га.

4. Уни­вер­са­ль­ные ал­го­рит­мы. Уни­вер­са­ль­ная ма­ши­на Тью­рин­га. Уни­вер­са­ль­ные фун­кции.

5. Ал­го­рит­ми­че­с­кая сво­ди­мость. 1-сво­ди­мость. m-сво­ди­мость. Сте­пе­ни не­раз­ре­ши­мо­сти. m-пол­ные. Про­дук­тив­ные и кре­а­тив­ные мно­же­ст­ва. Те­оре­ма Кли­ни о не­под­виж­ной точ­ке. Те­оре­ма Май­хил­ла. Таб­лич­ная сво­ди­мость. Сво­ди­мость по Тью­рин­гу.
1


1


1


1


1
1


1


1


1


1
4


6


4


2


2
6


8


6


4


4

Итого
24
20
46
90



4. Содержание разделов дисциплины


I. Введение. Уточнение понятия алгоритма.

1. Интуитивное опре­де­ле­ние по­ня­тия "ал­го­ритм".

2. Свой­ст­ва ал­го­рит­ма.

II. Рекурсивные функции.

1. Те­ория ре­кур­сив­ных фун­кций. Про­стей­шие фун­кции. Опе­ра­ция под­ста­но­вки. Свой­ст­ва опе­ра­ции под­ста­но­вки. Опе­ра­ция при­ми­тив­ной ре­кур­сии. Свой­ст­ва опе­ра­ции при­ми­тив­ной ре­кур­сии. При­ми­тив­но-ре­кур­сив­ное опи­са­ние фун­кции. При­ми­тив­но-ре­кур­сив­ная фун­кция. Свой­ст­ва при­ми­тив­но-ре­кур­сив­ных фун­к­ций. При­ме­ры при­ми­тив­но-ре­кур­сив­ных фун­к­ций. От­но­си­те­ль­ная при­ми­тив­ная ре­кур­сив­ность. Свой­ст­ва от­но­си­те­ль­ной при­ми­тив­ной ре­кур­сив­но­сти.

2. При­ми­тив­но-ре­кур­сив­ные опе­ра­ции (опе­ра­ция вве­де­ния фик­тив­ных пе­ре­мен­ных, опе­ра­ция под­ста­но­вки кон­стант, опе­ра­ция про­из­во­ль­ной под­ста­но­вки). Опе­ра­ции ко­неч­но­го сум­ми­ро­ва­ния и ко­неч­но­го про­из­ве­де­ния. При­мер ис­по­ль­зо­ва­ния опе­ра­ции ко­неч­но­го сум­ми­ро­ва­ния для до­ка­за­те­ль­ст­ва при­ми­тив­ной ре­кур­сив­но­сти фун­кции [x/y].

3. Пред­став­ля­ющая фун­кция пре­ди­ка­та. При­ми­тив­но-ре­кур­сив­ный пре­ди­кат. При­ми­тив­но-ре­кур­сив­ный пре­ди­кат от­но­си­те­ль­но со­во­куп­но­сти фун­кций и пре­ди­ка­тов. Ло­ги­че­с­кие опе­ра­ции. Опе­ра­ции на­ве­ши­ва­ния огра­ни­чен­ных кван­то­ров. Ку­со­чное за­да­ние фун­кции.

4. m-опе­ра­ция (опе­ра­ция ми­ни­ми­за­ции). Час­тич­но ре­кур­сив­ное опи­са­ние фун­к­ции. Час­тич­но ре­кур­сив­ная фун­кция. При­ме­ры час­тич­но ре­кур­сив­ных фун­кций. Об­ще­ре­кур­сив­ная фун­кция. При­ме­ры об­ще­ре­кур­сив­ных фун­кций.

Фор­ма­ль­ная сис­те­ма ре­кур­сив­ных фун­кций Эр­бра­на-Гё­де­ля. Фун­кция, вы­чис­ли­мая по Эр­бра­ну-Гё­де­лю.

5. Ре­кур­сив­но-пе­ре­чис­ли­мое мно­же­ст­во. Кри­те­рий ре­кур­сив­ной пе­ре­чис­ли­мо­сти мно­же­ст­ва. Ре­кур­сив­ное мно­же­ст­во. Кри­те­рий ре­кур­сив­но­сти мно­же­ст­ва (те­оре­ма По­ста).

III. Машины Тьюринга

1. Ма­ши­на Тью­рин­га. Опе­ра­ции над ма­ши­на­ми Тью­рин­га (опе­ра­ция ком­по­зи­ции, опе­ра­ция вет­вле­ния, опе­ра­ция за­цик­ли­ва­ния). Ба­зис эле­мен­тар­ных ма­шин Тью­рин­га. Гё­де­ле­ва ну­ме­ра­ция ма­шин Тью­рин­га.

2. Фун­кция, вы­чис­ли­мая по Тью­рин­гу. Фун­кция, пра­ви­ль­но-вы­чис­ли­мая по Тью­рин­гу. До­ка­за­те­ль­ст­во су­ще­ст­во­ва­ния фун­кций, не­вы­чис­ли­мых по Тью­рин­гу. При­мер не­вы­чис­ли­мой по Тью­рин­гу фун­кции.

При­ме­ры ал­го­рит­ми­че­с­ки не­раз­ре­ши­мых про­блем (про­бле­ма рас­по­зна­ва­ния са­мо­при­ме­ни­мо­сти, про­бле­ма при­ме­ни­мо­сти).

IV. Нормальные алгоритмы Маркова

1.Нор­ма­ль­ный ал­го­ритм Мар­ко­ва в ал­фа­ви­те и над ал­фа­ви­том. Нор­ма­ль­но-вы­чис­ли­мые фун­кции.

2. При­ме­ры нор­ма­ль­ных ал­го­ритмов (тож­де­ст­вен­ный нор­ма­ль­ный ал­го­ритм, нор­ма­ль­ный ал­го­ритм ле­во­го при­со­еди­не­ния, нор­ма­ль­ный ал­го­ритм пра­во­го при­со­еди­не­ния, нор­ма­ль­ный ал­го­ритм уд­во­ения, не­ко­то­рые ариф­ме­ти­че­с­кие ал­го­ритмы).

V. Дополнительные главы

1. "Ма­ши­на" По­ста. Ма­ши­на По­ста-Успен­ско­го.

2. Ма­ши­на с не­огра­ни­чен­ны­ми ре­ги­стра­ми (МНР).

3. Эк­ви­ва­ле­нт­ность ма­те­ма­ти­че­с­ких мо­де­лей по­ня­тия "ал­го­ритм".

Сов­па­де­ние клас­са фун­кций, пра­ви­ль­но-вы­чис­ли­мых по Тью­рин­гу, и клас­са час­тич­но ре­кур­сив­ных фун­кций.

4. Те­зи­сы те­ории ал­го­рит­мов. Те­зис Чёр­ча-Кли­ни. При­нцип нор­ма­ли­за­ции Мар­ко­ва. Те­зис Тью­рин­га. Уни­вер­са­ль­ные ал­го­рит­мы. Уни­вер­са­ль­ная ма­ши­на Тью­рин­га. Уни­вер­са­ль­ные фун­кции.

5. Ал­го­рит­ми­че­с­кая сво­ди­мость. 1-сво­ди­мость. m-сво­ди­мость. Сте­пе­ни не­раз­ре­ши­мо­сти. m-пол­ные. Про­дук­тив­ные и кре­атив­ные мно­же­ст­ва. Те­о­ре­ма Кли­ни о не­под­виж­ной точ­ке. Те­оре­ма Май­хил­ла. Таб­лич­ная сво­ди­мость. Сво­ди­мость по Тью­рин­гу.


5. Темы практических занятий


№
Темы практических занятий
Содержание занятий
Контроль усвоения

1
Интуитивное понятие алго­ритма.
Приметы алгоритмов в ма­тематике, некор­ректность интуитив­ного понятия.
К/р №1

2
Свойства алгоритмов.
Определение алго­ритма через его ос­новные свой­ства, не­зависимость свойств при различных под­ходах.
Самостоя­тельная ра­бота

3
Различные подходы к уточнению понятия алгоритма.
Краткое перечисле­ние раз­личных под­ходок к уточ­нению понятия алгорит­мов, взаимосвязь
Самостоя­тельная ра­бота

4
Основные функции и операции.
Нуль функция, функ­ция выбора аргу­мента, функ­ция сле­дования. Операция рекурсии, минимиза­ции, суперпозиции.

Самостоя­тельная ра­бота

5
Рекурсивность различных функций.
Доказательство ре­курсив­ности основ­ных функций ариф­метики. Иные функ­ции, их рекурсив­ность
К/р №2

6
Тезис Черча.
Связь интуитивного поня­тия вычислимой функции и рекурсив­ной функции.

Самостоя­тельная ра­бота

7
Ре­кур­сив­но-пе­ре­чис­ли­мое мно­же­ст­во. Кри­те­рий ре­кур­сив­но­сти мно­же­ст­ва.
Определение и при­меры перечислимых множеств. Рекурсив­ность перечисли­мого множества.
Самостоя­тельная ра­бота

8
Опе­ра­ции над ма­ши­на­ми Тью­рин­га. Гё­де­ле­ва ну­ме­ра­ция ма­шин Тью­рин­га.
Устройство машины Тью­ринга. Примеры построе­ния и реше­ния задач на их со­ставление. Нумера­ция Кантора и Ге­деля.
К/р №3

9
Фун­кция, вы­чис­ли­мая по Тью­рин­гу. Фун­кция, пра­ви­ль­но-вы­чис­ли­мая по Тью­рин­гу. До­ка­за­те­ль­ст­во су­ще­ст­во­ва­ния фун­кций, не­вы­чис­ли­мых по Тью­рин­гу. При­мер не­вы­чис­ли­мой по Тью­рин­гу фун­кции.
Примеры функций, вычис­лимых по Тью­рингу и со­ответст­вующие программы этих машин. Беско­нечно и конечные машины Тью­ринга. Невычислимые по Тьюрингу функции.
К/р №4

К/р №5

10
При­ме­ры ал­го­рит­ми­че­с­ки не­раз­ре­ши­мых про­блем (про­бле­ма рас­по­зна­ва­ния са­мопри­ме­ни­мо­сти, про­бле­ма при­ме­ни­мо­сти).
Проблема останова.

Проблема самопри­мени­мости.
Самостоя­тельная ра­бота

11
Нор­ма­ль­ный ал­го­ритм Мар­ко­ва в ал­фа­ви­те и над ал­фа­ви­том. Нор­ма­ль­но-вы­чис­ли­мые фун­кции. При­ме­ры нор­ма­ль­ных ал­го­ритмов.
Определение и при­меры алгоритмов Маркова. По­нятие алфавита. Нормаль­ные алфавиты и функции, нормально вычислимые по Мар­кову.
Самостоя­тельная ра­бота

12
Ма­ши­на По­ста. Ма­ши­на По­ста-Ус­пен­ско­го. Ма­ши­на с не­огра­ни­чен­ны­ми ре­ги­стра­ми (МНР).
Устройство и при­меры машины Поста, различия с машиной Тьюринга. МНР-уст­ройство и примеры.
К/р №6

13
Эк­ви­ва­ле­нт­ность ма­те­ма­ти­че­с­ких мо­де­лей по­ня­тия "ал­го­ритм". Сов­па­де­ние клас­са фун­кций, пра­ви­ль­но-вы­чис­ли­мых по Тью­рин­гу и клас­са час­тич­но ре­кур­сив­ных фун­кций.
Совпадение классов четко определенных и интуи­тивно опре­деленных, от­сутствие контрпримеров.
К/р №7

14
Те­зи­сы те­ории ал­го­рит­мов. Те­зис Чёр­ча-Кли­ни. При­нцип нор­ма­ли­за­ции Мар­ко­ва. Те­зис Тью­рин­га. Уни­вер­са­ль­ные ал­го­рит­мы. Уни­вер­са­ль­ная ма­ши­на Тью­рин­га. Уни­вер­са­ль­ные фун­кции.
Различные тезисы о совпа­дении того или иного спо­соба уточ­нения понятия алго­ритма и четко опи­сан­ных моделей. Те­зисы.

Самостоя­тельная ра­бота

15
Ал­го­рит­ми­че­с­кая сво­ди­мость. 1-сво­ди­мость. M-сво­ди­мость. Сте­пе­ни не­раз­ре­ши­мо­сти. M-пол­ные. Про­дук­тив­ные и кре­атив­ные мно­же­ст­ва. Те­оре­ма Кли­ни о не­под­виж­ной точ­ке. Те­оре­ма Май­хил­ла. Таб­лич­ная сво­ди­мость. Сво­ди­мость по Тью­рин­гу.
Различные подходы к сво­димости, типы и виды. Теоремы об исключитель­ных случаях. Сводимость.
Самостоя­тельная ра­бота, итого­вое тесто­вое задание


6. Примерные контрольные работы


№1. Алгоритмы в математике.

1. Составьте алгоритм сложения столбиком двух натуральных чисел.

2. Опишите правила перехода улицы для случаев:

а) перекресток регулируемый;

б) перекресток нерегулируемый (т.е. без светофора).

3. Опишите способ измерения длинной рейки с помощью линейки.

4. Укажите метод отыскания слова в орфографическом словаре.

5. Укажите алгоритм проведения перпендикуляра к прямой , в заданной точке D.

6. Опишите несколько алгоритмов решения задач на следующие темы:

а) рецепты приготовления пищи (один из способов получения таких рецеп­тов - воспользуйтесь поваренной книгой);

б) правила этикета (например, правило знакомства, алгоритм приветствия и т.п.);

в) правила дорожного движения;

г) правила поведения в бытовых ситуациях (алгоритм пользования газовой пли­той, правило пользования телефоном-автоматом и т.п.).

8. Составьте алгоритм нахождения цепной дроби рационального числа.

9. Составьте алгоритм нахождения цепной дроби для квадратичной ирра­циональ­ности.

10. Составьте алгоритм нахождения п-ой подходящей дроби некоторого рацио­нального числа.


№2. Исследование на рекурсивность функций.

f(x,y,z) = 2;

f(x,y) = x - y = ;

f(x) = ;

f(x,y) = x + y + 2;

f(x,y) = 3;

f(x,y,z) = x + y + z;

f(x,y) = x + 2;

9. f(x,y) = остатку от деления (x + y) на 2;

10. f(x,y) = остатку от деления х на 3;


№3. Операции над машинами Тьюринга.

1. На ленте машины Тьюринга записано целое положительное число в де­сятич­ной системе счисления. Найти произведение этого числа на 11,если каретка обо­зревает крайнюю правую цифру числа.

2. На ленте машины Тьюринга записано слово, состоящее из букв латин­ского алфавита {a, b, c, d }. Подсчитать число вхождений буквы a в за­данное слово. Полученное значение записать на ленту левее заданного слова через пробел. Каретка обозревает крайнюю левую букву.

3. На ленте машины Тьюринга записано десятичное число. Определить, делится ли это число не 5 без остатка. Если делится, то справа от числа записать слово «да», если не делится, то записать «нет». Каретка нахо­дится где-то над числом.

4. На ленте машины Тьюринга записано число в десятичной системе счис­ления. Каретка находится над правой цифрой. Запишите цифры этого числа в обратном порядке.

5. На ленте машины Тьюринга находится массив, состоящий только из символов А и В. Сожмите массив, удавив из него все элементы В.

6. Число n записано на ленте машины Тьюринга массивом меток.

Преобразуйте это значение n по формуле:

n – 2, если n > 5,

j (n) = 1, если n = 5,

2n, если n < 5.

Каретка обозревает крайнюю левую метку.

7. На ленте машины Тьюринга массив из 2n меток. Уменьшите этот мас­сив в 2 раза.

8. Даны два натуральных числа m и n, записанные в унарной системе счисле­ния. Между этими числами стоит знак «?». Выясните отношение между задан­ными числами и замените знак «?» на один из подходящих знаков «<», «>» или «=».

9. Найдите произведение двух натуральных чисел m и n, записанных в унар­ной системе счисления. Соответствующие наборы символов « | » раз­делены зна­ком «*», а справа от последнего символа стоит знак «=». По­местите результат умножение этих чисел вслед за знаком «=».


№4. Составление машин Тьюринга.

1. Дано число n в восьмеричной системе счисления. Постройте машину Тьюринга, которая бы увеличивала данное число на единицу.

2. Дана десятичная запись натурального числа n>1. Постройте машину Тью­ринга, которая уменьшала бы данное число на 1. При этом запись числа n – 1 не должна содержать левый нуль. Например, 100 – 1 = 99, а не 099. Начальное по­ложение головки – правое.

3. Дан массив из открывающихся и закрывающихся скобок. Построить ма- шину Тьюринга, которая удаляла бы пары взаимных скобок.

4. Дана строка из букв a и b. Построить машину Тьюринга, которая пе­ремес­тит все буквы a в левую часть строки, а все буквы b – в правую. Ка­ретка нахо­дится на крайнем левом символом строки.

5. Даны два целых положительных числа в десятичной системе счисления.

Построить машину Тьюринга, которая будет находить разность этих чи­сел, если известно, что первое число больше второго, а между ними стоит знак

« - ». Каретка находится над левой крайней цифрой левого числа.

6. Даны два целых положительных числа в различных системах счисле­ния, одно – в троичной системе счисления, другое – в десятичной. По­стройте машину Тью­ринга, которая будет находить сумму этих чисел в десятичной системе счисления.

7. Построите машину Тьюринга, которая преобразует запись числа в дво­ичной системе счисления в восьмеричную.

8. Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Построить машину Тьюринга, которая будет запи­сывать в деся­тичной системе счисления число этих меток.
  1. На ленте машины Тьюринга в трёх клетках записаны три различные бу­квы: А, В, С. Каретка в начальном состоянии обозревает букву, располо­женную справа. Построить машину Тьюринга, которая поменяет местами крайние буквы.
  2. На ленте машины Тьюринга записано число в десятичной системе счис­ления. Построить машину Тьюринга, которая бы умножала данное число на 2. В начале работы каретка находится над крайней левой цифрой числа.


№5. Функции, вычислимые по Тьюрингу.

1. Построить машину Тьюринга, вычисляющую функцию .

2. Построить машину Тьюринга, вычисляющую функцию .

3. Построить машину Тьюринга, вычисляющую функцию .

4. Построить машину Тьюринга, вычисляющую функцию .

5. Построить машину Тьюринга, вычисляющую функцию .

6. Построить машину Тьюринга, вычисляющую функцию .

7. Построить машину Тьюринга, вычисляющую функцию .

8. Построить машину Тьюринга, вычисляющую функцию .

9. Построить машину Тьюринга, вычисляющую функцию .

10. Построить машину Тьюринга, вычисляющую функцию .

11. Построить машину Тьюринга, вычисляющую функцию .

12. Построить машину Тьюринга, вычисляющую функцию

13. Построить машину Тьюринга, вычисляющую функцию , равную остатку от деления х на 2.


№6. Составление машины Поста.

1. На ленте машины Поста расположен массив в N отмеченных секциях. Необхо­димо справа от данного массива через одну пустую секцию раз­местить массив вдвое больший (он должен состоять из 2N меток). При этом исходный массив может быть стерт.

2. На ленте машины Поста расположен массив из N меток (метки распо­ложены через пробел). Надо сжать массив так, чтобы все N меток зани­мали N располо­женных подряд секций.

3. На информационной ленте машины Поста расположено N массивов ме­ток, от­деленных друг от друга свободной ячейкой. Каретка находится над крайней ле­вой меткой первого массива. Определите число массивов.

4. Игра Баше. В игре участвуют двое (человек и машина Поста). Напи­шите про­грамму, по которой всегда будет выигрывать машина Поста. Суть игры заключа­ется в следующем: имеется 21 предмет. Первым ходит человек. Каждый из иг­рающих может брать 1, 2, 3 или 4 предмета. Проиг­рывает тот, кто берет послед­ний предмет.

5. Число k представляется на ленте машины Поста k+1 идущими подряд мет­ками. Одна метка соответствует нулю. Составьте программу прибав­ления 1 к произвольному числу k. Каретка расположена над одной из ме­ток, принадлежа­щих заданному числу k.

6. Составьте программу сложения двух целых неотрицательных чисел а и b, рас­положенных на ленте машины Поста. Каретка расположена над од­ной из меток, принадлежащих числу а. Число b находится правее числа а через несколько пус­тых секций.

7. Составьте программу сложения произвольного количества целых неот­рица­тельных чисел, записанных на ленте машины Поста на расстоянии одной пустой секции друг от друга. Каретка находится над крайней левой меткой левого числа.

8. На ленте машины Поста расположен массив из N меток. Составьте про­грамму, действуя по которой машина выяснит, делится ли число на 3. Если да, то после массива через одну пустую секцию поставьте метку V.

9. Число k представлено на ленте машины Поста k+1 идущими подряд метками. Найдите остаток от деления целого неотрицательного числа k на 3, если из­вестно, что каретка находится справа от заданного числа.

10. Составьте программу нахождения разности двух неотрицательных це­лых чи­сел а и b, находящихся на ленте машины Поста. Каретка находится над левой меткой левого числа. Неизвестно, какое число больше: а или b.


№ 7. Фун­кции, пра­ви­ль­но-вы­чис­ли­мые по Тью­рин­гу.

1. Построить машину Тьюринга, вычисляющую функцию .

2. Построить машину Тьюринга, вычисляющую функцию .

3. Построить машину Тьюринга, вычисляющую функцию .

4. Построить машину Тьюринга, вычисляющую функцию .

5. Построить машину Тьюринга, вычисляющую функцию .

6. Построить машину Тьюринга, вычисляющую функцию .

7. Построить машину Тьюринга, вычисляющую функцию .

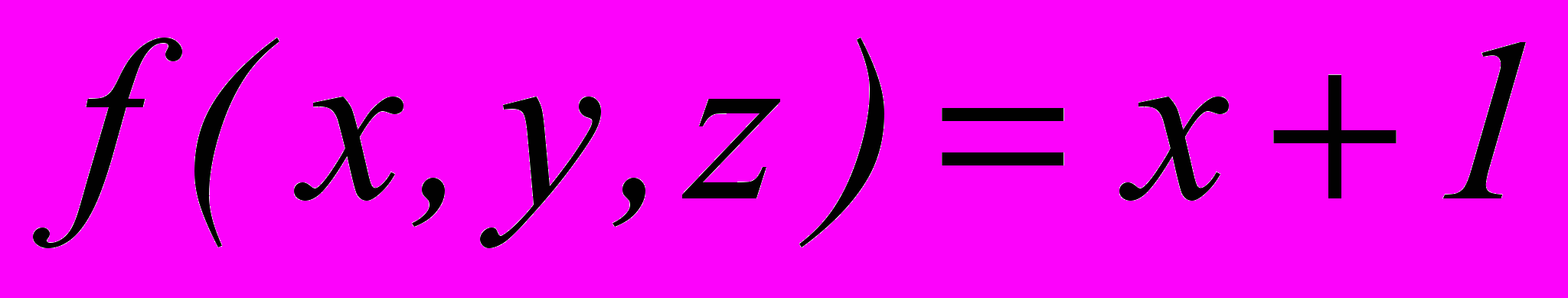8. Построить машину Тьюринга, вычисляющую функцию .

9. Построить машину Тьюринга, вычисляющую функцию .

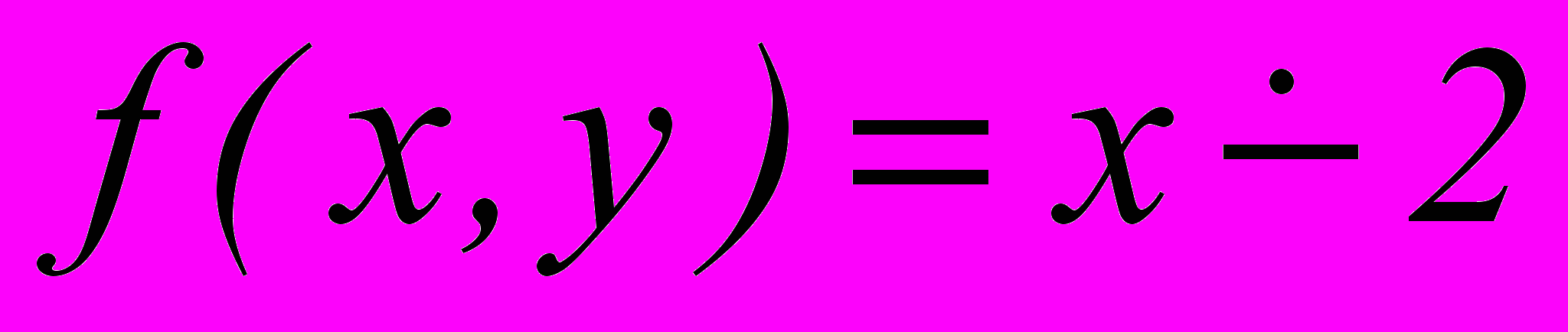10. Построить машину Тьюринга, вычисляющую функцию .

11. Построить машину Тьюринга, вычисляющую функцию .

12. Построить машину Тьюринга, вычисляющую функцию .

13. Построить машину Тьюринга, вычисляющую функцию , рав­ную ос­татку от деления х на 3.


7. Тематика рефератов по теории алгоритмов


1. Эк­ви­ва­ле­нт­ность ма­те­ма­ти­че­с­ких мо­де­лей по­ня­тия "ал­го­ритм".

2. Те­зи­сы те­ории ал­го­рит­мов. Те­зис Чёр­ча-Кли­ни. При­нцип нор­ма­ли­за­ции Мар­ко­ва. Те­зис Тью­рин­га.

3. Уни­вер­са­ль­ные ал­го­рит­мы. Уни­вер­са­ль­ная ма­ши­на Тью­рин­га. Уни­вер­са­ль­ные фун­кции.

4. Ал­го­рит­ми­че­с­кая сво­ди­мость: 1-сво­ди­мость, m-сво­ди­мость. Сте­пе­ни не­раз­ре­ши­мо­сти. m-пол­ные. Про­дук­тив­ные и кре­атив­ные мно­же­ст­ва.

5. Те­оре­ма Кли­ни о не­под­виж­ной точ­ке.

6. Те­оре­ма Май­хил­ла.

7. Таб­лич­ная сво­ди­мость. Сво­ди­мость по Тью­рин­гу.

8. Нор­ма­ль­ный ал­го­ритм Мар­ко­ва в ал­фа­ви­те и над ал­фа­ви­том. История возник­новения.

9. Десятая проблема Гильберта.

10. Примеры разрешимых и перечислимых множеств. Взаимосвязь поня­тий.

11. Примеры неразрешимых алгоритмических проблем.

12. Теорема Геделя о неполноте.

13. Рекурсивные функции.

14. Класс частично рекурсивных функций.

15. Класс рекурсивных функций.

16. Класс общерекурсивных функций.

17. Сов­па­де­ние клас­са фун­кций, вы­чис­ли­мых по Тью­рин­гу и клас­са час­тич­но ре­кур­сив­ных фун­кций.

18. Примеры функций невычислимых по Тьюрингу.

19. Нормальные алгоритмы.

20. Биография А.Тьюринга.

21. Биография А.Черча.

22. Биография Э.Поста.

23. Биография А.А.Маркова.

24. История возникновения термина «алгоритм».

25. Машинная арифметика.

26. Современное состояние теории алгоритмов.


8. Учебно-методическое обеспечение дисциплины

8.1. Литература

Основная:

  1. Кат­ленд Н. Вы­чис­ли­мость. Вве­де­ние в те­орию ре­кур­сив­ных фун­кций. - М.: Мир, 1983.
  2. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математиче­ской логике и теории алгоритмов. – М.: Наука, 1984.

Дополнительная:

1. Мар­ков А.А., На­гор­ный Н.М. Те­ория ал­го­риф­мов. - М.: ФАЗИС, 1996. -448с.

2. Мат­ро­сов В.Л. Те­ория ал­го­рит­мов. - М.: Про­ме­тей, 1989.

3. Мен­де­ль­сон Э. Вве­де­ние в ма­те­ма­ти­че­с­кую ло­ги­ку: - 3-е изд. -М.: На­ука, 1984.

4. Ми­хай­лов А.Б., Ры­жо­ва Н.И., Швец­кий М.В. Упраж­не­ния по ос­но­вам ма­те­ма­ти­че­с­кой ло­ги­ки. Вве­де­ние в те­орию ал­го­риф­мов. -СПб.: РГПУ им.А.И.Герцена, 1997.

5. Ми­хай­лов А.Б., Ры­жо­ва Н.И., Швец­кий М.В. Лек­ции по ос­но­вам ма­те­ма­ти­че­с­кой ло­ги­ки. Эле­мен­ты те­ории ал­го­риф­мов. - СПб.: РГПУ им. А.И.Герцена, 1997.

6. Род­жерс Х. Те­ория ре­кур­сив­ных фун­кций и эф­фе­к­тив­ная вы­чис­ли­мость. - М.: Мир, 1972.

7. Трах­те­нб­рот Б.А. Ал­го­рит­мы и вы­чис­ли­те­ль­ные ав­то­ма­ты. - М.: Сов.

радио, 1974.

8. Успен­ский В.А. Ма­ши­на По­ста. - М.: На­ука, 1979.

9. Успен­ский В.А. Се­мё­нов А.Л. Те­ория ал­го­рит­мов: осно­вные от­кры­тия и при­ло­же­ния. - М.: На­ука, 1987.


Электронные материалы