Элементы теории игр Определения
| Вид материала | Документы |
- Программа дисциплины Элементы теории управления и дифференциальных игр Семестры 7,8, 16.58kb.
- hulan ucoz, 73.13kb.
- Программа вступительного экзамена в магистратуру элементы теории погрешностей, 51.03kb.
- Ок. 365 300 до н э. древнегреческий математик. Работал в Александрии, 72.88kb.
- Методические указания Объектом исследования теории игр (ТИ) является принятие решений, 145.42kb.
- 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
- Программа дисциплины Принятие решений Семестр, 18.48kb.
- Краткий конспект курса по дням Предмет теории игр. Основные понятия: игрок, стратегия,, 57.2kb.
- Математика, 87.27kb.
- Практическое задание 11 Игровые модели. Классификация игровых моделей. Теория игр, 377.07kb.
Элементы теории игр
Определения
Имеются две стороны (игрок I и игрок II).
Игрок I может выбирать стратегию поведения из своего множества стратегий sS; игрок II – tT. Выборы (s,t) производятся независимо друг от друга. Пара (s,t) называется ситуацией в игре.
Зададим функцию (s,t): ST R2, которая оценивает выигрыш каждого игрока в ситуации (s,t). Эту функцию называют платежной функцией игры. Отрицательное значение платежной функции означает проигрыш.
Игрой будем называть тройку = <S, T, >, где S, T – произвольные множества, : ST R2.
Позиционные игры
Кроме антагонистических существуют и другие классы игр. Например, в шахматах любой ход игрока зависит от позиции, которая определяется количеством и составом фигур каждого игрока, а также их расположением в данный момент. Множество ходов, которые можно совершить из каждой позиции можно изобразить в виде дерева игры. Такие игры называют позиционными.
Упражнение 1 (домашнее задание).
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй – 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 24 камней. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Кооперативные игры
Реальные задачи принятия решений в условиях конфликта обычно характеризуются неантагонистичностью ситуации, то есть интересы игроков могут не быть противоположными. Это может приводить к ситуациям, взаимовыгодным обоим игрокам, что подразумевает выбор согласованного поведения, приводящего к увеличению выигрыша обоих игроков. Кооперативной игрой называют игру, в которой игрокам разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях. Основная задача в кооперативной игре состоит в дележе общего выигрыша между членами коалиции.
х/ф «Игры разума», Нэш: Адам Смит утверждает, что лучший результат получается тогда, когда каждый в группе делает так, как выгодно ему. Адама Смита надо пересмотреть! Подойти всем сразу не получится. Они друг друга блокируют. Так что она не достанется никому из нас. Можно подойти к подругам. Я предлагаю никому не подходить к блондинке, иначе все её подруги нам дадут от ворот поворот. Если к блондинке никто не подойдет, то мы не будем мешаться друг у друга под ногами и тем самым не оскорбим других девушек. Так каждый из нас выиграет… На самом деле лучший результат, когда каждый действует так, как лучше для него самого и для всей группы.
Пусть Q – множество точек плоскости (1,2), соответствующих всевозможным ситуациям в игре. Ситуация называется Парето-оптимальным решением, если в этой ситуации увеличение выигрыша одного игрока возможно только за счет уменьшения выигрыша другого (на рис. 1 это часть границы между точками A и B). Пусть T1 и T2 величины выигрыша, которые каждый из игроков может получить, не вступая в коалицию с партнёром. Ситуация, в которой игроки получают выигрыши T1 и T2 соответственно, называется точкой угрозы (точка T). Переговорным множеством называют все точки множества Q, являющиеся Парето-оптимальными решениями, выигрыши в которых не меньше выигрышей в точке угрозы, это те выигрыши, которых игроки не могут достичь в одиночку (на рис. точки границы между C и D). Ситуация в игре называется точкой равновесия по Нэшу, если ни одному из игроков не выгодно отклоняться от своей стратегии в одиночку. При этом выигрыши в равновесных точках могут быть различны. Решением Нэша называют точку, в которой достигается максимум величины H = (1 – T1)(2 – T2). В теории игр доказано, что если множество Q выпукло, замкнуто и ограничено сверху, то решение Нэша существует и единственно.
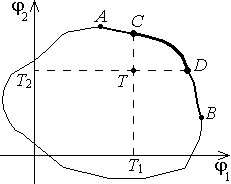
Рис.1. Иллюстрация понятий кооперативной игры:
точка угрозы точка T, часть границы между точками A и B Парето-оптимальные решения, точки границы между C и D переговорное множество.
Пример – игра «Семейный спор»
В городке есть два вида развлечений – театр и футбол. Семейная пара выбирает, как провести вечер. У каждого из супругов есть любимое зрелище: Жена предпочитает театр, Муж – футбол. Однако, супруги так привязаны друг к другу, что посещение любимого развлечения в одиночку доставляет им совсем не такое удовольствие, как присутствие на них вдвоем. Выигрыш (количественная оценка получаемого удовольствия) каждого из супругов описывается матрицей:
Жена
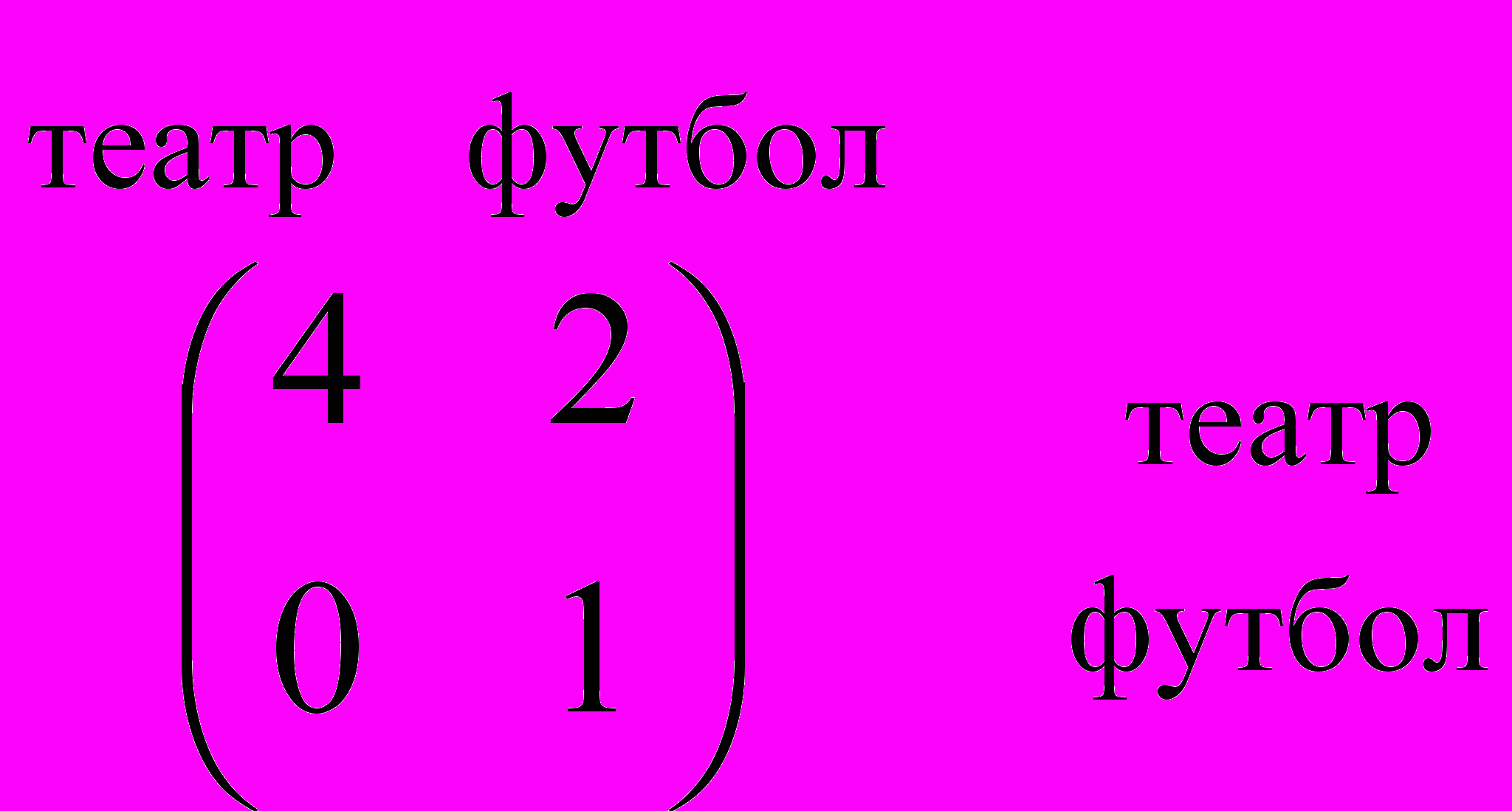
Муж

Как должны организовать свой досуг супруги, чтобы получить максимальное удовольствие?
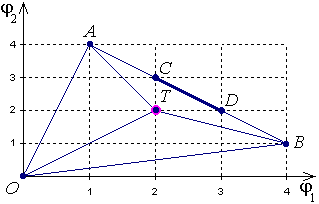
Рис. 2. Решение игры «Семейный спор»
На рис. 2: точка угрозы точка T (2, 2), отрезок AB Парето-оптимальные решения, отрезок CD переговорное множество. Единственная точка равновесия по Нэшу - точка T. Точки переговорного множества принадлежат прямой 2 = 5 – 1. Поэтому решение Нэша можно найти, исследовав на максимум функцию
H(1) = (1 – 2)( 2 – 2) = (1 – 2)( 3 – 1).
Максимум этой функции достигается при 1 = 2,5, следовательно, 2 = 2,5. Соответствующая точка является серединой отрезка между точками A и B. Это означает, что в чистых стратегиях решения не существует. Заметим, что точка A соответствует ситуации, когда оба супруга идут на футбол, а точка B оба идут в театр. Можно доказать, что при многократном повторении игры оптимальным будет выбор каждой из этих двух ситуаций с вероятностью 0,5.
Упражнение 2 – игра «Зачёт»
У студента есть две стратегии подготовки к зачету: учить или не учить. У преподавателя есть две стратегии – поставить зачет или не зачет. При этом выигрыши игроков описываются матрицами:
Студент

Преподаватель
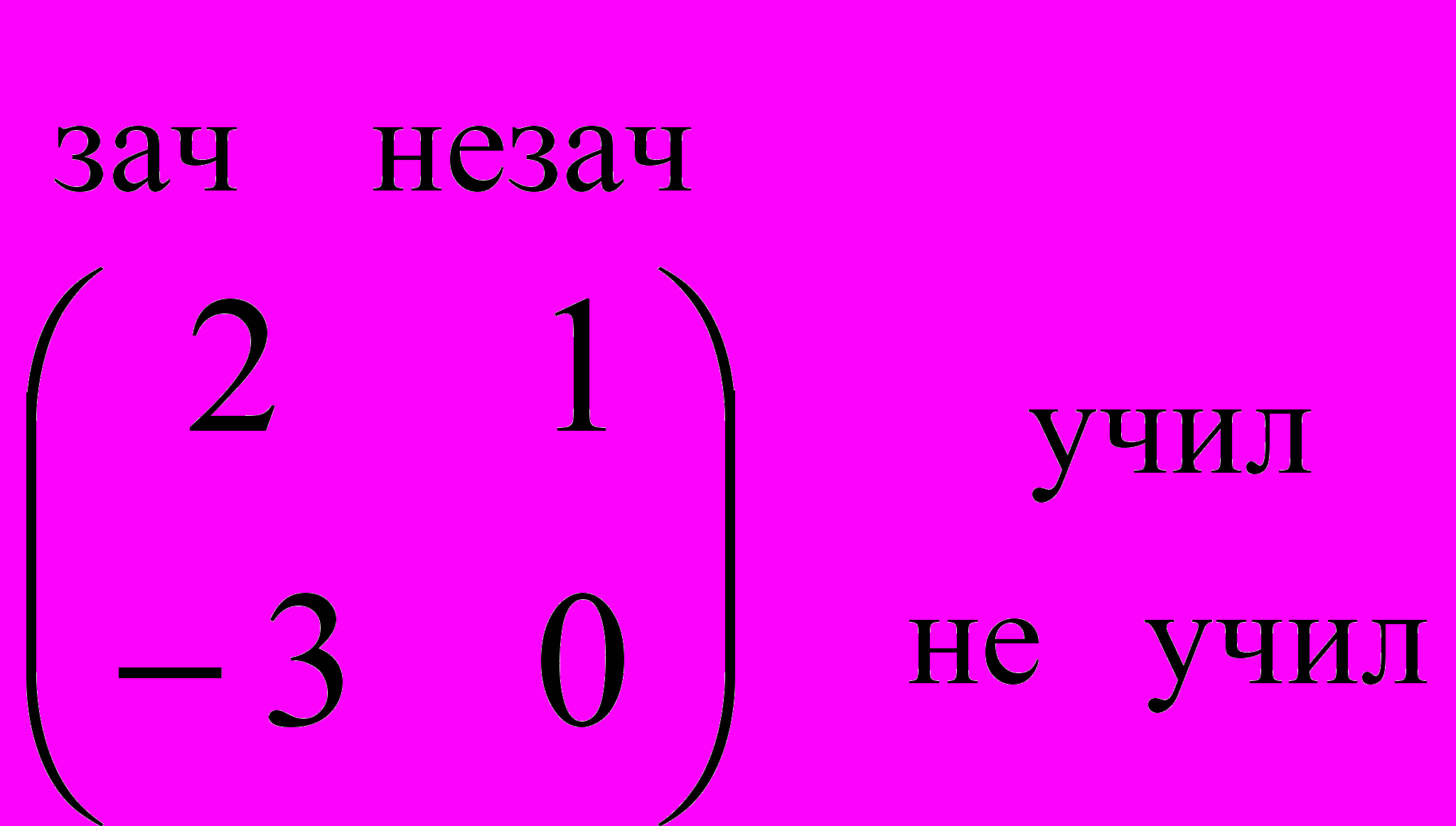
Какие стратегии должны выбрать студент и преподаватель?
Антагонистические игры
Пусть интересы игроков диаметрально противоположны, то есть выигрыш первого игрока равен проигрышу второго, тогда если (s,t) функция выигрышей игрока I, то выигрыш игрока II равен –(s,t). В этом случае игра называется антагонистической. Мы будем рассматривать антагонистические игры, в которых множества стратегий S и T конечны. В таких играх платежная функция представляет собой матрицу, а саму игру называют матричной. В матричной игре S = (s1, s2, …, sm), T = (t1, t2, …, tn), aij = (si, tj),
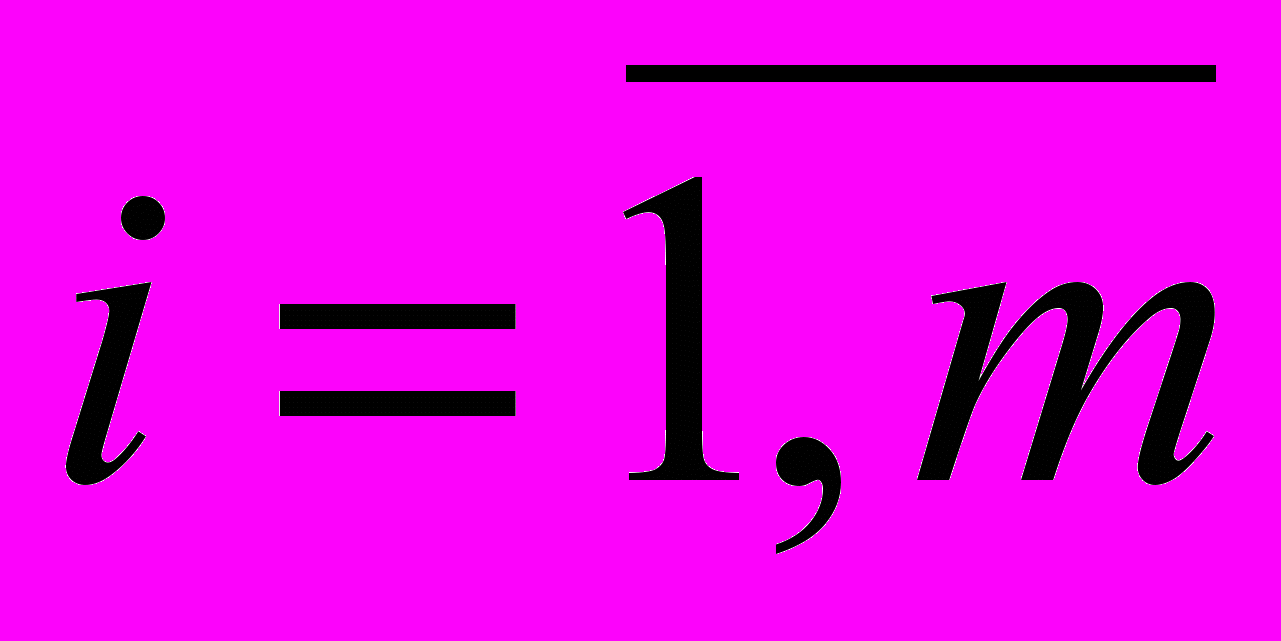 ,
, 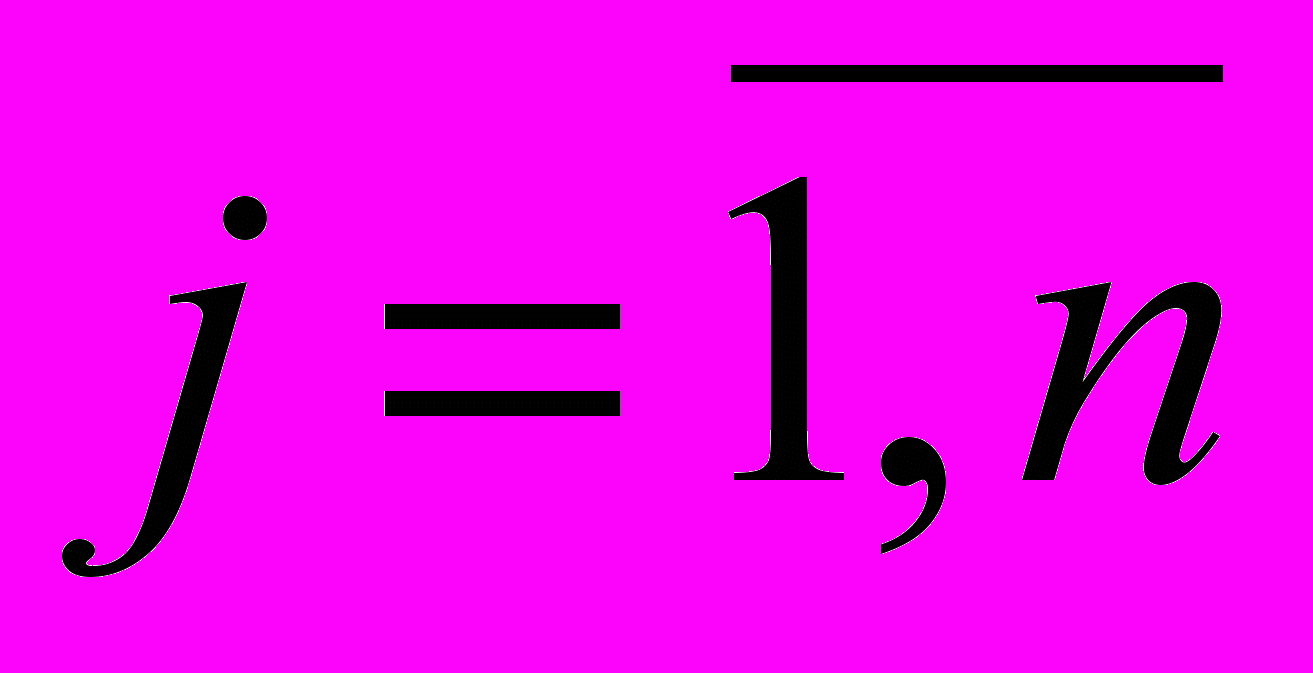 . То есть матричная игра полностью описывается матрицей
. То есть матричная игра полностью описывается матрицей 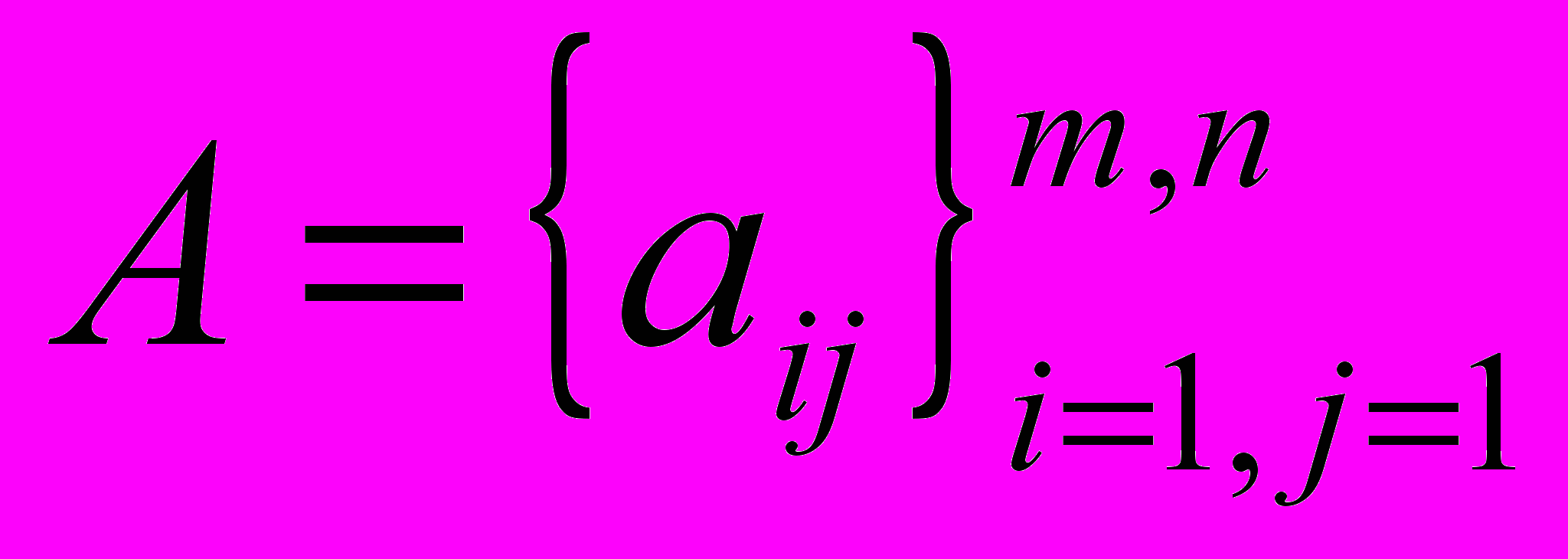 , которая называется платежной матрицей игры.
, которая называется платежной матрицей игры.Примеры
- Игра «Чёт-нечет»
Два игрока выбрасывают 1 или 2 пальца. Если сумма пальцев четная, то выигрывает первый, если сумма нечетна, то выигрывает второй (то есть выигрыш первого равен –1).
si = ti = {выброшено i пальцев}, i = 1, 2;
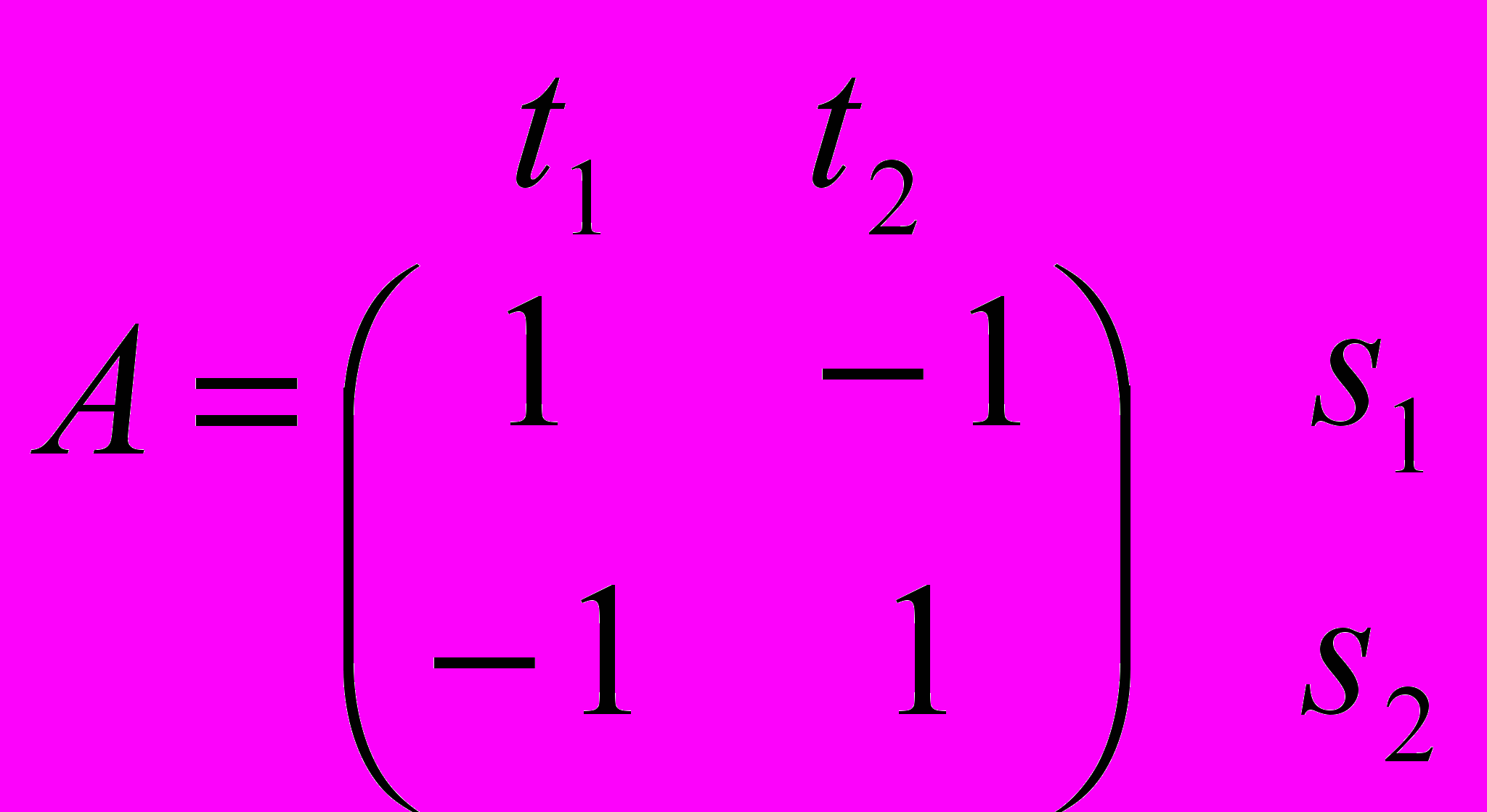
- Игра «Сравнение монет»
Два игрока выбрасывают по монетке. Если монетки выпадают обе вверх гербом или обе вверх решкой, то обе монетки забирает первый игрок (то есть выигрыш первого равен 1), в противном случае обе монетки забирает второй (то есть выигрыш первого равен –1).
Матрица этой игры совпадает с матрицей из первого примера.
- Игра «Камень, ножницы, бумага»
Два игрока выбрасывают кулак («камень»), два пальца («ножницы») или ладонь («бумага»). Камень побеждает ножницы, ножницы побеждают бумагу, бумага побеждает камень. Побеждающий получает с другого монетку.
Пусть s1 = t1 = {«камень»}, s2 = t2 = {«ножницы»}, s3 = t3 = {«бумага»}.

- Игра "Морра"
Два игрока показывают какое-либо количество пальцев и называют число (не обязательно равное количеству показанных пальцев). Если кто-то из игроков угадает сумму пальцев (назовет число, равное сумме), то этот игрок получает с другого выигрыш равный названному числу.
Построим матрицу игры для случая, когда можно показать один или два пальца.
sij = tij = {показано i пальцев, названо число j},
если i = 1, то j = 2, 3; если i = 2, то j = 3, 4;

- Игра "Война"
Имеется две стороны – обороняющаяся (I) и нападающая (II). I выбирает вид оружия, II – вид самолета, который должен прорвать оборону противника. Вероятность поражения самолета задана таблицей (платежная матрица игры):
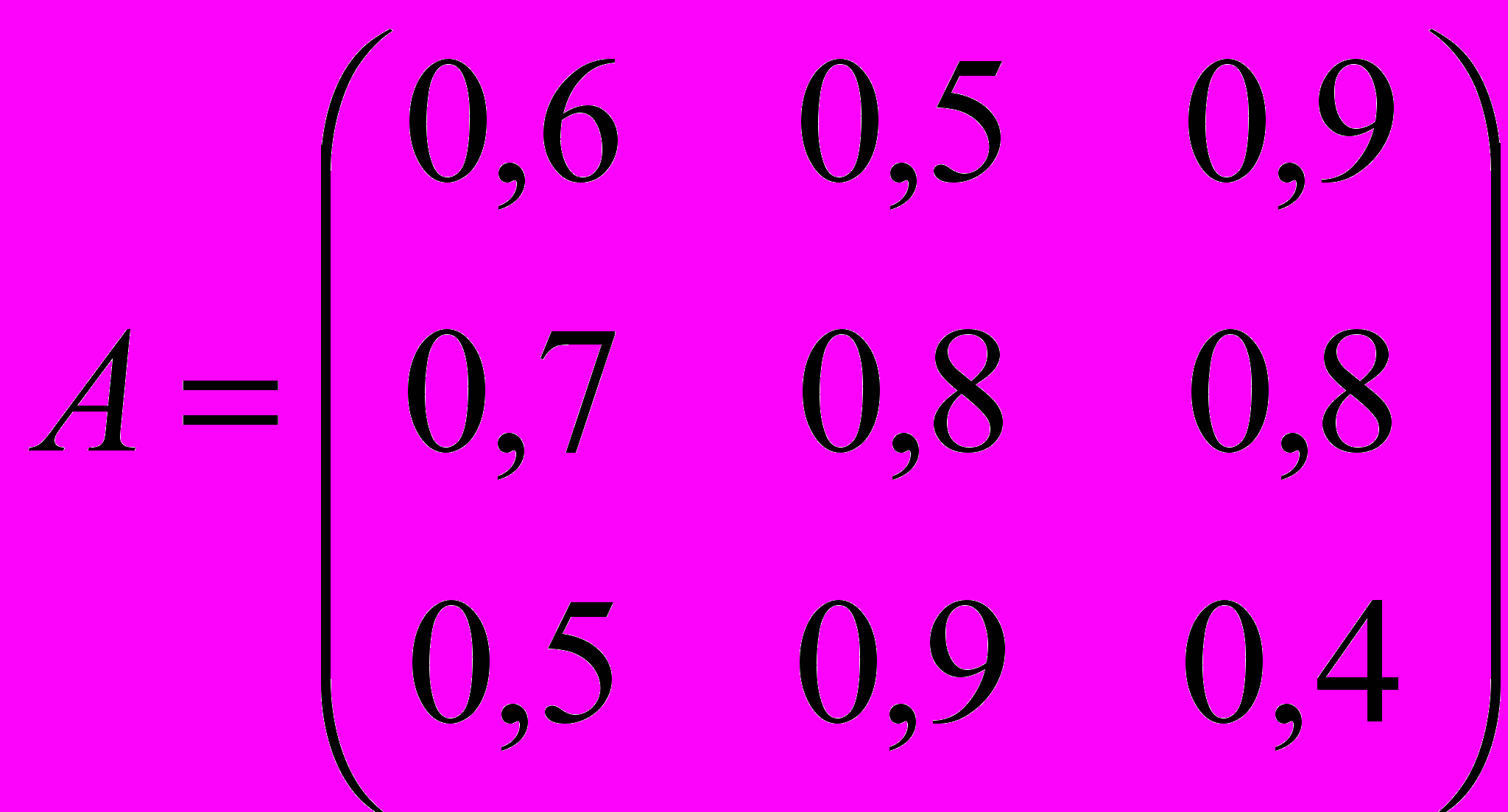
Нижнее и верхнее значение игры
Пусть A – платежная матрица игры. Пусть игрок I выбрал стратегию siS. Его выигрыш зависит от стратегии, выбранной игроком II. Худший вариант для игрока I заключается в том, что игрок II выберет ту стратегию, при которой выигрыш игрока I минимален. В этом случае игрок I получит
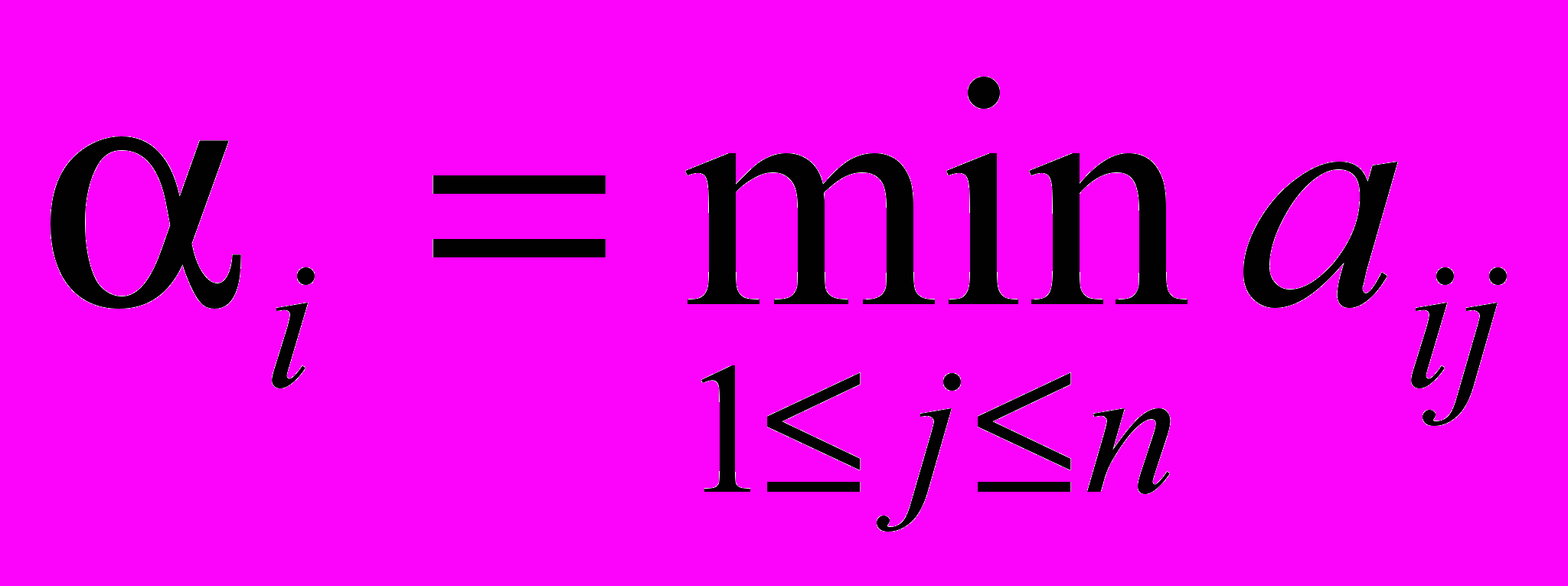 – это минимальный гарантированный выигрыш игрока I в случае выбора стратегии si. Естественно, при выборе i игрок I хочет получить как можно больший выигрыш:
– это минимальный гарантированный выигрыш игрока I в случае выбора стратегии si. Естественно, при выборе i игрок I хочет получить как можно больший выигрыш: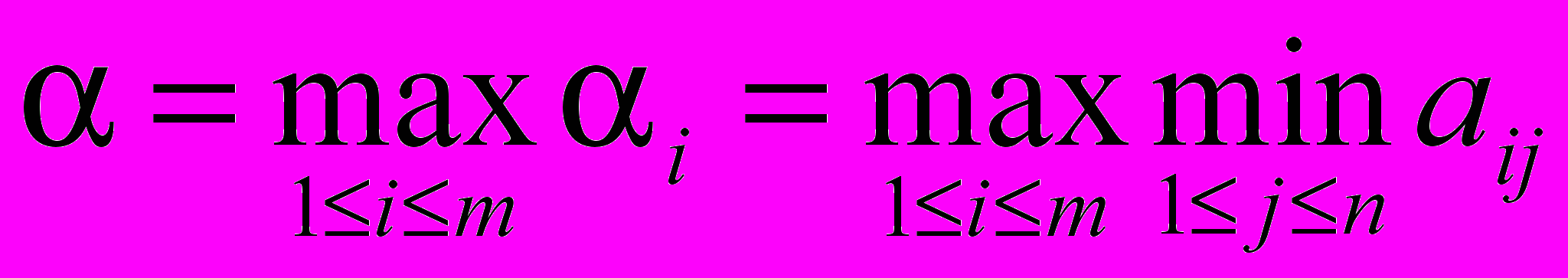 .
.Это число называется нижним значением игры (или максимином). Смысл этого числа – минимальный гарантированный выигрыш игрока I.
Пусть игрок II выбрал стратегию tjT. Его проигрыш зависит от стратегии, выбранной игроком I. Худший вариант для игрока II заключается в том, что игрок I выберет ту стратегию, при которой проигрыш игрока II максимален. В этом случае игрок II проиграет
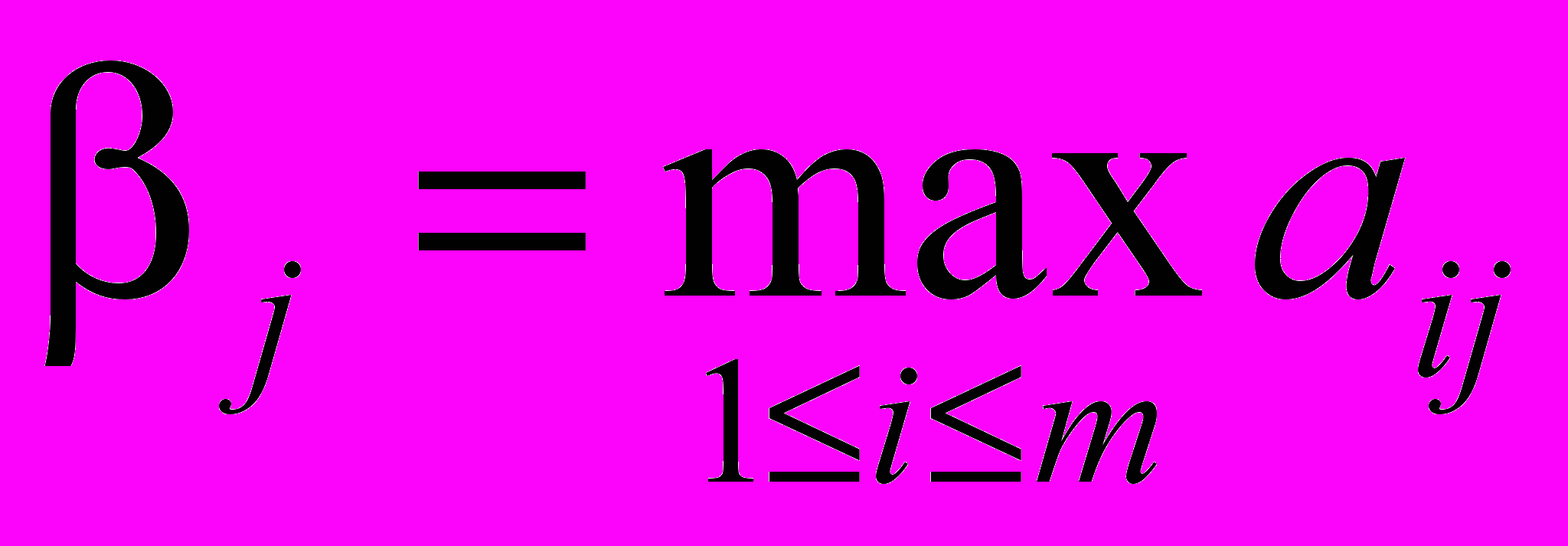 . Естественно, при выборе j игрок II хочет проиграть как можно меньше:
. Естественно, при выборе j игрок II хочет проиграть как можно меньше: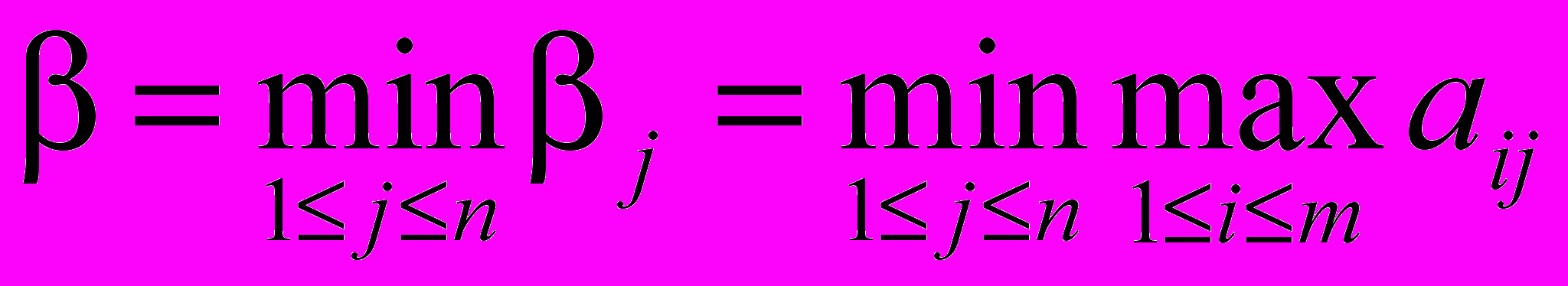 .
.Это число называется верхним значением игры (или минимаксом). Смысл этого числа –максимальный возможный проигрыш игрока II.
Стратегии si (tj), для которых достигается (соответственно ), называются максиминной (минимаксной) стратегиями.
В расмотренных выше примерах:
- Игра «Морра»: = –2 < = 2. Соответствующие стратегии s2, t2.
- Игра «Война»: = 0,7 = = 0,7. Соответствующие стратегии s2, t1.
Теорема 1 (о минимаксе и максимине).
Для любой матрицы A имеет место неравенство .
Доказательство.
i, j:
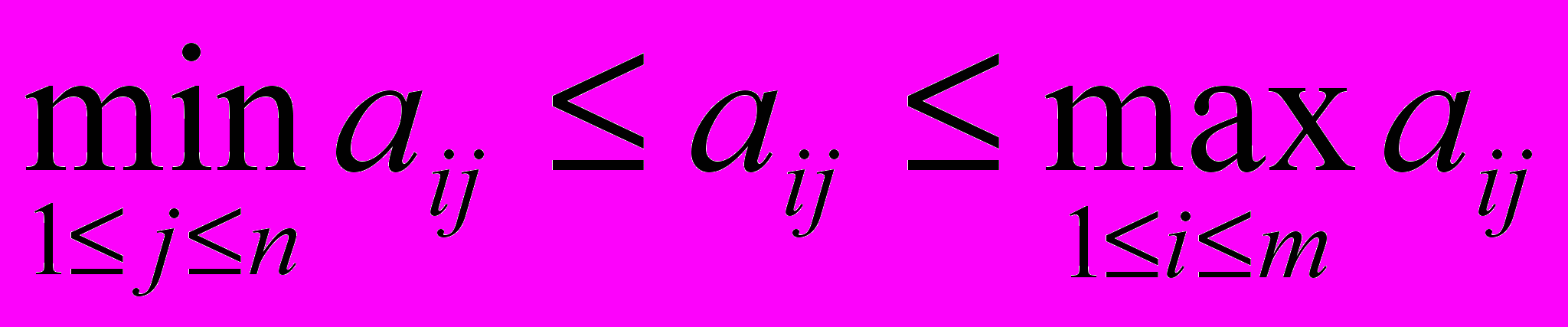
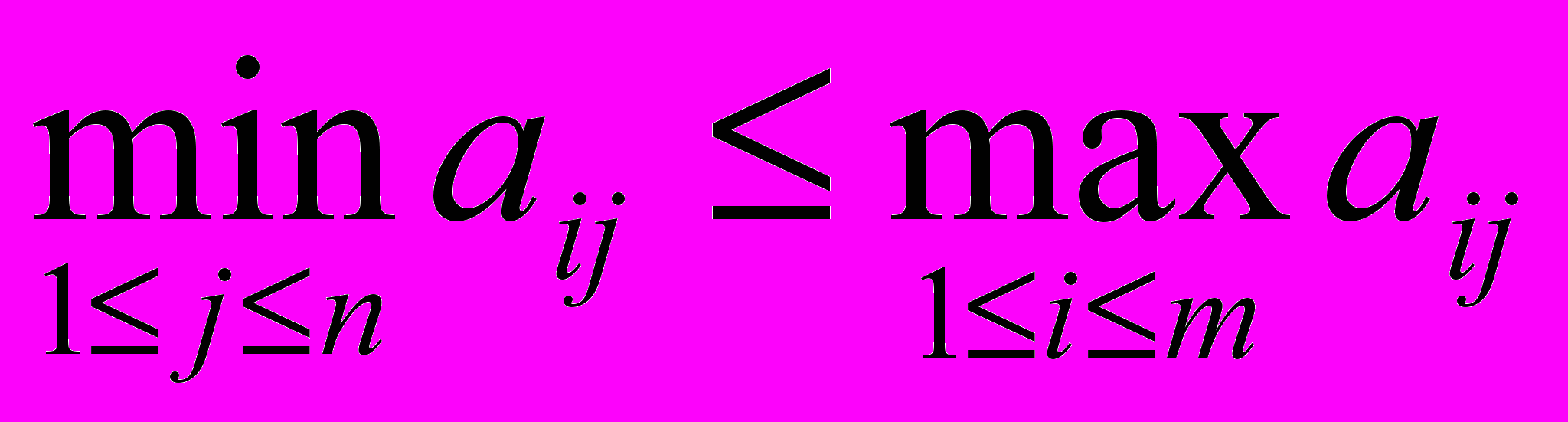 (1)
(1)Рассмотрим максимум по i от (1). Поскольку правая часть от i не зависит, то получим
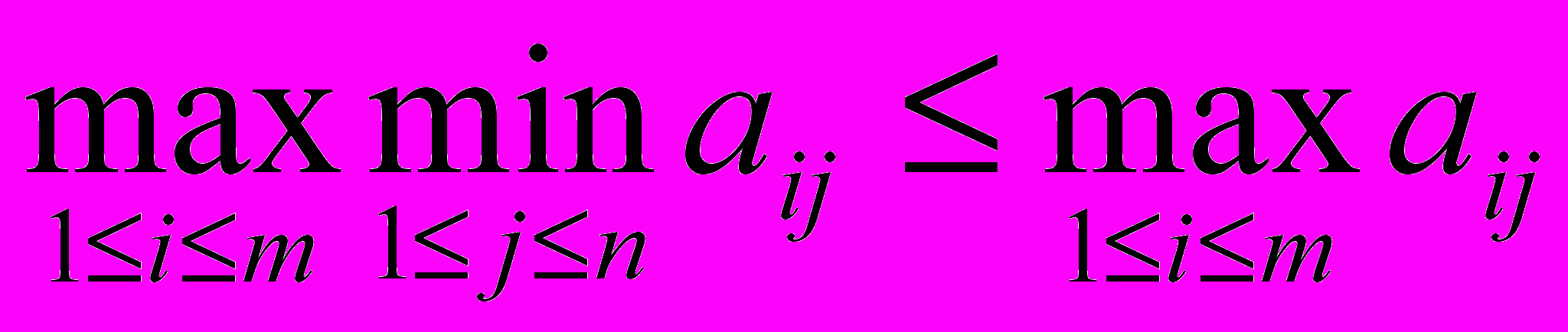 (2)
(2)Рассмотрим минимум по j от (2). Поскольку левая часть от j не зависит (это уже число), то получим
 , что и требовалось доказать.
, что и требовалось доказать.Седловые точки
Седловым элементом матрицы называется элемент, являющийся минимальным в своей строке и максимальным в своем столбце.
Ситуацию (s*, t*) назовем седловой точкой игры = <S, T, >, если
sS tT ( s, t*) ( s*, t*) ( s*, t). (3)
Теорема 2 (критерий существования седловой точки).
Для того, чтобы матричная игра = <S, T, > имела седловые точки необходимо и достаточно, чтобы были равны величины и .
Доказательство.
Необходимость.
Пусть (s*, t*) – седловая точка, т. е. выполнено (3).
- Так как ( si, t*) ( s*, t*), а ( s*, t*) – число, то
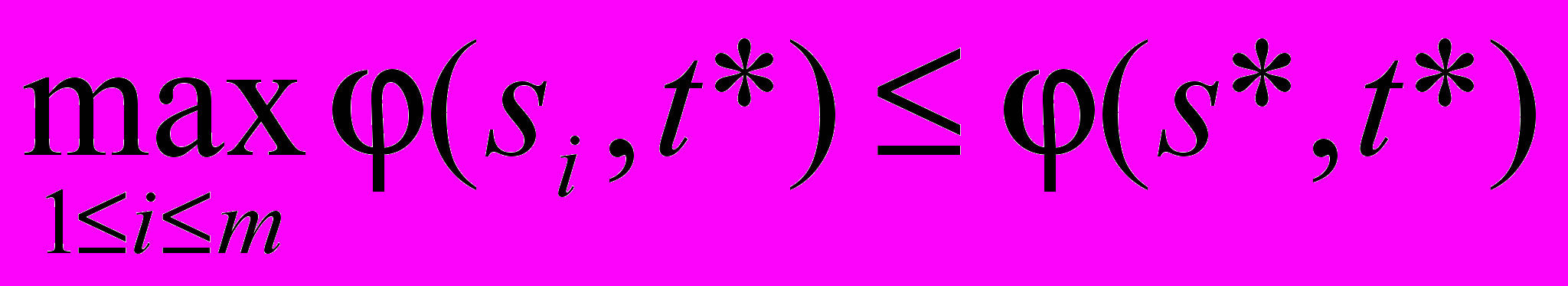 ,
,а отсюда следует (берем минимум по j, от которого левая часть не зависит), что
 (4)
(4)- Так как ( s*, t*) ( s*, tj), а ( s*, t*) – число, то
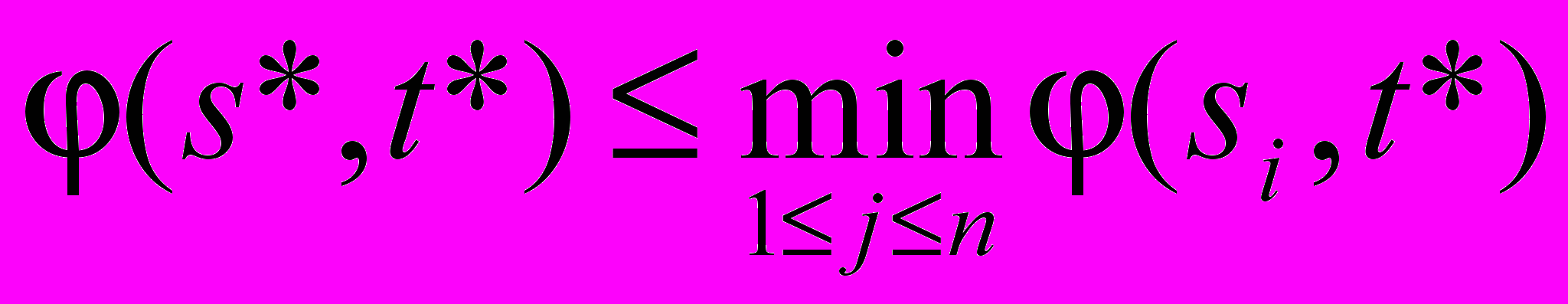 ,
,а отсюда следует, что
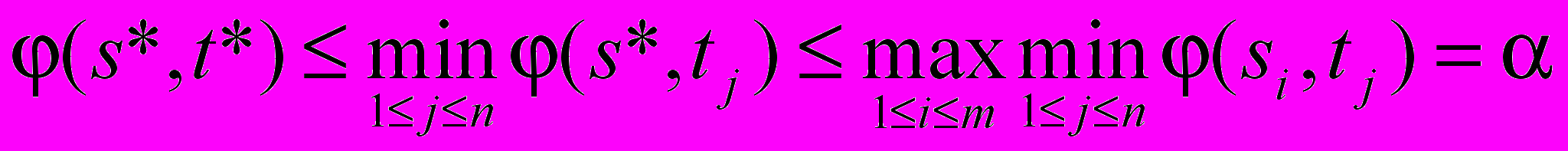 (5)
(5)- Объединяя (4) и (5), получаем ( s*, t*) .
Поскольку по теореме о минимаксе и максимине , то = .
Замечание 1.
В равенстве (3) s* и t* максиминная и минимаксная стратегии соответственно.
Достаточность.
Пусть выполнено = , т. е.
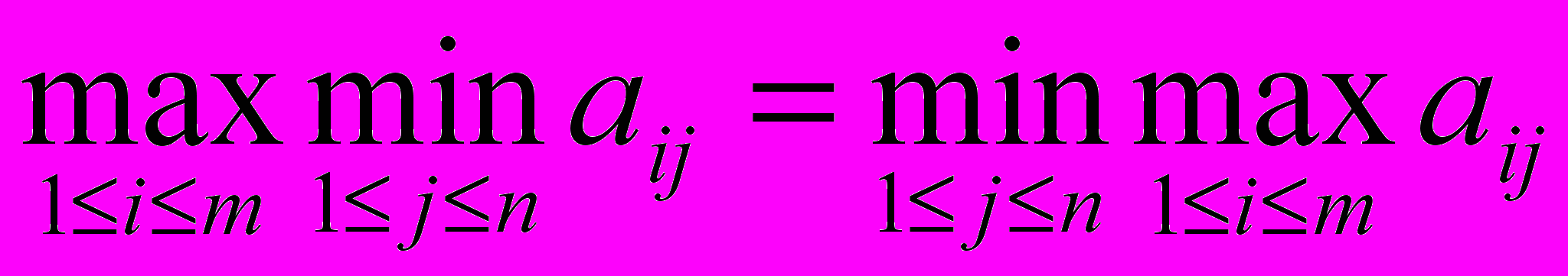 .
.Обозначим
s*S :
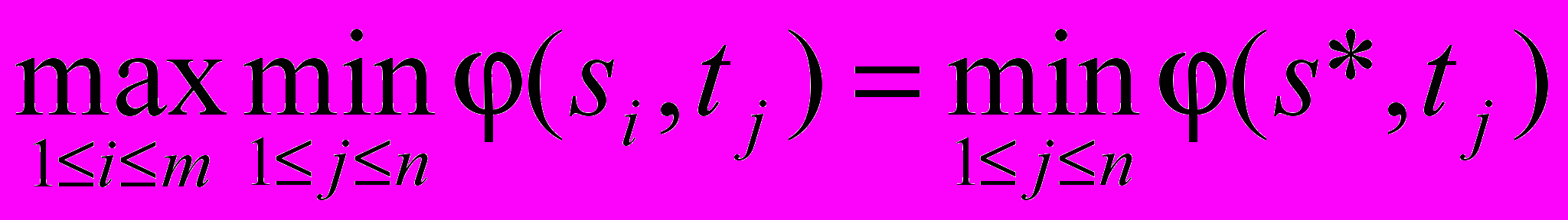 ,
,t*T :
 .
.Докажем, что (s*, t*) – седловая точка.
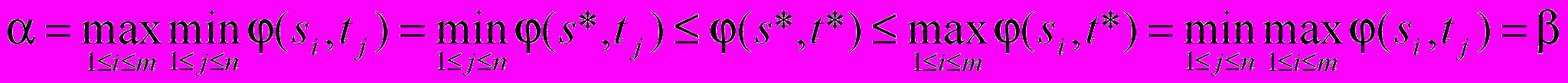
(а) (б)
Поскольку = , то в последней цепочке все неравенства выполняются в виде равенств. Следовательно, получаем:
Из (а):
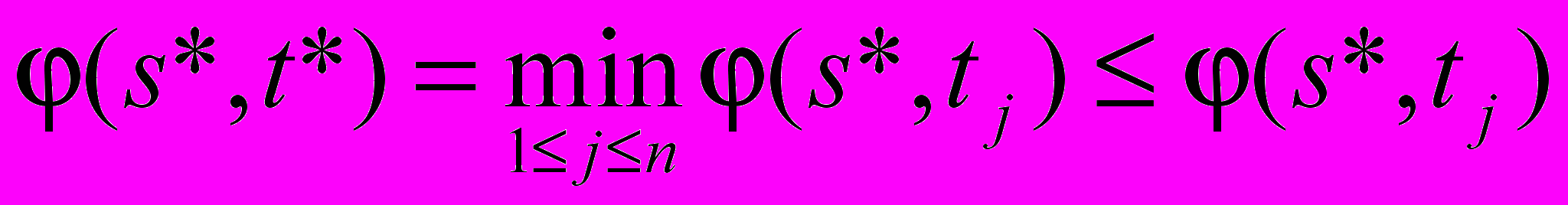 j
jИз (б):
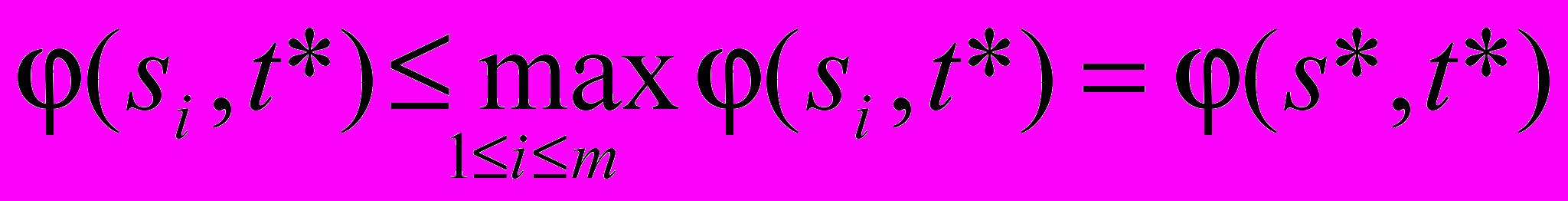 i
iПоследние два неравенства и дают (3).
Теорема доказана.
Следствие 1.
В качестве компонент седловой точки игры могут быть взяты независимо друг от друга стратегии (любые элементы множеств S и T), на которых достигается равенство = .
Доказательство – в достаточности.
Стратегию s*S назовем оптимальной стратегией игрока I, если при некотором tT точка (s*, t) является седловой. Оптимальной стратегией игрока II назовем стратегию t*T, если для некоторой sS точка (s, t*) является седловой.
Следствие 2.
Значение платежной функции игры во всех её седловых точках одинаково.
Доказательство – в необходимости.
Это свойство называется равноценностью, а число v = ( s*, t*) называется ценой игры. Смысл цены игры – это минимальный гарантированный выигрыш игрока I и максимальный неизбежный проигрыш игрока II.
Игры с седловой точкой называют вполне определенными. Совокупность оптимальных стратегий называют решением игры.
Решение игры обладает следующим свойством. Если один из игроков придерживается своей оптимальной стратегии, а другой отклоняется от своей оптимальной стратегии, то для игрока, допустившего отклонение, это никогда не может оказаться выгодным: в лучшем случае выигрыш/проигрыш остается неизменным, в худшем – выигрыш уменьшается, проигрыш – увеличивается.
Игра "Война" имеет седловую точку, то есть является вполне определенной. Остальные игры – игры без седловых точек. Решение этих игр существует, но оно указывает не оптимальную стратегию, а вероятности, с которыми следует выбирать ту или иную из возможных стратегий.
Упражнение 3
Платежная матрица игры имеет вид
 . Найдите верхнее и нижнее значение игры, максиминную и минимаксную стратегии. Является ли эта игра вполне определенной? Если да, то укажите цену игры и оптимальные стратегии игроков.
. Найдите верхнее и нижнее значение игры, максиминную и минимаксную стратегии. Является ли эта игра вполне определенной? Если да, то укажите цену игры и оптимальные стратегии игроков.Решения задач
Упражнение 1
Обозначения ходов игры:
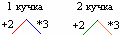 . Если после анализа окажется, что ход игроку невыгоден (поскольку следующим ходом выигрывает другой игрок), то будем изображать этот ход пунктирной линией.
. Если после анализа окажется, что ход игроку невыгоден (поскольку следующим ходом выигрывает другой игрок), то будем изображать этот ход пунктирной линией.1) Если первый игрок утроит какую-нибудь кучку, то выиграет второй:
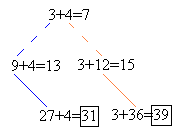
Поэтому при правильной игре такой ход первый игрок делать не будет.
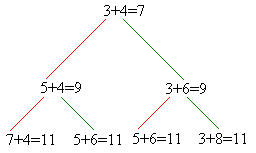
2) Значит, первым ходом первый игрок добавит два камня в какую-нибудь кучку. Если после этого второй игрок утроит количество камней в какой-нибудь кучке, то первый игрок сможет сделать следующий ход так, чтобы выиграть:
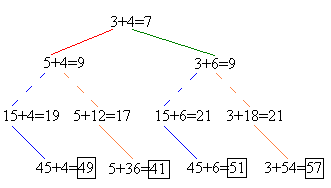
Поэтому при правильной игре такой ход второй игрок делать не будет. Значит, ход второго игрока будет заключаться в добавлении двух камней в какую-нибудь кучку:
3) Дальнейший анализ игры показывает, какие ходы являются невыгодными для второго игрока (поскольку приведут к выигрышу первого игрока).
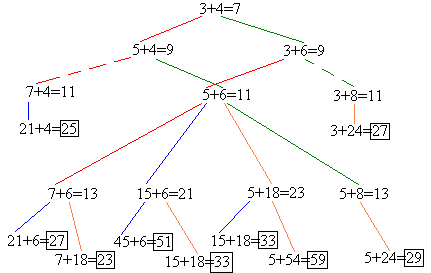
Заметим, что какой бы ход ни сделал первый игрок, выиграть на третьем ходе он не сможет (при правильной игре второго игрока). А четвертый ход второй игрок всегда может выбрать так, чтобы выиграть, причём утроение камне во второй кучке всегда ведёт к выигрышу.
Таким образом, при правильной игре всегда побеждает второй игрок. Для этого его первый ход должен быть таким:
- если первый игрок утроил количество камней в какой-нибудь кучке, то второму следует также утроить количество камней в той же кучке;
- если первый игрок добавил два камня в какую-нибудь кучку, то второму следует добавить два камня в другую кучку, а после любого хода первого игрока утроить количество камней во второй кучке;
Упражнение 2
Точка угрозы (2, 2) является точкой равновесия по Нэшу. Это единственная точка в переговорном множестве, поэтому она является решением. Оптимальные стратегии игроков: студенту – выучить предмет, а преподавателю – поставить зачет
Упражнение 3
Матрица имеет седловую точку a53 = 36. Поэтому игра является вполне определенной. Цена игры равна 36 (это же значение является верхней и нижней ценой игры). Оптимальными являются: для первого игрока максиминная стратегия (с номером 5), а для второго минимаксная (с номером 3).
Литература
- Вентцель Е. С. Элементы теории игр. – М.: Высш. шк., 1986.
- Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математиченские методы в экономике: Учебник/ Под общ. ред. д. э. н., проф. А. В. Сидоровича; МГУ им. М. В. Ломоносова. – 4-е изд., стереотип. – М.: Издательство «Дело и Сервис», 2004. – 368 с. – (Учебники МГУ им. М. В. Ломоносова).
- Берж К. Общая теория игр нескольких лиц
