Geum.ru

Курсовая работа

Вид материалаКурсовая

Содержание


9. Кооперативная игра двух лиц. Переговорное множество
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

9. Кооперативная игра двух лиц. Переговорное множество


Прежде, чем говорить о кооперативных играх, вернёмся еще раз к последнему примеру  игре “семейный спор”. Пусть первый игрок использует смешанную стратегию (p,1-p), второй  стратегию (q,1-q). Тогда средние выигрыши игроков будут равны

,

.

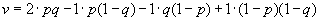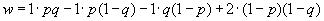Тем самым пара (p, q) превращается в пару .



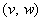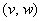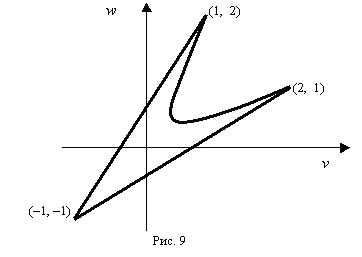
Рассмотрим плоскость . Перебирая все возможные значения пар (p, q) мы получим на плоскости 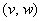некоторую область, которая изображена на рис. 9. Она ограничена прямыми, проходящими через пары точек ( 1,  1), (1, 2) и ( 1,  1), (2, 1), а также куском параболы 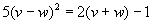. В ней есть “провал”, ограниченный именно этой параболой.

А теперь вернёмся к общему случаю игры двух лиц с платёжной матрицей



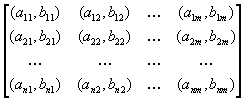
и допустим, что игроки имеют возможность договариваться о совместных действиях.

А теперь вернёмся к общему случаю игры двух лиц с платёжной матрицей



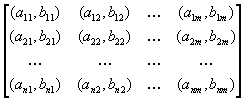
и допустим, что игроки имеют возможность договариваться о совместных действиях. В чем выразятся эти совместные действия?

Раньше ход номер i первого игрока выбирался с вероятностью 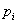и ход номер j второго игрока с вероятностью 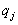и ходы обоих игроков были независимы так что комбинация (i, j) появлялась с вероятностью 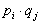. Сейчас ходы выбираются совместно и поэтому комбинация ходов 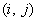появляется с некоторой совместной вероятностью . Совместная игра сводится таким образом к выбору совместной смешанной стратегии . При этом, очевидно,

.

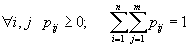При такой совместной смешанной стратегии средние выигрыши первого и второго игроков равны соответственно

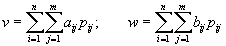. (9)

Представим себе плоскость 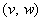.Какую область заполняют в ней значения 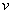и 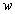, получаемые по формулам (9)?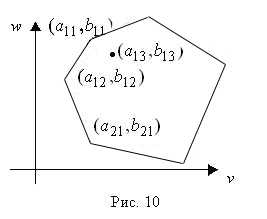



Эту область R можно построить следующим образом. Представим себе, что на плоскости 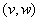мы поставили 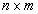точек с координатами 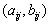. Тогда R есть так называемая выпуклая оболочка этих точек. Наглядно её можно представить так: вообразите себе, что в точках 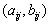вбиты гвоздики. Далее мы берём кольцо из резинки, растягиваем его, надеваем снаружи на все эти гвоздики и отпускаем резинку. Она сократится и обтянет всю эту систему гвоздей, ограничивая как раз ту область, которая и называется выпуклой оболочкой. Точки 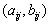окажутся при этом либо в вершинах получившегося многоугольника, либо внутри области.

Так в игре типа “семейный спор” область R есть выпуклая оболочка точек
(-1,-1), (2, 1) и (1, 2) (см. рис. 11).



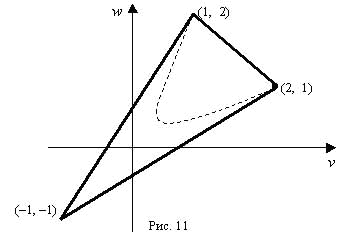
Сравните эту область с той, которая изображена на рис. 9. Мы видим, что применение совместных стратегий позволило заполнить ту “впадину”, которая была при некооперативной игре.

О чем же теперь могут договориться наши игроки? Пусть 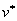и 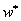есть максиминные выигрыши первого и второго игроков соответственно. Нанесём на наше множество R точку с координатами 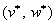. Эта точка называется точкой status quo. Очевидно, что ни один из игроков не согласится получать в результате совместной игры меньше, чем даёт ему максиминная стратегия  зачем ему такая договорённость, если он может

гарантировать себе 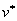или 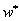без всяких договорённостей.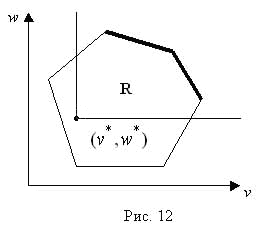



Поэтому из нашего множества R сразу исчезает область, где 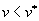или .

Рассмотрим теперь оставшуюся область, где 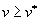и .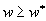

Определение 1. Точка 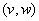называется подчинённой точке 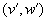если одновременно 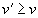и 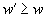, причем хотя бы одно из этих неравенств строгое.

Очевидно, что если точка 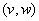подчинена точке 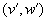, то в процессе торговли игроки безболезненно откажутся от точки 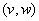в пользу точки 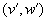, так как при таком переходе хотя бы одному становится лучше, а другому  не хуже. Очевидно также, что точки, которым подчинена точка 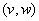, лежат правее и выше на множестве R.

Определение 2. Множество точек из R, которые не подчинены никаким другим точкам и для которых выполняется условие 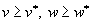, называется переговорным множеством или множеством Парето.

Легко догадаться, что переговорное множество это та часть правой верхней (или, как еще говорят, северо-восточной) границы множества R, для которой

выполнены условия .

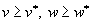Теперь очевидно, что собственно торговля и согласование стратегий игроков будут вестись на переговорном множестве. До чего они там доторгуются  сказать заранее нельзя, так как на этом множестве интересы игроков прямо противоположны. Результат зависит от умения вести переговоры и лежит за рамками математического исследования.

Итак, в определённом смысле, решить кооперативную игру двух лиц означает построить переговорное множество. Напомним основные этапы его построения.
  1. На плоскости 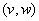нанести точки , , .
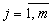  2. Построить выпуклую оболочку этих точек.
  3. Найти максиминные выигрыши обеих игроков 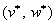и построить точку status quo.
  4. Нарисовать северо-восточную границу построенного множества, удовлетворяющую условиям

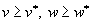
На этом работа математика заканчивается. А дальше  торгуйтесь, ребята!

Кстати, для игры типа “семейный спор” переговорное множество  это отрезок прямой, соединяющей точки (1, 2) и (2, 1). Вот на нём муж и жена и должны выяснять свои отношения.