Методы решения матричных игр. Метод линейного программирования
| Вид материала | Лекция |
- Темы курсовых работ «Методы оптимизации» Графический метод решения задачи линейного, 11.12kb.
- Методические указания Объектом исследования теории игр (ТИ) является принятие решений, 145.42kb.
- Кафедра «Прикладная математика» Экономические приложения линейного программирования, 27.15kb.
- Срс. Графический метод решения задачи линейного программирования, 22.8kb.
- Задачи математического и линейного программирования. Математическая модель задачи использования, 25.82kb.
- Optimization Toolbox – Оптимизация, 780.37kb.
- В. В. Панферов, 64.65kb.
- Задачи линейного программирования Геометрическая интерпретация задач линейного программирования, 132.4kb.
- Задачи линейного программирования Геометрическая интерпретация задач линейного программирования, 38.07kb.
- Краткий обзор моделей стохастического программирования и методов решения экономических, 59.55kb.
Лекция №8
Методы решения матричных игр.
Метод линейного программирования.
Этот метод используется в играх с произвольной матрицей игры G(m,n).
| Ai \ Bj | B1 | B2 | … | Bj | … | Bn |
| A1 | а11 | а12 | … | а1j | … | а1n |
| A2 | а21 | а22 | … | а2j | … | а2n |
| … | … | … | … | … | … | … |
| Ai | аi1 | аi2 | … | аij | … | аin |
| … | … | … | … | … | … | … |
| Am | аm1 | аm2 | … | аmj | … | аmn |
SA=(p1,p2,…, pi,…, pn) - вектор вероятностей выбора стратегий игроком А.
SB=(q1,q2,…, qj,…, qn) - вектор вероятностей выбора стратегий игроком B.
Требование, накладываемое на матрицу - i,j aij>0
Для того, чтобы произвольная матрица удовлетворяла этому требованию необходимо определить величину M>мах(|аij||aij0) и прибавить М ко всем элементам матрицы, т.е. получаем aij+M>0 (цена игры вычисляется VP=V–M).
Пусть А выбирает смешанную (оптимальную) стратегию, а В чистую:
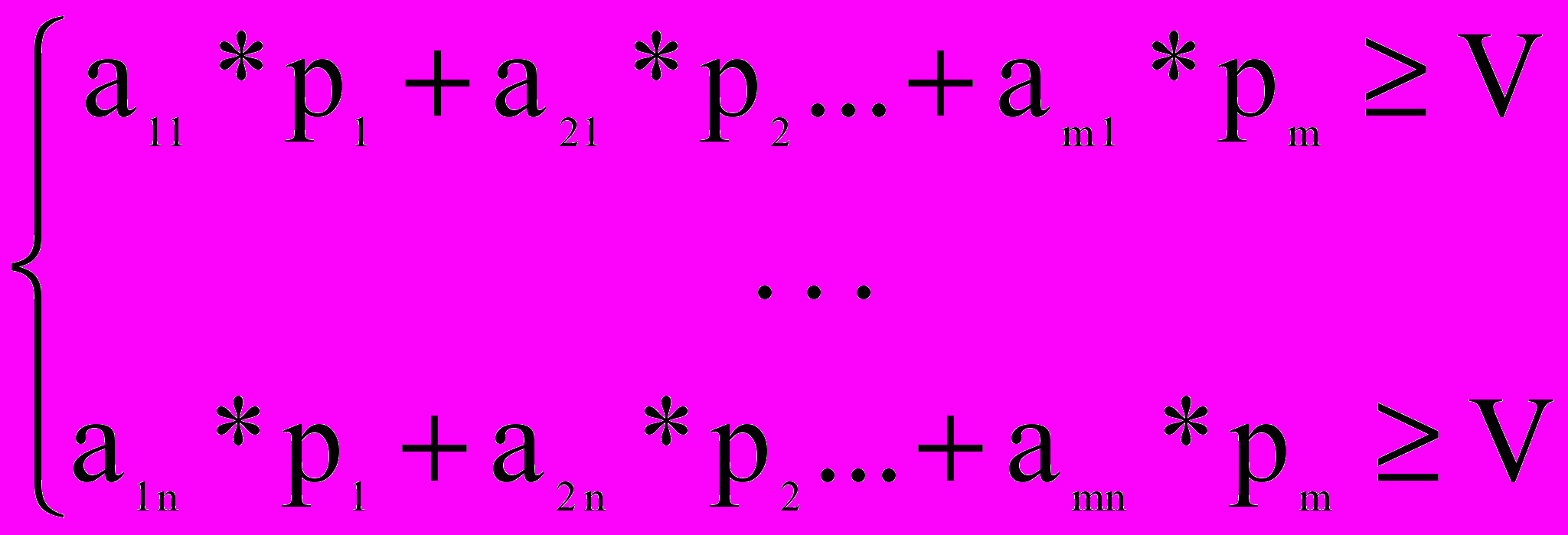
Введем величину
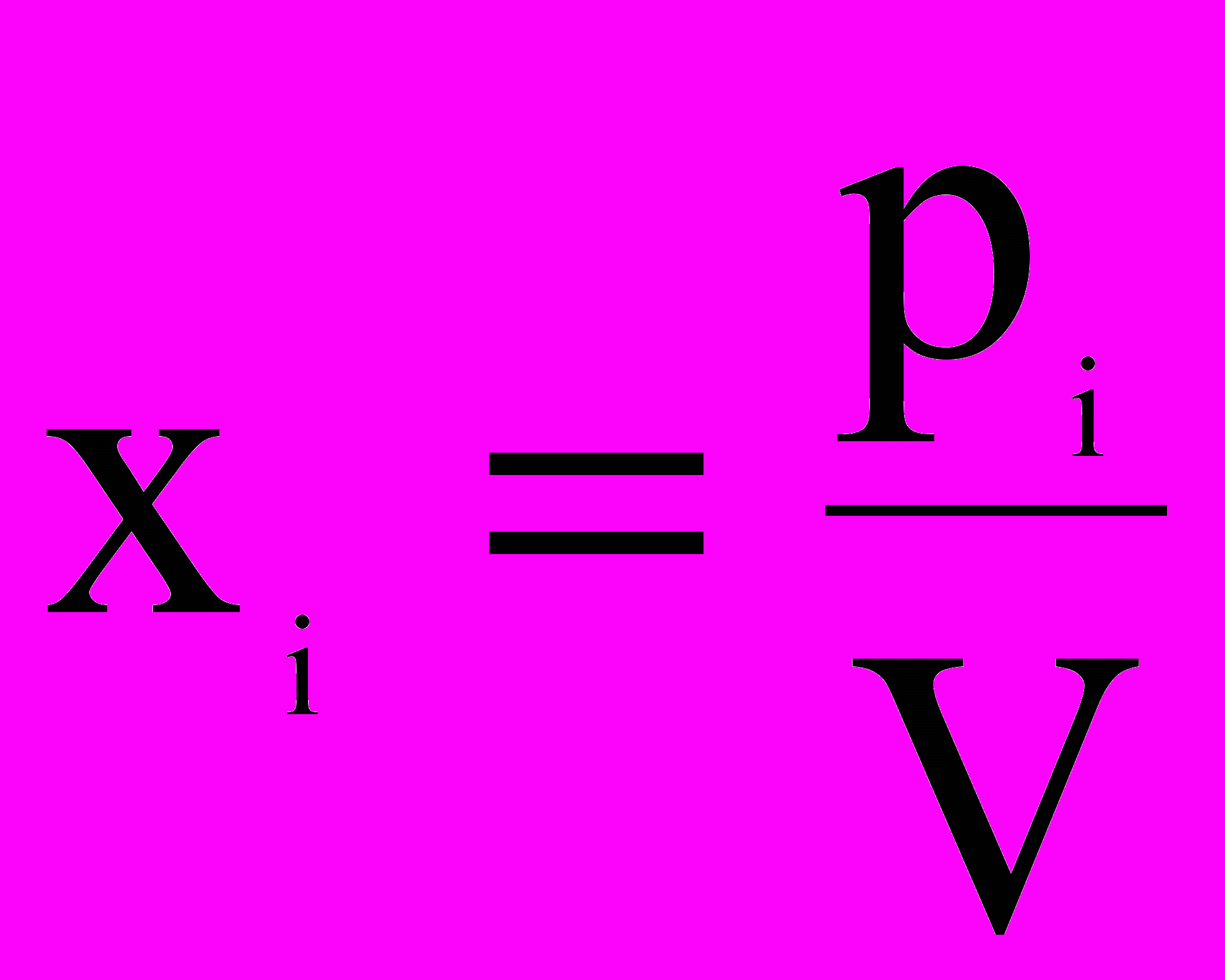 0, i=1, … , m
0, i=1, … , mТогда:
(*)
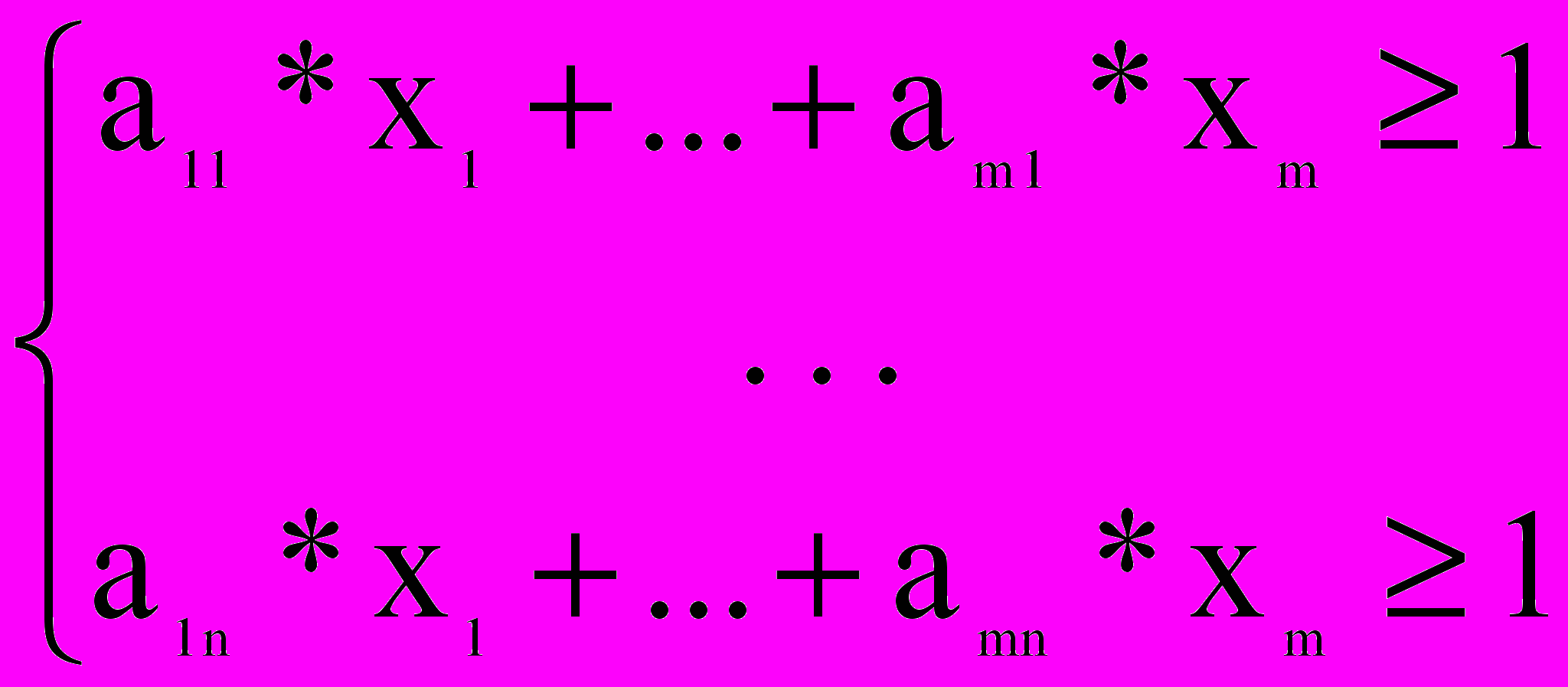 xi0 i=1,…,m
xi0 i=1,…,mт.к.
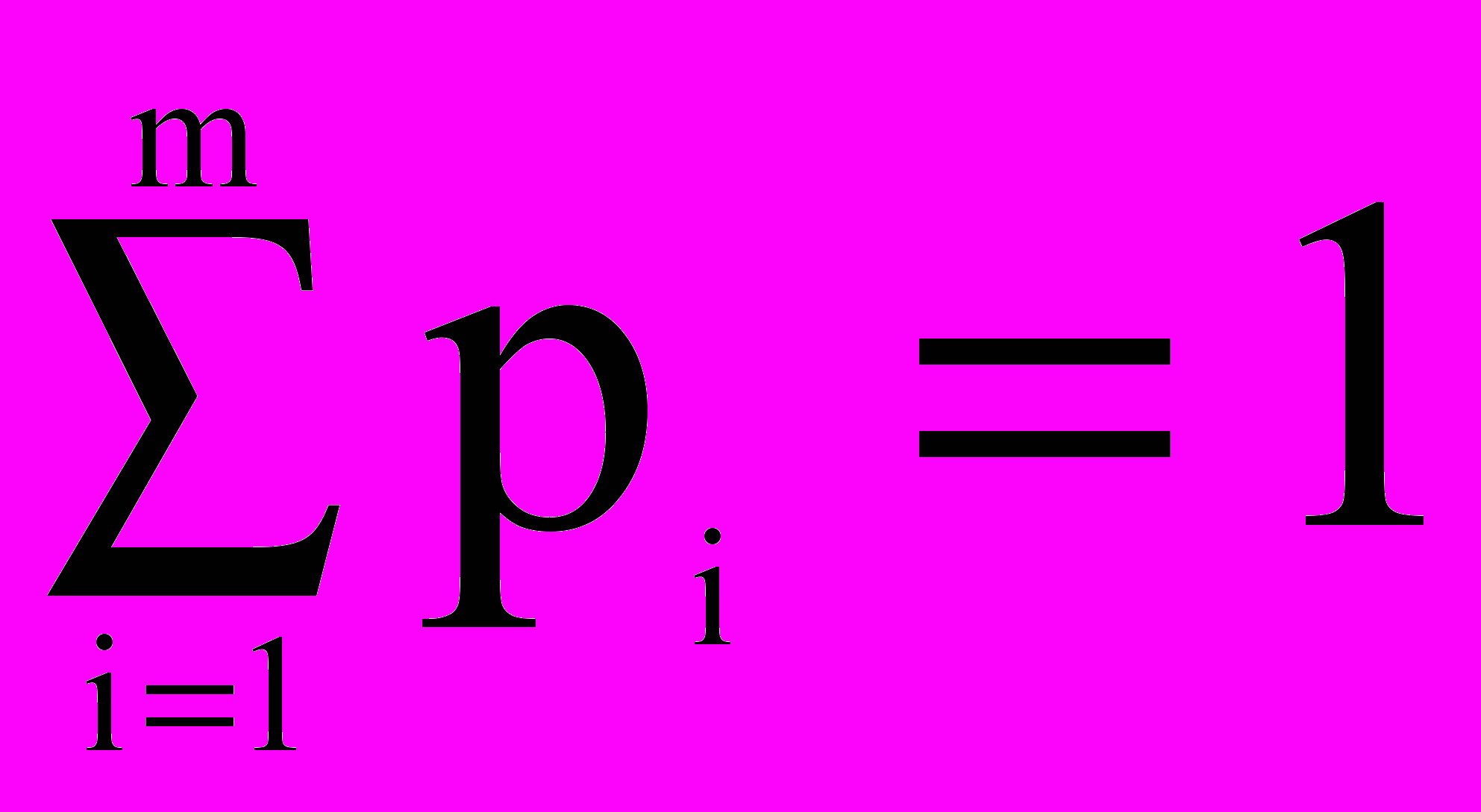
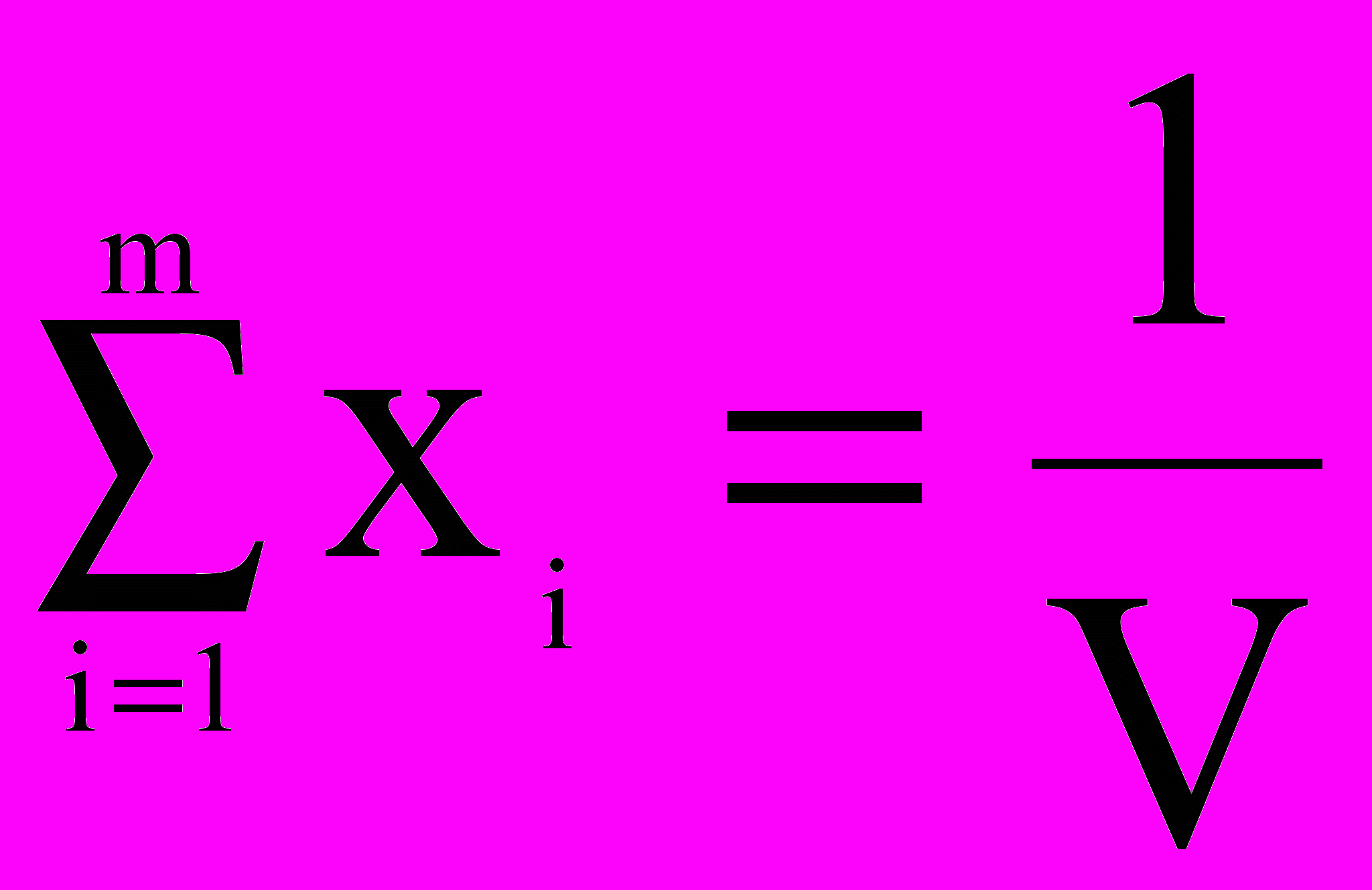
Получаем задачу линейного программирования (ЗЛП):
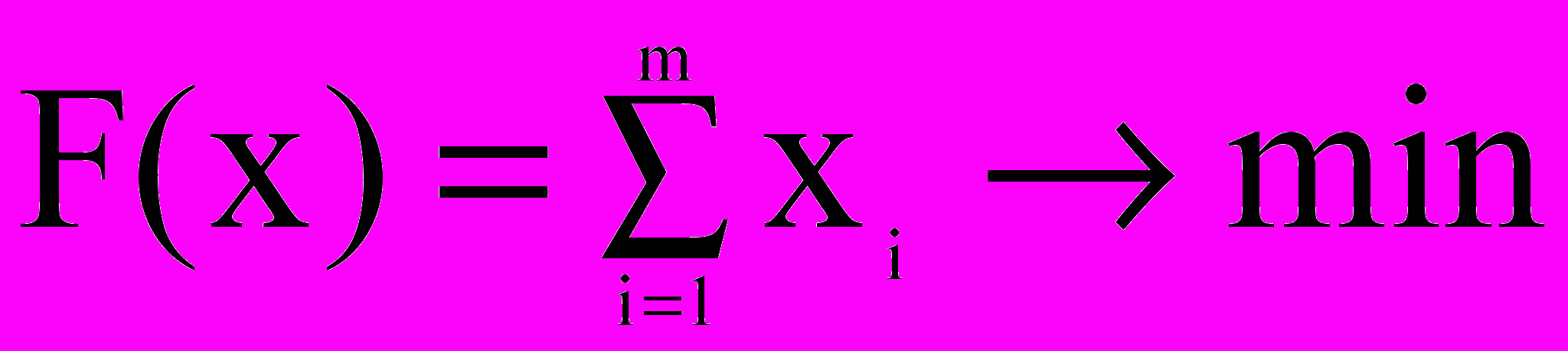
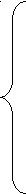
при системе ограничений (*)
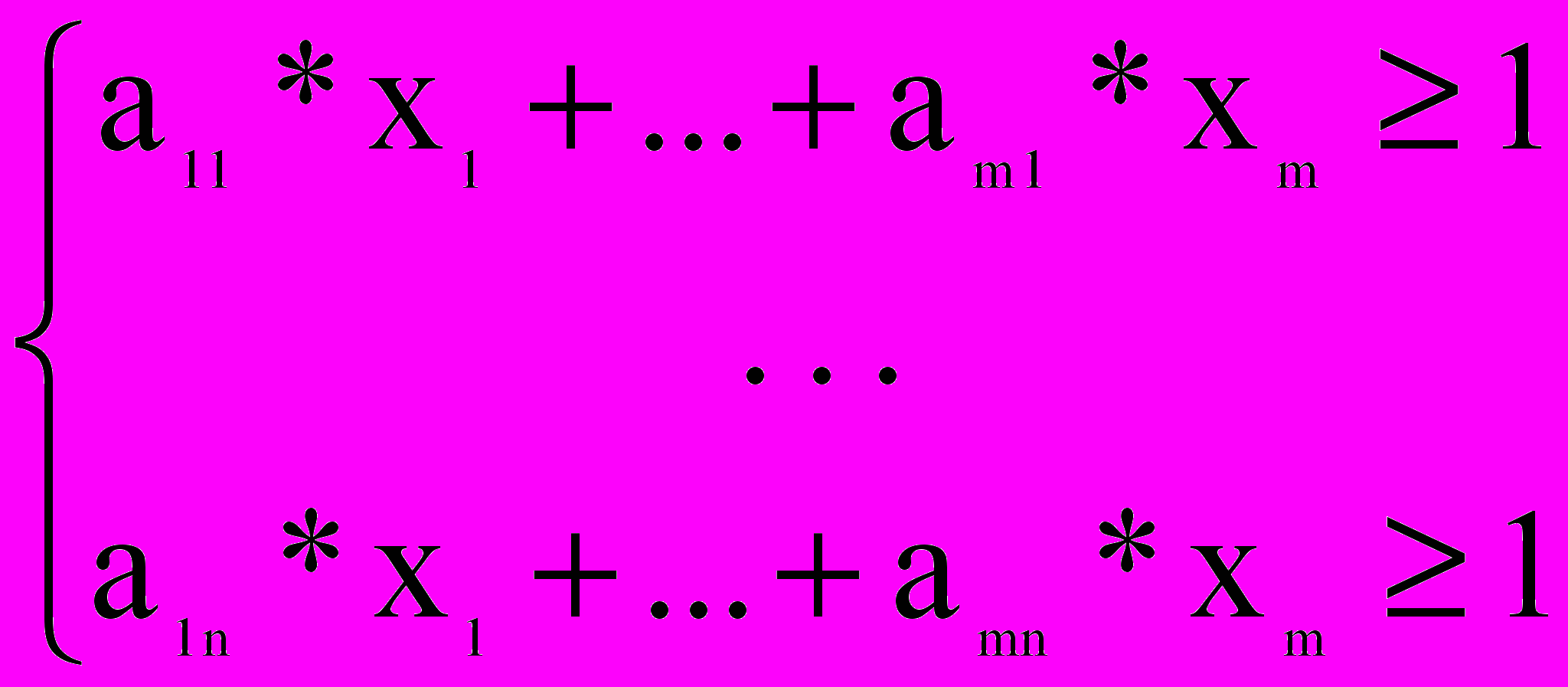
Решив ее, найдем (x1, x2,…, xm) и
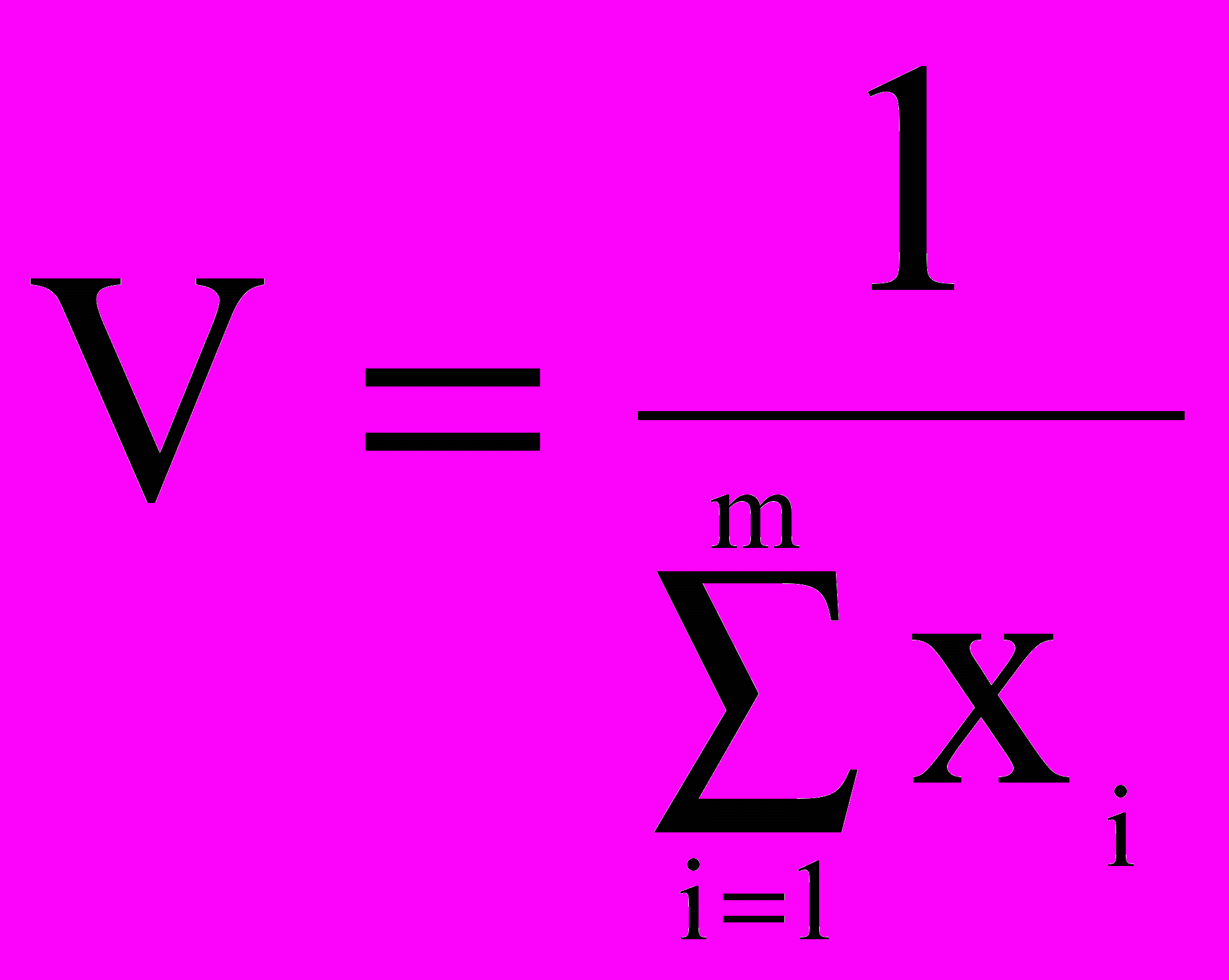
Зная V, найдем pi=xi*V.
Аналогично рассматривается решение для игрока В, только знаки неравенств меняются с на ≤ .
Введем величину
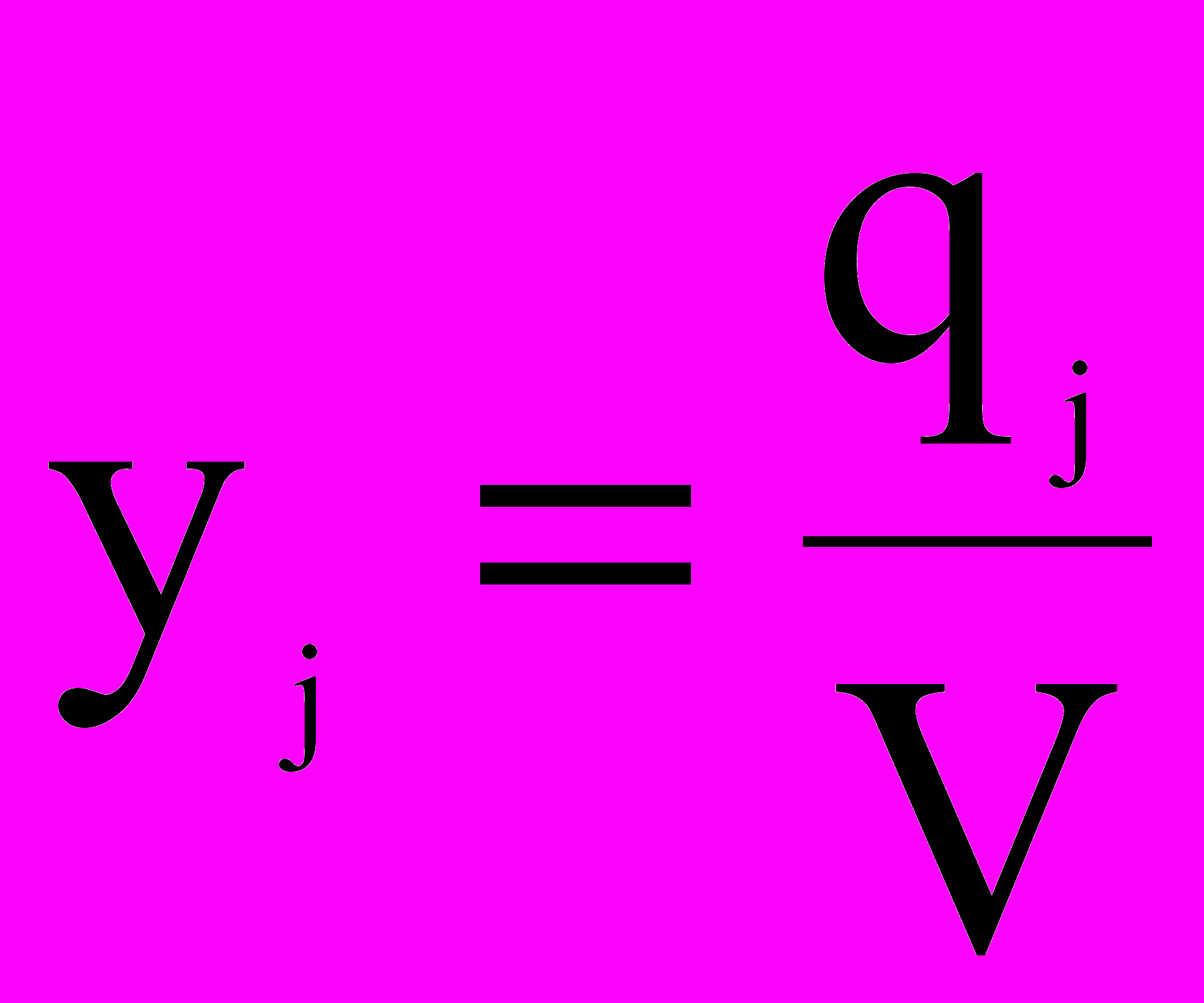 0, j=1, … , n
0, j=1, … , nПолучаем ЗЛП:
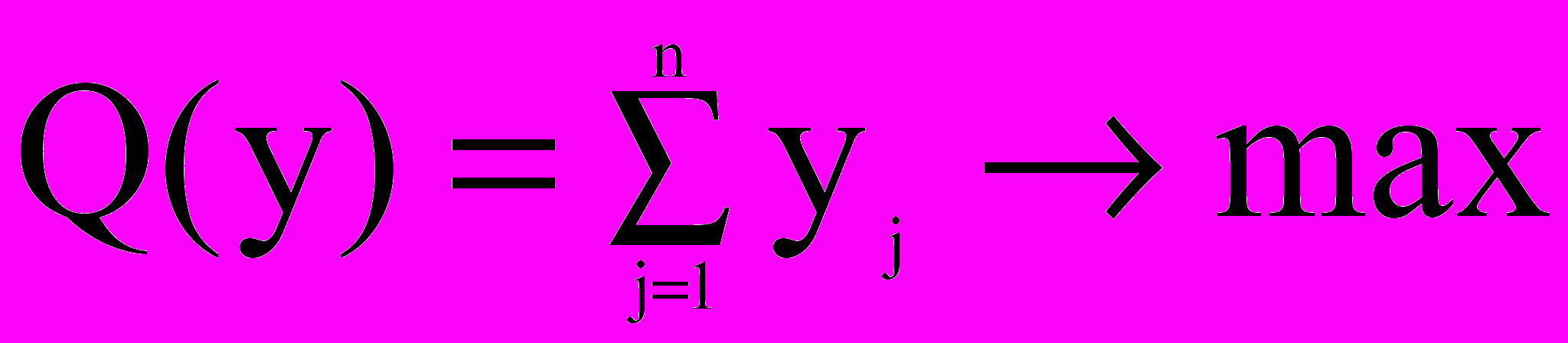
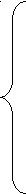
при системе ограничений (*)
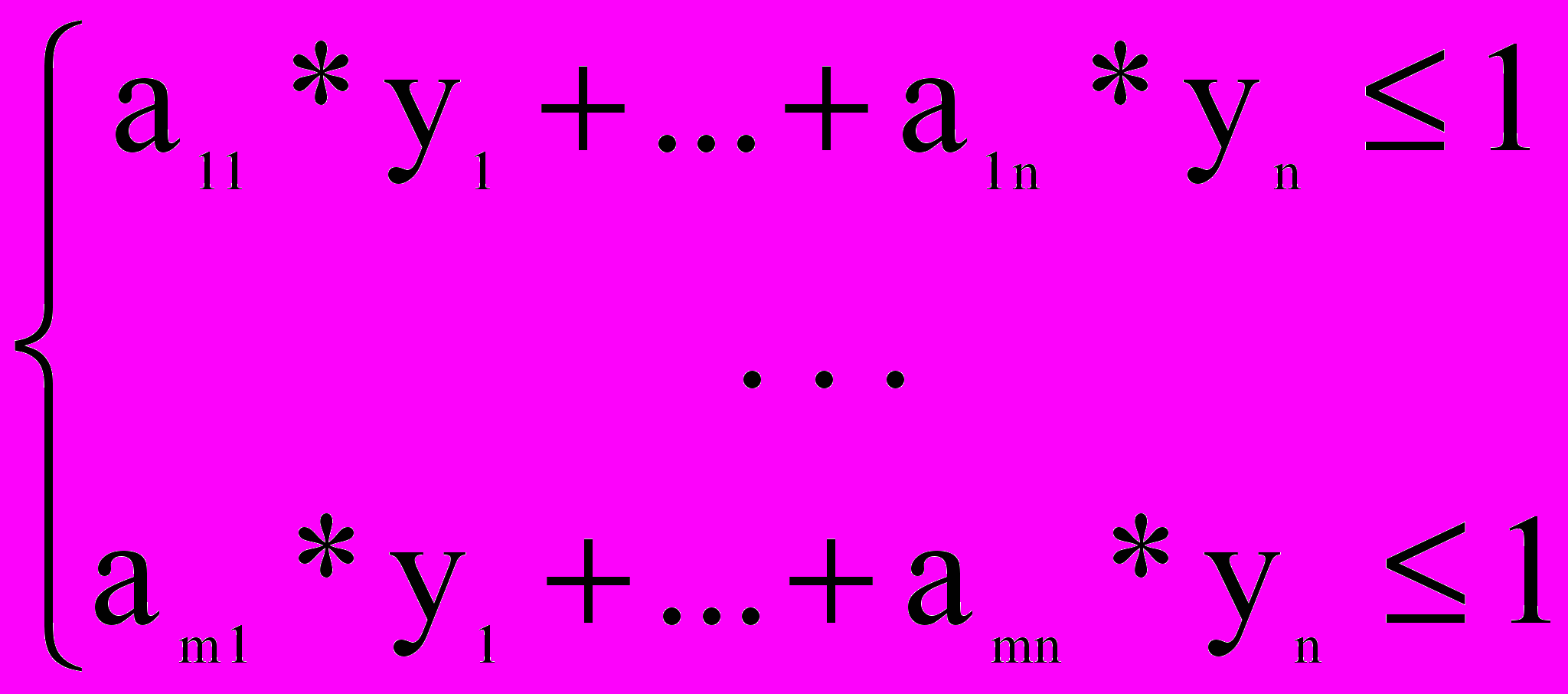
Решив ее, найдем (y1, y2,…, yn) и
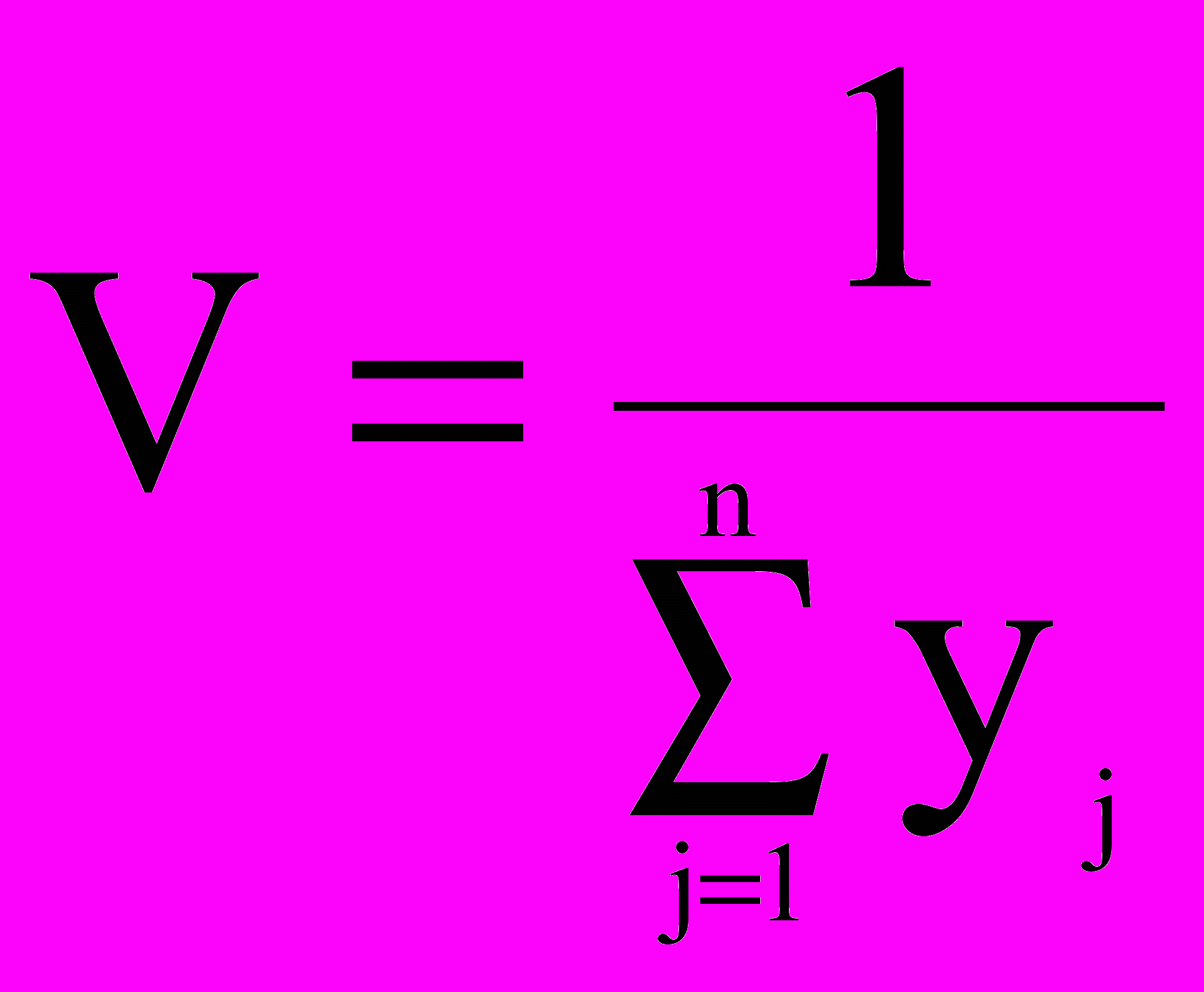
Зная V, найдем qj=yj*V.
