Будь процеси, стани або фізичні величини об'єктів матеріального світу, виражені у формі, зручній для передачі, обробки, зберігання І використання цих відомостей

Вид материала

Документы

Содержание Аналоговий сигнал Дискретний сигнал Цифровий сигнал Принцип дії

Подобный материал:

• Фізичної величини (гост 16263-70), 234.52kb.
• Теоретичні основи комп’ютеризації бухгалтерського обліку, 455.04kb.
• Ради Європейського Союзу от 24 жовтня 1995 року, Конституції України, закон, 298.89kb.
• Способи передачі даних в мережі Internet (на прикладі електронної пошти), 408.96kb.
• Комп'ютерні мережі, 1246.35kb.
• Це комплекс технічних засобів, який включає до свого складу обчислювальну техніку, 14.46kb.
• Інститут телекомунікацій, радіоелектроніки І електронної техніки, 72.54kb.
• Фестивалю-конкурсу: залучення молодих людей до соціальної активності в громадському,, 128.75kb.
• Міністерство охорони здоров'я україни, 249.63kb.
• Вплив магнітних ПоЛів на живі організми”, 40.38kb.

Модульне оцінювання

з дисципліни «Цифрова обробка сигналів та зображень»


Модуль 1

1. Сигнал, класифікація сигналів.
   

Сигнал - це певні відомості, повідомлення, інформація про які-небудь процеси, стани або фізичні величини об'єктів матеріального світу, виражені у формі, зручній для передачі, обробки, зберігання і використання цих відомостей.

З математичної точки зору сигнал являє собою функцію, тобто залежність однієї величини від іншої, незалежної змінної.

Найбільш поширене представлення сигналів - в електричній формі у вигляді залежності напруги від часу U (t).

Позначення сигналу – S(t).

Математична модель сигналу може бути представлена: S=F(t,z,w A,B,C)





Для періодичних сигналів виконується:

s(t) = s(t + kT), где k = 1, 2, 3, ... - любе ціле число(з множини цілих чисел I від -∞ до ∞)

Гармонічні сигнали (синусоїдальні), описуються наступними формулами:

s(t) = Asin (2f_оt+) = Asin (_оt+),

s(t) = Acos(_оt+), де А - амплитуда сигнала, f_о - циклічна частота в герцах, _о= 2f_о - кутова частота в радіанах,  и - початкові фазові кути в радіанах.

Полігармончі сигнали складають найбільш широко поширену групу періодичних сигналів і описуються сумою гармонічних коливань:

s(t) =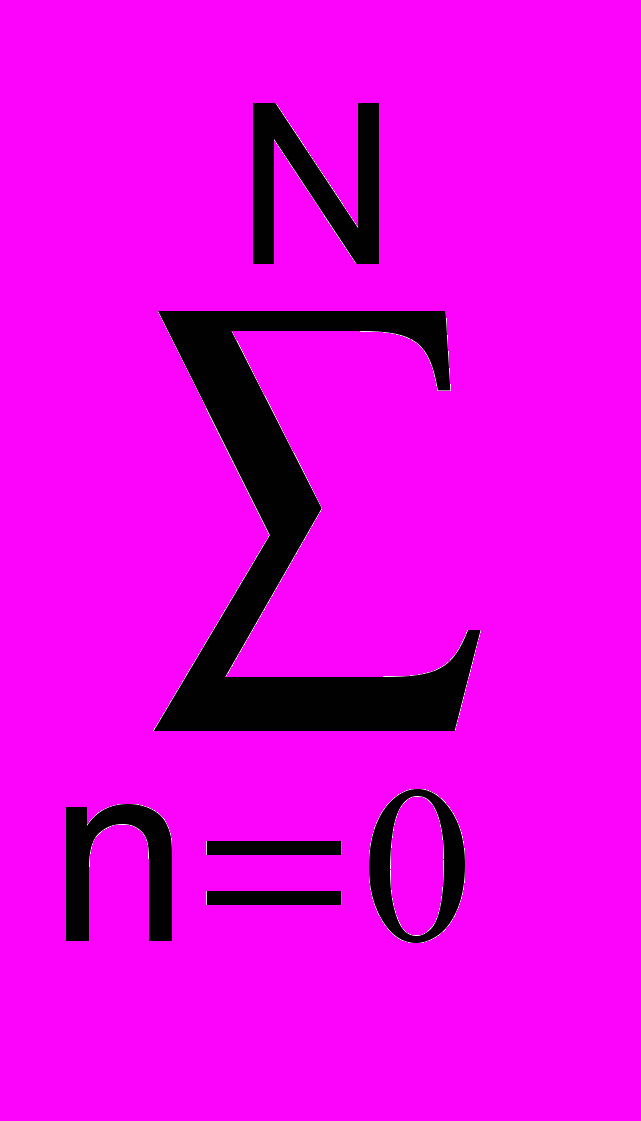A_n sin (2f_nt+_n),

або безпосередньо формулою: s(t) = y(t  kT_p), k = 1,2,3,...,

Математичний опис сигналу задається формулою:

s(t) =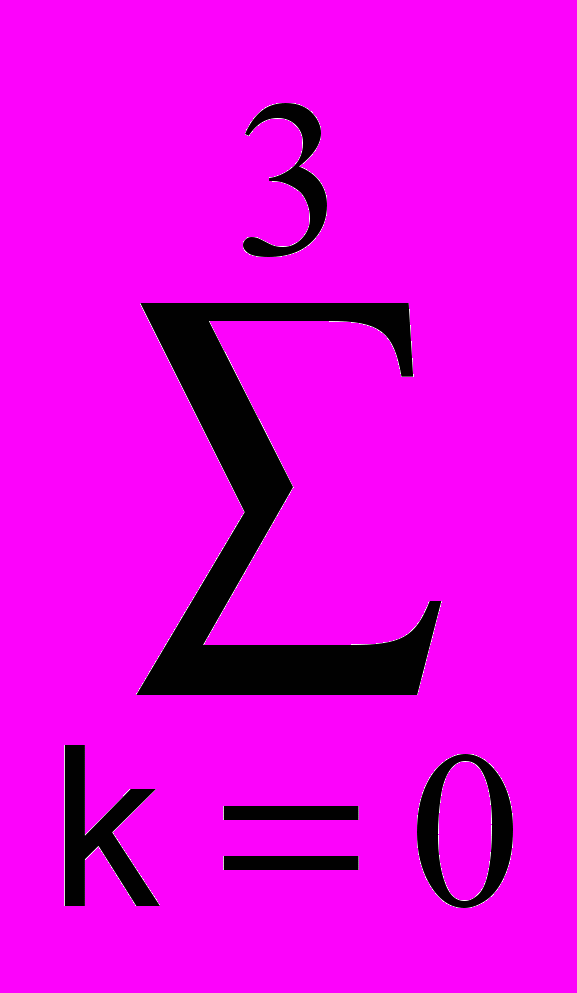A_kcos(2f_kt+_k),

Майже періодичні сигнали близькі за своєю формою до полігармонічних. Вони також являють собою суму двох і більше гармонічних сигналів, але не з кратними, а з довільними частотами.

Аперіодичні сигнали складають основну групу неперіодичних сигналів:

s(t) = exp(-at) - exp(-bt), де a і b – константи

Імпульсні сигнали: s(t) = u(t) cos(2f_ot+_o)

2. Типи сигналів.
   

Виділяють наступні|таких| типи|типи| сигналів, яким відповідають певні форми їх математичного опису.

А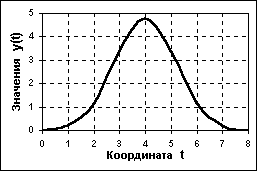налоговий сигнал (analog signal) є безперервною функцією безперервного аргументу, тобто визначений для будь-якого значення аргументів. Джерелами аналогових сигналів, як правило, є фізичні процеси і явища, безперервні в динаміці свого розвитку в часі, в просторі або по будь-якій іншій незалежній змінній, при цьому реєстрований сигнал подібний (“аналогічний”) до процесу, що породжує його. Приклад математичного запису сигналу: біля(t)= 4.8 exp[-(t-4) 2/2.8]. Приклади сигналів, аналогових за своєю природою, - зміна напруженості електричного, магнітного, електромагнітного поля в часі і в просторі.

Д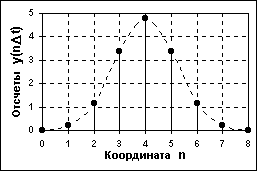искретний сигнал (discrete signal) по своїх значеннях також є безперервною функцією, але визначеною тільки по дискретних значеннях аргументу. По безлічі своїх значень він є кінцевим і описується дискретною послідовністю відліків біля(nDt), де y1  біля  y2, Dt - інтервал між відліками (інтервал або крок дискретизації), n = 0, 1, 2...,N. Величина, зворотна кроку дискретизації: f = 1/Dt, називається частотою дискретизації (sampling frequency). Якщо дискретний сигнал отриманий дискретизацією аналогового сигналу, то він є послідовністю відліків, значення яких в точності дорівнюють значенням початкового сигналу по координатах nDt. Приклади дискретних геофізичних сигналів - результати вертикального електричного зондування (дискретна величина рознесення струмових електродів), профілі геохімічного випробування, і тому подібне

Ц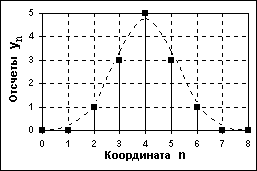ифровий сигнал (digital signal) квантований по своїх значеннях і дискретний по аргументу. Він описується квантованою гратчастою функцією yn = Qk[біля(nDt)], де Qk - функція квантування з числом рівнів квантування до, при цьому інтервали квантування можуть бути як з рівномірним розподілом, так і з нерівномірним, наприклад - логарифмічним. Задається цифровий сигнал, як правило, у вигляді дискретної лави числових даних - числового масиву по послідовних значеннях аргументу при Dt = const, але в спільному випадку сигнал може задаватися і у вигляді таблиці для довільних значень аргументу.

По суті, цифровий сигнал по своїх значеннях (відлікам) є|з'являється| формалізованим різновидом дискретного сигналу при округленні відліків останнього до певної кількості цифр. Цифровий сигнал кінцевий|скінченний| по безлічі своїх значень. Процес перетворення безкінечних|нескінченних| по значеннях аналогових відліків в кінцеве|скінченне| число цифрових значень називається квантуванням по рівню, а округлення відліків (відкидані значення), що виникають при квантуванні помилки, – шумами або помилками квантування |.




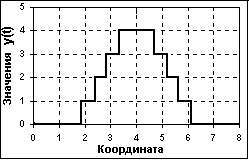
В принципі, квантованими по своїх значеннях можуть бути і аналогові сигнали, зареєстровані відповідною апаратурою які прийнято називати дискретно-аналоговими.

3. Система, лінійна система, властивості.
   

Перетворення і обробка сигналів здійснюється в системах. Поняття сигналу та системи нероздільні, тому що будь-який сигнал існує в межах якої-небудь системи. Система обробки сигналів може бути реалізована як у матеріальній формі (спеціальний пристрій, вимірювальний прилад, сукупність фізичних об'єктів з певною структурою взаємодії і т.п.), так і програмно на ЕОМ або будь-якому іншому спеціалізованому обчислювальному пристрої. Форма реалізації системи істотного значення не має, і визначає лише її можливості при аналізі і обробці сигналів.




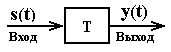
Графічне представлення

системи
Безвідносно до призначення система завжди має вхід, на який подається зовнішній вхідний сигнал, в загальному випадку багатомірний, і вихід, з якого знімається оброблений вихідний сигнал. Власне система являє собою системний оператор (алгоритм) перетворення вхідного сигналу s (t) - дії чи збудження, в сигнал на виході системи y (t) - відгук або вихідну реакцію системи. Символічне позначення операції перетворення (трансформації сигналу): y (t) = T [s (t)].

Системи поділяються на сиацірнарні і нестаціонарні.

Лінійні та нелінійні системи складають два основні класи систем обробки сигналів.

Термін лінійності означає, що система перетворення сигналів повинна мати довільний, але в обов'язковому порядку лінійний зв'язок між вхідним сигналом та вихідним сигналом з певним зміною спектрального складу вхідного . У нелінійних системах зв'язок між вхідним і вихідним сигналом визначається довільним нелінійним законом з доповненням частотного складу вхідного сигналу частотними складовими, відсутніми у вхідному сигналі.

Система вважається лінійною, якщо її реакція на вхідні сигнали адитивна (виконується принцип суперпозиції сигналів) і однорідна (виконується принцип пропорційнї подібності). Іншими словами, відгук лінійної системи на зважену суму вхідних сигналів повинен бути рівний зважені сумі відгуків на окремі вхідні сигнали незалежно від їх кількості і для будь-яких вагових коефіцієнтів, в тому числі комплексних.

До базових лінійних операцій, з яких можуть бути сформовані будь-які лінійні оператори перетворення, належать операції скалярного множення, зсуву та додавання сигналів:

y(t) = c  s(t), y(t) = s(t-t), y(t) = a(t)+b(t).

Система називається інваріантної до зсуву, якщо зсув вхідного сигналу по аргументах (часу, координатами простору і т.п.) викликає відповідний зсув вихідного сигналу:

y(x,t) = T[s(x,t)], T[s(x-x,t-t)] = y(x-x,t-t).


Лінійність і інваріантність до зсуву є незалежними властивостями систем і не визначають один одного.

4. Перешкоди, класифікація перешкод.
   

При детектуванні сигналів в сумі з основним інформаційним сигналом одночасно реєструються і сигнали, що заважають, - шуми і перешкоди самої різної природи. До перешкод відносять також спотворення інформаційних сигналів при впливі різних дестабілізуючих чинників на процеси вимірів, як, наприклад, вплив мікрокаверн в стінках свердловини на виміри в рентгенорадиометрических методах каротажу, грозових розрядів на електророзвідувальні методи вимірів і тому подібне.

Якщо перешкоди відомі і регулярні, як наприклад, фон змінного струму|току|, то боротьба з|із| ними особливої скрути|утруднення| не представляє|уявляє|. Найбільші труднощі представляє|уявляє| боротьба з|із| випадковими (непередбачуваними) перешкодами. У спільній|загальній| формі вплив перешкод на реєстрований сигнал записується|занотовує| в наступному|слідуючому| вигляді|виді|:

у|в|(t)= V(s(t), q(t)) (2.5.1)

де s(t) – інформаційна (корисна) частка|частина| сигналу, q(t) – перешкода.

Перешкода називається аддитивною, і зазвичай іменується шумом, якщо вираження (2.5.1) є простою сумою сигналу і перешкоди:

у|в|(t)= s(t)+ q(t). (2.5.2)

Якщо випадковий процес v(t), що робить вплив на сигнал, є|з'являється| ненегативним|заперечним|, а його вплив виражається|виказує| у формі:

у|в|(t)= v(t)·s(t), (2.5.3)

то перешкоду v(t) називають мультиплікативною.

У спільному|загальному| випадку в сигналі можуть бути присутніми обидва види перешкод:

у|в|(t)= v(t) s(t)+ q(t).

Як правило, випадкові шумові перешкоди (аддитивні) породжуються різного роду фізичними флюктуаціями – випадковими відхиленнями тих або інших фізичних величин від своїх середніх значень.

Природа мультиплікативних перешкод зазвичай|звично| пов'язана із змінами умов вимірів|вимірювань|, параметрів каналів передачі даних і систем їх обробки, тобто коли випадкові перешкоди накладаються не на сам сигнал безпосередньо, а на системи, в яких цей сигнал формується і звертається|обертається|, викликаючи|спричиняти| опосередковані спотворення сигналу, як лінійні, так і нелінійні.

Шуми поділяються на:

• Флюктуаційні
  
• Імпульсні
  
• Періодичні
  

5. Дискретизація (явище, властивості, інструменти дискретизації)
   

Операція дискретизації (discretization) здійснює перетворення аналогових сигналів (функцій), безперервних по аргументу, у функції миттєвих значень сигналів по дискретному аргументу. Дискретизація зазвичай проводиться з постійним кроком по аргументу (рівномірна дискретизація), при цьому s(t) Ю s(nDt), де значеннями s(nDt) є відліки функції s(t) в моменти часу t = nDt, n = 0, 1, 2..., N. Частота, з якою виконуються виміри аналогового сигналу, називається частотою дискретизації. У спільному випадку, сітка відліків по аргументу може бути довільною, як, наприклад, s(t) = s(tk), k=1, 2 ., K, або задаватися по певному закону. В результаті дискретизації безперервний (аналоговий) сигнал переводиться в послідовність чисел.

Сутність дискретизації аналогових сигналів полягає в тому, що безперервність у часі аналогової функції s (t) замінюється послідовністю коротких імпульсів, амплітудні значення яких cn визначаються за допомогою вагових функцій, або безпосередньо вибірками (відлік) миттєвих значень сигналу s (t) в моменти часу t_n. Представлення сигналу s (t) на інтервалі Т сукупністю дискретних зна-чений cn записується у вигляді:

(с1, с2, ..., cN) = А [s (t)],

де А - оператор дискретизації. Запис операції відновлення сигналу s (t):
s(t) = У [(с1, с2, ..., cN)].

Вибір операторів А і В визначається необхідної точністю відновлення сигналу. Найбільш простими є лінійні оператори. У загальному випадку:
с_n =q_n(t) s(t) dt,

де q_n(t) - система вагових функцій.

Властивості – крок дискретизації Δt, частота дискретезації f.

6. Відновлення сигналу. Теорема Котельникова-Шенона.
   

Операція відновлення аналогового сигналу з його дискретного уявлення зворотна операції дискретизації і представляє, по суті, інтерполяцію даних.

Дискретизація сигналів може приводити|наводити| до певної втрати інформації про поведінку сигналів в проміжках між відліками. Проте|однак| існують умови, визначені теоремою Котельникова-шеннона, згідно|згідно з| яким аналоговий сигнал з|із| обмеженим частотним спектром може бути без втрат інформації перетворений в дискретний сигнал, і потім|і тоді| абсолютно точно відновлений по значеннях своїх дискретних відліків.

Теоремою Котельникова-шеннона встановлюється, що якщо спектр сигналу обмежений частотою F, то після|потім| дискретизації сигналу з|із| частотою не менше 2F| можна відновити початковий|вихідний| безперервний сигнал по отриманому|одержувати| цифровому сигналу абсолютно точно. Для цього потрібно виконати інтерполяцію цифрового сигналу "між відліками" спеціальною функцією (Котельникова-шеннона).

На практиці ця теорема має величезне значення. Наприклад, відомо, що діапазон звукових сигналів, що сприймаються людиною, не перевищує 20 кГц|. Отже, при дискретизації записаних звукових сигналів з|із| частотою не менше 40 кГц| ми можемо точно відновити початковий|вихідний| аналоговий сигнал по його цифрових відліках, що і виконується в програвачах компакт-дисків для відновлення звуку. Частота дискретизації звукового сигналу при записі на компакт-диск складає 44100 Гц.

7. Інтерполяція, інтерполяційний ряд Котельникова.
   

Проведемо зворотне перетворення обох частин рівності :

FS(f) = F[S(f) _* Ш_F(f)]П_F(f)

Множення безперервного і нескінченного спектра на П-імпульс у межах головного діапазону відобразиться у динамічній області згортків двох функцій:

Fs(t) = Fs_(t) _* sinc(Ft).

s(t) = sinc(Ft) _*s(kt)(t-kt),

Звідси, з урахуванням рівності (t-kt) _* sinc(Ft) = sinc[F(t-kt)], отримуєм:

   s(t) =s(kt) sinc[F(t-kt)]

Ця формула має назву інтерполяційного ряду Котельникова-Шеннона і, по суті, є розкладанням сигналу по системі ортогональних функцій sinc(F(t-kt)) = sinc((t/t – k)).

Із сукупності вище наведених формул випливає, що якщо для частоти дискретизації сигналу справедливо нерівність F ³ 2fmax, де fmax - найбільша частота в спектрі довільній неперервної функції s (t), то функція s (t) може представлятися у вигляді числової послідовності дискретних значень s ( kDt), k = 0,1,2 ,..., і однозначно з цієї послідовності відновлюватися без втрати точності. У цьому й полягає суть теореми відліків Котельникова-Шеннона.

8. Спектральний аналіз (гребенева функція, спектри)
   

Спектральний аналіз — сукупність методів визначення складу (наприклад, хімічного) об'єкта, заснований на вивченні спектрів взаємодії матерії з випромінюванням: спектри електромагнітного випромінювання, радіації, акустичних хвиль, розподілу за масою та енергією елементарних частинок та інше. Спектральний аналіз, грунтується на явищі дисперсії світла. Традиційно розмежовують:

• атомарний та молекулярний спектральний аналіз,
  
• «емісійний» — за спектром випромінення та «абсорбційний» — за спектром поглинання,
  
• «мас-спектрометричний» — за спектром мас атомарних чи молекулярних іонів.
  

Принцип дії:Атоми кожного хімічного елемента мають певні резонансні частоти, внаслідок чого саме на цих частотах вони випромінюють або поглинають світло. Це призводить до того, що в спектроскопі на спектрах видимі лінії (темні або світлі) в певних місцях, характерних для кожної речовини. Інтенсивність ліній залежить від кількості речовини і її стану. У кількісному спектральному аналізі визначають зміст досліджуваної речовини по відносній або абсолютній інтенсивності ліній або смуг у спектрах.

Існують такі види спектрів земних джерел і небесних тіл:

* Суцільний, або неперервний спектр у вигляді райдужної смужки дають непрозорі розжарені тіла (вугілля, нитка електро­лампи) і досить протяжні густі маси газів.

* Лінійчастий спектр випромінювання дають розріджені гази й пара при сильному нагріванні. Кожний газ випромінює світло строго визначених довжин хвиль і дає характерний для даного хімічного елемента лінійчастий спектр.

* Лінійчастий спектр поглинання дають гази й пара, якщо за ними міститься яскраве джерело, що дає неперервний спектр — це неперервний спектр, перерізаний темни­ми лініями саме в тих місцях, де мають бути яскраві лінії, властиві даному газові.

9. Перетворення Фур’є
   

Перетворення Фур'є — інтегральне перетворення однієї комплекснозначної функції дійсної змінної на іншу. Це перетворення розкладає дану функцію на осциляторні функції. Використовується для того, щоби розрахувати спектр частот для сигналів змінних у часі (таких як мова або електрична напруга).

Перетворення Фур'є функції f(t )математично визначається як комплексна функція F(ω), яка задається інтегралом

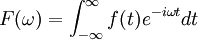
Обернене перетворення Фур'є задається виразом

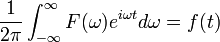
Властивості:

Якщо задані інтегровні функції f(x), g(x) та h(x) та іхні відповідні перетворення Фур'є 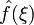, 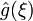та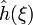, тоді самому перетворенню властиво наступне:

• Лінійність
  

Для довільних комплексних чисел a та b, якщо h(x) = aƒ(x) + bg(x), тоді  

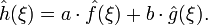
• Трансляція
  

Для довільного дійсного числа x₀, якщо h(x) = ƒ(x − x₀), тоді 

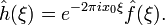
• Модуляція
  

Для довільного дійсного числа ξ₀, якщо h(x) = e^2πixξ₀ƒ(x), тоді  .

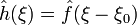• Маштабування
  

Для не рівного нулю дійсного числа a, якщо h(x) = ƒ(ax), тоді  .    

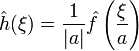• Спряження
  

Якщо 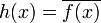, тоді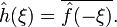 

• Згортка
  

Якщо 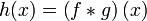, тоді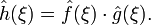 


Перетворення Фур'є застосовуються для отримання частотного спектру неперіодичної функції, наприклад, електричного сигналу, тобто для представлення сигналу у вигляді суми гармонічних коливань. При цьому використовується властивість згортки.

10. Дискретне перетворення Фур’є (ДПФ), властивості ДПФ.
    

Дискретне перетворення Фур'є (в англомовній літературі DFT, Discrete Fourier Transform) - це одне з перетворень Фур'є, широко застосовуються в алгоритмах цифрової обробки сигналів (його модифікації застосовуються в стисненні звуку в MP3, стиску зображень в JPEG і ін), а також в інших областях, пов'язаних з аналізом частот в дискретному (приміром, оцифрованому аналоговому) сигналі. Дискретне перетворення Фур'є вимагає як входу дискретну функцію. Такі функції часто створюються шляхом дискретизації (вибірки значень з неперервних функцій). Дискретні перетворення Фур'є допомагають вирішувати приватні диференціальні рівняння і виконувати такі операції, як згортки. Дискретні перетворення Фур'є також активно використовуються в статистиці, при аналізі часових рядів. Перетворення бувають одномірні, двовимірні і навіть тривимірні.

Пряме перетворення:



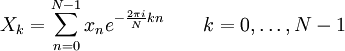
Обернене перетворення:



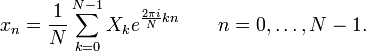
Властивості:

1. лінійність
   
   
2. зсув по часу
   
   
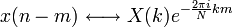
3. періодичність
   
   
4. виконується Теорема Парсеваля
   
5. володіє спектральною щільністю
   S(k) = | x(k) | ²
   
6. 
   
   
   
   

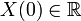
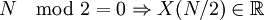
11. Комплексне ДПФ
    

Дискретне комплексне перетворення (ДКП) - дискретне ортогональне перетворення, що узагальнює всі інші перетворення. Має вигляд:







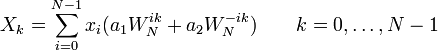
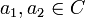
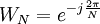
j - уявна одиниця.
Зворотне до нього перетворення має вигляд:

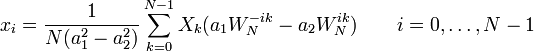
12. Двумірне ДПФ
    

Пряме і зворотне Фур'є-перетворення безперервної і інтергіруемой функції двох змінних виражаються співвідношеннями:



Тут x, y - координати в площині об'єкта, u, v - просторові частоти - координати в спектральної площині.

13. ДПФ в матричній формі
    

Дискретне перетворення Фур'є є лінійним перетворенням, яке переводить вектор тимчасових відліків 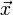у вектор спектральних відліків тієї ж довжини. Таким чином перетворення може бути реалізовано як множення квадратної матриці на вектор: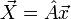



Матриця А має вигляд:




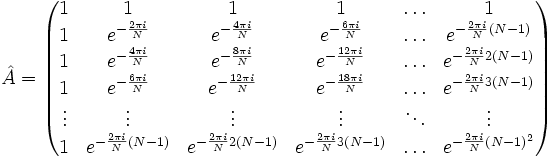
Елементи матриці задаються наступною формулою:

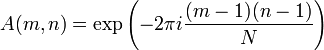
14. Вейвлет аналіз
    

Вейвлет-аналіз застосовується для аналізу нестаціонарних медичних сигналів, у тому числі в електрогастроентерографії.
Вейвлет-перетворення зазвичай ділять на дискретне вейвлет-перетворення (ДВП) і безперервне вейвлет-перетворення (НВП).

Дискретне:

ДВП сигналу x отримують застосуванням набору фільтрів. Спочатку сигнал пропускається через низькочастотний (low-pass) фільтр з імпульсним відгуком g, і виходить згортка:



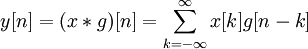
Одночасно сигнал розкладається за допомогою високочастотного (high-pass) фільтра h. У результаті виходять деталізуючі коефіцієнти (після ВЧ-фільтра) та коефіцієнти апроксимації (після НЧ-фільтра). Ці два фільтри пов'язані між собою і називаються квадратурних дзеркальними фільтрами (QMF).
Так як половина частотного діапазону сигналу була відфільтрована, то, згідно теоремі Котельникова, відліки сигналів можна прорідити в 2 рази:






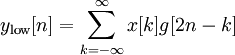
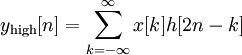
Безперервне: 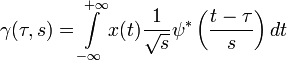,де τ представляє трансляцію, s представляє масштаб і ψ (t) - вейвлет-батько (mother wavelet).

15. Ряди Фур’є. Інтеграл Фур’є.
    

Ряд Фур'є - представлення довільної функції f з періодом τ у вигляді ряду



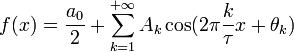
Цей ряд можна також переписаний у вигляді



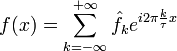
де

A_k — амплитуда k-го гармонічного коливання,

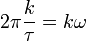 — круговая частота гармонічного коливання,

θ_k — початкова фаза k-го коливання,

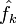 — k-я комплексна амплітуда

Розкладання функції в ряд Фур'є є потужним інструментом при вирішенні самих різних завдань завдяки тому, що ряд Фур'є прозорим чином веде себе при диференціюванні, інтегруванні, зсуві функції з аргументу і згортку функцій.

Інтеграл Фур’є:

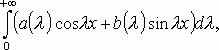де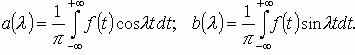

Інтеграл Фур’є в комплексній формі:

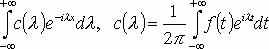або