Название диссертации
| Вид материала | Документы |
- Название диссертации, 236.78kb.
- Название диссертации, 326.98kb.
- Для заказа доставки диссертации введите ее название в форму поиска, 378.44kb.
- Название эксперимента, 62.85kb.
- Название эксперимента, 71.27kb.
- Название эксперимента, 42.5kb.
- Название эксперимента. Изучение эффектов двухнуклонных корреляций в адрон, 32.97kb.
- «название диссертации», 129.65kb.
- Структура диссертации, 1163.53kb.
- Ую информацию, являясь художественной обработкой диссертации, посвященной теме страха, 5036.87kb.
1 2
Объявление о защите кандидатской диссертации
| ФИО | Мо Чжо Чо |
| Название диссертации | Моделирование вычислительного процесса, разработка алгоритмов и пакета прикладных программ для вычисления экспоненциальной функции на программируемых логических интегральных схемах |
| Специальность | 05.13.05 – Математическое моделирование, численные методы и комплексы программ |
| Отрасль науки | Технические науки |
| Шифр совета | Д 212 .110 .08 |
| Телефон учёного секретаря Диссертационного совета | 8-499-141-94-55 |
| | electron_inform@mail.ru |
| Предполагаемый срок защиты диссертации | 12 ноября 2009г , в 14.00 |
| Место защиты диссертации | ул. Оршанская , 3 , ауд. 612А |
Ученый секретарь
Диссертационного совета Д 212.110.08
____________________/ Спыну М.В.
На правах рукописи
Мо Чжо Чо
Моделирование вычислительного процесса, разработка алгоритмов и пакета прикладных
программ для вычисления экспоненциальной функции на ПЛИС
Специальность:05.13.05 – Математическое моделирование, численные методы
и комплексы программ
Автореферат
Диссертации на соискание ученой степени
кандидата технических наук
Москва – 2009г
Работа выполнена в ГОУ ВПО «МАТИ» - Российском государственном технологическом университете имени К.Э. Циолковского.
Научный руководитель: доктор технических наук
Опадчий Юрий Федорович
Официальные оппоненты: доктор технических наук,
профессор
Руфицкий Михаил Всеволодович
кандидат физико-математических наук
доцент
Чумакова Екатерина Витальевна
Ведущая организация: ОАО «НПО «ЛЭМЗ»
Защита состоится «_______» ____________________2009 г. в ____ч._______мин. на заседании диссертационного совета Д 212.110.08 при «МАТИ» - Российском государственном технологическом университете им К.Э. Циолковского по адресу:121552, Москва, ул. Оршанская, д. 3, ауд. 612а.
С диссертацией можно ознакомиться в библиотеке «МАТИ» - Российского государственного технологического университета имени К.Э. Циолковского.
Ваш отзыв на автореферат диссертации в одном экземпляре, заверенный печатью организации, просим направлять по указанному адресу на имя ученого секретаря диссертационного совета.
Телефон для справок 8 (499) 141-94-55
Автореферат разослан «_____» _________________2009 г.
Ученый секретарь диссертационного совета Д212.110.08
Кандидат физико-математических наук
Спыну М.В.

Общая характеристика работы.
Актуальность темы. Существует два подхода к проектированию устройств вычислительной техники. Первый базируется на реализации принципов, сформулированных в 1945 году Джоном фон Нейманом. К основным из них относятся представление алгоритма обработки информации в виде последовательности управляющих команд и поочередному выполнению этих команд одними и теми же техническими средствами. Другими словами, при решении различных задач аппаратные средства компьютера остаются неизменными. Изменяется последовательность команд, то есть алгоритм работы. Использование этих принципов позволило разработать универсальное устройство способное решать широкий круг практических задач, однако последовательный принцип решения приводит к значительным временным затратам, что ограничивает применение таких устройств для решения задач в реальном масштабе времени.
Второй подход предполагает разработку для каждой конкретной задачи специализированного вычислителя, аппаратная структура которого ориентирована на выполнение заданного алгоритма. В этом случае возможны распараллеливание вычислительной процедуры и его конвейеризация, что значительно сокращает временные затраты на получение конечного результата. Вместе с тем такое устройство теряет универсальность и его применение оправдано только в тех случаях, когда алгоритм работы устройства неизменен в течение всего жизненного цикла изделия. Существует целый ряд задач, например задачи связанные с навигацией или управлением специализированным оборудованием, мобильными объектами и т.д., для которых такое решение является оправданным. Однако проектирование такого устройства, особенно с применение современной технологии БИС и СБИС является весьма дорогостоящим и оправдано только при больших сериях выпуска изделий, что не характерно для указанного класса задач.
Значительно сократить затраты и время проектирования можно при построении таких устройств с применением ПЛИС. Данный класс ИС позволяет в короткие сроки реализовать практически любой алгоритм обработки информации. Этому способствует наличие соответствующих САПР электронных схем, включающих большое число стандартных мегафункций, предназначенных для проектирования законченных узлов устройства. В этом случае разработчику нет необходимости полностью разрабатывать схему всего устройства. Достаточно собрать его структуру из уже имеющихся блоков.
В стандартных библиотеках таких САПР, например САПР Quartus II фирмы Altera, существуют мегафункции, предназначенные для аппаратной реализации основных математических операций. Однако их применение не во всех случаях позволяет получить устройство оптимизированное по времени вычисления и требуемым аппаратным ресурсом ПЛИС. К тому же в стандартном наборе отсутствуют мегафункции, предназначенные для вычисления специальных функций, таких как показательные, логарифмические и тригонометрические функции. Известные попытки реализовать вычисление таких функций сводятся к использованию случайных алгоритмов, не оптимизированных применительно к реализации на ПЛИС. К тому же при их разработке не учитываются вопросы, связанные с обеспечением требуемой точности вычисления, а именно вопросы минимизации остаточной погрешности, погрешностей округления и действия. Вследствие этого вопросы, связанные с разработкой алгоритмов вычисления специальных математических функций, ориентированные на разработку мегафункций стандартной библиотеки известных САПР электронных схем являются весьма актуальными.
Целью работы является разработка алгоритма нахождения численного значения функции
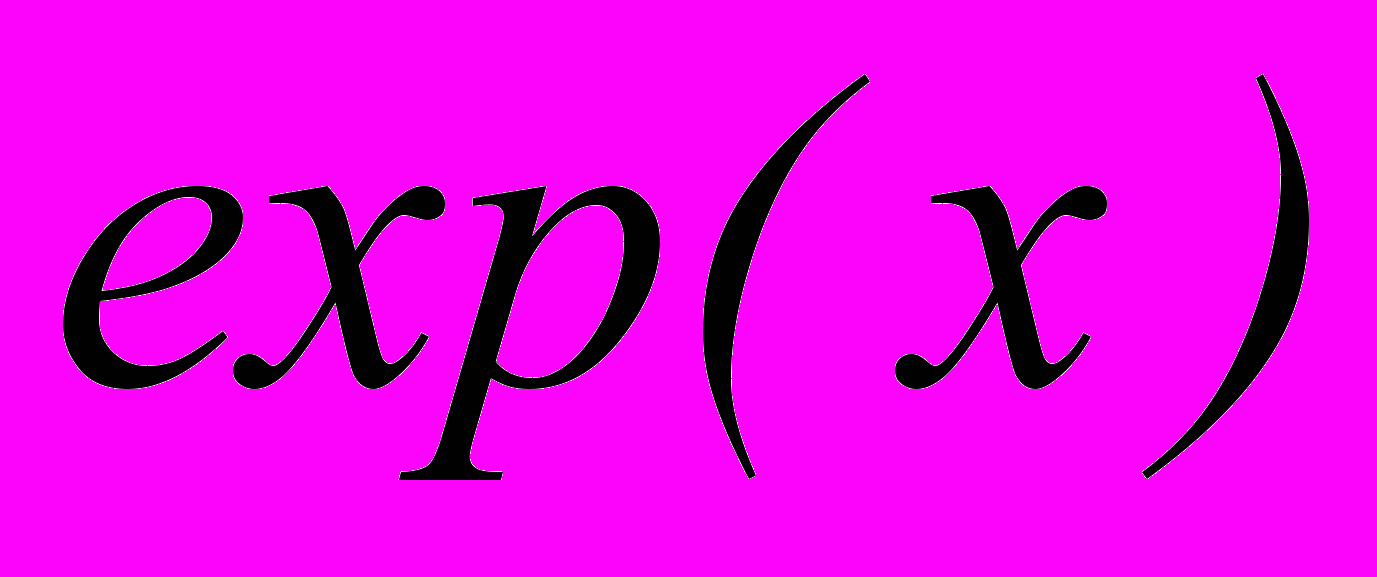 предназначенного для реализации в виде стандартной мегафункции САПР ПЛИС, обеспечивающего компромисс между быстродействием, точностью вычисления и затратами материальных ресурсов на реализацию и разработка на его основе комплекса программ для его практической реализации, учитывающего все виды погрешностей вычисления.
предназначенного для реализации в виде стандартной мегафункции САПР ПЛИС, обеспечивающего компромисс между быстродействием, точностью вычисления и затратами материальных ресурсов на реализацию и разработка на его основе комплекса программ для его практической реализации, учитывающего все виды погрешностей вычисления. Задачи исследования. Для достижения поставленной цели необходимо решить следующие задачи:
- Выявить для известных методов нахождения численного значения функции
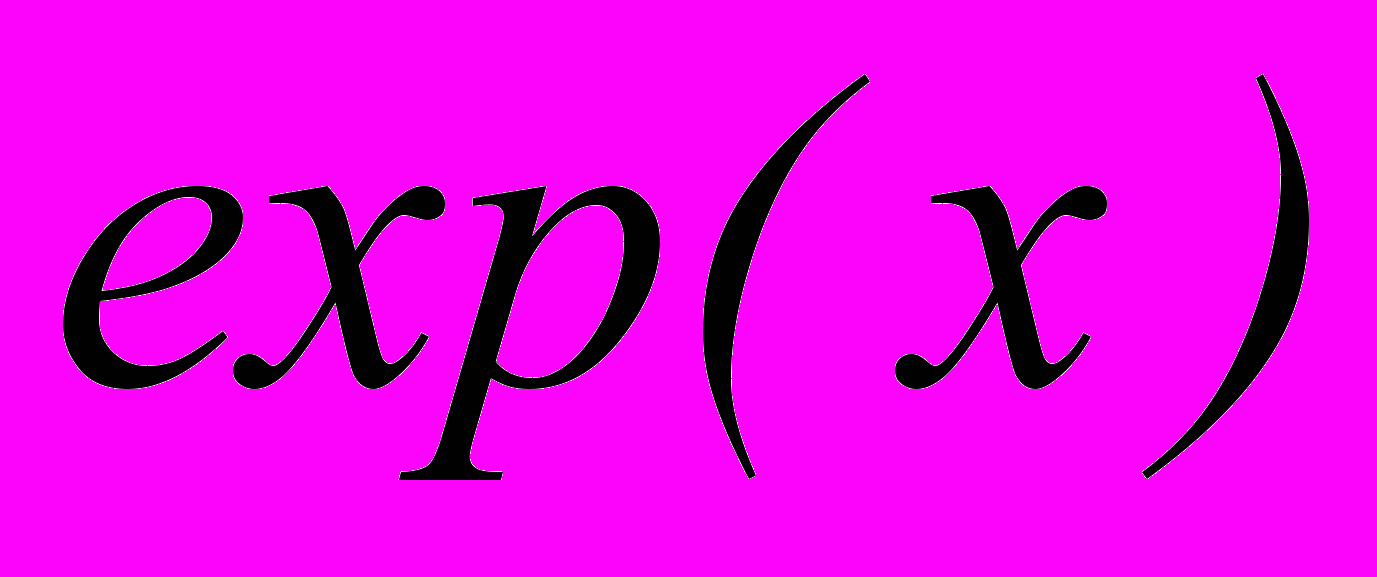 зависимость точности вычисления от вида используемой аппроксимации, диапазона изменения аргумента, и определить для каждого случая состав и количество выполняемых математических операций.
зависимость точности вычисления от вида используемой аппроксимации, диапазона изменения аргумента, и определить для каждого случая состав и количество выполняемых математических операций.
- Для различных типов ПЛИС проанализировать существующие алгоритмы выполнения основных математических операций, выявить зависимости аппаратных затрат и времени выполнения операции от разрядности аргументов и определить оптимальные диапазоны применения различных алгоритмов вычисления.
- Разработать алгоритм вычисления функции
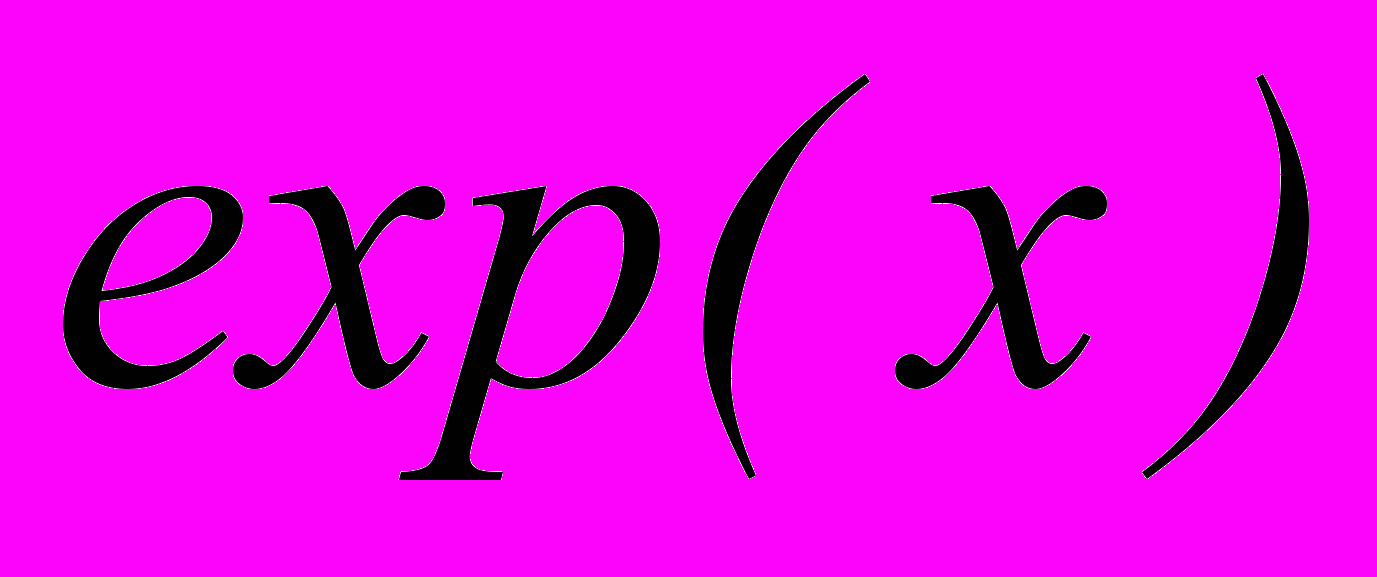 для произвольного диапазона изменения аргумента и произвести его оптимизацию с точки зрения минимизации требуемых аппаратных ресурсов ПЛИС и времени счета.
для произвольного диапазона изменения аргумента и произвести его оптимизацию с точки зрения минимизации требуемых аппаратных ресурсов ПЛИС и времени счета.
- Исследовать погрешности вычисления функции
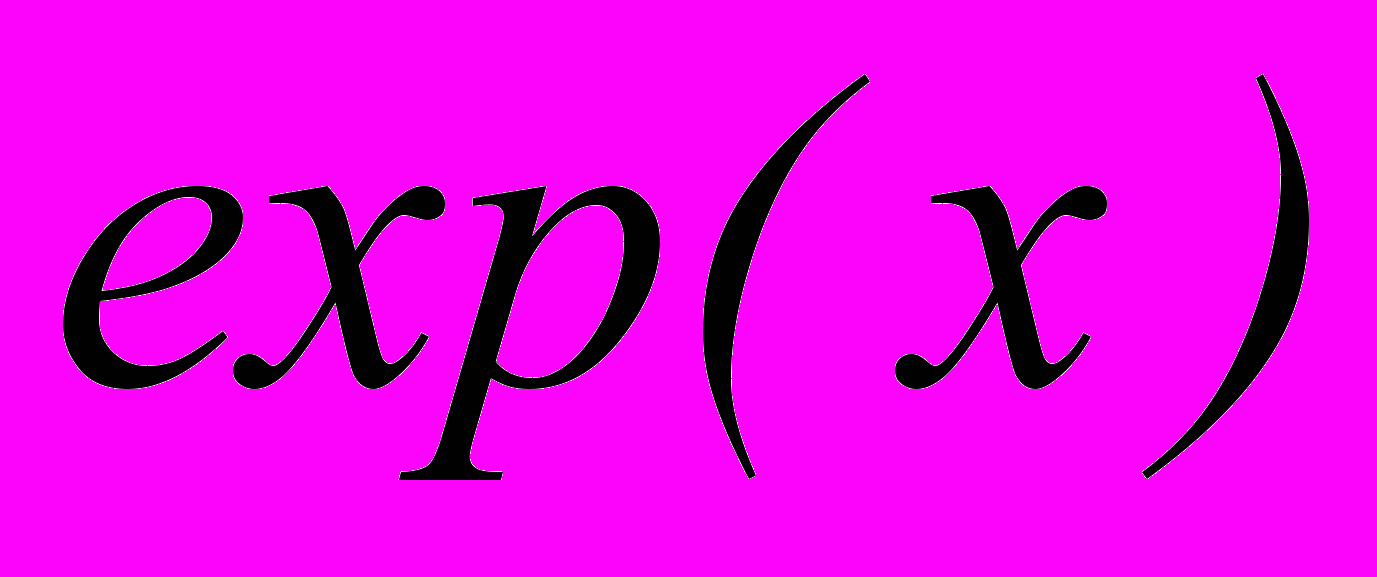 , обусловленные использованием разработанного метода реализации.
, обусловленные использованием разработанного метода реализации.
- Разработать пакет прикладных программ необходимый для разработки мегафункции вычисления функции
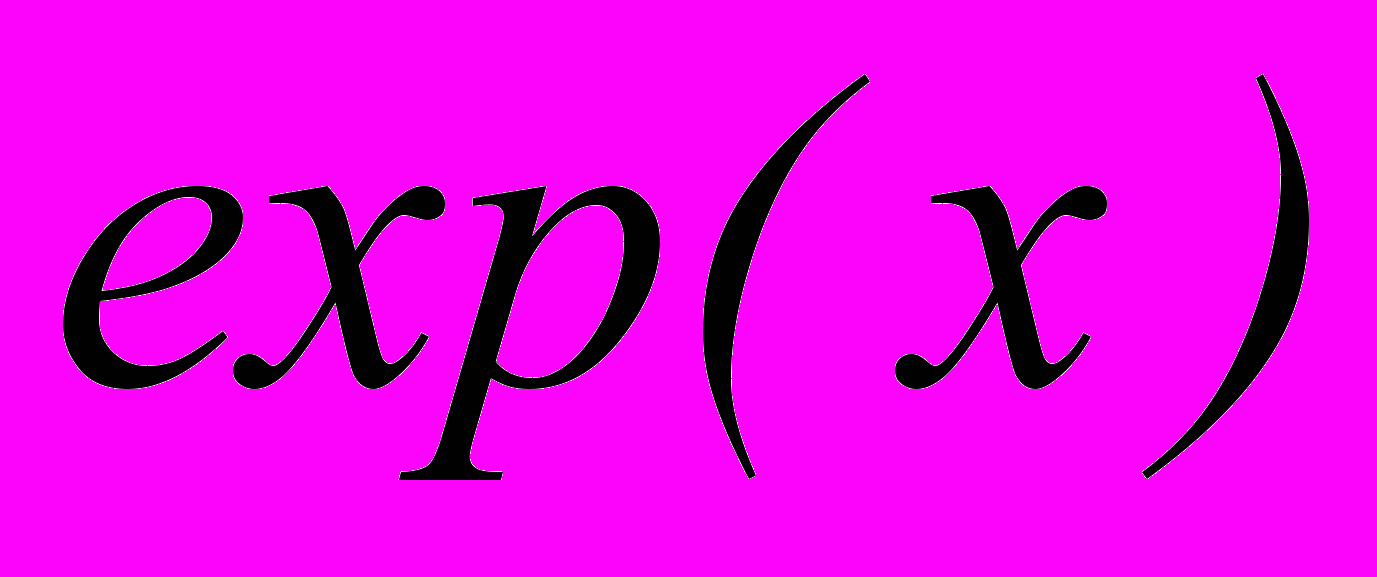 и проанализировать полученные программы с точки зрения обеспечения требуемой точности и аппаратных затрат ПЛИС на их реализацию.
и проанализировать полученные программы с точки зрения обеспечения требуемой точности и аппаратных затрат ПЛИС на их реализацию.
Научная новизна: К новым результатам проведенных исследований по теме диссертации относятся:
- Определение областей применения различных алгоритмов выполнения операции математического умножения, оптимальных с точки зрения быстродействия и затрат материальных ресурсов ПЛИС.
- Алгоритм вычисления функции
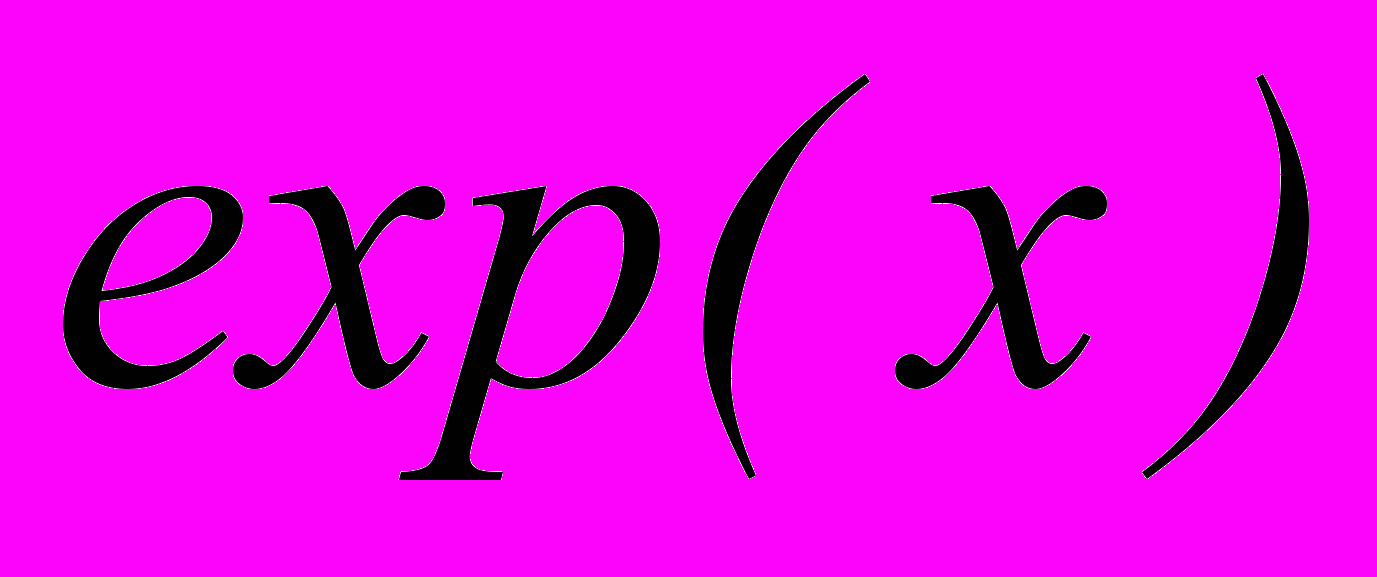 , обеспечивающий при получении требуемой точности и минимизации необходимых аппаратных ресурсов ПЛИС предельное снижение суммарного времени получения результата.
, обеспечивающий при получении требуемой точности и минимизации необходимых аппаратных ресурсов ПЛИС предельное снижение суммарного времени получения результата.
- Оптимальное для разработанного алгоритма соотношение между разбиением диапазона изменения аргумента функции на расчетные области и используемым методом замен переменных в многочленах Чебышева, обеспечивающее при заданной степени аппроксимирующего многочлена минимизацию погрешности вычисления функции.
- Функциональные зависимости точности вычисления функции
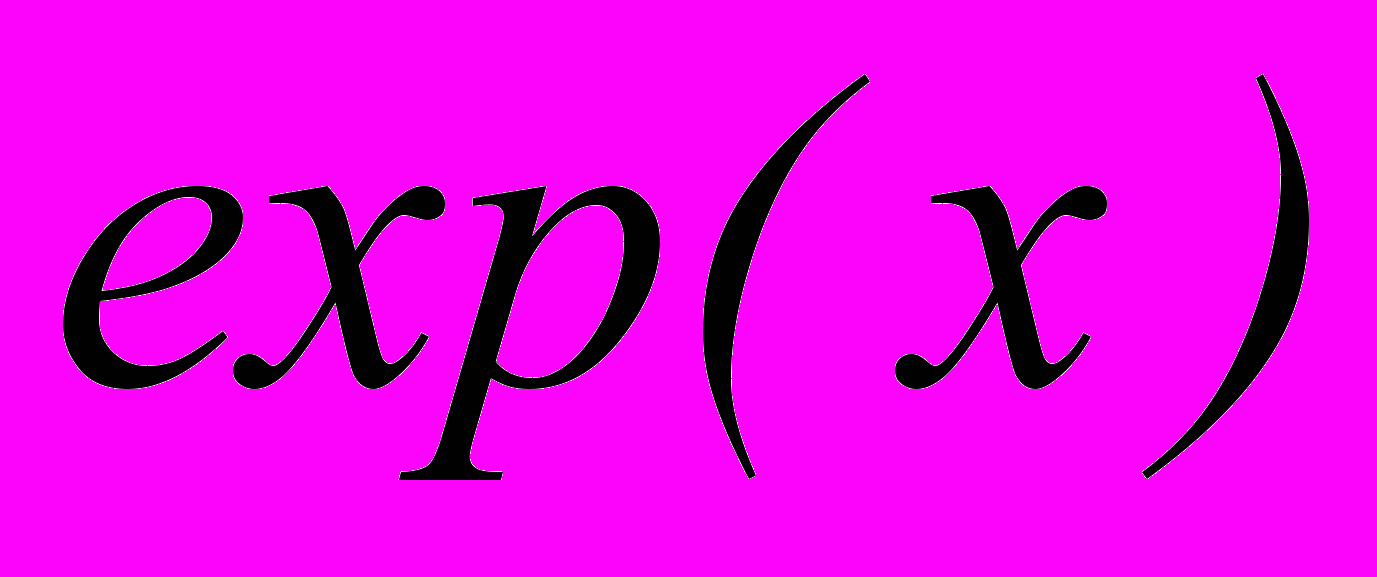 по разработанному алгоритму от числа разрядов исходного аргумента, учитывающие остаточную и начальную погрешности, а так же погрешность действия для различных методов замены переменных в многочленах Чебышева.
по разработанному алгоритму от числа разрядов исходного аргумента, учитывающие остаточную и начальную погрешности, а так же погрешность действия для различных методов замены переменных в многочленах Чебышева.
Практическая значимость проведенных исследований заключается в следующем:
- Разработан комплекс программ, предназначенных для аппаратного вычисления функции
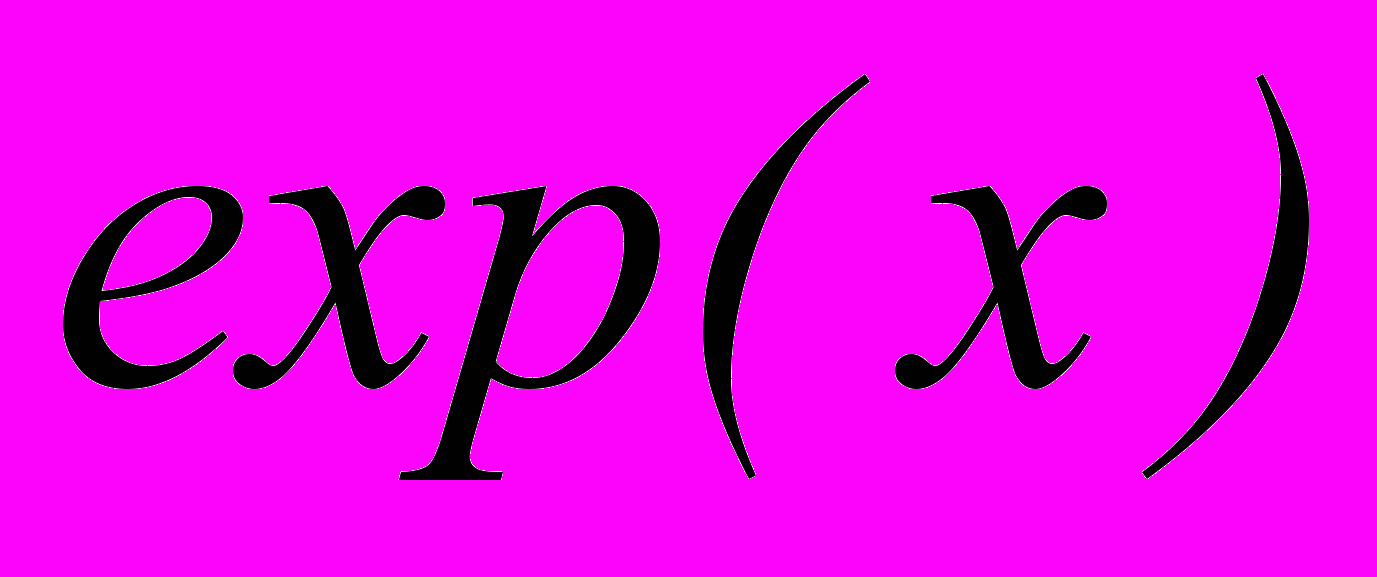 с помощью ПЛИС, обеспечивающих как минимизацию аппаратных ресурсов, так и время вычисления, реальное быстродействие которых определяется только возможностями используемой элементной базы.
с помощью ПЛИС, обеспечивающих как минимизацию аппаратных ресурсов, так и время вычисления, реальное быстродействие которых определяется только возможностями используемой элементной базы.
- Предложена процедура построения параллельной канонической формы графа вычисления степенного многочлена, и получены выражения определяющие зависимость длины его критического пути от степени используемого многочлена.
- Разработана программа для аппаратной реализации на ПЛИС операции математического умножения чисел большой разрядности, применение которой обеспечивает минимизацию необходимых аппаратных ресурсов ПЛИС и времени вычисления.
- Предложены рекомендации по выбору соотношения между разрядностями представления аргумента и используемых при вычислении коэффициентов степенного многочлена, обеспечивающего минимизацию погрешности вычисления.
- Для основных математических функций найдены соотношения между требуемыми аппаратными ресурсами ПЛИС, быстродействием и разрядностью используемых аргументов.
Достоверность полученных результатов, выводов и рекомендаций, сформулированных в работе, подтверждается использованием для их получения апробированного математического аппарата и стандартных средств формального описания цифровых устройств, а так же результатами вычислительного эксперимента, выполненного с использованием общепринятых в промышленности систем автоматизированного проектирования электронных средств (EDA), а именно, системы проектирования Quartus II фирмы Altera.
Основные положения, выносимые на защиту:
- Оптимизированный применительно к реализации на ПЛИС алгоритм выполнения операции арифметического умножения, и рекомендации по области его применения, гарантирующие относительно стандартных алгоритмов, реализованных в САПР Quartus II фирмы Altera как уменьшения требуемых на реализацию аппаратных ресурсов ПЛИС, так и сокращение временны вычисления.
- Алгоритм построения аппроксимирующего многочлена высокой степени, предназначенный для численного вычисления экспоненциальной функции, обеспечивающий при реализации на ПЛИС оптимальное разбиение аргумента на расчетные интервалы, что при произвольном диапазоне изменения аргумента и требуемой точности вычисления позволяет минимизировать как аппаратный затраты, так и время вычисления.
- Пакет прикладных программ, реализующий разработанные алгоритмы и включающий программы для реализации операции арифметического умножения и вычисления экспоненциальной функции от произвольного аргумента, применение которого позволяет сократить аппаратные ресурсы ПЛИС и время вычисления.
Апробация работы и публикации
Основные результаты работы докладывались на Международной молодежной научной конференции «Гагаринские чтения» 2006 и 2007 годов, III научной международной конференции «Современные проблемы науки и образования», г. Москва, 13-15 мая 2008г, Всероссийской научно-технической конференции «Новые материалы и технологии», Москва 11-13 ноября 2008г и международной научной конференции «Технические науки и современное производство», Китай (Пекин), 26 ноября - 4 декабря 2008 г.
Основные результаты работы опубликованы в 9 научных трудах, включая 1 работу [9] опубликованную в журнале, рекомендованном ВАК .
Структура диссертационной работы.
Диссертация состоит из введения, 5-и глав, заключения, списка использованных источников и приложений. Объем диссертации 185 страниц машинописного текста, приложений 16 страниц , 129 рисунков и 72 таблицы. Список литературы включает 62 наименования.
Краткое содержание работы
Во введении на основе анализа степени разработанности темы диссертации в отечественной и зарубежной литературе обоснована актуальность работы, определены цели и задачи исследования, сформулированы научная новизна и практическая значимость, а так же основные положения, выносимые на защиту, доказана достоверность полученных результатов и приведены сведения о ее апробации.
. В первой главе выполнен сопоставительный анализ известных методов вычисления экспоненциальной функции. В качестве исследуемых рассмотрены следующие методы:
- Метод разложения в степенной ряд;
- Методы ортогональных и других многочленных разложений, к которым можно отнести разложение по многочленам Чебышева или Лежандра;
- Метод многочленного приближения;
- Метод разложения в цепные дроби;
- Метод рациональных приближений;
Каждый из этих методов характеризуется собственным алгоритмом вычисления и, при реализации на ПЛИС, характеризуется некоторым временем вычисления и требуемыми аппаратными ресурсами, зависящими от количества и состава выполняемых математических операций. В качестве первичного критерия оценки различных методов рассматривалась зависимость относительной погрешности вычисления от сложности (количества членов) выражения и типа используемых математических операций.
Метод разложения в степенной ряд использует представление функции в виде:
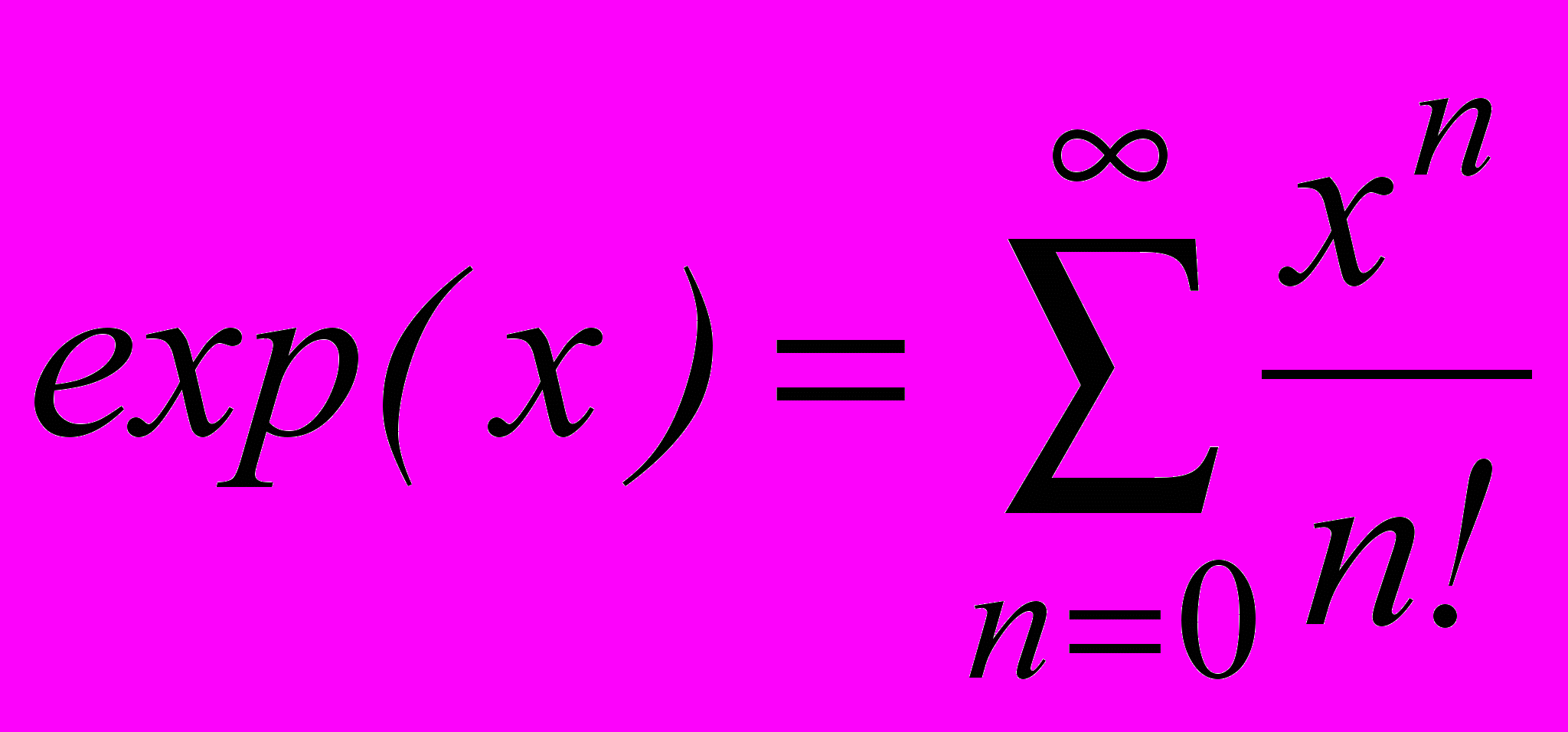 .
.Исследование данного разложения показали, что относительная ошибка вычисления при отрицательных значениях аргумента значительно превышает ошибку при положительных значениях аргумента и ошибка вычисления увеличивается при возрастании модуля аргумента.
 Рис.1 | Для данного метода найдена зависимость относительной ошибки вычисления (r) от количества членов (k) ряда (рис.1). Показано, что погрешность вычисления при ограничении числа членов ряда может быть уменьшена путем учета остаточного члена. Приведено несколько выражений для остаточного члена, учет которого позволяет уменьшить относительную погрешность до двух порядков (см.рис.1). |
Метод ортогональных приближений рассмотрен на примере разложения по многочленам Чебышева и Лежандра. Разложение экспоненциальной функции с использованием многочленов Чебышева, в общем случае приводит к выражению вида:
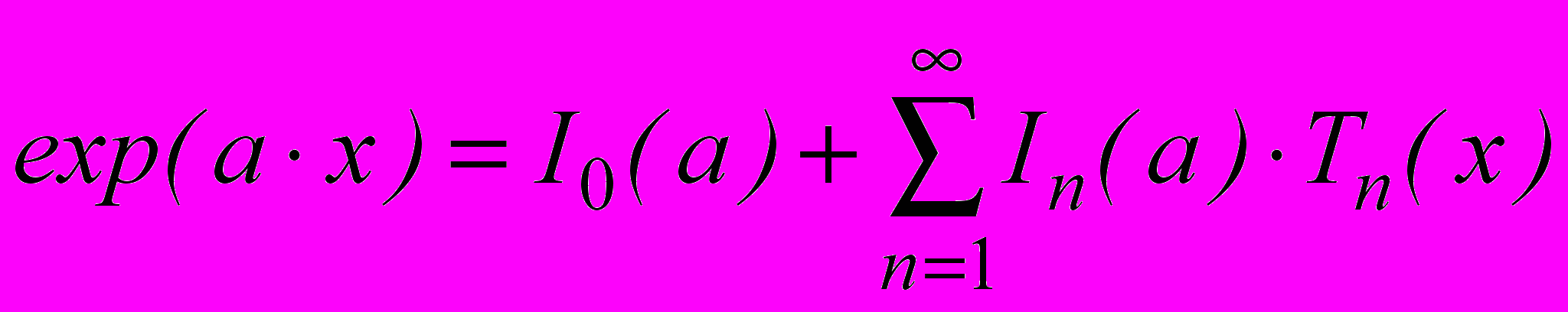 ,
,где: значения
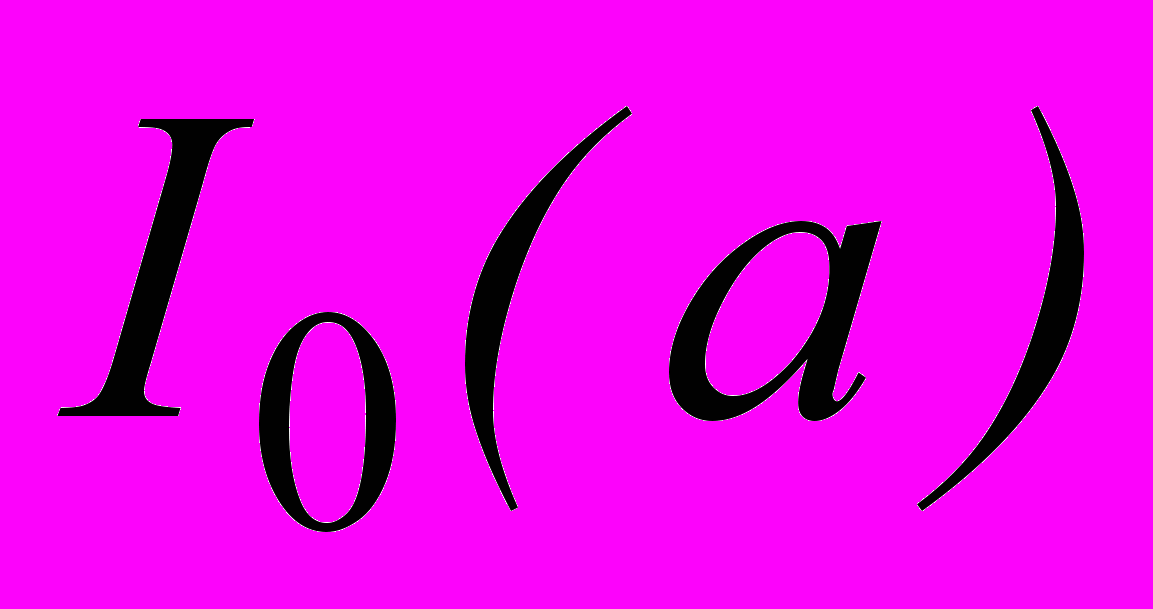 и
и 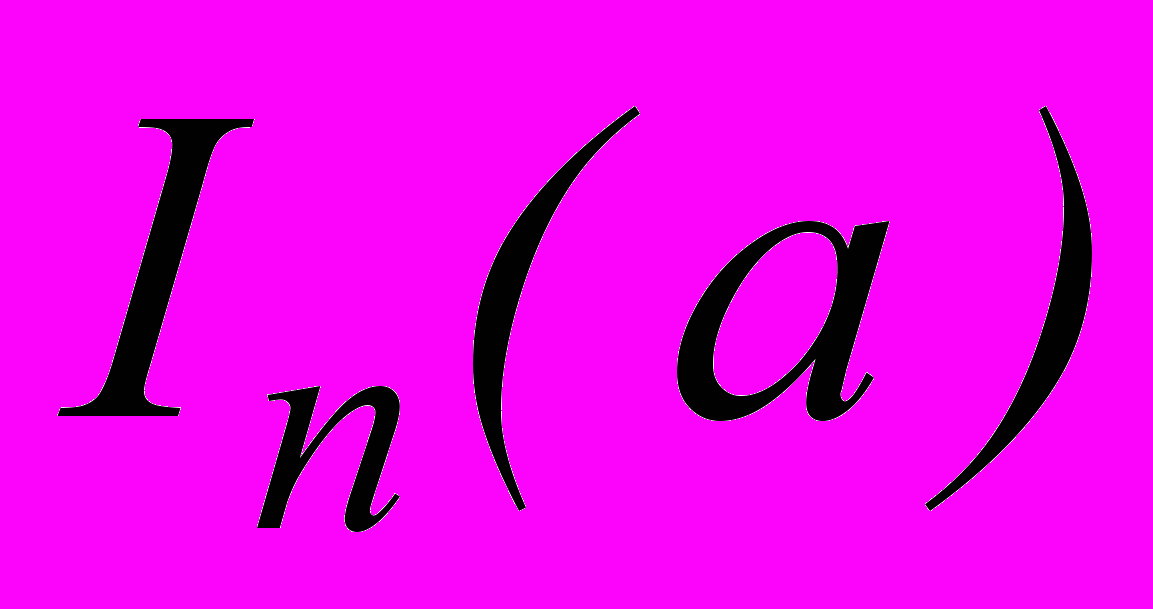 - функции Бесселя мнимого аргумента порядка
- функции Бесселя мнимого аргумента порядка 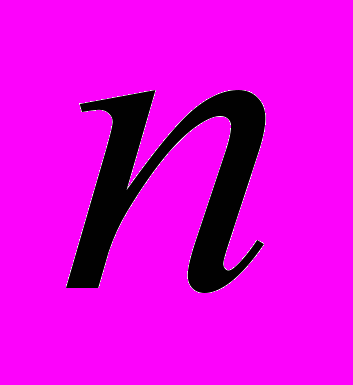 .
.Данное выражение справедливо для диапазона изменения аргумента
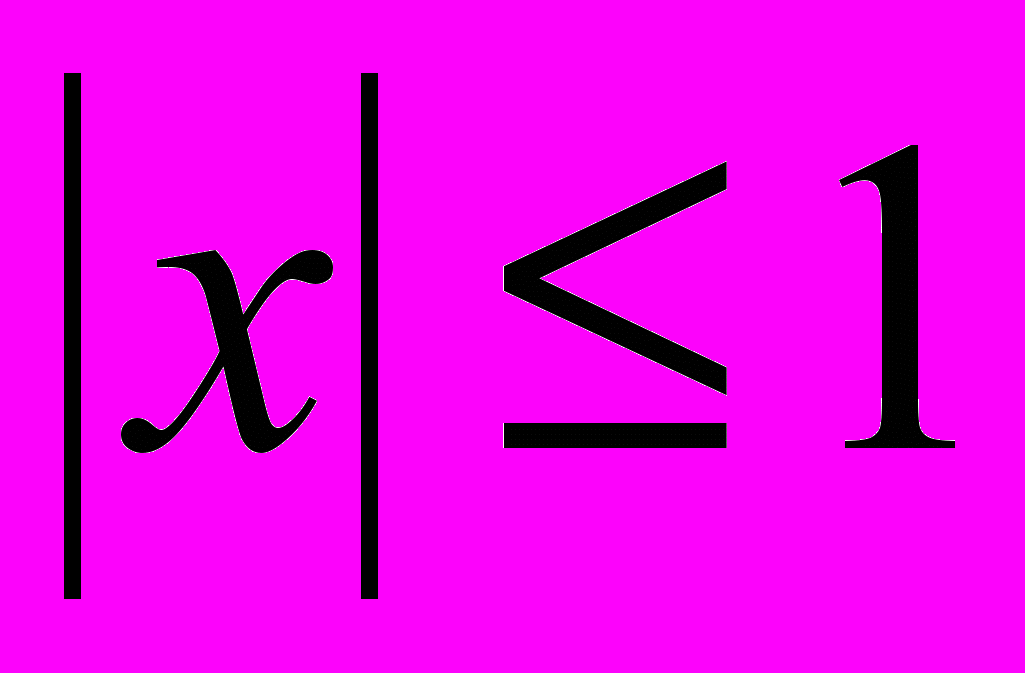 Показано, что сужение диапазона изменения аргумента позволяет значительно поднять точность вычисления функции. Этого можно добиться при использовании замены переменных в многочлене Чебышева вида:
Показано, что сужение диапазона изменения аргумента позволяет значительно поднять точность вычисления функции. Этого можно добиться при использовании замены переменных в многочлене Чебышева вида: 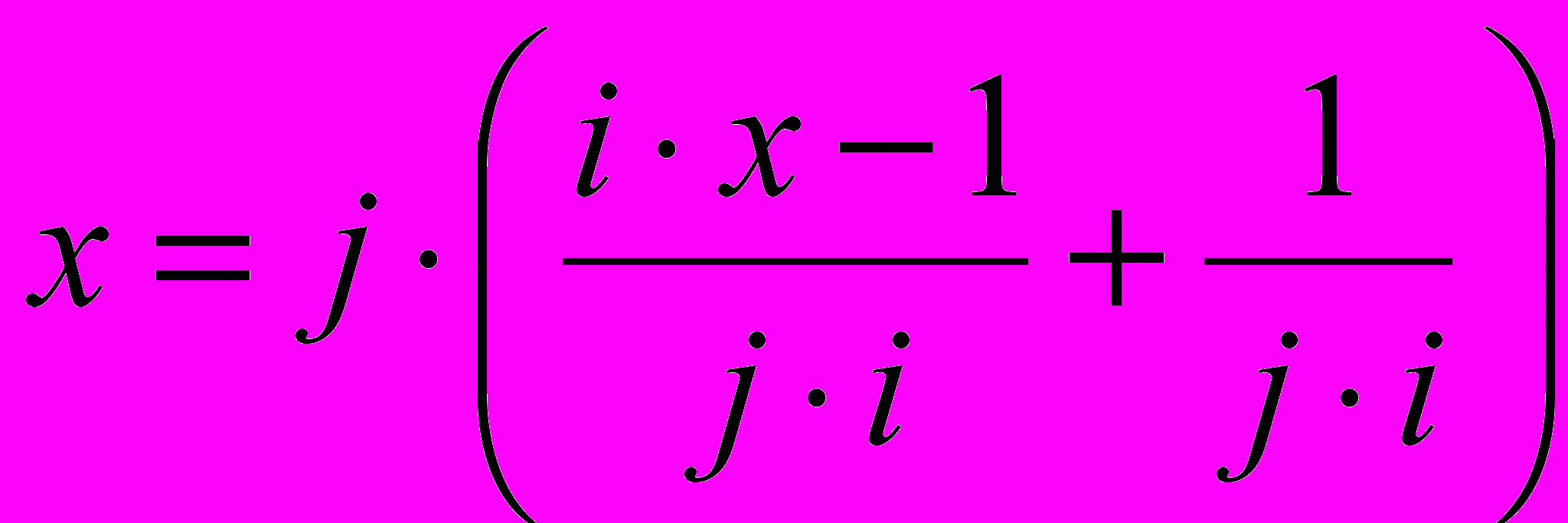 ,
,где: i и j – целые числа.
Использование данной замены приводит к получению следующего расчетного выражения:
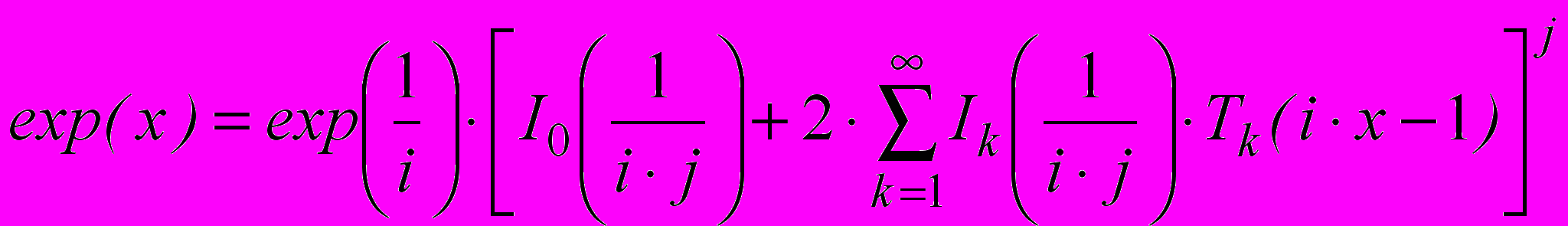
Исследования показали, что увеличение параметра
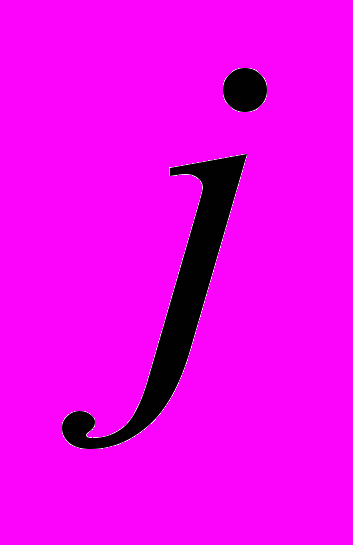 фактически приводит к повышению степени аппроксимирующего многочлена, то есть позволяет уменьшить относительную ошибку вычисления, а увеличение параметра
фактически приводит к повышению степени аппроксимирующего многочлена, то есть позволяет уменьшить относительную ошибку вычисления, а увеличение параметра 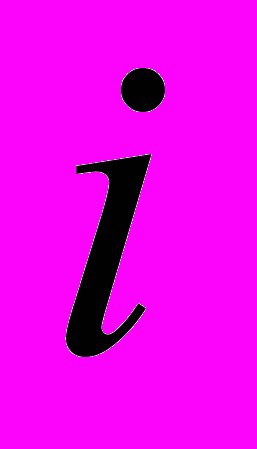 так же снижает относительную ошибку вычисления, но достигается это путем сужения реального диапазона изменения аргумента. Показано, что для каждого диапазона изменения переменной существует некоторое оптимальное с точки зрения повышения точности соотношение параметров i и j. Так если
так же снижает относительную ошибку вычисления, но достигается это путем сужения реального диапазона изменения аргумента. Показано, что для каждого диапазона изменения переменной существует некоторое оптимальное с точки зрения повышения точности соотношение параметров i и j. Так если 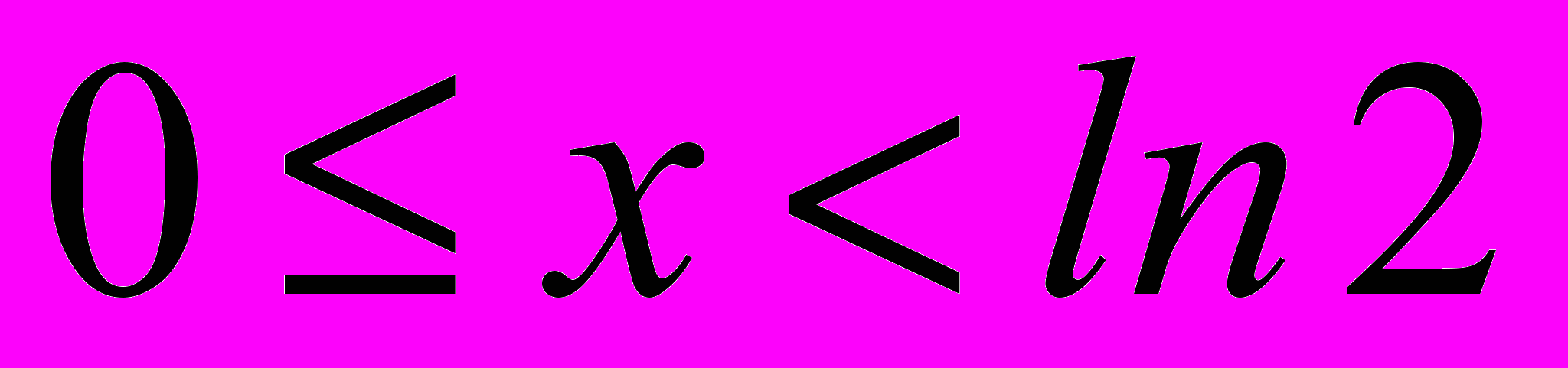 , то оптимальными являются значения j=2 и i=2.86.
, то оптимальными являются значения j=2 и i=2.86. 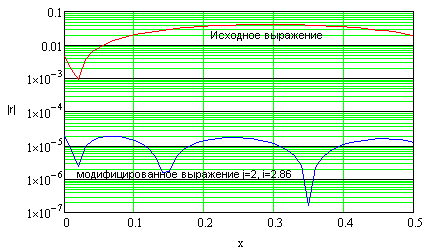 Рис.2. | На рис.2. приведены зависимости модулей относительной ошибки вычисления функции по исходному и модифицированному выражениям. В обоих случаях степень исходного аппроксимирующего многочлена равна четырем. Очевидно, что использование предлагаемой замены более чем на 3 порядка снижает относительную погрешность вычисления. |
Общий вид разложения в ряд произвольной функции
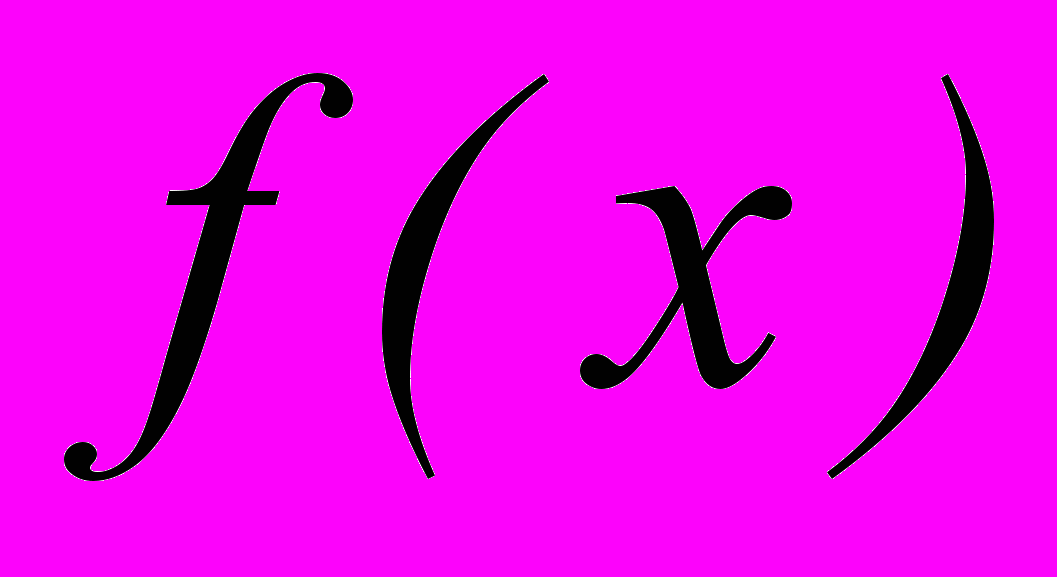 по многочленам Лежандра определяется выражением:
по многочленам Лежандра определяется выражением: 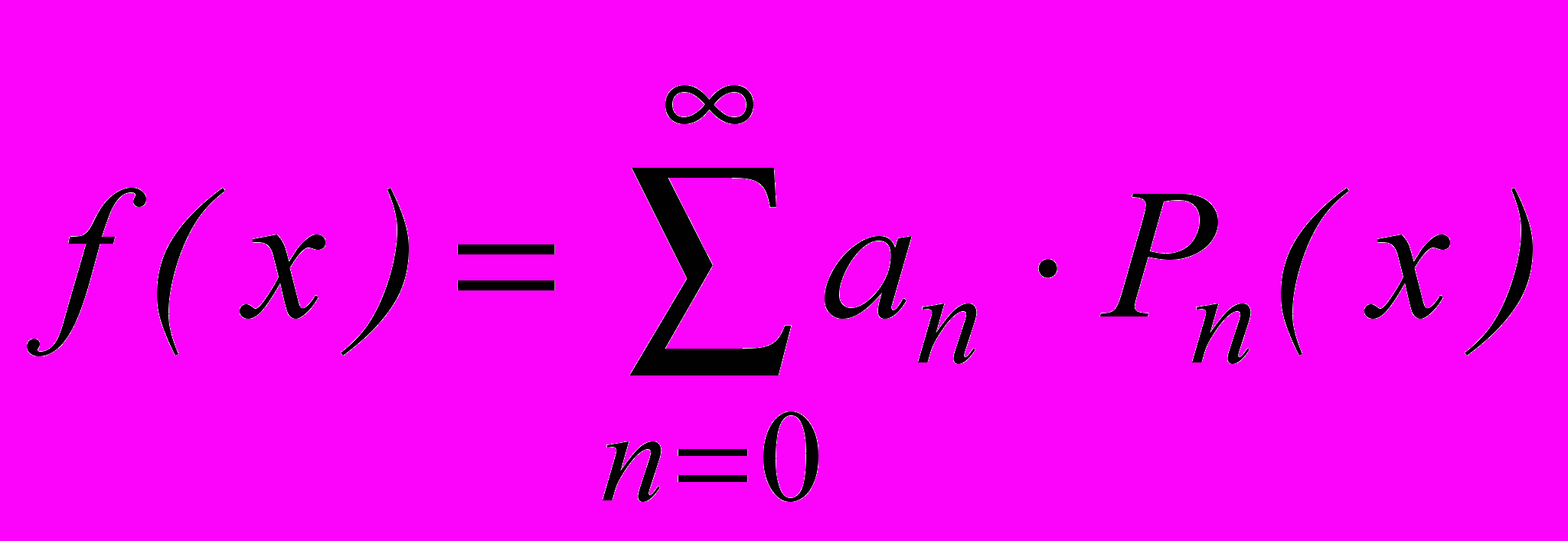 ,
,где:
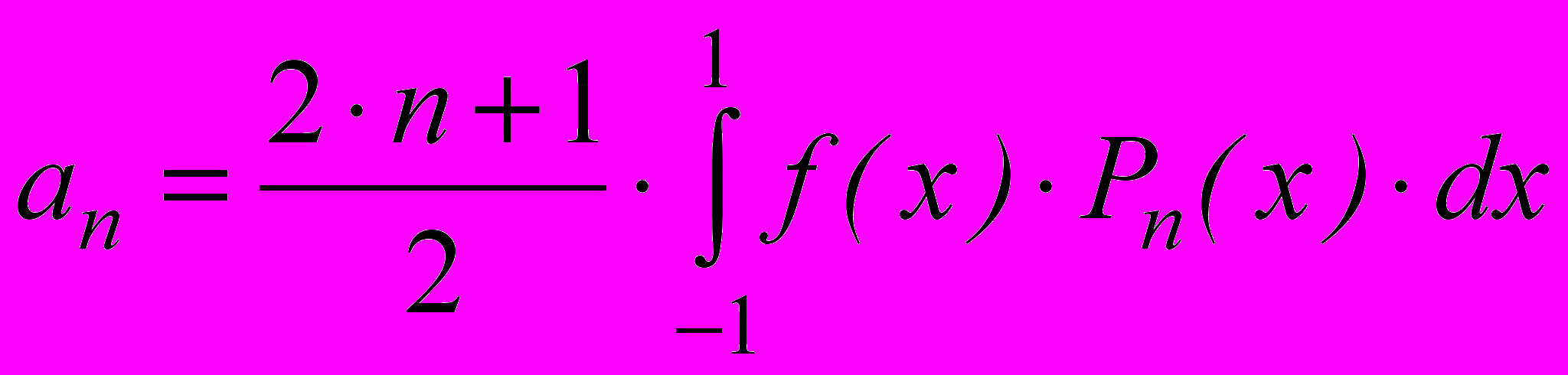 и
и 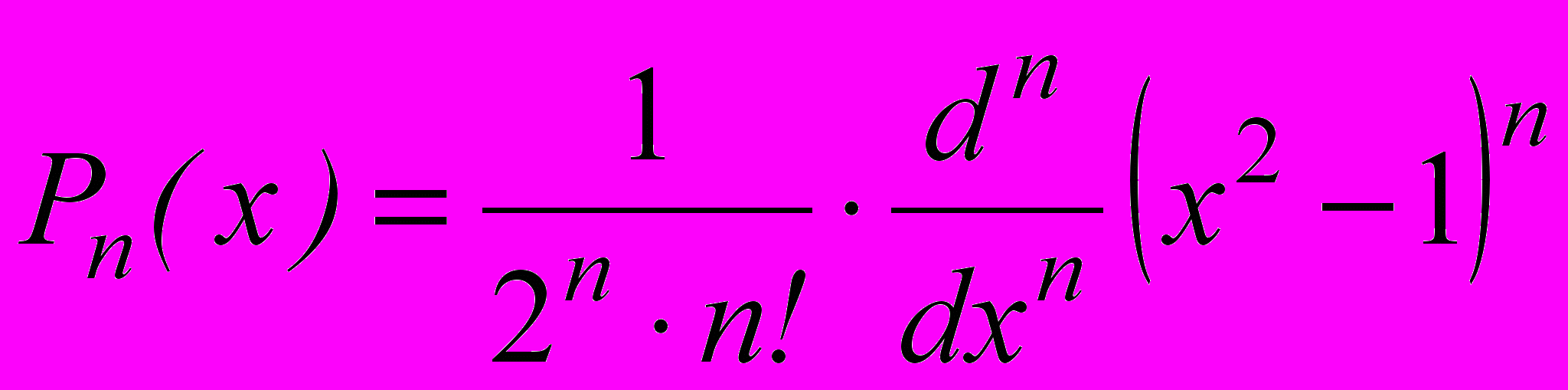
Показано, что при выполнении условия
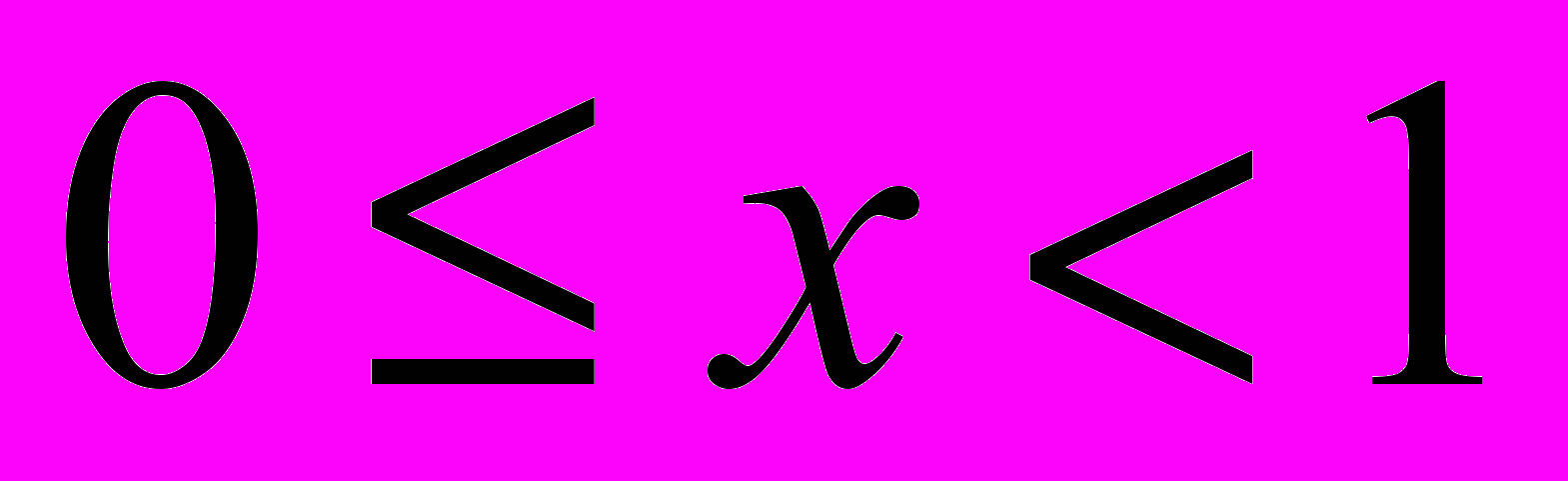 максимальное значение относительной ошибки соответствует значению
максимальное значение относительной ошибки соответствует значению 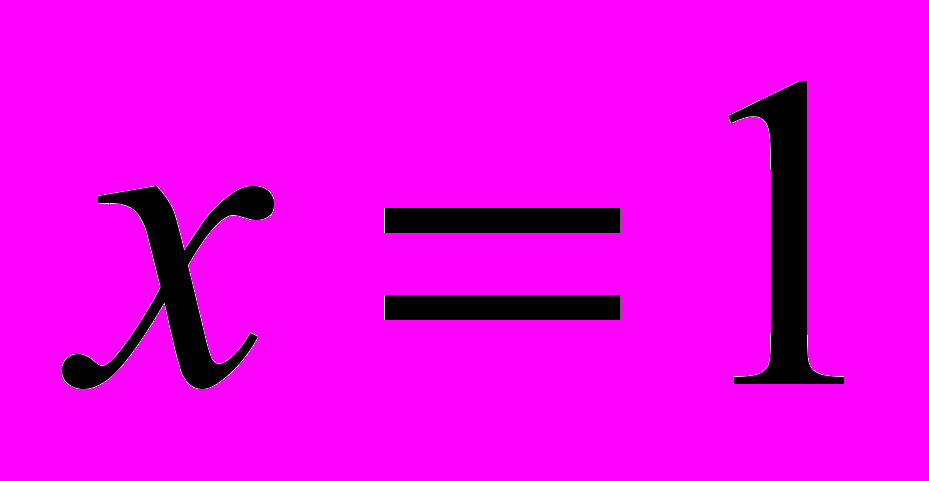 .На рис 3 приведена полученная с использованием данных выражений зависимость относительной ошибки вычисления от числа членов разложения. Следует отметить, что параметр n фактически равен степени реализуемого аппроксимирующего многочлена.
.На рис 3 приведена полученная с использованием данных выражений зависимость относительной ошибки вычисления от числа членов разложения. Следует отметить, что параметр n фактически равен степени реализуемого аппроксимирующего многочлена.  Рис.3. | Метод многочленного приближения базируется на работах Чебышева о минимизации равномерной нормы сходимости. Обычно многочлен наилучшего приближения для известного интервала ищется по значениям аппроксимирующих точек в виде степенного ряда: |
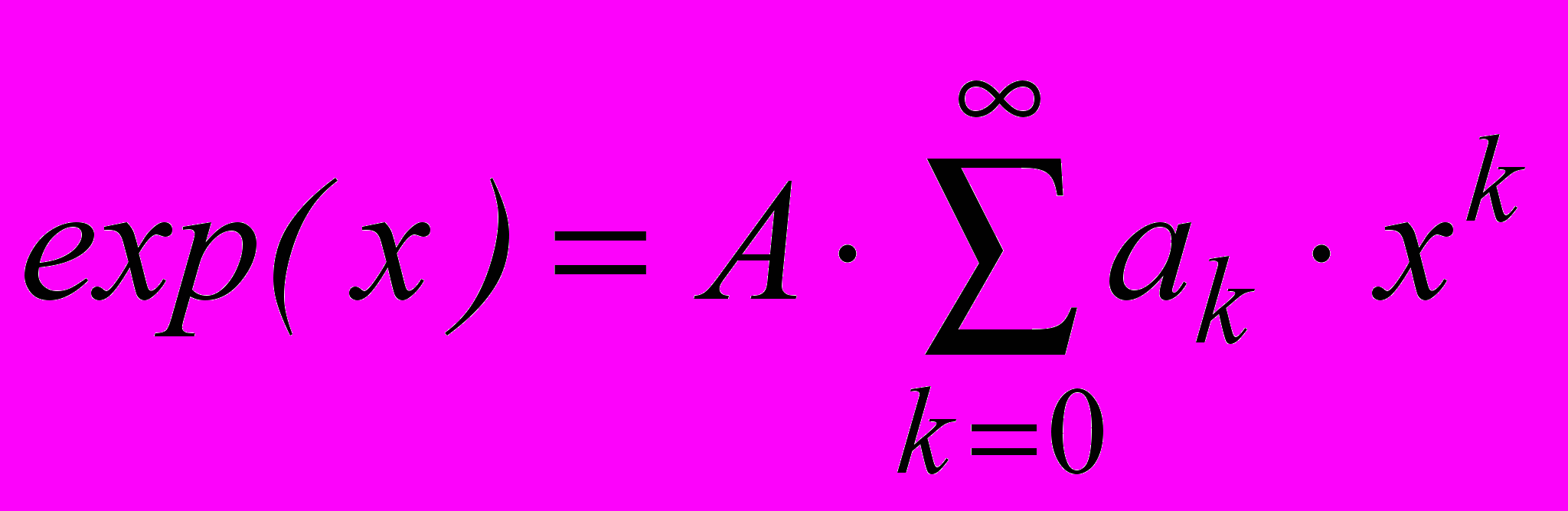
В работе показано, что такое разложение может обеспечить высокую точность вычисления функции только в случае конструирования аппроксимирующего многочлена под заданный вид функции и определенный диапазон изменения аргумента и оптимальном выборе координат аппроксимирующих точек. Отбрасывание членов в сконструированном многочлене и неоптимальный выбор координат ведут к резкому снижению точности вычисления. Предложена методика конструирования аппроксимирующего многочлена и с ее помощью получены коэффициенты для многочленов 3..9 степеней.
Метод разложения в цепные дроби базируется на использовании выражения вида:
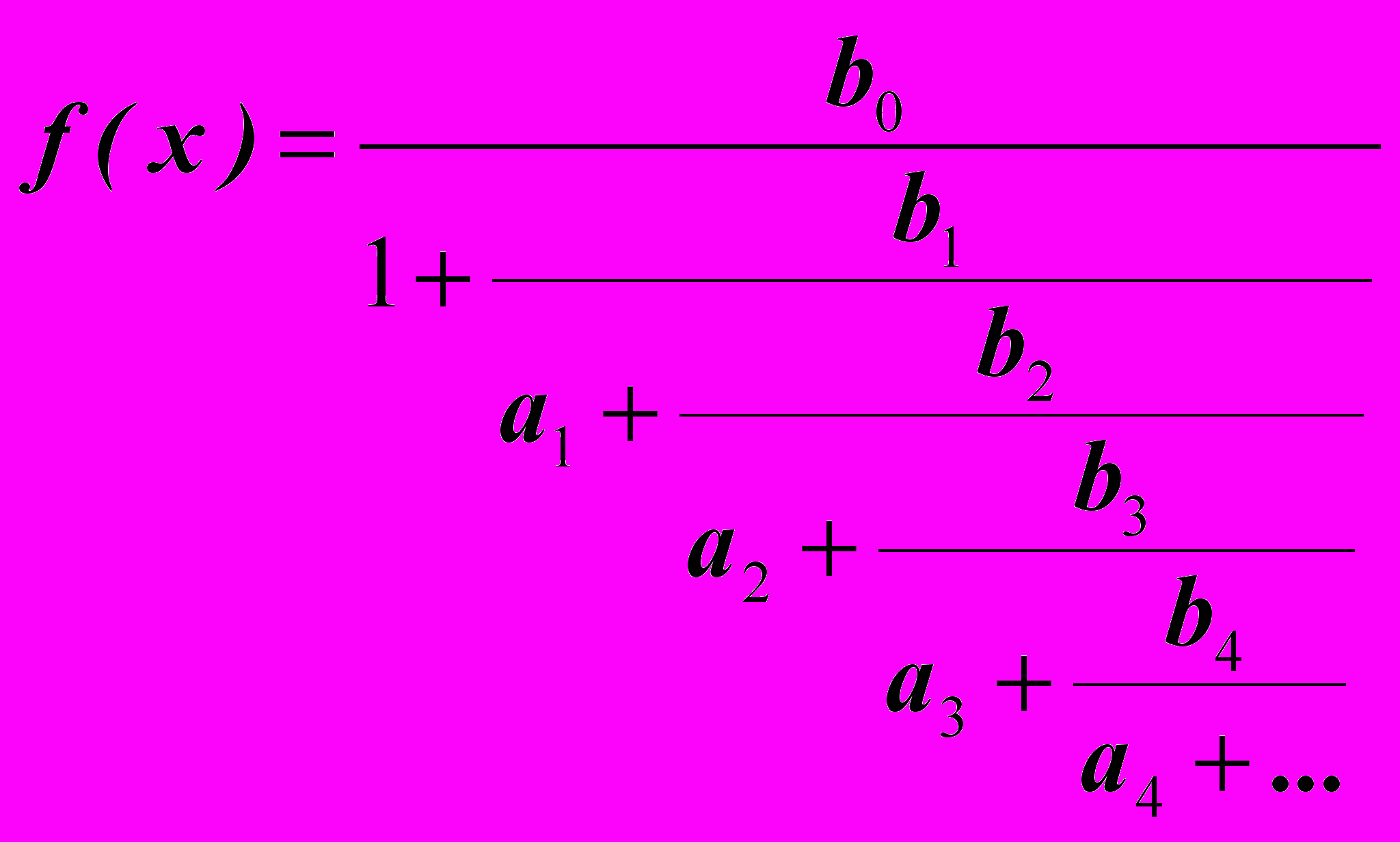 ,
,где: коэффициенты
 и
и 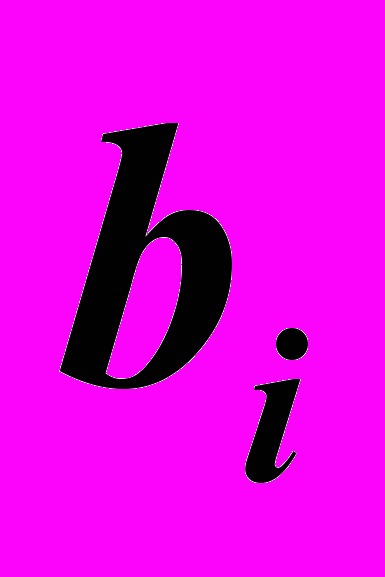 есть некоторые многочлены относительно аргументы искомой функции.
есть некоторые многочлены относительно аргументы искомой функции. В принципе, данное разложение бесконечно. Если используется конечное число членов разложения, то полученное выражение принято называть подходящей дробью, которая может быть представлена выражением:
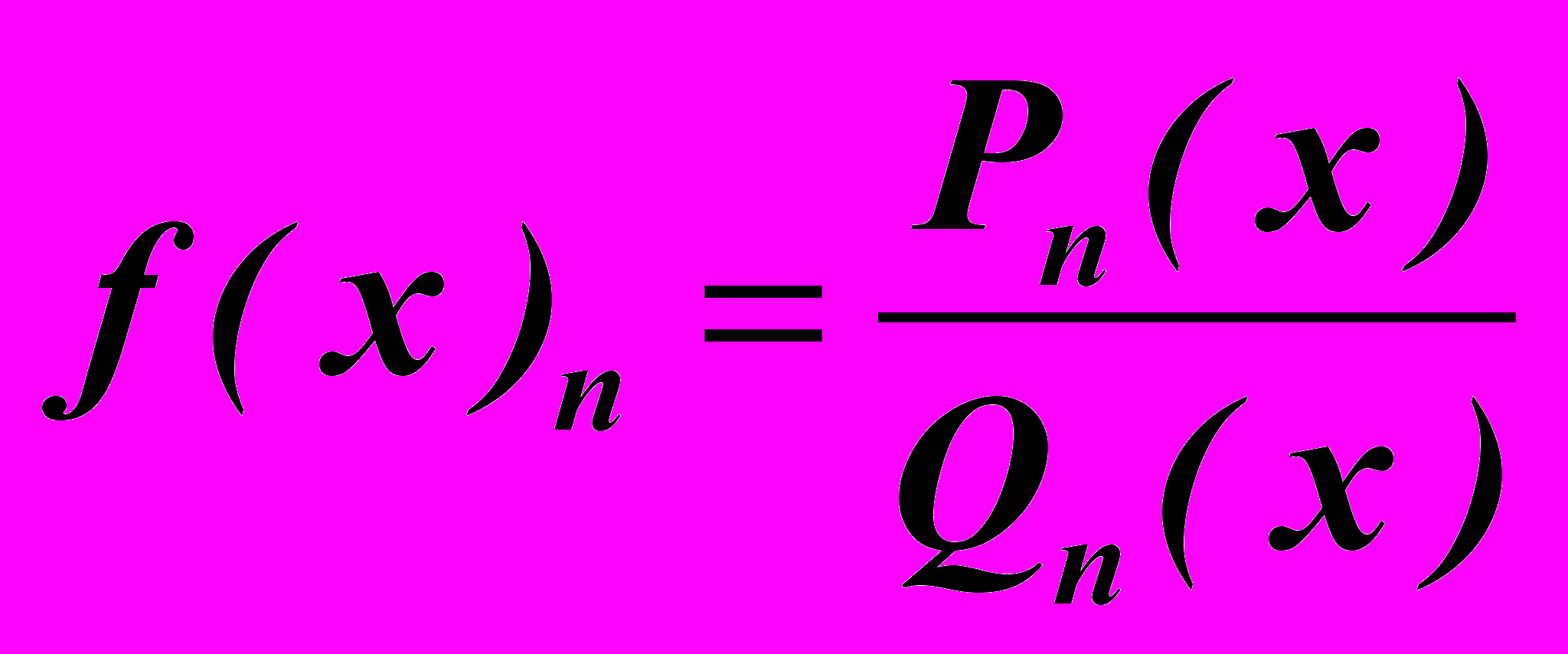 . Известно достаточно большое число разложений экспоненциальной функции в цепные дроби. Однако большинство из них приводят к выражению:
. Известно достаточно большое число разложений экспоненциальной функции в цепные дроби. Однако большинство из них приводят к выражению: 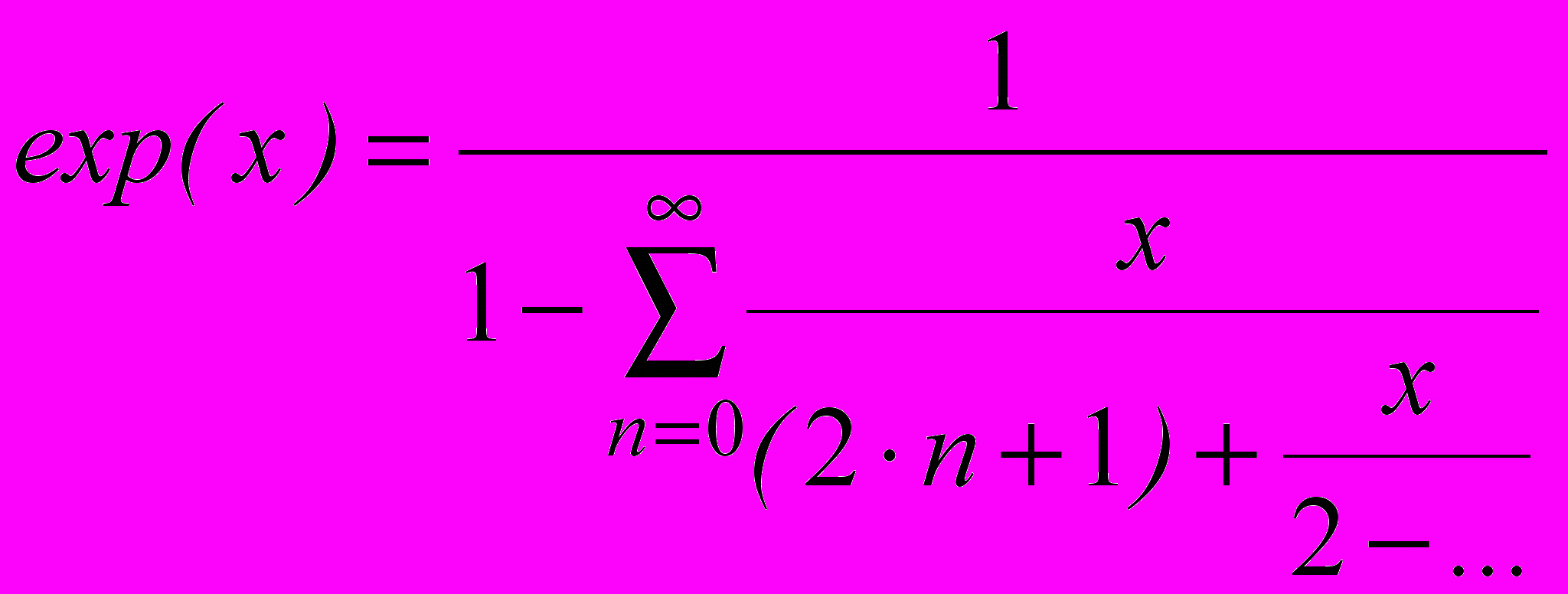 .
.В таблице 1 приведены подходящие дроби данного разложения для различных значений параметра n, а на рис.4 соответствующие им зависимости относительной ошибки вычисления от значения аргумента. Таблица 1
| Значение константы 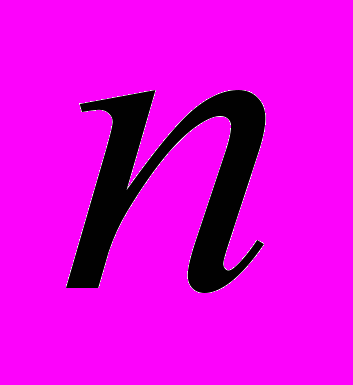 | Подходящая дробь | |
| 1 |  | |
| 2 |  | |
| 3 |  | |
| 4 |  | |
| 5 |  | |
 Рис.4. | Анализ полученных зависимостей показывает, что при использовании данного разложения может быть обеспечена высокая точность вычисления. Однако нахождение численного значения подходящей дроби сопряжено с вычислением двух мно- | |
гочленов и нахождением их отношения.
Методы рационального приближения базируются на вычислении некоторого отношения многочленов от аргумента. Например, известно разложение вида:
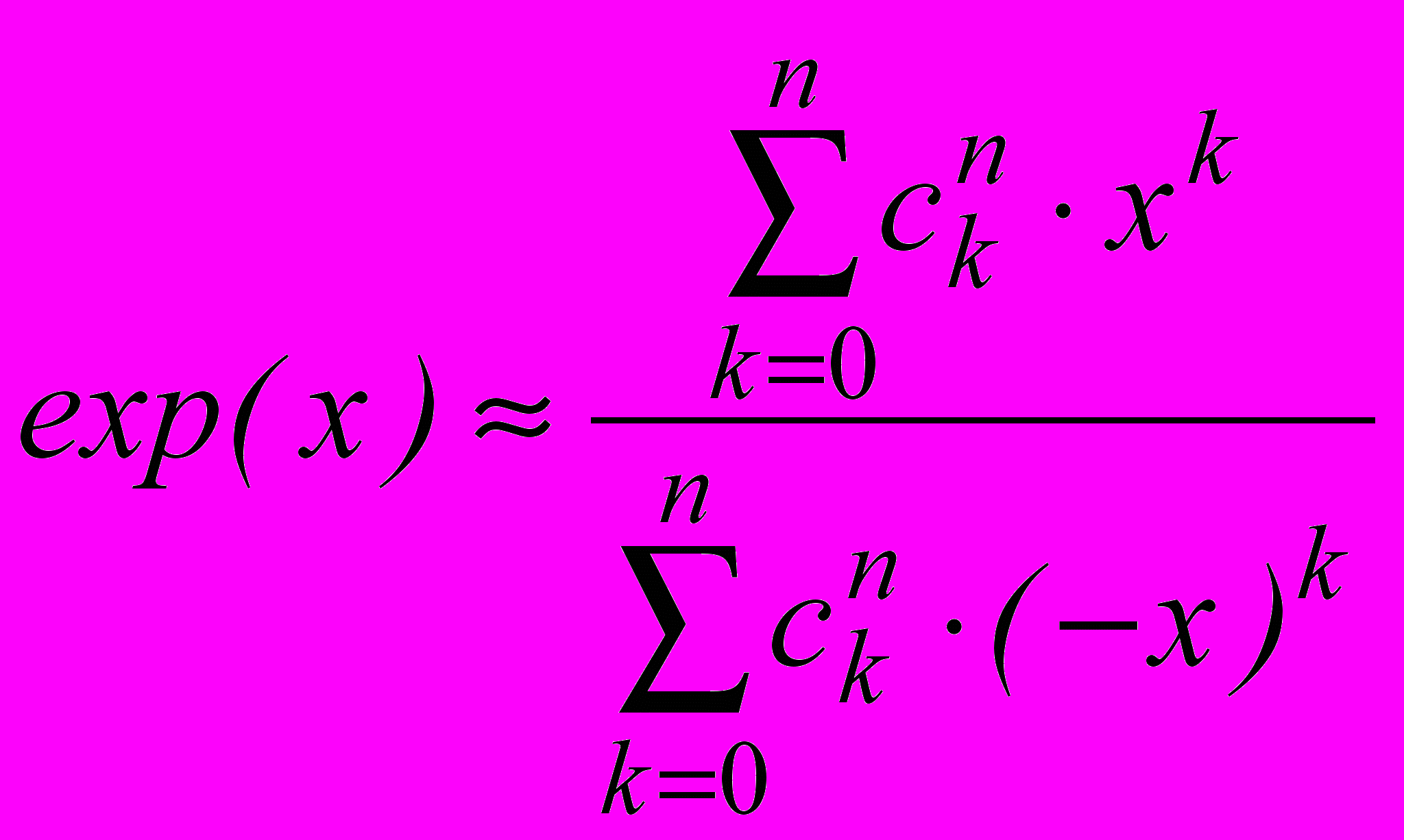 , где:
, где: 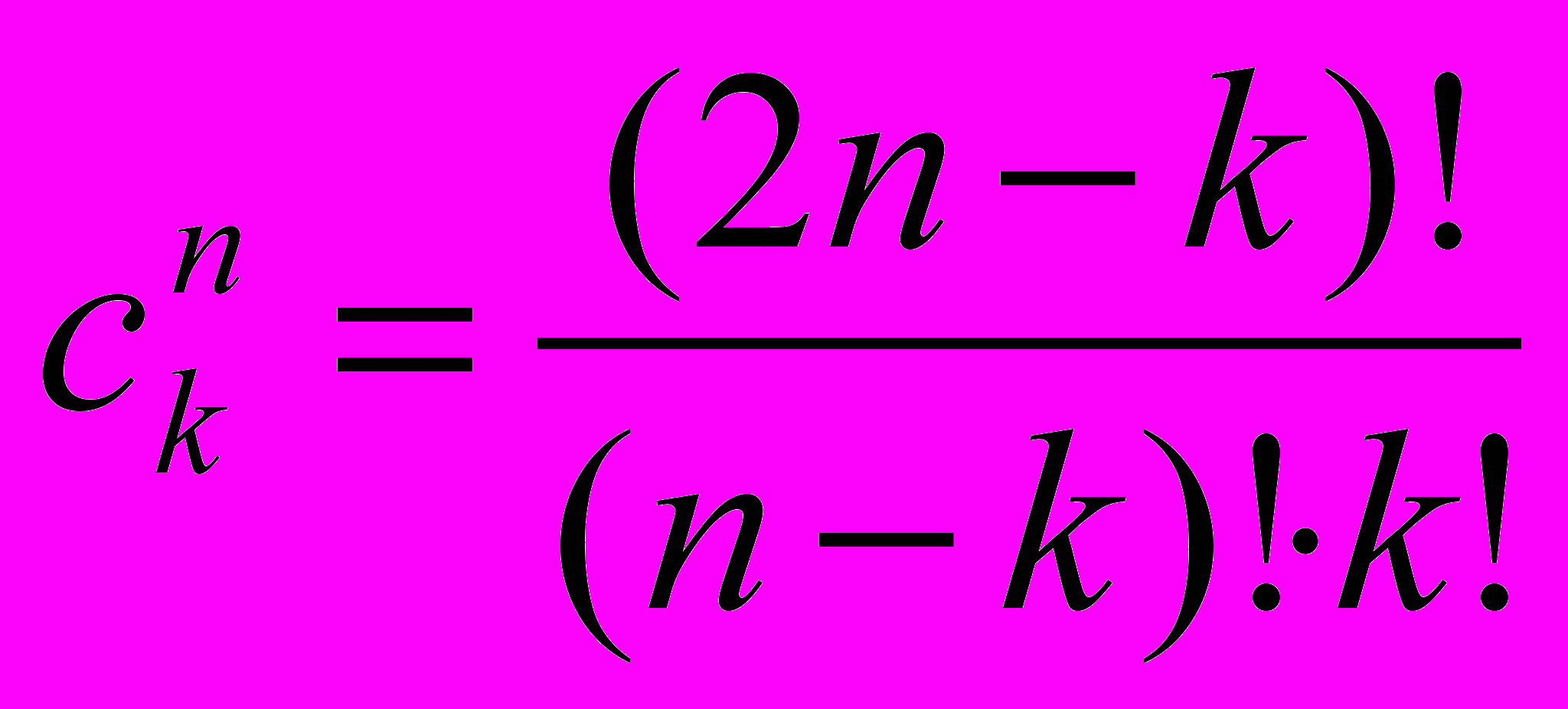 .
.Исследования показали, что подходящие дроби для этих разложений при ограниченном числе членов совпадают с приведенными выше для цепных дробей выражениями. Следовательно, данному методу присущи те же достоинства и недостатки, что и методу разложения в цепные дроби.
Сопоставительный анализ всех рассмотренных методов позволяет сделать вывод, что все они сводятся к вычислению некоторого многочлена высокой степени от аргумента. Отличия состоят только в составе и числе выполняемых операций необходимых для достижения требуемой точности получения результата. В таблице 2 для рассмотренных методов вычисления перечислены типы и количества выполняемых операций, необходимые для получения заданной точности вычисления. (Ns – количество сложений, Nm – количество умножений, Nd – количество делений)
Таблица 2
| Относительная погрешность | 10-1 % | 10-2 % | 10-3 % | 10-4 % | 10-5 % | 10-6 % | 10-7 % | 10-8 % | 10-9 % | 10-10 % | |
| Степенной ряд | Ns Nm Nd | 5 8 0 | 6 10 0 | 7 12 0 | 8 14 0 | 9 16 0 | 10 18 0 | 11 20 0 | 12 22 0 | 13 24 0 | 14 26 1 |
| Степенной ряд с остаточным членом | Ns Nm Nd | 4 6 0 | 5 8 0 | 6 10 0 | 7 12 0 | 8 14 0 | 9 16 0 | 10 18 0 | 10 18 0 | 11 20 0 | 12 24 0 |
| Многочлены Чебышева Выр-е 1.23 | Ns Nm Nd | 5 6 0 | 8 8 0 | 11 12 0 | 15 16 0 | 19 21 0 | 19 21 0 | | | | |
| Многочлены Чебышева Исходное выражение | Ns Nm Nd | 4 3 0 | 6 6 0 | 9 8 0 | 9 8 0 | 12 12 0 | 16 16 0 | 20 21 0 | 20 21 0 | | |
| Многочлены Чебышева Модифицированное выражение | Ns Nm Nd | 2 2 0 | 2 2 0 | 4 4 0 | 6 7 0 | 6 7 0 | 9 9 0 | 9 9 0 | 12 13 0 | 12 13 0 | 16 17 0 |
| Многочлены Лежандра | Ns Nm Nd | 6 9 0 | 7 11 0 | 9 13 0 | 10 15 0 | 12 17 0 | 13 19 0 | | | | |
| Многочленное приближение | Ns Nm Nd | 3 5 0 | 4 7 0 | 5 9 0 | 5 9 0 | 6 11 0 | 7 13 0 | 7 13 0 | 8 15 0 | 9 17 0 | 9 17 0 |
| Цепная дробь | Ns Nm Nd | 4 4 1 | 4 4 1 | 4 4 1 | 5 6 1 | 5 6 1 | 6 8 1 | 6 8 1 | 6 8 1 | 7 10 1 | 7 10 1 |
| Рациональное приближение | Ns Nm Nd | 6 8 1 | 6 8 1 | 6 8 1 | 8 11 1 | 8 11 1 | 8 11 1 | 8 11 1 | | | |
Анализ данных таблицы 2 показывает, что эффективность того или иного метода зависит от требуемой точности вычисления. Однако, в общем случае можно утверждать, что наиболее эффективным, с точки зрения получения заданной точности и минимизации количества выполняемых операций являются методы, основанные на использовании цепных дробей и многочленов Чебышева. При этом применения метода замены переменной, оптимизированной для заданного диапазона изменения аргумента, позволяет с меньшими затратами повысить степень аппроксимирующего многочлена, что делает его более предпочтительным с точки зрения экономии необходимых для реализации аппаратных ресурсов ПЛИС.
Во второй главе для основных математических операций, реализованных в САПР Quartus II фирмы Altera, исследуется взаимосвязь между разрядностью аргумента, ресурсами ПЛИС, и временем их выполнения. Исследования проведены для двух семейств ПЛИС: Cyclone II и STRATIX II.
Для реализации операции сложения-вычитания в САПР Quartus II фирмы Altera используется мегафункция lpm_add_sub. Исследование этой мегафункции показало, что аппаратные затраты на ее реализацию прямо пропорциональны разрядности аргумента, причем для обоих семейств аппаратные затраты практически одинаковы. Данная мегафункция предполагает оптимизацию получаемого технического решения либо по критерию минимизации скорости вычисления (параметр Maximize_Speed=10), либо требуемых аппаратных затрат (параметр Maximize_Speed=0) – логических блоков (ЛБ) ПЛИС. Проведенные исследования показали, что для выбранных семейств ПЛИС (Cyclone II и STRATIX II) в обоих случаях результат практической реализации получается одинаковым.
Для семейства Stratix II количество логических блоков ЛБ (Nлб), необходимое для реализации сумматора с разрядностью n равно:
Nлб = n + 1.
Для семейства Cyclone II при n≤48 справедлива аналогичная зависимость. При большем числе членов она приобретает вид:
Nлб = n + 3.
Для реализации блока умножения в САПР Quartus II используется стандартная мегафункция lpm_mult, которая, так же как и мегафункция lpm_add_sub предполагает оптимизацию умножителя либо по критерию минимизации скорости вычисления (параметр Maximize_Speed=10), либо по критерию уменьшения требуемых аппаратных затрат (параметр Maximize_Speed=0). Кроме этого, для реализации операции умножения могут быть использованы либо только логические блоки ПЛИС (ЛБ), либо специализированные аппаратные умножители, включенные в состав упомянутых семейств ПЛИС. В работе исследованы все возможные варианты реализации умножителей.
Исследования показали, что при реализации умножителя только с использованием ЛБ для ПЛИС семейства Stratix II оптимизация по параметру Maximize_Speed не дает различия в числе ЛБ и времени вычисления. Для ПЛИС семейства Cyclone II увеличения параметра Maximize_speed ведет к уменьшению времени вычисления и увеличению аппаратных затрат на реализацию. Зависимость числа ЛБ от разрядности аргумента носит квадратичный характер. В работе получены соответствующие аналитические зависимости. Для ПЛИС Cyclone II:
- при параметре maximize_speed = 0
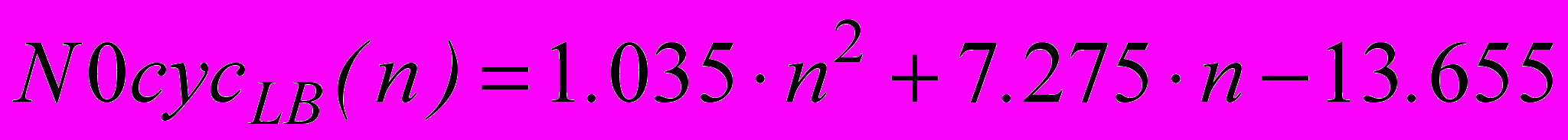 .
.
- при параметре maximize_speed = 10
 .
.
Для для ПЛИС семейства Stratix II
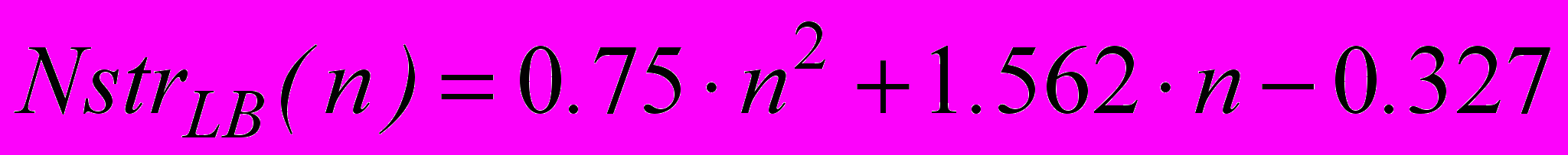 .
.Анализ результатов полученных для случая применения встроенных умножителей показывает, что оптимизация проекта по критерию speed для обоих типов ПЛИС не приводит к изменению требуемых аппаратных затрат и при увеличении разрядности сомножителей требуемое число дополнительных ЛБ для ПЛИС семейства Stratix II меньше, чем для ПЛИС семейства Cyclone II.
На рис.5 показаны полученные зависимости числа необходимых ЛБ (LB(n)) и встроенных умножителей (M(n)) от разрядности сомножителей (n). Из приведенных графиков следует, что искомые зависимости носят кусочно-линейных характер. При этом точками разрыва графиков являются переходы между числами разрядов
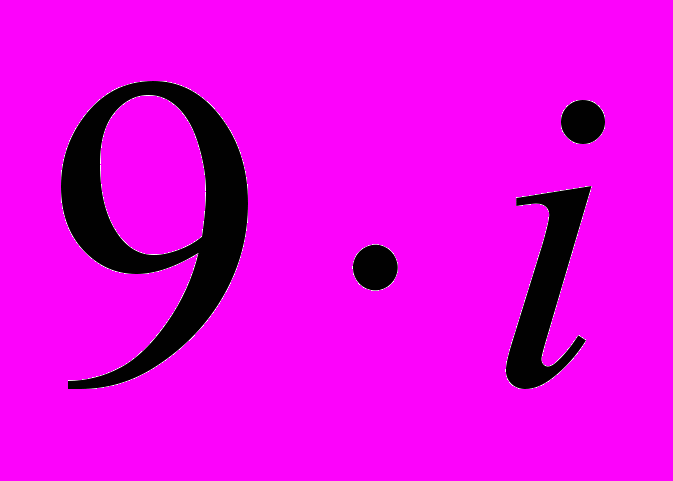 и
и 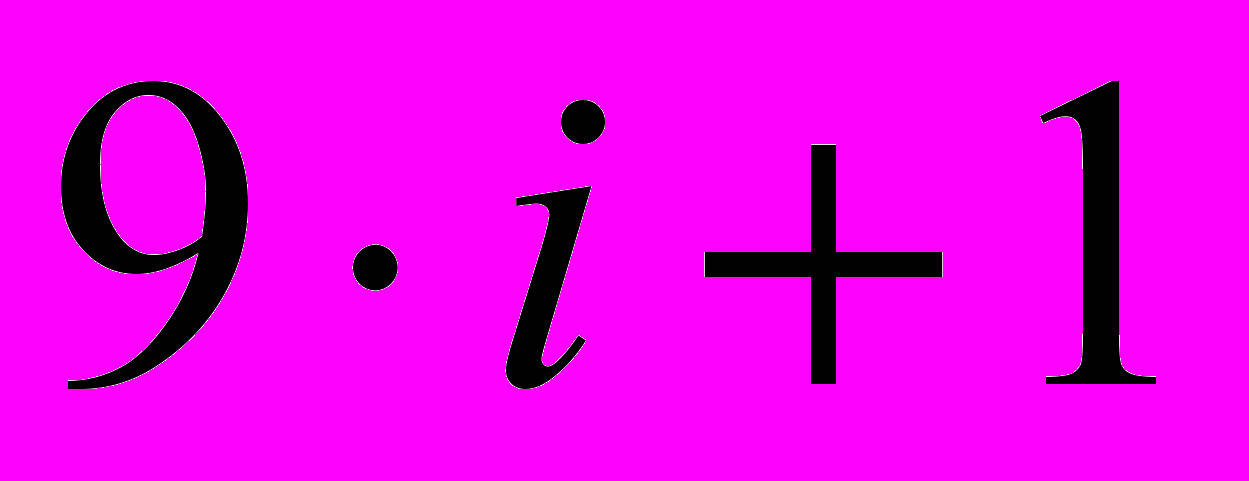 , что вполне объяснимо, так как в структуре ПЛИС использованы аппаратные умножители разрядности
, что вполне объяснимо, так как в структуре ПЛИС использованы аппаратные умножители разрядности 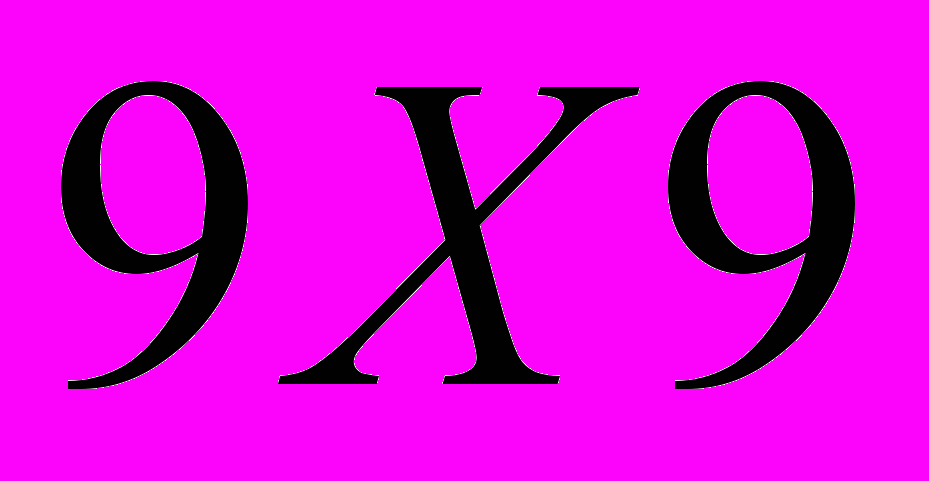 бит. Отметим так же, что для четных значений i (например, переход от 18 к 19 разрядам, или от 36 к 37 разрядам) сопровождается значительно большим увеличением требуемых аппаратных ресурсов, чем при нечетных i (9 разрядов 10 разрядов, или 27 разрядов 28 разрядов).
бит. Отметим так же, что для четных значений i (например, переход от 18 к 19 разрядам, или от 36 к 37 разрядам) сопровождается значительно большим увеличением требуемых аппаратных ресурсов, чем при нечетных i (9 разрядов 10 разрядов, или 27 разрядов 28 разрядов). 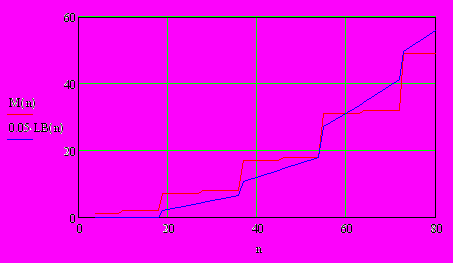 а) ПЛИС Cyclone II а) ПЛИС Cyclone II |  б) ПЛИС Stratix II б) ПЛИС Stratix II |
Рис.5
Полученная зависимость времени вычисления от разрядности аргументов, как и для операции сложения-вычитания носит линейный характер.
Полученные результаты подтверждают выдвинутую А. Н. Колмогоровым гипотезе n² о том, что сложность операции умножения, то есть количество простых операций выполняемых для получения произведения, пропорциональна квадрату разрядности сомножителей. Попытки уменьшить число простых операций при реализации умножения привели в разработке, так называемых методов быстрого умножения (метод "Divide and Conquer", его другие названия "Принцип Дихотомии", "Binary Splitting", и т.п.) является в настоящее время основой для построения различных алгоритмов быстрого вычисления различных функций. В работе с использованием этого подхода разработана программа для реализации быстрого умножения. Основой подхода является представление 2k разрядных двоичных аргументов в виде суммы двух чисел
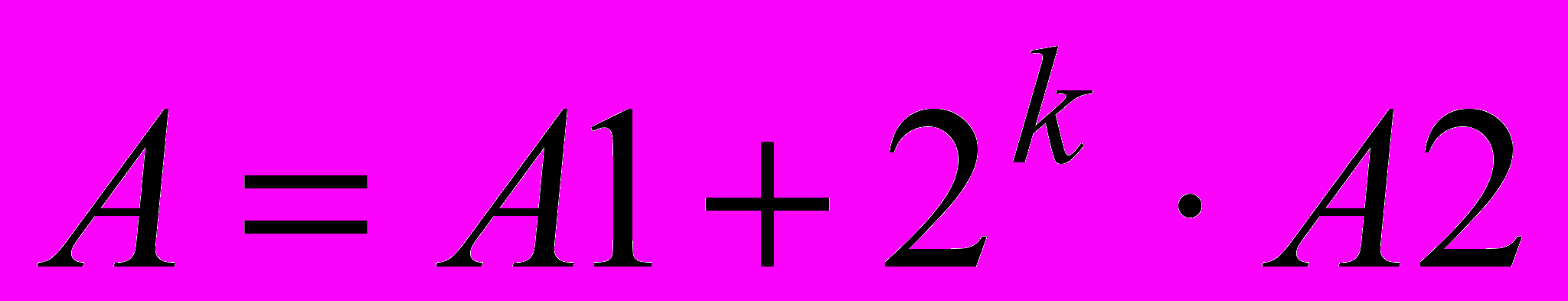 и
и 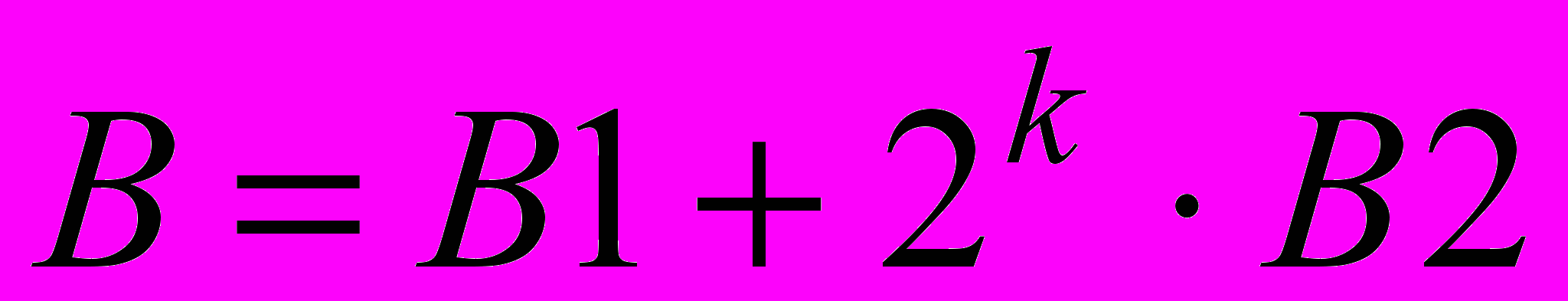 , где
, где  ,
, 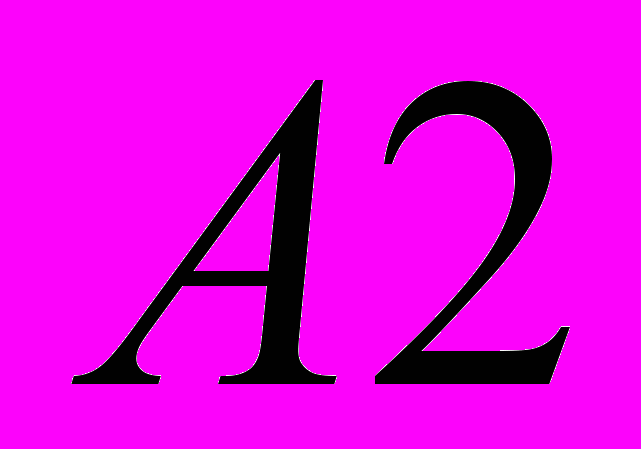 ,
, 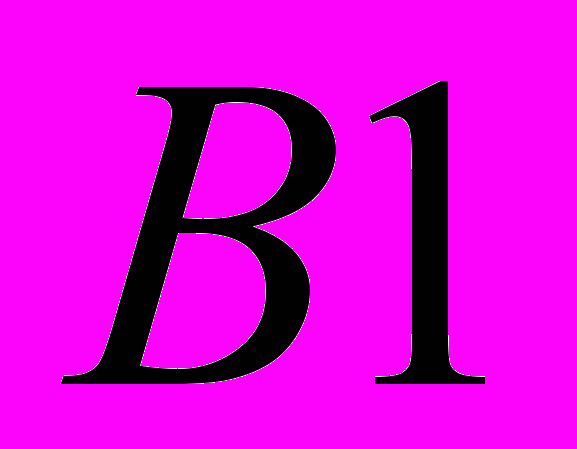 ,
, 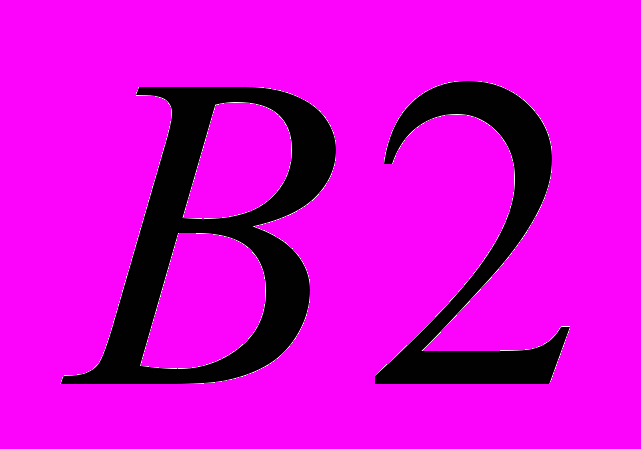 — k-значные числа и применения выражения
— k-значные числа и применения выражения 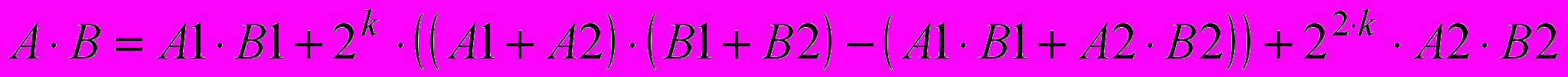
Уменьшения количества выполняемых операций достигается за счет выполнения умножений на целую степень используемой системы счисления. Для данного алгоритма разработана параллельная каноническая форма графа и программа, реализованная на языке AHDL. Проведенный вычислительный эксперимент показал, что при увеличении числа разрядов аргумента предложенная реализация операции умножения позволяет получить выигрыш как по требуемым ресурсам ПЛИС, так и по времени вычисления. Для различных методов компиляции и способов реализации получены области предпочтительного применения данного алгоритма.
Разработанный граф вычислительного процесса позволил определить длину его критического пути и оценить время вычисления:
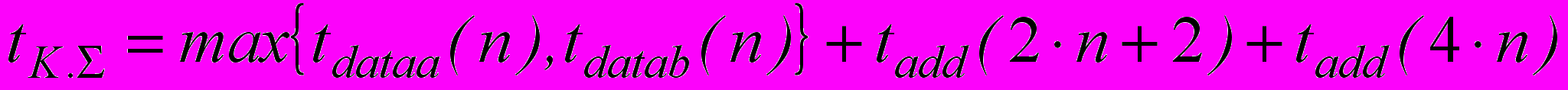 ,
,где:
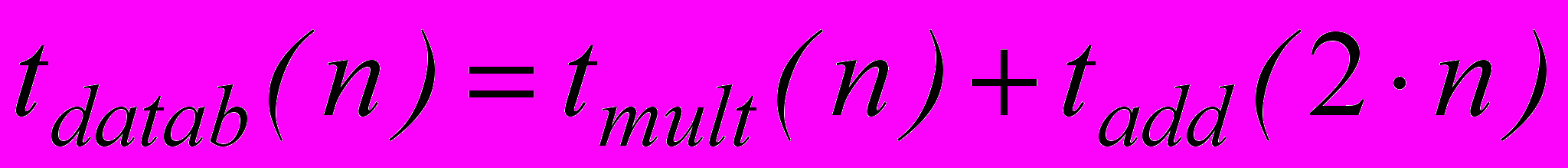 и
и 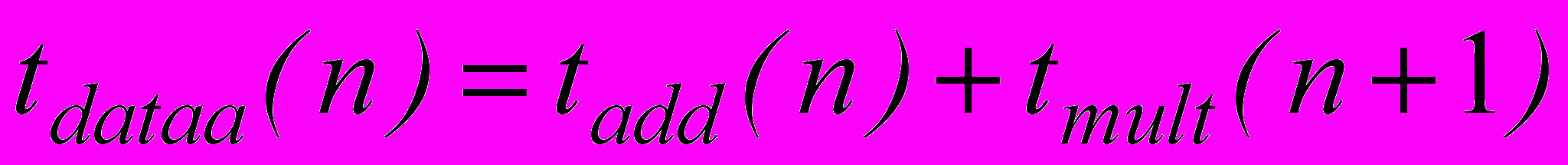 ;
;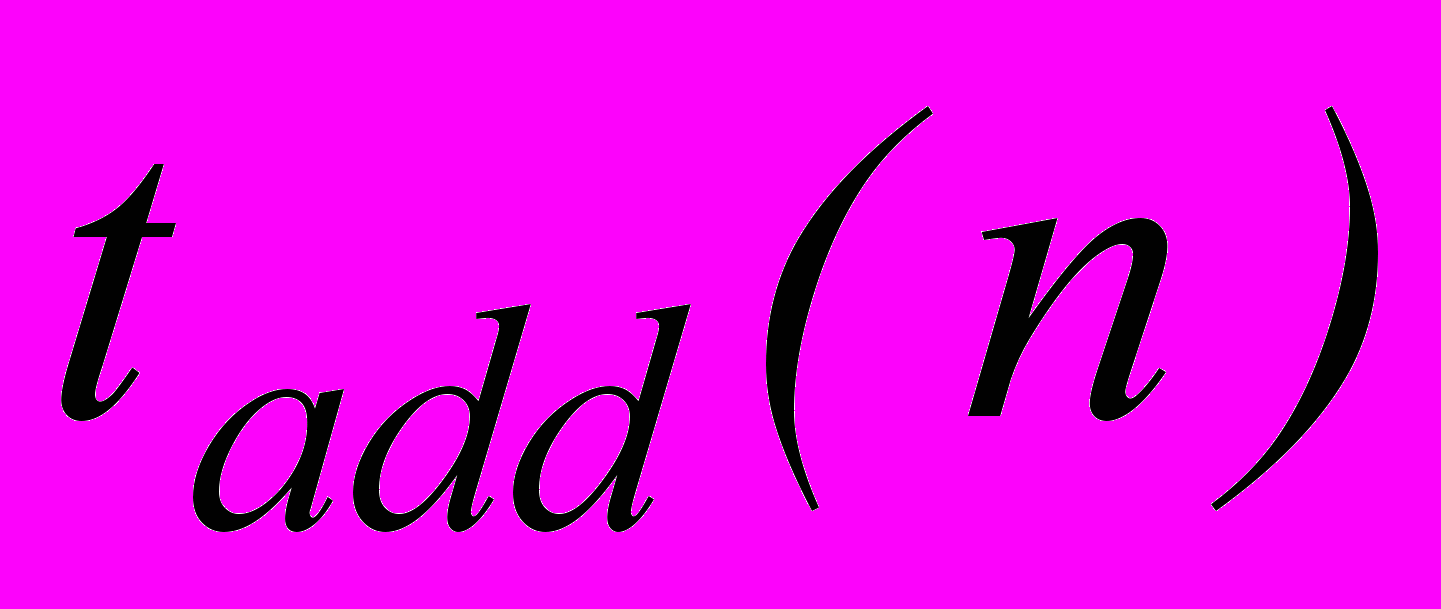 ,
, 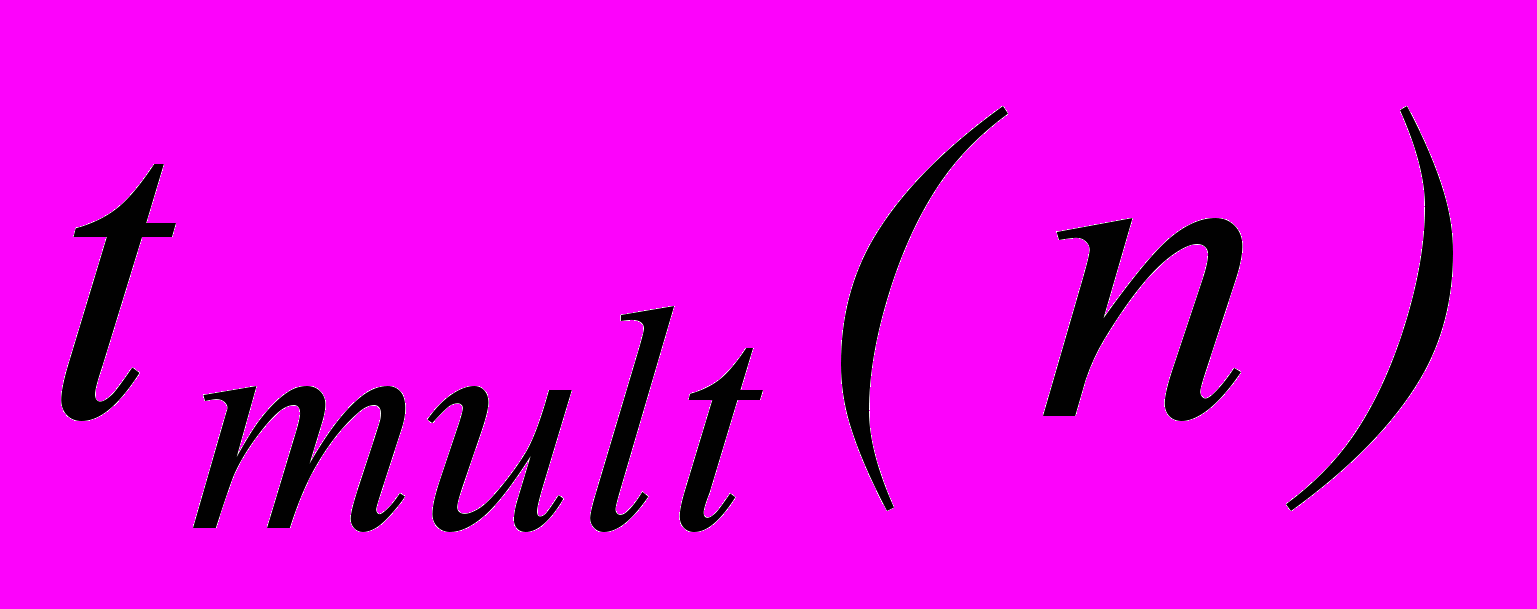 - соответственно времена выполнения операций сложения и умножения над n разрядными аргументами.
- соответственно времена выполнения операций сложения и умножения над n разрядными аргументами.Проведенные расчеты показали, что полученные ранее времена выполнения элементарных операций непосредственно не могут быть использованы в полученных выражениях.
 а) ПЛИС Cyclone II |  б) ПЛИС Stratix II |
Рис.6.
Объясняется это тем, что реально полученные времена складываются из трех составляющих: времени прохождения сигнал от входных выводов интегральной схемы до соответствующих логических блоков, времени выполнения операции (логической обработки сигнала) и времени прохождения сигнала от логических блоков до выходных выводов интегральной схемы. Для определения реального времени выполнения операции был проведен эксперимент, в котором исследовалась схема с двумя одинаковыми, последовательно включенными сумматорами. Результаты эксперимента показаны на рис.6 на которых
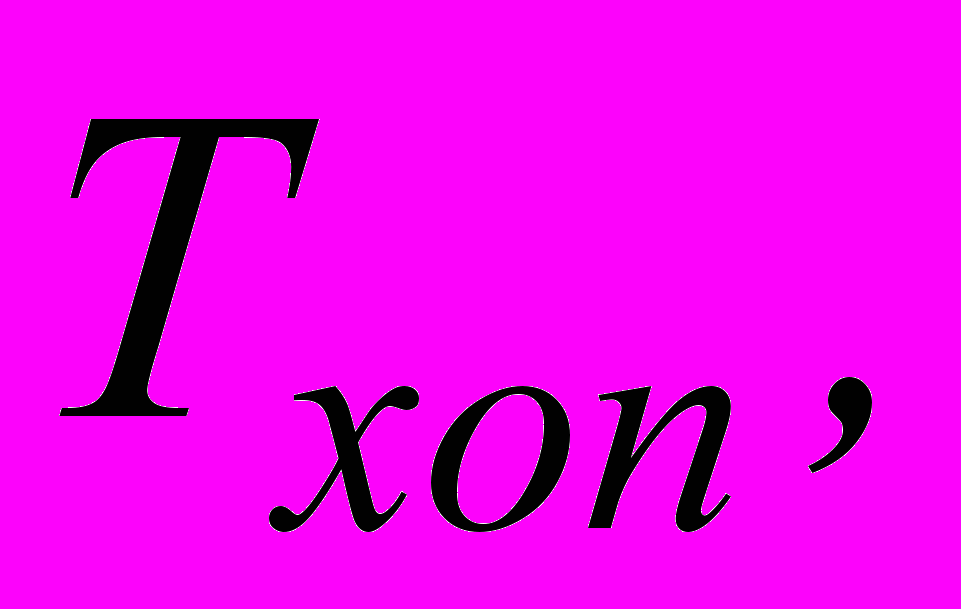
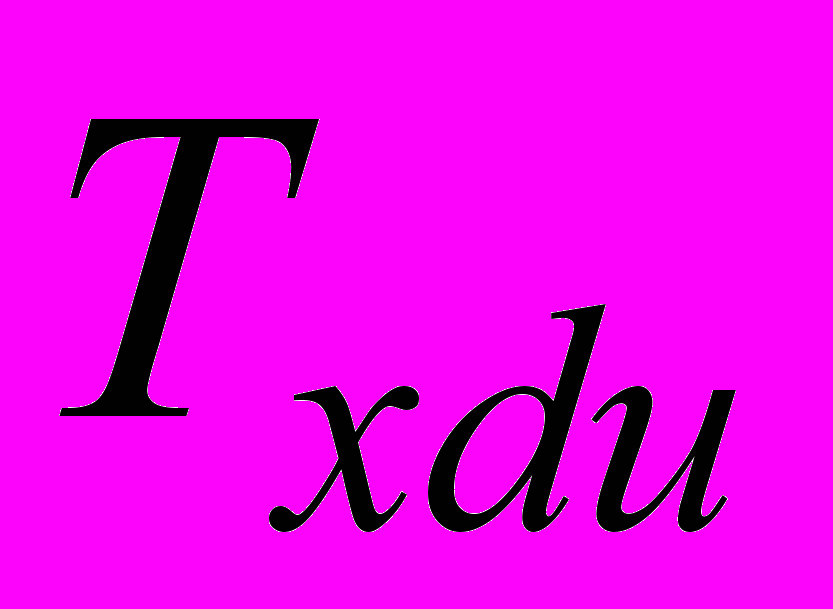 - соответственно времена вычисления с одним и двумя последовательно включенными сумматорами. Очевидно, что расстояние между приведенными зависимостями практически не зависит от разрядности аргументов. Отсюда следует вывод, что реально оценить время выполнения той или иной операции можно только путем проведения соответствующего эксперимента, так как времена передачи сигнала в ПЛИС соизмеримы с временем выполнения собственно операции.
- соответственно времена вычисления с одним и двумя последовательно включенными сумматорами. Очевидно, что расстояние между приведенными зависимостями практически не зависит от разрядности аргументов. Отсюда следует вывод, что реально оценить время выполнения той или иной операции можно только путем проведения соответствующего эксперимента, так как времена передачи сигнала в ПЛИС соизмеримы с временем выполнения собственно операции.Для операции целочисленного деления в САПР Quartus II существует мегафункцией lpm_devide. Ее исследование показало, что число ЛБ для реализации можно определить, используя следующие аппроксимирующие выражения:
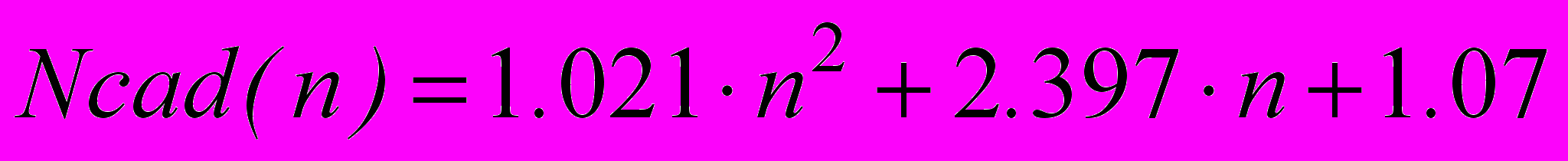
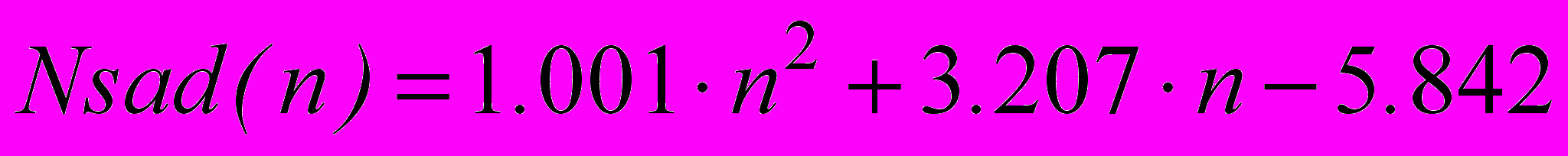
Реализация выполняется только на ЛБ, причем число этих блоков примерно на два порядка превышают ресурсы, необходимые для выполнения операции сложения-вычитания. При использовании только логических блоков требуемые аппаратные ресурсы на выполнения операций деления (мегафункция lpm_devide) и умножения (мегафункция lpm_mult) соизмеримы, однако время выполнения операции деления примерно на порядок превосходит время выполнения операции умножения, что говорит о последовательном алгоритме работы.
Проведенные исследования позволяют заключить, что при вычислении функции
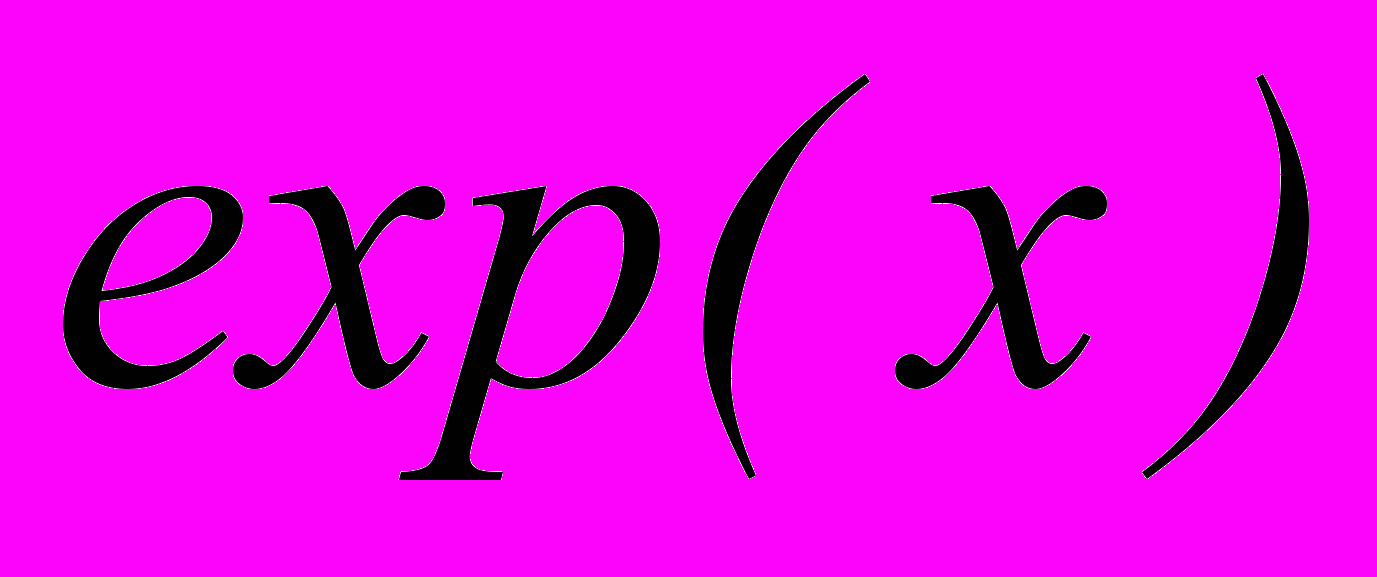 с помощью ПЛИС следует избегать алгоритмов, требующих выполнения операции деления и из двух выбранных в главе 1 методов предпочтение следует отдать методу, основанному на использовании многочленов Чебышева.
с помощью ПЛИС следует избегать алгоритмов, требующих выполнения операции деления и из двух выбранных в главе 1 методов предпочтение следует отдать методу, основанному на использовании многочленов Чебышева.В третьей главе рассмотрены способы организации вычисления, позволяющие уменьшить как время вычисления так и аппаратные затраты на реализацию вычислителя при произвольном диапазоне изменения аргумента. Показано, что для повышения точности вычисления аргумент целесообразно разбивать на две части: постоянную и расчетную. Окончательный вариант получается компиляцией значений функции для этих двух частей. Предложено два варианта реализации данного подхода. Первый (рис.7.а) предполагает выделение из аргумента целой и дробной частей. Значение функции от целой части хранится в блоке памяти, а значение от дробной части (внутренний аргумент) вычисляется вычислителем. Окончательный результат формируется умножением двух сомножителей. Второй вариант (рис.7.б) базируется на свойстве позиционной системы умножать или делить записанное число на основание системы счисления сдвигая его на требуемое число разрядов вправо или влево. В случае двоичной системы счисления это требует, чтобы постоянная часть аргумента была кратна
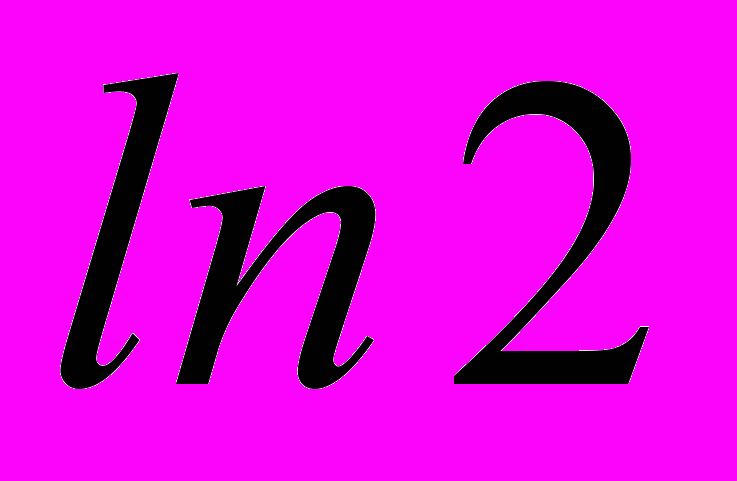 , а расчетная лежала в диапазоне
, а расчетная лежала в диапазоне 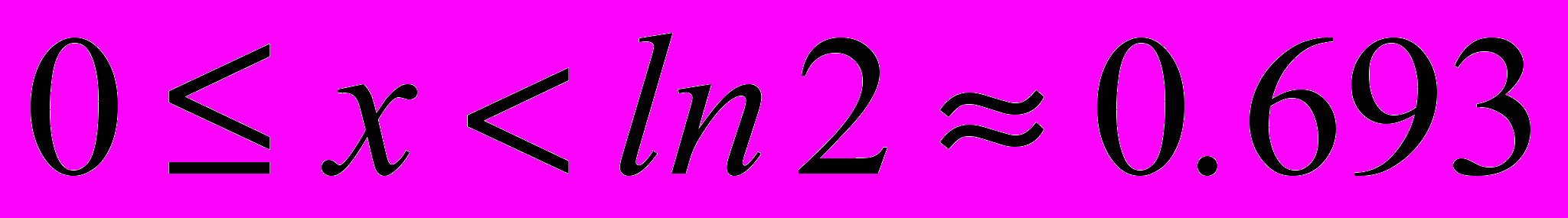 .
. В работе второй способ признан более предпочтительным. (Во-первых, дополнительный умножитель, заменяется на сдвиговый регистр, и, во-вторых, сужается расчетный диапазон изменения аргумента, что повышает точность вычисления.)
 а) |  б) |
Рис.7
Показано, что для аппроксимирующего многочлена 4-ой степени предлагаемое сужение диапазона расчетной части аргумента уменьшает относительную ошибку вычисления более чем в 50 раз.
В главе 1 было показано, что все методы вычисления сводятся к вычислению некоторого многочлена высокой степени. В главе рассмотрены вопросы построения последовательного и параллельного графов такого вычислительного процесса. Предложена процедура формирования параллельной канонической формы вычислительного процесса позволяющая по степени многочлена определить высоту и ширину графа, состав его ярусов. Последнее позволяет найти длину критического пути (фактически минимальное время вычисления) и аппаратные затраты на реализации. Результаты расчетов для некоторых многочленов сведены в таблицу 3
Таблица 3
| Степень многочлена | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Число ярусов умножения | 2 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 6 |
| Число ярусов сложения | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 |
| Число операций сложения | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Число операций умножения | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 |
