Geum.ru

Название диссертации

Вид материалаДокументы

Содержание


В четвертой главе
Пятая главы работы
Input→ (r)
Input→ (r)
Выводы по работе
Основные результаты
Подобный материал:
1   2

С использование предложенной процедуры построен граф вычислительного процесса для нахождения значения многочлена четвертой степени, соответствующего разложению функции по многочленам Чебышева при оптимизированной замене аргумента (i=2.86, j=2). Представленный граф содержит 6 ярусов. Последний ярус используется для фактического повышения степени аппроксимирующего многочлена до 8. Предложенное построение позволяет,



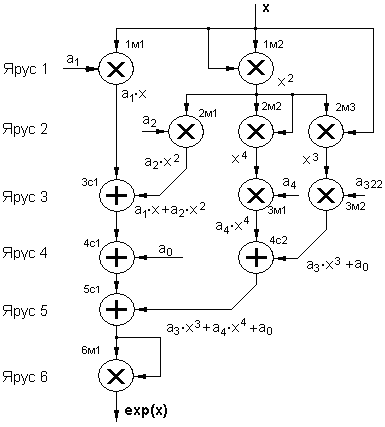Рис. 8.
во-первых, значительно сократить аппаратные затраты ПЛИС на реализацию, во-вторых, уменьшить время вычисления, и, в- третьих , значительно повысить точность вычисления.

В четвертой главе на базе основных положений теории погрешности рассмотрены вопросы, связанные с обеспечением требуемой точности при вычислении экспоненциальной функции. Показано, что точность вычисления функции определяется не только рассмотренной в главе 1 остаточной погрешностью, но и погрешностями округления и действия. Показана связь между числом

верных разрядов числа и предельной погрешностью его представления. Полученная связь между коэффициентами аппроксимирующего многочлена и параметрами многочленов Чебышева, позволила проводить дальнейшие исследования для обобщенного многочлена вида:

,

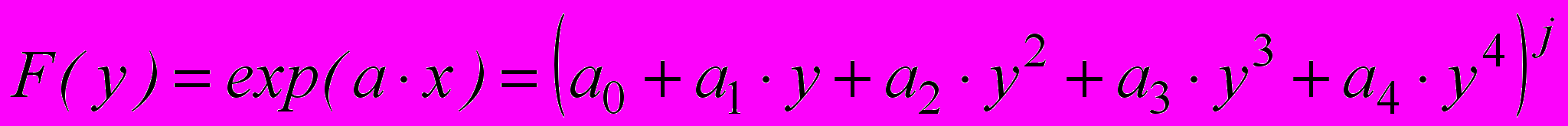где: ;

;

;

;

.

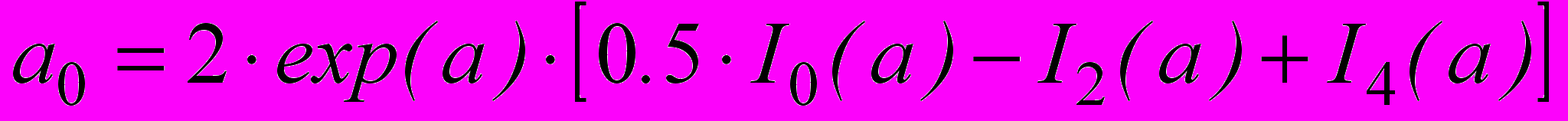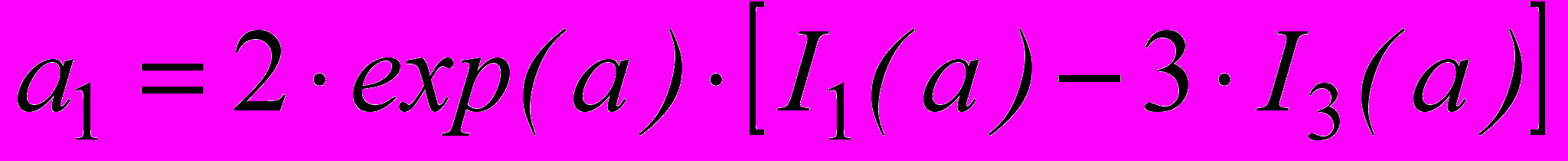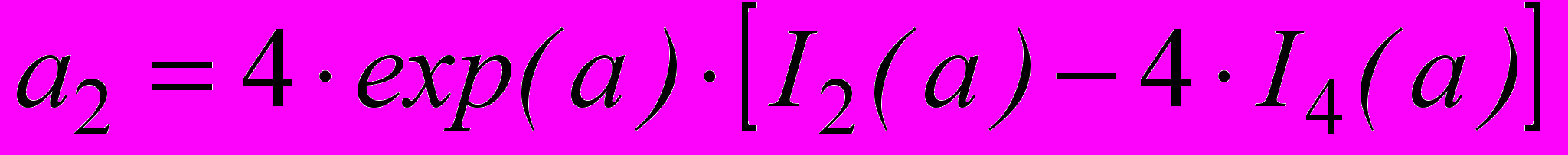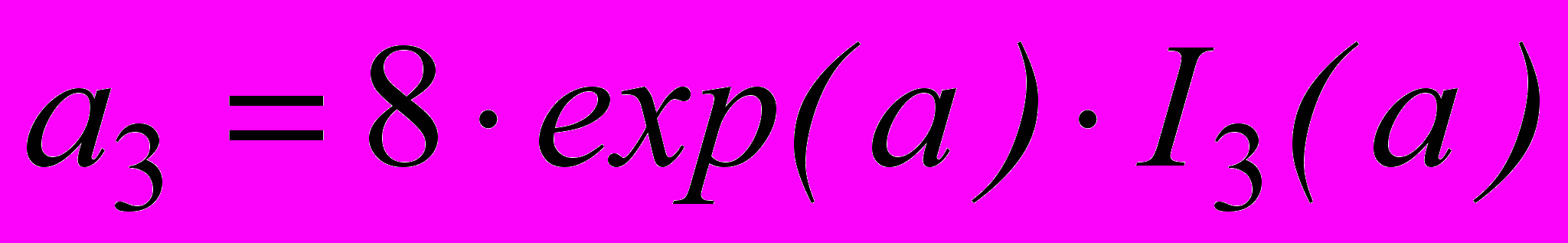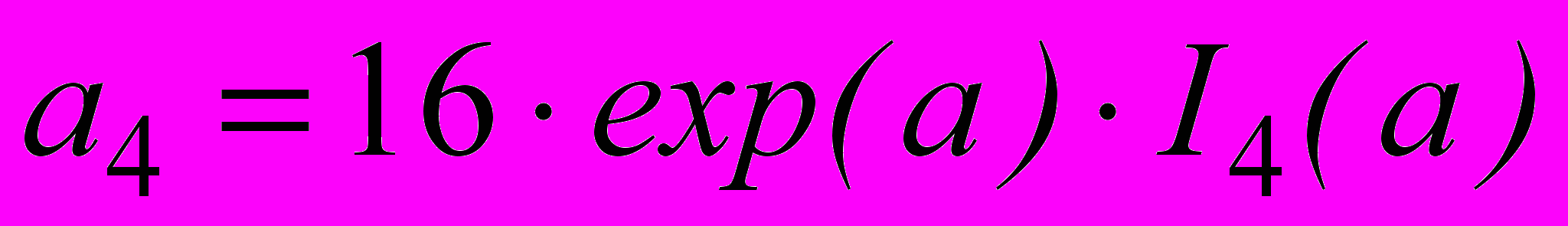В этом случае зависимость предельной абсолютной погрешности вычисления от параметров многочлена может быть представлена в виде:



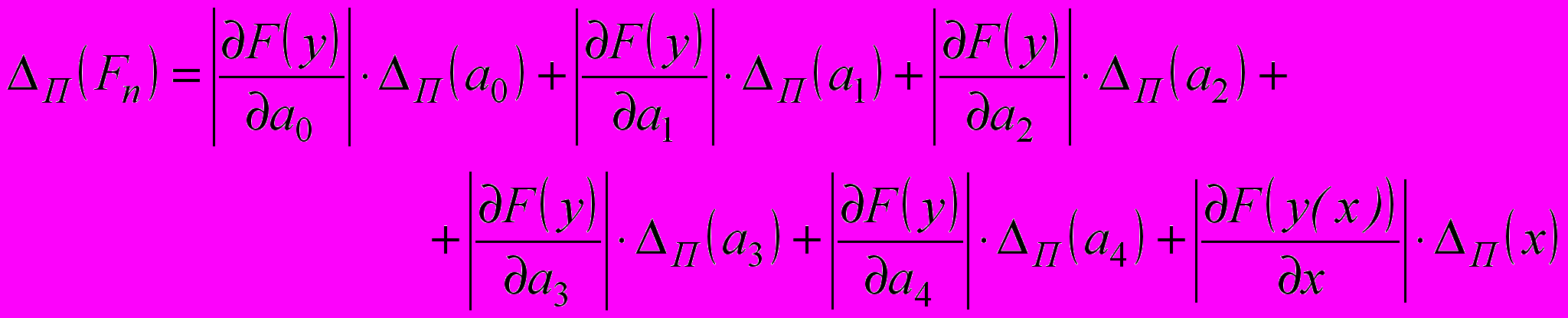
Для определения степени влияния абсолютных ошибок представления коэффициентов и аргумента функции на абсолютную ошибку вычисления предположим, было сделано предположение, что все исходные ошибки представления одинаковы 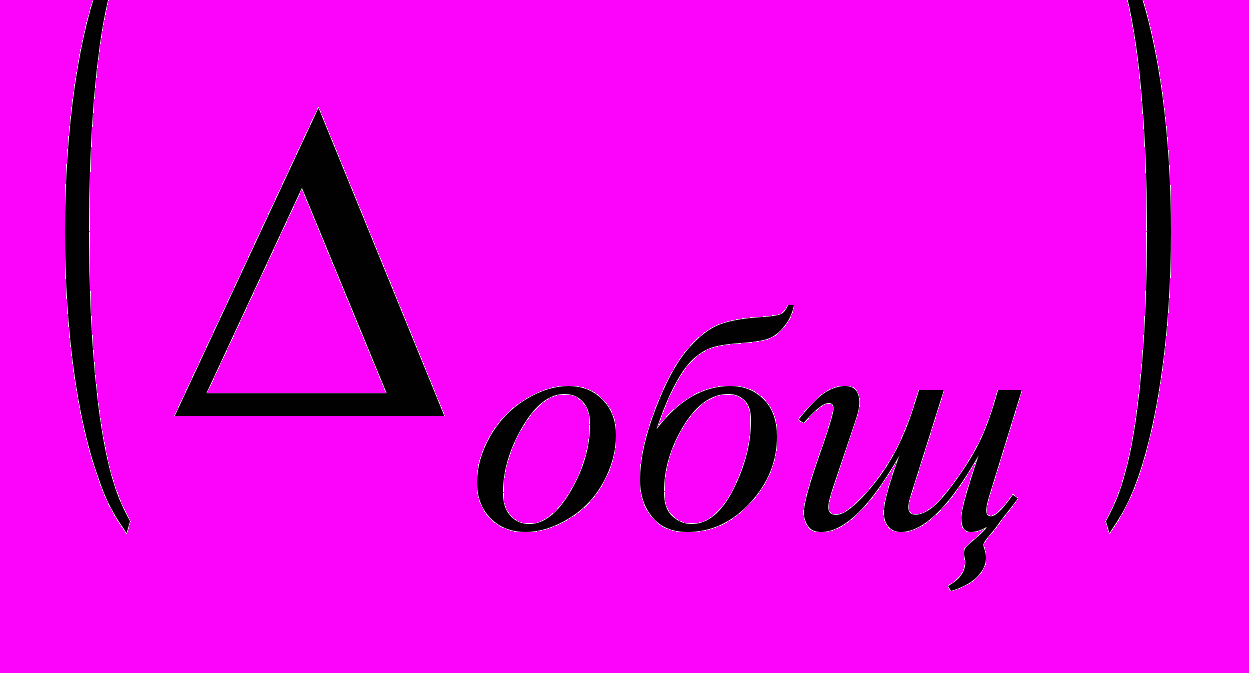. В этом случае полученное выражение можно переписать в следующем виде:

,

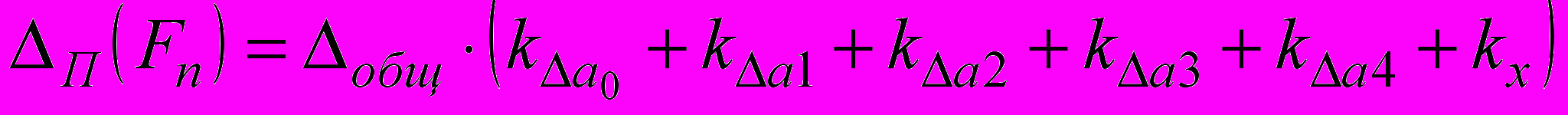где: 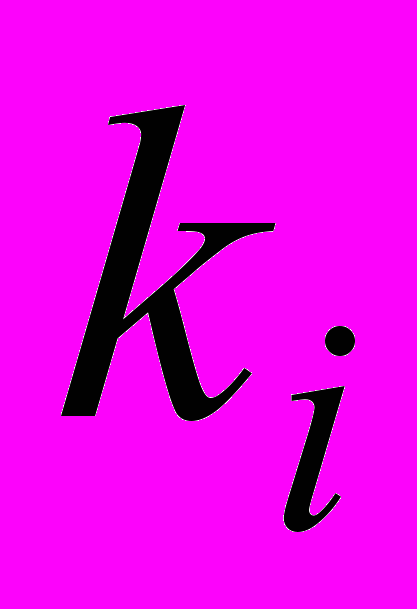- весовые коэффициенты влияния каждой составляющей на конечный результат.

Полученное выражение позволило определить весовые коэффициенты влияния на погрешность для следующих модификаций переменных в многочленах Чебышева: j=1, y=x; j=1, y=2x-1; j=1, y=2.86x-1; j=1, y=3x-1; j=2, y=2x-1; j=2, y=2.86x-1; j=2, y=3x-1. Для каждого из рассмотренных случаев получены значения весовых коэффициентов, позволившие определить оптимальные, с точки зрения точности вычисления, соотношения разрядностей представления аргумента и используемых коэффициентов аппроксимирующего многочлена.

Проведенные исследования позволили, для всех рассмотренных случает, получить зависимости суммарной относительной погрешности вычисления от разрядности аргументов (см.рис.9). Из приведенных зависимостей следует, что для каждого метода замены переменных в многочлене Чебышева существует предельное число разрядов представления аргумента, дальнейшее увеличение которого не ведет к повышению точности вычисления.



Рис.9.

Пятая главы работы посвящена разработке пакета прикладных программ, предназначенных для реализации предложенных алгоритмов и проведению вычислительного эксперимента, с целью подтверждение полученных в работе положений и рекомендаций.

Для структуры вычислителя рис.7.б предложено два варианта выполнения блока подготовки данных. Первый (рис.10.а) использует два дополнительных умножителя и реализует прямой метод преобразования. Это позволяет максимально сократить время получения результата. Второй (рис.10.б) построен на последовательном принципе, что сокращает необходимые ресурсы ПЛИС, но ведет к увеличению времени вычисления. В приложении работы представлены, написанные на языке AHDL программы для реализации обоих вариантов построения.



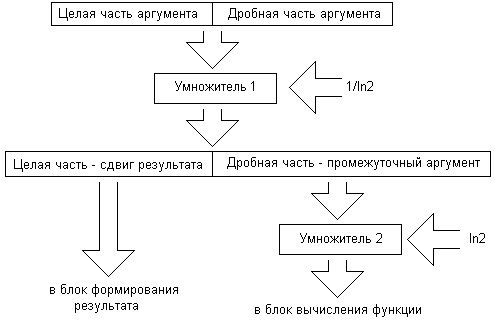а)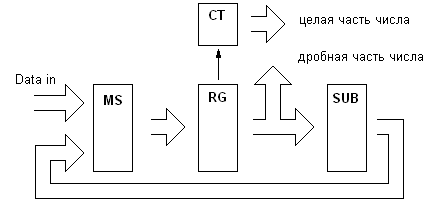


б)

Рис.10

В таблице 4 приведены рассчитанные с использованием результатов главы 4 рекомендуемые соотношения между разрядностями представления аргументов (R) и коэффициентов аппроксимирующего многочлена. С использованием графа рис.8 и рекомендаций таблицы 4 на языке AHDL была разработана программа для вычисления экспоненциальной функции при условии 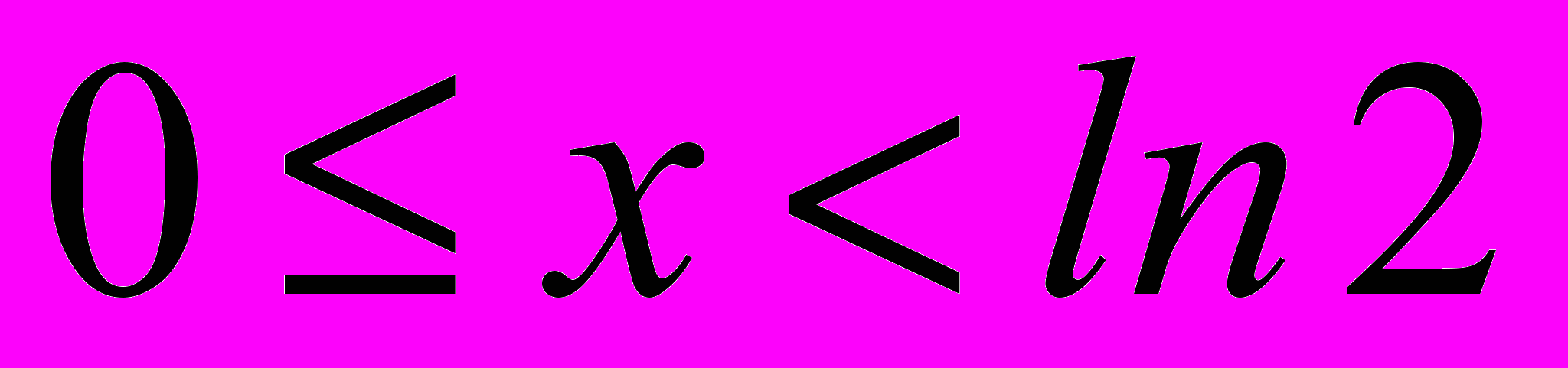. Данная программа явились основой для проведения вычислительного эксперимента с целью подтверждения полученных в работе теоретических положений.

Таблица 4.

Узел графа
dataA
dataB
Result

1м1
a1→(R+1)
INPUT→ (R)
(R)+1

1м2
INPUT→ (R)
INPUT→ (R)
(R-1)+2

2м1
a2→(R+1)
1M2→ (R-1)+2
(R-1)+2

2м2
1M2→ (R-1)+2
1M2→ (R-1)+2
(R-2)+2

2м3
1M2→ (R-1)+2
INPUT→ (R)
(R-1)+2

3с1
1M1→ (R)+1
2M1→ (R-1)+2
(R-1)+2

3м1
2M2→ (R-2)+2
a4→(R)
(R-2)+2

3м2
2M3→ (R-1)+2
a3→(R)
(R-1)+1

4с1
3S1→ 1+(R-1)+2
a0→(R+2)
(R)+2

4с2
3M1→ (R-2)+2
3M2→ (R-1)+1
(R-2)+2

5с1
4S1→ (R)+1
4S2→ 1+(R-2)+2
(R-1)+2

6м1
5S1→ (R-1)+2
5S1→ (R-1)+2
REZ→ (R-2)+2

В работе для всех рассмотренных ранее случаев (j=1, y=x; j=1, y=2x-1; j=1, y=2.86x-1; j=1, y=3x-1; j=2, y=2x-1; j=2, y=2.86x-1; j=2, y=3x-1) определены значения коэффициентов аппроксимирующего многочлена и получены зависимости ошибки вычисления от значения аргумента. Для случая j=2, y=2.86x-1 получена зависимость ошибки вычисления от числа разрядов аргумента, подтвердившая положение о том, что для каждого случая представления существует некоторое предельное число разрядов аргумента, дальнейшее увеличение которого не ведет к повышению точности вычисления.

В таблице 5 приведены основные результаты вычислительного эксперимента. В графе «Число разрядов результата» приведено количество правильных разрядов результата, соответствующее данному методу аппроксимации. Таблица 5

Метод замены
Число разрядов
Относительная ошибка %
Число ЛБ
Число умножителей
Время счета

аргумент
результат

j=1, y=x
17
12
5.25·10-4
72
14
29.25nS

j=1, y=2x-1
18
16
3.08·10-5
214
26

33.75nS

j=1, y=3x-1
23
18
9.66·10-6
1322
26

48.54nS

j=1, y=2.86x-1
23
19
4.05·10-6
1290
26

47.15nS

j=2, y=2x-1
25
21
1.9·10-6
1696
36

60,02nS

j=2, y=2.86x-1
29
23
3.18·10-7
3552
36

76.61nS

j=2, y=3x-1
28
22
7.05·10-7
3304
36
72.85nS

В этой же таблице приведено число необходимых для реализации логических блоков и встроенных умножителей ПЛИС. Эксперимент показал, что нехватка для реализации выбранного алгоритма встроенных умножителей ведет к резкому возрастанию числа необходимых логических блоков и времени вычисления. В таблице 6 приведены результаты вычислительного эксперимента для случая j=2, y=2.86x-1 при условии, что ПЛИС содержит требуемое число встроенных умножителей. Таблица 6

Число разрядов
Время счета
Число логических блоков (LB2)
Число 9 бит умножителей (M2)

29
61,56 nS
875
64

27
60,01 nS
786
62

24
57,62 nS
655
56

22
55,55 nS
543
56

20
54,09 nS
457
56

18
44,25 nS
236
37

16
33,85 nS
50
16

14
33,79 nS
44
16

12
33,68 nS
38
16

10
32,76 nS
32
16

8
30,38 nS
26
8

Из таблицы следует, что для 29 разрядного аргумента полученное время вычисления уменьшилось примерно на четверть. Полагая, что времена прохождения сигнала от входных выводов к логической части ПЛИС и обратно в обоих экспериментах остаются неизменными, можно утверждать, что получаемый в этом случае выигрыш по быстродействию значительно превышает 25%.


Выводы по работе

Проведенные исследования позволили получить следующие результаты:
  1. Проведен сопоставительный анализ известных методов численного определения значения экспоненциальной функции и выявлена зависимость остаточной погрешности вычисления от вида аппроксимирующего многочлена. Показано, что все известные методы могут быть сведены к вычислению многочлена высокого порядка. При этом повышение точности требует сужения диапазона изменения аргумента и использовании для вычисления значения функции от отрицательного аргумента соотношения .
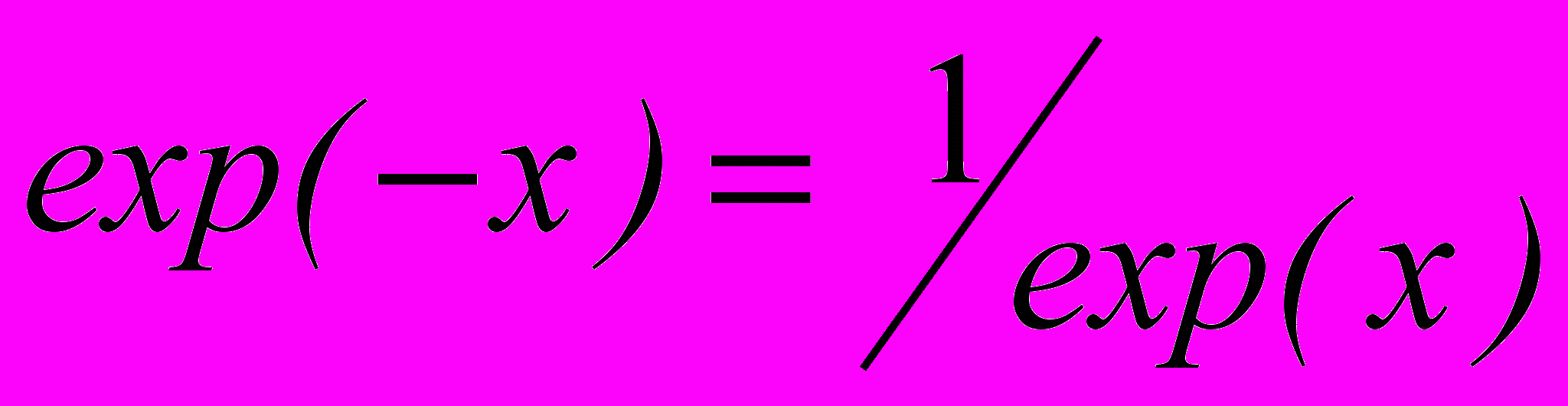  2. Для разложения функции в степенной ряд вида 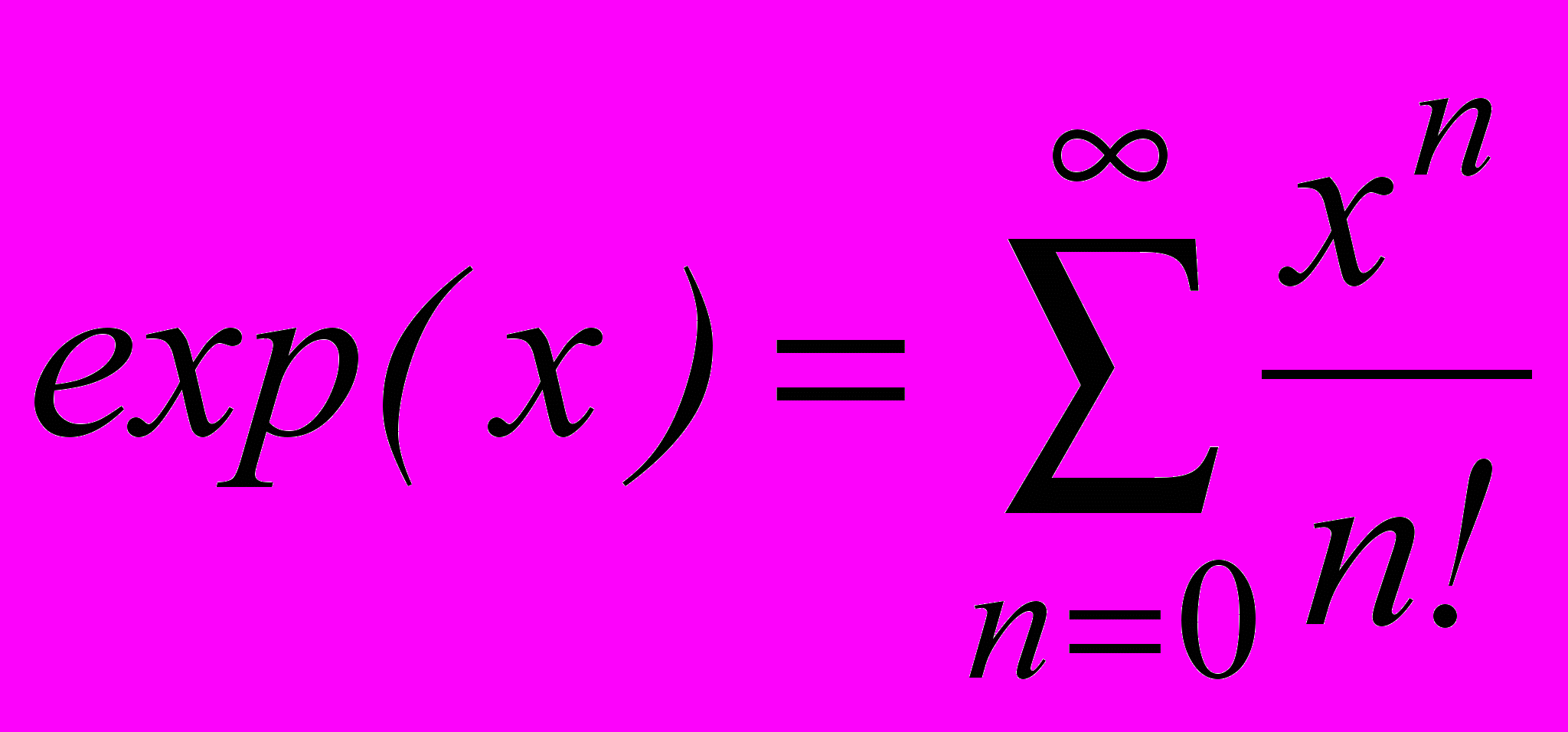предложена методика получения корректирующего коэффициента, компенсирующего остаточную погрешность, обусловленную ограничением числа членов расчетного степенного ряда. Получены аналитические выражения для корректирующего коэффициента при 5 членах ряда, позволяющие на 3 порядка повысить точность вычисления функции.
  3. Для метода многочленного приближения предложена методика определения коэффициентов аппроксимирующего многочлена из условия равенства максимумов модулей относительной ошибки на всем диапазоне изменения аргумента. Составлен алгоритм и программа вычислений и определены коэффициенты аппроксимирующих многочленов степеней 3..9. Показано, что аппроксимирующий многочлен необходимо конструировать под заданное число членов и их отбрасывание приводит к резкому снижению точности вычисления. Применение предложенных разложений для многочлена 7 степени позволило относительно известного разложения поднять точность вычисления на 3 порядка.
  4. Показано, что с точки зрения реализации на ПЛИС, наиболее перспективным является метод использующий многочлены Чебышева, с оптимизированной под заданный диапазон изменения аргумента заменой переменных. Предложена методика модификации переменной в многочлене Чебышева из условия получения максимальной точности вычисления при заданном диапазоне изменения аргумента. На основе предложенной методики найдено, что для диапазона изменения аргумента 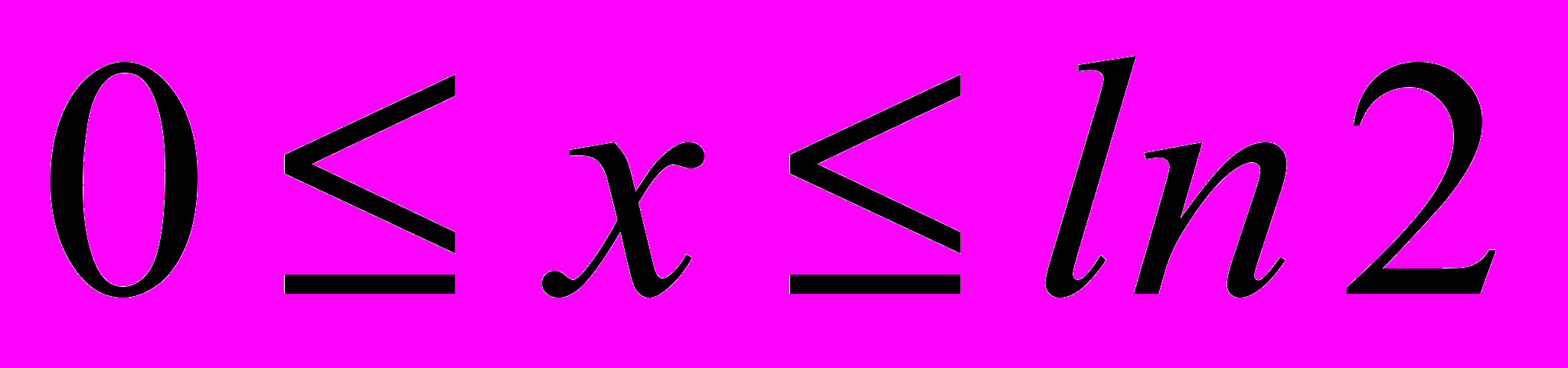оптимальной является подстановка переменной в многочлене Чебышева вида 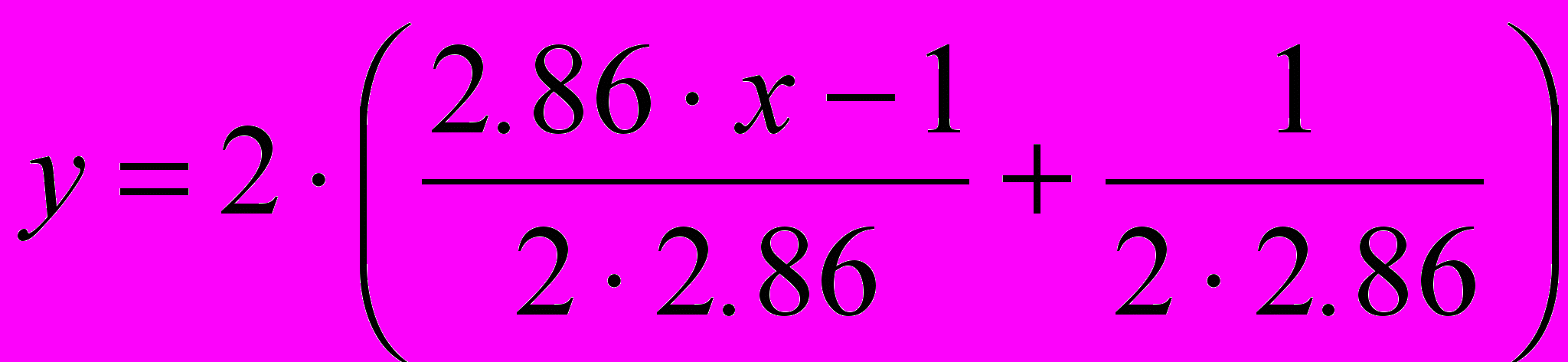. Это при минимизации аппаратных затрат на реализацию позволяет в два раза повысить степень аппроксимирующего многочлена, что для случая аппроксимирующего многочлена четвертого порядка более чем на три порядок повышает точность вычисления функции. Повышение порядка исходного аппроксимирующего многочлена приводит к еще большему выигрышу по точности вычисления.
  5. Для стандартных мегафункций САПР Quartus II lpm_add_sub и lpm_mult, реализующих операции сложения-вычитания и умножения, получены аналитические зависимости, связывающие необходимые аппаратные ресурсы ПЛИС и время выполнения операции с разрядностью операндов.
  6. Разработан и применительно к реализации на ПЛИС оптимизирован по требуемым аппаратным ресурсам алгоритм быстрого умножения, обеспечивающий сокращение битовой сложности вычисления. Для разработанного алгоритма получена аналитическая зависимость требуемых аппаратных ресурсов от разрядности аргументов. Показано, что при увеличении разрядности аргументов применение разработанного алгоритма позволяет сократить как требуемые аппаратные ресурсы, так и время вычисления. Для различных методов реализации и типов ПЛИС определены предпочтительные области применения разработанного алгоритма.
  7. Разработаны алгоритмы вычисления, позволяющие вычислять значение функции при произвольном диапазоне изменения аргумента. Получены зависимости точности вычисления и количества выполняемых математических операций от расчетного диапазона изменения аргумента. Показано, что с точки зрения обеспечения требуемой точности вычисления при требовании минимизации аппаратных ресурсов ПЛИС на реализацию, оптимальным является расчетный диапазон изменения аргумента, определяемый условием .
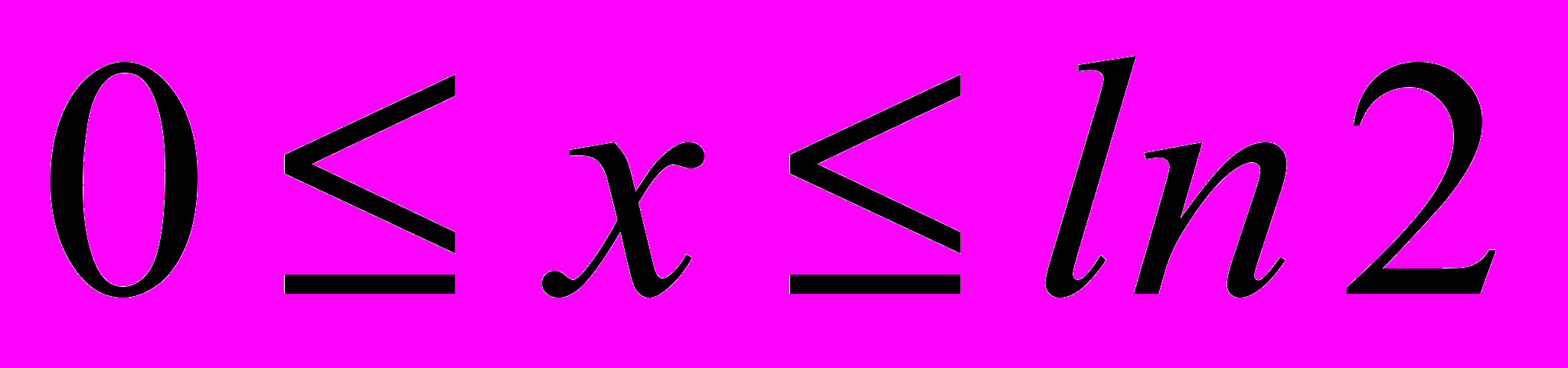  8. Предложена процедура построения параллельной канонической формы графа, определяющего вычисление степенного многочлена, и получены выражения определяющие зависимость длины его критического пути от степени используемого многочлена. С использованием предложенной процедуры разработана оптимальная с точки зрения времени вычисления и требуемых аппаратных ресурсов параллельная каноническая форма графа вычислительного процесса, базирующаяся на использовании разложения функции по многочленам Чебышева. Найдены зависимости времени вычисления и необходимых аппаратных ресурсов при реализации на ПЛИС от степени аппроксимирующего многочлена.
  9. Показано, что при вычислении функции 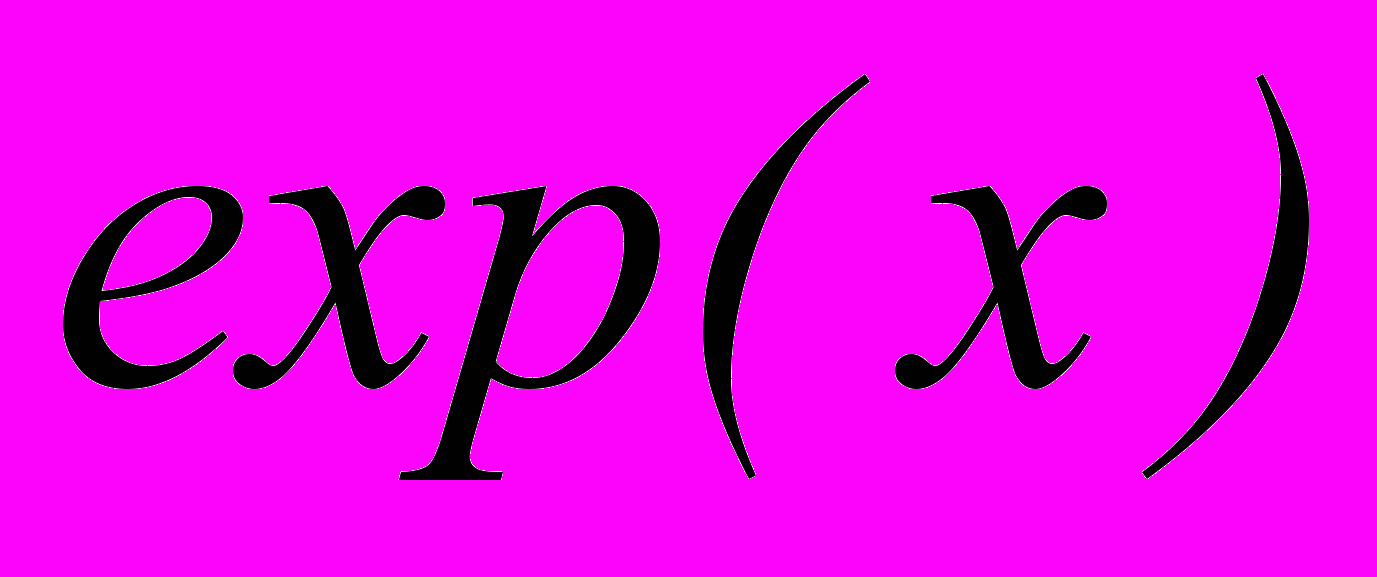ошибка вычисления определяется суммой остаточной погрешности, погрешности округления и погрешности действия. При этом последние две составляющие могут быть сколь угодно уменьшены увеличением числа разрядов используемых констант и аргумента. Поэтому определяющее значение при выборе метода вычисления играет остаточная погрешность. Получены соотношения, позволяющие оценить долю всех существующих погрешностей в суммарной ошибке вычисления функции.
  10. Для различных методов представления аргумента в многочленах Чебышева найдено граничное значение максимального числа разрядов представления аргумента и показано, что его дальнейшее увеличение не ведет к повышению точности вычисления. При числе разрядов аргумента менее критического, значение предельной относительной ошибки вычисления практически не зависит от вида используемого аппроксимирующего многочлена, что создает предпосылки для унификации вычислительной процедуры и алгоритма функционирования устройства, предназначенного для вычисления значения экспоненциальной функции, то есть позволяет на основе предложенного алгоритма синтезировать стандартную мегафенкцию.
  11. Разработана структура вычислителя, обеспечивающего вычисление экспоненциальной функции от произвольного аргумента. С применением языка описания аппаратуры AHDL разработаны подпрограммы для реализации всех блоков разработанной структуры.
  12. С использованием предложенной структуры вычислителя проведен вычислительный эксперимент, показавший достоверность полученных в диссертации теоретических положений. Поэтому предложенный алгоритм работы может быть положен в основу разработки специализированной мегафункции для вычисления значения экспоненциальной функции. При этом изложенные в работе методические подходы могут явиться основой для разработки алгоритмов вычисления многочленов более высоких степеней.


Основные результаты диссертации опубликованы в следующих работах:
  1. Мо Чжо Чо. Особенности организации вычисления экспоненциальной функции на ПЛИС – Тезисы докладов Международной молодежной научной конференции «ХХХII Гагаринские чтения», том 4, секция 29 стр. 90, 2006 г.
  2. Мо Чжо Чо. Организация вычисления экспоненциальной функции на ПЛИС – Тезисы докладов Международной молодежной научной конференции «ХХХIII Гагаринские чтения», том 4, секция 20 стр. 138, 2007 г.
  3. Мо Чжо Чо. Вычисления экспоненциальной функции на ПЛИС – Журнал «Современные наукоемкие технологии» Российская академия естествознания, № 4, стр. 113..114 , 2008г.
  4. Мо Чжо Чо. Особенности организации операции умножения на ПЛИС – Журнал «Современные наукоемкие технологии» Российская академия естествознания, № 4, 2008г. стр. 99.
  5. Мо Чжо Чо. Опадчий Ю.Ф. Алгоритм вычисления показательной функции на ПЛИС. – Сб. трудов Всероссийской научно-технической конференции «Новые материалы и технологии» том.3 Москва., 11..13 ноября 2008г. стр. 113…115
  6. Мо Чжо Чо. Опадчий Ю.Ф. Оптимизация алгоритма операции умножения на ПЛИС. – Сб. трудов Всероссийской научно-технической конференции «Новые материалы и технологии» том.3 Москва., 11..13 ноября 2008г. стр.115..116.
  7. Мо Чжо Чо. “Optimization algorithm of exponential function calculation at CPLD” Пекин 26.11 – 04.12 2008. Материалы конференции международной научной конференции «Технические науки и современное производство», Китай (Пекин), 26 ноября - 4 декабря 2008 г.
  8. Мо Чжо Чо. Оптимизация алгоритма вычисления показательной функции на ПЛИС ПЛИС – Журнал «Современные наукоемкие технологии» Российская академия естествознания, № 11, 2008г. стр. 61-62.
  9. Мо Чжо Чо. Опадчий Ю.Ф. Мониторинг температурных режимов работы автономных объектов. Измерительная техника. 2009, № 9, стр. 26…28.



Подписано в печать ____ _____ 2009. Объем 1,5 п.л., тираж 100 экз.

Ротапринт МАТИ, 109240, г. Москва, Берниковская наб., 14