Курс. Занятие №8 Определение достоверности различий по критерию Х 2

Вид материала

Документы

Подобный материал:

• Международное гуманитарное право. Вводное занятие, 62.07kb.
• Н. И. Дереклеева модульный курс учебной и коммуникативной мотивации учащихся или учимся, 1679.79kb.
• Ит в физической культуре и спорте. 1 Курс. Занятие, 94.54kb.
• Курс план практических занятий по курсу общественного здоровья и здравоохранения, 119.11kb.
• Элективный курс по музыке в предпрофильной подготовке учащихся 9 класса. Использование, 51.13kb.
• Элективный курс «практическая стилистика» Соколова О. В., Рябинина Л. А. Ссылка, 61.61kb.
• Кросскультурные аспекты обучения деловому иностранному языку, 40.16kb.
• Предлагаем вам пройти дистанционный курс «Обучение в сотрудничестве». Каждое занятие, 171.18kb.
• 9 6 Контрольные вопросы, 851.81kb.
• Тема : «Эрмитаж-место уединения особо приближенных к императрице», 34.7kb.

Определение достоверности различий по критерию х². Критерий Х² (хи-квадрат) применяется для сравнения распре­делений испытуемых двух групп по состоянию некоторого свой­ства на основе измерений по шкале наименований.

Для расчета достоверности различий результаты, полученные в обеих груп­пах, распределяются в четырехпольные или многопольные «табли­цы» в зависимости от того, на сколько классов (категорий) эти результаты подразделяются.

Случай четырехпольной «таблицы». Допустим, проверяется эффективность использования специальной методики обучения переворота рычагом. Отберем для этой цели две равноценные группы по 25 человек в каждой (экспериментальную, в которой обучение ведется по экспериментальной методике, и контрольную, в которой обучение проводится по общеприня­той, традиционной, методике).

Результаты обучения будем изме­рять по шкале наименований, имеющей только две взаимоиск­лючающие категории: «выполнил» – «не выполнил». На основе та­ких измерений результатов обучения занимающихся в экспе­риментальной и контрольной группах составляется четырехполь­ная «таблица» (2x2):

	Категория 1	Категория 2
Эксперимен­тальная группа	Э1	Э2	nэ=Э1+Э2
Контрольная группа	К1	К2	nк=К1+К2
	Э1+К1	Э2+К2	N=nэ+nк

В этой «таблице» Э₁ – число занимающихся в эксперимен­тальной группе, попавших в первую категорию (класс), то есть те, кто выполнил прием; Э₂ – число занимающихся в экспериментальной группе, попавших во вто­рую категорию, которые не выполнили прием; соответственно К₁ и К₂; N – общее число наблюдаемых (испытуемых), равное Э₁+Э₂+К₁+К₂ или n_э+n_к.

На осно­ве данных такой «таблицы» можно проверить гипотезу о ра­венстве вероятностей выполнения приема в экспериментальной и контрольной группах, и на этой основе судить об эффективности той или иной методики обучения.

Для проверки гипотезы подсчитывается значение хи-квадрат по следующей формуле:





Полученное значение Х² сравнивается с критическим значени­ем (Х²_крит.) при числе степеней свободы V=С-1 и уровне значи­мости 0,05, где С – число категорий.

Если наблюдаемое значе­ние хи-квадрат больше критического, т.е.





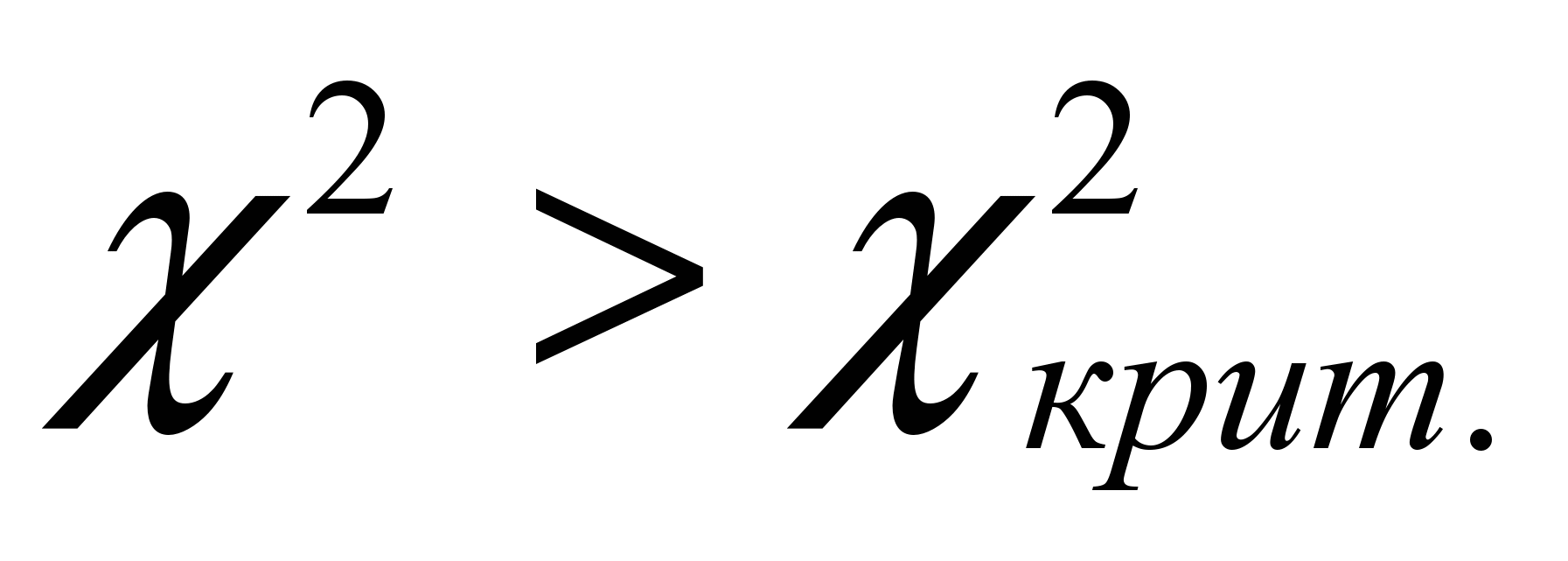
то считается, что распределение полученных результатов в ту или иную категорию не случайное и, следовательно, одна из приме­няемых методик обучения более эффективна, и наоборот, когда





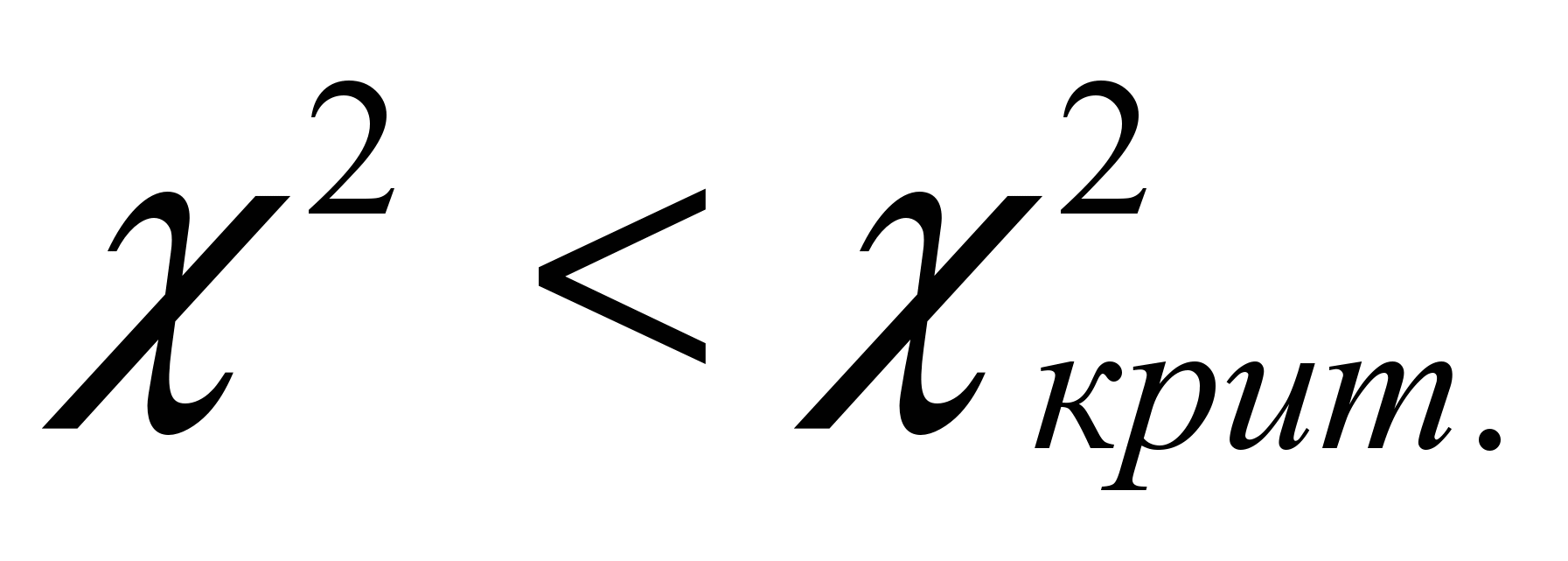
распределение полученных результатов в ту или иную категорию не считается случайным, а следовательно нет осно­ваний говорить о преимуществах какой-либо из применявшихся методик.

Критерий не рекомендуется использовать, если N=n_э+n_к<20 и в случае, когда хотя бы одно из абсолютных значений (Э₁, Э₂, К₁, К₂) в таблице 2x2, составленной на основе экспериментальных данных, меньше 5.

В случае же если хотя бы одно из абсолютных значений имеет заключено в пределах от 5 до 10, применение критерия возможно при внесении следующих изме­нений в формулу:





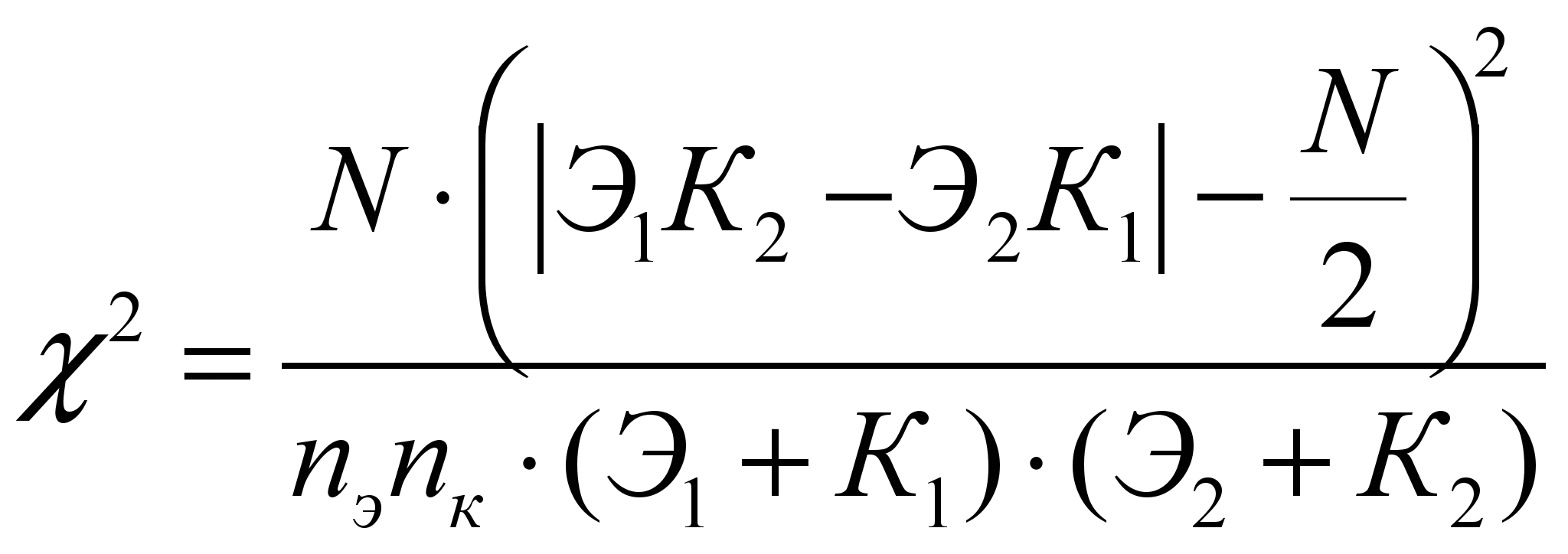
Для наглядности проставим конкретные значения в четырех­дольную «таблицу» с учетом нашего примера и выявим достовер­ность различий между полученными результатами.

Например, из 25 занимающихся в экспериментальной группе после обучения переворот рычагом выполнили 20 человек, не смогли выполнить 5 человек. контрольной – 13 и 12 соответственно.

Составим на основе этих результатов четырехпольную «таблицу»:

	Выполнили	Не выполнили
Эксперимен­тальная группа	Э1=20	Э2=5	nэ=Э1+Э2=25
Контрольная группа	К1=13	К2=12	nк=К1+К2=25
	Э1+К1=33	Э2+К2=17	N=nэ+nк=50

Из «таблицы» видно, что все абсолютные значения не меньше 5, но одно значение (Э₂) равно 5, поэтому подсчет необ­ходимо произвести по второй формуле:





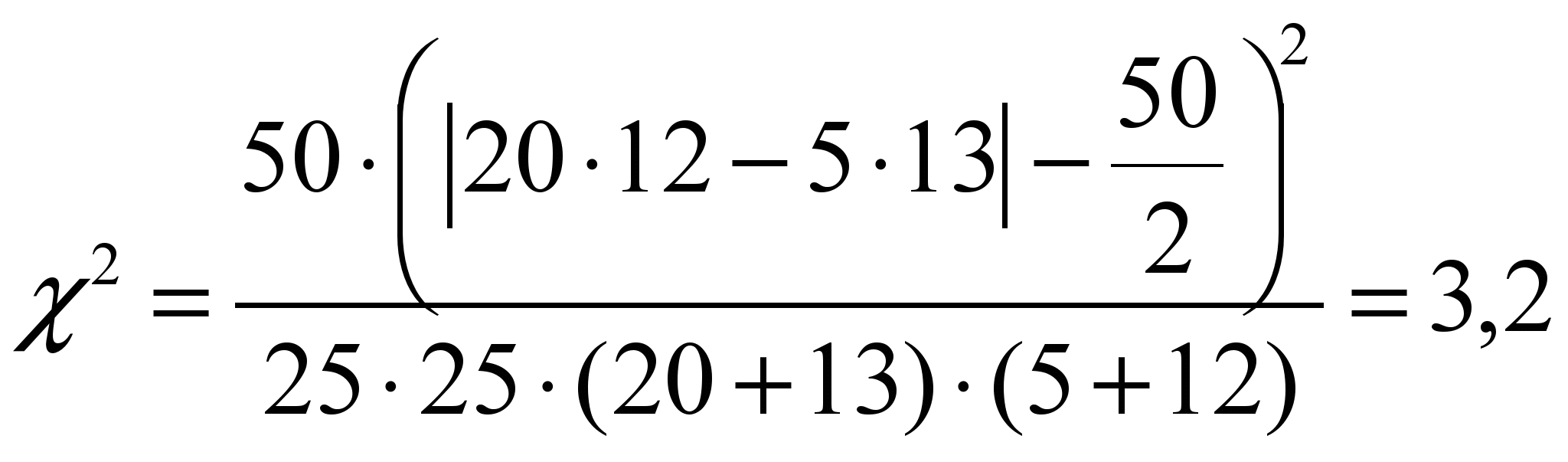
Теперь необходимо полученное значение Х² с критиче­ским (Х²_крит.), для чего вначале определяем число степеней свободы
V=C-1=2-1=1.

Дальше из специальной таблицы находим значение Х²_крит., которое равно 3,8, что больше нашего значения 3,2. Следовательно, большее количе­ство занимающихся в экспериментальной группе, сумевших в дан­ном случае выполнить прием, имеет случайный характер и, видимо, зависит от других факторов. Поэтому говорить о том, что экспериментальная методика была более эффективной, оснований нет.