Ит в физической культуре и спорте. 1 Курс. Занятие №9

Вид материала

Документы

Содержание Определение коэффициента корреляции при оценке качественных признаков.

Подобный материал:

• Ит в физической культуре и спорте. 1 Курс. Занятие, 120.8kb.
• Российская федерация федеральный закон о физической культуре и спорте в российской, 858.17kb.
• Управление алтайского края по физической культуре и спорту, 241.55kb.
• Темы рефератов по дисциплине "Экономика физической культуры и спорта", 7.34kb.
• Распоряжение от 3 марта 2011 г. N 15-р о составе совета по физической культуре и спорту, 72.98kb.
• Роль медицины в спортЕ, физическОй реабилитациИ и адаптивнОй физическОй культурЕ, 89.26kb.
• Об утверждении районной целевой программы «Развитие физической культуры и спорта, 135.24kb.
• Цели и задачи курса, 66kb.
• Краткая информация по составу дисциплин обязательного, 254.18kb.
• Общие положения Статья Предмет регулирования настоящего Федерального закона, 706.2kb.

Определение меры связи между явлениями. Исследователей часто интересует вопрос о том, как связаны между собой различные факторы, влияющие на результаты учеб­но-тренировочного процесса.

Например, имеют ли спортсмены, начавшие заниматься каким-либо видом спорта в более раннем возрасте, тенденцию к достижению более высоких результатов? Или как влияет гибкость гимнаста на качество выступлений на соревнованиях и т.п.

Такого рода связи и зависимости называют­ся корреляционными или просто корреляцией. Изучение этих связей с помощью математических методов осуществляется на основе корреляционного анализа, основные задачи которого – измерение тесноты, а также определение формы и направления существующей между рассматриваемыми явлениями и факторами зависимости.

По направлению корреляция бывает положительной (прямой) или отрицательной (обратной), а по форме – линейной и нелинейной. При положительной корреляции с возрастанием при­знаков одного фактора они увеличиваются и у другого. Например, с увеличением силовых показателей у штангистов улучшаются их результаты на соревнованиях.

При отрицательной корреляции на­оборот – при увеличении признаков одного фактора признаки другого уменьшаются. Например, увеличение веса у гимнасток может вызвать ухудшение спортивных результатов.

Корреляция называется линейной, когда направление связи между изучаемы­ми признаками графически и аналитически выражается прямой линией. Если же корреляционная зависимость имеет иное направ­ление, она называется нелинейной.

Анализ линейной корреляции осуществляется с помощью вычисления коэффициентов корреля­ций (r). Для измерения криволинейной, т.е. нелинейной зависи­мости используется показатель, называемый корреляционным от­ношением. Здесь мы рассмотрим только линейную корреляцию, с анализом которой в исследованиях в области физического воспи­тания и спорта приходится сталкиваться наиболее часто.

При на­личии положительной связи между изучаемыми признаками ве­личина коэффициента корреляции имеет положительный знак (+), а при отрицательной – знак (–). Величина этого коэффициента может колебаться от -1 до +1.

Если коэффициент корреляции меньше 0,3, считается, что связь слабая, при коэффициенте от 0,31 до 0,69 – средняя и при значениях коэффициента от 0,70 до 0,99 – сильная.

Значение коэффициента корреляции выражается десятичными дробями с точностью до второго знака после запя­той. Для изучения меры связи при линейной корреляции в зави­симости от того, по какой шкале произведены измерения, вы­числяется тот или иной вид коэффициента.

Определение коэффициента корреляции при оценке качественных признаков. Когда признаки, свойства, параметры и т.п. не поддаются ко­личественному измерению и не распределяются в вариационный ряд, т.е. тогда, когда мы пользуемся шкалой наименований, кор­реляция между ними устанавливается по наличию этих признаков.

В случае, когда анализируется связь только между двумя качествен­ными признаками, прибегают к вычислению коэффициента ас­социации (r_a). При этом данные о наличии или отсутствии каждо­го признака группируются в четырехпольную корреляционную таблицу:

	Есть	Нет
1-й признак	а	б	n1=а+б
2-й признак	в	г	n2=в+г
	а+в	б+г	N=n1+n2

Коэффициент ассоциации вычисляется по следующей фор­муле:





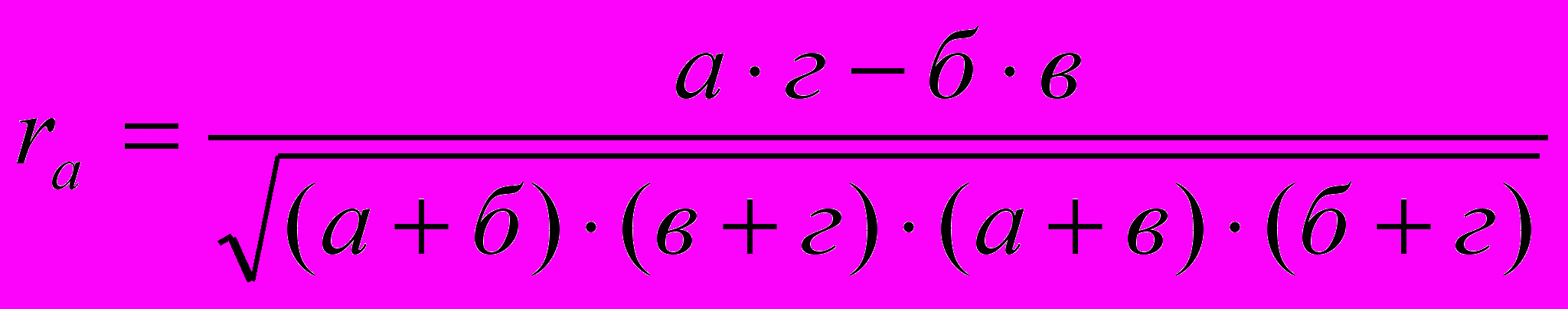
где а, б, в, г – численности альтернативных признаков, располо­женные в клетках корреляционной таблицы. Одним из условий правильного применения коэффициента ассоциации является тре­бование, чтобы ни одна из частот четырехпольной таблицы не была меньше 5. Для того чтобы легче понять методику расчета ко­эффициента ассоциации, снова обратимся к примеру.

Допустим, вы хотите изучить связь между чрезмерно строгой дисциплиной в семье и проявлением упрямства и непослушания у занимающихся в отделении ДЮСШ. Результаты наблюдений внесем в четырехпольную корреляционную таблицу:

	Есть	Нет
Упрямство	а=7	б=8	n1=а+б=15
Строгая дисциплина	в=5	г=10	n2=в+г=15
	а+в=12	б+г=18	N=n1+n2=30

Подставим эти значения в формулу и рассчитаем коэффици­ент ассоциации:





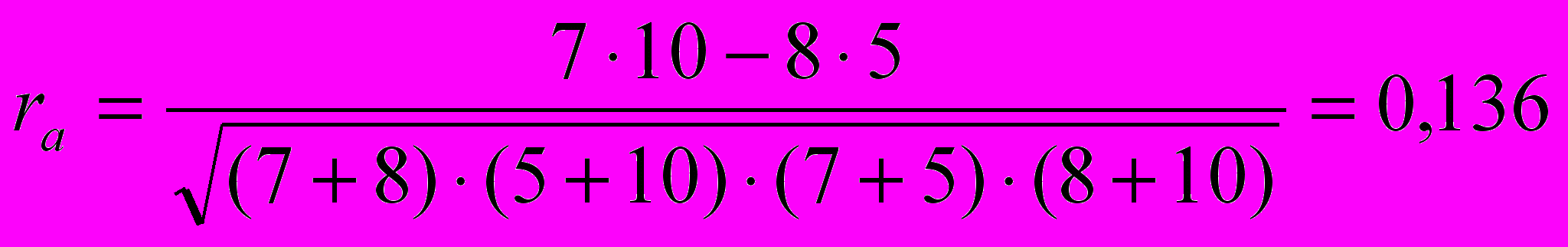
Значение полученного коэффициента показывает, что между строгой дисциплиной в семье и проявлением у занимающихся упрямства и непослушания обнаруживается слабая положитель­ная связь. Однако прежде чем делать окончательные выводы, не­обходимо проверить достоверность этого коэффициента: не яв­ляется ли эта величина случайной. Проверка достоверности в дан­ном случае осуществляется следующим образом.

Если величина 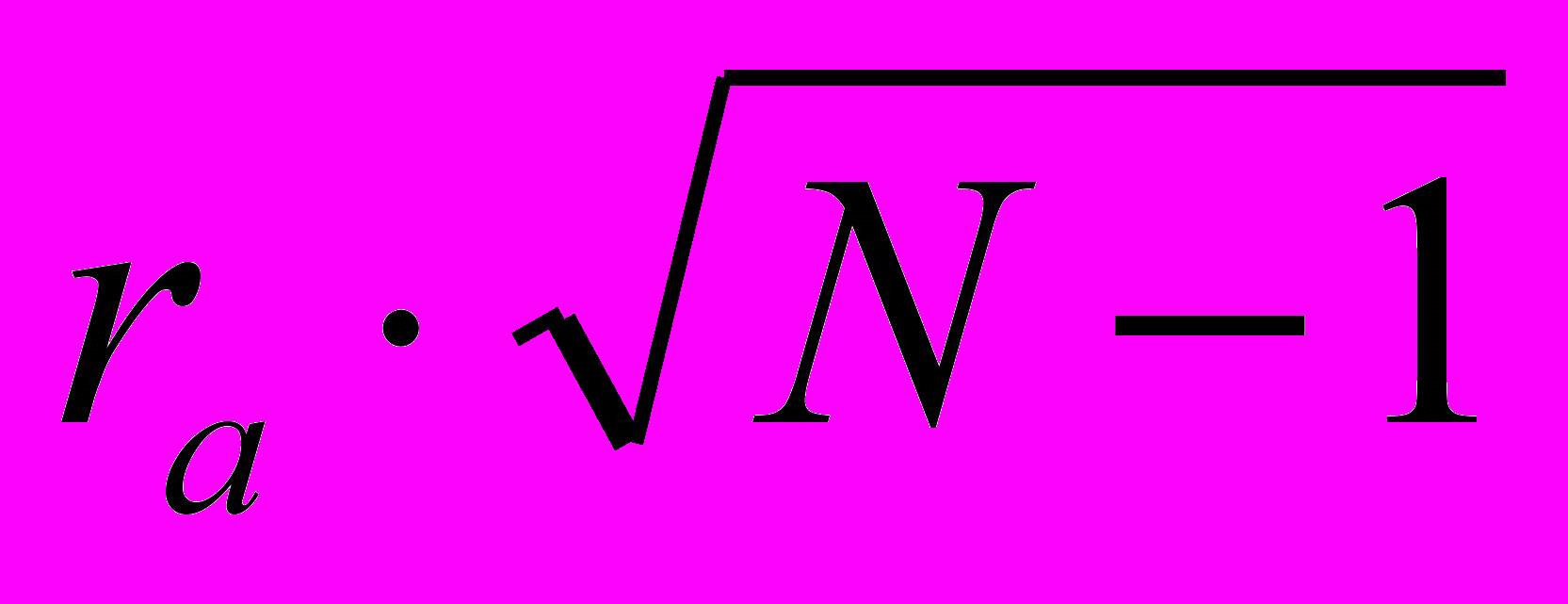превосходит указанное в таблице критическое значе­ние для принятого уровня значимости и числа степеней свободы (K=N-2), то наличие связи считается достоверным, и наоборот.

В нашем примере 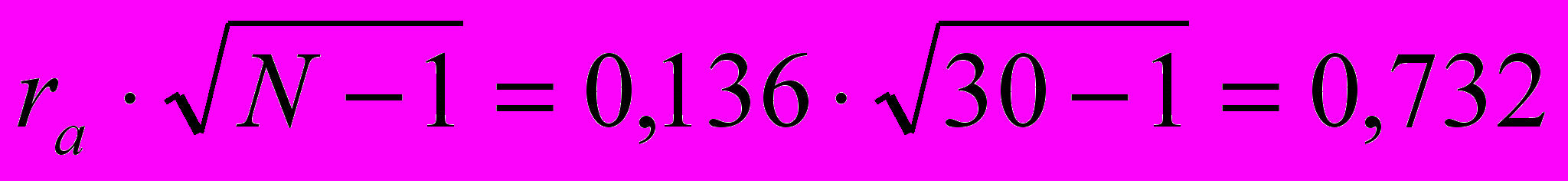. Теперь по таб­лице найдем значение коэффициента корреля­ции при р=0,05 и числе степеней свободы К=N-2=30-2=28. Это значение равно 0,36.

Вычислим величину 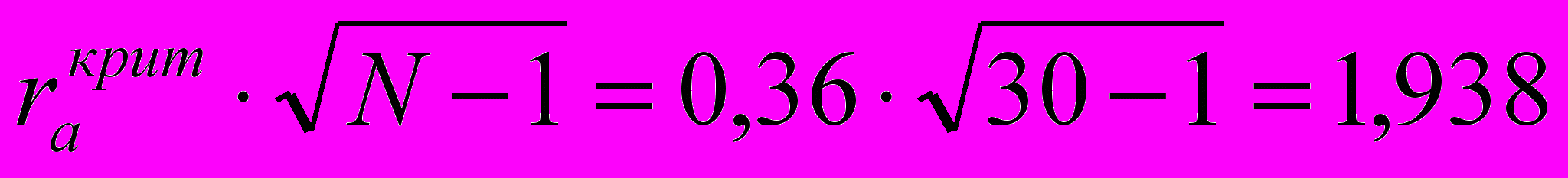. Произведенный расчет показывает, что 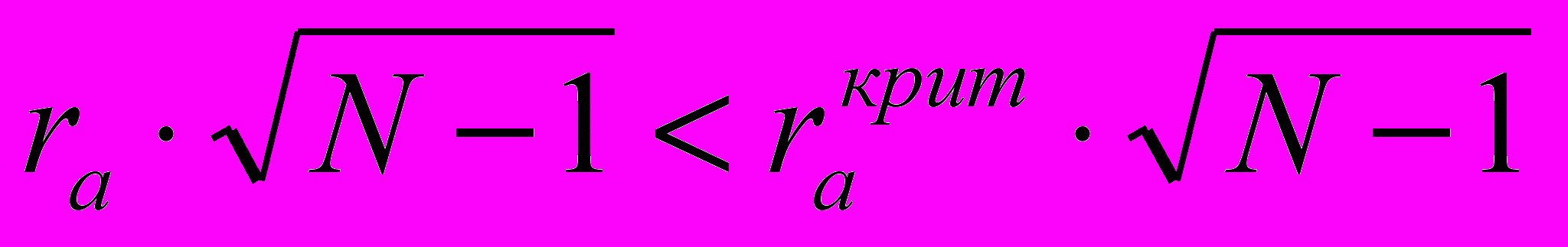(0,732<1,938). Следовательно, обнаруженная поло­жительная связь между чрезмерно строгой дисциплиной в семье и проявлениями упрямства и непослушания у детей считается не­достоверной (r_a=0,136 при р>0,05). Очевидно, при увеличении числа наблюдений наличие такой связи может оказаться досто­верным.