Ит в физической культуре и спорте. 1 Курс. Занятие №9

Вид материала

Документы

Содержание Методика определения моды. Методика определения медианы.

Подобный материал:

• Ит в физической культуре и спорте. 1 Курс. Занятие, 94.54kb.
• Российская федерация федеральный закон о физической культуре и спорте в российской, 858.17kb.
• Управление алтайского края по физической культуре и спорту, 241.55kb.
• Темы рефератов по дисциплине "Экономика физической культуры и спорта", 7.34kb.
• Распоряжение от 3 марта 2011 г. N 15-р о составе совета по физической культуре и спорту, 72.98kb.
• Роль медицины в спортЕ, физическОй реабилитациИ и адаптивнОй физическОй культурЕ, 89.26kb.
• Об утверждении районной целевой программы «Развитие физической культуры и спорта, 135.24kb.
• Цели и задачи курса, 66kb.
• Краткая информация по составу дисциплин обязательного, 254.18kb.
• Общие положения Статья Предмет регулирования настоящего Федерального закона, 706.2kb.

Меры центральной тенденции (средние величины). Одной из важнейших обобщающих характеристик варьирую­щих признаков является средняя величина. Значение средних за­ключается в их свойстве нивелировать индивидуальные разли­чия, в результате чего выступает более или менее устойчивая числовая характеристика признака – не отдельных измерений, а целой группы статистических единиц.

Средняя величина харак­теризует групповые свойства, является центром распределения, занимает центральное положение в общей массе варьирующих значений признака. Существует несколько видов сред­них величин.

Наиболее часто в педагогических исследованиях ис­пользуются такие средние, как мода, медиана и средняя арифме­тическая величина. Первые два вида – непараметрические, а сред­няя арифметическая представляет собой параметрическую вели­чину.

Методика определения моды. Мода (Mo) – это такое значение в множестве наблюдений, которое встречается наиболее часто. На­пример, в ряду из цифр: 2, 6, 8, 9, 9, 9, 10 модой является 9, потому что она встречается чаще любого другого значения. Обра­тите внимание, что мода представляет собой наиболее частое зна­чение (в данном примере 9), а не частоту этого значения (в при­мере равную 3). Мода, как мера центральной тенденции, имеет определенные особенности, которые необходимо учитывать при ее вычислении (определении):

1. В случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа не имеет моды. Например, 6 легкоатлетов пробежали дистанцию 100 м и показали результа­ты: 10, 10, 11, 11, 12, 12, 13, 13 с. В данном случае моду обнару­жить невозможно.

2. Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Например, 10 гимнастов за упражнения на коне получают следующие оценки: 6,9; 7,0; 7,5; 8,0; 8,0; 8,0; 9,0; 9,0; 9,0; 9,5. В этом случае мода будет равна 8,5.

3. Если два несмежных значения в группе имеют равные часто­ты и они больше частот любого значения, то существуют две моды. Например, в группе значений: 9, 10, 10, 10, 13, 15, 16, 16, 16, 17 модами являются 10 и 16. В этом случае можно говорить, что дан­ные бимодальны.

Значение моды можно определить фактически при любом способе измерений, сделанных на основе всех шкал изме­рения. Однако наибольшее применение она находит в измерениях по шкале наименований, так как другие меры центральной тен­денции к таким измерениям неприменимы.

Методика определения медианы. Медиана (Md) – это такое значение, которое делит упорядо­ченное множество пополам так, что одна половина значений ока­зывается больше медианы, а другая — меньше. Определение ме­дианы возможно лишь в том случае, когда измерения выполнены не ниже шкалы порядка. Способы вычисления медианы могут быть следующие:

1. Если данные содержат нечетное число различных значений, и они представляют упорядоченный ряд, то медианой является сред­нее значение ряда. Например, в ряду 5, 8, 12, 25, 30 медиана равна 12.

2. Если данные содержат четное число различных значений, упорядоченных в ряд, например 3, 8, 16, 17, то медианой является точка, лежащая посередине между двумя центральными значе­ниями:
Md=(8+16):2=12.

3. Для более точного определения медианы можно воспользоваться специальной формулой. Но прежде чем привести эту фор­мулу, ознакомимся с некоторыми дополнительными понятиями, знание которых при этом необходимо:

– класс – группы одинаковых чисел в данном ряду;

– медианный класс – класс, в котором находится медиана;

– классовый промежуток – разность между числами соседних классов;

– частота класса – количество одинаковых чисел в классе;

– частота медианного класса – количество одинаковых чисел в медианном классе.

Закрепим эти понятия на конкретном примере. Допустим, что на экзаменах по легкой атлетике студенты получи­ли следующие оценки: 4, 3, 2, 4, 3, 3, 5, 3, 3, 4, 4, 3, 5, 4, 2, 5, 3, 3, 4, 2, 2, 3, 4; расположим эти оценки в порядке возрастания: 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5.

Этот ряд подразделя­ется на четыре класса: «2», «3», «4», «5». Медианным классом явля­ется класс «3», классовый промежуток в этом ряду равен 1, частота класса «2» – 4 (т. е. оценка 2 встречается 4 раза); класса «3» – 8; клас­са «4» – 7; класса «5» – 4.

Если определять медиану простыми способами, то и она будет равняться 3, двенадцатое значение, кото­рое занимает центральное положение в ряду из 23 данных.

Однако довольно приблизительное значение, определяемое этими способами, иногда может не удовлетворить ис­следователя. Поэтому ее можно вычислить по следующей формуле:





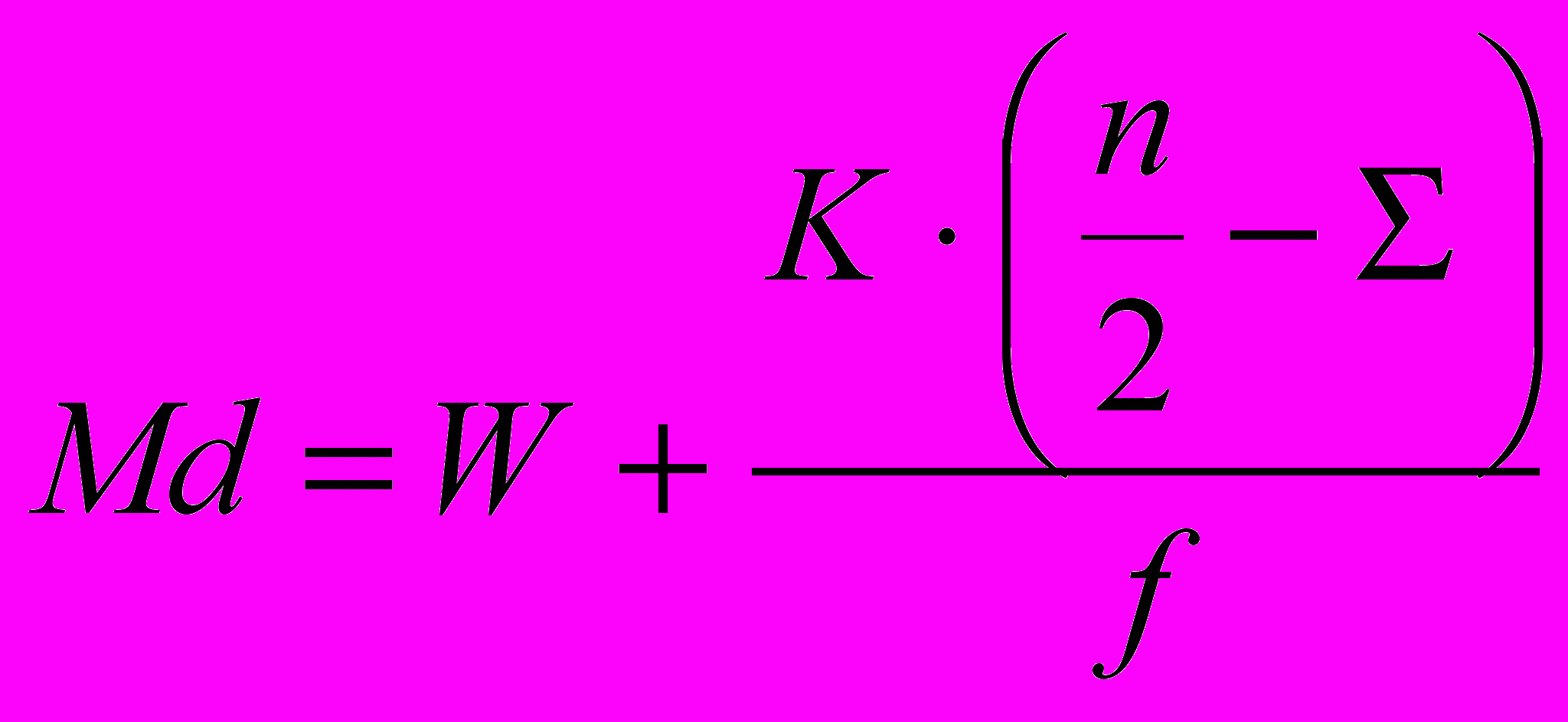
где W – начало класса, в котором находится медиана; n – общее число данных; К – величина классового промежутка;  – сумма частот классов, предшествующих медианному классу; f – частота медианного класса.


Составим для приведенного выше ряда таблицу частот каждой оценки:

Оценка	Частота оценок
2 3 4 5	4 8 7 4
Итого	23

Используя данные таблицы W=3; К=1; n=23; =4; f=8, вычислим значение медианы по формуле:





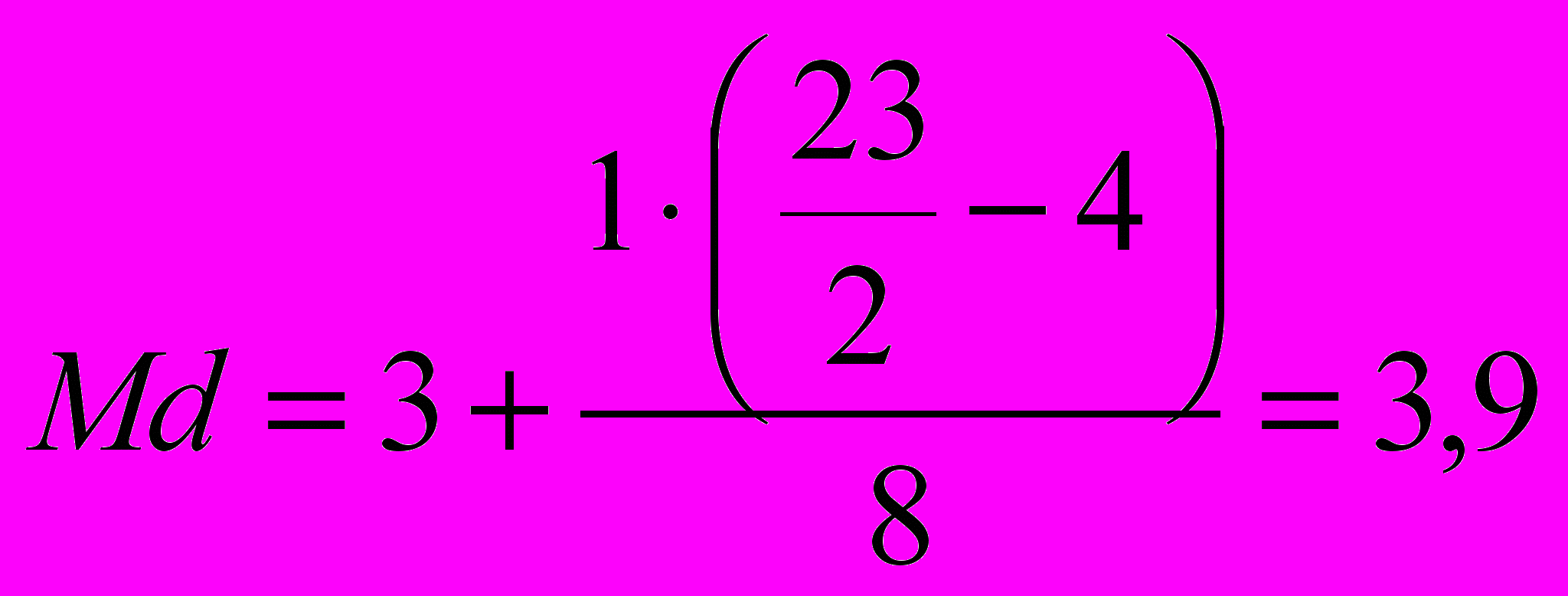
В случае, когда измерения сделаны по шкале интервалов и от­ношений, основной мерой центральной тенденции является сред­няя арифметическая величина, а мода и медиана могут использо­ваться для вспомогательных целей.

В заключение раздела необходимо отметить, что математико-статистическая обработка результатов педагогического экспери­мента – один из трудоемких и ответственных моментов в подго­товке дипломной работы.

Она требует умелого и правильного вы­бора статистических критериев и методов анализа в соответствии с полученными результатами и задачами проведенных исследова­ний. Значительную помощь при обработке результатов могут ока­зать современные компьютеры.

Следует также иметь в виду, что сама математико-статистическая обработка еще не может полно­стью раскрыть сущность того или иного педагогического явления. Например, с помощью количественных методов с определенной точностью можно выявить преимущество какого-либо метода обу­чения и тренировки или обнаружить общую тенденцию, опреде­ленные связи и зависимости, доказать, что проверяемое научное предположение оправдалось, и т.п.

Однако эти методы не могут дать ответ на вопрос о том, почему одна методика обучения луч­ше другой. Поэтому наряду с математико-статистической обработкой полученных результатов нужно проводить и качествен­ный анализ этих данных.