Лабораторная работа №4
| Вид материала | Лабораторная работа |
СодержаниеОписание установки Порядок выполнения работы Обработка результатов измерений |
- Методические указания к лабораторным работам Лабораторная работа, 357.24kb.
- Лабораторная работа №3 кпк лабораторная работа №3 Тема: карманный персональный компьютер, 173.34kb.
- Методические возможности стенда Особенности работы на стендах уилс-1 Ознакомительное, 1487.3kb.
- Лабораторная работа по курсу «Физические основы микроэлектроники», 136.21kb.
- Лабораторная работа, 166.92kb.
- Самостоятельная работа по учебным пособиям, 471.48kb.
- Конспект урока в 9 классе по теме: «Магний», 84.54kb.
- Лабораторная работа №1 Введение в Windows. Работа с окнами и приложениями в Windows, 67.41kb.
- Знакомство c Excel, 1212.51kb.
- Лабораторная работа, 105.21kb.
Лабораторные работы по механике
Лабораторная работа № 4
определение коэффициента трения качения
методом наклонного маятника
Цель работы
Изучение закономерностей при внешнем трении и экспериментальное измерение коэффициента трения качения для различных материалов.
ТеоретическИе ОСНОВЫ РАБОТЫ
Во всех механических явлениях имеют место силы трения, действие которых практически всегда связано с переходом механической энергии в тепловую. Силы всемирного тяготения, упругие силы, рассматриваемые в механике, а также силы взаимодействия электрически заряженных тел зависят только от конфигурации тел, то есть от их взаимного расположения, но не от их скоростей. Отличие сил трения от указанных сил состоит в том, что силы трения, помимо конфигурации, зависят от относительной скорости тех тел, между которыми они действуют.
Силы трения могут возникать между соприкасающимися телами или их частями как при их относительном перемещении, так и при их относительном покое.
Внешнее трение действует в плоскости касания двух прижатых друг к другу тел при их относительном движении (например, трение между бруском и наклонной плоскостью, с которой он соскальзывает).
Внутреннее трение проявляется между различными частями одного и того же тела (между различными слоями жидкости или газа).
Т
 рение между поверхностями двух соприкасающихся тел при отсутствии между ними жидкой, газообразной прослойки, называется сухим. Если между твердыми телами имеется тонкий слой жидкости (смазочного масла), то в этом случае трение называется жидкостным.
рение между поверхностями двух соприкасающихся тел при отсутствии между ними жидкой, газообразной прослойки, называется сухим. Если между твердыми телами имеется тонкий слой жидкости (смазочного масла), то в этом случае трение называется жидкостным.По кинематическому признаку внешнее трение можно разделить на трение скольжения и трение качения.
Рассмотрим движение (качение) шара (или цилиндра) по горизонтальной поверхности и возникающее при этом движении трение качения.
Для объяснения сил трения качения следует считать деформации шара (цилиндра) и плоскости качения неупругими, причем для простоты будем полагать, что деформируется только поверхность качения, и только она имеет некоторые пластические деформации (в реальных условиях возникают упругие и пластические деформации как шара (цилиндра), так и плоскости).
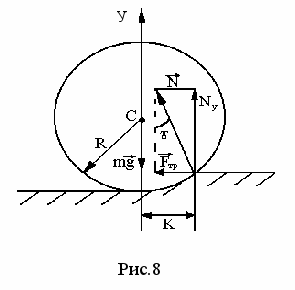
Точка приложения и направление реакции опоры (
 ), или силы воздействия плоскости на катящийся шар (цилиндр) представлены на рис.8.
), или силы воздействия плоскости на катящийся шар (цилиндр) представлены на рис.8.Уравнение проекций сил
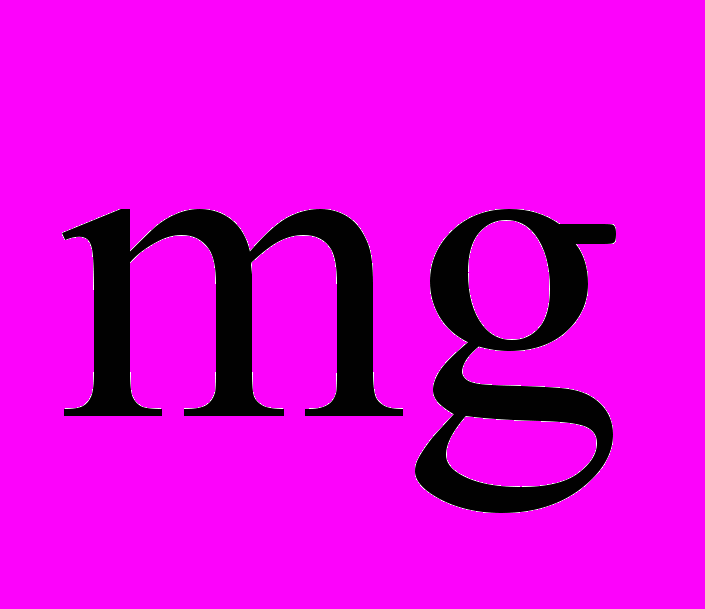 и
и  на ось У имеет вид:
на ось У имеет вид:-mg +N·cosγ=0. (1)
Угол γ практически мал, cosγ 1, то есть
Nmg. (2)
Горизонтальная составляющая реакции опоры представляет собой силу трения качения
 .
.Так как вращение шара (цилиндра) равномерное, и угловое ускорение его равно нулю, то должно выполняться условие равенства моментов* сил, то есть момент силы трения качения относительно точки С равен проекции силы нормального давления Ny, умноженной на К:
Fтр·R=Nу·K, (3)
где R - радиус шара (цилиндра);
Nу = Ncosγ = N;
К - линейная величина, называемая коэффициентом трения качения.
Коэффициент трения качения имеет размерность длины, поэтому он называется также «плечом» силы трения качения шара (цилиндра).
Из равенства (3) с учетом, что NуN получаем следующее выражение для силы трения качения:
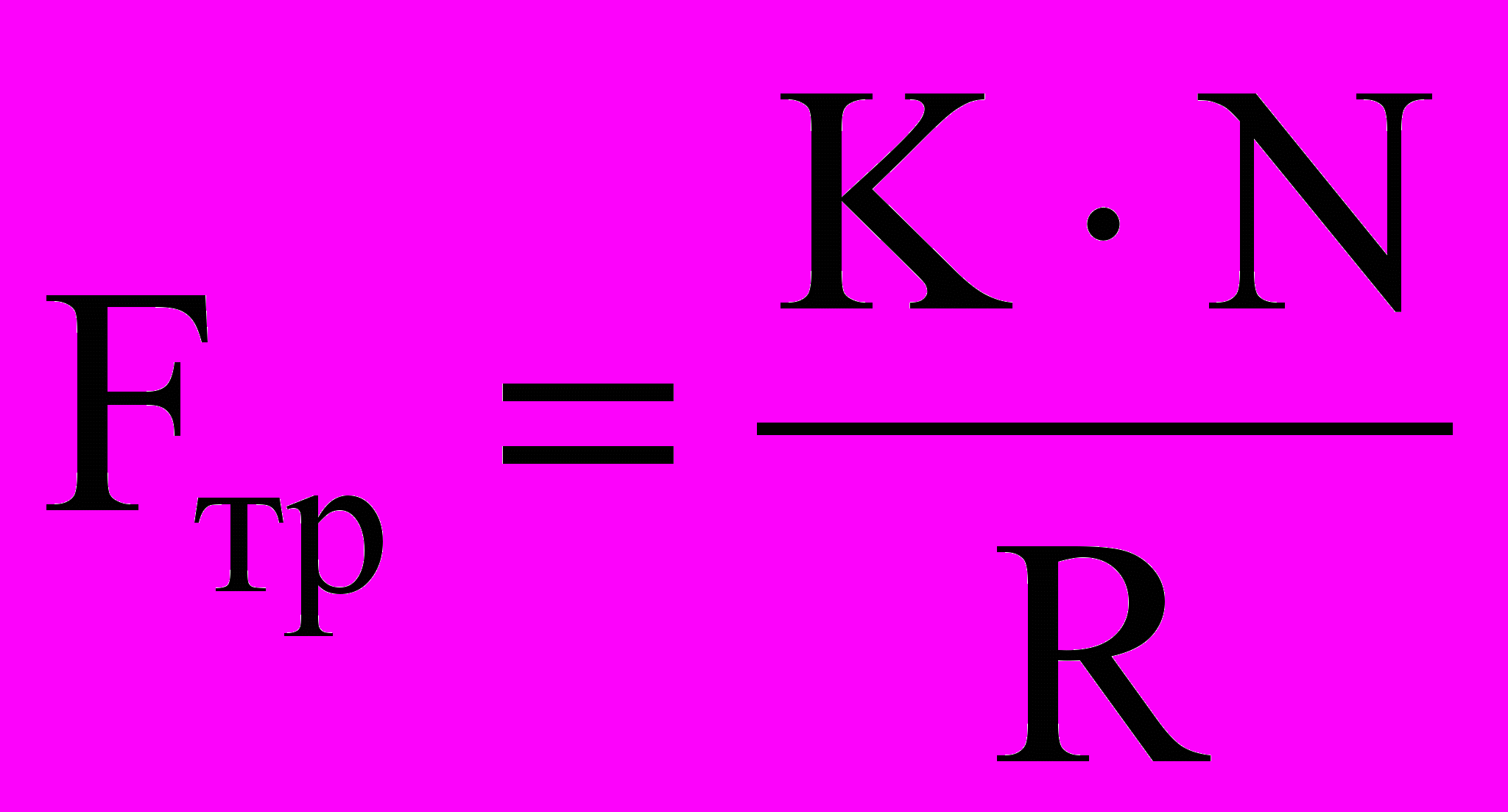 . (4)
. (4) В данной лабораторной работе предлагается один из способов исследования процесса трения качения - метод наклонного маятника.
Шарик 1, подвешенный в точке О на нити длиной L, может катиться по наклонной плоскости 2, составляющей регулируемый угол α с горизонтальной поверхностью (рис.9а).
ОО1 - направление (ось), фиксирующее положение равновесия наклонного маятника, точки А| и В| - проекции точек А и В на ось ОО1.
Идея данного метода заключается в определении связи уменьшения угла φ отклонения нити маятника с коэффициентом трения качения К.
Если маятник отклонить от положения равновесия на угол φ (точка А, рис.9а) и отпустить, то при отсутствии трения шарик 1 через половину периода* оказался бы в точке А1. Но при наличии трения качения шарик окажется (остановится) в точке В, нить маятника составит угол (φ-φ) с осью ОО1, причем точка В расположена ниже, чем точка А. Это означает, что происходит уменьшение потенциальной энергии маятника (U), равное работе сил трения качения на пути АВ.
С

ледует отметить, что работой по преодолению сопротивления среды и трения в подвесе маятника ввиду их малости можно пренебречь.
U = Aтр,
mgh = FтрS, (5)
где m - масса шарика;
h - потеря высоты (рис.9б);
S - длина дуги АВ;
Fтр - сила трения качения, определяемая по формуле (4), в которой сила нормального давления тела (шара) на наклонной плоскости равна
N = mgcosα. (6)
Из геометрических соображений определим h и S.
Длина дуги АВ равна (рис.9а)
S = L(2φ-φ), (7)
где L - длина нити или радиус дуги АВ окружности.
Изменение высоты h определяется как проекция отрезка A|B| на вертикальную ось (рис.9,б):
h = (A|B|)sin = Lsin,
где L = A|B| = OB| - OA| = Lcos( - ) - Lcos,
h = Lsin[cos( - ) - cos]. (8)
Подставив в (5) формулы (4), (6), (7) и (8), получим следующее выражение:
mgLsin[cos( - ) - cos] = (Kmgcos/R)L(2 - ) . (9)
Учитывая, что << 1 (за половину полного колебания потеря угла составляет порядка 0,3 = 5,210-3 рад), то можно считать, что
cos 1, sin
и cos( - ) = coscos + sinsin = cos + sin .
С учетом указанных упрощений выражение (9) можно представить в виде:
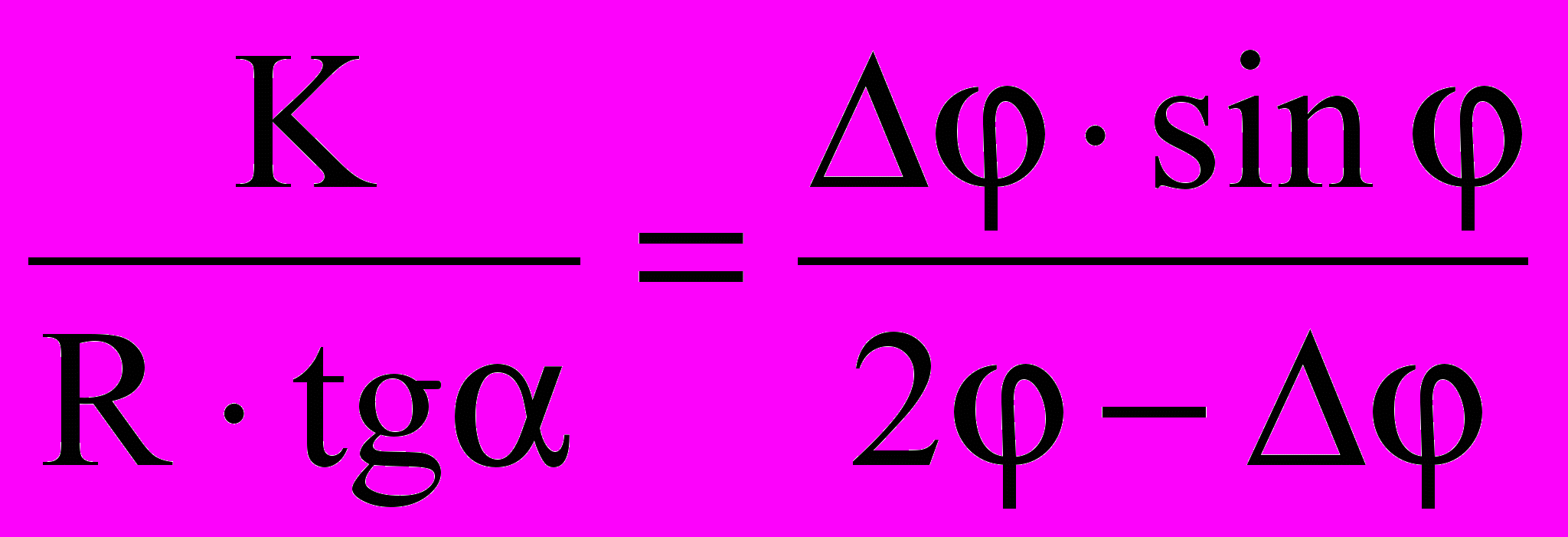 .
.Откуда
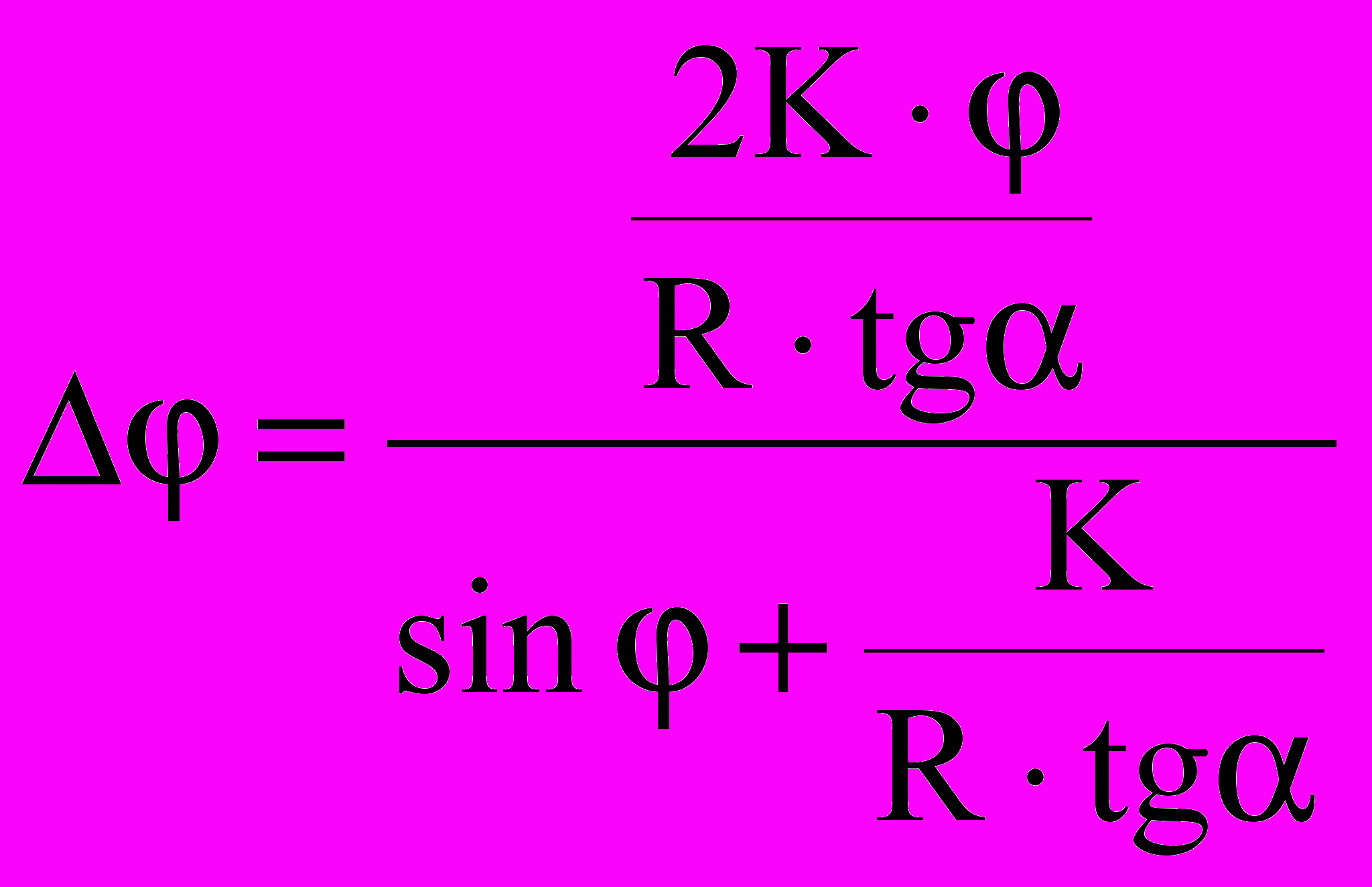 . (10)
. (10)Так как коэффициент трения качения мал, например, порядка 10-5 м при движении стали по стали [1], то
sin >> K/(Rtg),
и при малых углах отклонения шарика от положения равновесия
(=6=0,1 (рад))
sin ,
тогда уменьшение угла отклонения шарика от положения равновесия за половину полного колебания равно
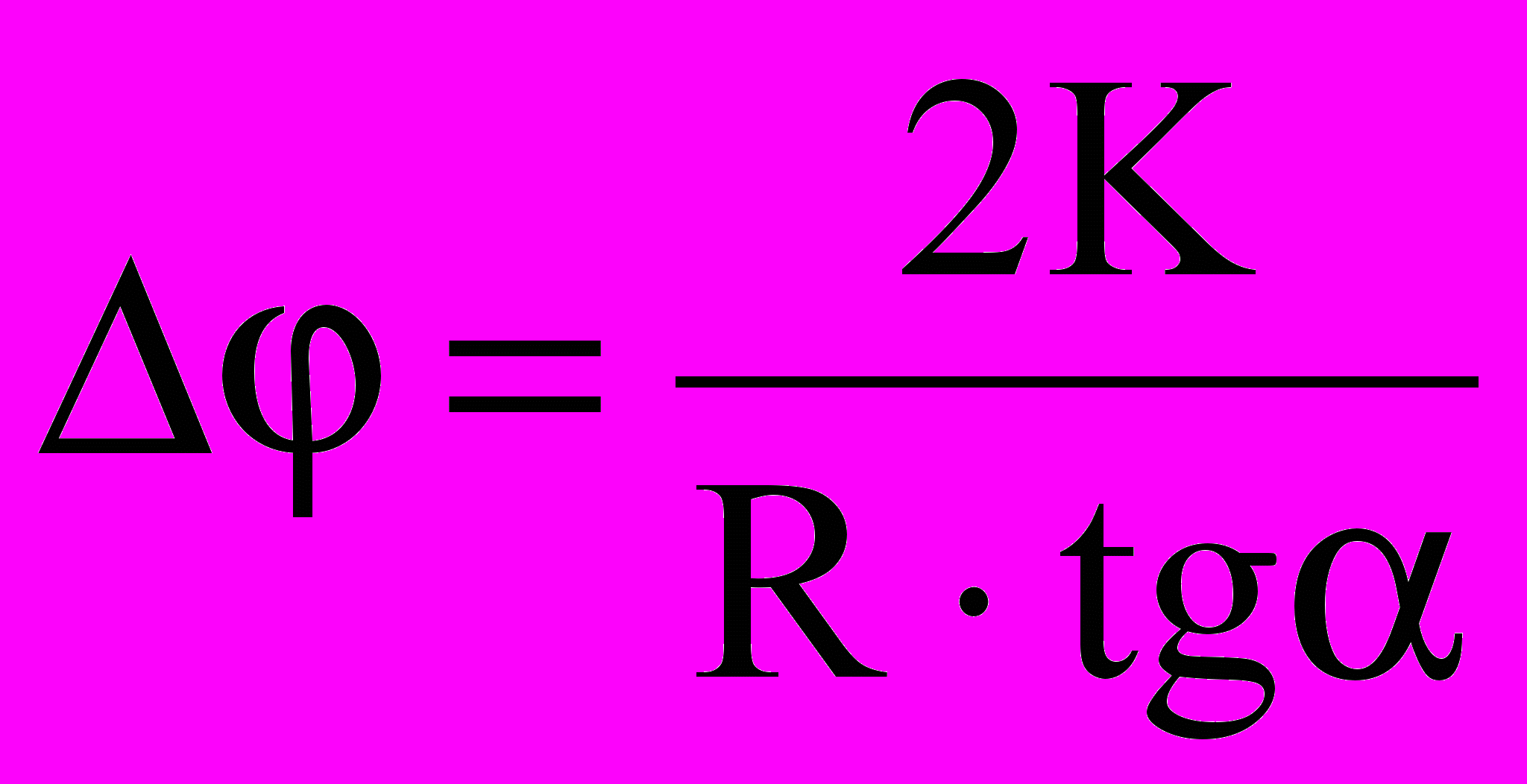 . (11)
. (11)Тогда за одно полное колебание уменьшение угла отклонения удвоится,
т. е.
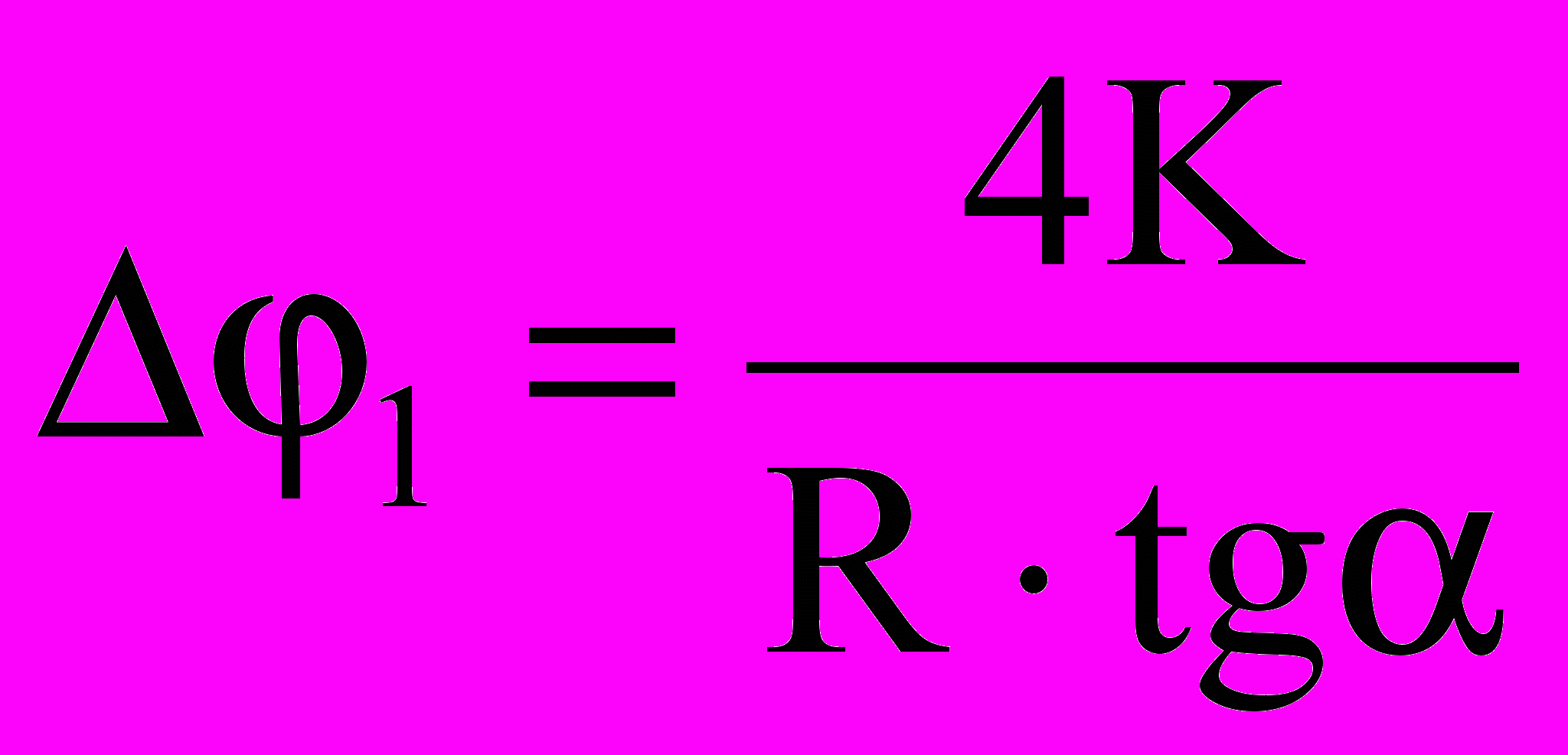 ,
,а за n полных колебаний
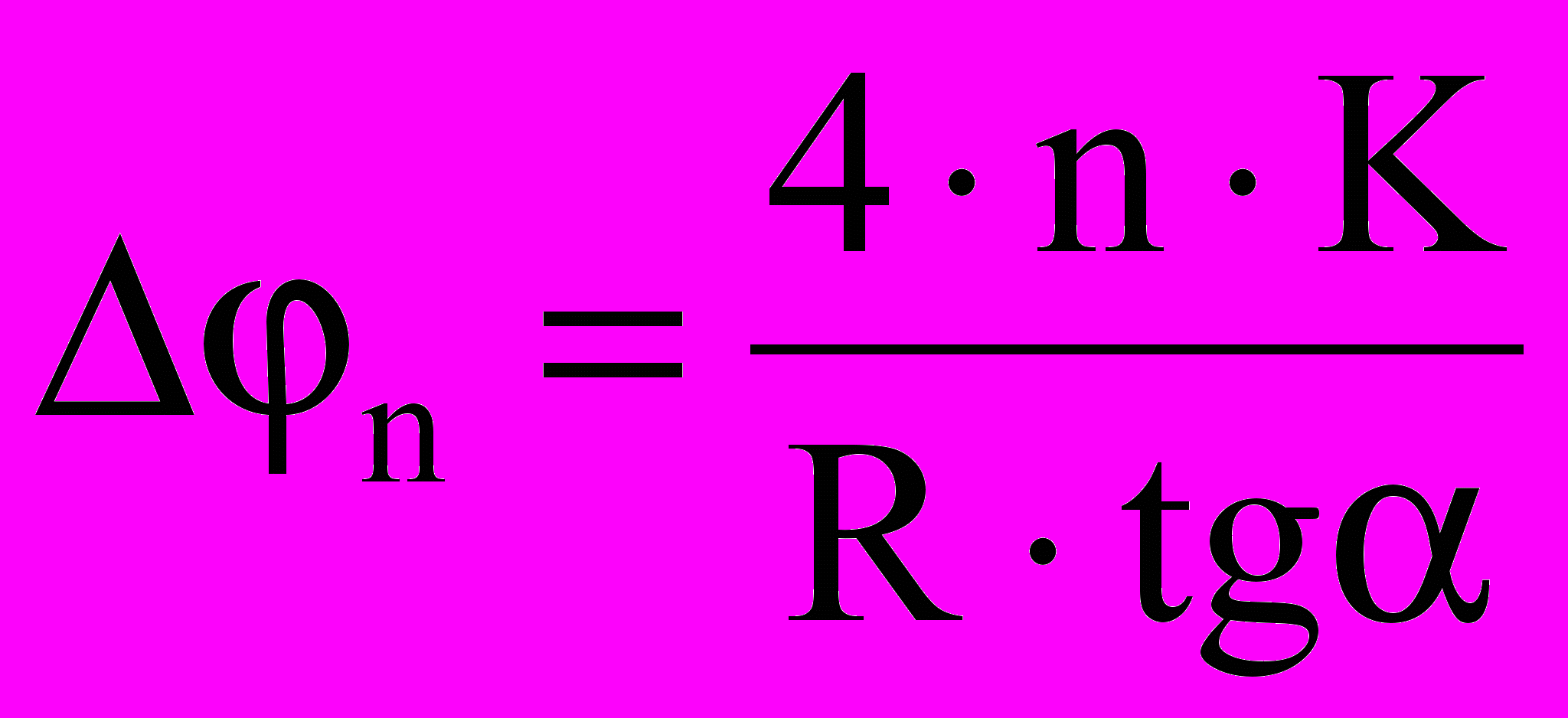 .
.Итак, коэффициент трения качения при вышеуказанных упрощениях рассчитывается по формуле:
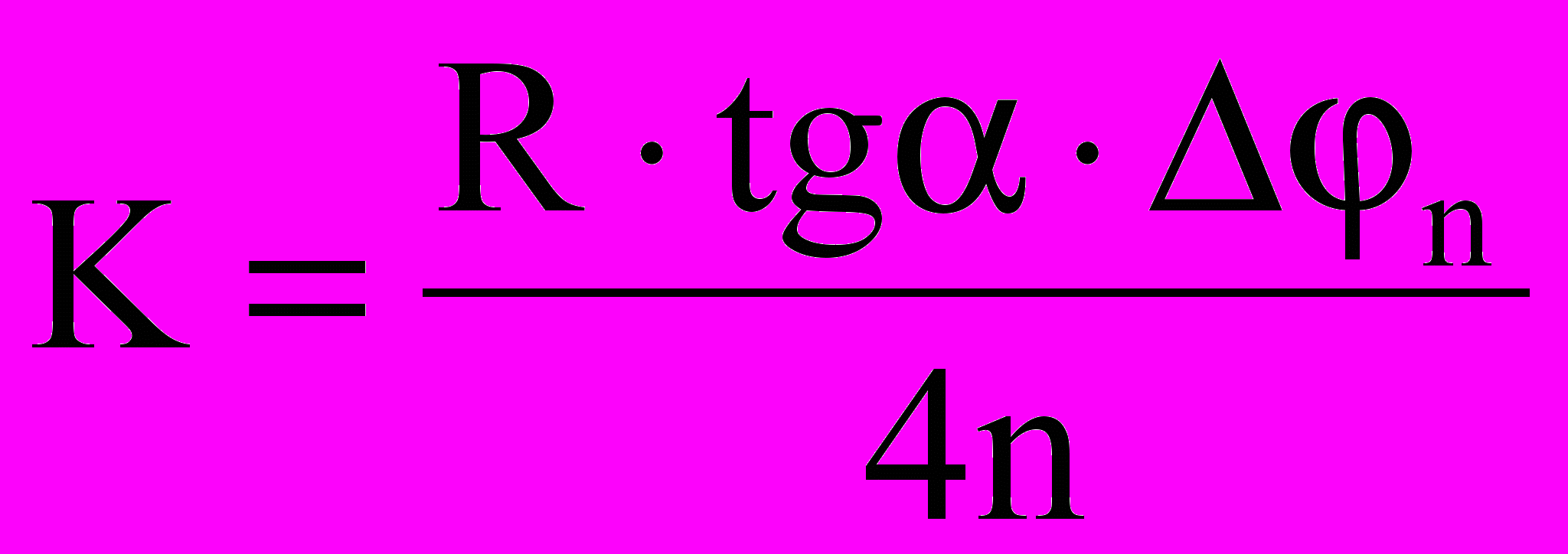 или
или 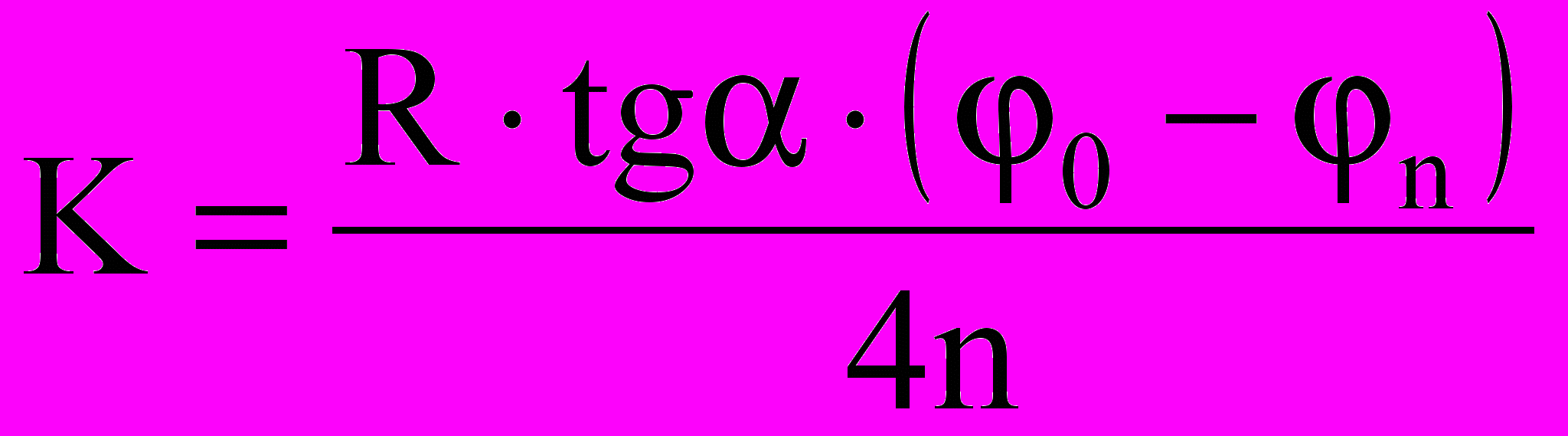 , (12)
, (12)где n = (0 - n) - уменьшение угла отклонения маятника за n колебаний, выраженное в радианах.
Описание установки
Приборы и принадлежности: измерительная установка (наклонный маятник) и набор плоских образцов, изготовленных из различных материалов.
На рис.10 представлен наклонный маятник, представляющий собой шар
с указателем 1, подвешенный на нити к стойке 2.
Н
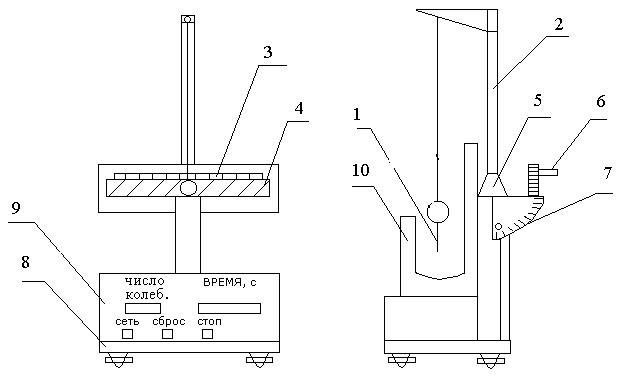
ить с шаром отклоняется от положения равновесия на заданные углы в градусах, которые отсчитываются по шкале 3, расположенной над плоским образцом 4, по которому происходит качение исследуемого шарика. Направляющие, в которые вставляется плоский образец, крепятся в кронштейне 5. Угол наклона плоскости качения меняется с помощью маховика 6 и регистрируется по шкале 7 в градусах, причем угол наклона = 90 - , где - показание шкалы 7 прибора.
Рис.10
В
 ся установка расположена на основании 8 с регулируемыми по высоте ножками (опорных винтов). На этом же основании расположен измерительный блок (миллисекундомер) 9, соединенный с фотоэлектрическим датчиком 10. На лицевой панели миллисекундомера 9 расположены табло “ЧИСЛО КОЛЕБ.” и “ВРЕМЯ, С”, а также кнопки “СЕТЬ” (включение установки), “СБРОС” (установка нуля измерителя) и “СТОП” (остановка счета измерителя).
ся установка расположена на основании 8 с регулируемыми по высоте ножками (опорных винтов). На этом же основании расположен измерительный блок (миллисекундомер) 9, соединенный с фотоэлектрическим датчиком 10. На лицевой панели миллисекундомера 9 расположены табло “ЧИСЛО КОЛЕБ.” и “ВРЕМЯ, С”, а также кнопки “СЕТЬ” (включение установки), “СБРОС” (установка нуля измерителя) и “СТОП” (остановка счета измерителя).Порядок выполнения работы
- Включите установку в сеть.
- При помощи опорных винтов установите маятник в такое положение, чтобы нить маятника находилась против нулевого деления шкалы 3, а указатель 1 пересекал световой луч фотоэлектрического датчика.
- Установите и закрепите шкалу 7 углов на отметку 90 и установите с помощью маховика 6 стойку 2 маятника под углами i. Значения углов наклона плоскости качения i = 90 - i указаны в таблице.
- При заданном угле наклона плоскости отклоните шарик на угол 0 = 6 и без толчка отпустите. После того как маятник совершит n = 5 полных колебаний, нажмите кнопку “СТОП” и по шкале 3 измерьте визуально угол n отклонения маятника.
Таблица
| R = 0,1 м; 0 = 6 = 0,104 рад; n = 5 | ||||||||
| 1 = 65 | 2 = 75 | 3 = 80 | ||||||
| №№ | t,с | n град | №№ | t,с | n град | №№ | t,с | n град |
| 1 | | | 1 | | | 1 | | |
| 2 | | | 2 | | | 2 | | |
| 3 | | | 3 | | | 3 | | |
| 4 | | | 4 | | | 4 | | |
| 5 | | | 5 | | | 5 | | |
| t = ; n = ; | t = ; n = ; | t = ; n = ; | ||||||
| T = | T = | T = | ||||||
- Показания миллисекундомера 9 (время полных колебаний t,с) и значения угла n занесите в таблицу.
- Для каждого угла наклона плоскости i повторите опыты, проводимые по пунктам 4 и 5 не менее 5 раз, и результаты измерений занесите в таблицу.
ВНИМАНИЕ: после каждого измерения следует нажать кнопку “СБРОС” для установки нуля измерителя.
- Указанные измерения проделайте для плоских образцов 4 (рис.10), изготовленных из различных материалов (стали, бронзы, латуни, алюминиевого сплава).
Обработка результатов измерений
- Выразите (0 - n) в радианах и по формуле (12), используя данные таблицы, вычислите коэффициент трения качения при различных углах наклона плоскости качения .
- Постройте график зависимости коэффициента трения качения от угла наклона , то есть К = К (tg).
- Методику расчета абсолютной ошибки при прямых измерениях смотрите в гл.Ι данного пособия. Найдите абсолютные ошибки t, n, 0, , R.
- Рассчитайте относительную ошибку измерения коэффициента трения качения по формуле
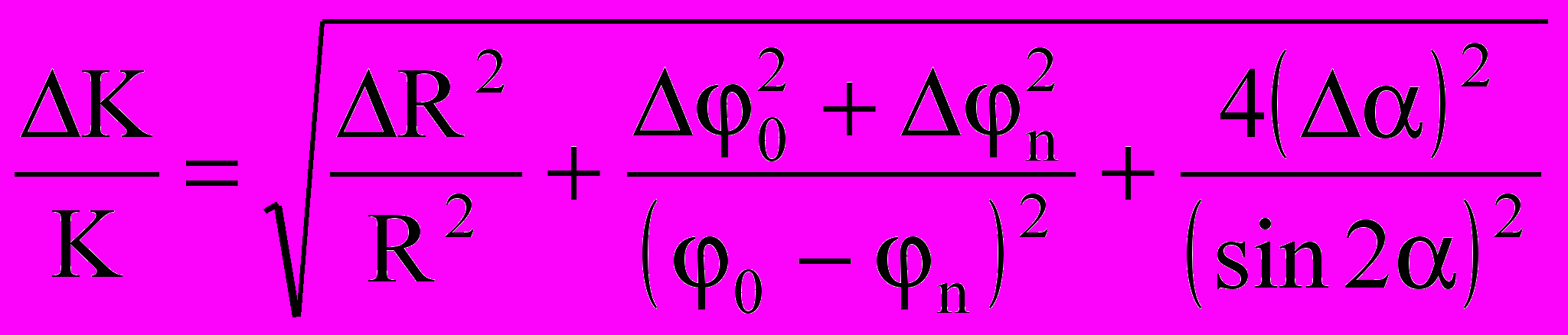 .
.- Вычислите периоды колебаний маятника при различных углах наклона плоскости качения по формуле
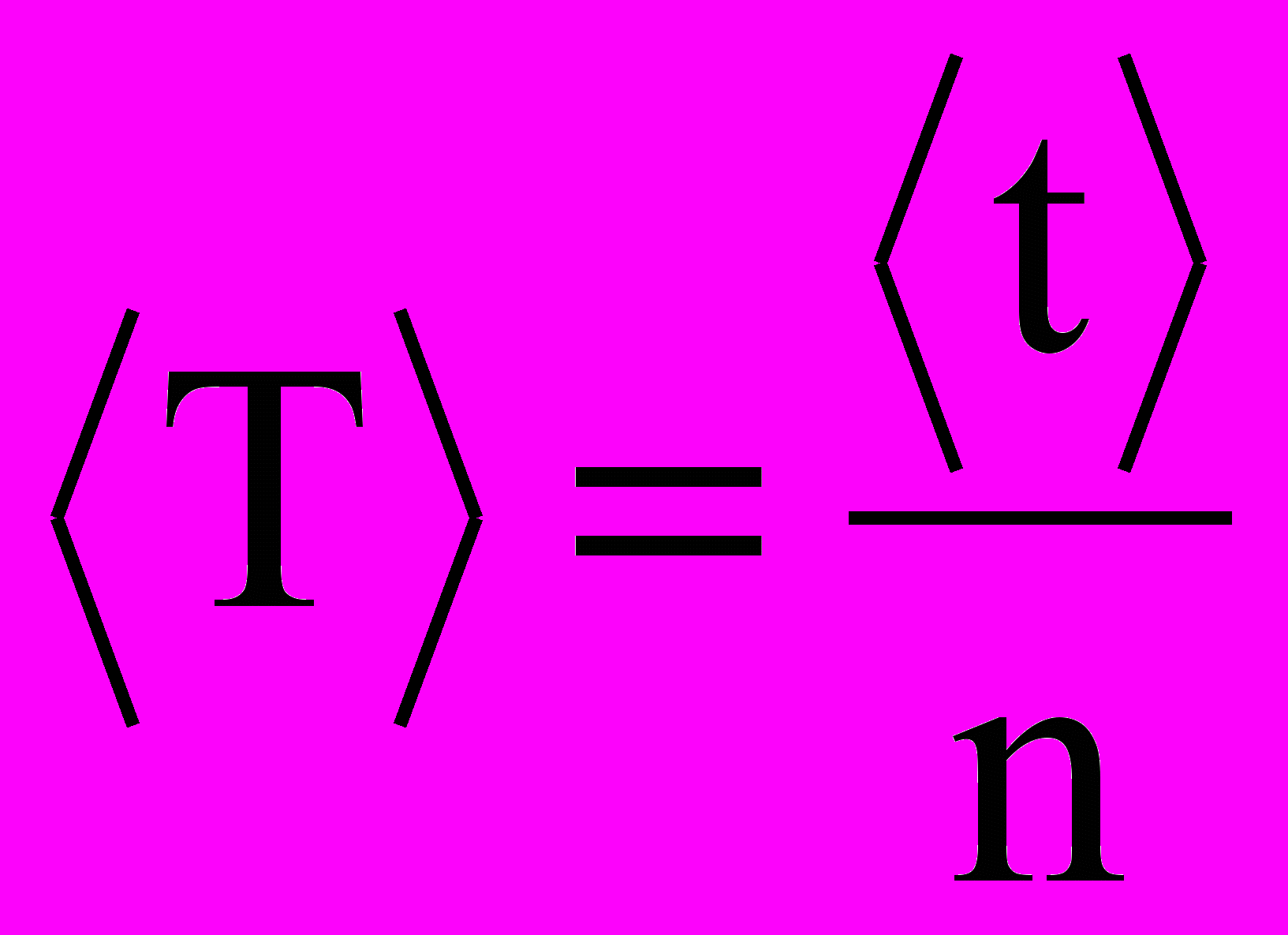 ,
,а абсолютную ошибку по формуле
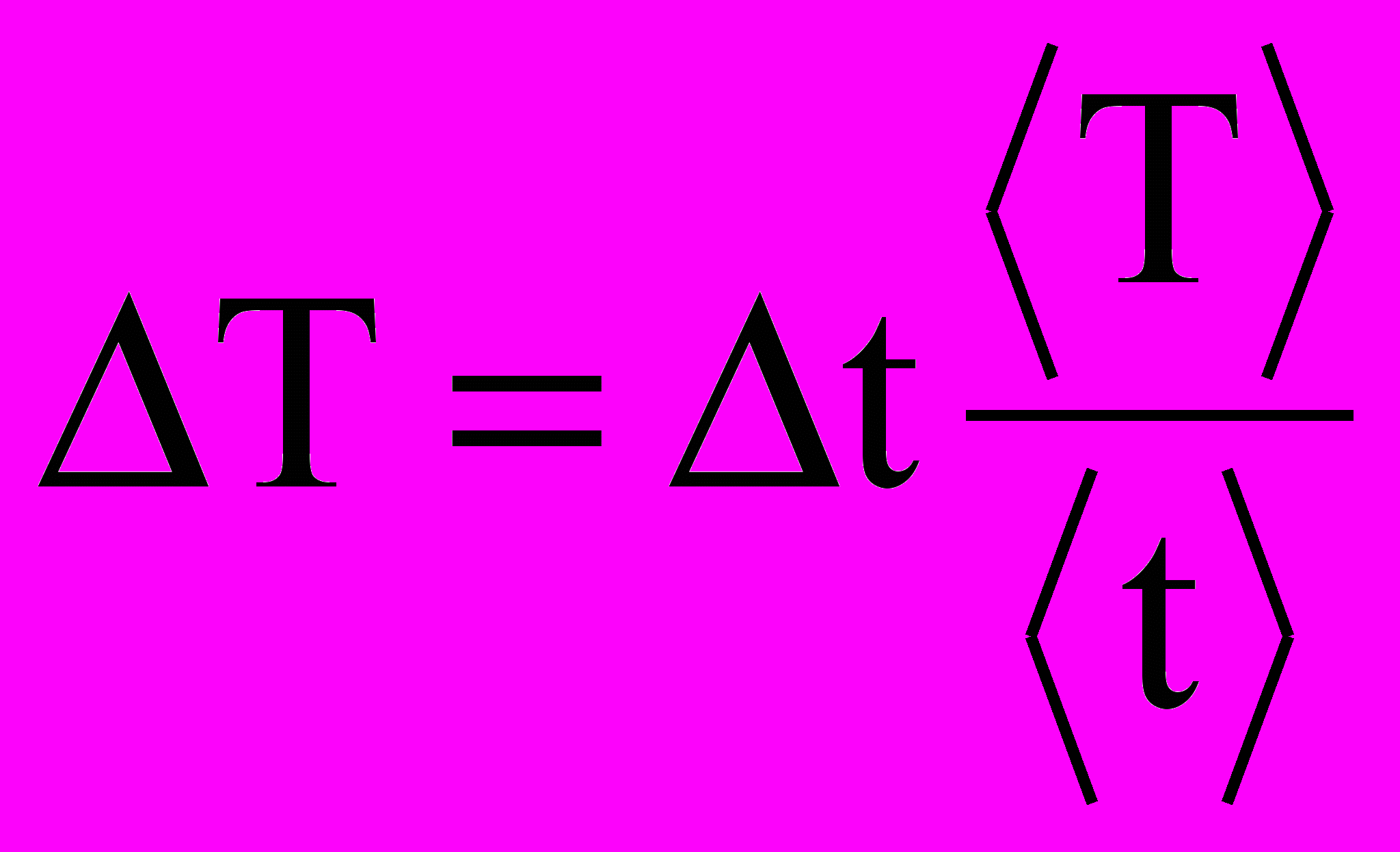
и результаты вычислений занесите в таблицу:
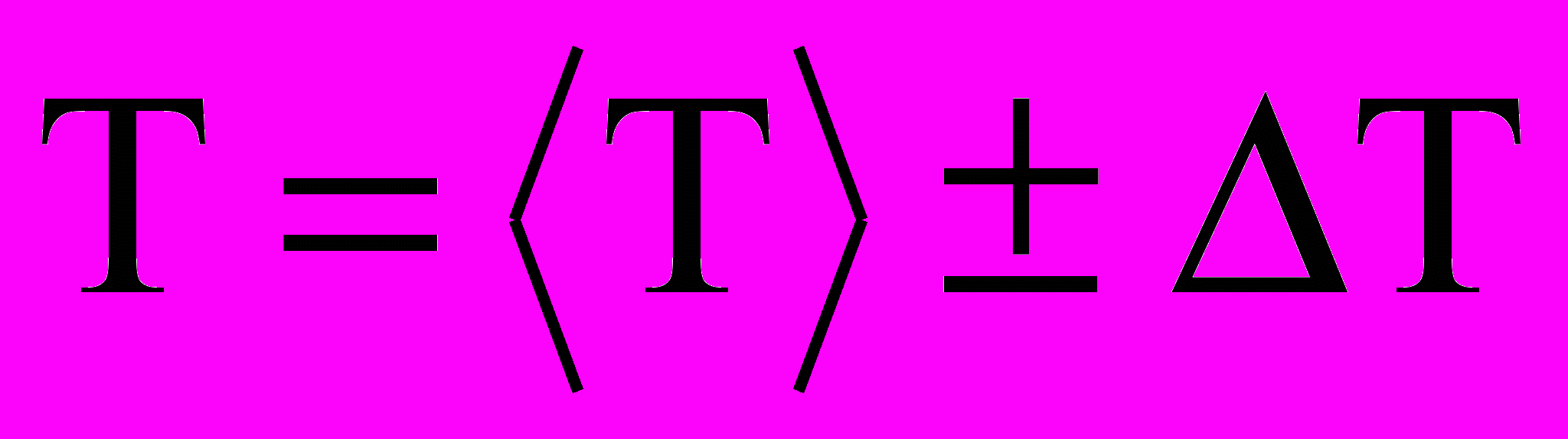 .
.- Постройте график зависимости периода колебаний от угла наклона плоскости качения , то есть T = T (), учитывая, что при = 90 (наклонная плоскость установлена вертикально и шар почти касается плоскости) период колебаний можно вычислить по формуле
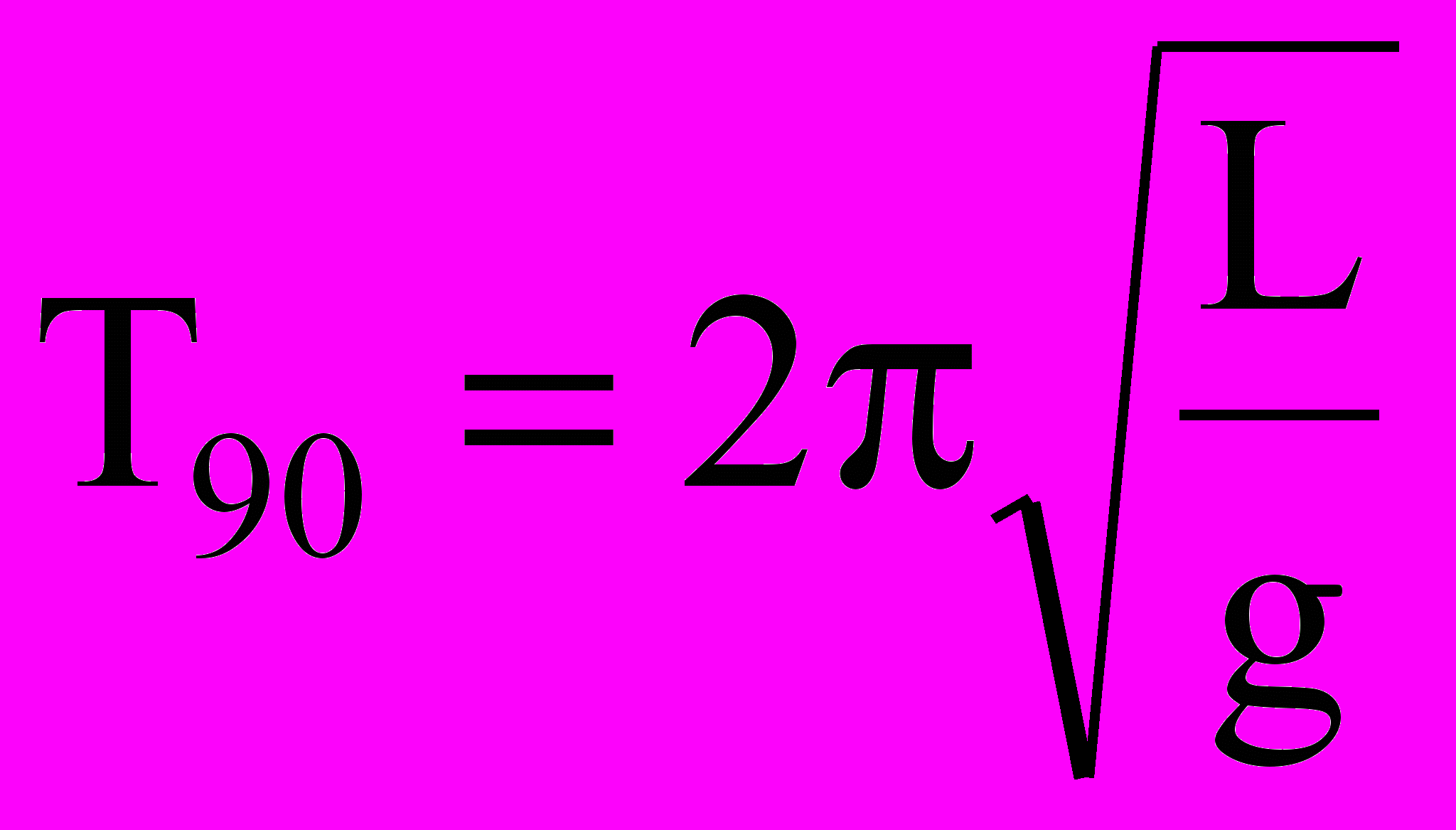 .
.Контрольные вопросы
- От каких факторов зависит величина сил трения?
- Дайте определение внешнего трения.
- Что такое внутреннее трение?
- Какие виды внешнего трения Вы знаете?
- При каких условиях возникают сухое или жидкостное трение?
- Чему равна сила трения скольжения?
- Какова размерность коэффициента трения скольжения?
- Объясните, какие деформации твердого тела называются упругими, пластическими?
- Чему равен момент силы относительно неподвижной точки?
- Что такое сила нормального давления и чему она равна в случае горизонтальной поверхности и в случае наклонной поверхности?
- Чему равна сила трения качения?
- Какова размерность коэффициента трения качения?
- Что такое полное колебание и его период?
- На основании какого закона выводится формула (12) для вычисления коэффициента трения качения?
- Какие упрощения вводятся при выводе расчетной формулы коэффициента трения качения?
- Опишите работу данной лабораторной установки.
- Какое явление используется для автоматической регистрации времени колебаний маятника?
- Объясните порядок выполнения данной лабораторной работы.
- Почему нить с шариком следует отклонять от положения равновесия на малые углы?
- Используя формулу периода колебаний математического маятника, вычислите время одного полного колебания, если длина маятника равна 0,9 м.
- М
 аятник (рис.11) длиной L = 1 м и массой m = 0,2 кг отклонили от положения равновесия на угол = 60. Найдите изменение потенциальной энергии в момент прохождения шариком положения равновесия. Ускорение свободного падения принять равным g = 10 м/с2.
аятник (рис.11) длиной L = 1 м и массой m = 0,2 кг отклонили от положения равновесия на угол = 60. Найдите изменение потенциальной энергии в момент прохождения шариком положения равновесия. Ускорение свободного падения принять равным g = 10 м/с2.
- Почему происходит уменьшение амплитуды колебаний наклонного маятника?
- Ц
 илиндр (рис.12) массой 1кг и радиусом 0,4 м пытаются поднять на ступеньку высотой 0,1 м горизонтальной силой F, приложенной к центру С. Найдите момент силы тяжести (
илиндр (рис.12) массой 1кг и радиусом 0,4 м пытаются поднять на ступеньку высотой 0,1 м горизонтальной силой F, приложенной к центру С. Найдите момент силы тяжести (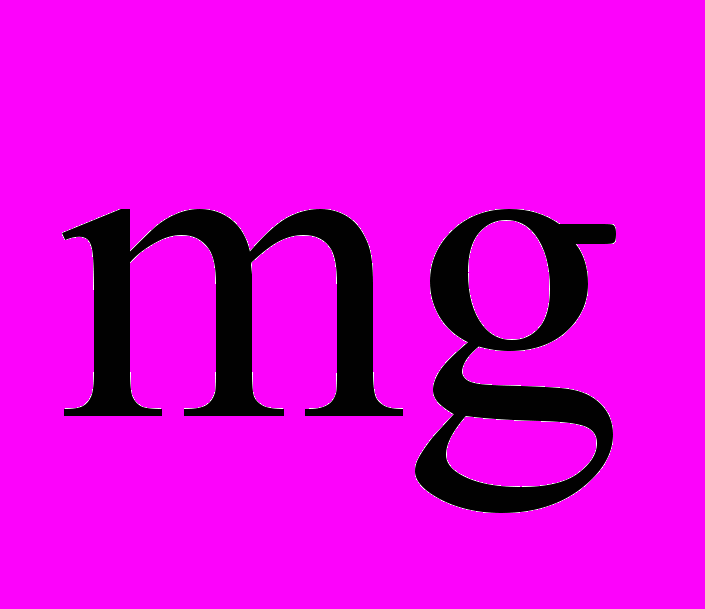 ) и силы
) и силы  относительно точки поворота (т.О).
относительно точки поворота (т.О).
- Как изменится коэффициент трения качения, если стальную пластину заменить на алюминиевую?
- Как зависит период колебаний маятника от угла наклона плоскости качения?
- Какие виды погрешностей Вы знаете?
- Назовите виды измерений физических величин.
- Как вычисляются абсолютные и относительные ошибки при прямых измерениях ?
- Что такое доверительный интервал?
- Напишите формулу для вычисления относительной погрешности
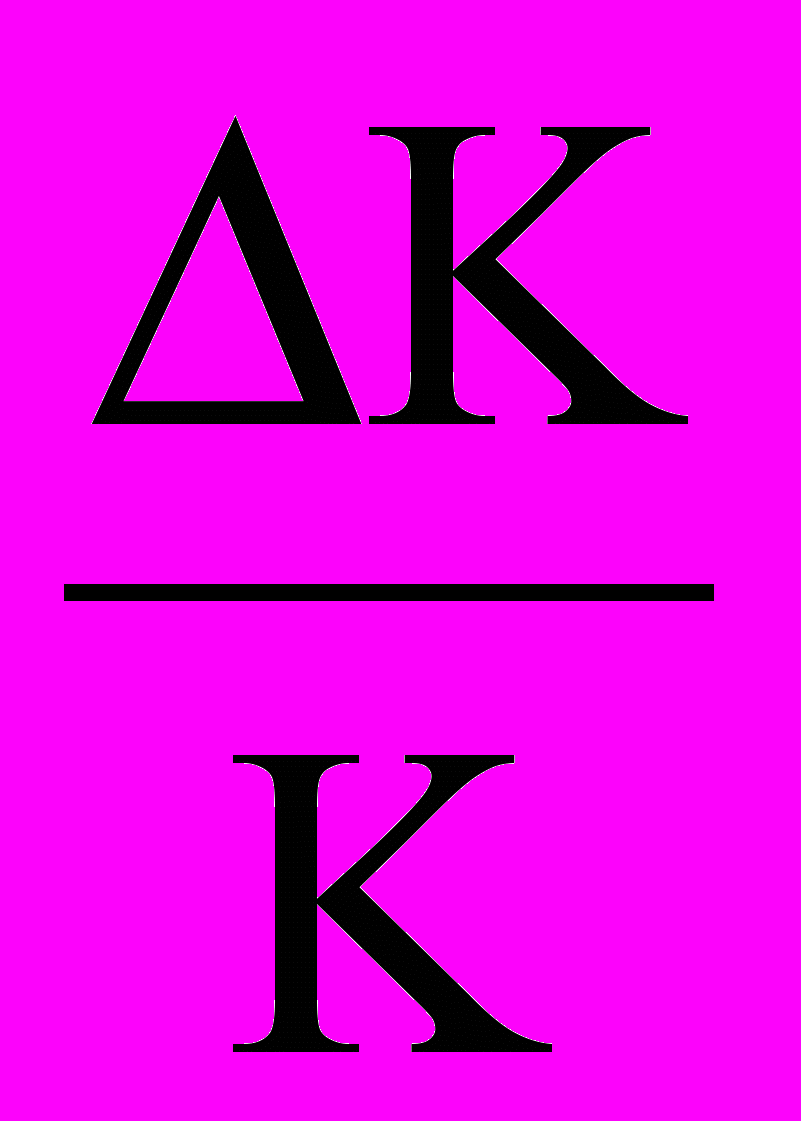 .
.
* Момент силы относительно оси, проходящей через точку С, численно равен произведению силы на плечо (кратчайшее расстояние между линией действия силы и осью вращения, проходящей через точку С).
* Период колебаний Т (с) - это время одного полного колебания.
©МАТИ, 2003
