«Алгоритмизация и решение физических задач на эвм»
| Вид материала | Решение |
- Решение физических задач на эвм" Лекции 20 ч. Практические занятия 96 ч. Учебная, 40.03kb.
- Календарно-тематическое планирование элективного курса " методы решения физических, 107.87kb.
- Лекция №11, 100.42kb.
- Лекция №10, 126.75kb.
- Методы решения задач, 160.67kb.
- Программы общего назначения в решении медицинских задач. История развития средств вычислительной, 59.78kb.
- Утверждаю, 187.71kb.
- Урок физики, литературы, русского языка. Решение задач по теме: "Законы Ньютона"на, 124.36kb.
- 1 История развития компьютерной техники, поколения ЭВМ и их классификация Развитие, 1329.92kb.
- I. Решение логических задач средствами алгебры логики 22 >II. Решение логических задач, 486.64kb.
Для их выполнения требуется знакомство с средой программирования Turbo Pascal и Mathcad (версии 5 и выше). Обязательными являются задания № 1…7. По каждому из заданий оформляется отчет (в текстовом или электронном виде), содержащий следующие обязательные пункты:
- постановка задачи, исходные данные для расчета;
- сведения о численном методе, которым будет решаться задача;
- блок-схема программы или словесное описание алгоритма;
- результаты расчета с оценкой погрешности вычислений;
- если требуется сравнить решение задачи на Pascal и Mathcad, приводится текст документа Mathcad с подробными комментариями и проводится анализ полученных результатов.
Вариант №4 заданий по курсу
«Алгоритмизация и решение физических задач на ЭВМ».
| N | Содержание задания | Данные (в терминах Mathcad) | ||||||||||||||||||||||||||||||||
| 1 | Составить программу на языке Паскаль, вычисляющую определенные интегралы методом Симпсона с точностью 0.00001. С помощью среды Mathcad попытаться найти аналитическое решение этих интегралов, а также получить численное решение с той же точностью и сравнить полученные результаты. | 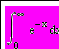 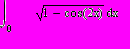 | ||||||||||||||||||||||||||||||||
| 2 | Составить программу на языке Паскаль, решающую систему линейных алгебраических уравнений методом Гаусса. Рассчитать невязки. С помощью среды Mathcad найти решение этой системы двумя способами: путем вычисления обратной матрицы и используя функцию lsolve. | 0.5x-z=y z+2-y=0 y-2z=4.2 | ||||||||||||||||||||||||||||||||
| 3 | На языке Паскаль составить программу, аппроксимирующую предложенный набор экспериментальных точек полиномом по методу наименьших квадратов. Обосновать, какая степень полинома необходима для правильной аппроксимации (абсолютная погрешность исходных данных 1.5). Построить график полученного полинома, аппроксимирующего экспериментальные значения. |
| ||||||||||||||||||||||||||||||||
| 4 | На языке Паскаль составить программу, вычисляющую корни уравнения с точностью 10-6 методами бисекций и касательных. Сравнить количество итераций при использовании каждого из методов. В среде Mathcad исследовать график уравнения и найти все его корни с помощью функции root, используя различные начальные приближения. | 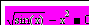 | ||||||||||||||||||||||||||||||||
| 5 | На языке Паскаль составить программу, решающую систему нелинейных уравнений методом Ньютона с точностью 0.0001. Найти все корни этой системы в среде Mathcad, используя решающий блок Given…Find. |  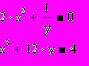 | ||||||||||||||||||||||||||||||||
| 6 | В среде Mathcad графически исследовать предложенную функцию двух переменных и с помощью решающего блока Given…Minerr найти ее минимум с точностью 0.0001. |  | ||||||||||||||||||||||||||||||||
| 7 | В среде Mathcad написать программу, численно решающую предложенную задачу Коши для обыкновенного дифференциального уравнения простейшим методом Эйлера. Оценить погрешность решения по методу Рунге. Построить график полученной функции. Сравнить результат с решениями, полученными с помощью встроенных функций rkfixed (метод Рунге-Кутта 4 порядка) и Bulstoer (метод Булириш-Штёра). | 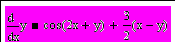 y(0) = 0 | ||||||||||||||||||||||||||||||||
| 8* | На языке Паскаль реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений. Вывести на график полученные функции. В среде Mathcad попытаться найти аналитическое решение данной системы уравнений. |  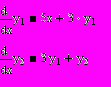 y1(0) = 3; y2(0) = 2 |
Для их выполнения требуется знакомство с средой программирования Turbo Pascal и Mathcad (версии 5 и выше). Обязательными являются задания № 1…7. По каждому из заданий оформляется отчет (в текстовом или электронном виде), содержащий следующие обязательные пункты:
- постановка задачи, исходные данные для расчета;
- сведения о численном методе, которым будет решаться задача;
- блок-схема программы или словесное описание алгоритма;
- результаты расчета с оценкой погрешности вычислений;
- если требуется сравнить решение задачи на Pascal и Mathcad, приводится текст документа Mathcad с подробными комментариями и проводится анализ полученных результатов.
Вариант №5 заданий по курсу
«Алгоритмизация и решение физических задач на ЭВМ».
| N | Содержание задания | Данные (в терминах Mathcad) | ||||||||||||||||||||||||||||||||
| 1 | Составить программу на языке Паскаль, вычисляющую определенные интегралы методом Симпсона с точностью 0.00001. С помощью среды Mathcad попытаться найти аналитическое решение этих интегралов, а также получить численное решение с той же точностью и сравнить полученные результаты. | 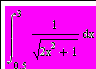 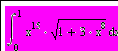 | ||||||||||||||||||||||||||||||||
| 2 | Составить программу на языке Паскаль, решающую систему линейных алгебраических уравнений методом Гаусса. Рассчитать невязки. С помощью среды Mathcad найти решение этой системы двумя способами: путем вычисления обратной матрицы и используя функцию lsolve. | y-5z=7 x+2-y-1.1z=0 y-15=3x | ||||||||||||||||||||||||||||||||
| 3 | На языке Паскаль составить программу, аппроксимирующую предложенный набор экспериментальных точек полиномом по методу наименьших квадратов. Обосновать, какая степень полинома необходима для правильной аппроксимации (абсолютная погрешность исходных данных 1.5). Построить график полученного полинома, аппроксимирующего экспериментальные значения. |
| ||||||||||||||||||||||||||||||||
| 4 | На языке Паскаль составить программу, вычисляющую корни уравнения с точностью 10-6 методами бисекций и касательных. Сравнить количество итераций при использовании каждого из методов. В среде Mathcad исследовать график уравнения и найти все его корни с помощью функции root, используя различные начальные приближения. |  | ||||||||||||||||||||||||||||||||
| 5 | На языке Паскаль составить программу, решающую систему нелинейных уравнений методом Ньютона с точностью 0.0001. Найти все корни этой системы в среде Mathcad, используя решающий блок Given…Find. |  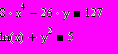 | ||||||||||||||||||||||||||||||||
| 6 | В среде Mathcad графически исследовать предложенную функцию двух переменных и с помощью решающего блока Given…Minerr найти ее минимум с точностью 0.0001. |  | ||||||||||||||||||||||||||||||||
| 7 | В среде Mathcad написать программу, численно решающую предложенную задачу Коши для обыкновенного дифференциального уравнения простейшим методом Эйлера. Оценить погрешность решения по методу Рунге. Построить график полученной функции. Сравнить результат с решениями, полученными с помощью встроенных функций rkfixed (метод Рунге-Кутта 4 порядка) и Bulstoer (метод Булириш-Штёра). | 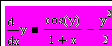 y(0) = 0 | ||||||||||||||||||||||||||||||||
| 8* | На языке Паскаль реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений. Вывести на график полученные функции. В среде Mathcad попытаться найти аналитическое решение данной системы уравнений. |  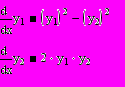 y1(0) = -1; y2(0) = 0 |
Для их выполнения требуется знакомство с средой программирования Turbo Pascal и Mathcad (версии 5 и выше). Обязательными являются задания № 1…7. По каждому из заданий оформляется отчет (в текстовом или электронном виде), содержащий следующие обязательные пункты:
- постановка задачи, исходные данные для расчета;
- сведения о численном методе, которым будет решаться задача;
- блок-схема программы или словесное описание алгоритма;
- результаты расчета с оценкой погрешности вычислений;
- если требуется сравнить решение задачи на Pascal и Mathcad, приводится текст документа Mathcad с подробными комментариями и проводится анализ полученных результатов.
Вариант №6 заданий по курсу
«Алгоритмизация и решение физических задач на ЭВМ».
| N | Содержание задания | Данные (в терминах Mathcad) | ||||||||||||||||||||||||||||||||
| 1 | Составить программу на языке Паскаль, вычисляющую определенные интегралы методом Симпсона с точностью 0.00001. С помощью среды Mathcad попытаться найти аналитическое решение этих интегралов, а также получить численное решение с той же точностью и сравнить полученные результаты. |  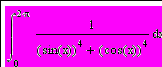 | ||||||||||||||||||||||||||||||||
| 2 | Составить программу на языке Паскаль, решающую систему линейных алгебраических уравнений методом Гаусса. Рассчитать невязки. С помощью среды Mathcad найти решение этой системы двумя способами: путем вычисления обратной матрицы и используя функцию lsolve. | 3y-12v+0.1z=1 -x+3v=0 y+23x+z=2v 1-8y-1.5z=x | ||||||||||||||||||||||||||||||||
| 3 | На языке Паскаль составить программу, аппроксимирующую предложенный набор экспериментальных точек полиномом по методу наименьших квадратов. Обосновать, какая степень полинома необходима для правильной аппроксимации (абсолютная погрешность исходных данных 1.5). Построить график полученного полинома, аппроксимирующего экспериментальные значения. |
| ||||||||||||||||||||||||||||||||
| 4 | На языке Паскаль составить программу, вычисляющую корни уравнения с точностью 10-6 методами бисекций и касательных. Сравнить количество итераций при использовании каждого из методов. В среде Mathcad исследовать график уравнения и найти все его корни с помощью функции root, используя различные начальные приближения. | 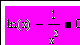 | ||||||||||||||||||||||||||||||||
| 5 | На языке Паскаль составить программу, решающую систему нелинейных уравнений методом Ньютона с точностью 0.0001. Найти все корни этой системы в среде Mathcad, используя решающий блок Given…Find. |  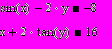 | ||||||||||||||||||||||||||||||||
| 6 | В среде Mathcad графически исследовать предложенную функцию двух переменных и с помощью решающего блока Given…Minerr найти ее минимум с точностью 0.0001. | 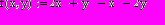 | ||||||||||||||||||||||||||||||||
| 7 | В среде Mathcad написать программу, численно решающую предложенную задачу Коши для обыкновенного дифференциального уравнения простейшим методом Эйлера. Оценить погрешность решения по методу Рунге. Построить график полученной функции. Сравнить результат с решениями, полученными с помощью встроенных функций rkfixed (метод Рунге-Кутта 4 порядка) и Bulstoer (метод Булириш-Штёра). | 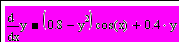 y(0) = 0 | ||||||||||||||||||||||||||||||||
| 8* | На языке Паскаль реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений. Вывести на график полученные функции. В среде Mathcad попытаться найти аналитическое решение данной системы уравнений. |  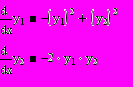 y1(0) = 0; y2(0) = 1 |
