Geum.ru

А. В. Сакало математическое моделирование профилей

Вид материалаДокументы

Содержание


Получение информации о топологии изношенных поверхностей.
Оцифровка координат точек профиля
Аппроксимация профиля полиномом 4-й степени.
Список литературы
Подобный материал:

Вестник Брянского государственного технического университета. 2009. № 3(23)


УДК 539.3

А.В. Сакало


МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОФИЛЕЙ

ИЗНОШЕННЫХ ПОВЕРХНОСТЕЙ ТЕЛ КАЧЕНИЯ


Предложен способ аппроксимации профилей поверхностей тел качения с использованием на их участках полиномов 4-й степени со стыковкой по координатам граничных точек и первых производных от аппроксимирующих функций.


Ключевые слова: профиль поверхности, аппроксимирующая функция, полином.


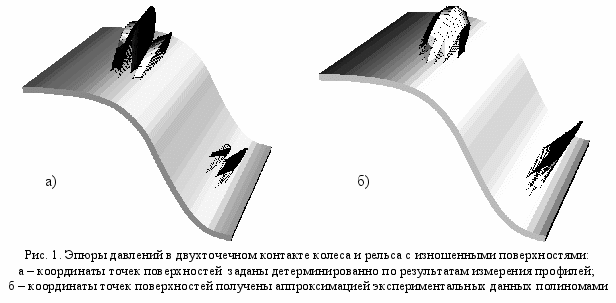
При моделировании движения сложных механических систем и процессов изнашивания возникает необходимость решения контактных задач. В процессе эксплуатации тела изнашиваются, и их поверхности приобретают сложные геометрические формы. Особо актуальной проблемой является описание их профилей. Для замера координат точек профилей изношенных поверхностей используются приборы, не обеспечивающие достаточной точности измерений. Численные эксперименты показывают, что погрешность в задании координат точек контактирующих поверхностей порядка 2-3 мкм приводит к значительным погрешностям при решении контактной задачи в определении законов распределения давлений. На рис.1а представлены эпюры давлений в двухточечном контакте колеса и рельса с изношенными поверхностями при задании координат точек поверхностей детерминированно по результатам измерения профилей. А на рис.1б представлено решение этой задачи для профилей, полученных аппроксимацией экспериментальных данных полиномами. В первом случае давление представлено эпюрами, не характерными для контакта изношенных поверхностей, выглаженных в результате приработки.

Для сглаживания профилей используют аппроксимирующие функции, позволяющие правильно представить закон изменения кривизны их участков в пределах потенциального контакта. В [1] для аппроксимации профиля изношенного локомотивного колеса использованы две функции: вида 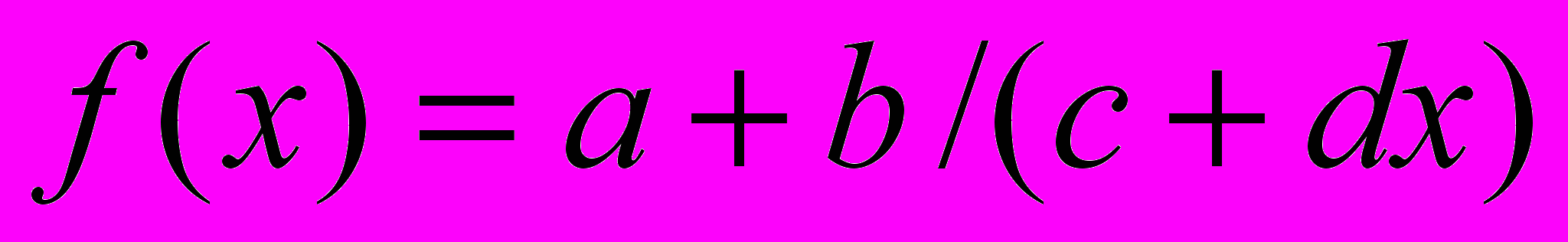– на участке от круга катания до гребня и 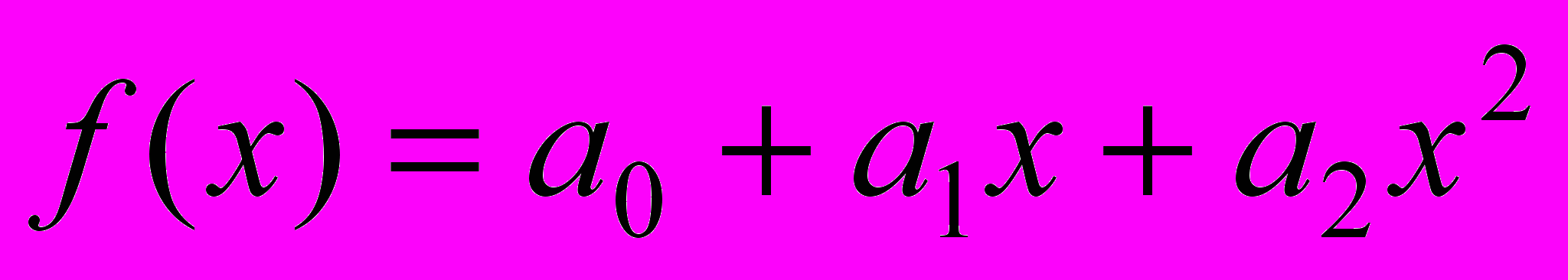– на внешнем участке контура. В [2] контур разбивается на несколько участков и на каждом из них аппроксимируется кубическим сплайном.

В статье исследуется возможность применения в качестве аппроксимирующих функций полиномов 2-5-й степени с различными условиями стыковки участков.

Получение информации о топологии изношенных поверхностей. Для получения формы профилей изношенных колес и рельсов с них снимались гипсовые слепки с помощью приспособлений, показанных на рис.2 и 3. Приспособление, показанное на рис.2, предназначено для снятия слепка поверхности вагонного колеса. Оно состоит из двух щек (1, 2) и прокладок (3, 4) между ними, определяющих толщину снимаемого слепка. Контур щеки воспроизводит профиль поверхности неизношенного колеса. Приспособление устанавливается на колесо, базируясь плоскостью А на его внутреннюю торцевую плоскость, и фиксируется на нем с помощью винта 5. Раствор гипса или алебастра заливается в свободное пространство между щеками. Аналогично устроено приспособление для снятия слепка поверхности рельса. На рельсе оно базируется по наклонным граням головки рельса. Приспособление, установленное на рельсе, показано на рис.3.

Оцифровка координат точек профиля проводилась путём сканирования слепка с высоким разрешением. На контуре слепка выбиралось начало координат: в точке, расположенной на круге катания колеса, и в точке, лежащей на оси симметрии неизношенного рельса. Координата x отсчитывалась в поперечном относительно рельса направлении. С использованием программы CorelDraw определялись координаты xi, yi точек (с точностью до трех знаков после запятой), расположенных с шагом 1 мм на контуре профиля.

С использованием шаблона измерен прокат более 200 колес полувагонов и вагонов-цистерн. По значению проката они разделены на 5 групп: с прокатом 1, 2, 3, 4 и 5 мм. С помощью слепков исследованы характерные для выделенных групп профили.

Исследованы также профили рельсов, уложенных в кривых радиусов 600 и 1000 м. Сняты слепки наружного рельса на различных участках переходной кривой и кривой постоянного радиуса, где боковой износ составил 1,8; 5; 8,8; 12 и 14 мм.

Аппроксимация профиля полиномом 4-й степени. В качестве аппроксимирующей функции в работе использован полином .

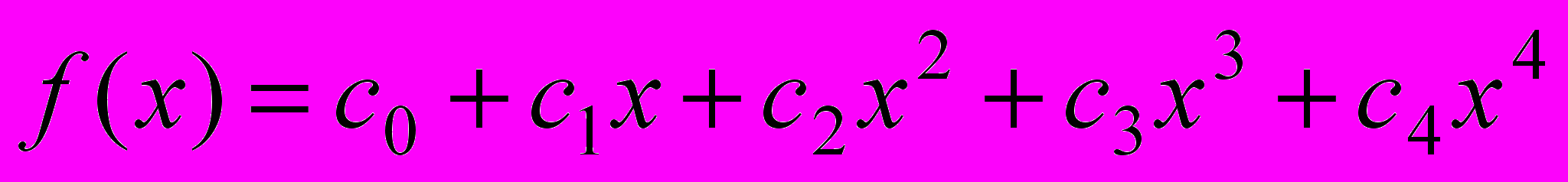Для определения его коэффициентов воспользуемся методом наименьших квадратов [3]. Он предполагает условие: коэффициенты должны быть определены так, чтобы сумма квадратов разности детерминированно заданных значений ординат точек профиля 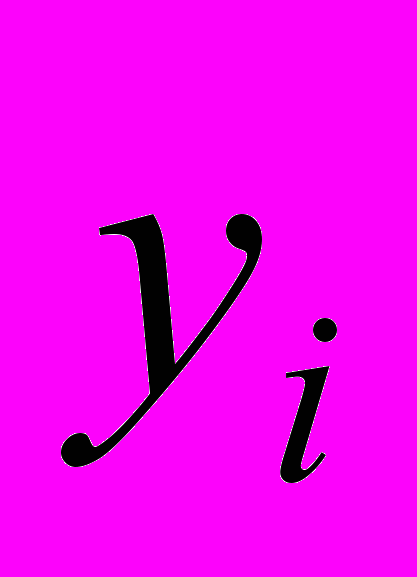и значений функции 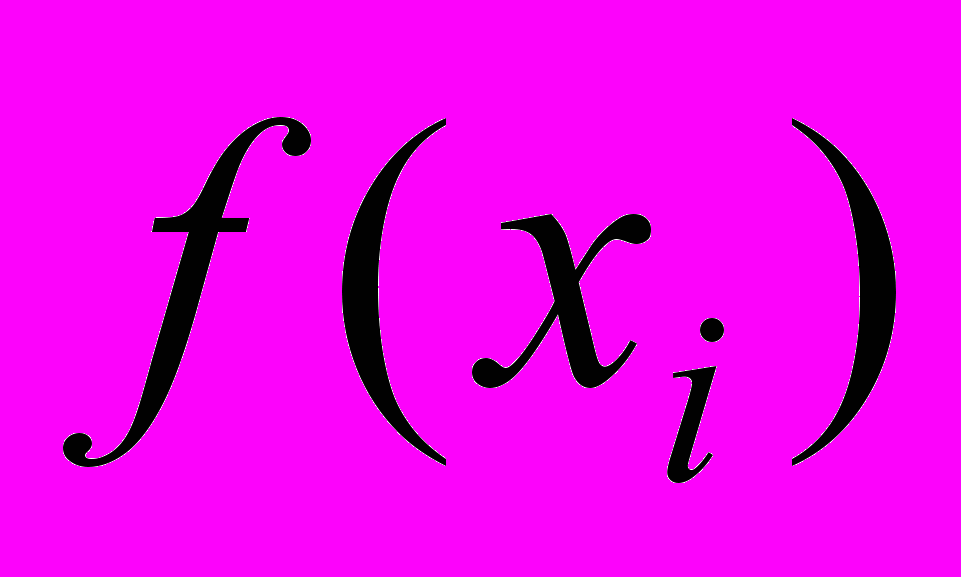, где 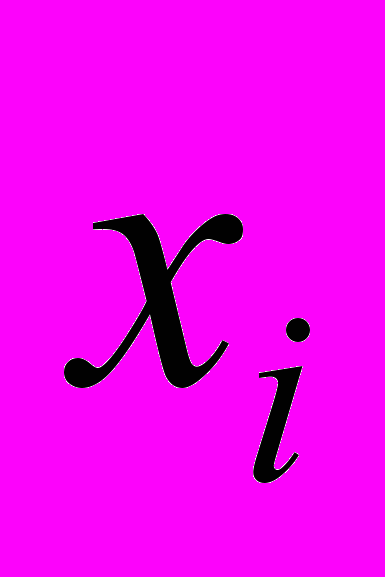- абсцисса точки i, была минимальной:

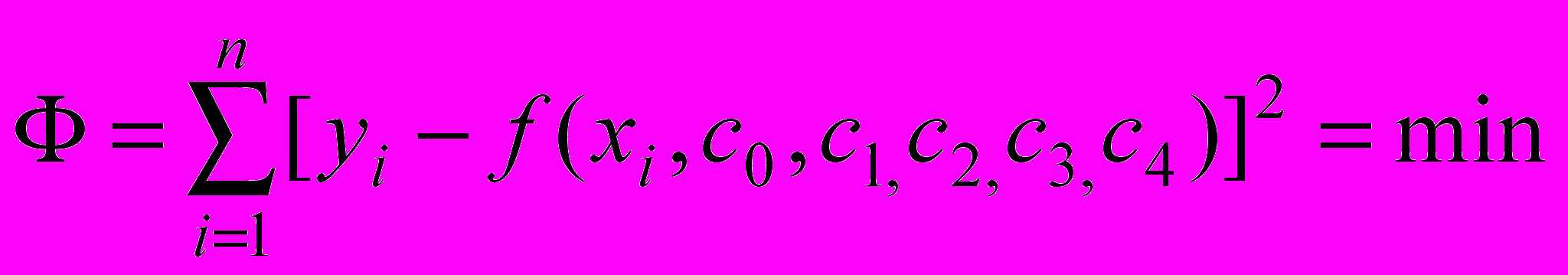. (1)

Это условие выполняется при равенстве нулю производных 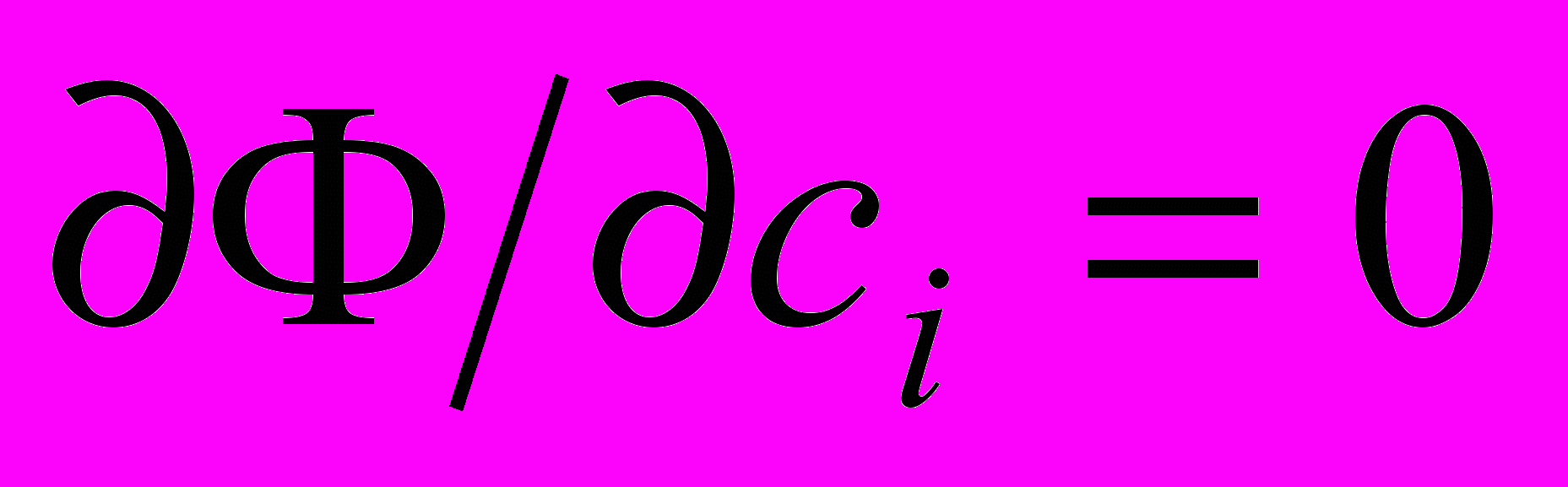. Получим систему из пяти алгебраических уравнений с коэффициентами: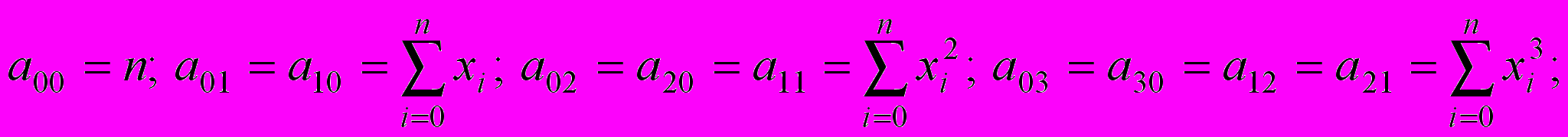



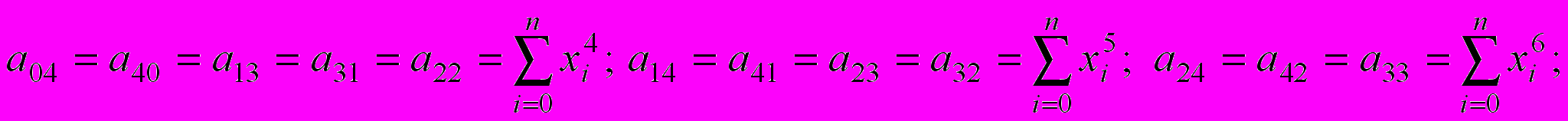(2)



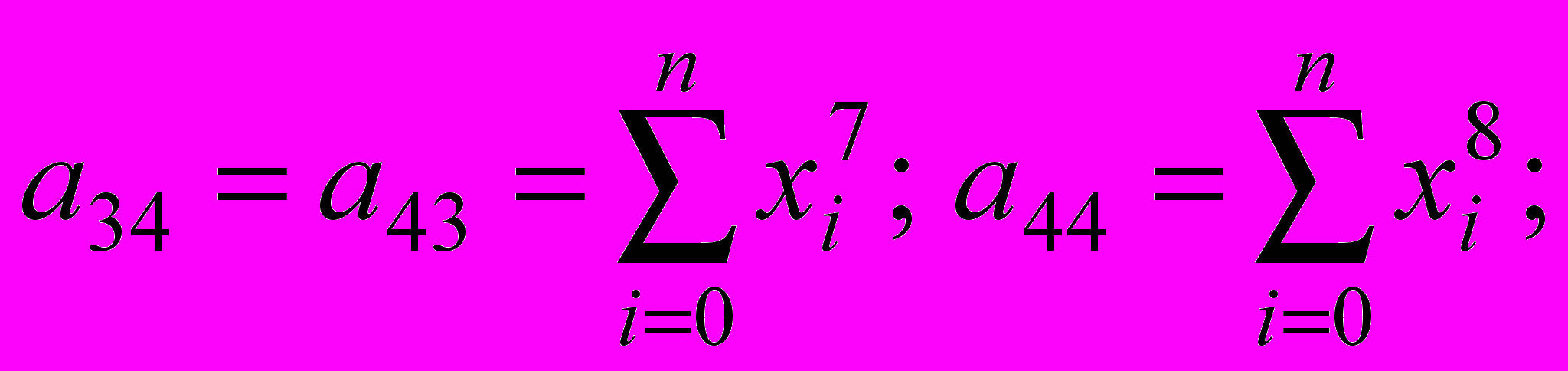
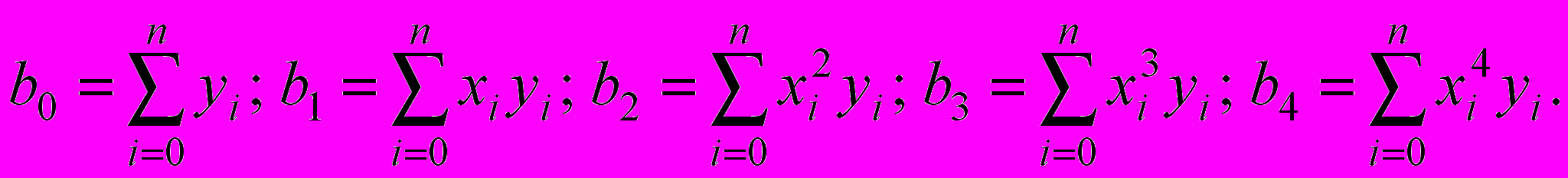
Из нее определяются коэффициенты аппроксимирующего полинома.

Аппроксимируемый профиль разбивается на участки. Присвоим номер 0 участку, для которого определены коэффициенты полинома, и номер 1 – участку, для которого они определяются. Обозначим 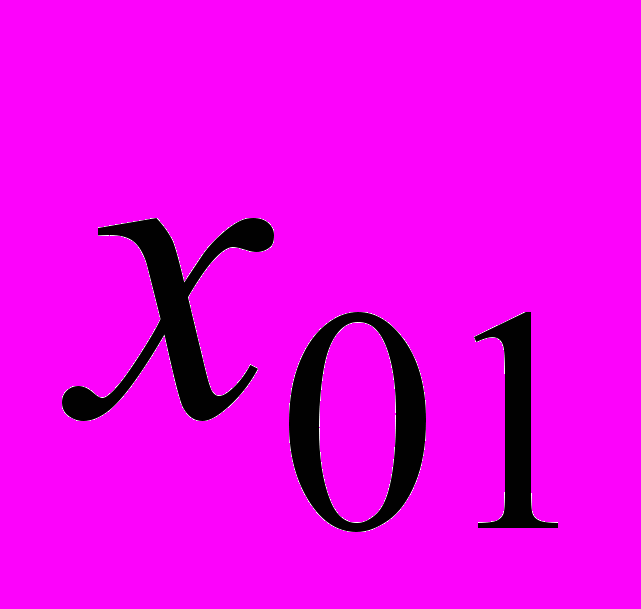абсциссу точки, расположенной на стыке двух участков, и 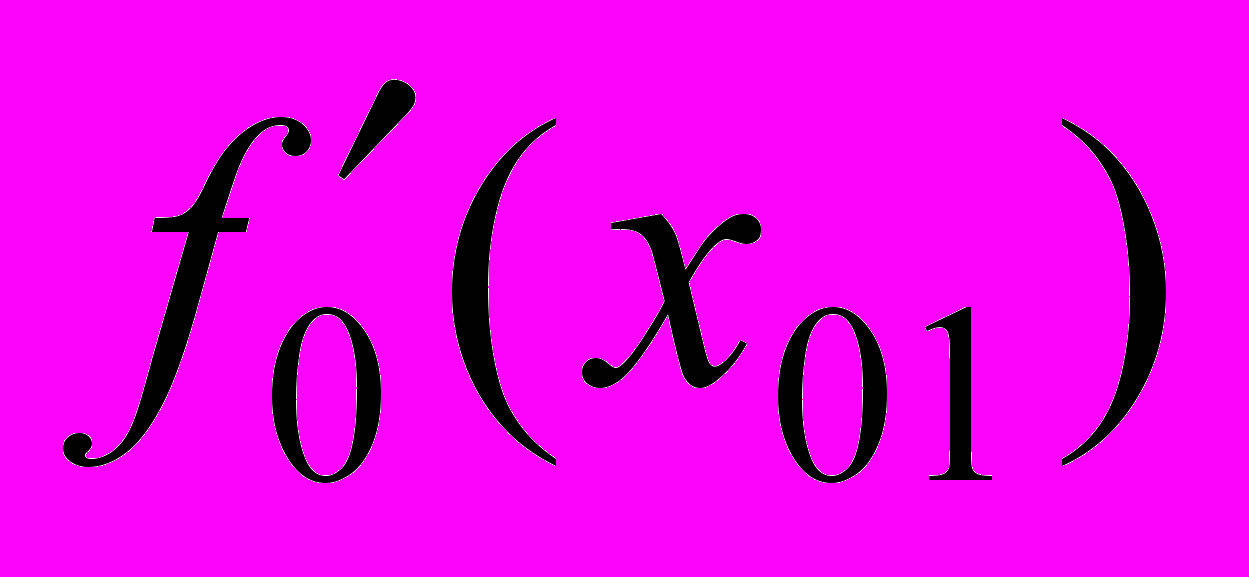– значение производной в ней. Пусть аппроксимирующие функции стыкуются на границе по координатам граничной точки 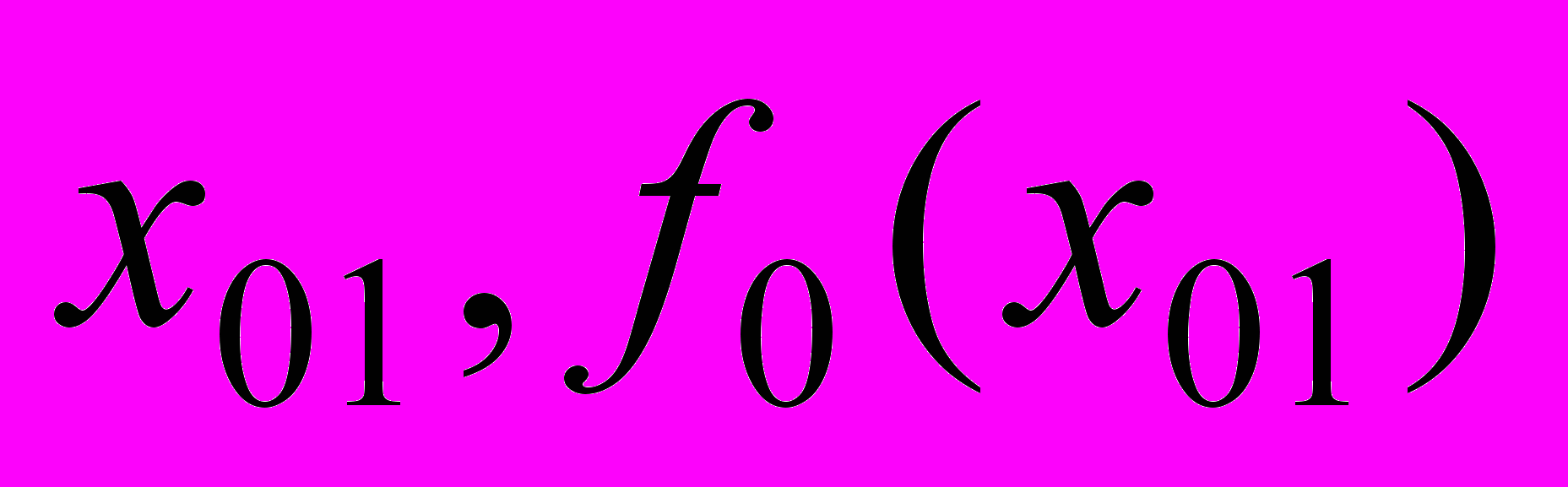и первой производной 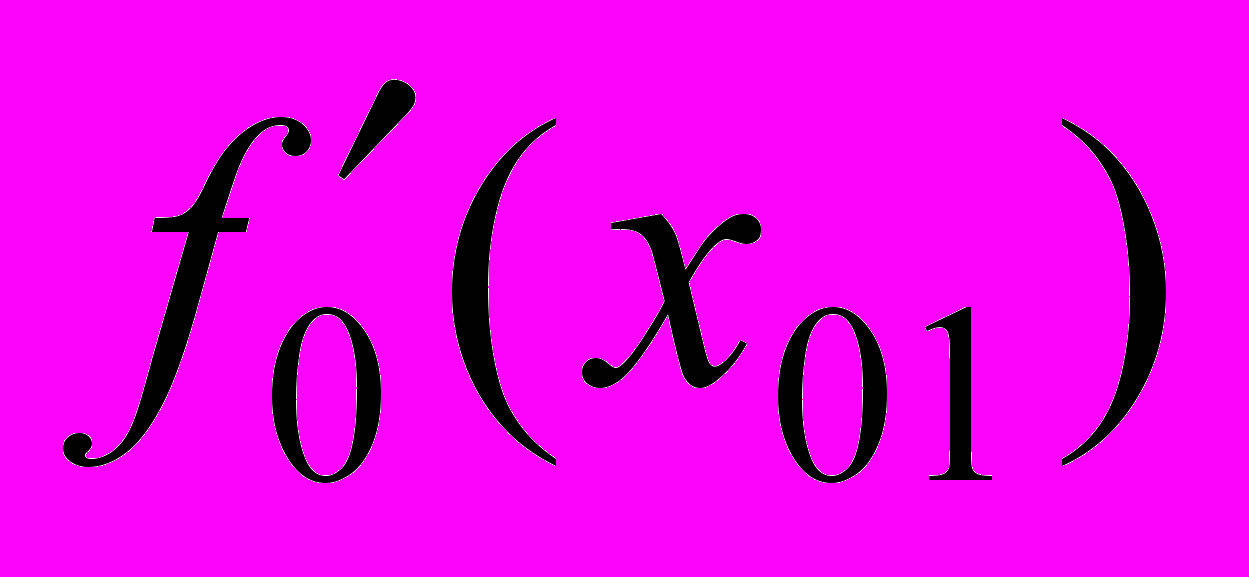. Уравнение полинома на участке представим в виде 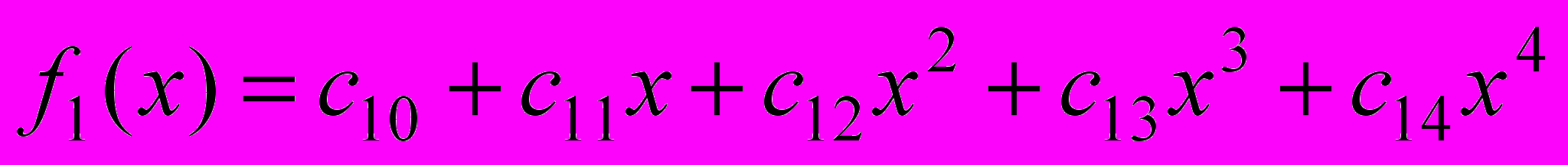. Первая производная от него равна .

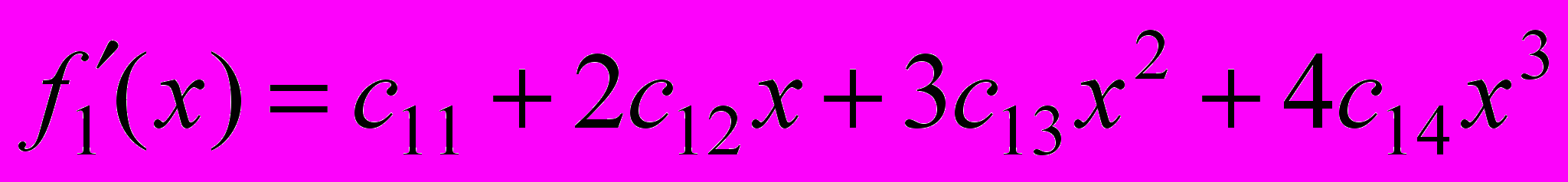Из условий стыковки на границе участков

;

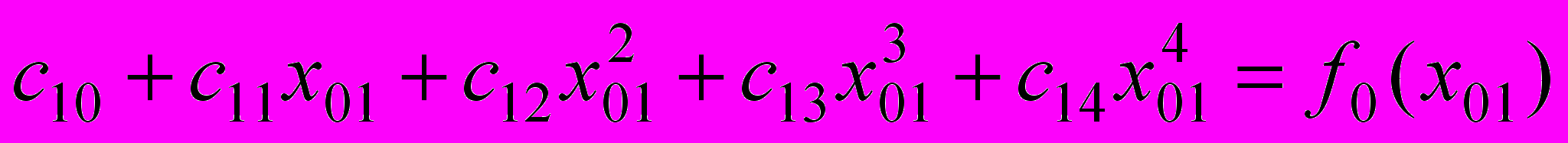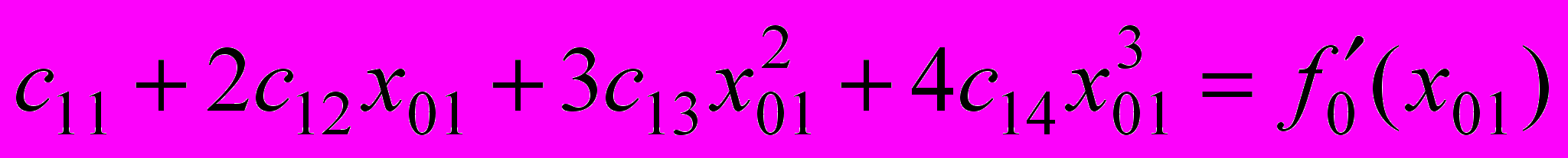
получаем

; .

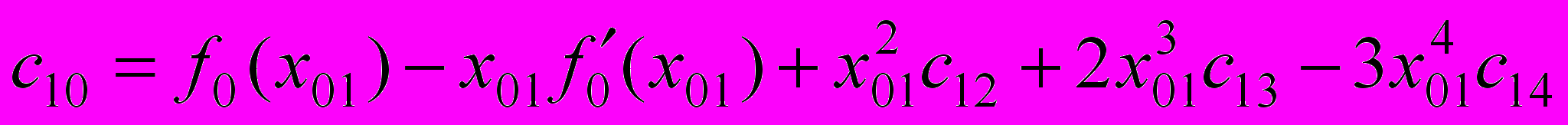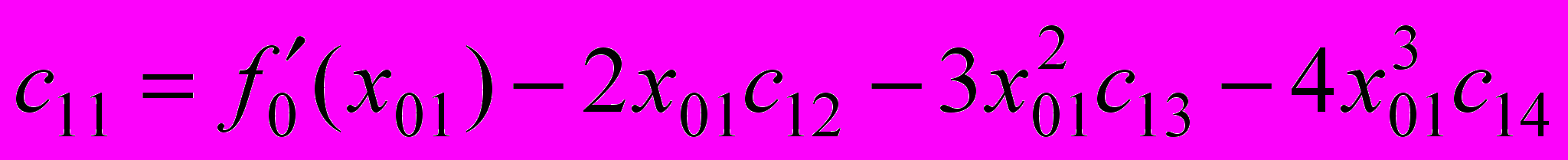Построив минимизируемую функцию по аналогии с условием (1) и взяв производные по коэффициентам с12, с13 и с14, получим систему из трех алгебраических уравнений с коэффициентами:







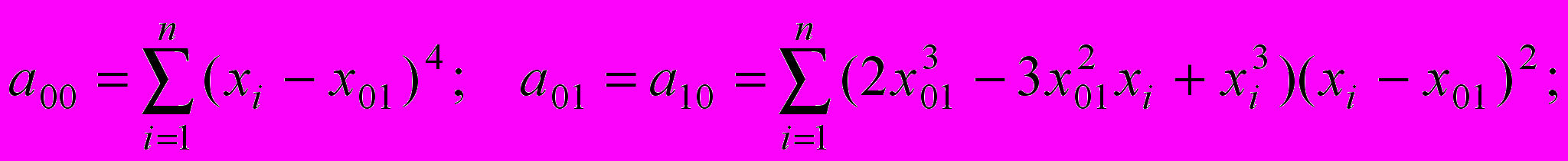
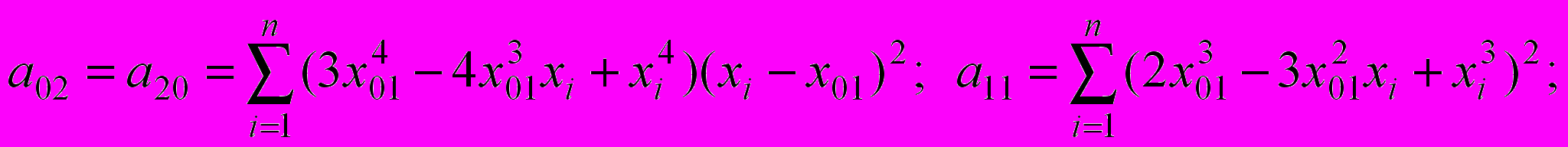
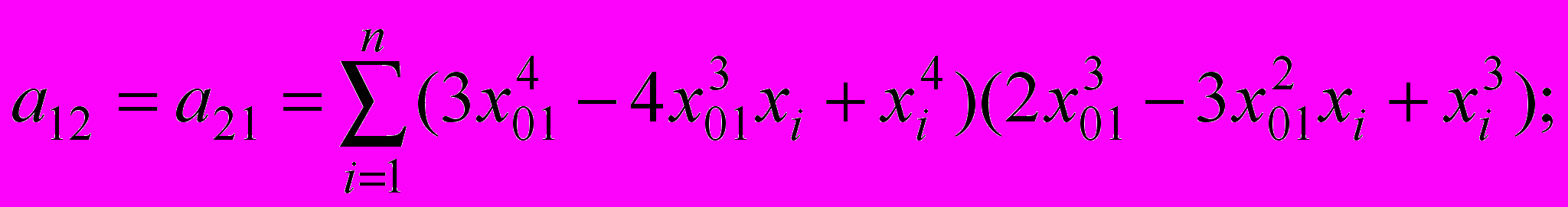
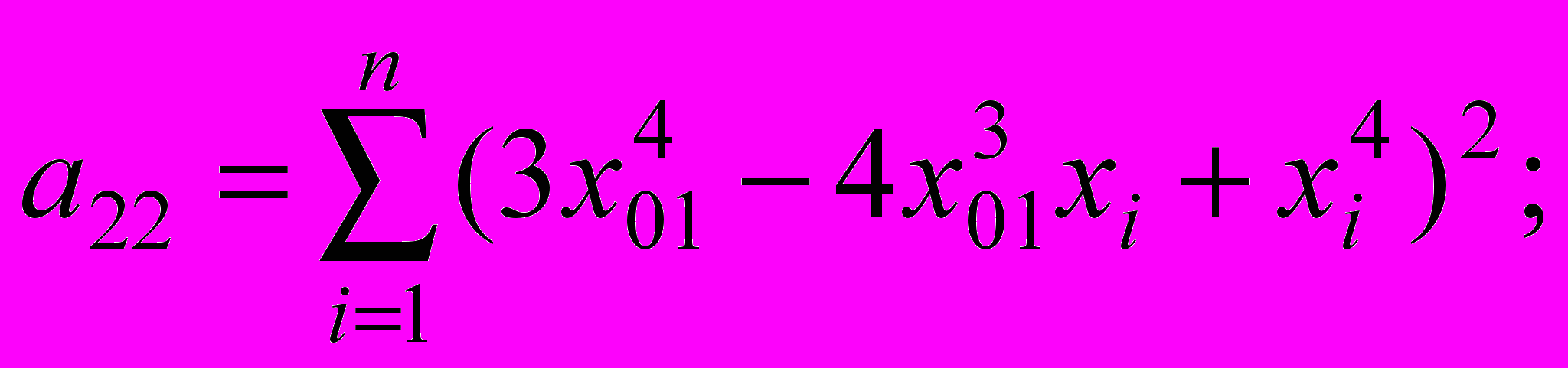
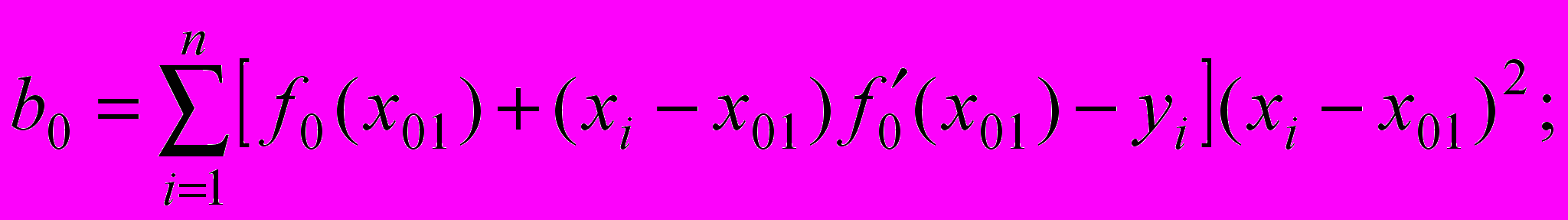(3)





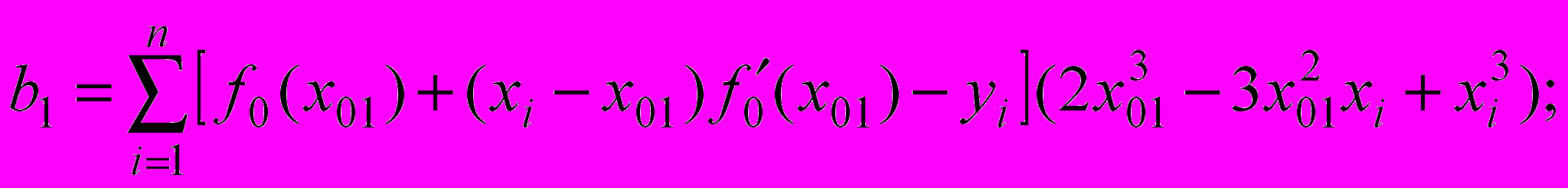
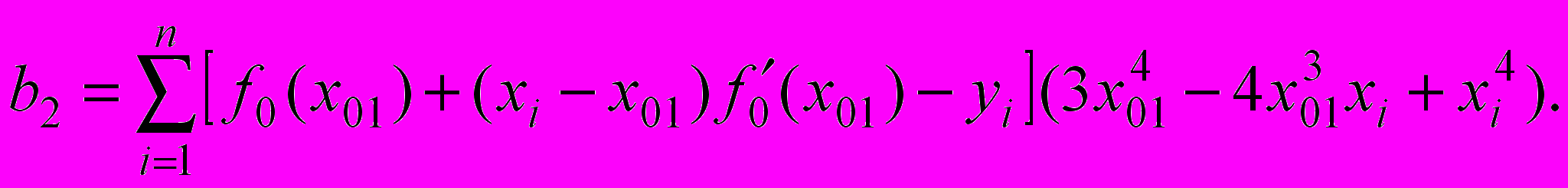
Алгоритм предполагает разбивку профиля на несколько участков и построение аппроксимирующего полинома для каждого из них. Коэффициенты полинома для начального участка определяются из решения системы из пяти уравнений с коэффициентами (2). Для последовательно пристыковываемых к нему участков коэффициенты определяются из решения системы из трех уравнений с коэффициентами (3).

Алгоритм использован для сглаживания профилей поверхностей изношенных колес полувагонов и рельсов. Аппроксимированы профили колеса с прокатом 1 мм и рельса Р65 с боковым износом 1,8 мм.

Структурная схема алгоритма сглаживания профиля поверхности контакта представлена на рис. 4. На первом этапе проводится разделение профиля на участки. Характер разделения существенно влияет на качество сглаживания. Лучшие результаты получаются, если участки выбираются так, чтобы кривизна профиля не сильно менялась в пределах участка. Число точек участка должно быть больше числа определяемых коэффициентов функции: больше 5 для начального участка и больше 3 для стыкуемого. В противном случае аппроксимирующая функция превращается в интерполирующую, её график проходит через заданные точки и сглаживания профиля не происходит.

О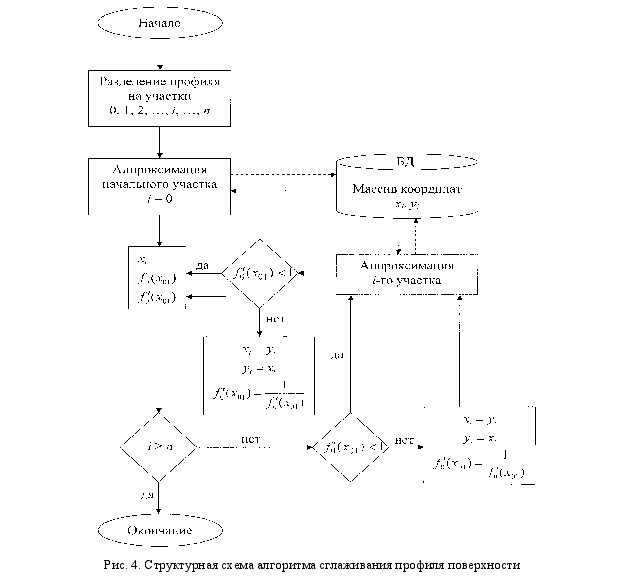пределяются коэффициенты аппроксимирующей функции для первого участка, значение функции 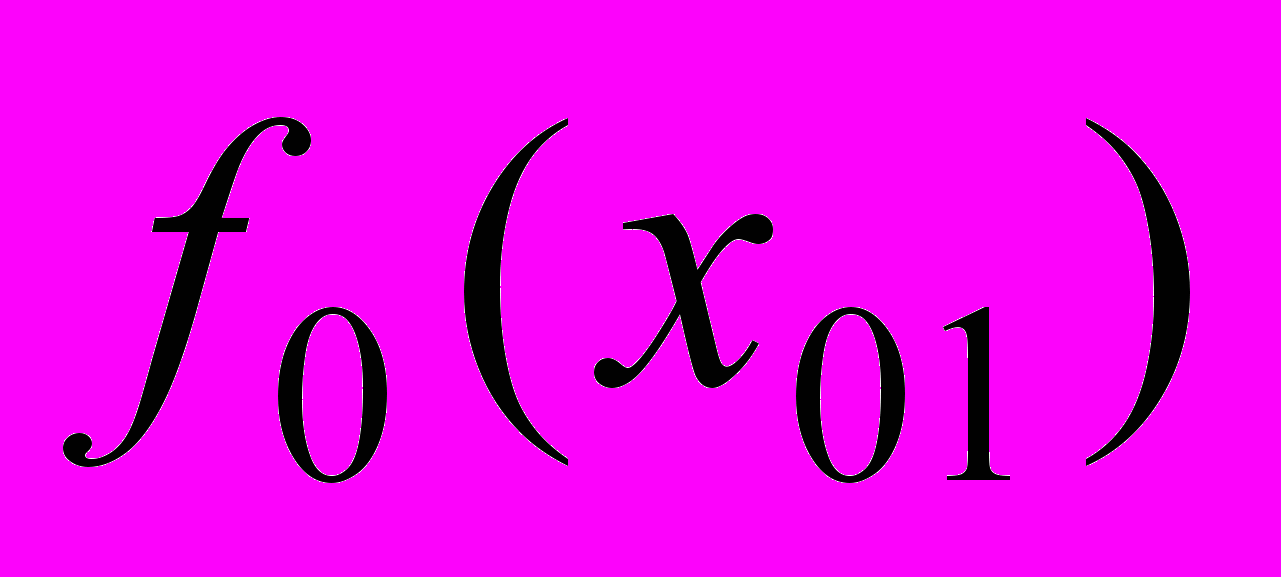и её первой производной 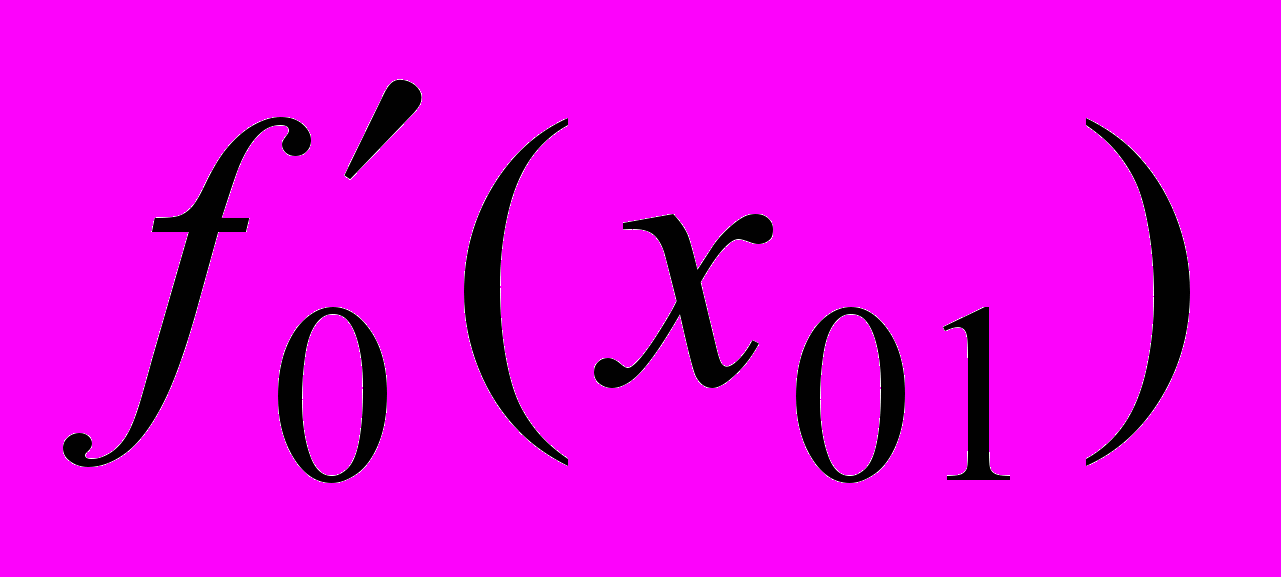в точке стыковки со следующим участком. Далее строится аппроксимирующая функция для следующего участка. Если угол его наклона больше 45º, уравнение аппроксимирующей функции представляется в виде f(y). В связи с этим, если тангенс угла наклона в начале участка 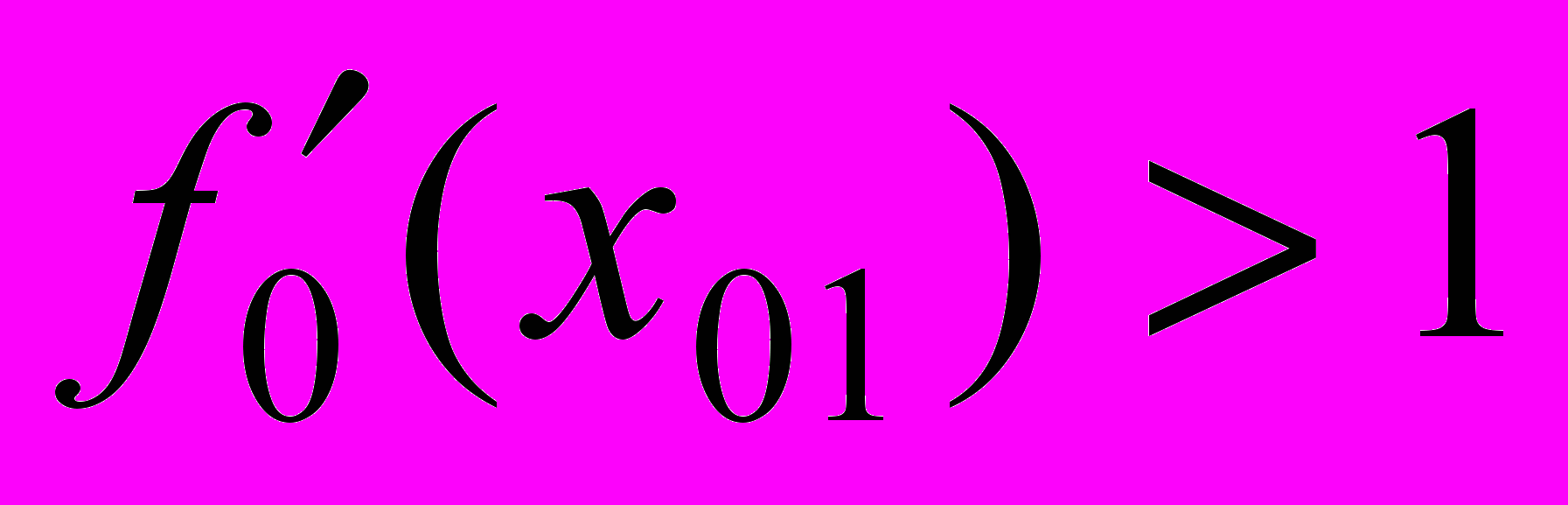, в алгоритме предусмотрен переход к построению аппроксимирующей функции f(y). Эта операция выполняется для каждого последующего участка. С использованием аппроксимирующей функции для участка вычисляются ординаты точек профиля и заносятся в базу данных.

Исследована возможность применения в качестве аппроксимирующих функций полиномов 2, 3 и 5-й степени с различными условиями стыковки участков. Если условия стыковки таковы, что методом наименьших квадратов определяется лишь один коэффициент полинома, то аппроксимация получается неприемлемой. Такая ситуация возникает при стыковке полиномов 2-й степени по координатам граничной точки и первой производной и полиномов 3 й степени, стыкуемых, кроме того, и по второй производной. Если методом наименьших квадратов определяются два коэффициента, то получаемая при этом система из двух уравнений не имеет решения.

Выбор в качестве аппроксимирующей функции полинома 4-й степени обусловлен тем, что им могут быть представлены условия тесного контакта с несимметричным распределением давлений и двугорбостью эпюры давлений, характерными для контакта тел с изношенными поверхностями. Задача хорошо решается, если методом наименьших квадратов определяются три коэффициента полинома. Это условие выполняется при стыковке участков по координатам граничной точки и первой производной.

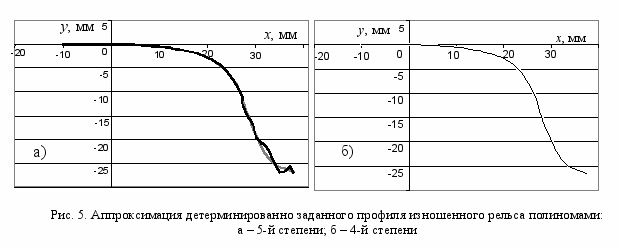
Полином 5-й степени позволяет провести стыковку и по второй производной, вследствие чего на границе участков нет ступенчатого изменения кривизны. Однако такая функция более склонна к осцилляции, чем полином 4-й степени (рис.5).

Использование в качестве аппроксимирующей функции полинома 4-й степени позволяет решать контактные задачи для случаев несимметричного тесного контакта, характерного для тел с изношенными поверхностями. При надлежащем разделении профиля поверхности на участки достигается достаточная для решения контактных задач точность аппроксимации. С помощью предложенных аппроксимирующих функций составлены таблицы координат точек профилей изношенных колёс и рельсов, которые могут быть использованы при решении контактных задач.


СПИСОК ЛИТЕРАТУРЫ

  1. Царев, И.В. Исследование влияния геометрии профиля бандажа и характеристик упругодиссипативных связей на горизонтальную динамику тепловоза: дис.... канд. техн. наук / И.В. Царёв.– Ворошиловград, 1982. –233с.
  2. Шевченко, К.В. Математическое моделирование напряженно-деформированного состояния железнодорожных колес для оценки их работоспособности: дис.... канд. техн. наук / К.В. Шевченко.– Брянск, 2001. –145с.
  3. Гутер, Р.С. Элементы численного анализа и математической обработки результатов опыта / Р.С. Гутер, Б.В. Овчинский.– М.: Наука, 1970.– 432с.


Материал поступил в редколлегию 21.07.09.