Программа вступительного испытания собеседования для магистерской программы «математическое моделирование»

Вид материала

Программа

Содержание 2. Содержание программы вступительного собеседования II. Уравнения математической физики IV. Дополнительные главы математического анализа V. Теория разностных схем Литература для подготовки к вступительному собеседованию 4. Варианты билетов для проведения собеседования.

Подобный материал:

• Программа вступительного испытания по предмету «Механика и математическое моделирование», 15.82kb.
• Программа вступительного испытания собеседования для магистерской программы «интеллектуальные, 135.51kb.
• Материалы для подготовки к вступительному собеседованию включают в себя: Программу, 133.4kb.
• Магистерской программы «Математическое моделирование» реализуемой на кафедре №31 «Прикладная, 20.67kb.
• Программа государственного квалификационного экзамена по дисциплине «Математическая, 43.58kb.
• Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
• Программа собеседования совместной российско-германской магистерской программы двойных, 14.8kb.
• Программа вступительного испытания в магистратуру, 68.92kb.
• Программа вступительного испытания по истории, 47.75kb.
• Программа вступительного испытания (собеседования по профилю подготовки) по дисциплине, 308.66kb.

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ

УНИВЕРСИТЕТ МИФИ


Факультет экспериментальной и теоретической физики


Утверждено

Ученым советом факультета «ЭТФ»

протокол № ____ от ____________


ПРОГРАММА

ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ – СОБЕСЕДОВАНИЯ

ДЛЯ МАГИСТЕРСКОЙ ПРОГРАММЫ


«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»


НАПРАВЛЕНИЕ ПОДГОТОВКИ 010400 «ПРИКЛАДНАЯ МАТЕМАТИКА И ИНФОРМАТИКА»


МОСКВА, 2011г.


1. Общие положения


Вступительный экзамен по магистерской программе «Математическое моделирование» включает 5 блоков дисциплин:

Теоретические дисциплины:

- обыкновенные дифференциальные уравнения;

- уравнения математической физики,

- теория функций комплексного переменного,

- дополнительные главы математического анализа.

Дисциплины специализации:

- теория разностных схем.

Вступительное собеседование по программе «Математическое моделирование» осуществляется в письменной форме в виде вопросов (тестов и задач) по темам дисциплин.

Билет для собеседования включает в себя 60% вопросов по теоретическим дисциплинам и 40% по остальным разделам.

Оценка выставляется по 100-балльной системе. Неудовлетворительной оценкой является оценка от 1 до 20 баллов.


^ 2. Содержание программы вступительного собеседования


I. Обыкновенные дифференциальные уравнения

1. Нормальная система дифференциальных уравнений. Задача Коши.
   
2. Нормальная система линейных дифференциальных уравнений. Метод вариации постоянных. Линейное дифференциальное уравнение n-го порядка.
   
3. Структура решения линейной однородной системы дифференциальных уравнений с постоянными коэффициентами. Линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами.
   
4. Теоремы существования и единственности. Понятие о непродолжаемых решениях.
   
5. Зависимость решения задачи Коши от параметров и начальных условий.
   
6. Приближенные методы решения задачи Коши.
   
7. Поведение траекторий линейной однородной системы дифференциальных уравнений второго порядка с постоянными действительными коэффициентами.
   
8. Понятие устойчивости решения нормальной системы дифференциальных уравнений. Устойчивость тривиального решения линейной однородной системы дифференциальных уравнений с постоянными коэффициентами. Теоремы Ляпунова об устойчивости.
   

^ II. Уравнения математической физики

1. Основные уравнения математической физики. Классификация линейных дифференциальных уравнений с частными производными второго порядка с двумя независимыми переменными.
   
2. Постановка краевых задач и задачи Коши. Корректно и некорректно поставленные задачи.
   
3. Решение краевых задач для уравнений гиперболического и параболического типов методом Фурье.
   
4. Понятие обобщенных функций, 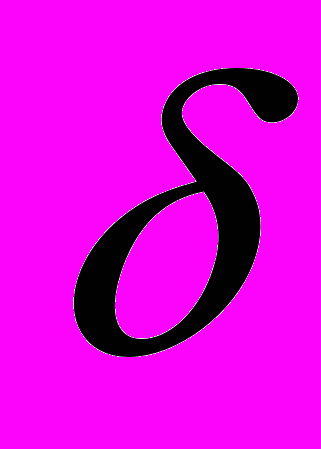- функция и ее свойства.
   
5. Метод функций Грина решения краевых задач и задачи Коши для уравнений параболического типа.
   
6. Принцип максимума и минимума для решений уравнений теплопроводности. Корректность задачи Коши.
   
7. Гармонические функции и их основные свойства. Метод функций Грина решения краевых задач для уравнений эллиптического типа. Единственность решения краевых задач.
   
8. Решение задачи Коши для волнового уравнения в одномерном, двумерном и трехмерном случае. Непрерывная зависимость решения задачи Коши от начальных данных.
   
9. Потенциалы и их основные свойства. Применение потенциалов к решению краевых задач.
   
10. Цилиндрические функции. Асимптотические представления цилиндрических функций. Ортогональные многочлены. Сферические функции.
    

III. Функции комплексного переменного

1. Понятие аналитической функции. Условия Коши-Римана. Непрерывные ветви обратных функций. Примеры римановых поверхностей.
   
2. Интегральная теорема Коши. Интеграл типа Коши. Бесконечная дифференцируемость аналитической функции. Теорема Морера. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций.
   
3. Разложение функций в ряд Тейлора. Теорема единственности. Понятие аналитического продолжения.
   
4. Разложение функции, аналитической в кольце, в ряд Лорана. Классификация изолированных особых точек. Вычеты. Основная теорема о вычетах и ее приложения. Принцип аргумента.
   
5. Преобразование Лапласа и его основные свойства.
   
6. Понятие конформного отображения. Дробно-линейная функция и другие элементарные функции.
   
7. Теорема Римана. Принцип соответствия границ. Принцип симметрии. (Без доказательства).
   

^ IV. Дополнительные главы математического анализа

1. Понятие метрического пространства. Полное метрическое пространство. Понятие компакта. Свойства непрерывных функций на компакте.
   
2. Линейное нормированное пространство. Гильбертово пространство. Понятие ряда Фурье вектора по ортонормированной системе векторов в гильбертовом пространстве. Полные ортонормированные системы векторов.
   
3. Понятие ограниченного линейного функционала на линейном нормированном пространстве.
   
4. Понятие линейного оператора (ограниченного, неограниченного) в линейном нормированном пространстве. Норма ограниченного линейного оператора.
   
5. Понятие сопряженного оператора в конечномерном евклидовом пространстве. Существование ортонормированного базиса из собственных векторов у самосопряженного оператора.
   
6. Простейшая вариационная задача. Экстремум функционала. Вариация функционала. Необходимое условие экстремума. Уравнение Эйлера.
   

^ V. Теория разностных схем

1. Основные понятия теории разностных схем.

2. Примеры исследования устойчивости разностных схем с помощью признака Неймана.


^ ЛИТЕРАТУРА ДЛЯ ПОДГОТОВКИ К ВСТУПИТЕЛЬНОМУ СОБЕСЕДОВАНИЮ

1.	517 К27	А.П. Карташев, Б.Л. Рождественский. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М.: Наука,1980.
2.	517 П56	Л.С. Понтрягин. Обыкновенные дифференциальные уравнения. М.: Наука, 1974.
3.	517 Э53	Л.Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Эдиториал УРСС, 2000.
4.	517 А85	В.Я. Арсенин. Методы математической физики и специальные функции. М.: Наука, 1974, 1984.
5.	517 Т47	А.Н. Тихонов, А.А. Самарский. Уравнения Математической физики. М.: Наука, 1966, 1972, 1977, 2004.
6.	517 Л13	М.А. Лаврентьев, Б.Т. Шабат. Методы теории функций комплексного переменного. М., 2002.
7.	517 К60	А.Н. Колмогоров, С.В. Фомин. Элементы теории функции и функционального анализа. М.: Наука, Изд. 3, 1989.
8.	517 Г59	С.К. Годунов, В.С. Рябенький. Разностные схемы. М.: Наука, 1977.
9.	517 С17	Ю.П. Попов, А.А. Самарский. Разностные методы решения задач газовой динамики. М., наука, 1992, 1980.
10.	519 К17	Н.Н. Калиткин, Численные методы. М., Наука, 1978.

^ 4. Варианты билетов для проведения собеседования.


Билет 1.

1. Представимость решения линейной однородной системы дифференциальных уравнений в виде линейной комбинации решений фундаментальной системы решений.

2. Решение задачи Коши для волнового уравнения в одномерном случае. Непрерывная зависимость решения задачи Коши от начальных данных.

3. Составить разностную схему для уравнения теплопроводности 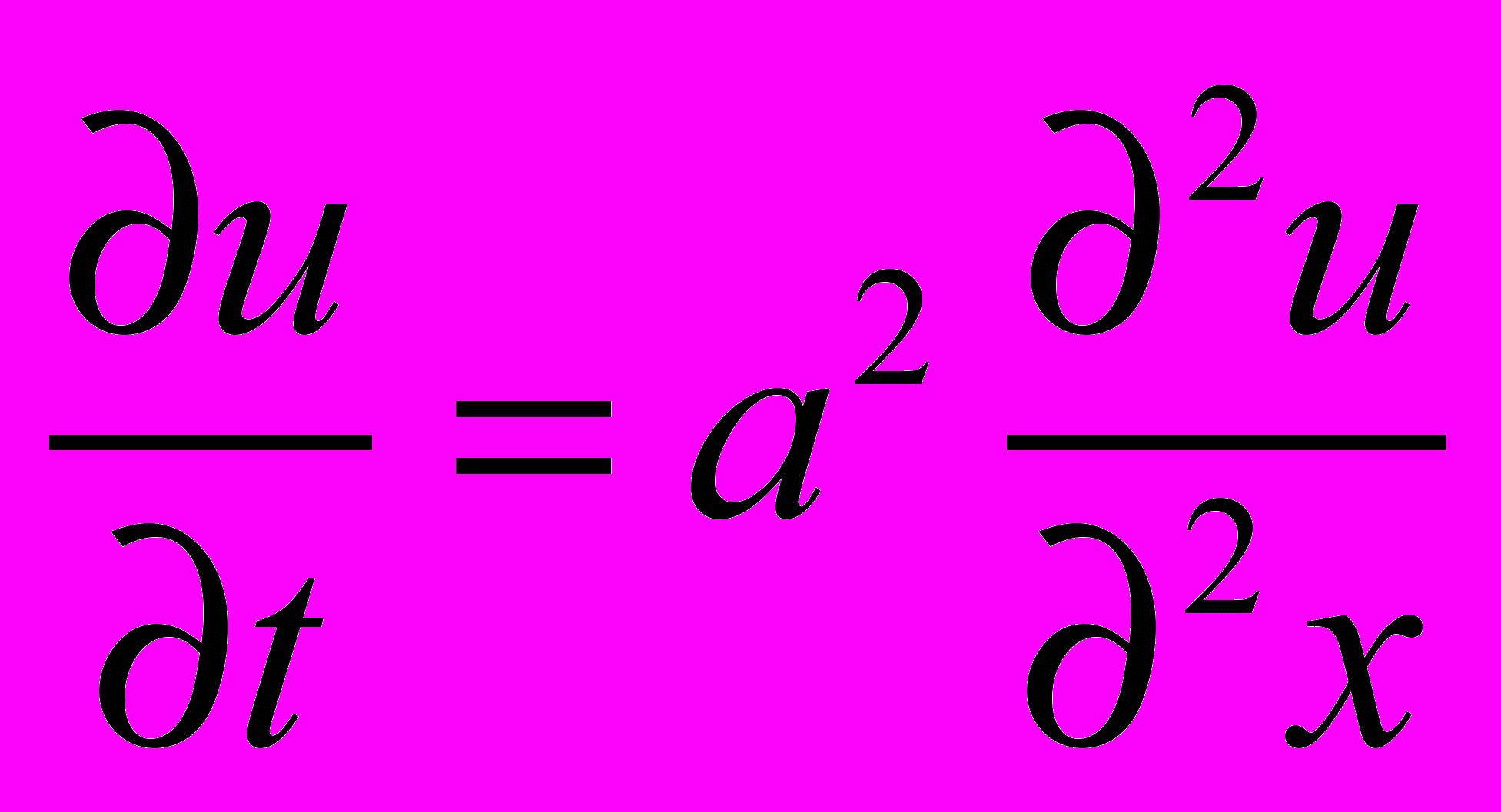соответствующую шаблону , и исследовать ее устойчивость с помощью спектрального признака Неймана.


Билет 2.

1. Решение линейной неоднородной системы дифференциальных уравнений методом вариации постоянных.

2. Вариация функционала в линейном нормированном пространстве. Необходимое условие экстремума функционала.

3. Составить разностную схему для уравнения переноса 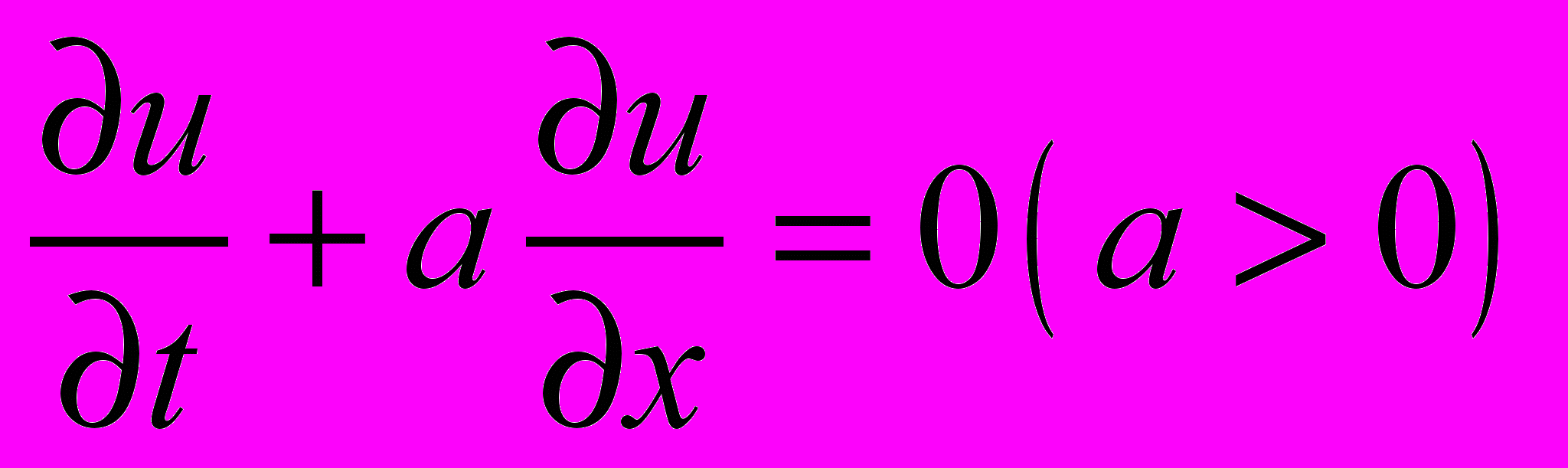соответствующую шаблону , и исследовать ее устойчивость с помощью спектрального признака Неймана.


Руководитель профиля

«Математическое моделирование»,

направление подготовки 010400

«Прикладная математика и информатика»

профессор /Н.А. Кудряшов/