Учебное пособие 9-11 классы Министерство образования и науки Российской Федерации
| Вид материала | Учебное пособие |
- Учебное пособие Министерство образования и науки Российской Федерации Владивостокский, 861.04kb.
- Учебное пособие Министерство образования и науки Российской Федерации Владивостокский, 1116.36kb.
- Учебное пособие Оренбург 2004 Министерство образования и науки Российской Федерации, 3542.12kb.
- Учебное пособие Челябинск 2006 Министерство образования и науки Российской Федерации, 864.53kb.
- Министерство образования и науки Российской Федерации гоу впо «Сыктывкарский государственный, 653.44kb.
- Российской Федерации Министерство образования и науки Российской Федерации Государственный, 343.55kb.
- Учебное пособие Министерство общего и профессионального образования Российской Федерации, 936.13kb.
- Учебное пособие Чебоксары 2009 Министерство образования и науки Российской Федерации, 1938.24kb.
- Министерство образования и науки Российской Федерации Уссурийский государственный педагогический, 1207.04kb.
- Министерство образования и науки российской федерации, 2585.99kb.
4.1 Общая характеристика методов и первичная статистическая обработка.
«Статистика знает все», - утверждали Ильф и Петров в своем знаменитом романе «Двенадцать стульев». Статистика знает обо всем: сколько и какой пищи съедает человек, чего и сколько он изнашивает за год, сколько в стране школьников, студентов и др. Авторы знаменитого романа иронично продолжают: «…Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц!…». Веселое, но довольно точное определение статистики (от лат. Status – состояние) - науки, изучающей, обрабатывающей и анализирующей количественные данные о самых разнообразных массовых явлениях в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления. Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, социума, привычек, прогнозирует распространение эпидемий. Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный). Есть еще статистика налоговая, финансовая, биологическая, метеорологическая и т.д.
Статистика как наука имеет многовековую историю. Еще в древности вели статистический учет населения. Однако, статистические данные толковались произвольно, отсутствовала научная база статистических прогнозов. Статистика вносила больше неразберихи, чем помогала науке. В конце XIX века английский премьер-министр Б. Дизраэли заметил : «Есть три вида лжи: просто ложь, наглая ложь и статистика».
И вот в XX веке появилась математическая статистика – наука, основанная на законах теории вероятностей. Статистические методы обработки данных из самых разнообразных областей жизни имеют много общего. Это позволило создать универсальные научные методы статистических исследований и проверки статистических гипотез.
Мы рассмотрим некоторые комплексные статистические исследования, в процессе которых будем использовать такие понятия как: мода, размах, медиана и другие, которые уже рассматривались нами ранее. Цель данного раздела – познакомиться с применением математики для обработки собственных исследований.
В результате наблюдений и регистрации массовых случайных событий получаются статистические данные или статистический материал. В частности, статистическим материалом являются ошибки различных измерений.
Если наблюдаемая величина есть - случайная величина, то она изучается методами теории вероятностей. Для понимания характера этой случайной величины нужно знать ее закон распределения. Определение законов распределения рассматриваемых величин и оценка значений параметров распределения на основании наблюдаемых значений – задача математической статистики.
Еще одной задачей математической статистики является создание методов обработки и анализа статистического материала с целью получения определенных выводов, нужных для организации оптимального процесса, где участвуют рассматриваемые величины.
Приведем примеры различных наблюдений явлений, в результате которых получается статистический материал.
Пример 1. При многократном измерении некоторого объекта с помощью измерительного инструмента, в частности при определении дальности до некоторого объекта, получаются различные значения наблюдаемой величины. Эти значения называют наблюденными значениями.
Полученные таким образом значения требуют систематизации и обработки, прежде чем на их основании можно было бы сделать какие-либо выводы. Разность δ между наблюденным значением х и истинным значением наблюдаемой величины a (х – а= δ) называется ошибкой измерения. Ошибки измерения требуют математической обработки с целью получения определенных выводов.
Пример 2. При массовом производстве приходится рассматривать величину отклонения некоторого размера полученного изделия (например, длины) от заданного размера для полученных изделий ( ошибка изготовления)
Пример 3. Разность между координатой точки попадания при стрельбе и координатой точки прицеливания есть ошибка стрельбы (рассеивание).
Пример 4. Результаты измерений величины отклонения размера детали после эксплуатации от ее размеров до эксплуатации ( проектных) требуют математического анализа.
Из приведенных примеров следует, что рассматриваемые величины есть случайные величины, а каждое наблюденное значение следует рассматривать как частное значение случайной величины.. Обработав результаты наблюдений, исследователь может выдвинуть ряд гипотез о том - какой вероятностной теоретической моделью данное явление можно описать. Если данные эксперимента носят количественный характер, то проводят первичную, а затем и вторичную статистическую обработку.
Если исследователь выполняет первичную статистическую обработку, то необходимо: определить необходимое число элементарных математических статистик, характеризующих выборочное распределение данных ( выборочное обследование, дисперсия, среднее арифметическое, мода, медиана и другое.)
Выполняя вторичную статистическую обработку исследователь занимается сравнением средних, дисперсии, корреляционный и факторный анализы и т.д., она проводится тогда, когда требуется определить закономерности, скрытые в первичных данных эксперимента.
Для выбора вторичных математических статистик рекомендуется:
Если гипотеза содержит предположение о том, что в результате обучающего эксперимента возрастут ( уменьшатся) показатели какого-либо качества, то для сравнения до и после экспериментальных данных рекомендуется использовать критерий Стьюдента или χ² - критерий. χ² - критерий применяется в том случае, если первичные экспериментальные данные относительны и выражены, например, в процентах.
- Если гипотеза включает в себя причинно-следственные зависимости между некоторыми переменными, то применяется коэффициент линейной корреляции (с которым познакомимся в этом разделе). Он используется в том случае, когда измерения независимой и зависимой переменных после эксперимента небольшие.
- Когда гипотеза включает в себя предположение о том, что в результате эксперимента возрастут или уменьшатся индивидуальные различия , тогда применяется критерий Фишера, позволяющий сравнить дисперсии до и после эксперимента.
Полученные в результате исследований данные всегда представляют собой результаты измерений различных процессов, явлений, качеств. На основе анализа качественных и количественных характеристик и строятся дальнейшие выводы. В жизни даже самое простое действие обусловлено большим количеством одновременно действующих факторов, часть которых практически не поддается контролю даже в условиях строгого лабораторного эксперимента. Поэтому многие используемые показатели представляют собой случайные величины.
Но научные выводы базируются не на единичном факте, а на их достаточном множестве. Чтобы вскрыть в полученном числовом материале определенные закономерности и сделать обоснованные выводы, необходима его специальная обработка с помощью методов математической статистики. С помощью математической статистики можно заменить множество числовых значений измеряемого показателя двумя обобщенными величинами, выражающими наиболее типичное значение показателя и степень разброса значений и их статистическое оценивание; определить статистическую достоверность различий между двумя однородными показателями; определить меры связи между двумя показателями и оценить ее статистическую достоверность.
Математическая обработка результатов обеспечивает доказательность исследований, но достоверность выводов в большей степени зависит от того, насколько адекватны величины, которыми оперирует исследователь, отражает реальные количественные характеристики изучаемых явлений. Несоблюдение этого требования превращает математическую обработку в пустое манипулирование формулами.
Простейший способ приписывания числовых характеристик предметам или явлениям – их регистрация. Она заключается в том, что выделяют какой-нибудь признак и отмечают каждый случай, когда в наблюдении появляется явление с этим признаком. Важная особенность регистрации состоит в том, что она позволяет применять количественное изучение даже там, где невозможно определить сами свойства изучаемых явлений (например, в педагогических исследованиях).
Для определения границы применимости регистрации нужно как можно более точно сформировать критерий. Позволяющий однозначно отличать объект с регистрируемым признаком от объекта без него.
Следующий способ количественной характеристики данных – операция упорядочения. Сущность ее заключается в том, что изучаемые явления распределяются в порядке возрастания или убывания величины определяемого признака. Затем каждой группе объекта приписывается число, соответствующее месту этой группы в нарастающем или убывающем ряду. Это число, показывающее порядок изучаемого признака у данных объектов, называется их рангом.
Сбор эмпирической информации может быть осуществлен двумя путями: 1) исследование всей совокупности объектов; 2) изучение лишь части объектов.
В первом случае исследование называется сплошным, а множество субъектов (объектов) – генеральной совокупностью. Во втором случае исследование называется выборочным, а выборочная часть субъектов (объектов) – выборкой. Так как сплошное исследование требует большого количества времени и затрат, то ученые предложили более дешевый и удобный метод – выборочный.
Выборка конструируется таким образом, чтобы при минимуме исследуемых объектов удавалось с необходимой степенью гарантии представить всю генеральную совокупность. Для этого необходимо соблюдать определенные условия и принципы:
- Основа. Основой выборки называется перечень элементов генеральной совокупности, если он удовлетворяет требованиям полноты, точности, адекватности, удобства работы с ним, отсутствия дублирования.
- Полнота. Под полнотой подразумевается представительность всех единиц данной генеральной совокупности в основе выборки.
- Точность. Информация о каждой единице отбора должна быть точной.
- Адекватность (приравненный, соответствующий, эквивалентный). Характеристики выборки должны быть эквивалентны характеристикам объектов или субъектов генеральной совокупности.
- Удобство. Если основа выборки находится в одном месте и ее структура соответствует реальной структуре изучаемых объектов, то это не только облегчает работу исследователю, но и значительно повышает ее качество.
- Репрезентативность выборки. Выборка в определенном смысле должна быть моделью генеральной совокупности, что и позволяет на ее основе оценить характеристики этой совокупности.
По сформированной основе выборки легко реализовать процедуру простого случайного отбора. Для этого требуется соблюдение равенства шансов попадания единиц отбора в выборку. Решая вопрос построения выборки, следует помнить, что нет общих правил, которые были бы применимы к любой поставленной задаче. Ее следует обосновать в программе исследования.
Прежде всего, следует определить какой объем выборки позволит распространить полученные результаты на исследуемую совокупность с необходимой для данного исследования степенью точности или вероятностью.
Вероятности, признанные достаточными для того, чтобы можно было уверенно судить о генеральной совокупности на основании выборки, называются доверительными. Доверительная вероятность характеризует надежность выборки, так как она определяет степень уверенности в том, что в отдельно взятой выборке расхождение между величинами выборочной и генеральной средней не превышают допустимой величины.
Различают три уровня значимости, или степени риска допустить ошибку измерения: на 5% уровне , или Δ < 0,05; на 1 % уровне, или Δ < 0,01 ; на 0,1% уровне, или Δ < 0,001.
При однообразном составе генеральной совокупности, когда дисперсия близка к нулю, требуется небольшой объем выборки. Объем выборки можно определить по формуле:
N = t²*S²/Δ²
где Δ – величина предельной ошибки, S² - дисперсия генеральной совокупности. Можно воспользоваться максимальным значением дисперсии S²=0,25. Это позволяет рассчитывать завышенное число выбранной совокупности, которое гарантирует более высокую точность оцениваемых параметров; t – нормированная переменная выборочных средних является аргументом функции распределения Лапласа или Стьюдента для малых n. Она выбирается из таблицы (см. ниже), задавшись величиной доверительной вероятности (γ=0,95)
№1
Таблица значений t□ =t( □ ,n)
| n | γ=0,95 | γ=0,99 | n | γ=0,95 | γ=0,99 |
| 5 | 2,78 | 4,60 | 15 | 2,15 | 2,98 |
| 6 | 2,57 | 403 | 16 | 2,13 | 2,95 |
| 7 | 2,45 | 3,71 | 17 | 2,12 | 2,92 |
| 8 | 2,37 | 3.50 | 18 | 2,11 | 2,90 |
| 9 | 2,31 | 3,36 | 19 | 2,10 | 2,88 |
| 10 | 2,26 | 3,25 | 20 | 2,093 | 2,861 |
| 11 | 2,23 | 3,17 | 25 | 2,064 | 2,797 |
| 12 | 2,20 | 3,11 | 30 | 2,045 | 2,756 |
| 13 | 2,18 | 3,06 | 60 | 2,001 | 2,662 |
| 14 | 2,16 | 3,01 | ∞ | 1,960 | 2576 |
Чтобы избежать ошибок во время эксперимента рекомендуется проводить его в соответствии с одной из заранее продуманных логических схем доказательства, гарантирующих установление причинно-следственных зависимостей между изучаемыми переменными.
Логическая схема, позволяющая добиться хорошего результата имеет следующий вид. Схема включает в себя проведение исследования не на одной группе объектов, а на двух и более группах, одна из которых является экспериментальной, а другие – контрольными.
В экспериментальной группе выделяется и целенаправленно изменяется переменная, которая рассматривается как вероятная причина объясняемого явления, а в контрольной группе объект помещается в стандартные условия. При завершении эксперимента оцениваются и сравниваются между собой изменения, которые в экспериментальной и контрольной группах произошли, а если оказывается, что в экспериментальной группе эти изменения больше, чем в контрольной, то делается вывод о том, что подлинной их причиной являются вновь вводимые условия или средства.
Существует два плана проведения эксперимента:
1. Эксперимент, организованный по плану типа «только после».
В этом случае экспериментальные и контрольные группы оцениваются только после окончания эксперимента и не оцениваются в его начале. Если в итоге обнаруживается существенная разница между экспериментальной и контрольной группами, не имевшая место в начале, то можно сделать вывод о том, что различия между этими группами вызваны именно экспериментальными действиями. Тогда требуется доказать, что группы до эксперимента были эквивалентны.
Для определения однородности «выборок» по выбранным критериям до эксперимента используют коэффициент вариации CV, который определяется как отношение среднего квадратичного к среднему арифметическому, выраженное в процентах:
CV = S/X *100%
2. Эксперимент, организованный по плану типа «до и после».
В этом случае предполагаемые причины и следствия оцениваются и до, и после эксперимента и делается это как в экспериментальной, так и контрольной группах. Тем самым заранее отбрасывается альтернативная гипотеза о том, что обнаруженные по окончании эксперимента различия между экспериментальной и контрольной группами были вызваны теми различиями между ними, которые имелись еще до начала проведения эксперимента.
Теперь вспомним некоторые уже изученные нами понятия, которые понадобятся для проведения исследования. Для того, чтобы установить является ли распределение частных значений изучаемого признака симметричным и приближающимся к нормальному распределению, то определяют медиану.
Медиана – это значение, которое делит выборку пополам. Например, для выборки 2, 3, 4, 4, 5, 5, 6, 6,7, 8, 9 медиана равна 5. Если ряд включает в себя четное число признаков, то медианой будет среднее, взятое как полусумма двух центральных значений ряда. Например, для ряда 0, 1, 1, 2, 3, 4, 5, 5, 6, 7, медиана будет равна Ме*=(3+4)/2=3,5.
Среднее и медиана для нормального распределения обычно совпадают или очень мало различаются. Если выборочное распределение признаков нормально, то к нему можно применять методы вторичных статистических расчетов . В противном случае, этого делать нельзя, так как в расчеты могут вкрасться серьезные ошибки.
Мода – количественное значение исследуемого признака, наиболее часто встречаются в выборке.
Для симметричных распределений признаков, в том числе для нормального распределения, значение моды совпадает со значением среднего и медианы. Для других типов распределения это не характерно.
Интервал – группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. Это делается для сокращения расчетов. Пример: 0,1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 8, 8, 8, 9, 9, 10, 10, 11, 11, 11, …,30. Всего 30 значений. Разбиваем на 6 подгрупп по 5 значений в каждой. Вычисляем среднее для каждой подгруппы, они будут равны: 1,2; 3,4; 5,2; 6,8; 8,6; 10,6 и теперь все расчеты можно вести с этим сокращенным рядом.
При замене множества числовых значений показателя одним числом – средним арифметическим и медианой – мы, выигрывая в простоте и наглядности, теряем часть информации. Наиболее применяемыми мерами рассеивания данных являются размах и стандартные отклонения.
Напомним, что размах – это разность максимального и минимального значений в ряду данных. Главным преимуществом этой меры рассеивания данных является легкость ее определения. Однако, это и самая грубая мера, пригодная лишь для приблизительного сравнения двух или более рядов данных в отношении их степени рассеивания, поскольку при определении размаха используются лишь крайние члены ряда, которые подвержены резким колебаниям, особенно при малом количестве данных.
Более точной мерой рассеивания данных является стандартное отклонение (σ), вычисляется по формуле
Σ = √(∑(xi-M)²)/(n-1), i=1,…,n;
где xi - числовое значение показателя; n – их количество ( если n> 30, то в знаменателе вместо n-1 будет только n); М – среднее арифметическое.
При n≤20 можно воспользоваться экспресс- методом для определения стандартного отклонения, который менее громоздкий для расчетов. Расчет осуществляется по формуле:
σ = W/dn ,
где W – размах, dn – табличный коэффициент.
№2
Таблица значений коэффициента dn для оценки стандартного отклонения по размаху
| n | dn | n | dn |
| 5 | 2,33 | 13 | 3,34 |
| 6 | 2,53 | 14 | 3,41 |
| 7 | 2,70 | 15 | 347 |
| 8 | 2,85 | 16 | 353 |
| 9 | 2,97 | 17 | 3,59 |
| 10 | 3,08 | 18 | 3,64 |
| 11 | 3,17 | 19 | 3,69 |
| 12 | 3,26 | 20 | 3,74 |
Зная средне арифметическое, разброс и стандартное отклонение, можно определить довольно полную статистическую характеристику совокупности данных. Однако исследователь всегда стремится выйти за пределы своих данных, полученных на ограниченном числе объектов или испытуемых и распространить полученные результаты на более широкий круг объектов. Эта задача решается с помощью методов статистического вывода – точечного или интервального оценивания.
Например, допустим, что нужно сравнить между собой два множества данных, полученных при различных условиях или на разных группах испытуемых. Такое сравнение осуществляется чаще всего по средним арифметическим или медианам.
Пусть два множества данных представлены двумя средними арифметическими: М1=10 и М2=15. Разница между ними составляет 5 единиц и на первый взгляд этот факт ни в каком дополнительном доказательстве не нуждается. Однако нужно помнить, что числовые значения показателя, образующие множество данных, являются случайными величинами; следовательно оба средних также величины случайные. Тогда вполне возможно, что и различие между ними всего лишь случайное явление.
Для установления факта случайности различных средних (или медиан) или его опровержения (то есть доказательства достоверности различий) пользуются статистическими критериями. Причем в этом случае нужно иметь в виду, что когда применение критерия указывает на случайность обнаруженных различий, это иногда может быть вызвано не объективным положением вещей, а просто малым объемом имеющихся в распоряжении данных.
При проверке любых статистических гипотез решение в пользу одной из них никогда не принимается с полной уверенностью; всегда остается вероятность (контролируемая исследователем) принятия неправильного решения. Обычно принимается близко к 95% уровень достоверности, тогда вероятность принять ошибочное решение составит 5%. Эта величина называется уровнем значимости и всегда указывается в статистическом выводе.
Наряду с анализом различий межу множествами данных часто используют оценку в статистической связи (корреляции) между двумя сравнительными рядами данных. В качестве меры статистической связи используются (в зависимости от характера данных) различные виды коэффициентов корреляции.
№3
Таблица пограничных значений U-критерия (95%-ный уровень достоверности)
| | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 10 | 23 77 | 26 84 | 29 91 | 33 97 | 36 104 | 39 111 | 42 118 | 45 125 | 48 132 | 52 138 | 55 145 |
| 11 | 26 84 | 30 91 | 33 99 | 37 106 | 40 114 | 44 121 | 47 129 | 51 134 | 55 143 | 58 151 | 62 158 |
| 12 | 24 91 | 33 99 | 37 107 | 41 115 | 45 123 | 49 131 | 53 139 | 57 147 | 61 155 | 65 163 | 69 171 |
| 13 | 33 97 | 37 106 | 41 115 | 45 124 | 50 132 | 54 141 | 59 149 | 63 158 | 67 167 | 72 175 | 76 184 |
| 14 | 36 104 | 40 114 | 45 123 | 50 132 | 55 141 | 59 151 | 64 160 | 67 171 | 74 178 | 78 188 | 83 197 |
| 15 | 39 111 | 44 121 | 49 131 | 54 141 | 59 151 | 64 161 | 70 170 | 75 180 | 80 190 | 85 200 | 90 210 |
| 16 | 41 118 | 47 129 | 53 139 | 59 149 | 64 160 | 70 170 | 75 181 | 81 191 | 86 202 | 92 212 | 98 222 |
| 17 | 45 125 | 51 136 | 57 147 | 63 158 | 67 171 | 75 180 | 81 191 | 87 202 | 93 213 | 99 224 | 105 235 |
| 18 | 48 132 | 55 143 | 61 155 | 67 167 | 74 178 | 80 190 | 86 202 | 93 213 | 99 225 | 106 236 | 112 248 |
| 19 | 52 138 | 58 151 | 65 163 | 72 175 | 78 188 | 85 200 | 92 212 | 99 224 | 106 236 | 113 248 | 119 261 |
| 20 | 55 145 | 62 158 | 69 171 | 76 184 | 83 197 | 90 21 | 98 222 | 105 235 | 112 248 | 119 261 | 127 273 |
К
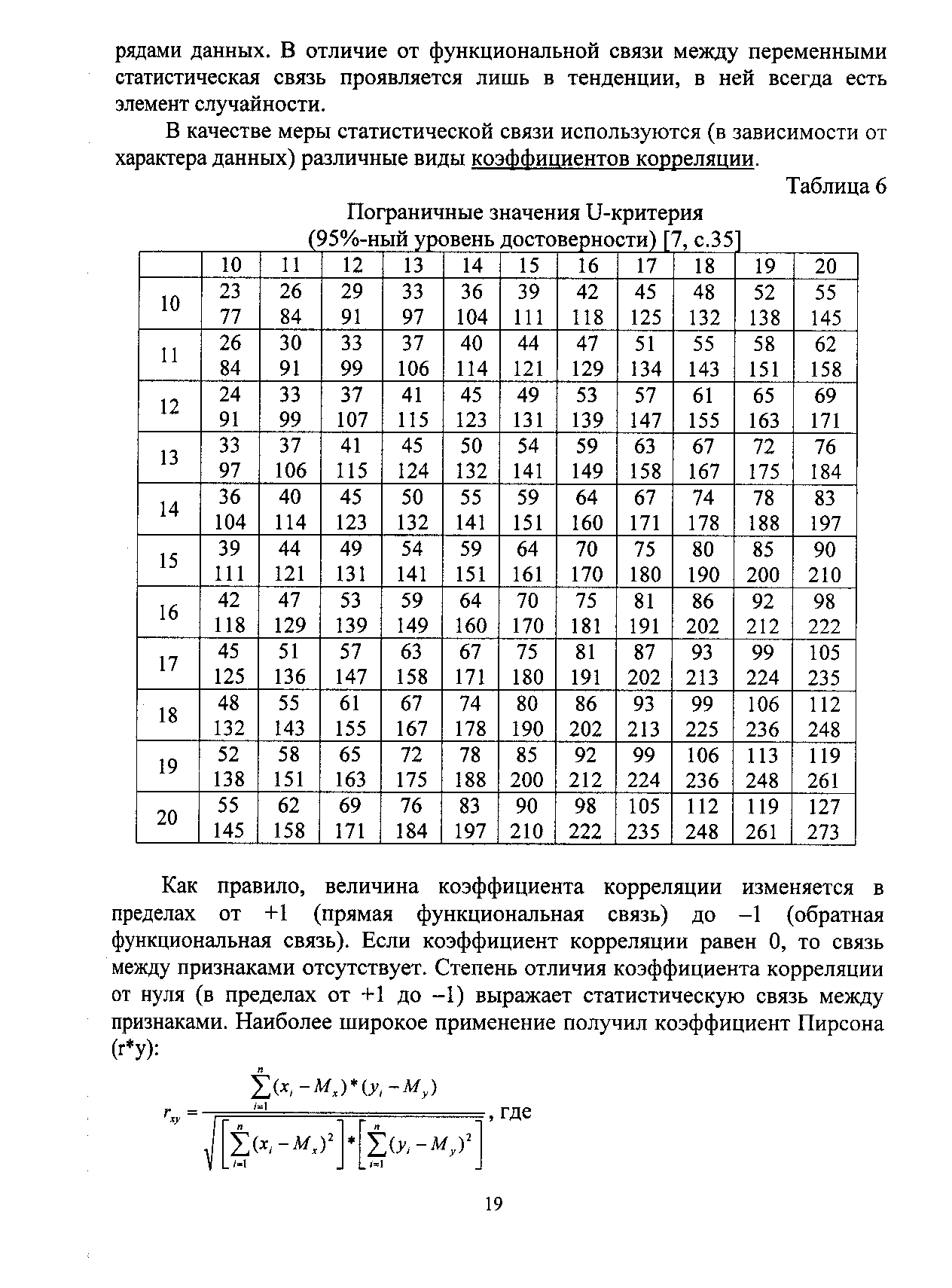
ак правило, величина коэффициента корреляции изменяется в пределах от +1 (прямая функциональная связь) до –1 (обратная функциональная связь). Если коэффициент корреляции равен 0, то связь между признаками отсутствует. Степень отличия коэффициента корреляции от нуля ( в пределах от +1 до –1) выражает статистическую связь между признаками. Наиболее широкое применение получил коэффициент Пирсона
Где xi, уi - числовые значения коррелируемых признаков; Мх и Му – соответствующие средние арифметические; n – количество пар числовых значений.
Для оценки значения rху можно воспользоваться следующей таблицей.
№4
Таблица критических значений rху (для уровней значимости 0,05 и 0,01)
| n | 0,05 | 0,01 | n | 0,05 | 0,01 | n | 0,05 | 0,01 |
| 10 | 0,63 | 0,77 | 21 | 0,43 | 0,5 | 32 | 0,35 | 0,45 |
| 11 | 0,60 | 0,74 | 22 | 0,42 | 0,5 | 33 | 0,34 | 0,44 |
| 12 | 0,58 | 0,71 | 23 | 0,41 | 0,5 | 34 | 0,34 | 0,44 |
| 13 | 0,55 | 0,68 | 24 | 0,40 | 0,5 | 35 | 0,33 | 0,43 |
| 14 | 0,53 | 0,66 | 25 | 0,40 | 0,41 | 36 | 0,33 | 0,42 |
| 15 | 0,51 | 0,64 | 26 | 0,39 | 0,50 | 37 | 0,32 | 0,42 |
| 16 | 0,50 | 0,62 | 27 | 0,38 | 0,4 | 38 | 0,32 | 0,41 |
| 17 | 0,48 | 0,61 | 28 | 0,37 | 0,4 | 39 | 0,31 | 0,41 |
| 18 | 0,47 | 0,59 | 29 | 0,37 | 0,4 | 40 | 0,311 | 0,40 |
| 19 | 0,46 | 0,58 | 30 | 0,36 | 0,4 | 41 | 0,31 | 0,40 |
| 20 | 0,44 | 0,56 | 31 | 0,36 | 0,4 | 42 | 0,30 | 0,39 |
Если полученный rху > rтабл на каком-либо из уровней значимости, то он является статистически достоверным. При вычислении rху следует иметь ввиду, что он является мерой линейной связи между переменными. Если связь между переменными носит иной характер, то величина rху окажется близкорй 0, хотя объективно связь между переменными можети быть очень сильной. С другой стороны, точность rху зависит от характера распределения обеих переменных (оно должно быть нормальным). Наконец, строгое использование rху в качестве меры связи требует, чтобы переменные были измерены на уровне шкал, имеющих единицы измерения (метр, кг, и т. д.).
Когда перечисленные требования не могут быть соблюдены, а переменные измерены не на уровне порядковой шкалы (или переведены в нее), предпочтительнее использовать (особенно при малом объеме данных) в качестве меры связи коэффициент ранговой корреляции Спирмена (р).
