Качественные и приближенно-аналитические методы и алгоритмы исследования характеристик динамических систем

Вид материала

Автореферат

Содержание Обзор содержания диссертации

Подобный материал:

• А. В. Язенин 2010 г. Программа, 58.59kb.
• Определение динамических характеристик диссипативной механической системы на основе, 18.68kb.
• Учебная программа профилирующей дисциплины теория автоматического управления, 36.13kb.
• Методы исследования Метод исследования, 68.93kb.
• Рабочая программа по дисциплине " Методы анализа динамических систем " для специальности, 143.06kb.
• План Методы психологии Основные методы психологического исследования Вспомогательные, 128.12kb.
• 1 Анализ динамических процессов систем управления, 45.71kb.
• «Численные методы в химии» Общая трудоёмкость дисциплины составляет, 22.46kb.
• «Устойчивость систем электроснабжения» Общая трудоёмкость изучения дисциплины составляет, 44.18kb.
• Лекция №12. Аналитические методы расчета нц при периодических воздействиях метод гармонического, 90.9kb.

ОБЗОР СОДЕРЖАНИЯ ДИССЕРТАЦИИ

В настоящей диссертации дано развитие качественных, приближенно-аналитических и численных методов и алгоритмов исследования математических моделей динамических систем, моделируемых дифференциальными уравнениями в форме Коши и ньютоновского типа. С помощью названных методов изучаются качественные, асимптотические и количественные характеристики математических моделей динамических систем типов 1  6.

Во Введении содержится обоснование актуальности темы диссертации и характеристика области исследований. Дан обзор и сравнительный анализ научных результатов, относящихся к теме диссертации, приведены основные цели и задачи исследований, охарактеризованы методы решения задач, основные результаты, отмечены их научная новизна и практическая ценность. Приведено краткое содержание работы, а также представлена общая характеристика диссертации.

Первая глава «Качественные методы исследования характеристик динамических систем» диссертации посвящена качественному и асимптотическому изучению характеристик решений математических моделей динамических систем типов 1  5. В частности, приведены изучаемые математические модели (модели типов 1 − 5) и предварительные сведения.

В первой главе развиты качественные методы исследования характеристик динамических систем. Здесь разработан обобщенный прямой метод Ляпунова исследования математических моделей, описываемых многомерными нелинейными дифференциальными уравнениями первого порядка в форме Коши. Эти модели являются моделями пространства состояний динамической системы и названы моделями типа 1. Для модели типа 1 установлены предложения о локализации положительного предельного множества, из которых вытекают новые условия об асимптотической устойчивости. Для модели типа 1 получен также признак об эвентуальной ограниченности решений и рассмотрены некоторые качественные свойства решений. В данной главе проведен качественный анализ ньютоновской модели (модели типа 2) с неограниченной функцией диссипации и обобщенной матричной модели (модели типа 3). Кроме того, проведен качественный анализ скалярной и векторной моделей (моделей типов 4 и 5), а именно, установлены условия существования периодических решений и дана оценка зон стабильности движения железнодорожного состава. Результаты первой главы служат теоретической основой для первого этапа математического моделирования широкого класса динамических систем нелинейной механики, в частности, в тех случаях, когда рассматривается неограниченная диссипация.

Пусть V(x) есть функция Ляпунова автономной модели типа 1, Ω  положительное предельное множество решений φ(t) автономной модели типа 1,  множество с-уровня функции V, 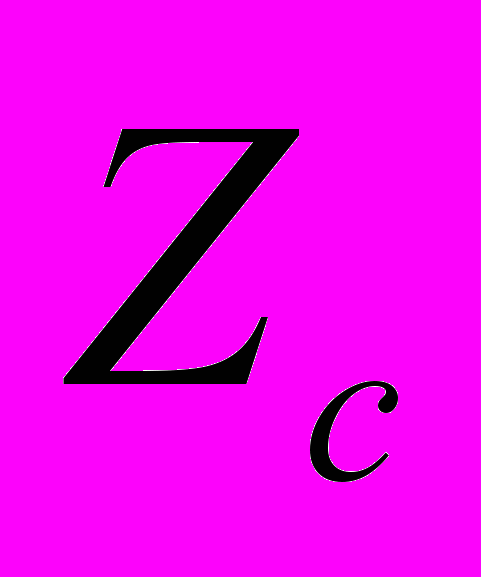 множество нулей производной функции Ляпунова V в силу автономной модели типа 1 для . Показано, что если множество ограничено и 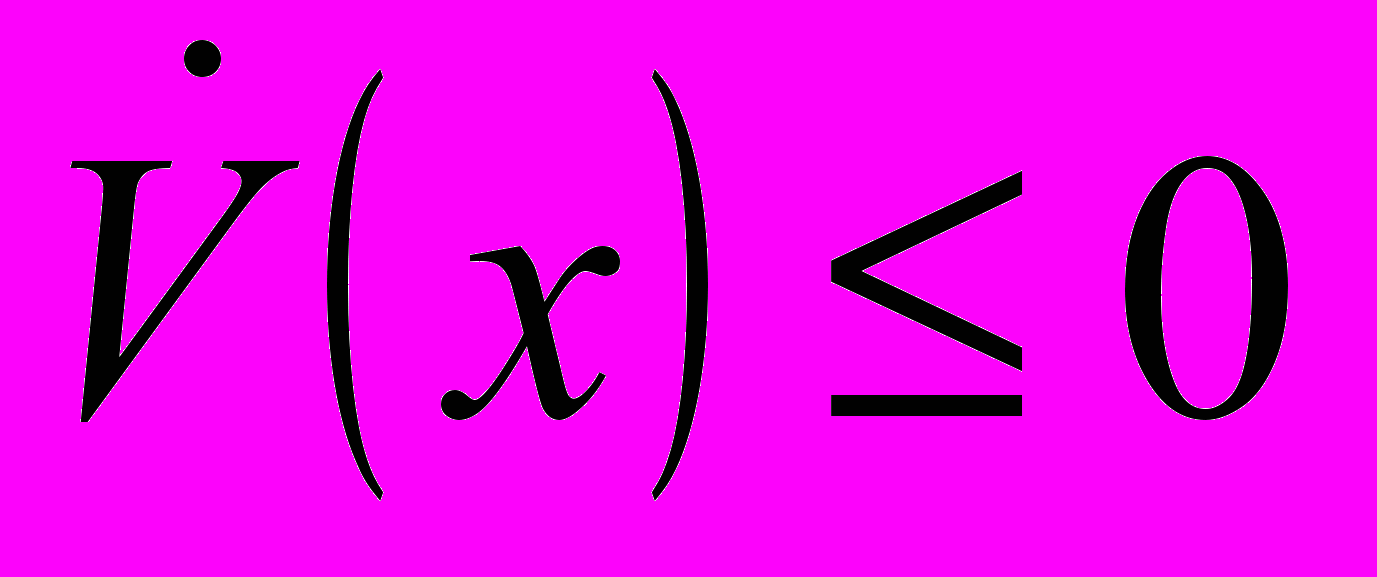, то: 1) множество положительно инвариантно , 2) имеют место включения

,

3) для каждого справедливо соотношение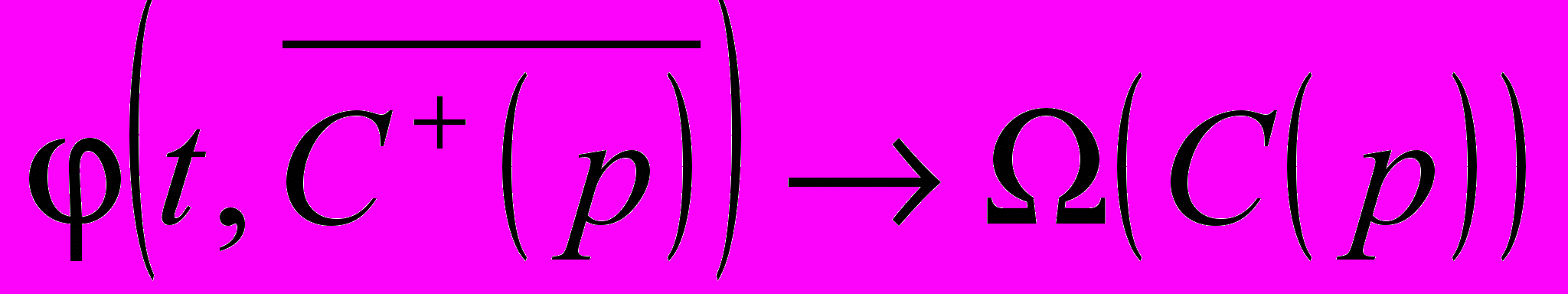

, .

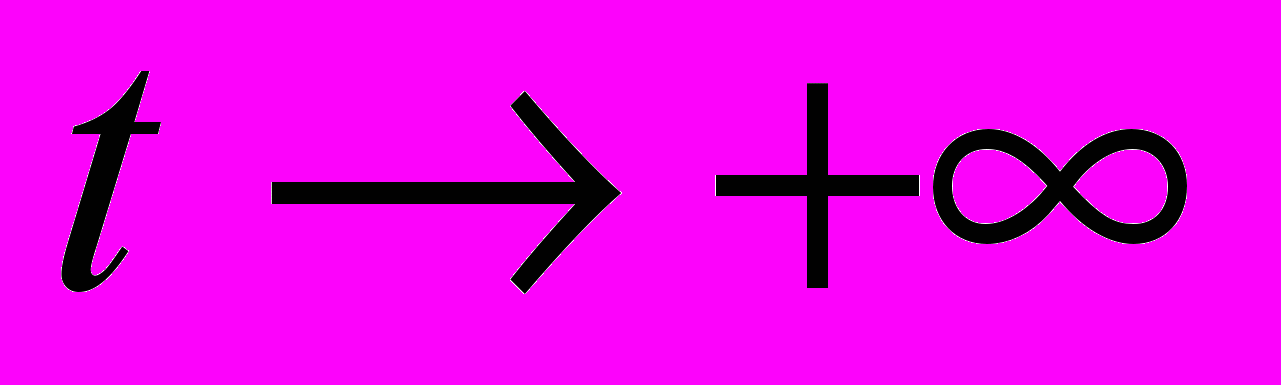Этот результат является обобщением и модификацией теоремы

А.А. Шестакова о локализации предельного множества относительно всех фазовых переменных автономной модели типа 1 на базе сходимости в хаусдорфовой метрике. Кроме того, в главе установлен аналогичный результат для случая не всех, а части переменных. Полученные в главе 1 результаты позволяют проводить качественный анализ и исследовать динамические характеристики, что проиллюстрировано на примерах двумерной и четырехмерной динамических систем.

В главе также рассмотрен вопрос о сохранении свойства ограниченности решений при возмущении неавтономной нелинейной модели типа 1. Наряду с системой (1) рассмотрена возмущенная система

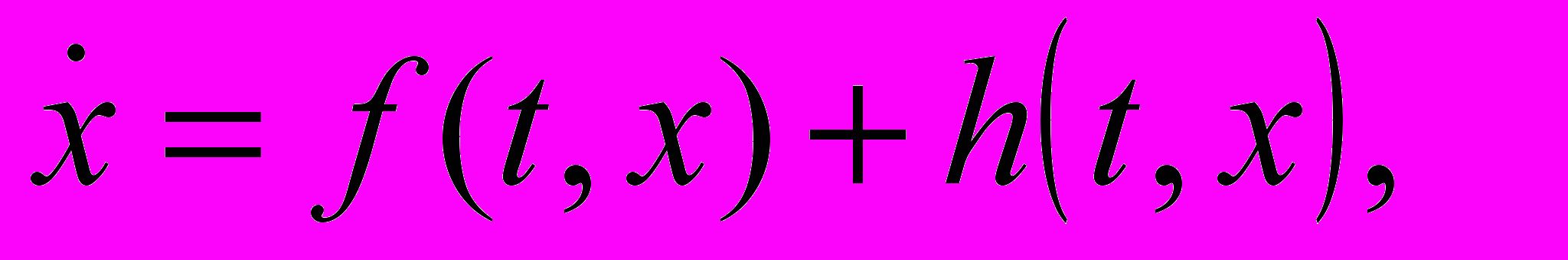(7)

где f, h непрерывны на 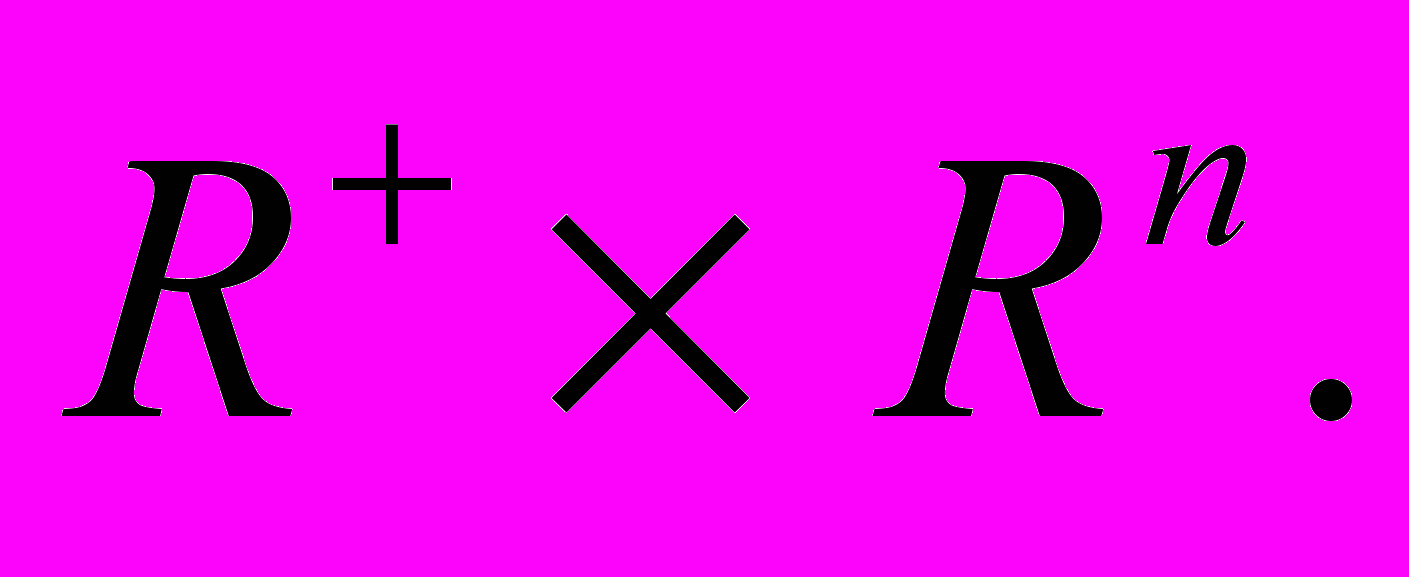Показано, что если для системы (1) выполнено обобщенное условие Липшица, решения системы (1) ограничены и если для возмущенной системы (7) выполнено условие интегральной сходимости, то решения возмущенной системы ограничены.

Указанный результат обобщает исследования Т. Иосидзавы и позволяет изучать свойства ограниченности решений широкого класса моделей, описываемых дифференциальными уравнениями в форме Коши.

Кроме того, в главе 1 дан качественный анализ обобщенной матричной модели движения колесных транспортных средств, описываемой матричным дифференциальным уравнением (3). Рассмотрена модель колебаний грузового вагона и модель движения колесной пары. На основе использования первого метода Ляпунова изучена устойчивость и асимптотическая устойчивость состояний равновесия.

В этой же главе рассмотрены модели типов 4 и 5, описываемые соответственно уравнениями (4) и (5). Известно, что модель, описываемая уравнением движения железнодорожного состава, имеет вид

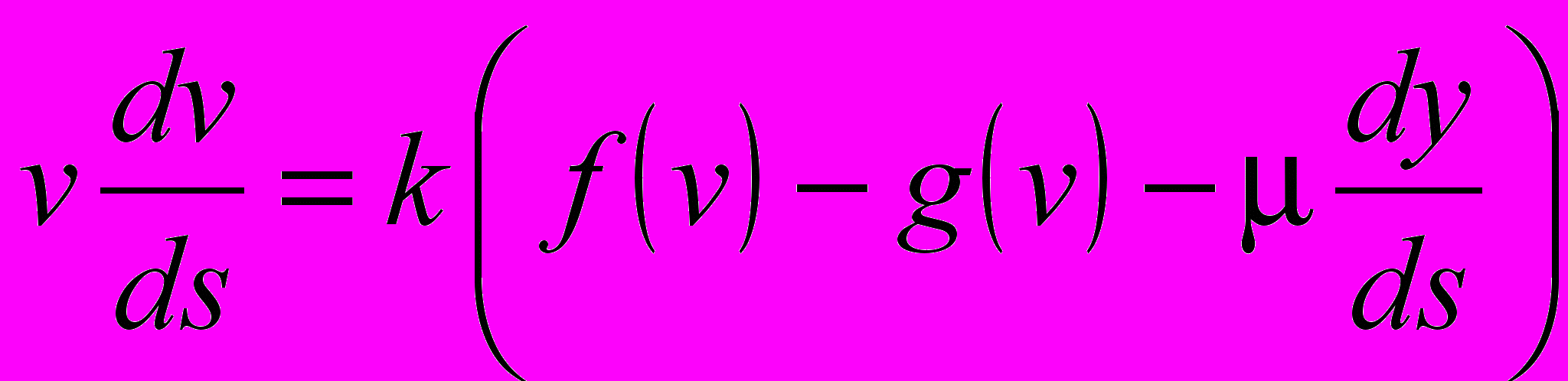, (8)

где v  cкорость движения, s  длина пути по данному криволинейному профилю, f(v)g(v)  сила, движущая состав и зависящая только от скорости, dy/ds  синус угла наклона касательной профиля пути к горизонту, μ  постоянная. Нетрудно показать, что с математической точки зрения модель, описываемая уравнением (8), эквивалентна модели типа 4, описываемой уравнением (4).

Для моделей типов 4 и 5 изучены вопросы существования периодических решений и дана оценка зон стабильности движения. Для векторной модели типа 5 показано, что если выполнены условия: 1) P(s)  непрерывная ограниченная функция и Q(u)  непрерывно дифференцируемая функция, 2) симметризованная матрица Якоби DQ(u) функции Q(u) является знакоопределенной. Тогда существует единственное ограниченное на R решение u*(s) матричной модели типа 5, к которому стремится произвольное решение u(s)  u*(s) при s + или при s  .

Во второй главе «Приближенно-аналитические методы и алгоритмы исследования характеристик динамических систем» рассмотрены вопросы, связанные с дальнейшим развитием и модификацией приближенно-аналитического метода Чаплыгина исследования математических моделей динамических систем. Результатом второй главы является модификация метода Чаплыгина, следствием которой является единообразие метода Чаплыгина для моделей типа 1 в конечномерном и бесконечномерном пространствах. Это дает возможность применять приближенно-аналитический метод Чаплыгина для исследования моделей, описываемых уравнениями с частными производными. В главе показано совпадение последовательности Ньютона для модели типа 1 и последовательности Чаплыгина для оператора, сопоставляемого с этой моделью, и выполнено обобщение метода Чаплыгина, позволяющее накладывать более слабые ограничения на модели по сравнению с предыдущими исследованиями. Указанное обобщение использовано для интегрирования модели, описывающей движение рельсового экипажа (модели типа 4). В главе предложен упрощенный итерационный алгоритм численного решения алгебраической матричной модели Ляпунова (модели типа 6).

Дана оценка ошибки сходимости последовательности Чаплыгина к единственному решению х интегрального уравнения

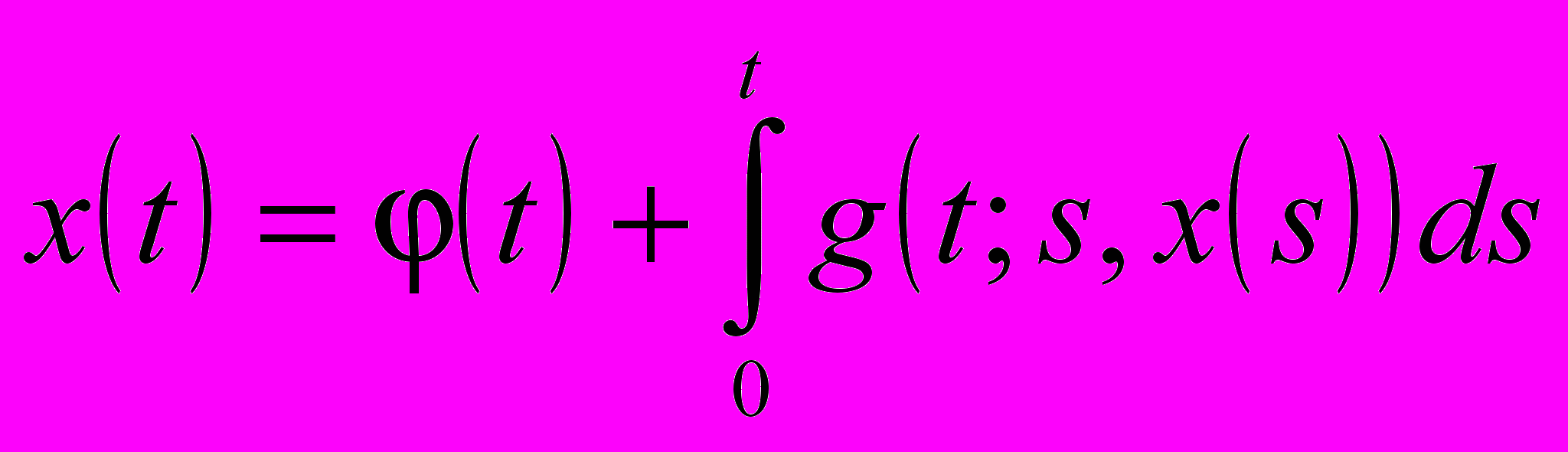, (9)

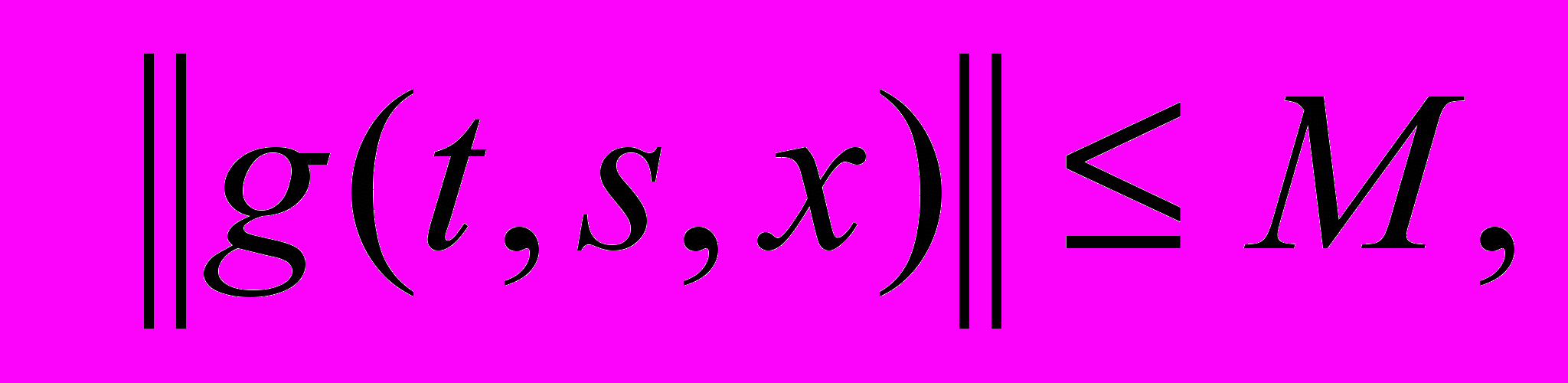
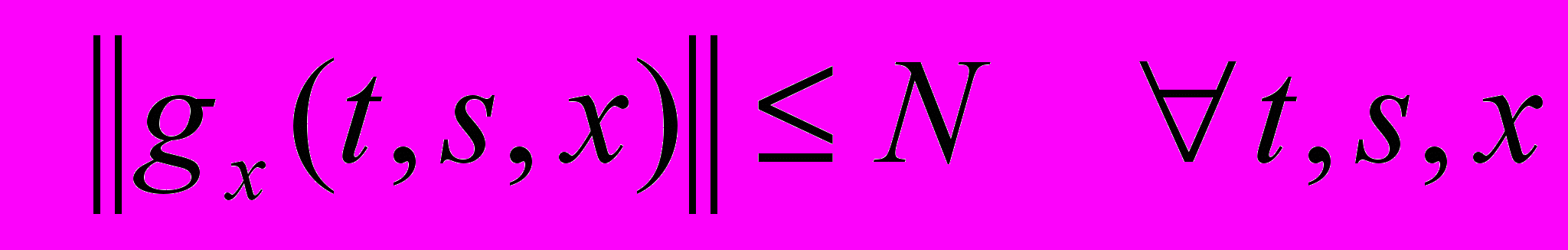сопоставляемого с уравнением (1). Пусть выполнены условия: 1) – открытое множество в пространстве , 2) функция непрерывна, причем такая, что существует непрерывная и , где 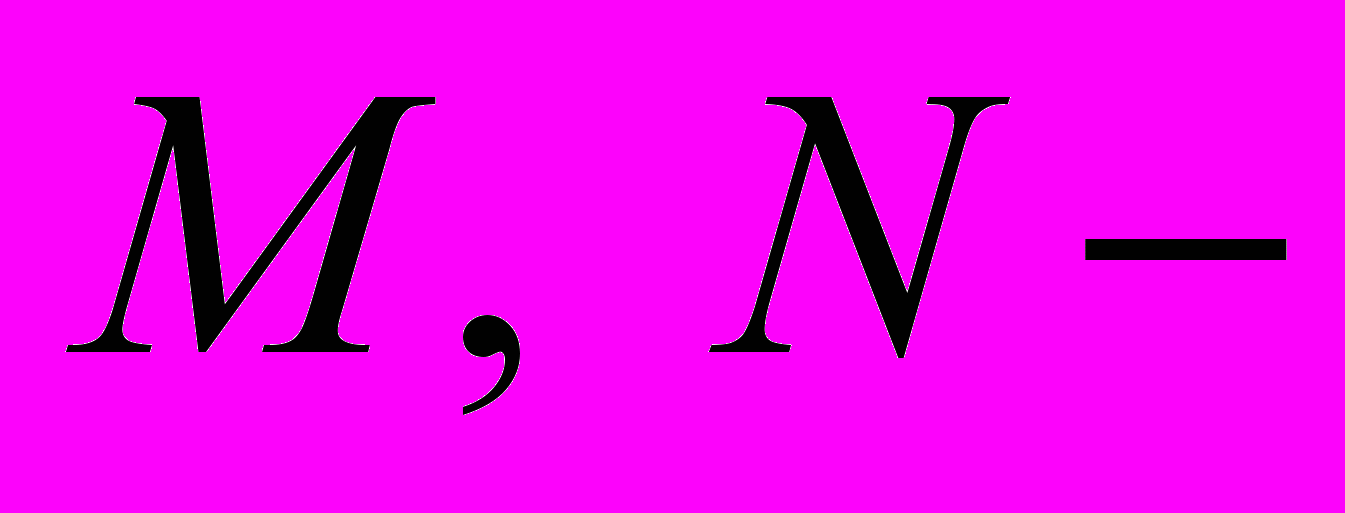положительные постоянные, 3) существует 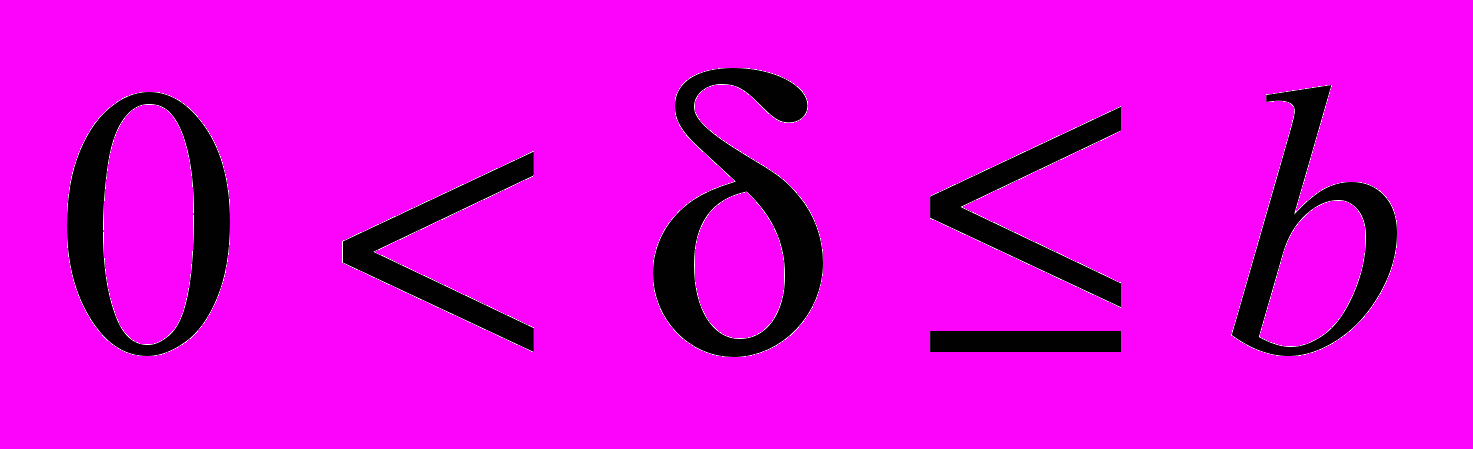такое, что для любой функции при 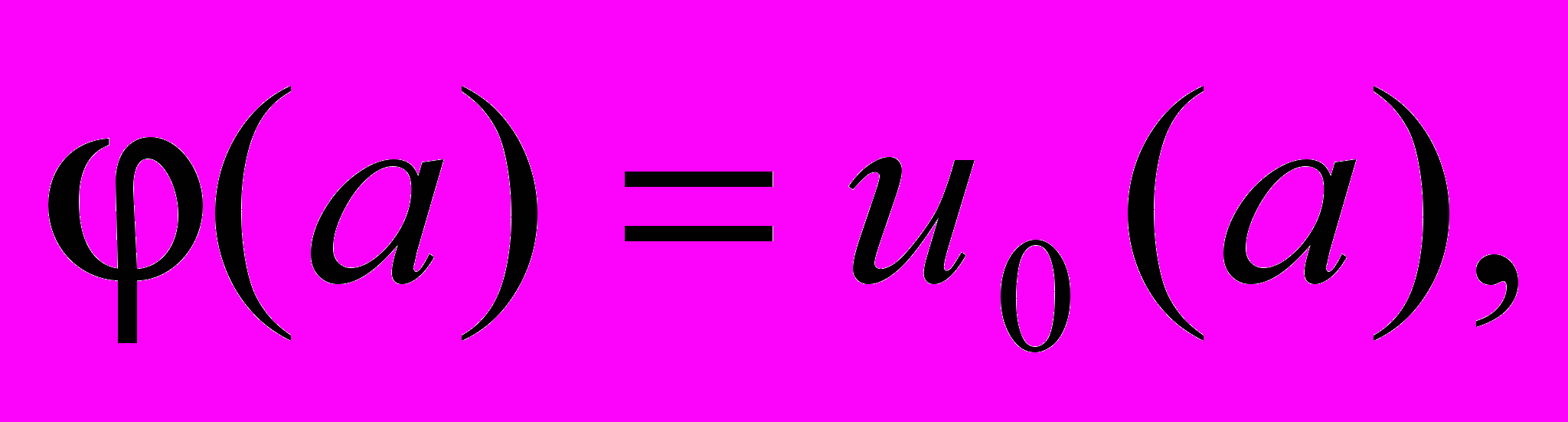последовательность Чаплыгина

,

отвечающая интегральному уравнению (9), определена на отрезке и совпадает с последовательностью Ньютона для оператора

начинающегося в точке .

При перечисленных условиях показано, что последовательность 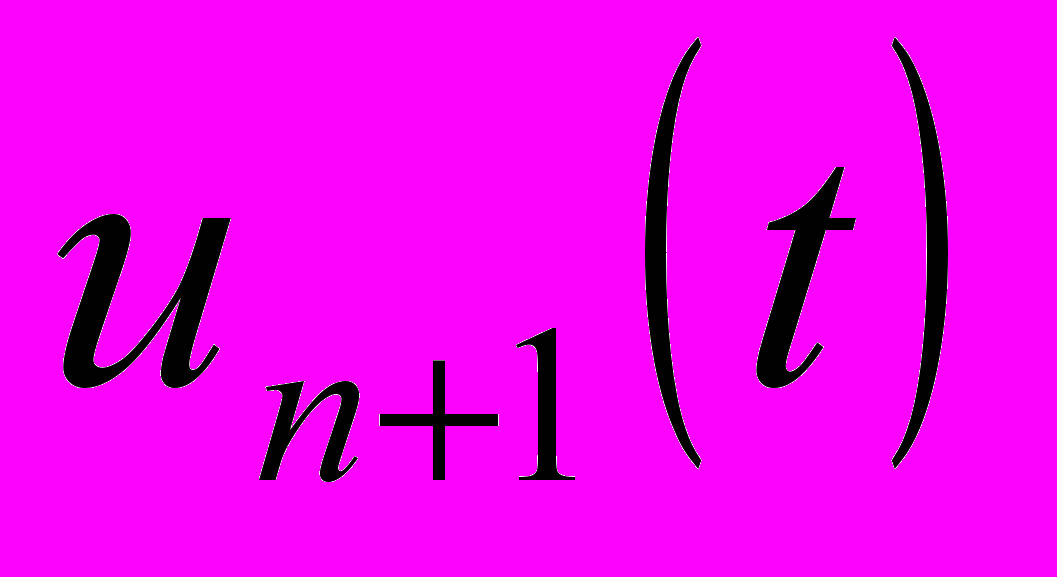сходится равномерно на отрезке к единственному решению х интегрального уравнения (9) с ошибкой



где .

Установлена сходимость последовательности Чаплыгина в большом, т. е. на всем отрезке [а, b], обобщающая результаты Н.Н. Лузина, С. Олеха,

Ж. Видоссича. Полученные результаты дают возможность получить точную оценку интервала сходимости.

Разработана модификация метода Чаплыгина на основе преобразования Лапласа и приведен соответствующий алгоритм. Модифицированный метод Чаплыгина применен для интегрирования модели типа 4, описывающей движение железнодорожного состава.

Доказано также существование на заданном отрезке асимптотически оптимальной сетки с минимальным числом шагов для численного решения задачи Коши модели типа 1 при заданной погрешности вычислений и предложен соответствующий алгоритм. Приведен иллюстрирующий пример.

Построен алгоритм численного решения задачи Коши модели типа 2, основанный на использовании специальной последовательности целых функций, показана улучшенная сходимость предложенного метода. Установлена связь между задачей численного интегрирования и устойчивостью численного решения задачи Коши для неавтономной скалярной модели типа 1.

Разработан упрощенный алгоритм численного решения матричной модели Ляпунова типа 6, где матрица А устойчива, а матрица W симметрична. Показано, что решение 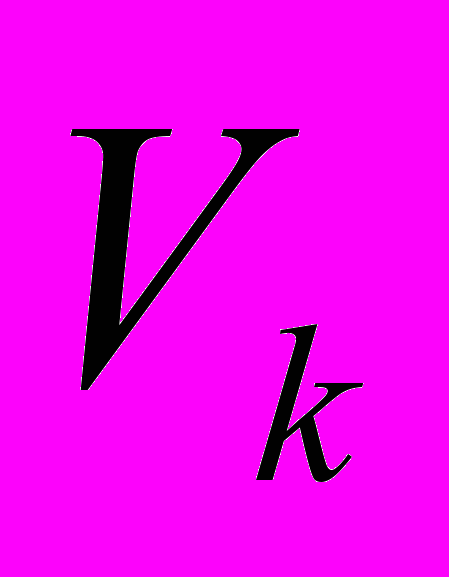модели типа 6 находится по рекуррентной формуле следующего вида 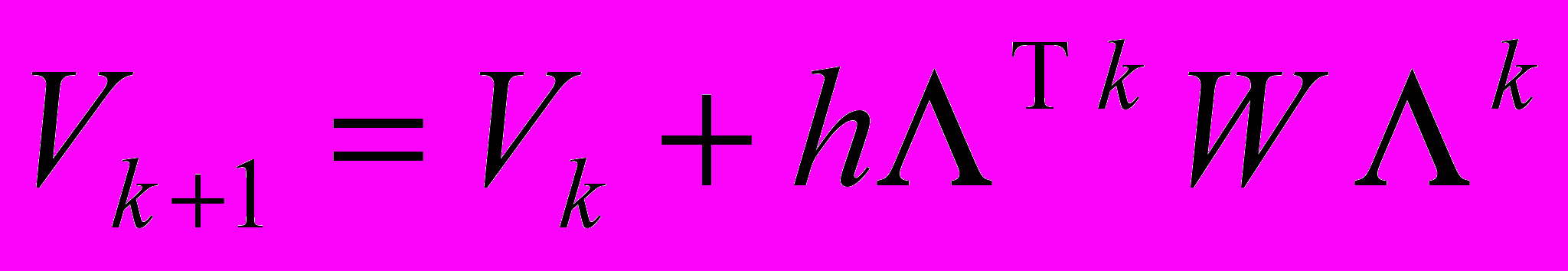, где 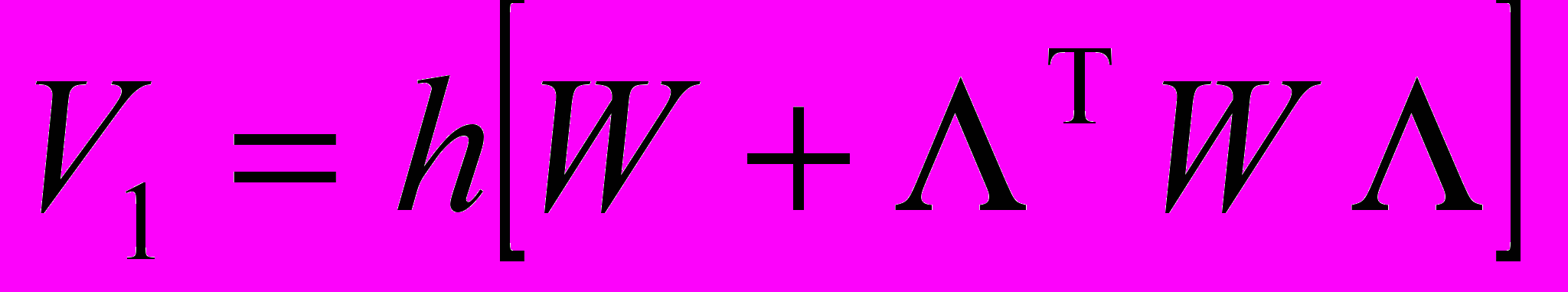, h > 0. Приведен иллюстрирующий пример.

Результаты, полученные во второй главе, дают возможность применять приближенно-аналитический метод Чаплыгина для исследования моделей, описываемых уравнениями с частными производными. Обобщение метода Чаплыгина, выполненное в главе 2, позволяет накладывать более слабые ограничения на исследуемые модели. Модифицированный метод Чаплыгина интегрирования скалярной модели типа 4, описывающей движение железнодорожного состава, может быть легко распространен на многомерное дифференциальное уравнение (5). Построенный в главе алгоритм выбора узлов оптимальной сетки численного решения задачи Коши для модели типа 1 доказывает существование асимптотически оптимальной сетки, обеспечивающей минимальный объем вычислительной работы численного решения задачи Коши для модели типа 1 при наперед заданной погрешности вычислений ε > 0. В главе разработан алгоритм численного решения специальной модели типа 2 на основе последовательности целых функций. Соответствующая программа, написанная в главе 3, обладает быстрой сходимостью и полезна при численном решении дифференциальных уравнений на больших промежутках изменения независимой переменной без существенной потери точности вычислений. В главе 2 предложен также упрощенный алгоритм численного решения алгебраической матричной модели Ляпунова (модели типа 6), в соответствии с которым в главе 3 написана компьютерная программа.

Третья глава диссертации «Проблемно-ориентированные программы исследования характеристик динамических систем» посвящена разработке проблемно-ориентированных программ расчета характеристик динамических транспортных систем, моделируемых матричными дифференциальными уравнениями (модели типа 3) и содержит описания и тексты программ в интегрированной математической среде Maple. Указанные программы позволяют производить расчет характеристик вертикальных колебаний элементов конструкций колесных транспортных систем при движении по неровному пути с заданной формой неровностей, учитывать влияние характеристик демпфирования и жесткости на частоту колебаний кузова и других деталей подвижного состава железнодорожного транспорта. В третьей главе разработаны программы численного решения задачи Коши специальной модели типа 2 с помощью целых функций, а также численного решения матричной модели Ляпунова типа 6, написанные в интегрированной математической среде Mathcad согласно алгоритмам, предложенным в главе 2.

Комплекс программ, содержащийся в этой главе, позволяет проводить исследования математических моделей при решении задач динамики подвижного состава железнодорожного и автомобильного транспорта. В частности, разработанный комплекс программ включает в себя следующие программы: программу численного решения специальной модели типа 2 на основе специальной последовательности целых функций, программу численного решения матричной модели Ляпунова типа 6, программу численного расчета динамических характеристик колесных транспортных средств на основе модели типа 3, программу графической иллюстрации результатов расчета динамических характеристик колесных транспортных средств и программу исследования влияния характеристик демпфирования, геометрических и инерционных характеристик колесных транспортных средств на устойчивость вертикальных колебаний железнодорожного или автомобильного экипажа.

Программа численного решения специальной модели типа 2 составлена согласно алгоритму, предложенному в главе 2. В ней использованы операторы simplify, expand, collect, for , while и др. среды Mathcad. Она позволяет вычислять значения 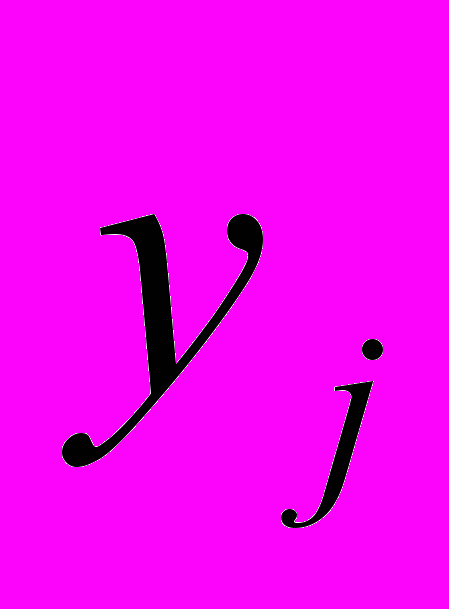и 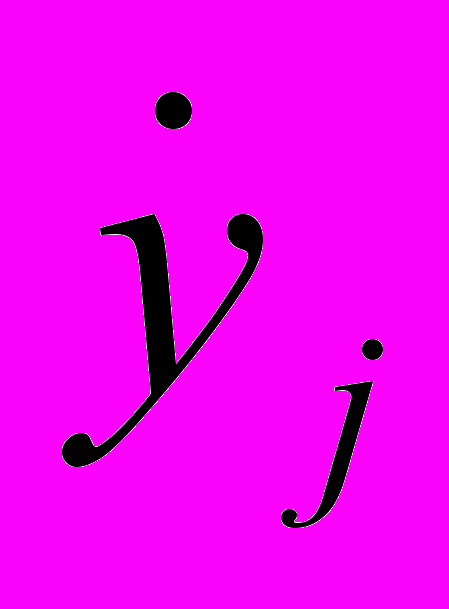в точках 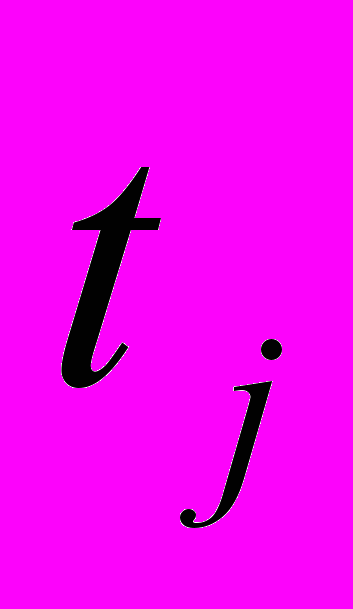на промежутках 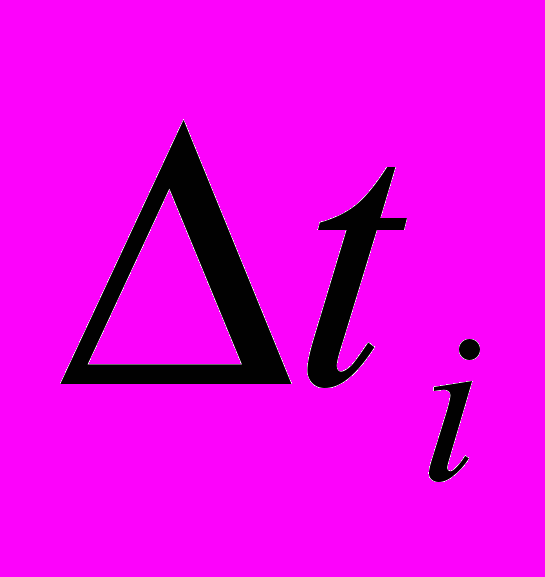с определенным шагом, а также производить учет заданного числа точек 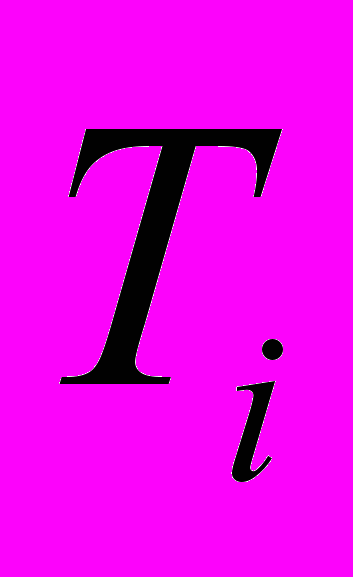, в которых находится решение исходной математической модели, и обладает улучшенной сходимостью, которая достигается за счет использования специальной последовательности целых функций 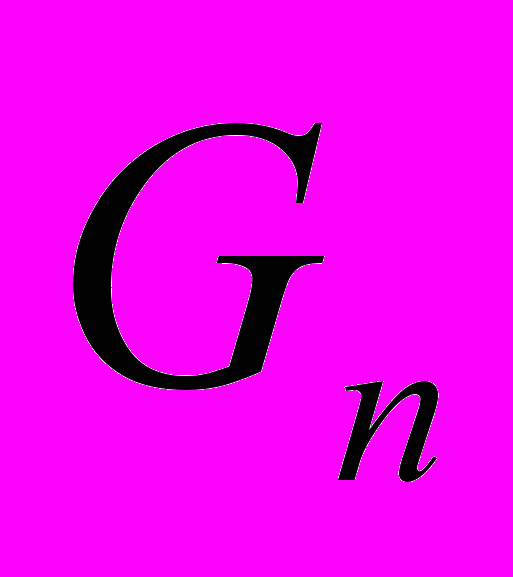. Перед запуском данной программы необходимо указать число (N) членов степенного ряда; число (M) функций 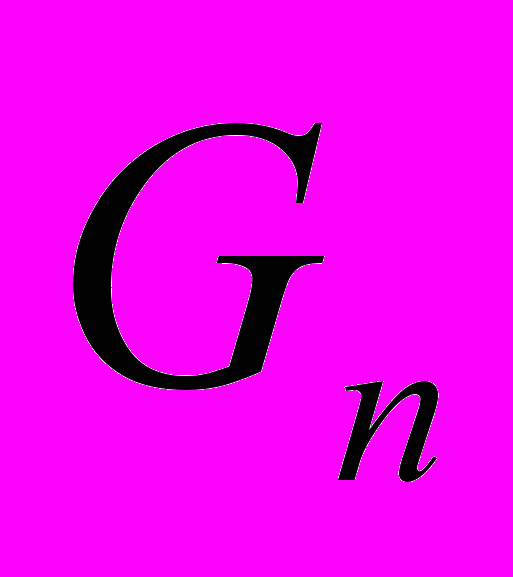, вычисляемых на каждом шаге; число (P) и значения точек 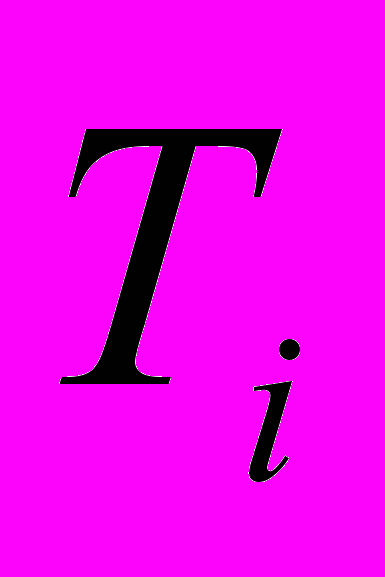, в которых находится решение математической модели; величину шага (h) вычислений. Решение представляется в виде матрицы, содержащей три столбца: 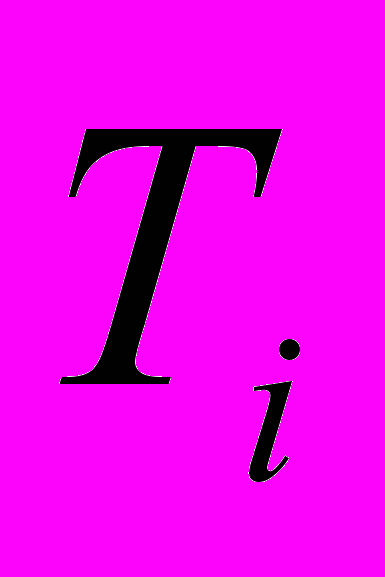, 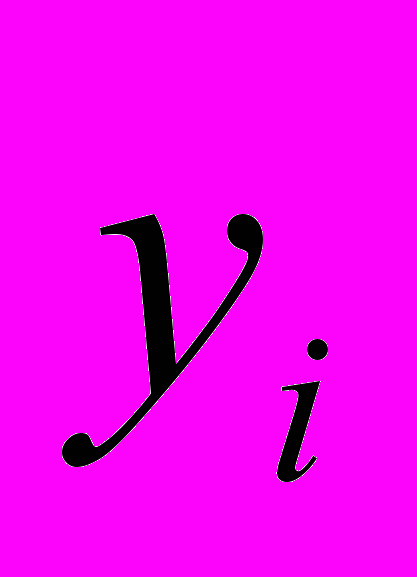и 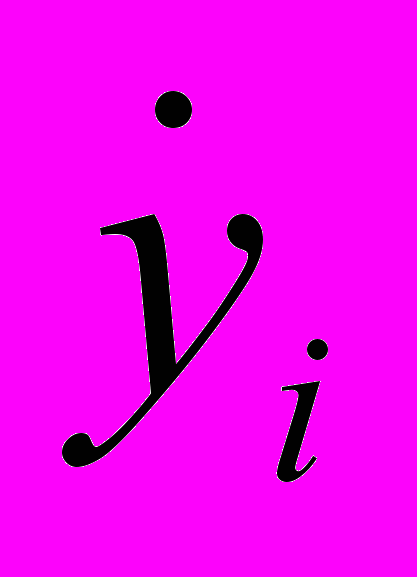. Особенность программы состоит также в том, что для больших значений независимой переменной t 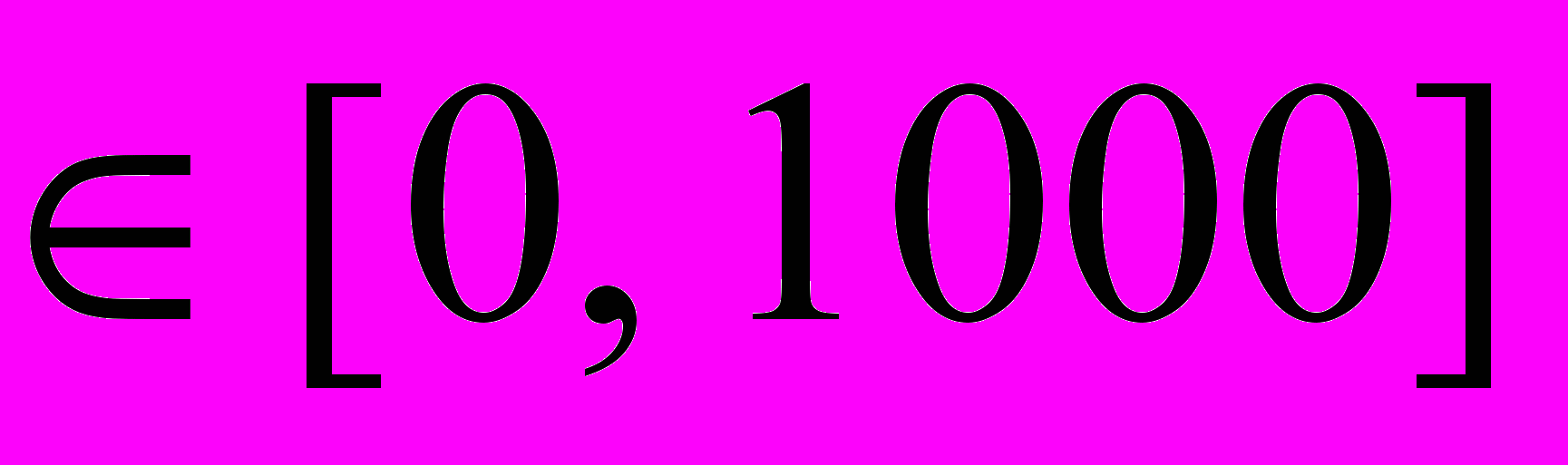точность вычислений в конце промежутка задания независимой переменной уменьшается примерно на один знак.

Программа численного решения матричной модели Ляпунова типа 6 также написана в соответствии с алгоритмом из главы 2. Достаточно простые итерационные вычисления организованы с помощью оператора while среды Mathcad. Итерационный процесс завершается при выполнении неравенства 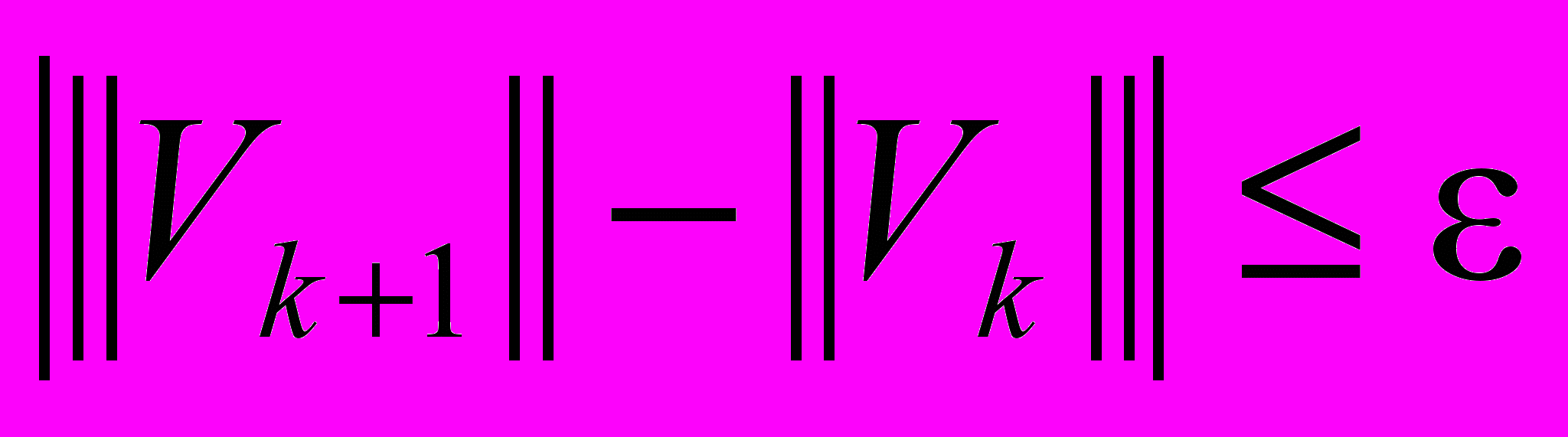, где  евклидова норма матрицы,   заданная погрешность вычислений. Для запуска этой программы необходимо задать матрицы A и W и погрешность вычислений  > 0.

Программа расчета динамических параметров колесных транспортных средств написана в среде Maple в соответствии с алгоритмами, приведенными в главы 3 диссертации. Данная программа состоит из трех проблемно-ориентированных подпрограмм: подпрограмма 1, подпрограмма 2 и подпрограмма 3. Подпрограмма 1 предназначена для расчета собственных частот колебаний, перемещений, скоростей и ускорений перемещений узлов колесного транспортного средства при движении по заданному профилю неровностей пути. Подпрограмма 2 позволяет определить характеристики случайных колебаний колесного транспортного средства при движении по пути, поверхность которого имеет случайную последовательность выступов и впадин. Подпрограмма 3, наконец, осуществляет вычисление собственных частот колебаний, перемещений, скоростей и ускорений перемещений элементов железнодорожного вагона в вертикальной плоскости при его движении по неровному железнодорожному пути.

Указанные подпрограммы состоят из вспомогательных программных модулей и основной программы. Вспомогательные программные модули можно разделить на три группы: модули для ввода данных, для расчета и для вывода результатов. Исходные данные моделируемых транспортных динамических систем в соответствии с решаемыми задачами предварительно должны быть помещены в файлы: data_1, data_2 и data_3 соответственно. Результаты расчетов выводятся на дисплей ПЭВМ и записываются в принимающие файлы: rez_1, rez_2, rez_3 и rez_4.

Строки с командами программы пронумерованы в порядке возрастания. Текст подпрограммы 1 содержится в строках с номерами: 1172, подпрограммы 2  в строках: 173326, подпрограммы 3  в строках: 327467. Запуск подпрограмм 1, 2 и 3 осуществляется соответственно в строках с номерами: 158, 317 и 450.

При необходимости с помощью программы, программные модули которой приведены в строках 1–83, возможно произвести графическую иллюстрацию расчетов, выполненных с помощью подпрограмм 1, 2 и 3 соответственно. Запуск графических подпрограмм осуществляется соответственно в строках 1, 45, 57. Перед запуском программы необходимо указать директории расположения принимающих файлов: rez_1, rez_2, rez_3 и rez_4.

Программа исследования влияния геометрических характеристик G, инерционных характеристик I и характеристик демпфирования J колесных транспортных средств на устойчивость вертикальных колебаний железнодорожного экипажа включает строки 1–12. Она используется совместно с подпрограммой 3 программы численного расчета динамических характеристик колесных транспортных средств. В построении алгоритма программы исследования влияния характеристик G, I и J колесных транспортных средств на устойчивость вертикальных колебаний железнодорожного экипажа использованы положения первого метода Ляпунова. Результаты расчетов выводятся на дисплей в числовом и графическом виде и дают представление о влиянии геометрических G и инерционных I характеристик, а также характеристик демпфирования и жесткости J на устойчивость вертикальных колебаний железнодорожного экипажа, выраженное в процентах.

Глава 3 содержит комплекс проблемно-ориентированных программ расчета характеристик динамических транспортных систем типов 35 и численного решения моделей типов 2 и 6.

Четвертая глава «Организация и проведение вычислительного эксперимента, анализ результатов моделирования характеристик динамических систем» посвящена проведению вычислительного эксперимента и анализу результатов моделирования характеристик динамических систем. В частности, с помощью комплекса проблемно-ориентированных программ расчета характеристик динамических транспортных систем проведен вычислительный эксперимент по математическому моделированию характеристик движения: колесного транспортного средства по неровному пути, колесного транспортного средства по неровному пути со случайным характером неровностей и моделирование вертикальных колебаний при движении железнодорожного вагона. Далее дан анализ результатов моделирования вертикальных колебаний при движении колесных транспортных средств, показателей устойчивости движения железнодорожного экипажа со многими колесными парами, показателей устойчивости движения железнодорожного транспортного средства посредством комбинированного метода и устойчивости установок двухосной тележки при движении железнодорожного экипажа в кривых. Анализ характеристик транспортных динамических систем, оцененных в процессе вычислительного эксперимента, дает возможность вносить усовершенствования в конструкции транспортных средств, повышать безопасность и комфортабельность передвижения пассажиров и сохранность перевозимых грузов.

Математическое моделирование движения колесных транспортных средств, выполненное в главе 4, предусматривает, в частности, решение следующих задач: расчет нагрузок, которым подвергаются элементы подвески и само транспортное средство, сохранность перевозимых грузов, безопасность и комфортабельность передвижения пассажиров и т.д. Для исследования транспортных моделей типа 3 и решения указанных выше задач в диссертационной работе использован комплекс проблемно-ориентированных программ, разработанный в главе 3.

В главе описан вычислительный эксперимент, в котором изучено движение в вертикальной плоскости автомобильного транспортного средства, состоящего из кабины, сиденья водителя, рамы, кузова, подвески и шин, через препятствие заданной формы. Общая система уравнения движения данного транспортного средства получается на основе частного случая транспортной модели типа 3:



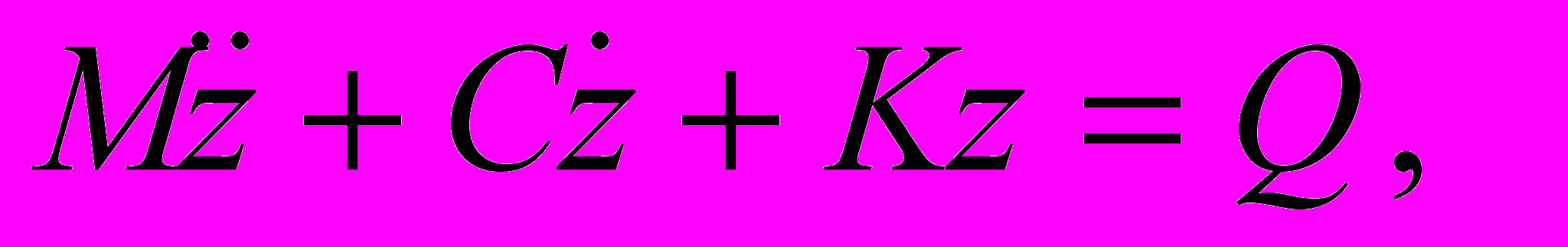
где М, С, К – соответственно матрицы масс, демпфирования и жесткости, Q – вектор обобщенных сил, z – вектор обобщенных координат, равный 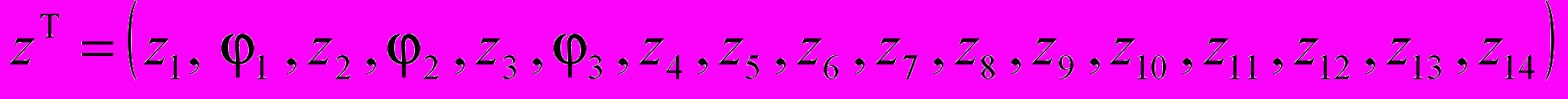, 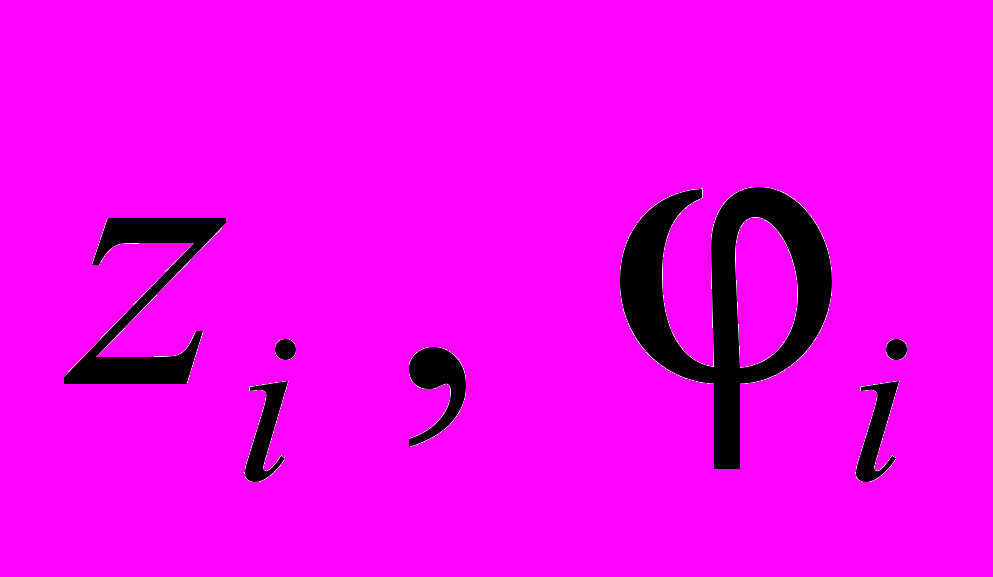– обобщенные перемещения i-го тела.

На рис. 1 и 2 представлены результаты расчетов с помощью комплекса проблемно-ориентированных программ зависимостей перемещений z₁, z₂, z₃ и z₉ и линейных ускорени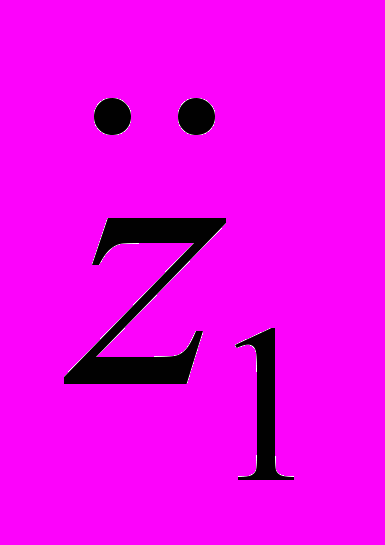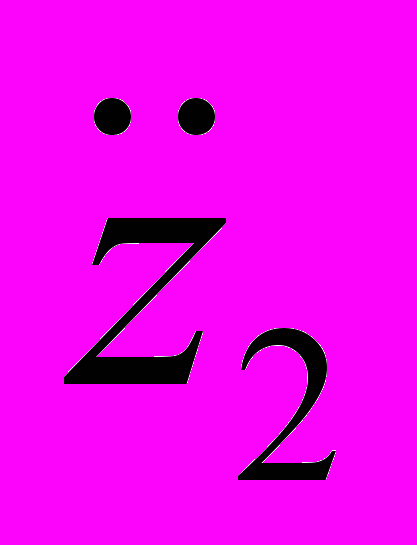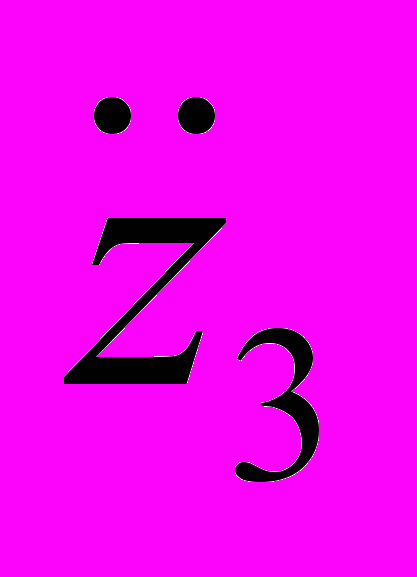й , , и 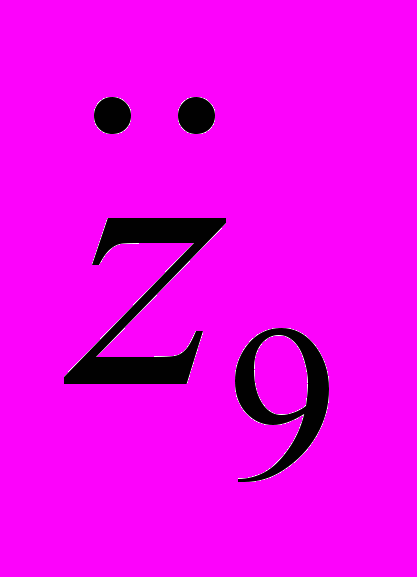от времени t для v = 50 км/час концентрированных масс соответственно кабины, рамы, кузова и сиденья водителя моделируемого транспортного средства (толщина линий увеличивается с ростом номера соответствующей зависимости).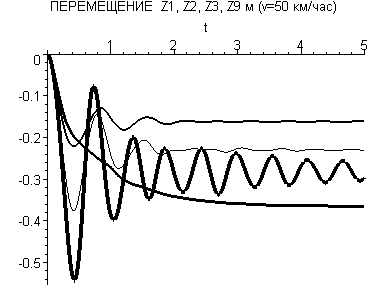




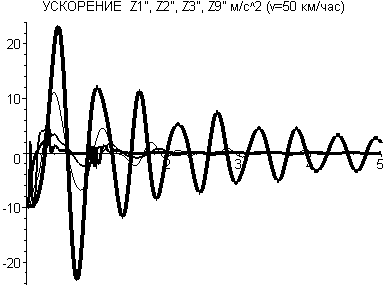
Рис. 1 Рис. 2

Установлено, что собственная частота колебаний frequency[9]=0,66 Hz сиденья водителя соответствует зоне комфортности, а при движении через препятствие сиденье подвергается значительным перегрузкам; на скорости v = 60 км/час происходит отрыв колес от поверхности пути.

В главе 4 проведено также моделирование движения желез­нодорожного вагона, состоящего из кузова и двух рам тележек с подбуксовым подвешиванием, вдоль желез­нодорожного полотна. Изучены вертикальные колебания вагона на стыках железнодорожной колеи. Закон движения вагона в вертикальной плоскости соответствует частному случаю транспортной модели типа 3:



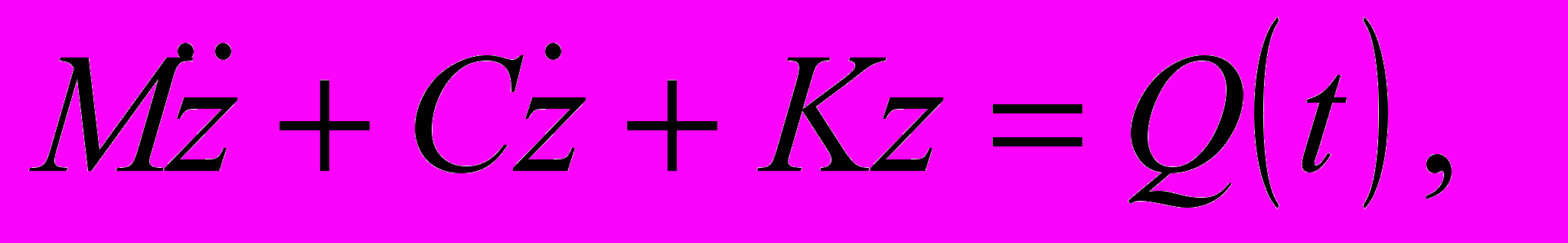
где М, С, К – соответственно матрицы масс, демпфирования и жесткости, Q(t) – вектор обобщенных сил, z – вектор обобщенных координат, 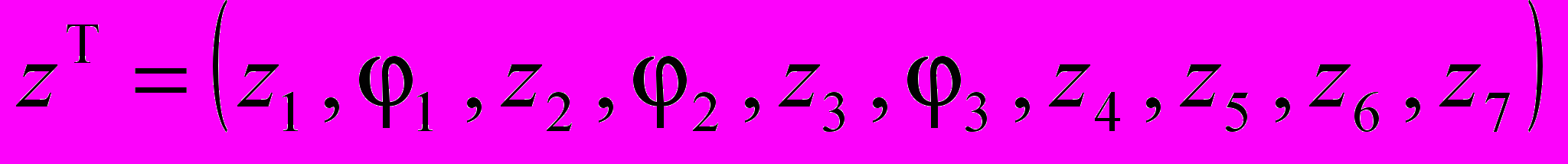, 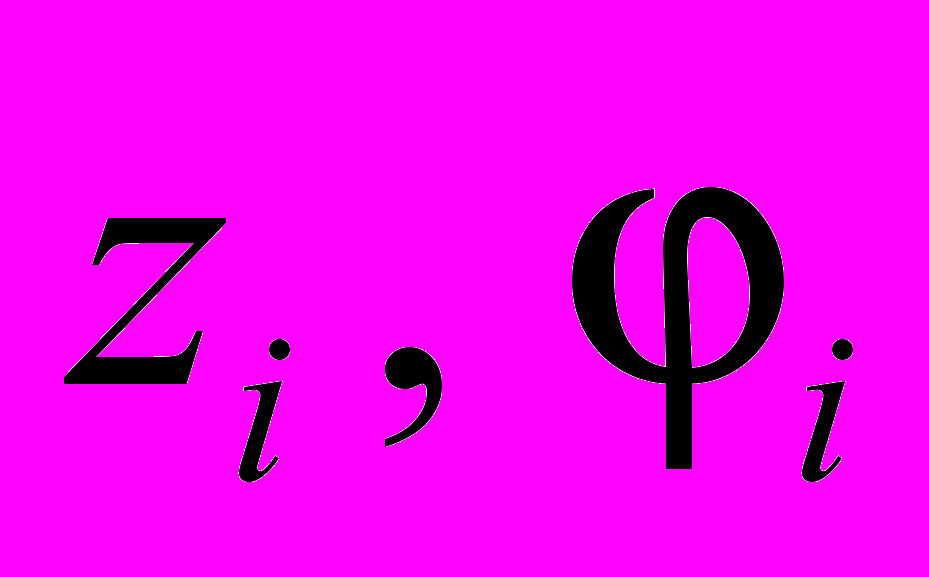– обобщенные перемещения i-го тела.

Расчеты с помощью комплекса проблемно-ориентированных программ показывают, что перемещение кузова вагона невелико и практически не зависит от скорости движения вагона. Частота линейного ускорения возрастает с увеличением скорости вагона от 120 до 200 км/час и не принадлежит зоне комфортабельного передвижения.

Изучение влияния параметров G, I и Ј на устойчивость вертикальных колебаний вагона показывает, что параметры демпфирования и жесткости Ј оказывают значительно более существенное влияние на устойчивость вертикальных колебаний вагона, чем инер­ционные I и геометрические G параметры (см. рис. 3).



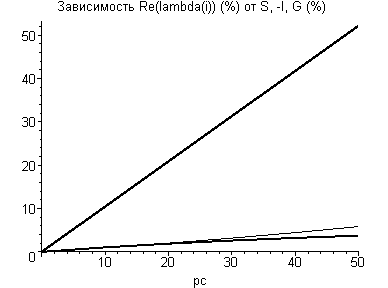
Рис. 3

Результаты четвертой главы позволяют дать рекомендации по улучшению конструкции колесных транспортных средств и совершенствованию функционирования транспортных систем с точки зрения устойчивости движения, повышения безопасности и комфортабельности передвижения пассажиров и сохранности перевозимых грузов. Кроме того, разработанные методы и алгоритмы расчета позволяют выполнять расчет показателей устойчивости движения железнодорожного экипажа со многими колесными парами, показателей устойчивости движения железнодорожного транспортного средства посредством комбинированного метода и устойчивости установок двухосной тележки при движении железнодорожного экипажа в кривых.

В Заключении диссертации перечислены основные результаты работы, отмечены некоторые нерешенные задачи и перспективные направления, связанные с темой диссертации.