А. И. Акимов Оренбургский государственный педагогический университет
| Вид материала | Документы |
СодержаниеНа первом этапе |
- «Оренбургский государственный педагогический университет», 374.47kb.
- «романы с ключом» Т. Л. Пикока, 276.46kb.
- «группы риска», 1693.05kb.
- Механизмы гетерогенной организации системы русского языка (на материале рефлексов праславянских, 845.94kb.
- «Оренбургский государственный педагогический университет», 2561.05kb.
- "Философские науки", 789.13kb.
- Педагогика, 1821.51kb.
- Нестеров Александр Климентьевич формирование духовной культуры, 468.3kb.
- Педагогическое сопровождение развития толерантности в межличностном взаимодействии, 433.77kb.
- Творческое саморазвитие старшеклассника в креативном образовании 13. 00. 01 общая педагогика,, 440.76kb.
Акимов А.И. Математическое моделирование теплофизических процессов в автоматических установках производства композиционных материалов. // Проблемы информатики в образовании, управлении, экономике и технике: Сб. статей Всерос. научно-техн. конф.– Пенза: ПДЗ, 2008. – С. 271-274.
Математическое моделирование теплофизических процессов
в автоматических установках производства композиционных материалов
А.И. Акимов
Оренбургский государственный педагогический университет,
г. Оренбург
Управление процессом полимеризации связано с разработкой теплофизических математических моделей. Основные трудности при создании таких моделей возникают из-за необходимости учета:
многослойности конструкций с различными теплофизическими свойствами;
фазовых переходов при полимеризации, которые описываются моделями Стефана;
многостадийности процесса нагрева.
Температурный процесс полимеризации разделяется на этапы. Своеобразие теплофизических процессов на каждом из этапов создает необходимость использования различных математических моделей.
На первом этапе процесса математическая постановка задачи в цилиндрической системе координат для многослойной конструкции имеет вид:
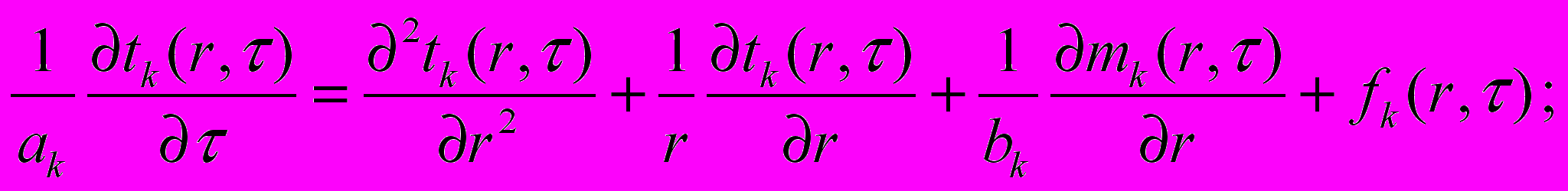 (1)
(1)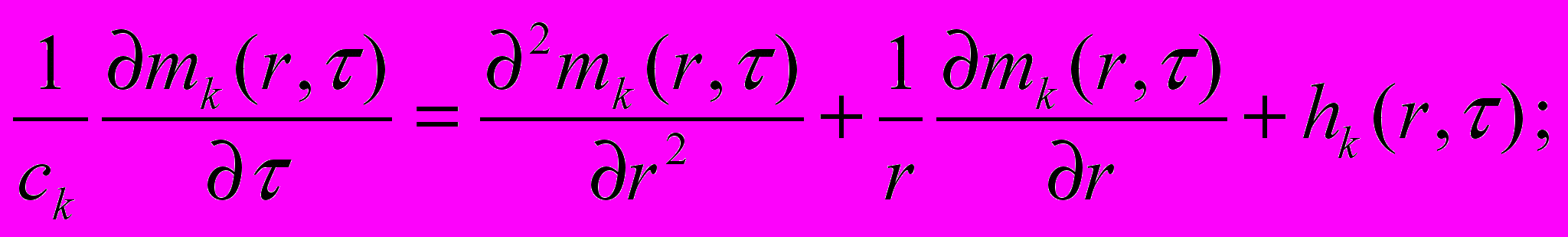 (2)
(2)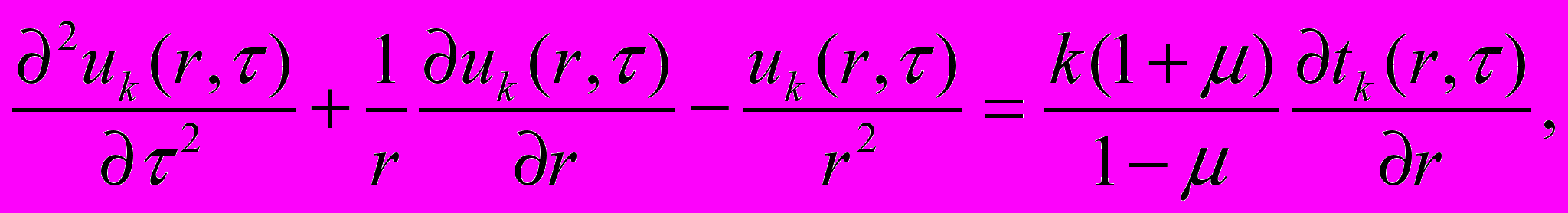 (3)
(3)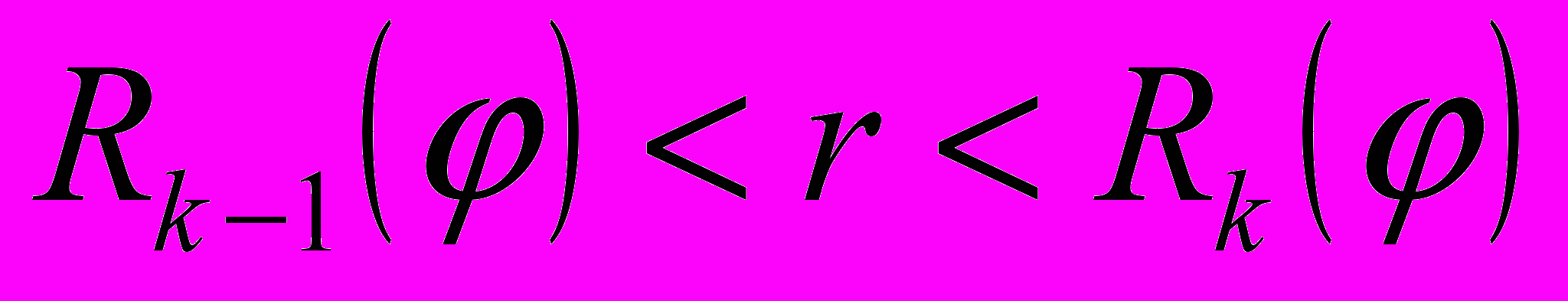 для к=1,2,….n,
для к=1,2,….n,при начальных условиях
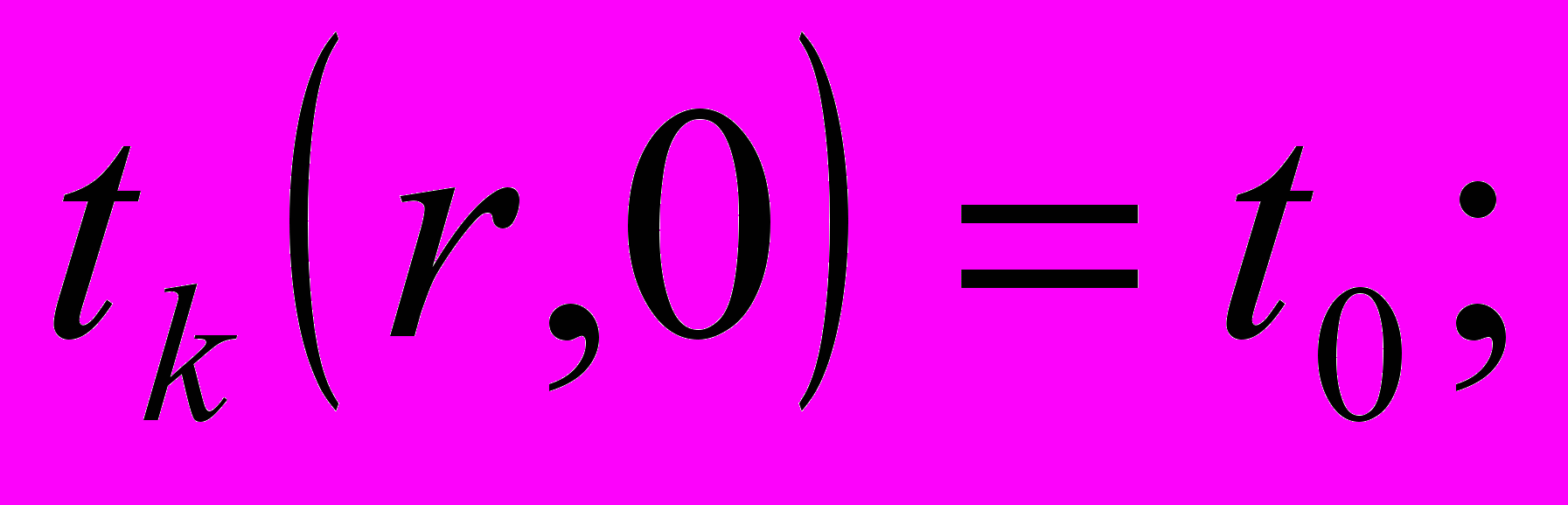 (4)
(4)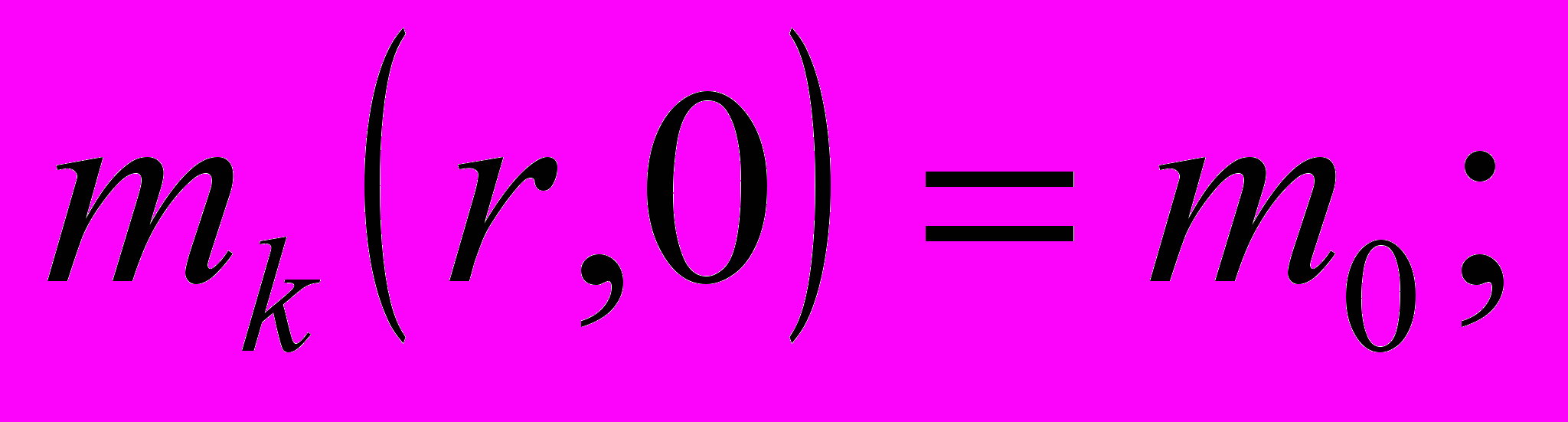 (5)
(5)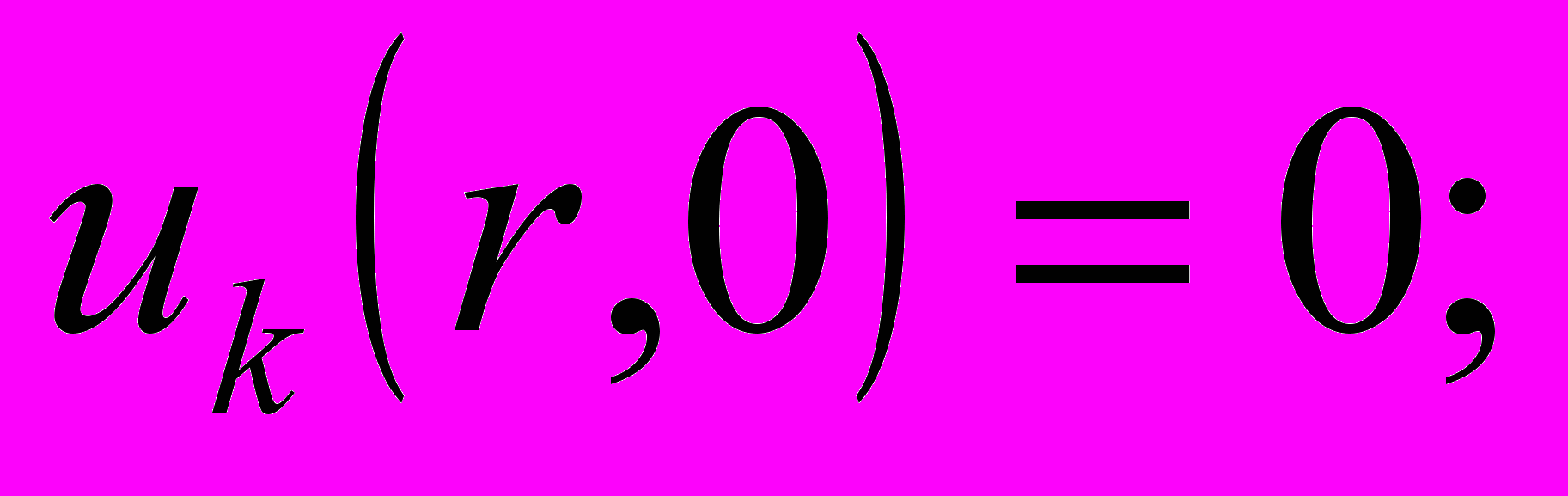 (6)
(6)и при граничных условиях
 (7)
(7) (8)
(8)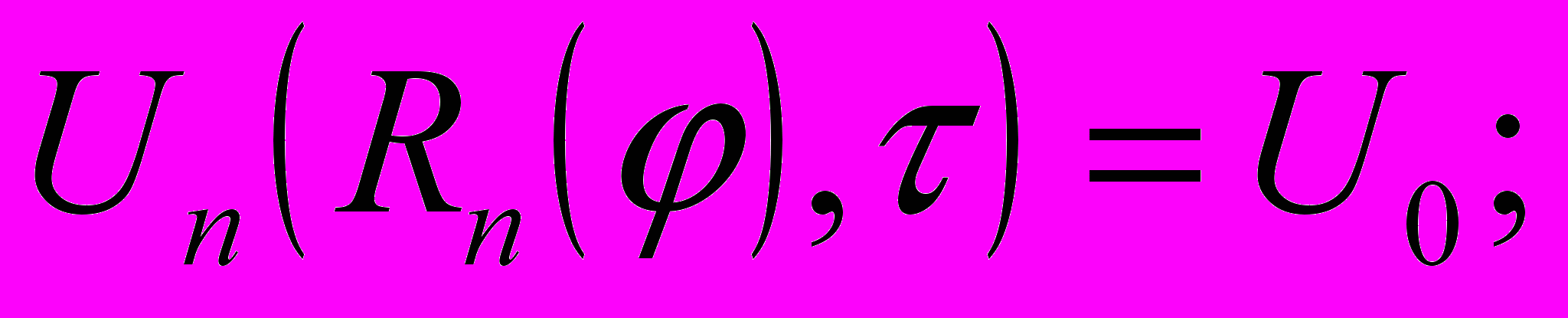 (9)
(9)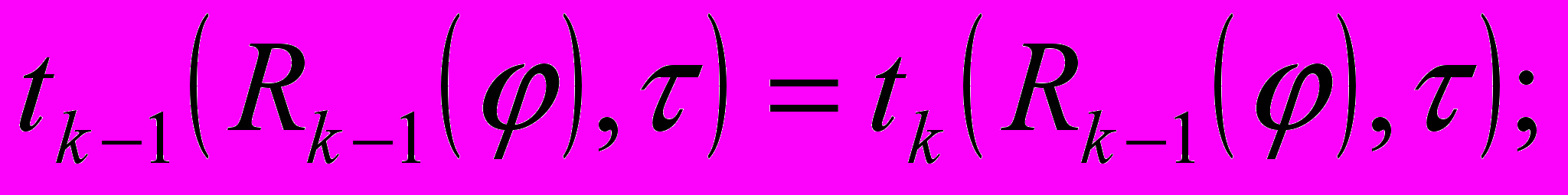 (10)
(10)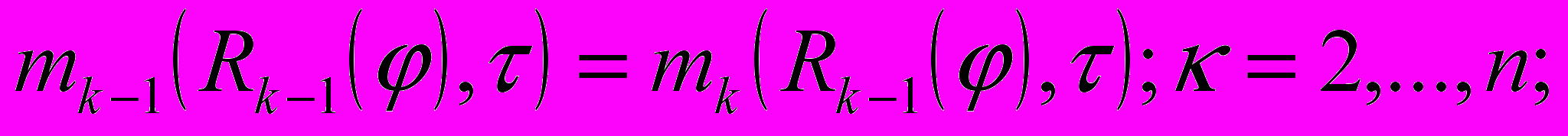 (11)
(11) (12)
(12)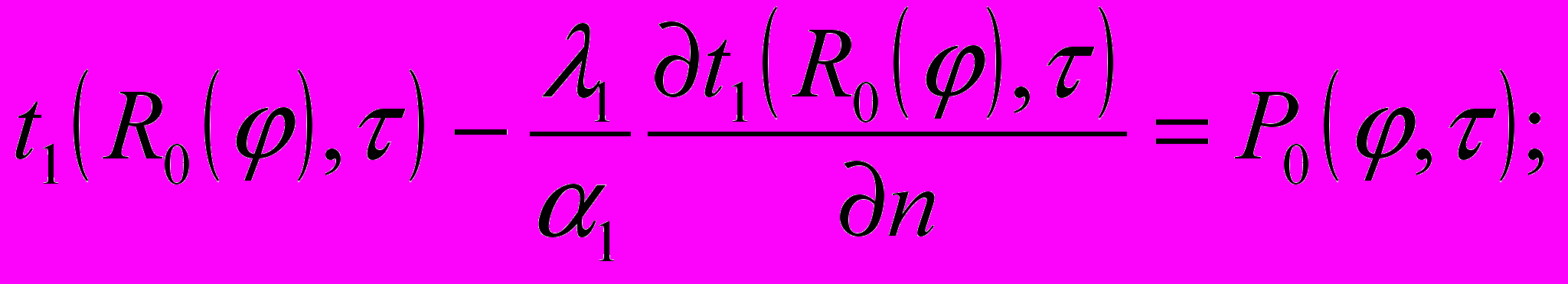 (13)
(13)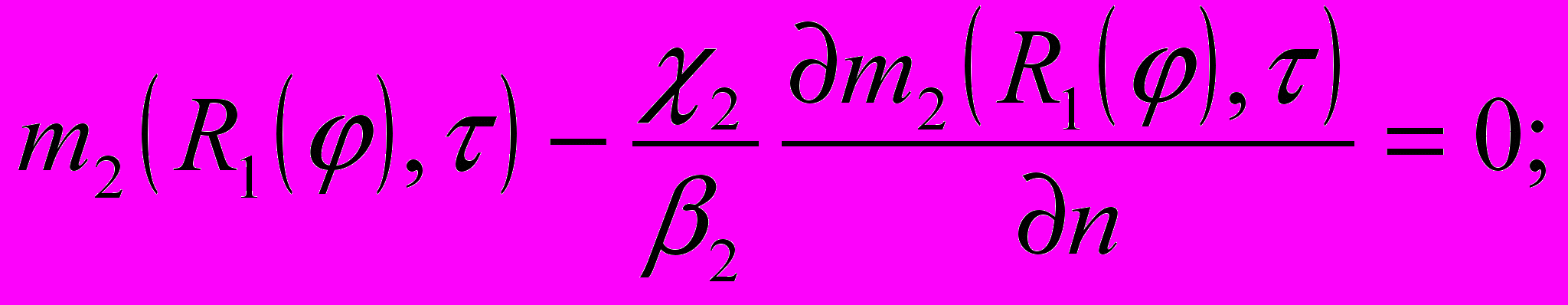 (14)
(14)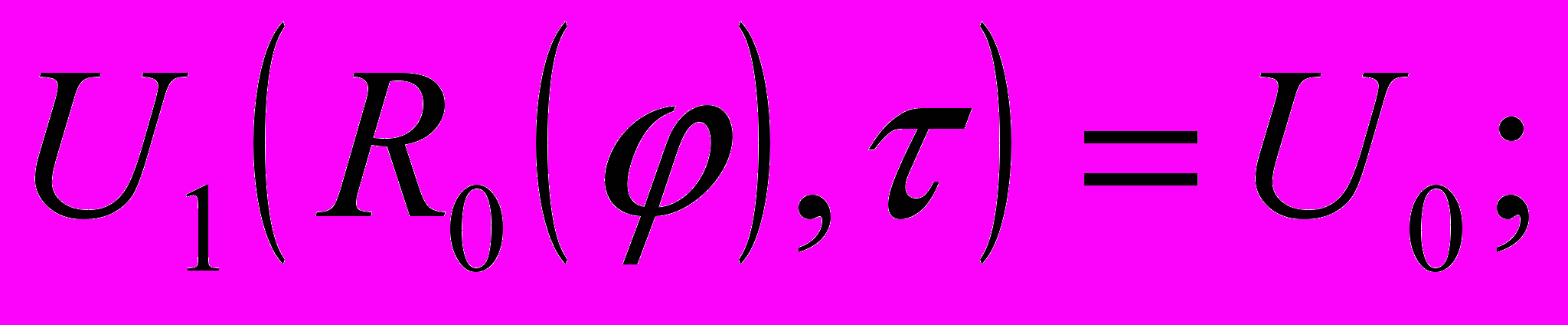 (15)
(15)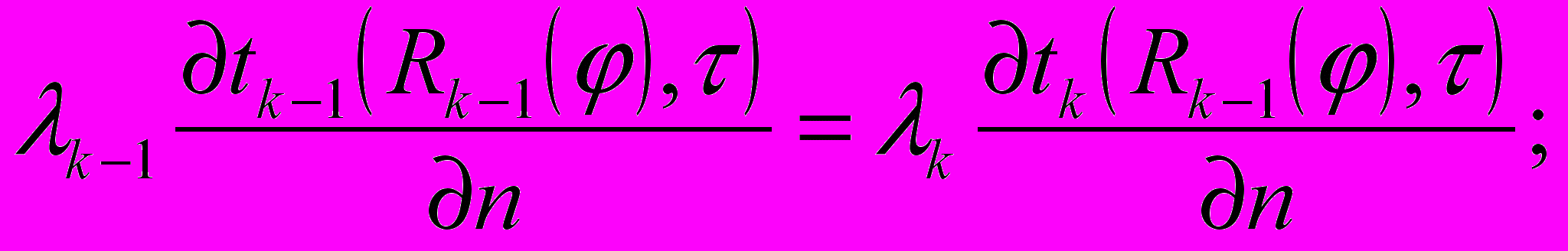 (16)
(16)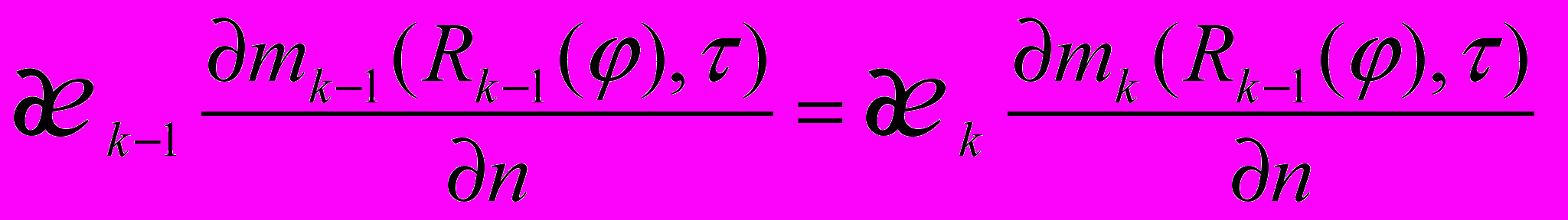 (17)
(17)где
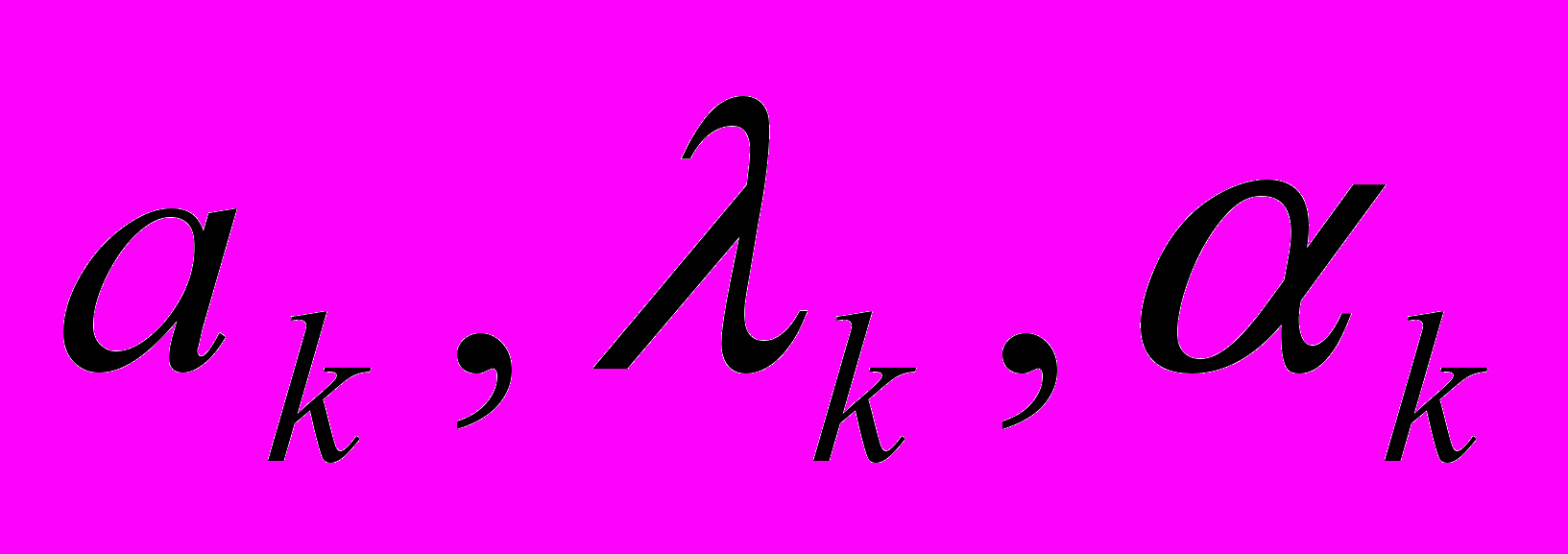 – коэффициенты температуропроводности, теплопроводности и теплопередачи соответственно;
– коэффициенты температуропроводности, теплопроводности и теплопередачи соответственно;  – коэффициенты проводности потенциала массы, массопередачи и массоотдачи; W – доля жидкого состояния рассматриваемой среды (при затвердевании вещества); – плотность этой части среды; – скрытая теплота кристаллизации; – время;
– коэффициенты проводности потенциала массы, массопередачи и массоотдачи; W – доля жидкого состояния рассматриваемой среды (при затвердевании вещества); – плотность этой части среды; – скрытая теплота кристаллизации; – время; х – пространственная координата; tk – температура области DK,, k = 1,2;
mk – объёмная концентрация k-го компонента; uk – поле скоростей или деформации.
Отметим, что в задаче (1)-(17) описываются взаимосвязанные процессы тепло- и массообмена. Уравнение теплопроводности (1) содержит наряду с источниками тепла
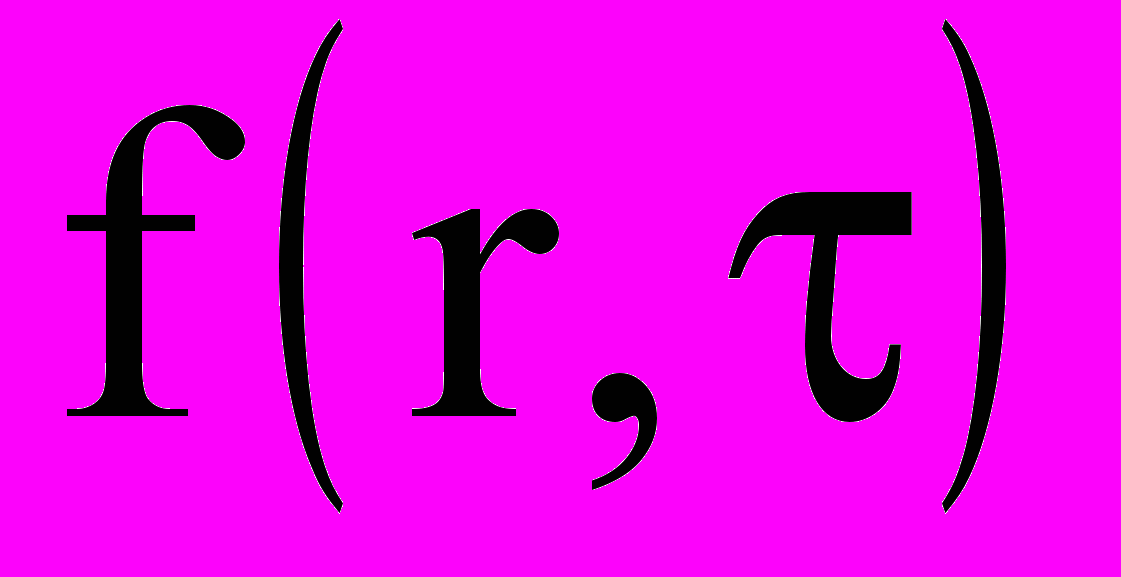 слагаемые, обусловленные тепловыделениями за счет градиента
слагаемые, обусловленные тепловыделениями за счет градиента 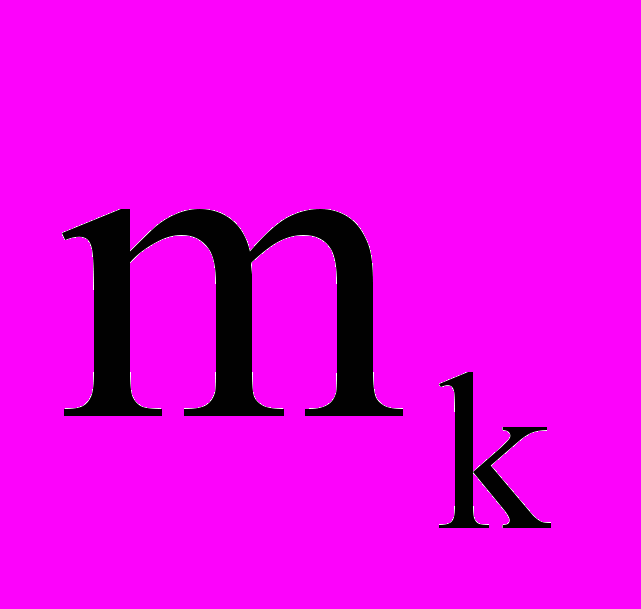 , и дополнено соответствующими уравнениями (2) и (3), где
, и дополнено соответствующими уравнениями (2) и (3), где  – безразмерный коэффициент, характеризующий свойства термонапряжений.
– безразмерный коэффициент, характеризующий свойства термонапряжений.На втором этапе теплофизические процессы описываются следующей задачей:

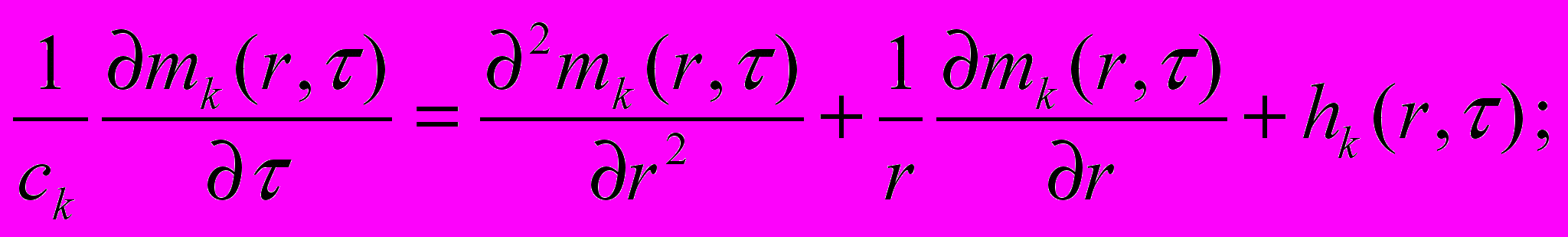
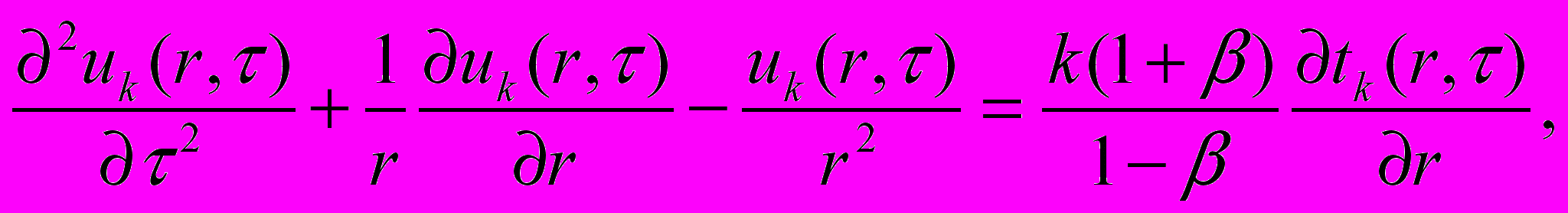
где
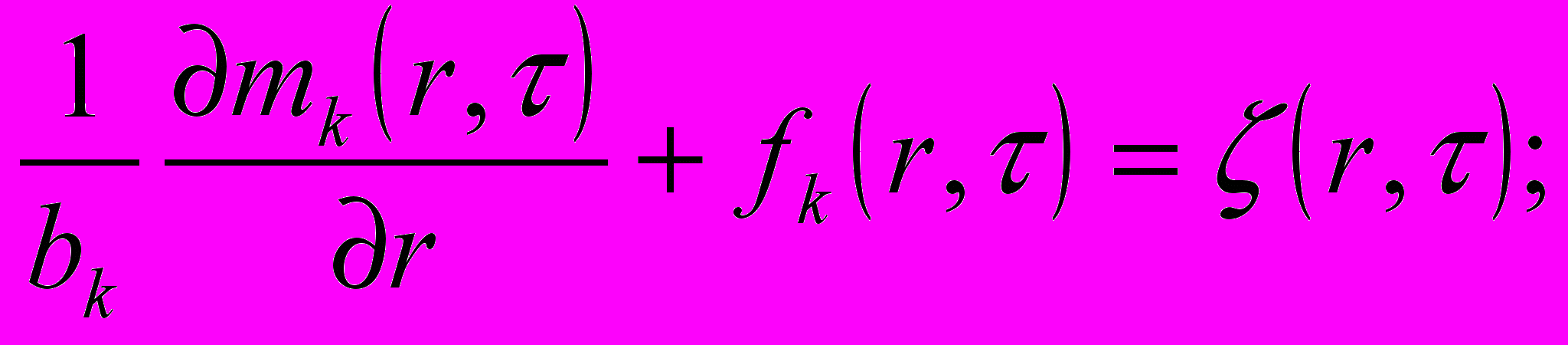
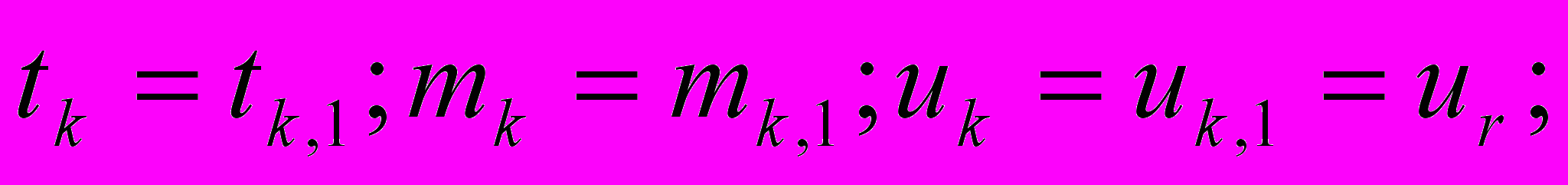
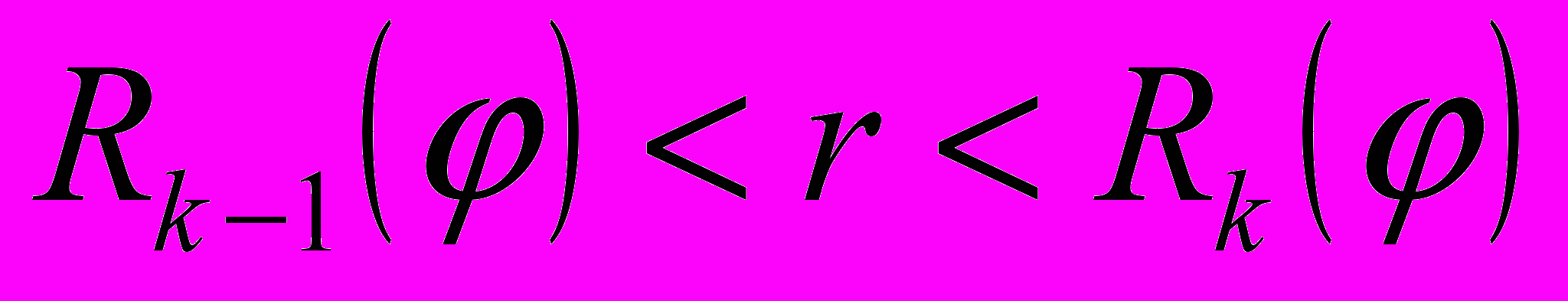 для к=1,2,….,j,….n;
для к=1,2,….,j,….n;Ro()r () при 1=I,() r Rn () при 1=II,
при начальных условиях
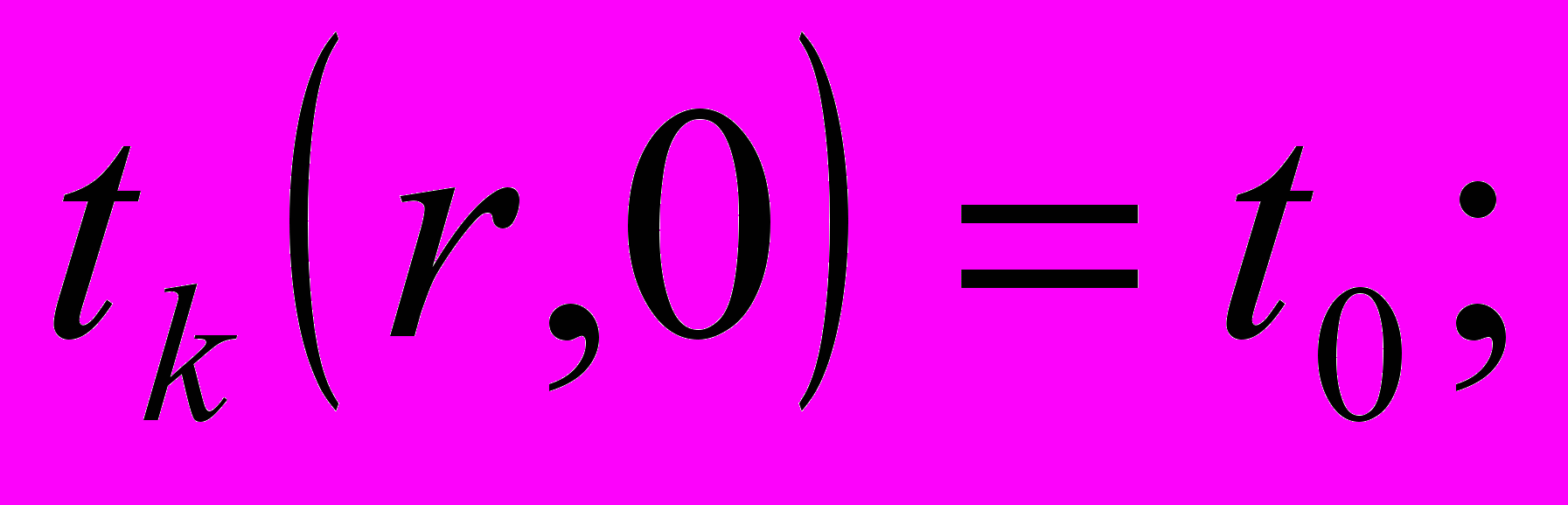
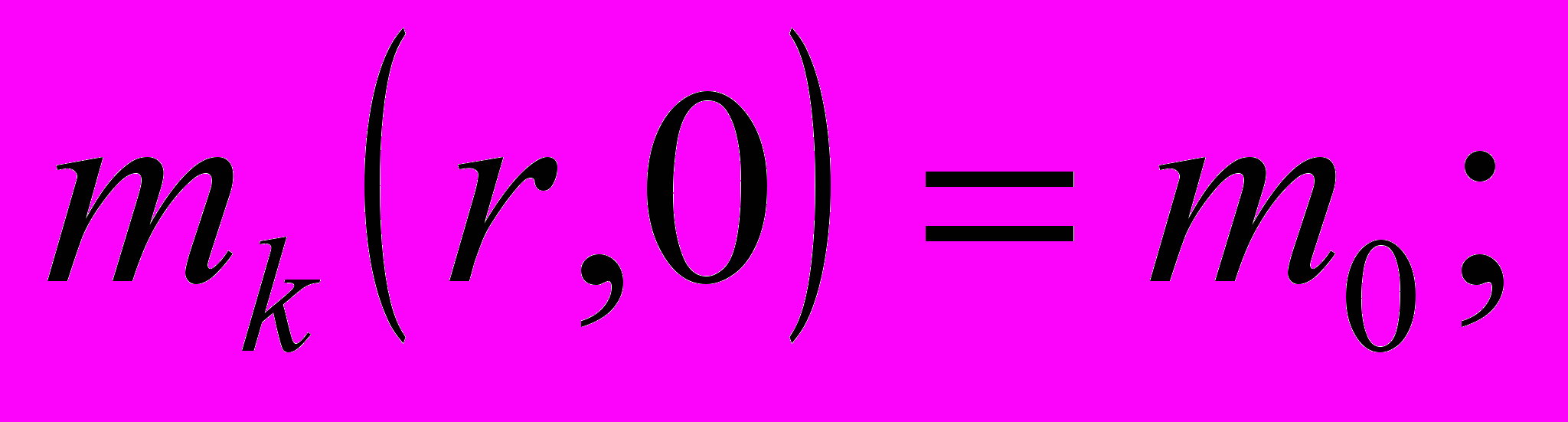
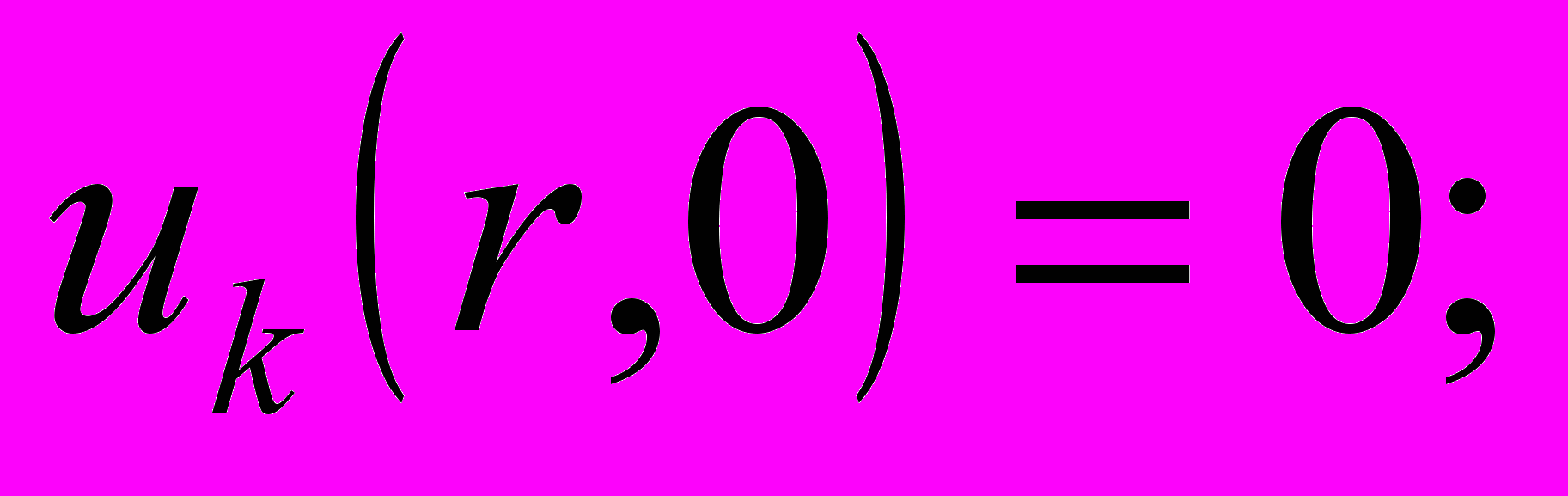
и при граничных условиях
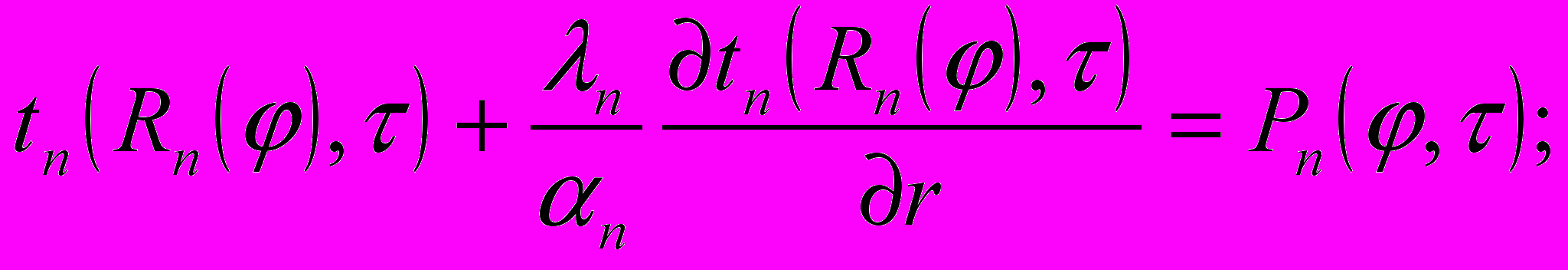
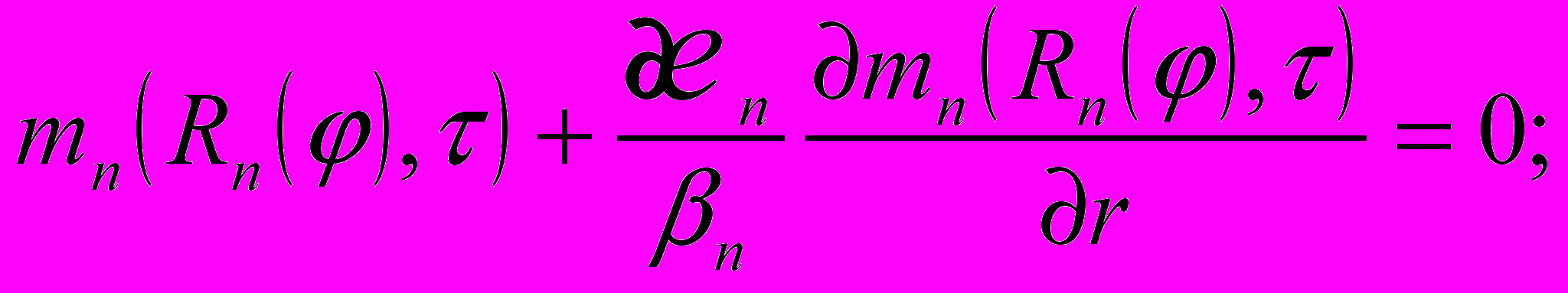


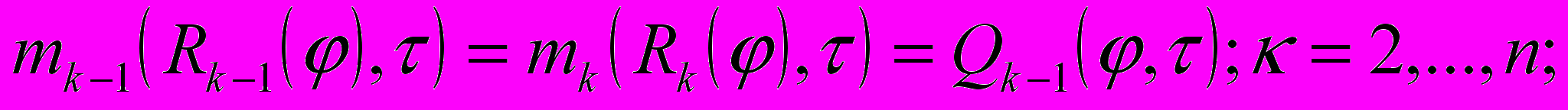


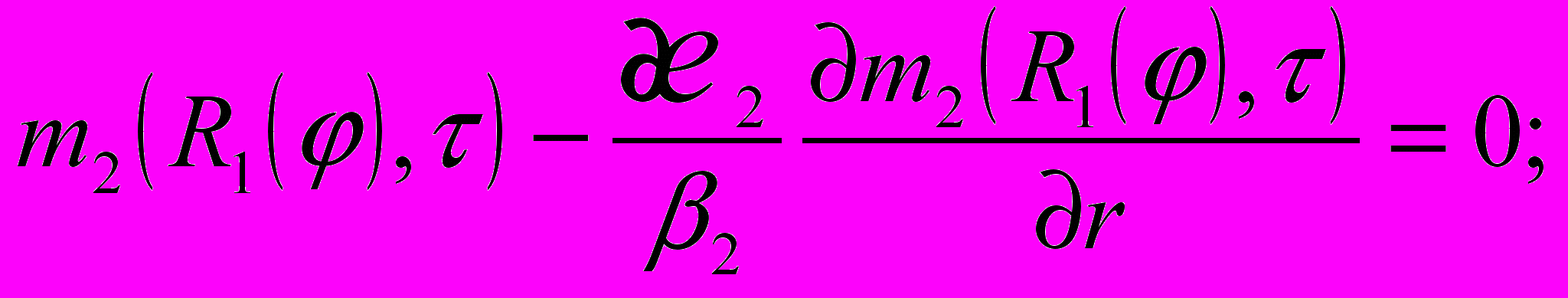
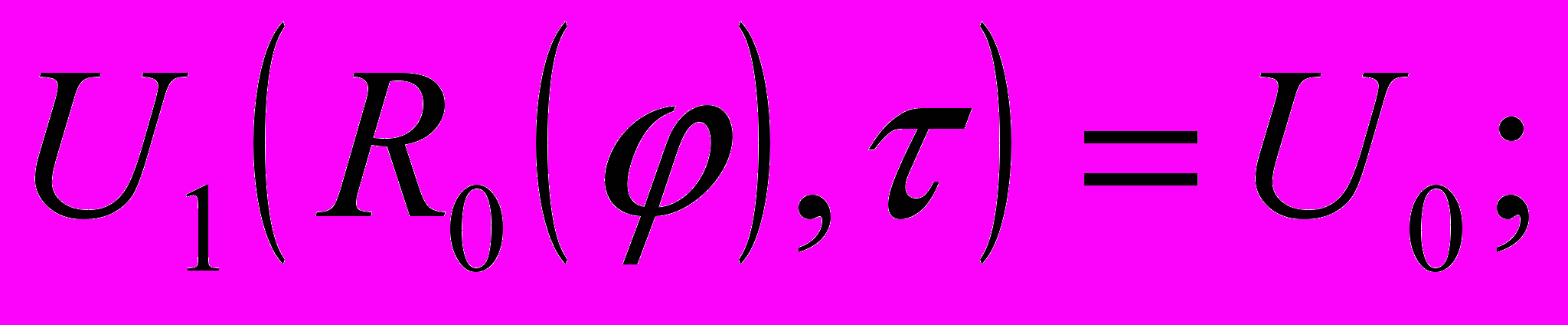
с условиями полимеризации
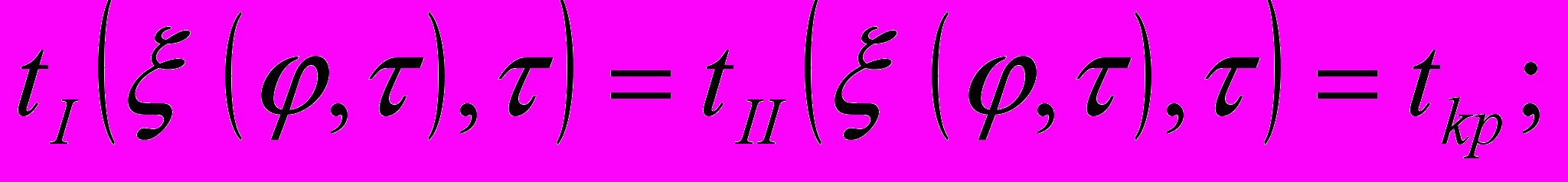
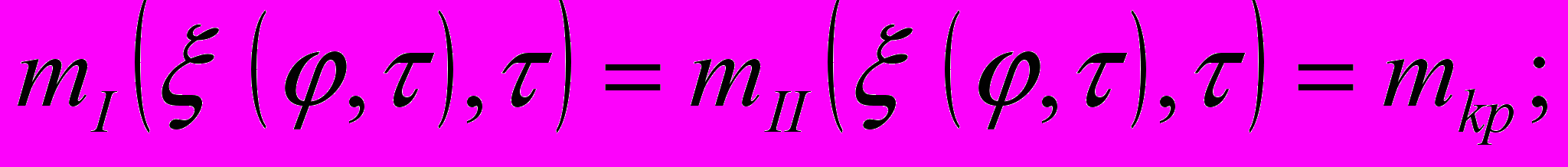



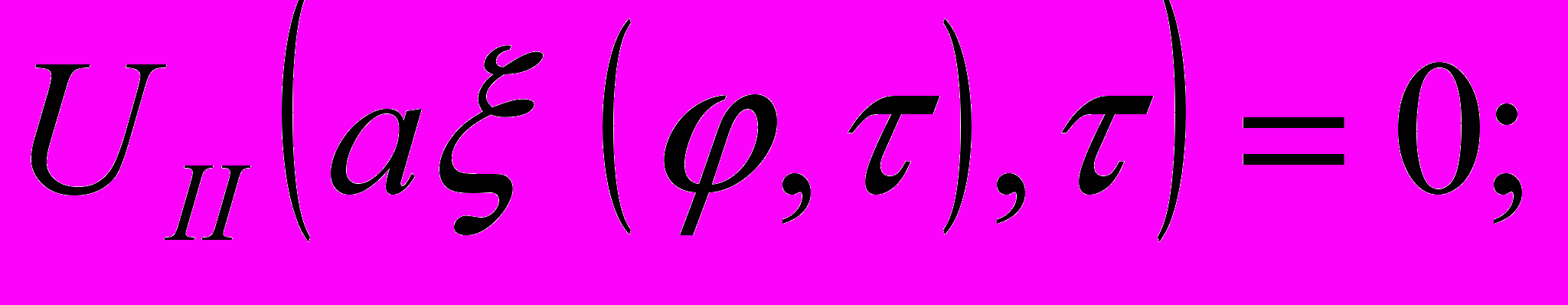
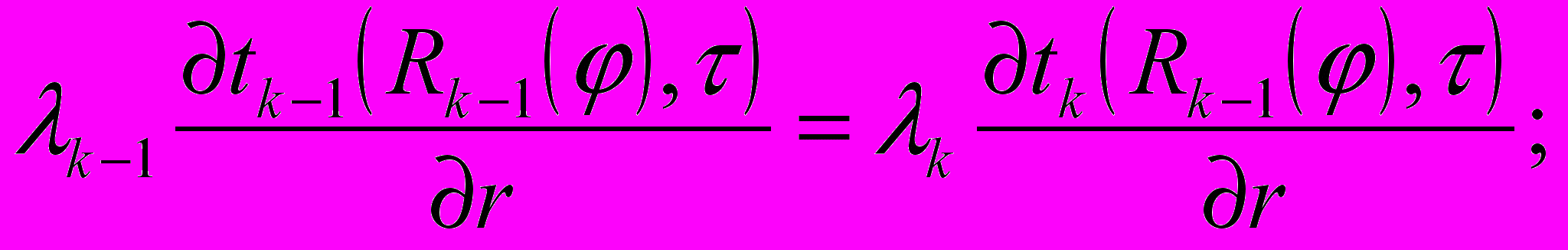
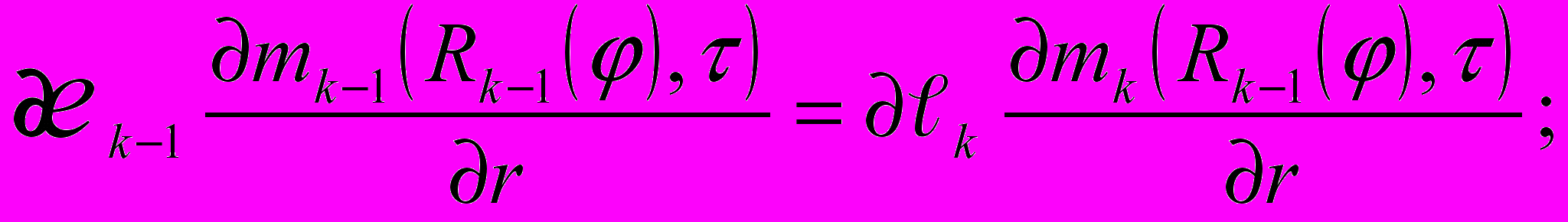
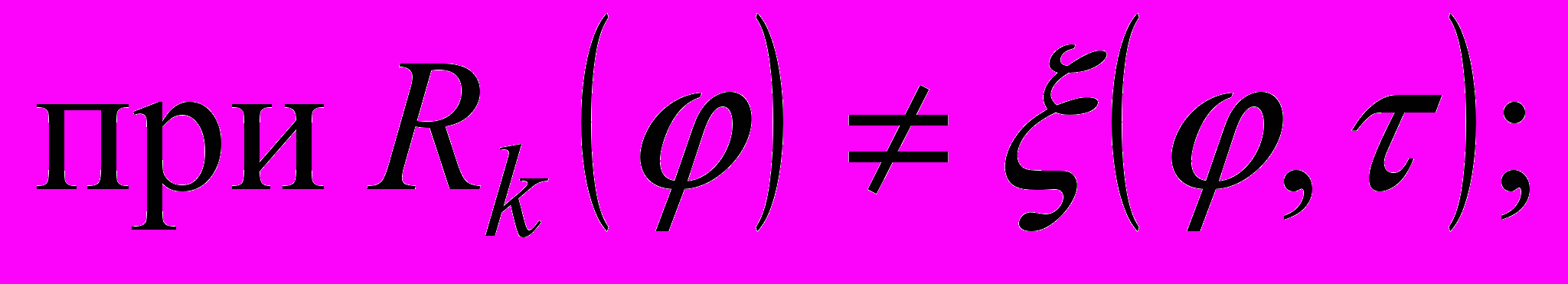
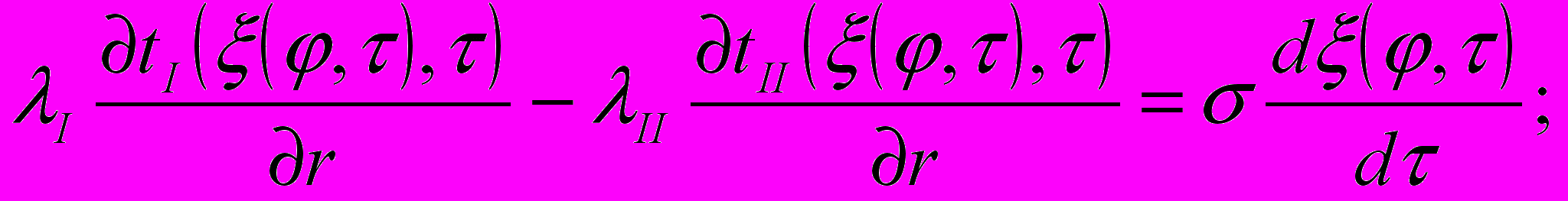

При решении этой задачи использован метод изотермических поверхностей.
