Нестационарный тепло- и массоперенос в многослойных ограждающих конструкциях
| Вид материала | Автореферат |
- Вестник ргу им. Иммануила, вып. 10, 2007г., с. 8-14, 89.44kb.
- Название проекта, 9.18kb.
- Рабочая программа наименование дисциплины Тепло- и массоперенос в материалах и процессах, 102.48kb.
- Краткое содержание дисциплин, основные разделы, 55.77kb.
- О надежности дюбельного крепления в системах наружного утепления 'мокрого типа', 241.2kb.
- Од знаменателен тем, что в его середине исполняется 10 лет со дня принятия новых нормативов, 182.16kb.
- Проект «Тепло слів» 26 серпня в рамках всеукраїнської програми «Спілкування заради, 95.52kb.
- А. И. Герцена Способы выражения предикатного актанта в конструкциях с фазовыми глаголами, 47.54kb.
- Потенциальным участникам, 16.93kb.
- Гагарин В. Г., Козлов В. В. Математическая модель и инженерный метод расчета влажностного, 113.96kb.
Уравнение теплопроводности в общем случае имеет нелинейный вид:
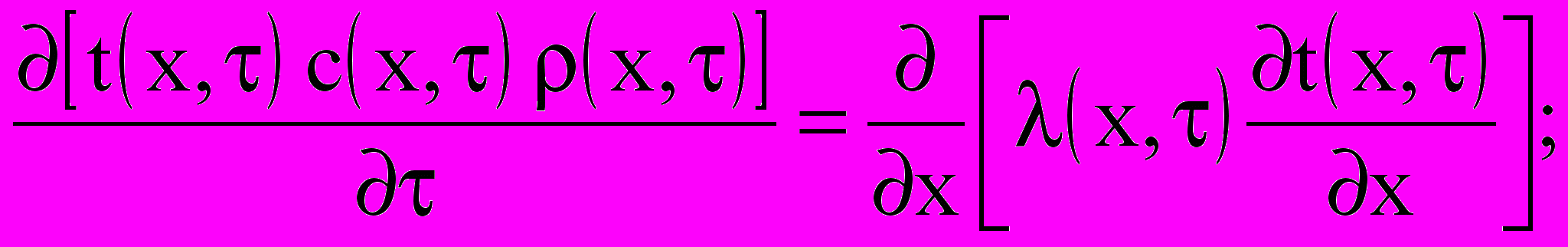 (1)
(1)Физическая картина процесса может быть представлена следующим образом (Рис. 1а): многослойная (для простоты рассматривается трехслойная) стенка имеет начальное распределение температур:
t1(x,0) = t0; t2(x,0) = t0; t3(x,0) = t0;
В
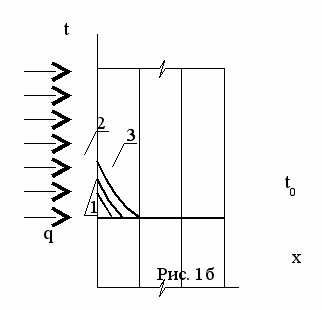
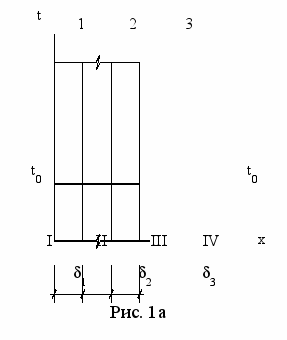 момент времени =0 c левой стороны стенки подается тепловой поток q, под влиянием которого первый слой начинает прогреваться (Рис. 1б). Изменение полей температур характеризуется кривыми 1 и 2. При этом второй и третий слои имеют темпе-ратуру t0.
момент времени =0 c левой стороны стенки подается тепловой поток q, под влиянием которого первый слой начинает прогреваться (Рис. 1б). Изменение полей температур характеризуется кривыми 1 и 2. При этом второй и третий слои имеют темпе-ратуру t0. В момент времени 1* (кривая 3) тепловой фронт достигает границы первого и второго слоев, и в этом месте появляется градиент температур:
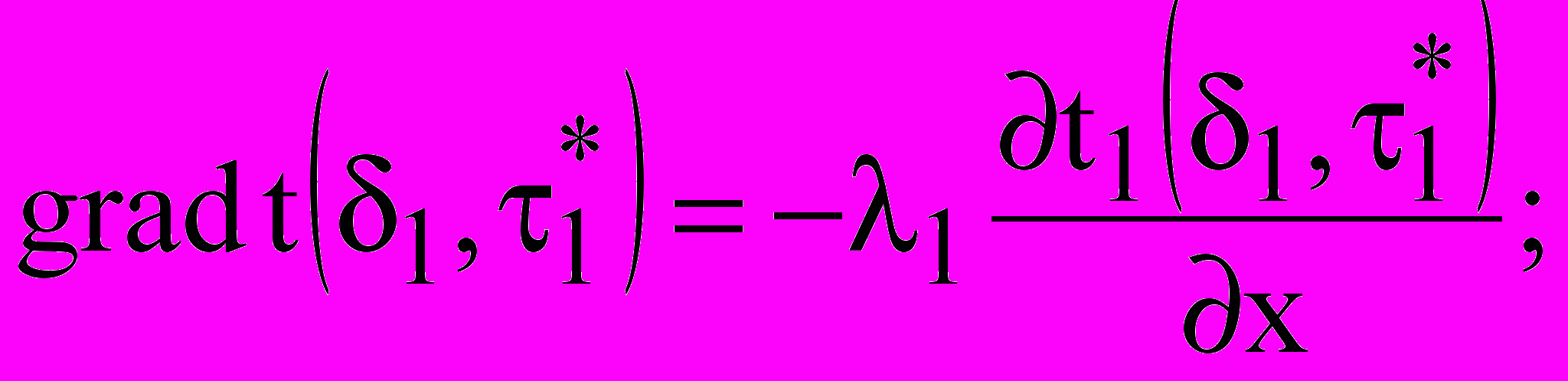 (2)
(2)После этого момента поле темпера-тур будет проникать глубже в стенку, как показывают кривые 4 и 5. Температура третьего слоя остается равной t0 до момента времени 2*, когда температурный градиент достигнет стыка второго и третьего слоя. И так далее. В момент в
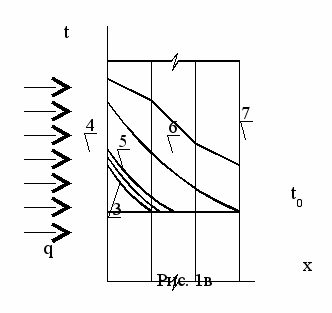 ремени 3*, когда температурный градиент достигнет внешней границы последнего слоя ограждения, в процессе теплопереноса оказываются задействованы все слои ограждения. При достаточно большом значении времени процесса, (теоретически при ) в конструкции сформируется стационарное поле температур (ломаная линия 7 Рис. 1в), значения которого используется для расчета R, по методике СНиП II-3-79 **.
ремени 3*, когда температурный градиент достигнет внешней границы последнего слоя ограждения, в процессе теплопереноса оказываются задействованы все слои ограждения. При достаточно большом значении времени процесса, (теоретически при ) в конструкции сформируется стационарное поле температур (ломаная линия 7 Рис. 1в), значения которого используется для расчета R, по методике СНиП II-3-79 **.Предлагаемая методика позволяет методом решения обратной задачи непосредственно рассчитывать значение R из нестационарного температурного поля.
В математической постановке используем комбинированный метод решения краевых задач теплопереноса, идею которого впервые разработал С.В. Федосов более 20 лет назад. Метод базируются на основе сочетания элементов аналитического и численного решения. Суть метода состоит в том, что весь процесс теплопереноса делится на ряд малых временных интервалов. В пределах каждого интервала предполагаем, что температура одинакова на границе II и III и постоянна плотность теплового потока через соприкасающиеся поверхности, т.е. идеальный тепловой контакт.
Общая задача разбивается на три автономные, но взаимосвязанные между собой.
Задача 1. Теплоперенос в слое 1 с граничными условиями третьего рода, которые учитывают конвективный обмен на границе I, и первого рода, которые характеризуют постоянство температуры на границе II слоев 1 и 2.
Задача 2. Теплоперенос в слое 2 с граничными условиями второго рода, которые характеризуют постоянство плотности теплового потока через границу II, и первого рода, характеризующие постоянство температуры на границе III.
Задача 3. Теплоперенос в слое 3 с граничными условиями второго рода на границе III и граничными условиями третьего рода, которые характеризуют теплообмен между поверхностью слоя 3 на границе IV с окружающей средой по закону Ньютона.
Каждая из этих задач решается аналитически. Решение общей задачи нестационарной теплопроводности можно получить в результате сопряжения этих аналитических решений на каждом временном интервале. Это позволяет перейти от граничных условий четвертого рода к граничным условиям первого и второго рода на поверхностях раздела слоев 1 и 2, 2 и 3, что облегчает решение задачи.
Общее решение для задачи 1 получено С.В. Федосовым и имеет вид:
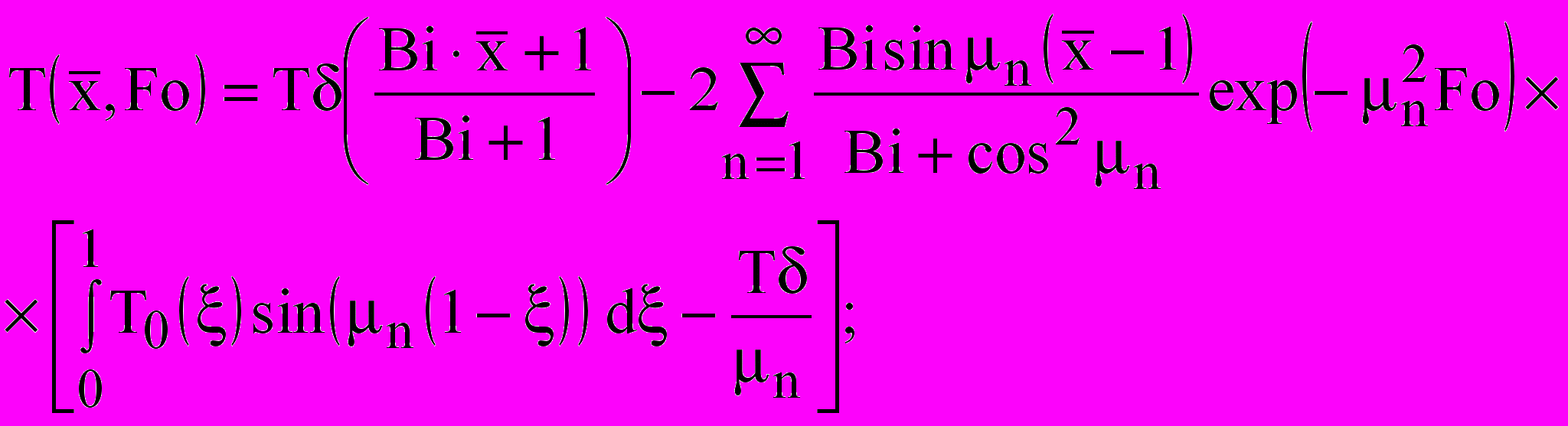 (3)
(3)Общее решение для задачи 2 получено в виде:
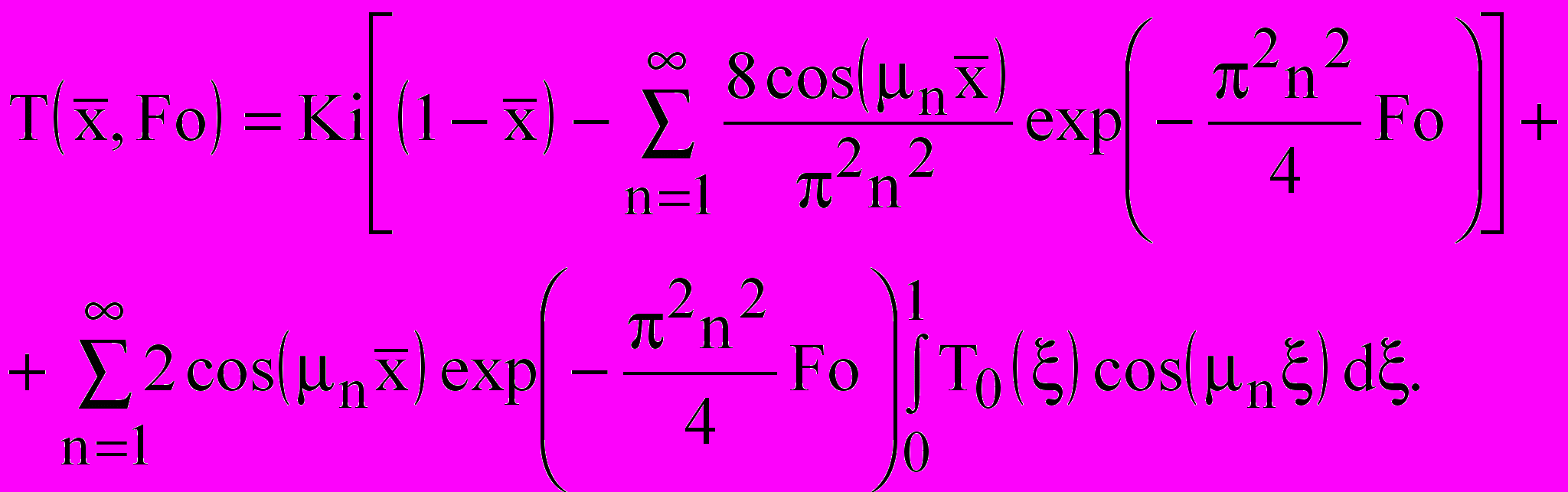 (4)
(4)Общее решение для задачи 3 получено в виде:
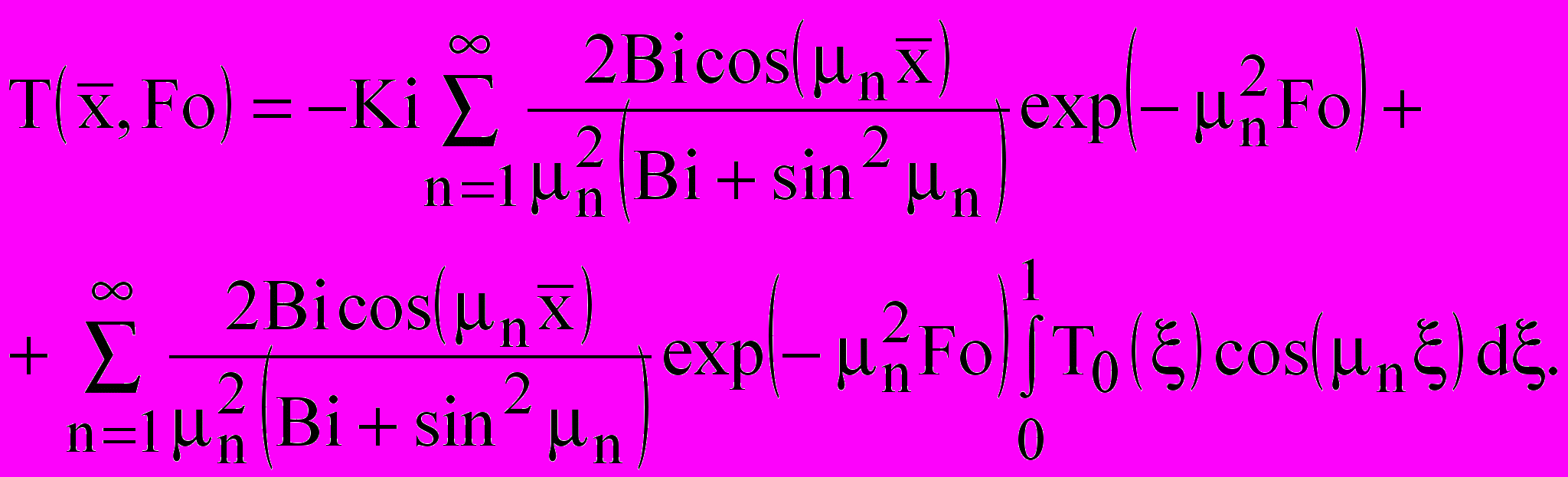 (5)
(5)Величина температурных градиентов для каждого слоя имеет вид:
- для задачи 1:
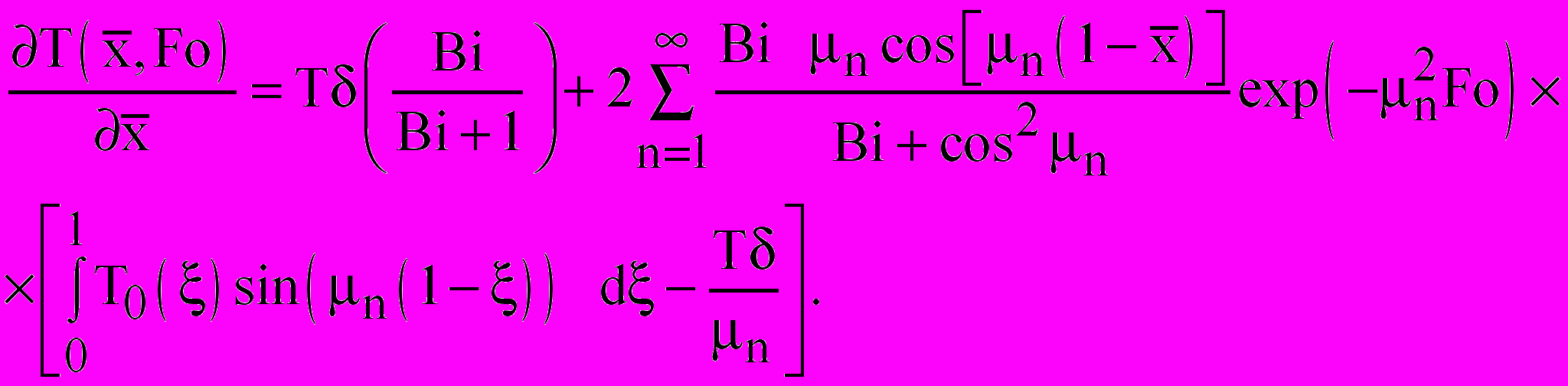 (6)
(6)- для задачи 2:
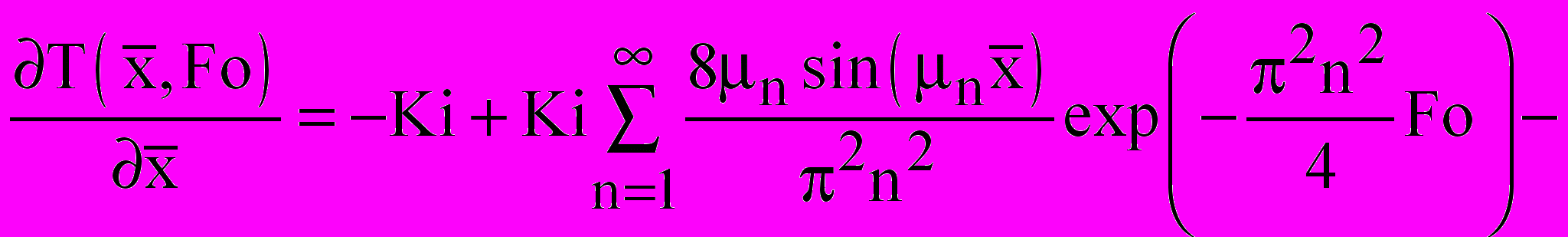
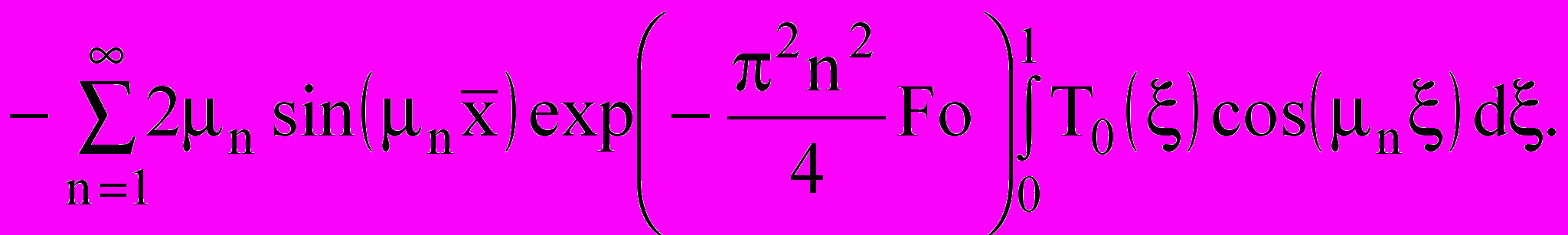 (7)
(7)- для задачи 3:
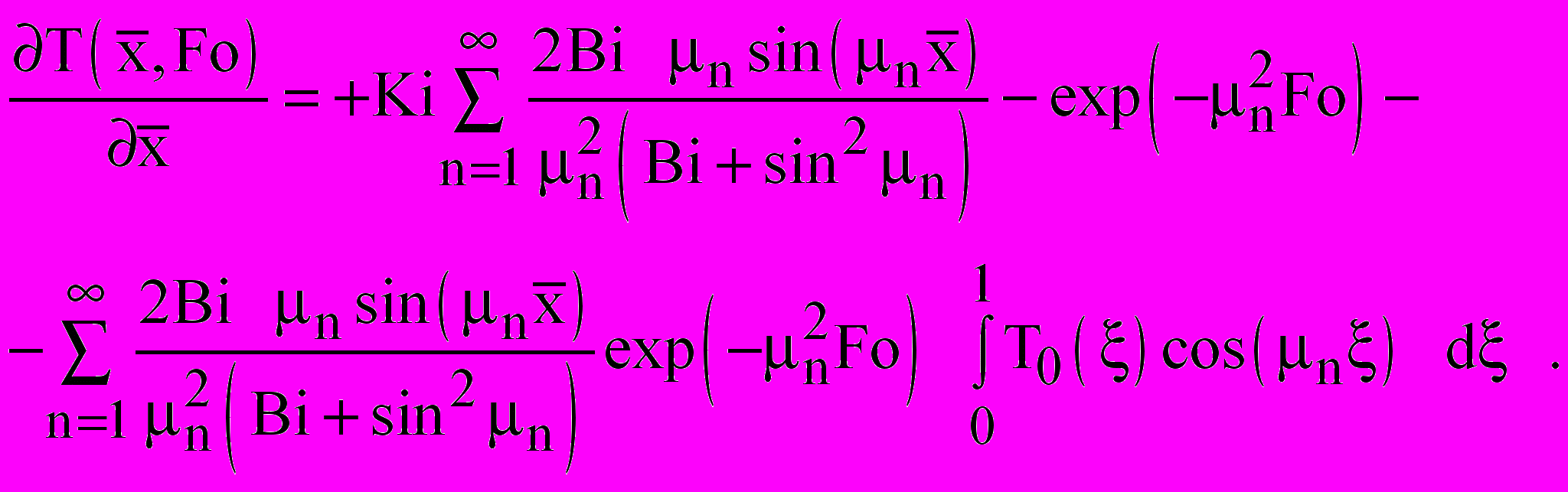 (8)
(8)Расчет температурных полей в многослойной конструкции с помощью аналитических решений (3), (4) и (5) и их сопряжений на каждом временном интервале осуществляем следующим образом: в начальный момент времени температура материалов ограждающей конструкции имеет равномерное распределение и равна t (Рис. 2а). По уравнению (3) рассчитывают поле температуры в первом слое конструкции для первого малого интервала времени (Рис. 2б). Далее определяют величину температурного градиента на границе II слоев 1 и 2 по выражению (6). В том случае, если градиент температуры (Г1) равен нулю, то по выражению (3) рассчитывают температурное поле в первом слое для следующего временного интервала. Если температурный градиент (Г1) отличен от нуля (Рис. 2в), то его величина закладывается в качестве граничного условия второго рода в задаче 2. В этом случае величина теплового потока (q2) и критерий Кирпичева (Кi) определяются путем умножения величины температурного градиента (Г1) на коэффициент теплопроводности первого слоя (1). По выражению (4) рассчитывают поле температур во втором слое (Рис. 2д). Полученное новое значение температуры второго слоя в месте контакта слоев 1 и 2 задается в качестве граничного условия первого рода в задаче 1. С новым значением граничного условия задачи 1 рассчитывают поле температур в первом слое для следующего интервала времени (Рис. 2д) и так далее, до момента, когда градиент (Г2), определяемый выражением (7), не станет отличен от нуля (Рис. 2е). Величина отличного от нуля градиента (Г2) закладывается в качестве граничного условия второго рода в задаче 3. В этом случае величина теплового потока (q3) и критерий Кi определяются путем умножения величины температурного градиента (Г2) на коэффициент теплопроводности второго слоя (2). По выражению (5) рассчитывают поле температур в третьем слое (Рис. 2ж). Полученное новое значение температуры третьего слоя на границе III в месте контакта слоев 2 и 3 задается в качестве граничного условия первого рода в задаче 2. С новым значением граничного условия первого рода в задаче 2 рассчитывается поле температур во втором слое (Рис. 2и). Полученное новое значение температуры второго слоя в месте контакта слоев 1 и 2 задается в качестве граничного условия первого рода в задаче 1. С новым значением граничного условия задачи 1 рассчитывают поле температур в первом слое для следующего интервала времени (Рис. 2к) и так далее, до момента, когда градиент (Г3), определяемый выражением (8), не станет отличен от нуля (Рис. 2л). Тогда методом последовательных приближений рассчитывается момент, когда t3=tн, именно для этого момента, в зависимости от поставленной задачи, окончательно рассчитывают все параметры многослойной ограждающей конструкции.
Не составляет особого труда распространить этот алгоритм на n-слойную конструкцию.
Теоретически весь процесс теплообмена можно разделить на три стадии.
Стадия 1. Нерегулярный режим. Тепловой режим не упорядочен и существенно зависит от начального распределения температуры. При стадии 1 необходимо исследовать ряды (3), (4) и (5) при малых значениях Fо, но именно эта стадия наиболее близко описывает реальные условия теплопередачи через ограждение, например, колебания внешних температур, включение и выключение отопительных приборов, режимы сезонной эксплуатации и т.д.
Стадия 2. Регулярный режим. Изменение температуры описывается первым членом рядов выражений (3), (4) и (5) и не зависит от начального распределения температуры. Методы стадии 2 называют методами регулярного теплового режима, они заложены в методику теплотехнического расчета по СНиП II-3-79**.
Стадия 3. Температура всех точек тела одинакова и равна температуре окружающей среды.
С теоретической точки зрения одной из сторон анализа решений вида (3), (4) и (5) является определение времени и последовательности наступления регулярного теплового режима, именно временной фактор является существенным при решении многих задач теплопередачи.
Предлагаемая математическая модель позволяет решить следующие задачи: оценить тепло-физическое состояние проектируемых конструкций при различных режимах эксплуатации и, как следствие, рационально их запроектировать под конкретный режим или диапазон режимов, подобрать соответствующие материалы слоев; рассчитать поле температур в сложных в конструктивном отношении многослойных конструкциях, например, когда расположение слоев дискретно; при замере температуры в характерных точках (на стыках слоев и поверхностях конструкции) определить тепло-физические характеристики материалов, составляющих обследуемую конструкцию; при лабораторных испытаниях существенно сократить время испытания, у исследователей появляется возможность не дожидаться установления регулярного режима, а также отказаться от климатической камеры и дорогостоящего приборного обеспечения экспериментов и исследований; при решении обратной задачи непосредственно определить сопротивление теплопередаче всей слоистой конструкции и отдельных ее слоев из неустановившегося температурного поля.
Р
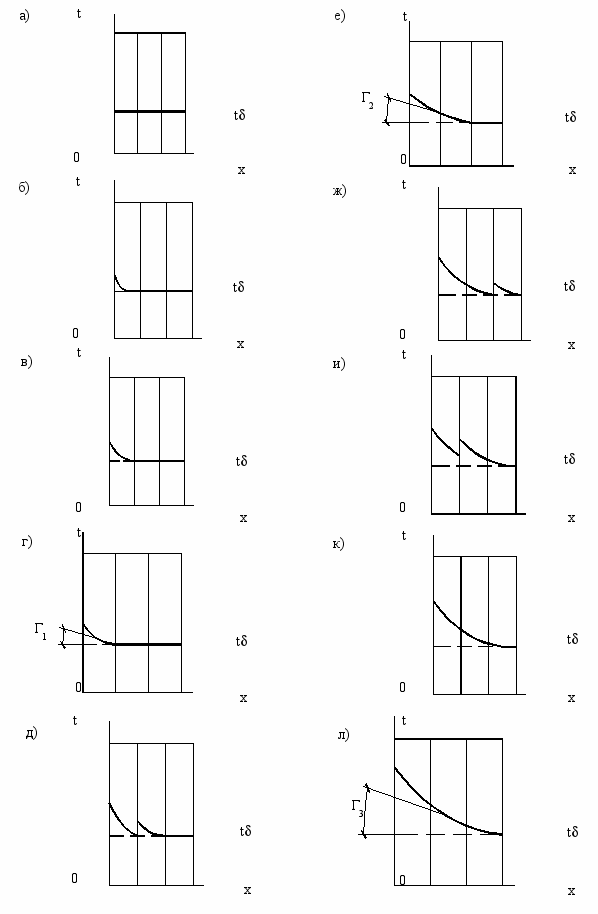
ис. 2
Критериями достоверности разработанной методики расчета явились:
- тождественность решений, полученных по методике СНиП и предлагаемой методике при =;
- отклонение расчетных данных от экспериментальных не превышает 14%;
-апробация методики при натурных исследованиях многослойной конструкции (ограждающей панели жилого дома) с последующим вскрытием тех мест конструкции, в которых методика показала отсутствие утеплителя.
Предлагаемая методика расчета реализована на персональной ЭВМ типа IBM и позволяет моделировать во времени распределение температурного поля в толще ограждающей конструкции. Некоторые примеры результатов расчета нестационарных температурных полей в теле в многослойных конструкциях приведены в ЧАСТИ II настоящей работы, а блок-схема программы в приложении.
Представление результатов счета в цифровом и графическом виде, а также возможность варьирования различных параметров задачи позволяют смоделировать практически любую ситуацию и провести ее всесторонний анализ. Достоверность полученных результатов зависит от адекватности математического моделирования кинетики процессов.
Все вышеизложенное позволяет рекомендовать разработанную математическую модель нестационарного теплопереноса в многослойной ограждающей конструкции к практическому применению.
Влажность материалов реальных строительных конструкций в различные периоды эксплуатации изменяется в широких пределах и впрямую влияет на процесс теплопереноса. Поэтому в главе 3 предложена математическая модель комбинированного метода расчета нестационарного процесса теплопереноса во влажных слоистых средах.
Ф
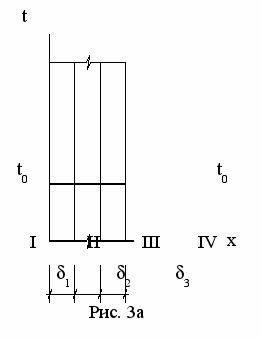 изико-математическую постановку задачи проследим на примере промерзания многослойной кирпичной кладки. Три остальных случая (оттаивание, испарение, конденсация) аналогичны по физической картине рассматриваемому примеру.
изико-математическую постановку задачи проследим на примере промерзания многослойной кирпичной кладки. Три остальных случая (оттаивание, испарение, конденсация) аналогичны по физической картине рассматриваемому примеру.Физическая картина процесса может быть представлена следующим образом (Рис. 3а): многослойная (для простоты рассматривается трехслойная) стенка находится в стационарном (талом) состоянии, вся влага в конструкции находится в виде пара и жидкости, распределение температур по слоям имеет вид:
t1(x,0) = t0; t2(x,0) = t0; t3(x,0) = t0.
Слева от конструкции располагается помещение, поверхность I омывается воз-духом внутренней (в) среды, справа от конструкции располагается наружная (н) среда. Теплообмен на поверхности I и IV происходит по закону Ньютона. В момент времени =0 температура наружной среды внезапно понижается ниже температуры замерзания влаги в материале. В слое 3 начинает образовываться зона промер-зания, правая граница которой совпад
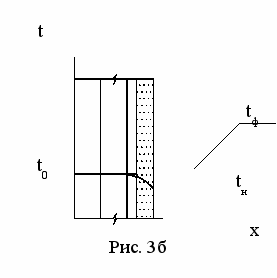 ает с плоскостью IV, а левой является изотер-мическая плоскость фронт промерзания с температурой tф =0С, т.е. равной темпера-туре замерзания влаги на открытом воздухе. При этом, второй и первый слои остаются с температурой t0 (см. Рис. 3б). С течением времени фронт начинает прод-вигаться в глубь слоя 3. Температура спра-ва начинает понижаться и в определенный момент времени достигает температуры tпзв - равной температуре полного замерза-ния влаги в матер
ает с плоскостью IV, а левой является изотер-мическая плоскость фронт промерзания с температурой tф =0С, т.е. равной темпера-туре замерзания влаги на открытом воздухе. При этом, второй и первый слои остаются с температурой t0 (см. Рис. 3б). С течением времени фронт начинает прод-вигаться в глубь слоя 3. Температура спра-ва начинает понижаться и в определенный момент времени достигает температуры tпзв - равной температуре полного замерза-ния влаги в матер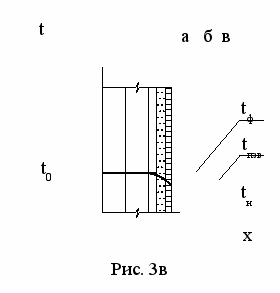 иале, которая определяется опытным путем для каждого конкретного материала. Согласно учению П.А. Ребиндера влага в материале может находиться в пяти видах: химически связанная вода, адсорбционно связанная вода, капиллярно связанная вода, осмотически связанная вода и свободная вода, удерживаемая в дисперсной структуре, захваченная телом механически. Температура tф соответствует температуре замерзания свободной воды, а температура tпзв может быть принята равной температуре замерзания осмотически связанной или капиллярно связанной воды, так как для большинства строительных материалов именно эти два вида влаги - адсорбционная и капиллярная являются основными. Таким образом, в слое 3 образуется три зоны (см. Рис. 3в):
иале, которая определяется опытным путем для каждого конкретного материала. Согласно учению П.А. Ребиндера влага в материале может находиться в пяти видах: химически связанная вода, адсорбционно связанная вода, капиллярно связанная вода, осмотически связанная вода и свободная вода, удерживаемая в дисперсной структуре, захваченная телом механически. Температура tф соответствует температуре замерзания свободной воды, а температура tпзв может быть принята равной температуре замерзания осмотически связанной или капиллярно связанной воды, так как для большинства строительных материалов именно эти два вида влаги - адсорбционная и капиллярная являются основными. Таким образом, в слое 3 образуется три зоны (см. Рис. 3в):(а) - талая зона, левая плоскость ее ограничена плоскостью III (плоскость физического контакта слоев 2 и 3), а правая - фронтом промерзания - изотермической плоскостью с температурой равной tф;
(б) - зона промерзания, левая, ограничивающая ее плоскость, совпадает с изотермической плоскостью фронта промерзания tф, а правая плоскость зоны ограничена изотермической плоскостью с температурой равной tпзв;
(в) - мерзлая зона, левая плоскость зоны имеет температуру tпзв, а правая совпадает с плоскостью IV, разграничивающую физическую поверхность конструкции (слой 3) с наружной средой.
В каждой зоне (а), (б) и (в) будет свой коэффициент теплопроводности: а3; б3; в3 соответственно. Индекс (3) номер слоя.
При достижении фронтом промерзания физической границы III сопряжения слоев в процесс промерзания начнет вовлекаться слой 2 и в расчете необходимо будет учитывать а2; б2. И так далее. Всего возможны двадцать четыре характерных случая взаимного расположения физических границ I...IV и изотермических плоскостей с температурами tф и tпзв.
В зоне промерзания происходят фазовые превращения влаги, не вся влага одновременно превращается в лед при температуре 0С, а происходит постепенное ее замерзание по мере снижения температуры. Температура на левой границе этой зоны равна температуре фронта промерзания tф=0С, а на правой границе некоторой температуре полного замораживания влаги tпзв в материале. Температура tпзв различна для различных материалов и, согласно современным исследованиям может достигать минус 70...90С для адсорбционной влаги, которая наиболее связана с материалом. Современные представления насчитывают до девяти видов льда. В мерзлой зоне вся влага или большая ее часть находится в виде льда. Ее правая граница определяется наружной поверхностью слоя 3 и соответствующей температурой среды tн, а левая температурой tпзв.
Для решения задачи в зоне промерзания и определения скорости продвижения фронта промерзания в тело слоя первоначально получим решение краевой задачи теплопроводности с фиксированными границами и условиями первого рода на этих границах. Поместим начало координат на стыке мерзлой зоны и зоны промерзания. Математически запись этой краевой задачи может быть представлена следующей системой уравнений:
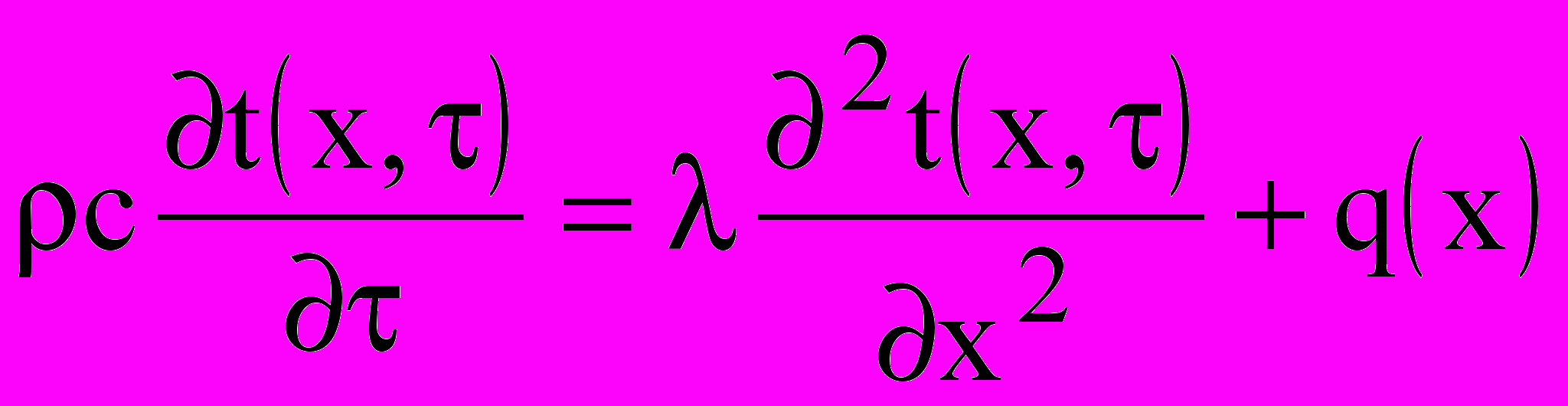 ,
, 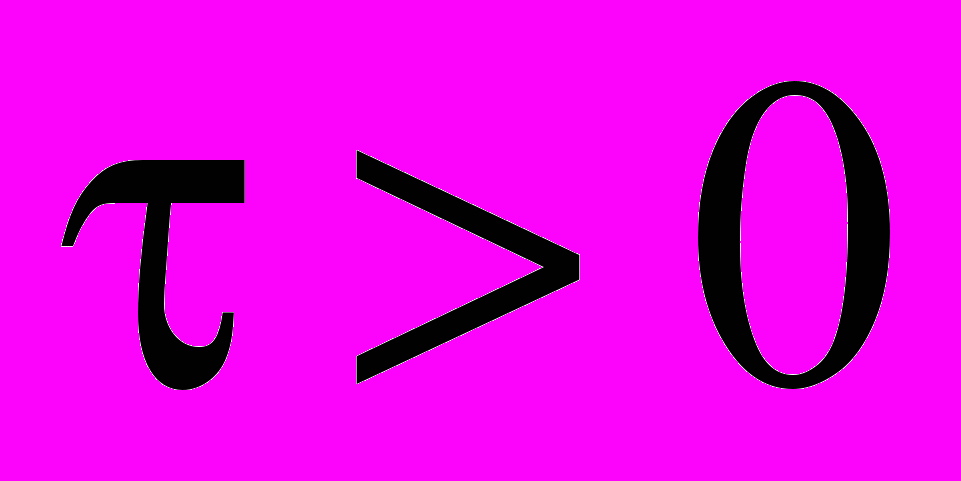 ,
, 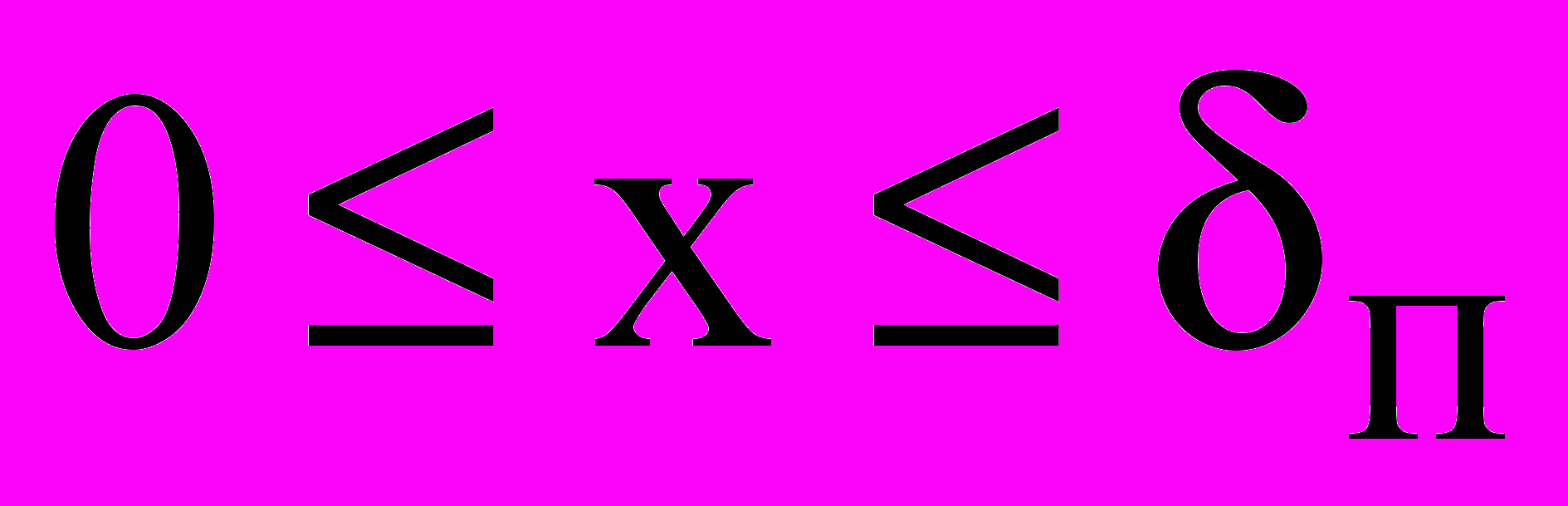 ; (9)
; (9)t(x,0)=t0(x); (10)
t(0,)=tпзв; (11)
t(п,)=tф, (12)
здесь: q(x) - мощность объемного источника тепла, возникающего в зоне промерзания при превращении жидкости в лед (теплота льдообразования), при условии пренебрежения облимацией. Значение q(x) максимально у изотермической плоскости tпзв и минимально у фронта промерзания tф. Функция, в первом приближении, может быть линейна или иметь гиперболический характер распределения.
Решение краевой задачи (9)...(12) имеет вид:
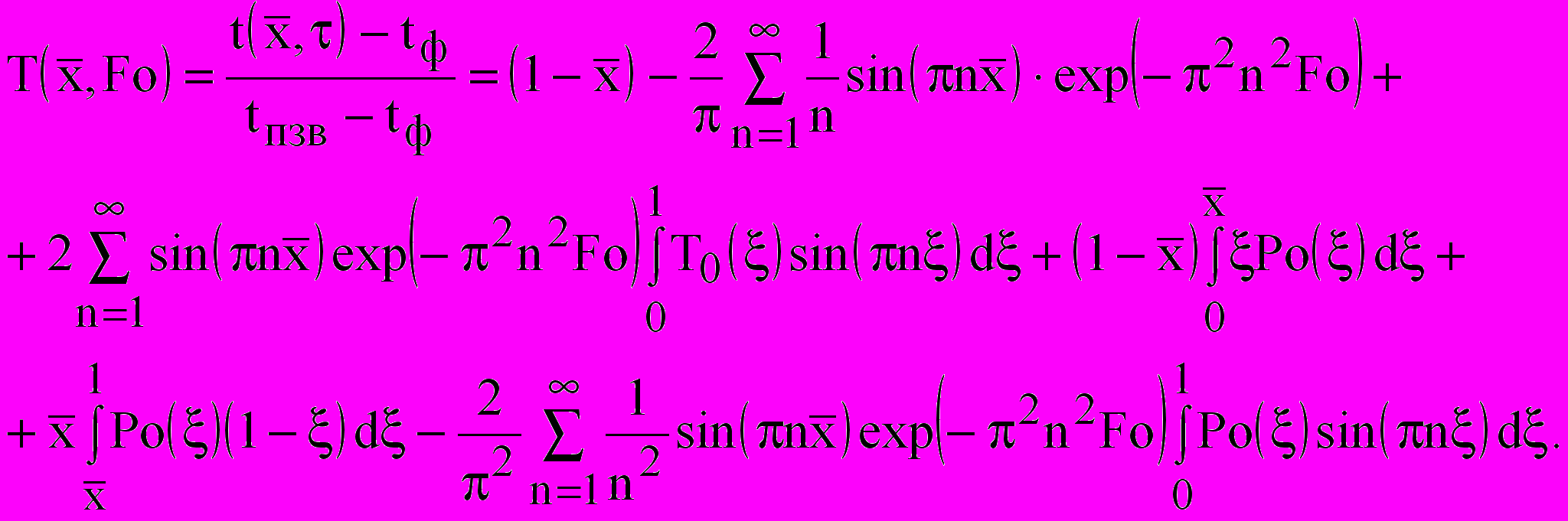 (13)
(13)Если для упрощения принять, что в зоне промерзания лед образуется по всей толщине зоны с одинаковой интенсивностью, т.е. источник льдообразования имеет равномерное распределение, то получаем частный, но очень важный случай. Этот случай можно принять в качестве первого приближения для оценки скорости промерзания. Решение (13) упрощается и принимает вид:
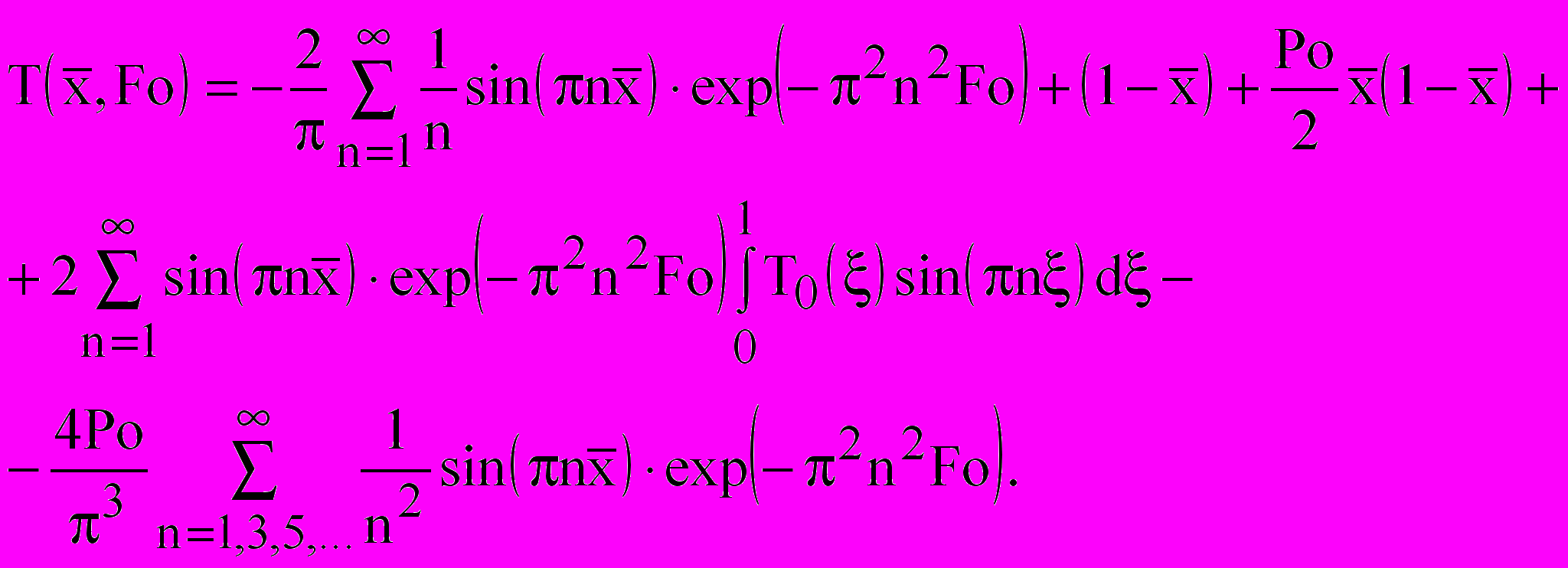 (14)
(14)Решение для малых временных интервалов (Fo<0,1) имеет вид:
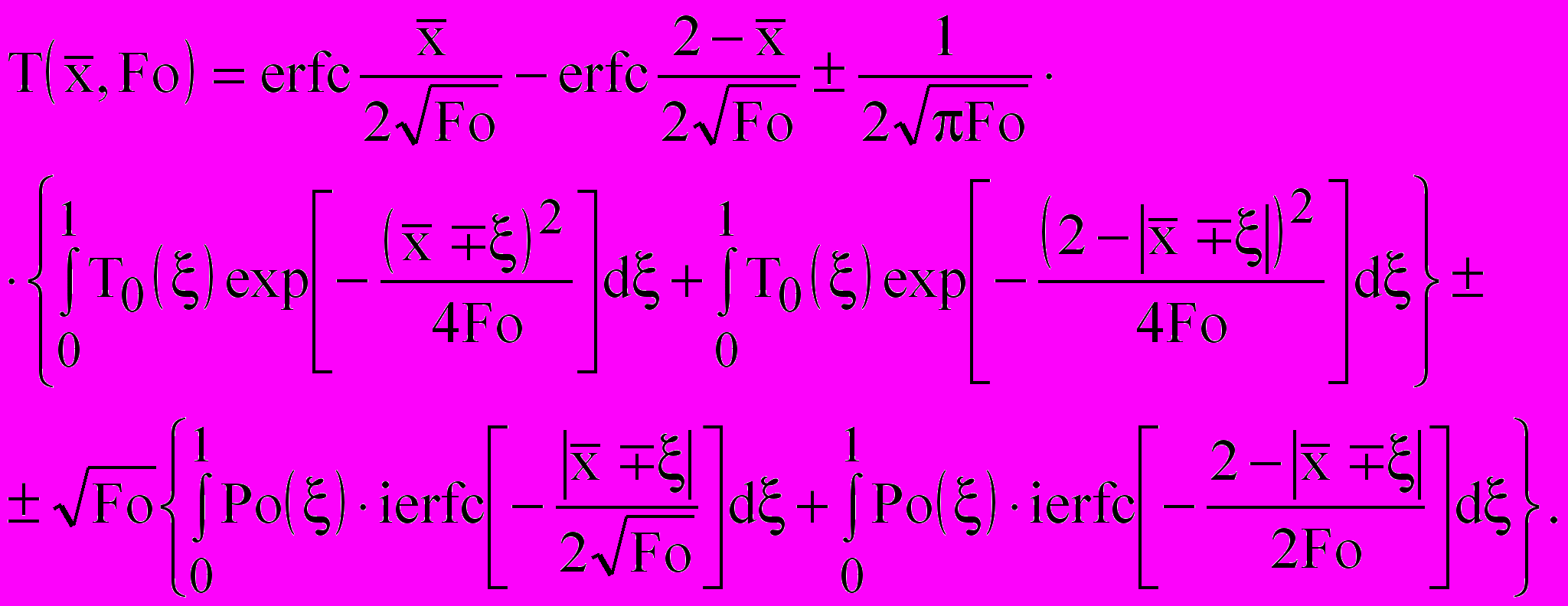 (15)
(15)В мерзлой зоне к ее внешней (правой) поверхности подается холодный воздух, левая граница определяется температурой tпзв и с течением времени продвигается в тело ограждения вслед за зоной замораживания (б). Анализ кинетики процесса приводит к необходимости постановки и решению краевой задачи теплопереноса с неравномерным начальным распределением температур и источника теплоты.
Граничные условия для рассматриваемой задачи сформулируются следующим образом:
- на границе мерзлой зоны и зоны промерзания температура равна tпвз, т.е. условие первого рода;
- на внешней поверхности мерзлой зоны постоянство теплового потока от атмосферного воздуха к поверхности слоя, т.е. условие второго рода. Постановка такого условия возможна только при расчете комбинированным методом, идея которого представлена выше, т.е., когда в условиях i-го микропроцесса можно считать, что не изменяются теплофизические свойства материала и границы зон. Тогда для i-го микропроцесса теплопереноса в мерзлой зоне математическая запись краевой задачи примет вид:
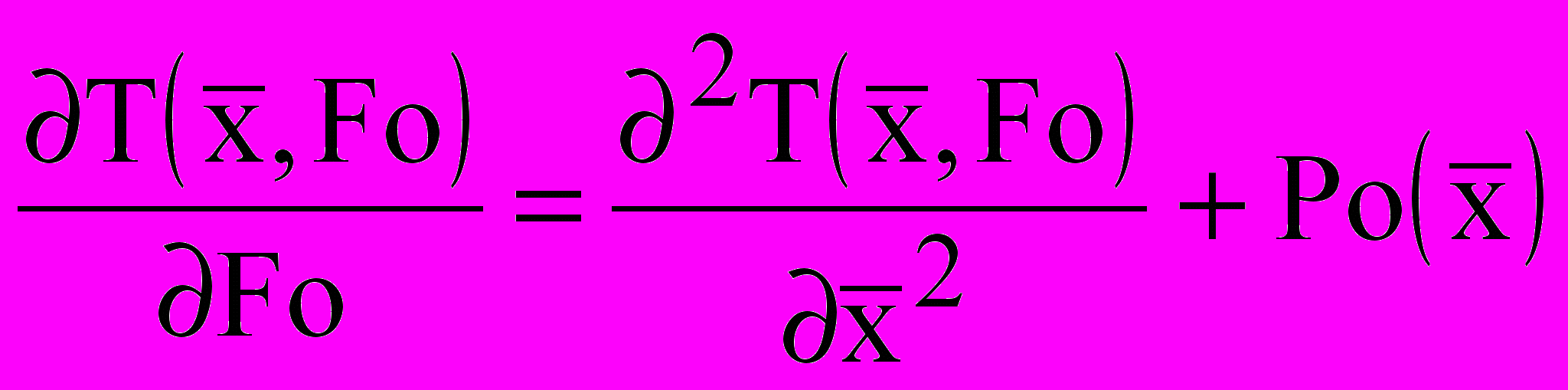 ,
, 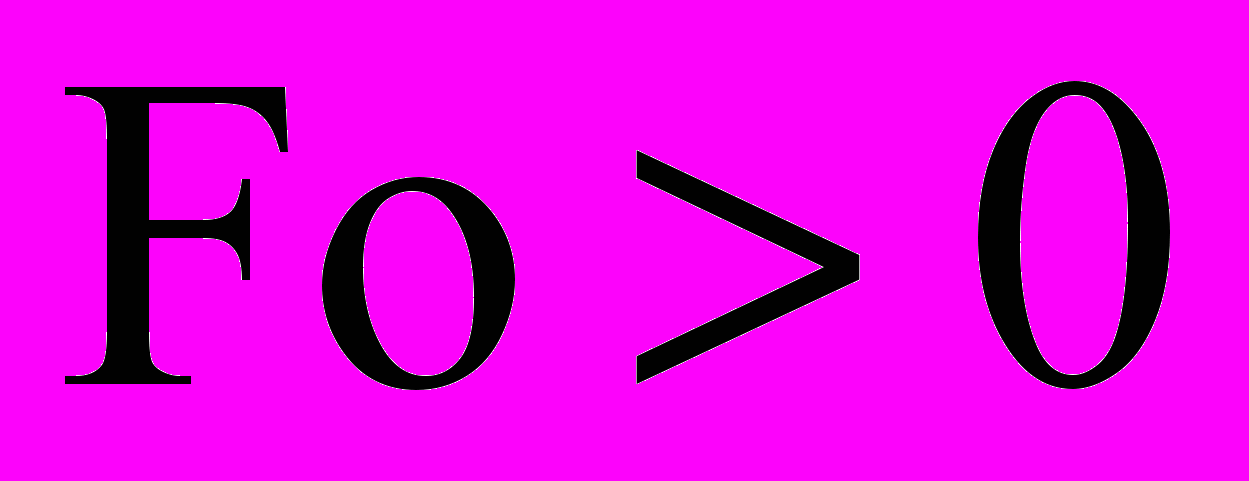 ,
, 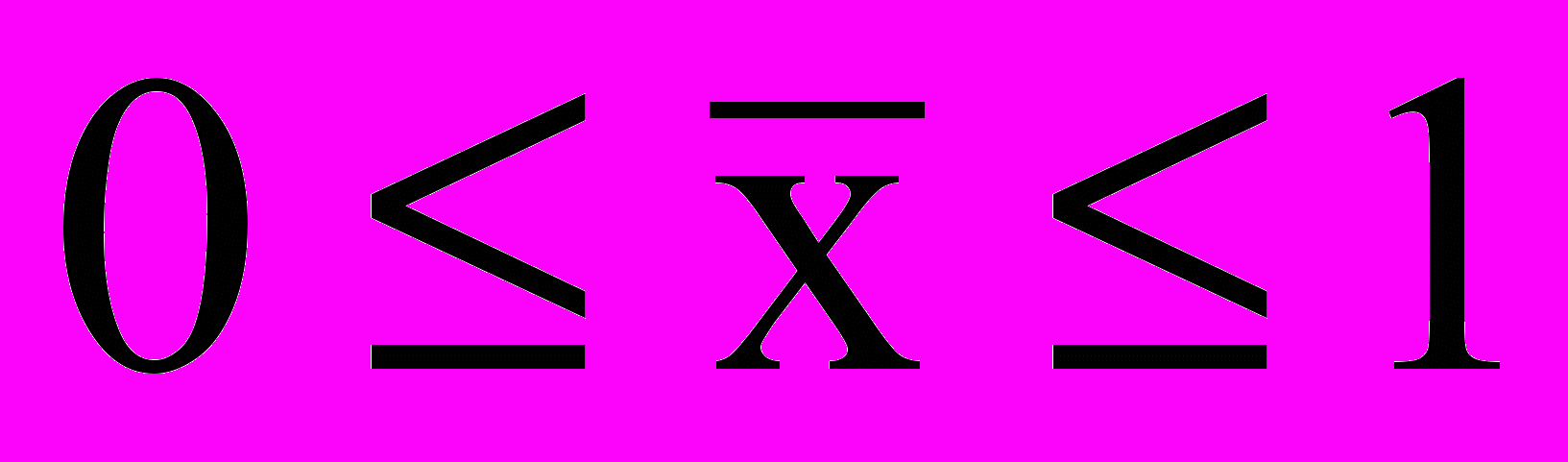 ; (16)
; (16)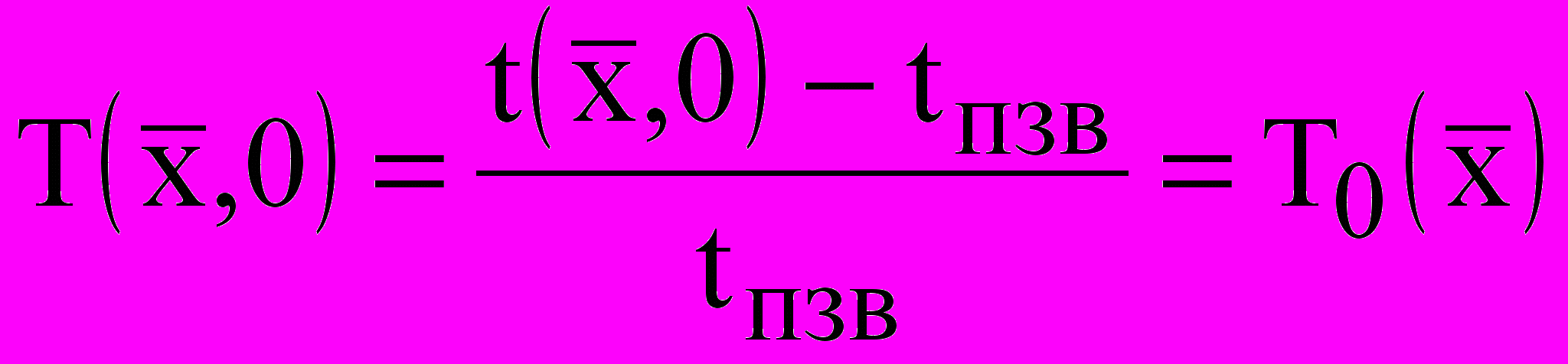 ; (17)
; (17)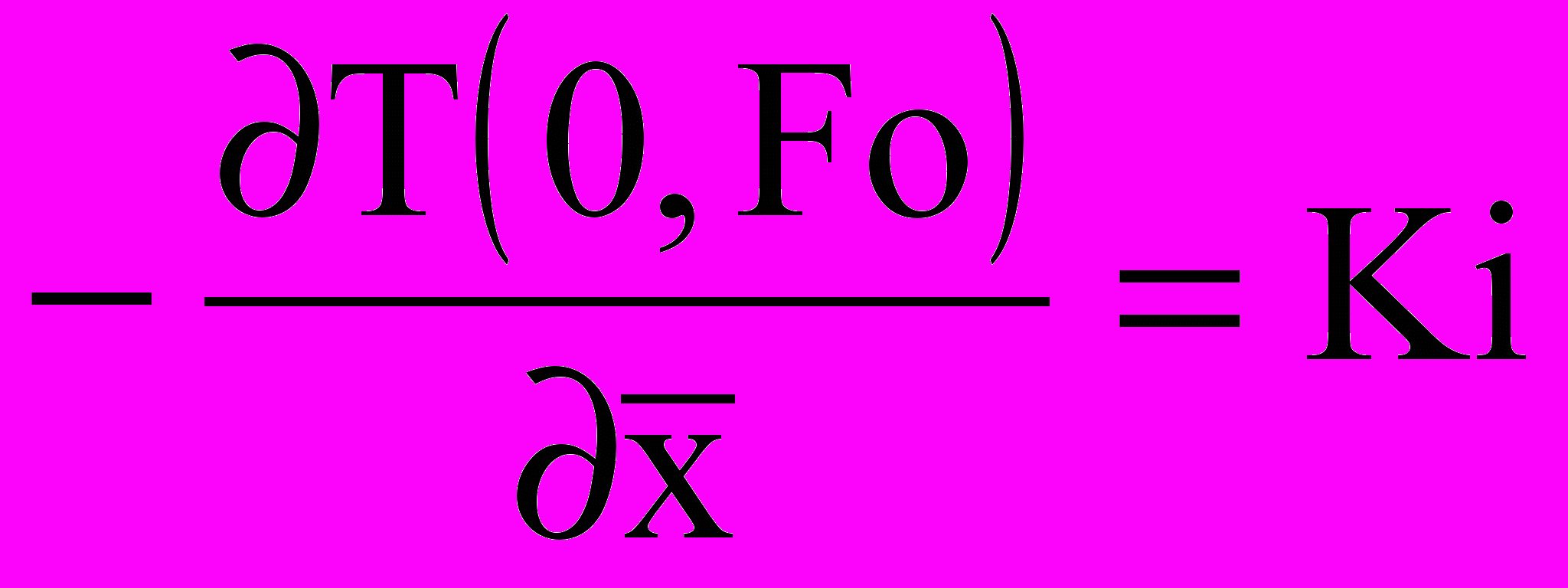 ; (18)
; (18)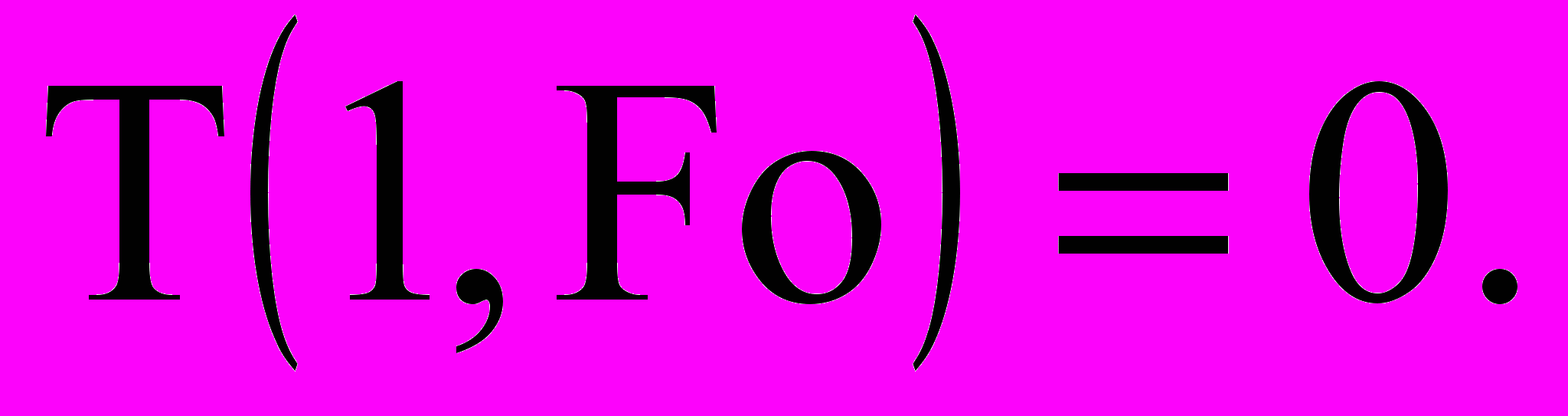 (19)
(19)В (16)...(19) приняты обозначения:
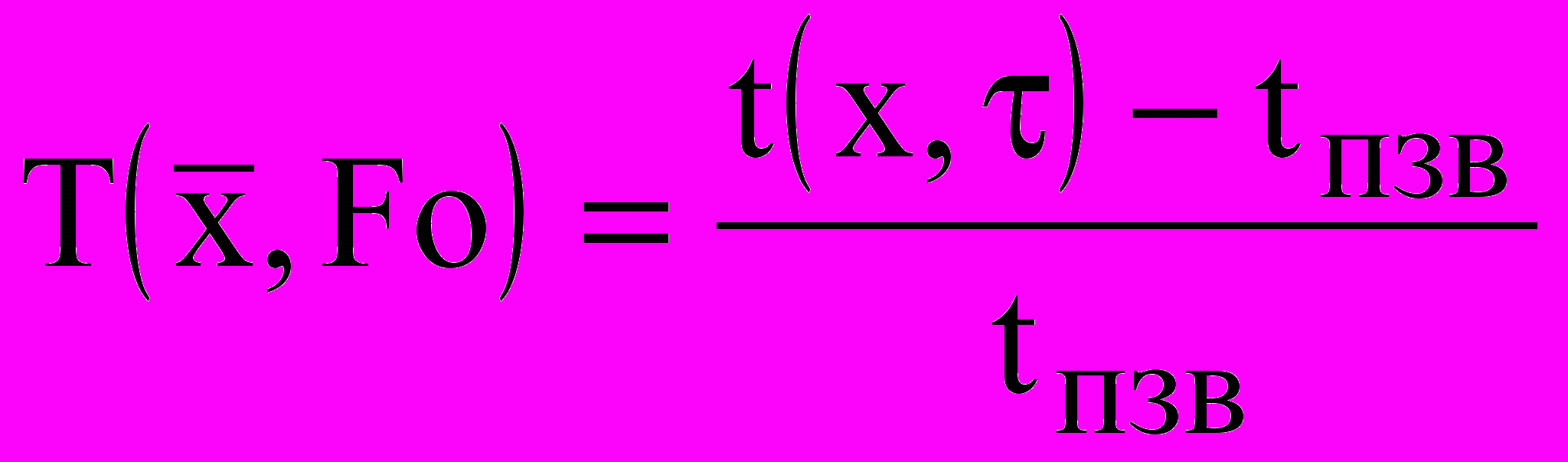 ;
; 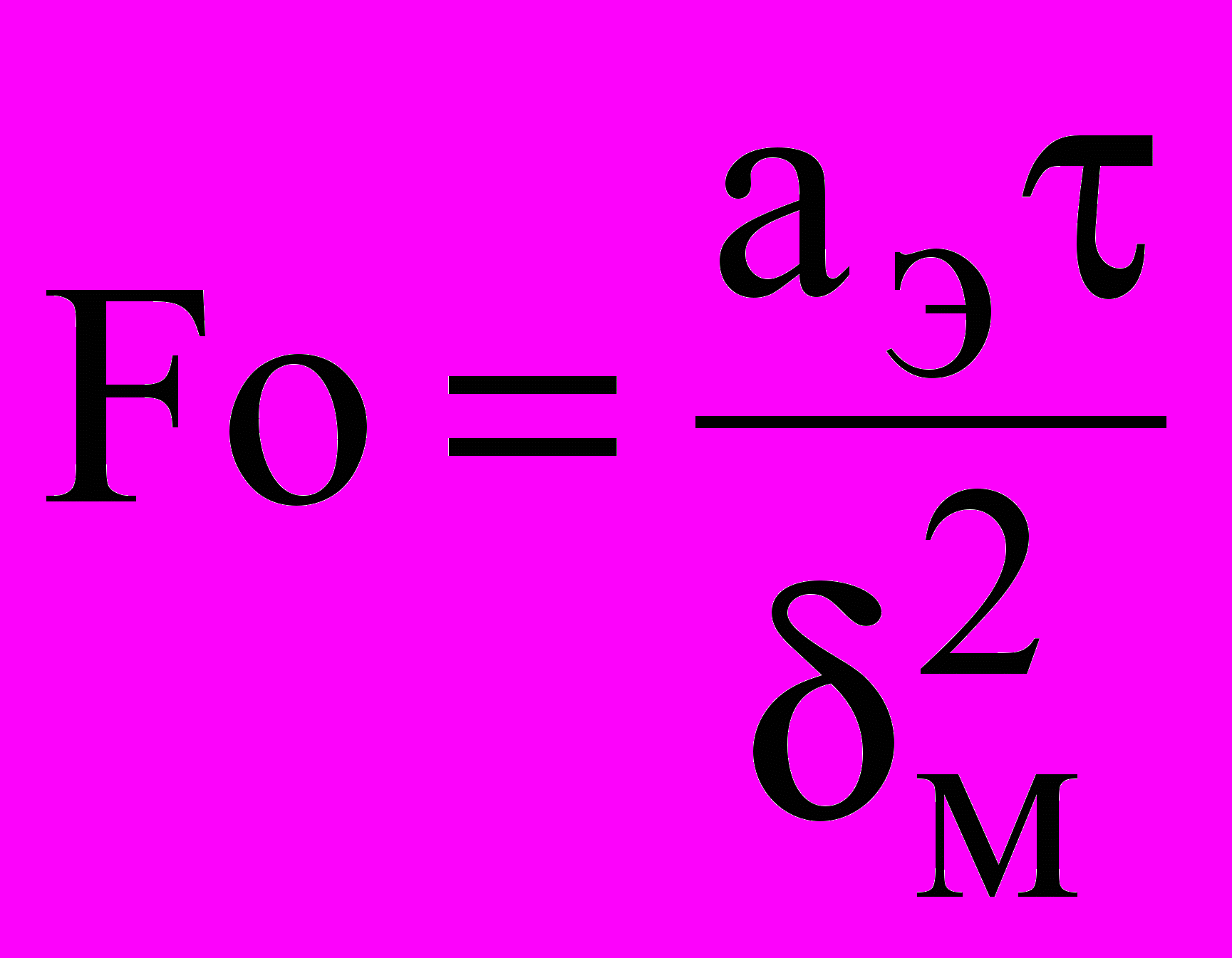 ;
; 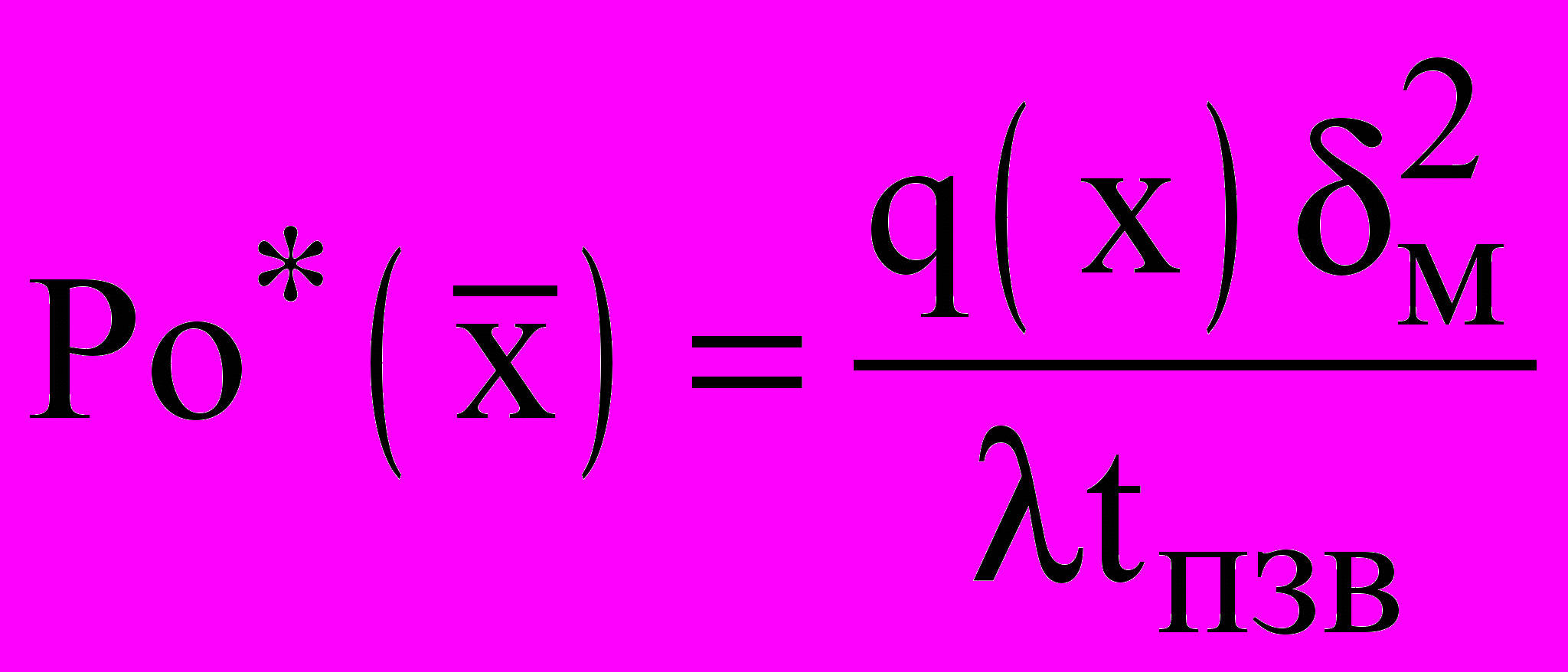 ;
; 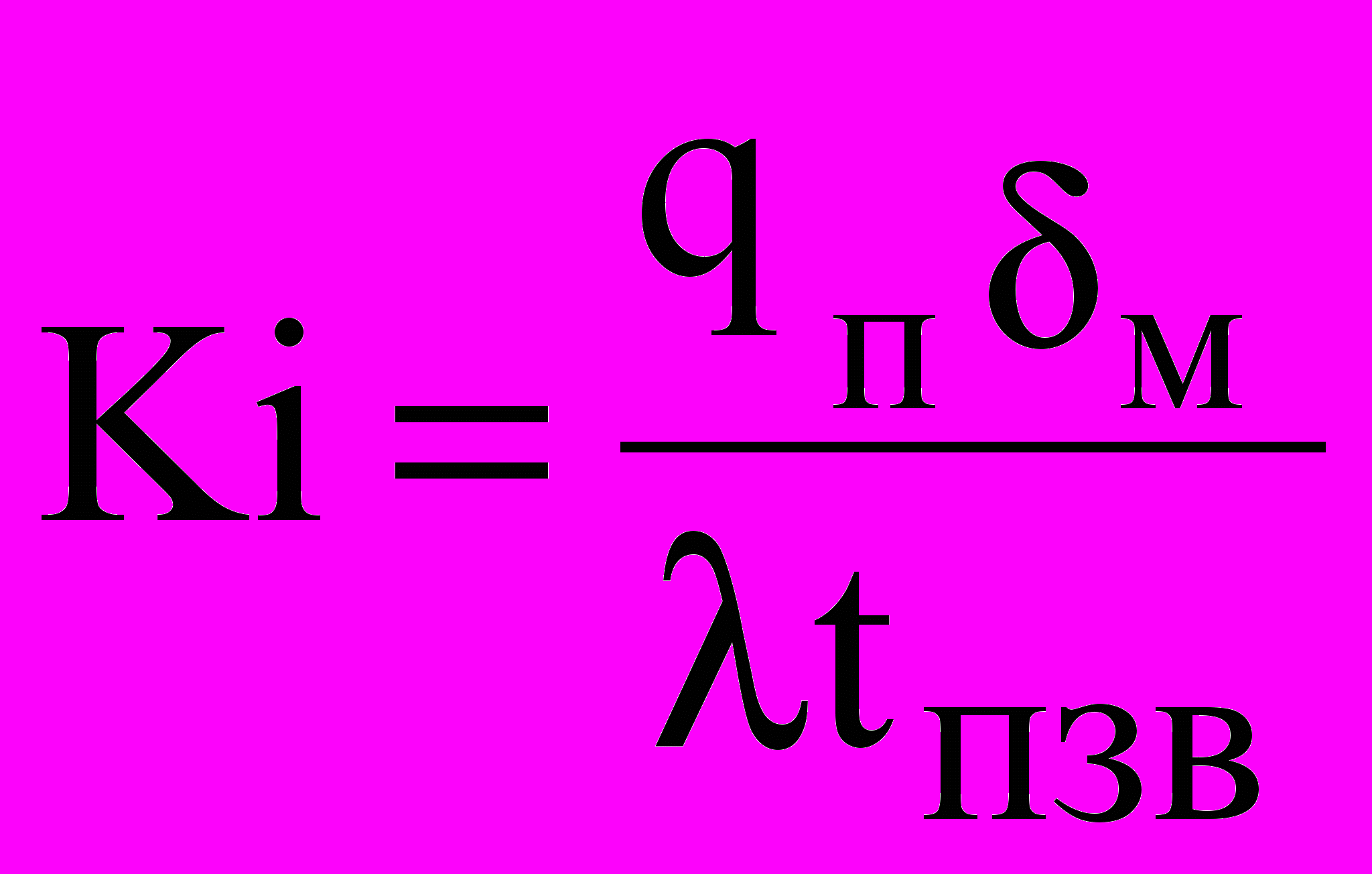 , (20)
, (20)здесь м - толщина мерзлой зоны, qп - плотность потока теплоты от газа к поверхности ограждения (Втм-2).
Решение рассматриваемой краевой задачи для мерзлой зоны имеет вид:
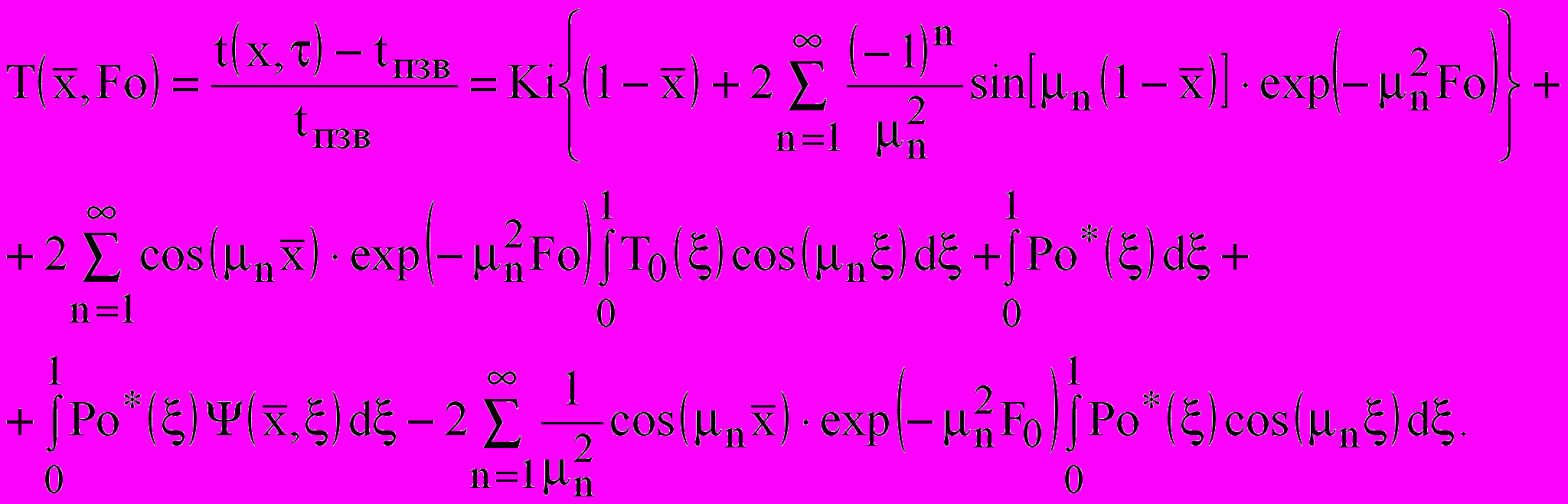
(21)
Для равномерно распределенного по толщине зоны источника выражение (21) принимает вид:
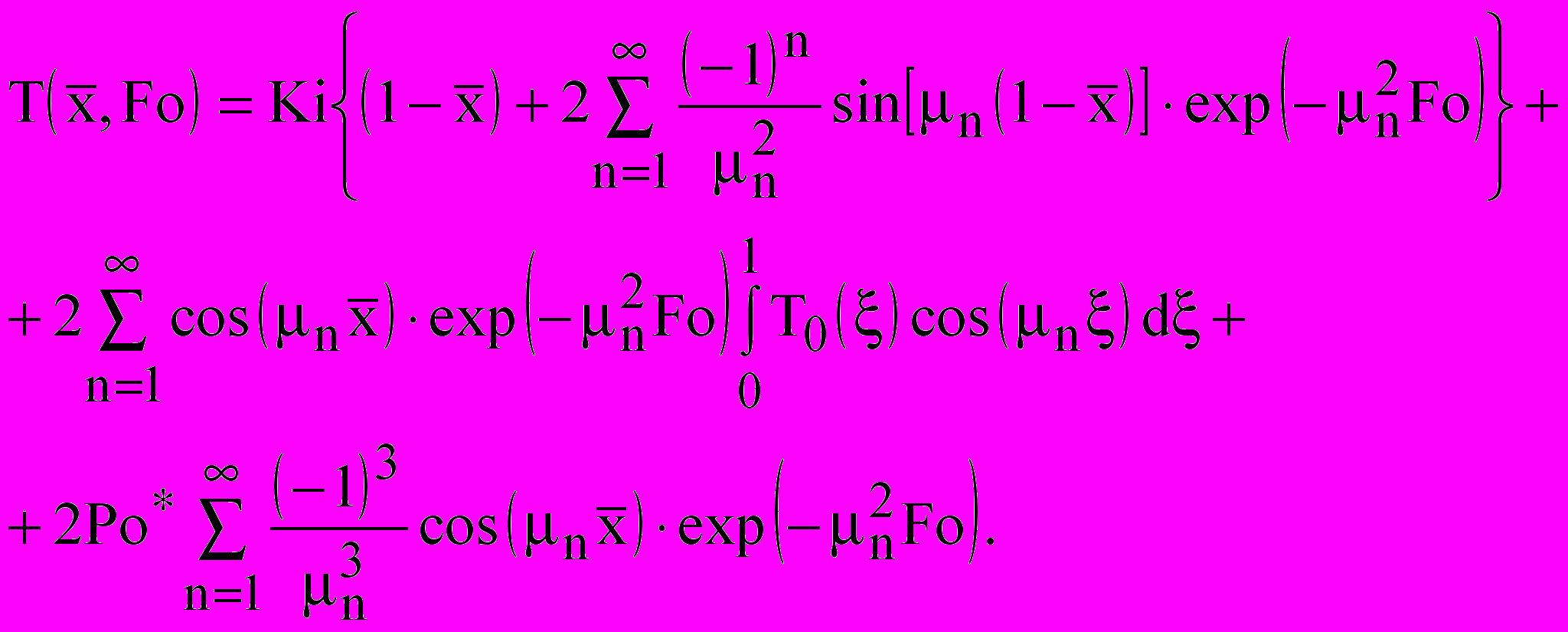 (22)
(22)Приближенное решение для малых чисел Фурье, полученное по аналогии с предыдущей задачей, будет иметь вид:
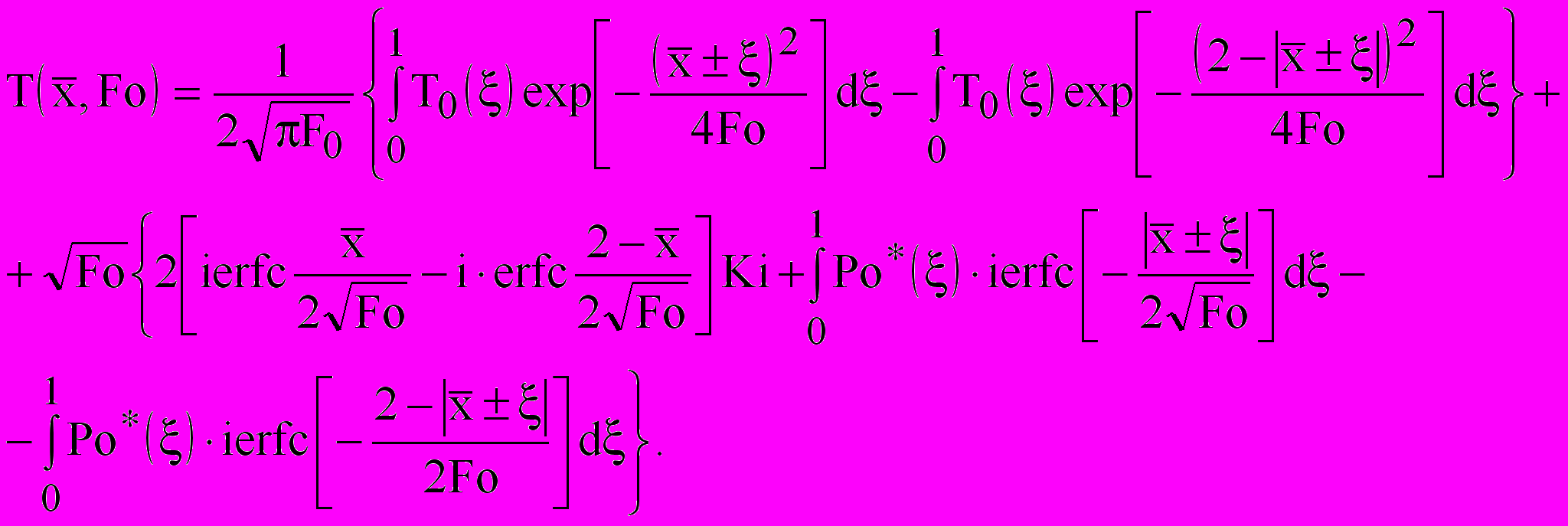
(23)
Если в выражениях (13), (14), (15), (21), (22) и (23) положить
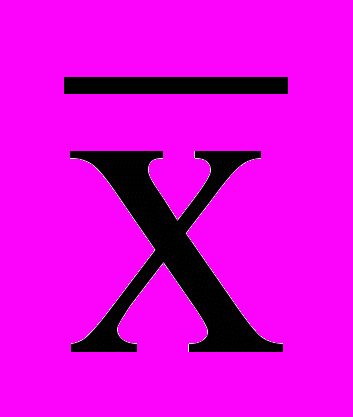 =1 и решить их относительно , то можно определить время промерзания слоя (в зоне промерзания и мерзлой зоне).
=1 и решить их относительно , то можно определить время промерзания слоя (в зоне промерзания и мерзлой зоне).Особый интерес инженеров-проектировщиков и эксплуатационников вызывает необходимость определения скорости промерзания, т.е. скорости продвижения фронтов в тело конструкции. Для определения этих скоростей воспользуемся подходом П.Г. Романкова и В.Ф. Фролова. Эффект переноса массы (в нашем случае промерзания) вследствие неоднородности температурного поля несомненно носит градиентный характер, поэтому возможно использование уравнения Фика:
j=-D gradC, (24)
где коэффициент D имеет смысл суммарной массопроводности реального капиллярно-пористого материала, С - массосодержание рассматриваемого компонента (вода, лед) в порах материала. Дифференциальное уравнение для определения координаты () фронта фазового превращения внутри слоя имеет вид:
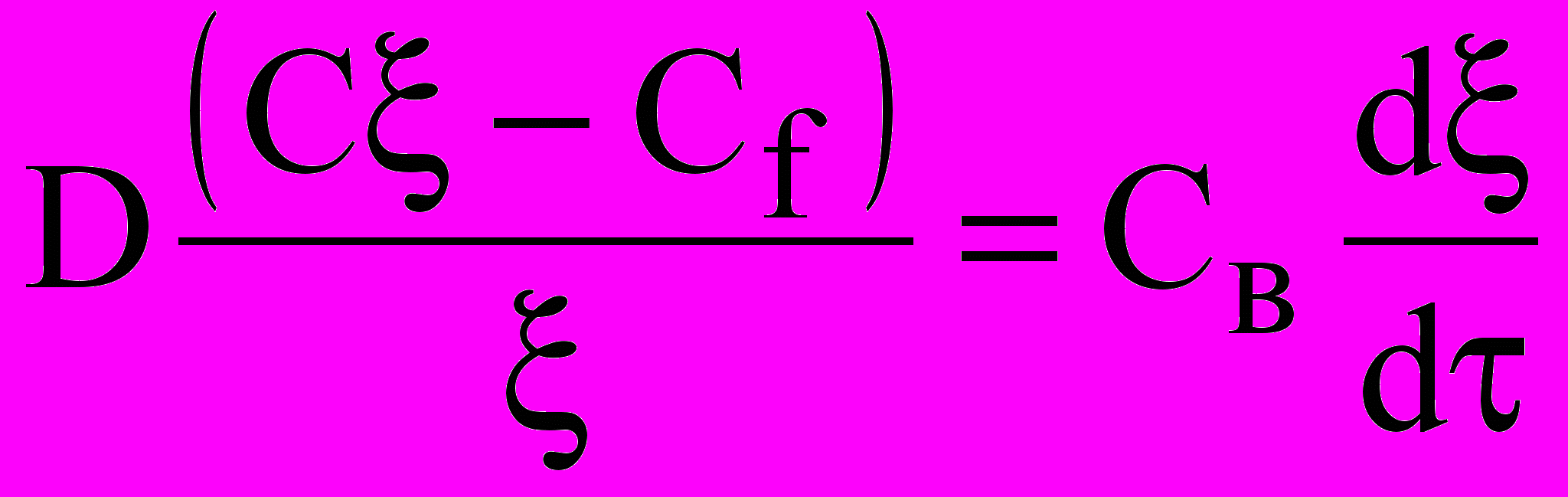 . (25)
. (25)где Сf = сonst - концентрация льда в порах материала при отрицательной температуре воздуха на поверхности слоя, С - концентрация льда в порах на фронте фазового превращения воды в лед, Св - концентрация влаги в порах материала слоя в талой зоне.
Анализ выражения (25) позволяет сделать вывод о замедлении с течением времени скорости процесса промерзания конструкции, что соответствует реальной физике процесса.
Задача еще более усложняется, если в многослойной конструкции присутствует утеплитель, практически не содержащий в своем объеме влагу (например, пенополистирол) или слой пароизоляции. Решение для такого слоя получено в главе 2 настоящей работы, его необходимо состыковать с полученными.
Выражения (13), (14), (15), (21), (22) и (23) пригодны для решения широкого класса задач, так как процесс промерзания конструкции может быть с успехом заменен на процесс оттаивания промерзшей конструкции. В этом случае зона промерзания заменяется на зону конденсации, а место мерзлой зоны займет зона сушки. Однако необходимо иметь в виду, что процесс оттаивания мерзлой ограждающей конструкции должен протекать за более короткое время, чем процесс промерзания, так как оттаивание в реальных условиях происходит с обеих сторон мерзлой зоны. Особенностью постановки задач промораживания талой конструкции и оттаивания мерзлой конструкции является то, что эти два процесса рассматриваются в отдельности и в течение процесса температура среды (внутренней для промерзания и наружной для оттаивания) остаются фиксированными. На самом деле эти процессы происходят одновременно: внутри включаются отопительные приборы, снаружи температура падает ниже нуля. Фронты движутся навстречу друг другу и стыкуются между собой через определенный промежуток времени, который определяется условиями на поверхностях ограждения. Особенность решения такой задачи состоит в выборе первоначальной температуры ограждающей конструкции и температуры стыковки решений задач промерзания и оттаивания. Решение такой задачи совершенно четко позволяет ответить на вопросы, тесно связанные с рациональным проектированием ограждения: где зона конденсации влаги в теле многослойного ограждения; какой применить утеплитель и где рационально его разместить; какие конструктивные мероприятия необходимо предусмотреть для удаления влаги из конструкции; каким должен быть температурно-влажностный режим помещения для нормальной эксплуатации ограждающей конструкции; какова долговечность конструкции с точки зрения морозостойкости материалов ее составляющих, и так далее. С помощью полученных решений вполне адекватно можно смоделировать и описать процесс аварии теплоцентрали или водовода и условие проникновения влаги в ограждающую конструкцию.
В главе 4 рассматривается математическая модель нестационарного теплопереноса в многослойной железобетонной ограждающей конструкции при тепловлажностной обработке с учетом наличия в слоях бетона объемного источника тепла (гидратация цемента), изменяющегося по толщине конструкции и во времени.
Глава содержит аналитические решения краевых задач, как для отдельных слоев, так и для многослойной конструкции в целом.
При моделировании было учтено, что изделие формуется “лицом” вниз как это показано на рисунке 4.
При горизонтальном расположении изделия на поверхность слоя 4 подается постоянный тепловой поток к границе IV, который обусловлен технологическими параметрами пропарочных камер. Исследованиями установлено, что на границах III и II температура не должна превышать температуры деструктивного разрушения утеплителя. В слоях 2 и 4 происходит реакция гидратации цемента с выделением тепла. На границах I и IV постоянство теплового потока и условие II рода, а на границах II и III постоянная температура, т.е. условие I рода.
Тепловой поток из слоя 4 не может проникнуть через утеплитель к слою 2 и наоборот.
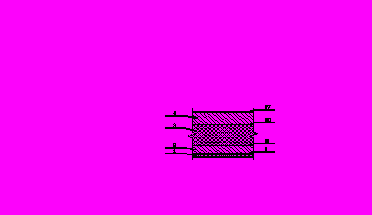
Рис. 4 Фрагмент вертикального разреза по конструкции и опалубке:
1 – дно металлической опалубки; 2 – лицевой слой бетона; 3 – слой пенополистирола; 4 – внутренний слой бетона.
Общая задача для трехслойной конструкции разобьется на три:
Задача 1. (рис. 5)
Т
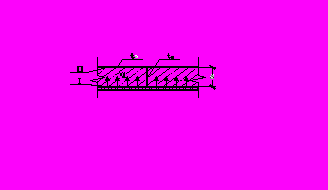
Рис. 5 Расчетная схема лицевого слоя
бетона панели
еплоперенос в слое 2 конст-рукции с граничными условиями на границе I – второго рода, и гра-ничными условиями первого рода на границе II, где максимум темпе-ратуры ограничен температурой деструктивного разложения утеп-лителя (пенополистирола).
Предположим, что начальная температура слоя одинакова по всей толщине (рис. 5).
Граничные условия:
- граница I:
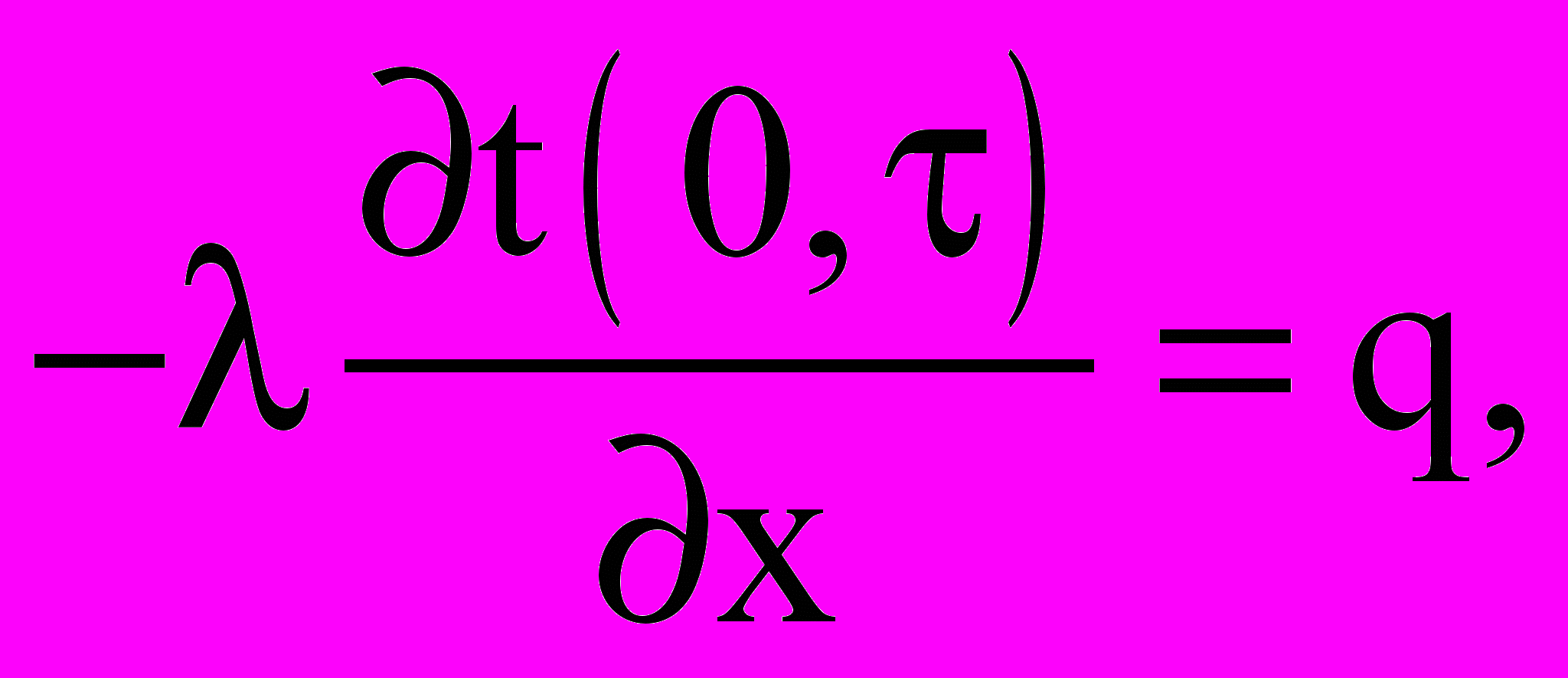 (26)
(26)где
 - теплопоток, действующий на границу I.
- теплопоток, действующий на границу I.- граница II:
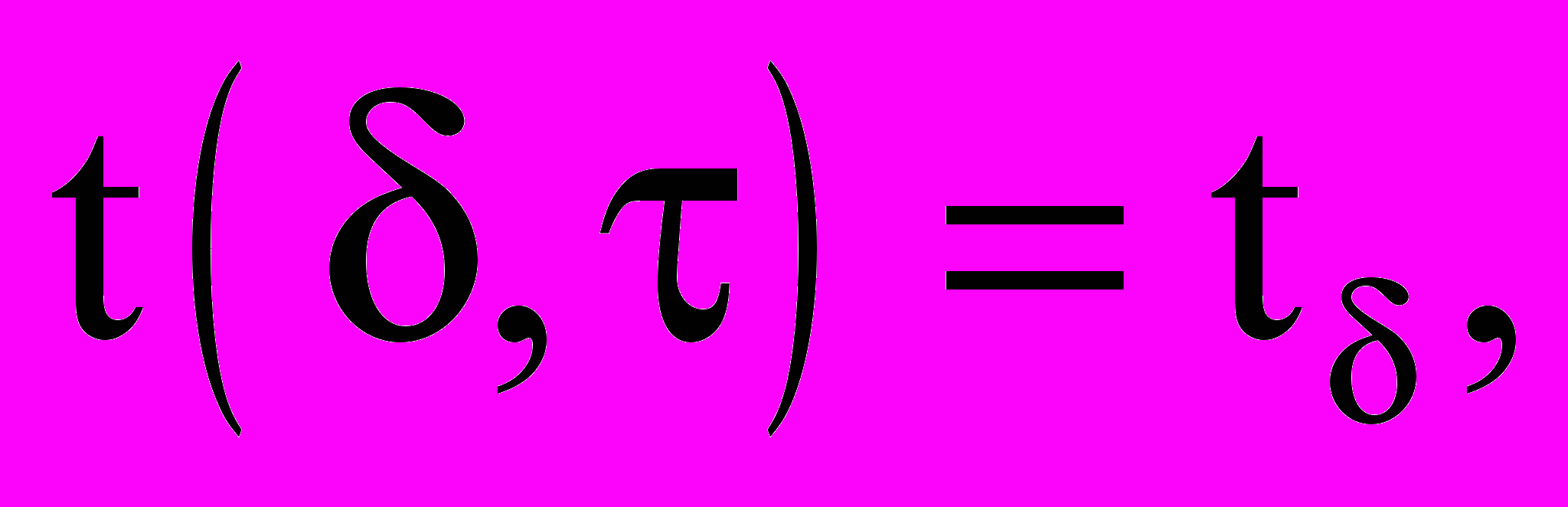 (27)
(27)где
 - температура на границе II.
- температура на границе II.Начальные условия:
Для начала расчетов принимается
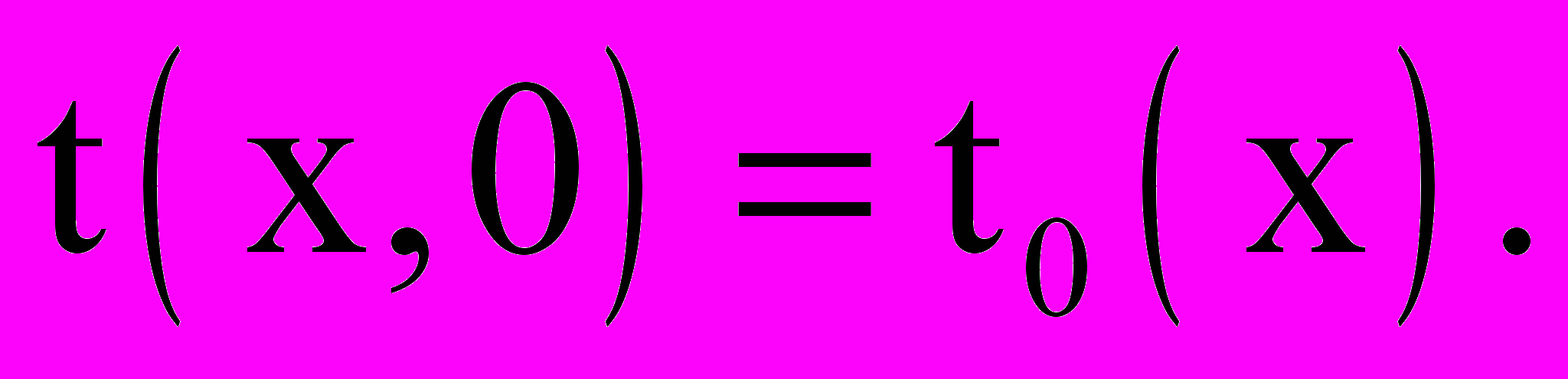 (28)
(28)Уравнение теплопроводности:
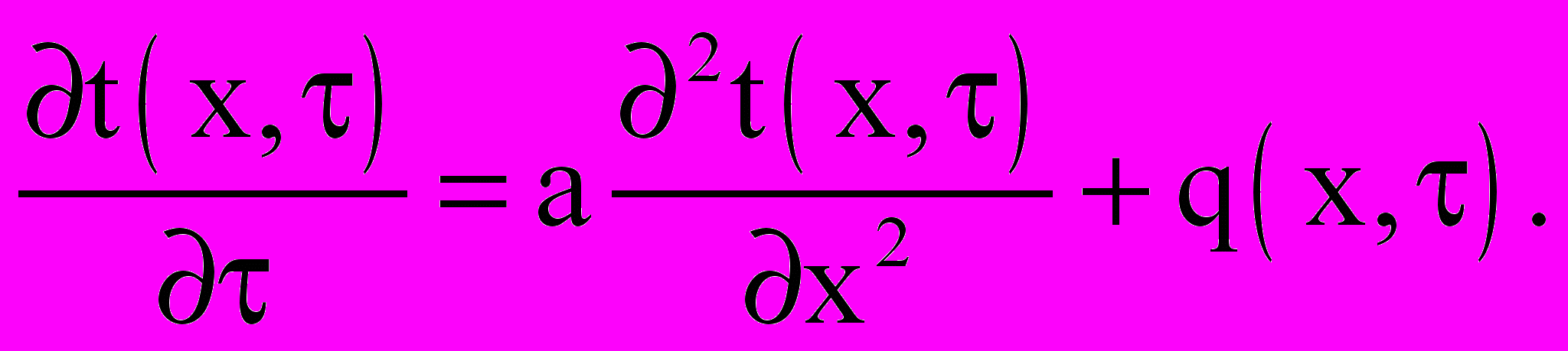 (29)
(29)где
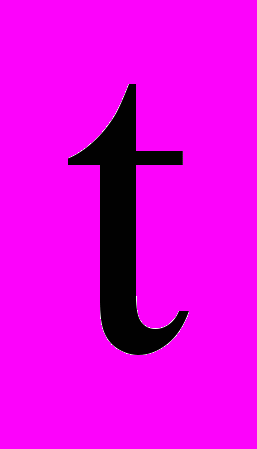 - температура;
- температура;  - время;
- время; 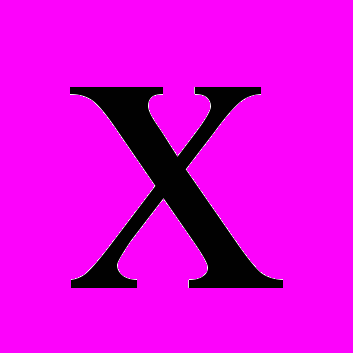 - координата;
- координата;  - коэффициент теплопроводности;
- коэффициент теплопроводности; 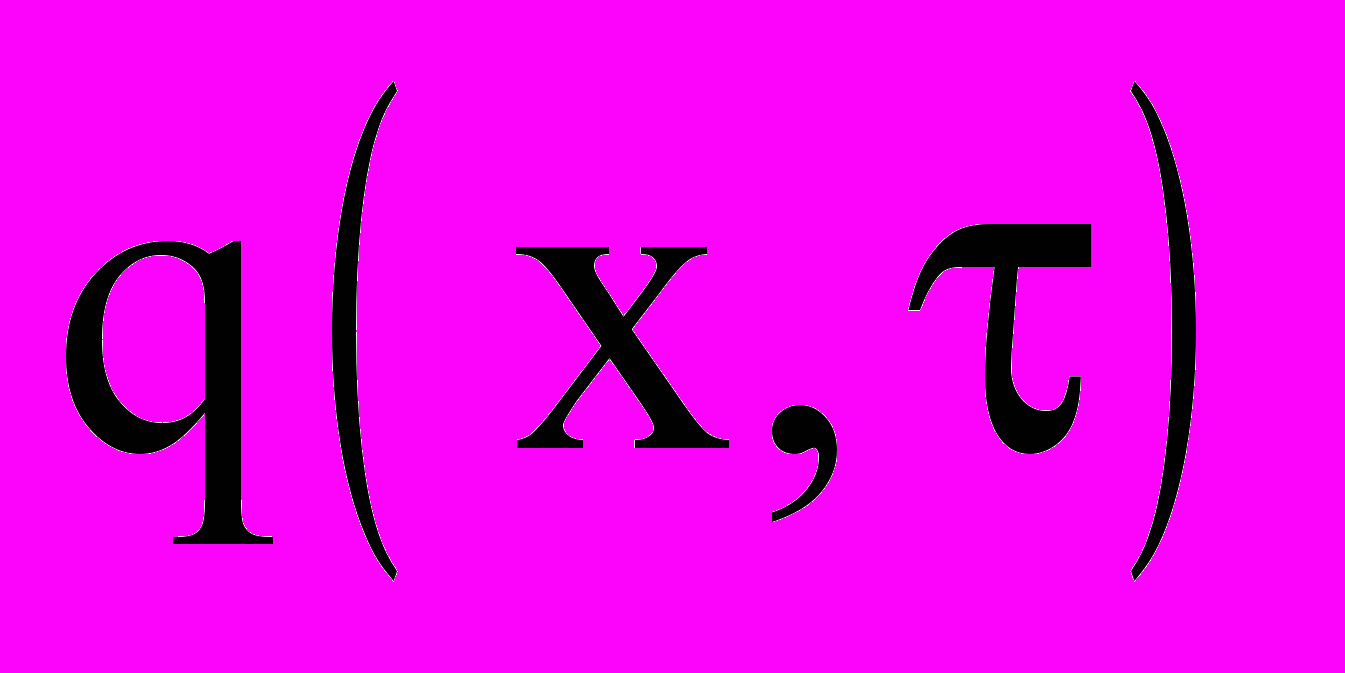 - объемный источник тепла, обусловленный тепловым эффектом, возникающим при гидратации цемента. В общем случае эта величина зависит от соотношения компонентов в бетонной смеси, и ее числовое значение изменяется во времени процесса тепловлажностной обработки и по толщине обрабатываемого слоя.
- объемный источник тепла, обусловленный тепловым эффектом, возникающим при гидратации цемента. В общем случае эта величина зависит от соотношения компонентов в бетонной смеси, и ее числовое значение изменяется во времени процесса тепловлажностной обработки и по толщине обрабатываемого слоя.Методом интегральных преобразований Лапласа получим общее решение системы в виде:
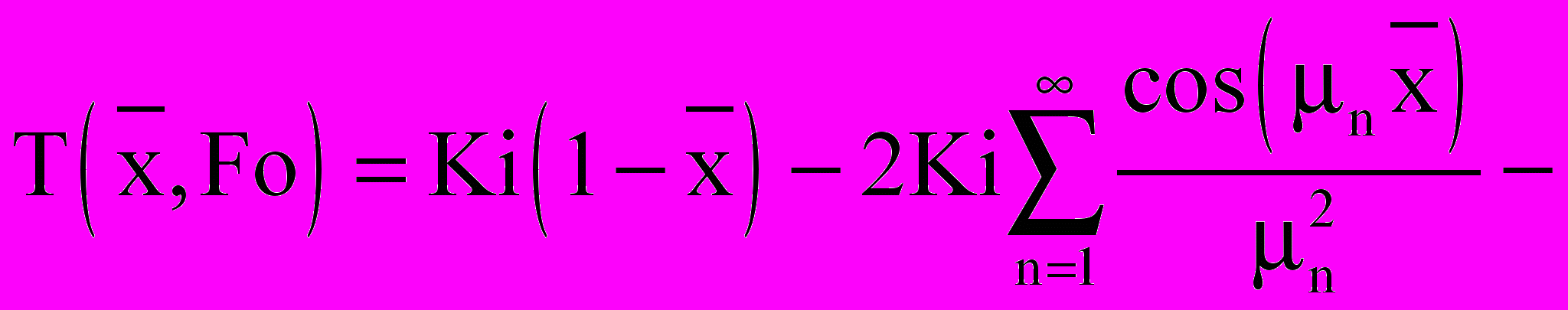
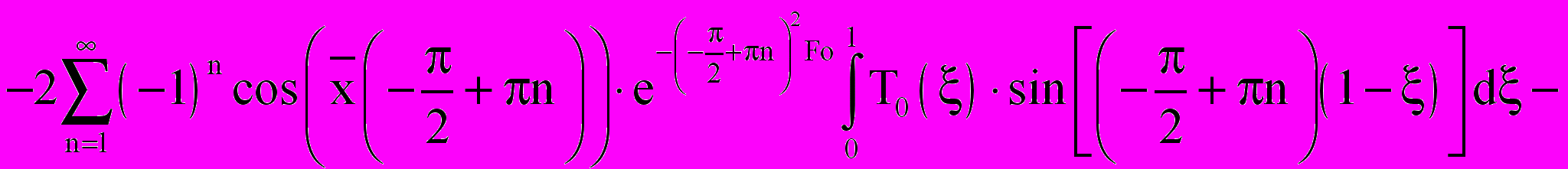 (30)
(30)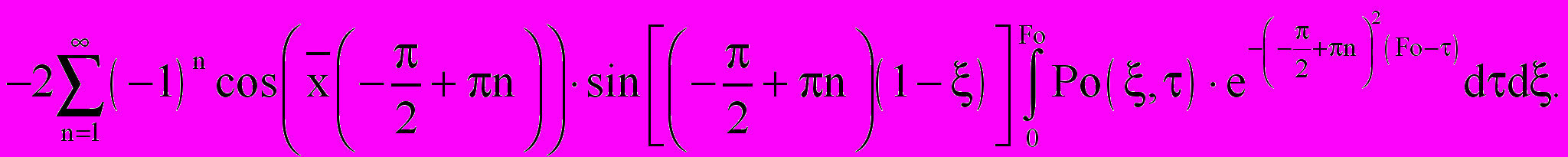
где
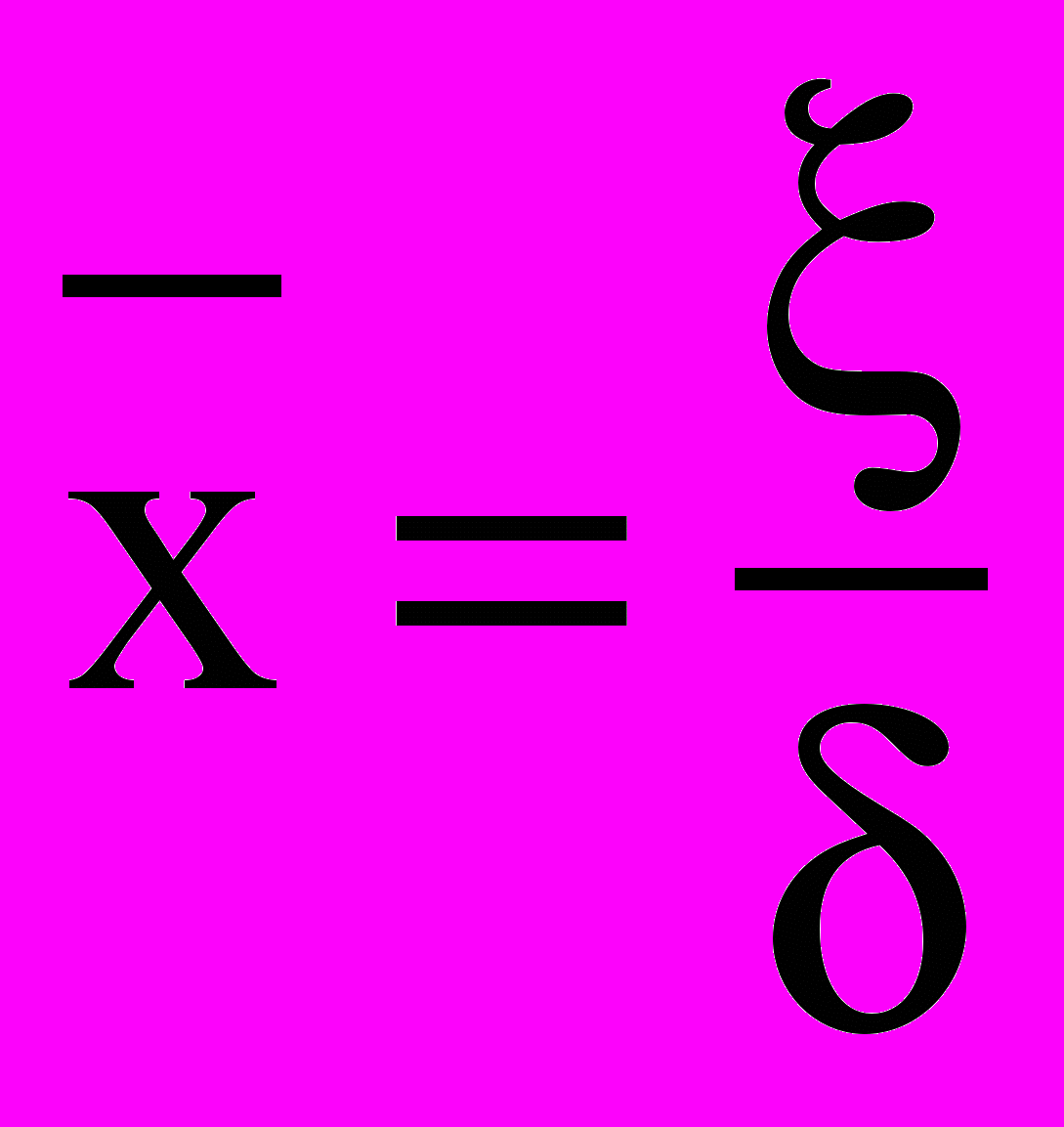 ;
; 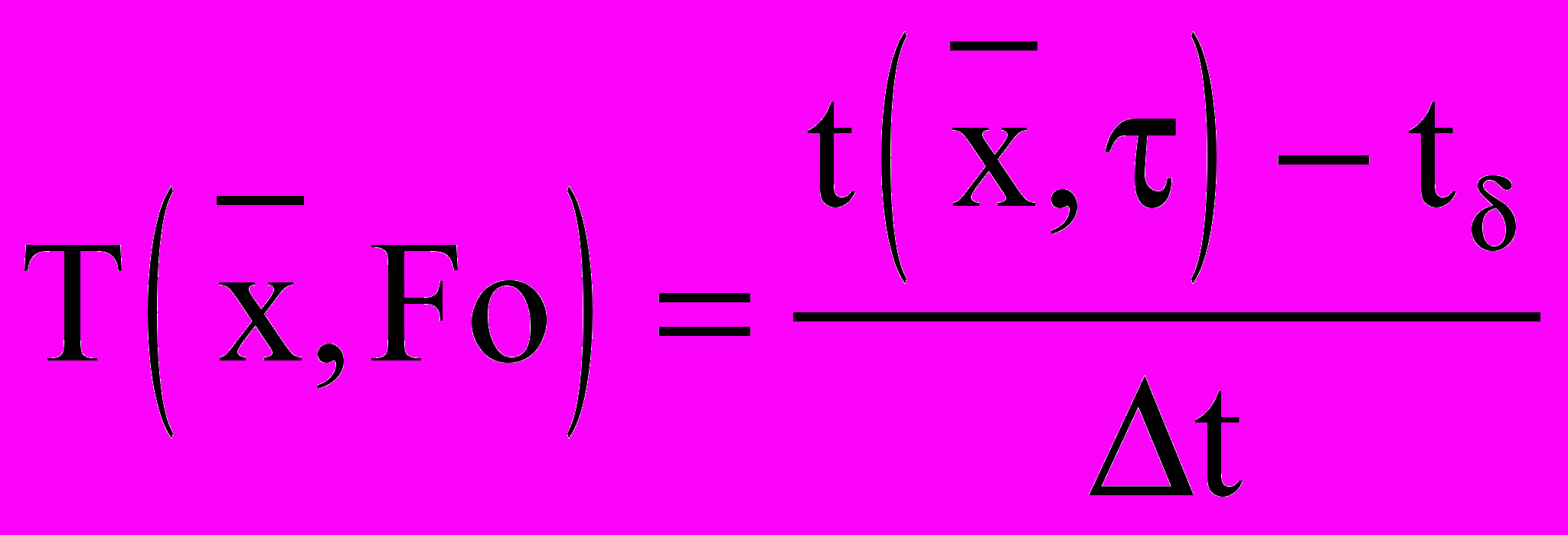 ;
; 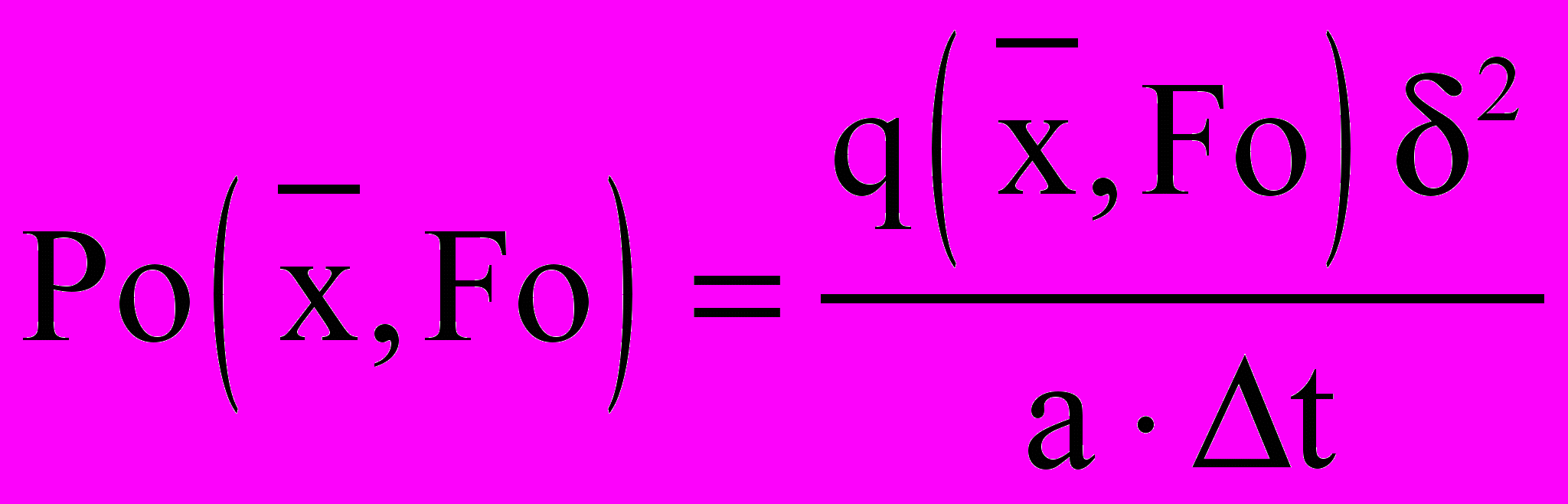 - критерий Померанцева;
- критерий Померанцева;  - температура на границе II;
- температура на границе II; 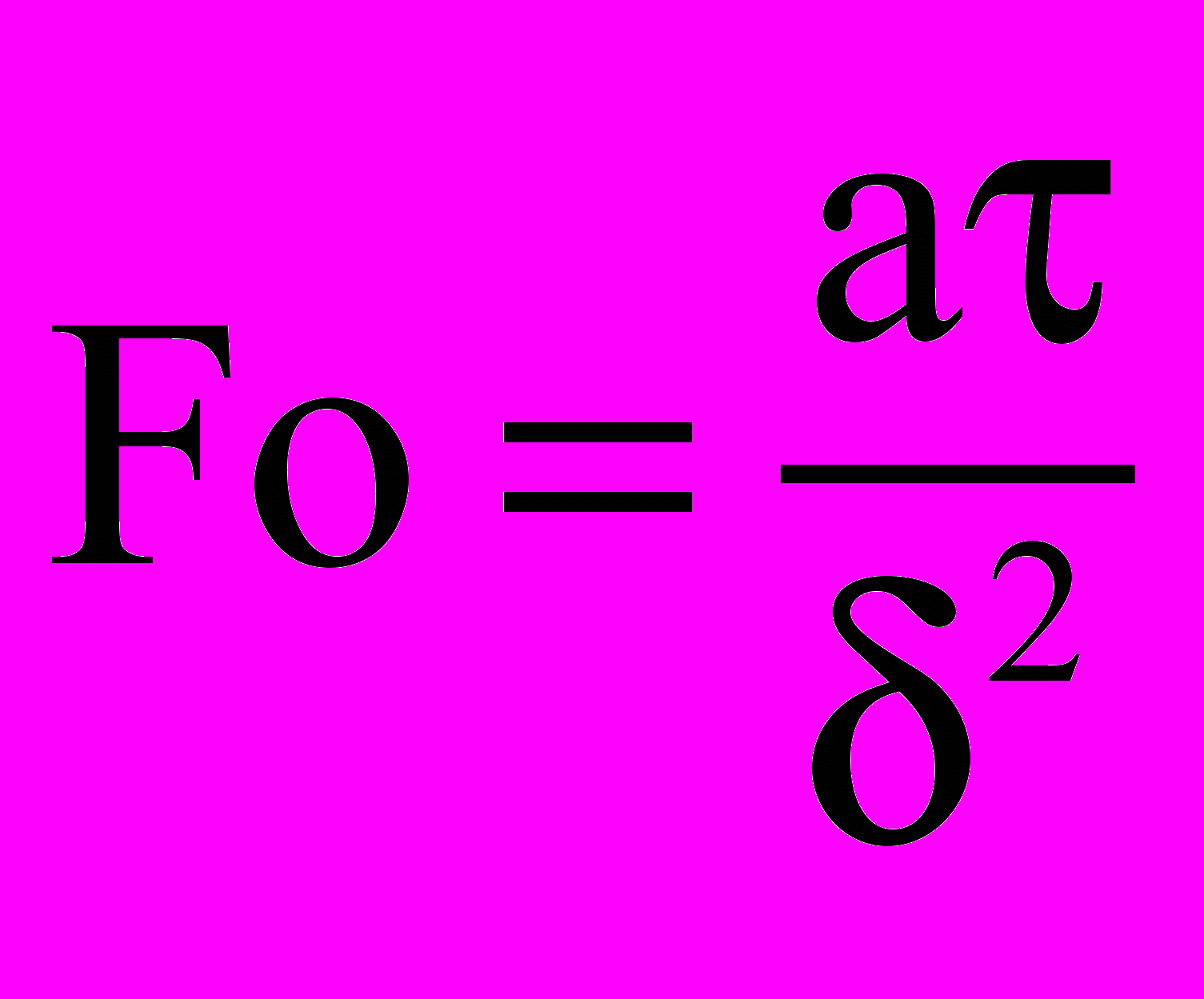 - критерий Фурье;
- критерий Фурье; 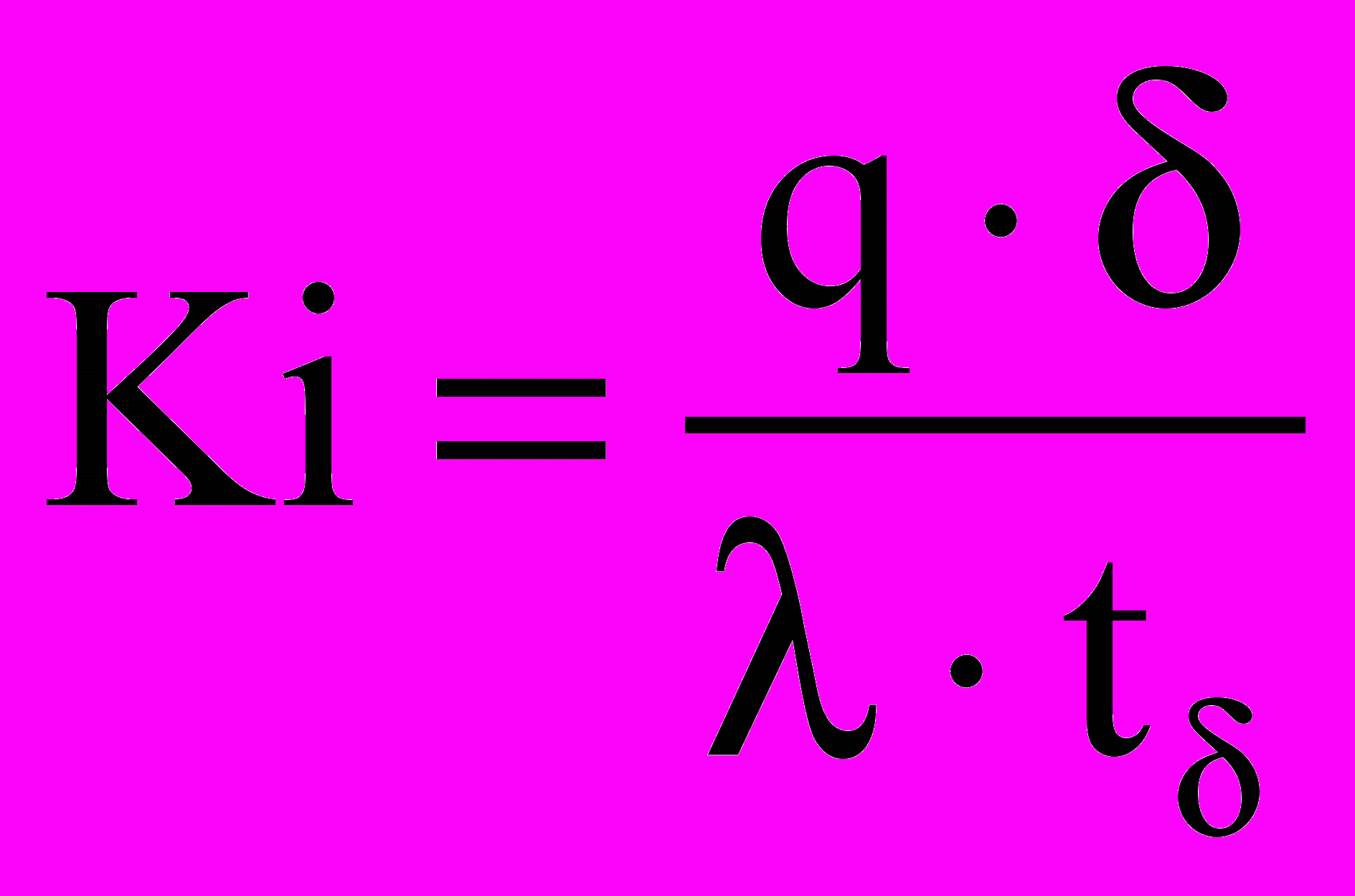 - критерий Кирпичева;
- критерий Кирпичева;  – безразмерная температура в начальный момент времени;
– безразмерная температура в начальный момент времени;  - корни характеристического уравнения
- корни характеристического уравнения 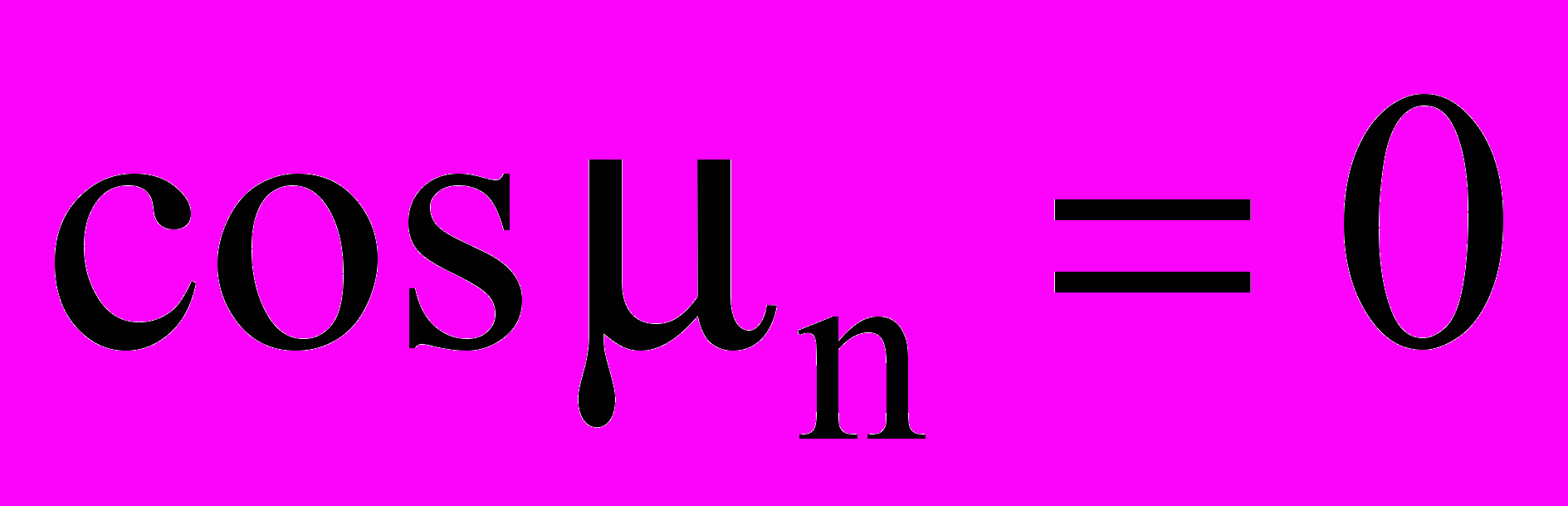 ;
; 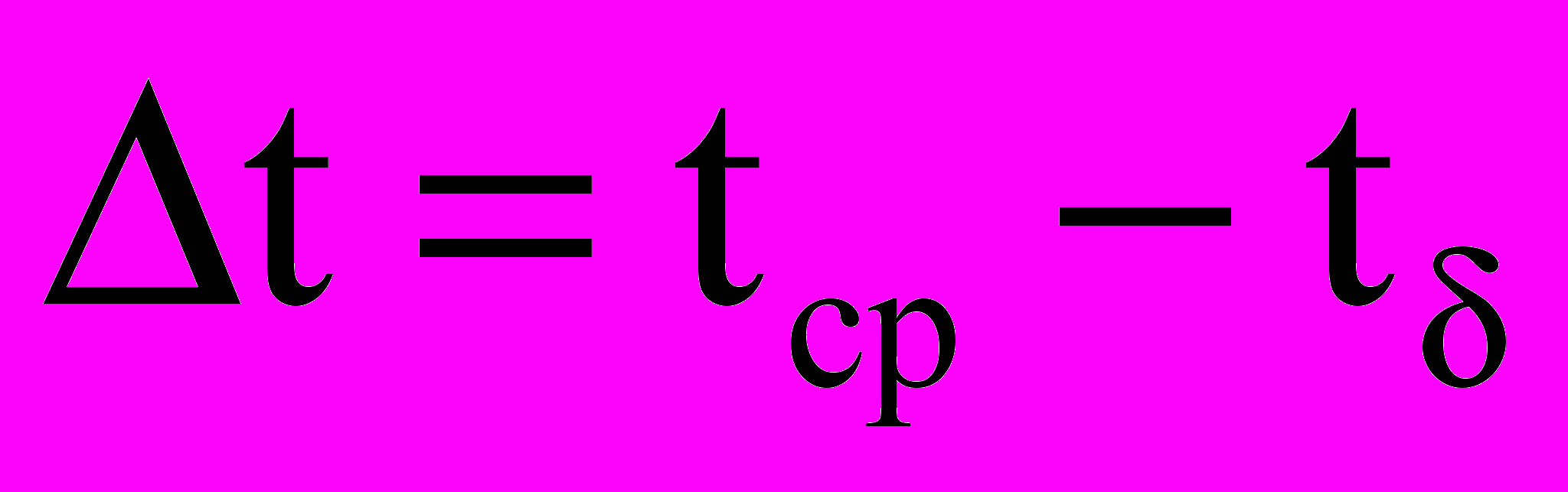 - температура среды у границы II.
- температура среды у границы II.Задача 2.
Для четвертого (несущего) слоя приняв с допущением, что интенсивность теплового воздействия на границе IV достаточно продолжительна на этапе изотермического прогревания, с достаточной степенью достоверности можно принять, что через границу IV идет постоянный тепловой поток, т.е. (1) – условие второго рода, а на границе III граничные условия аналогичны граничным условиям границы II – (2). Таким образом, задача для слоя 2 и 4 имеет “зеркальную” аналогию, с разницей только в толщине слоя и направлении оси координат (х).
Решение задачи для слоя 4 аналогично решению для слоя 2.
Задача 3.
Для слоя 3 учитывая, что это утепляющий слой (пенополистирол), не являющийся источником внутреннего теплового эффекта (нет гидратации цемента, как в предыдущих задачах) и независимо от какой границы I или IV будет направлен тепловой поток от пропарочной камеры, уравнение теплопроводности примет вид:
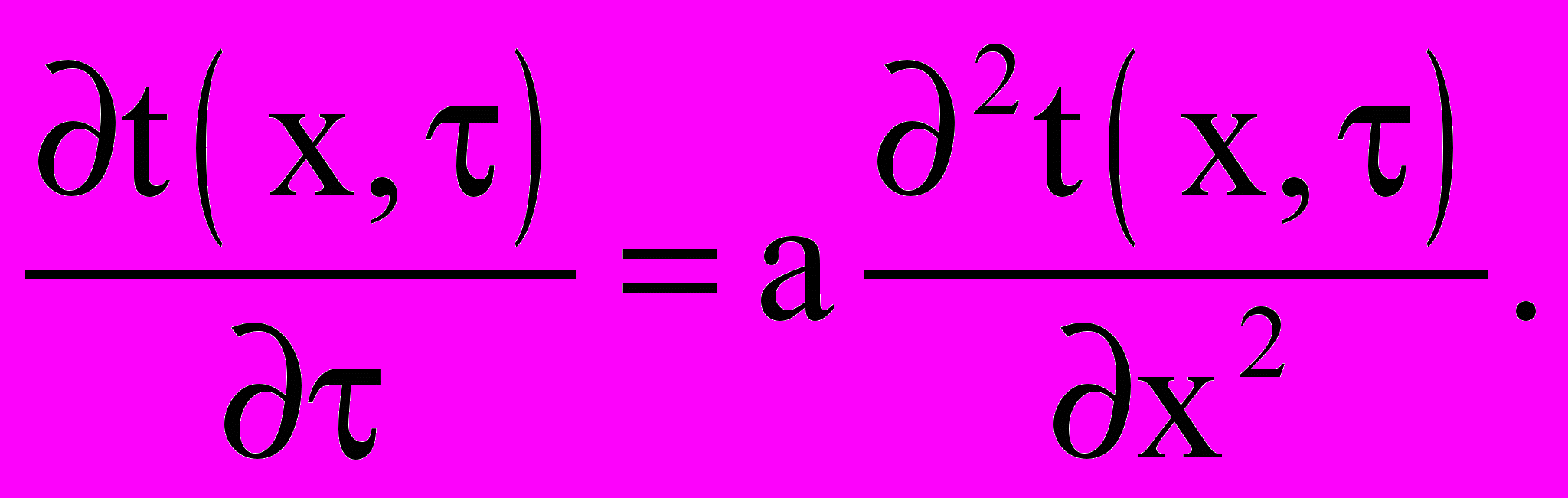 (31)
(31)Общее решение задачи имеет вид (4).
Алгоритм расчета трехслойной конструкции таков. В начальный момент времени температура во всех слоях конструкции одинакова и равна
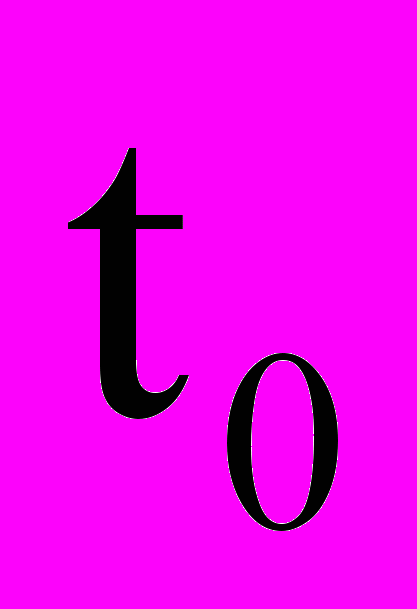 . Для первого малого интервала времени по выведенным зависимостям рассчитывают поле температуры в первом слое 2 или 4 конструкции. После этого определяют величины градиентов температуры на границах II и III. Если градиент равен нулю, то поток тепла от опалубки и от паро-воздушной среды пропарочной камеры не достиг границ II и III.
. Для первого малого интервала времени по выведенным зависимостям рассчитывают поле температуры в первом слое 2 или 4 конструкции. После этого определяют величины градиентов температуры на границах II и III. Если градиент равен нулю, то поток тепла от опалубки и от паро-воздушной среды пропарочной камеры не достиг границ II и III.Далее производят расчет для следующего временного интервала в слое 4 (2) и так далее.
Осуществляется поиск режимов, при которых происходит одновременное достижение температуры близкой к температуре деструктивного разложения пенополистирола на границах II и III. Этого можно добиться лишь тогда, когда в процессе бетонирования и тепловлажностной обработки будут четко выполняться все расчетные технологические режимы и параметры.
Решение (30) можно использовать при расчете процессов, происходящих в монолитной палубе при зимнем бетонировании с применением термоопалубки и утеплением открытой поверхности бетона.
В главе 5 приведена предлагаемая методология расчета нестационарных полей взаимосвязанного тепло- и массопереноса в слоистых средах.
Создание точной математической модели описания процессов переноса тепла и влаги в ограждающей конструкции представляет сложную задачу, поэтому в настоящее время при решении используют различного рода упрощения и допущения. Например, нормы II-3-79** рекомендуют рассчитывать сопротивление теплопередаче ограждающей конструкции исходя из того, что процесс теплопередачи стационарный, а влажностные условия определены значениями таблиц приложений 2 и 3 норм.
В данном исследовании была поставлена задача разработки методики расчета многослойных ограждающих конструкций, работающих в нестационарных условиях эксплуатации. За основу математического моделирования взяты уравнения взаимосвязанного тепломассопереноса в слое, имеющие вид:
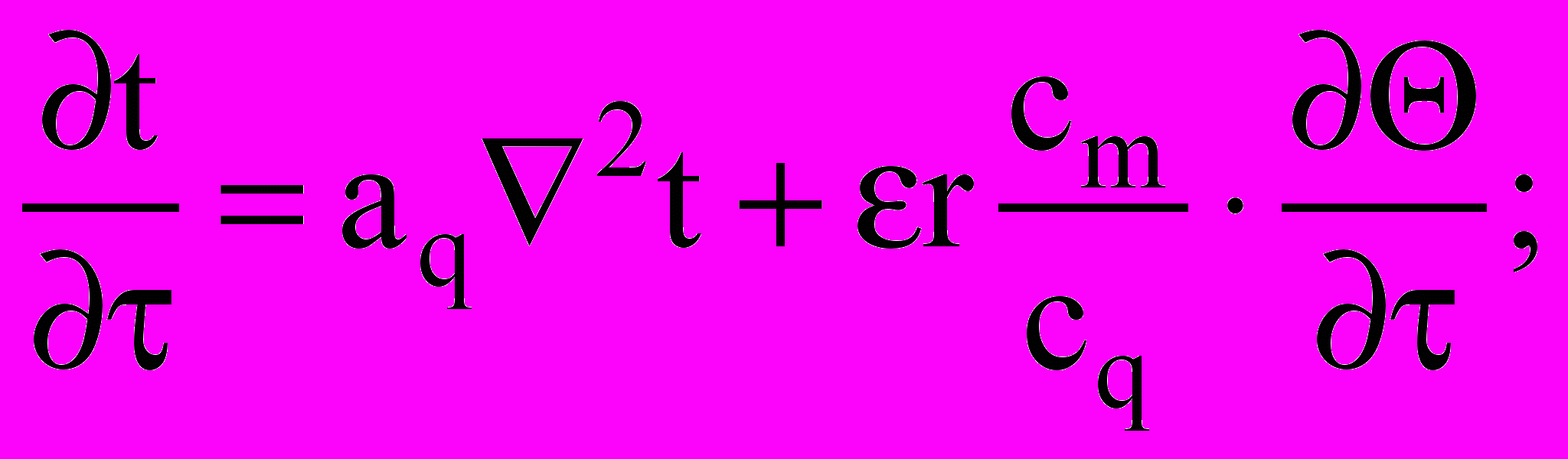 (32)
(32)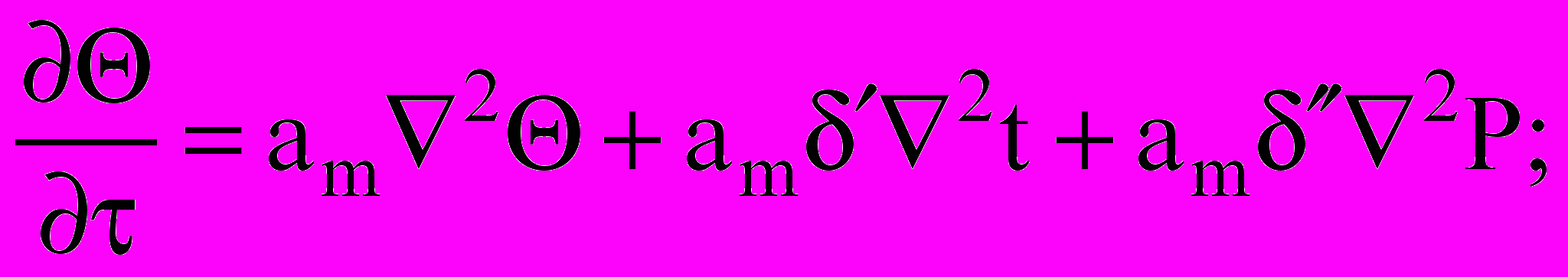 (33)
(33)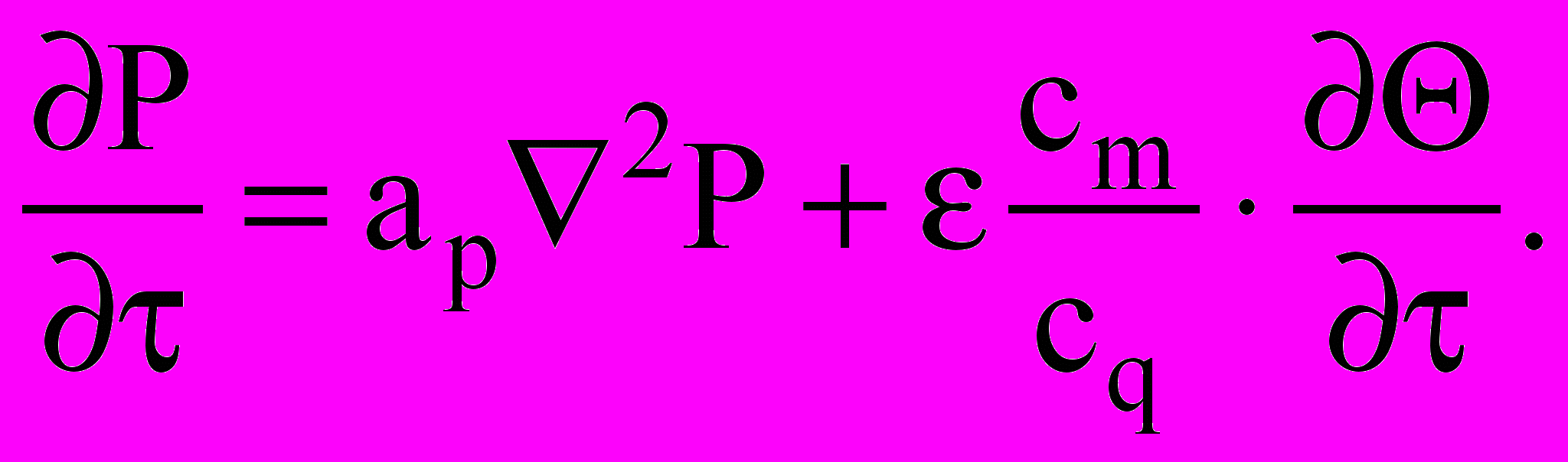 (34)
(34)Для решения системы (32)...(34) должны быть поставлены краевые условия, которые в общем виде можно записать следующим образом:
- начальные условия: обычно задаются на начальный момент времени (=0) распределение потенциалов тепло- и массопереноса в виде функции координаты для одномерной задачи t(x, 0) и (x, 0). (35)
- граничные условия:
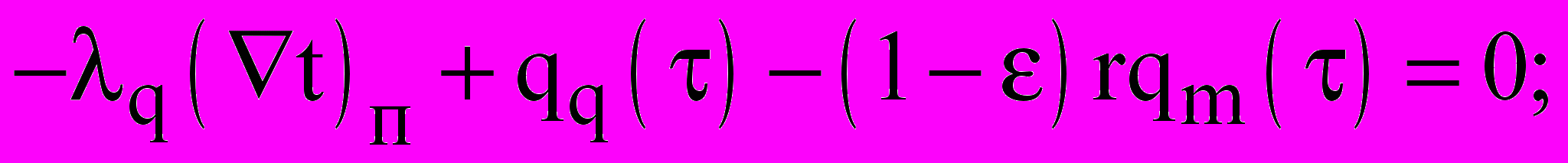 (36)
(36)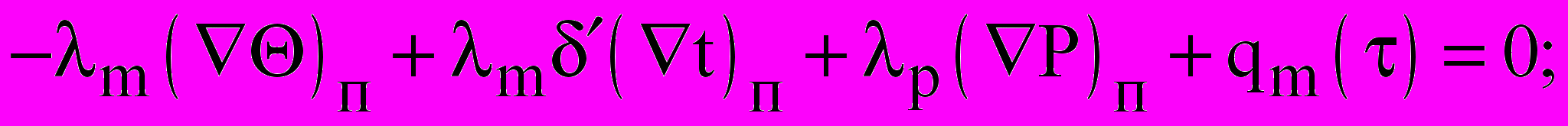 (37)
(37)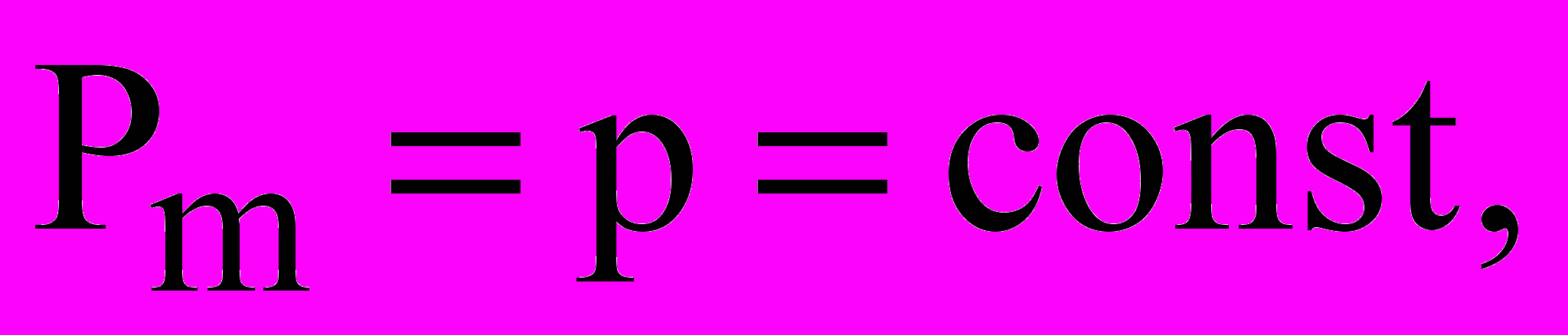 (38)
(38)где qq и qm - плотность потоков тепла и вещества, индекс (п) означает поверхность тела.
Первый член равенства (36) -q(t)п в физическом смысле представляет количество тепла, ушедшего от поверхности внутрь ограждения; второй qq() - количество тепла, подведенное к поверхности ограждения; третий -(1-)rqm() - количество тепла, затраченного на испарение жидкости. Если =1, то испарение происходит внутри тела конструкции, если =0, то поток влаги состоит из потока жидкости и испарение происходит только на поверхности. Равенство (37) носит название балансового уравнения массы вещества. К поверхности тела влага подводится под действием градиентов потенциала m()п - массопереноса, m(t)п -теплопереноса и p(P)п - градиента общего давления. С поверхности тела в окружающую среду отводится поток массы влаги qm(). Равенство (38) отображает равенство давлений парогазовой смеси у поверхности ограждения Pm и барометрического давления окружающей среды p.
Для многослойной конструкции должны быть поставлены условия сопряжения слоев, а при учете фазовых превращений наложены дополнительное условие внутри каждого слоя на подвижной границе раздела фаз. Использовав идею метода зонального расчета, который разработал С.П. Рудобашта, для решения задачи применяем комбинированный метод, который базируются на основе сочетания элементов аналитического и численного решения. Предлагаемая методика расчета позволяет упростить решение задачи без существенного ущерба для точности решения. Суть метода состоит в том, что весь процесс тепловлагопереноса делится на ряд малых временных интервалов. В пределах каждого интервала предполагаем, что температура одинакова на границе II и III, и постоянна плотность теплового потока через соприкасающиеся поверхности, т.е. идеальный тепловой контакт, а также массовый контакт.
Общая задача разбивается на три автономные, но взаимосвязанные между собой.
Задача 1. Тепловлагоперенос в слое 1 с граничными условиями третьего рода, которые учитывают конвективный теплообмен на границе I по закону Ньютона, влагообмен поверхности с окружающей средой по закону Дальтона и первого рода, которые характеризуют постоянство температуры на границе II слоев 1 и 2 и постоянство влагосодержания.
Задача 2. Тепловлагоперенос в слое 2 с граничными условиями второго рода, которые характеризуют постоянство плотности теплового и массового потока через границу II, и первого рода, характеризующие постоянство температуры и постоянство влагосодержания на границе III.
Задача 3. Тепловлагоперенос в слое 3 с граничными условиями второго рода, которые характеризуют постоянство плотности теплового и массового потока через границу III и граничными условиями третьего рода, которые характеризуют теплообмен между поверхностью слоя 3 на границе IV с окружающей средой по закону Ньютона и массообмена по закону Дальтона.
Каждая из этих задач решается аналитически. Решение общей задачи нестационарного тепловлагопереноса можно получить в результате сопряжения этих аналитических решений на каждом временном интервале.
При решении краевых задач учитывались три вида зависимости:
а) Kim = const; б) Kim = Bim[1-(0, Fo)]; в) Kim = Kim (Fo).
В диссертации получены решения для всех трех задач и зависимостей Kim, но в автореферате они не приводятся ввиду громоздкости записи
Полученные решения для задачи 1, 2, 3 с успехом реализуются в алгоритме расчета многослойной конструкции, идея которого и детальная разработка представлены в главе 2 настоящей работы. Некоторая громоздкость записи выражений практически не влияет на качество расчета, так как возможности современной вычислительной техники позволяют получить итоговое решение за 10…15 минут машинного счета. Трудоемкость заключается в аккуратной подготовке и задании исходных данных, а также получении (выявлении) недостающих для расчета теплофизических характеристик материалов, которые можно получить только опытным путем (методика их получения приведена в части II диссертации). Блок-схема программы расчета приведена в приложении к диссертационной работе.
Часть II. «Расчетно-экспериментальные исследования и разработки»
В главе 6 представлены разработки методик определения различных параметров, необходимых для расчета и проектирования различного рода конструкций, материалов, грунтов и оснований, а также описание установок для проведения экспериментов и описания самих экспериментов.
- Методика определения сопротивления теплопередаче многослойных кирпичных кладок;
- Методика определения сопротивления теплопередаче утеплителей;
- Методика определения температурных полей во влажных образцах при их промерзании;
Особенностью разработанных методик является то, что у исследователей появилась возможность отказаться от климатической камеры и проводить как модельные, так и натурные исследования и испытания строительных материалов, конструкций, изделий.
В главе 7 для иллюстрации эффективности теоретических и экспериментальных исследований с помощью предлагаемых математических моделей и методов расчета рассмотрены некоторые прикладные задачи, приведен анализ решений и рекомендации по проектированию конструкций.
Оптимальное проектирование многослойных ограждающих конструкций с точки зрения теплопереноса. Анализ теоретических и экспериментальных разработок позволил сделать следующие выводы:
- плитный утеплитель в многослойных ограждающих конструкциях следует устраивать в местах, как можно ближе расположенных к наружной поверхности конструкции, либо вообще вынести утеплитель на наружную поверхность, т.к. только в этом случае исключается пагубное влияние влаги на несущую способность стен и обеспечивается надлежащий микроклимат в помещении;
- применение утеплителей с < 0,04 Вт/(м °К) и толщиной 120...140 мм позволяет сохранить модульные размеры (толщины) кладок 380, 510, 640 и 770 мм, что облегчает перевязку швов;
- при увеличении сопротивления теплопередаче ограждающих конструкций из полнотелого силикатного кирпича на 29% и из силикатного одиннадцатипустотного кирпича на 26% по сравнению с существующими и запроектированными конструкциями без учета изменений №3 к СНиП в климатических условиях Ивановского региона в зимний период конденсат не образуется;
- при реконструкции существующих зданий, памятников архитектуры или наличия сложного, архитектурно-выразительного фасада зачастую единственно возможное решение – это размещение утепляющего слоя внутри помещения. Конструктивным решением, в этом случае, для исключения образования конденсата является устройство вентилируемой воздушной прослойки толщиной 40 мм между стеной и слоем утеплителя.
Расчет многослойного ограждения на промерзание
В качестве примера смоделирована ситуация. Рассмотрена трехслойная стенка: 1 слой - кладка из силикатного кирпича =380 мм; 2 слой- утеплитель (пенополистирол) =140 мм; 3 слой - кладка из силикатного кирпича =120 мм. Внутренняя температура воздуха +20С. Начальная наружная температура +10С - случай (а); -10С - случай (б); -20С - случай (в). Наружная температура воздуха понижается (похолодание) с интенсивностью 1С в час.
Расчет показывает, что на границе III (стык второго и третьего слоя) температура при похолодании уменьшится на 1С: для случая (а) через 6 ч 20 мин; для случая (б) через 5 ч 40 мин; для случая (в) через 5 ч 10 мин. Таким образом, чем ниже начальная температура наружного воздуха, тем за более короткий срок промерзает конструкция при дальнейшем понижении этой температуры (похолодание в ночные часы).
Если скорость понижения температуры наружного воздуха увеличивается вдвое, т.е. 1С за 30 минут, то разница между температурой наружной поверхности ограждения (граница IV) и температурой наружного воздуха возрастает, например, при -25С (случай а) с 2,4С до 2,68С.
По классической теории суточные колебания температуры носят затухающий маятниковый (гармонический) характер, что приводит к установлению стационарного распределения температуры в толще ограждения (это положено в основу современных нормативных теплотехнических расчетов), однако полученные результаты убедительно показывают, что игнорирование нестационарности процессов, особенно в наружном слое ограждения, который работает в худших термовлажностных условиях, приводит к ошибке при подсчете циклов замораживания и оттаивания в зимний период эксплуатации зданий, а именно к занижению их числа. На самом деле число циклов значительно выше нормативных, что приводит к преждевременному старению материала и, как следствие, снижению несущей способности и надежности конструкции.
Расчет температурных полей многослойных влажных конструкций.
Н
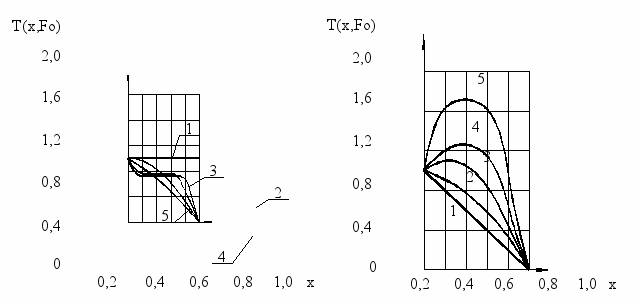 а рисунке 6 графически представлены некоторые результаты расчетов, произведенных по формулам (13) и (14). При малоинтенсивном источнике теплоты (Рис. 6а) внешний перенос оказывает определяющее воздействие на процесс, поэтому температура внутренних слоев непрерывно уменьшается и стремится к стационарному распределению при значении числа Фурье, равным 0,5. Если источник тепла более мощный (Рис. 6б), то характер процесса изменяется. В этом случае стационарное распределение температур также достигается при Fо=0,5, однако, в начальный период развития процесса количество выделившейся теплоты льдообразования превышает количество теплоты, отводимой от поверхности ограждения, т.е. наблюдается непрерывный рост потенциала переноса. С течением времени устанавливается баланс между выделившимся и отводимым количеством теплоты и распределение температур остается неизменным.
а рисунке 6 графически представлены некоторые результаты расчетов, произведенных по формулам (13) и (14). При малоинтенсивном источнике теплоты (Рис. 6а) внешний перенос оказывает определяющее воздействие на процесс, поэтому температура внутренних слоев непрерывно уменьшается и стремится к стационарному распределению при значении числа Фурье, равным 0,5. Если источник тепла более мощный (Рис. 6б), то характер процесса изменяется. В этом случае стационарное распределение температур также достигается при Fо=0,5, однако, в начальный период развития процесса количество выделившейся теплоты льдообразования превышает количество теплоты, отводимой от поверхности ограждения, т.е. наблюдается непрерывный рост потенциала переноса. С течением времени устанавливается баланс между выделившимся и отводимым количеством теплоты и распределение температур остается неизменным.а) Ро=1; Т0(х)=1; б) Т0(х)=1-х; Ро=10;
Fo: (1)-0; (2)-0,005; (3)-0,01; Fo: (1)-0; (2)-0,01; (3)-0,05;
(4)-0,05; (5)-0,5. (4)-0,1; (5)-0,5.
Рис. 6 Динамика полей безразмерных температур
по толщине зоны промерзания
Н
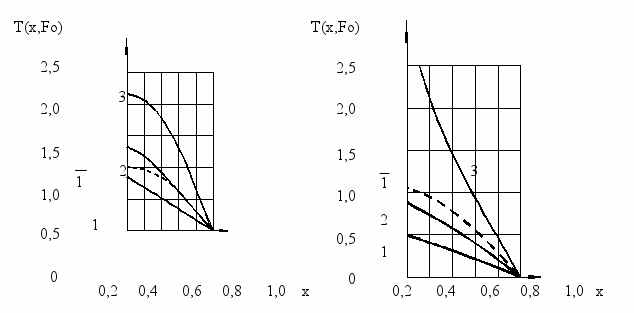 екоторые результаты расчетов по формуле (22) приведены на рисунке 7.
екоторые результаты расчетов по формуле (22) приведены на рисунке 7.а) Кi=1,0; б) Pо=0;
Po: (1)-0,1; (2)-1,0; (3)-3,0; Ki: (1)-0,5; (2)-1,0; (3)-3,0.
Рис. 7 Динамика полей безразмерных температур по толщине мерзлой зоны в
зависимости от чисел Померанцева (а)
и Кирпичева (б) при Т0(х)= 1-х2; (1) Fo=1,0.
Анализ полученных результатов позволяет сделать следующие выводы:
1. При увеличении мощности внутренних источников теплоты (другими словами – «чем интенсивнее образуется лед»), а также плотности теплового потока к поверхности ограждения приводит к быстрому повышению температуры во внутренних слоях материала.
2. При замораживании влажных талых конструкций и оттаивании мерзлых конструкций можно говорить о гистерезисной петле процессов. Однако, на вид гистерезисных петель очень сильно влияет реальная ситуация, например:
- процесс оттаивания промерзшей ограждающей конструкции менее продолжителен по времени, чем процесс промерзания, так как оттаивание происходит с обеих сторон замороженной зоны;
- при наличии чередующихся в теле конструкции мерзлых и талых зон, возникающих при нестационарных процессах, общие векторы замораживания и оттаивания в количественном отношении совпасть по гистерезису практически не имеют возможности.
- нестационарность процессов, при детальном их рассмотрении, вообще не позволяют построить гистерезисную петлю в общепринятом понимании, так как петли имеют ступени - разрывы перехода фазового состояния влаги, временные характеристики действия внутренних и внешних факторов, массивность (тепловая инерция) материалов также накладывают свои поправки на график гистерезиса, и петли зачастую имеют очень причудливое начертание.
Пример решения комплексной задачи проектирования ограждающих конструкций жилого помещения, фундамента и основания.
В качестве примера рассмотрено распределение полей температур в наиболее характерных местах ограждения первого этажа, подвала и прилегающей к подвальной части толще грунта.
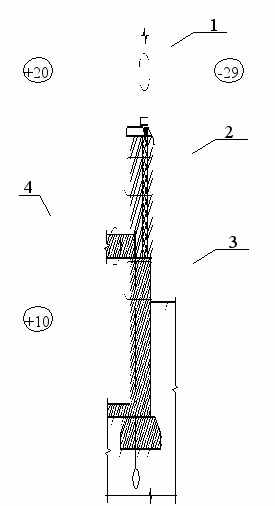 Рис. 8 К комплексной задаче проектирования ограждения здания | Схема конструкций приведена на Рис. 8. За исходные данные приняты следующие параметры: здание расположено в третьей климатической зоне (г. Иваново); температура внутренней среды (жилое помещение) tв=+20С; температура воздушной среды подвального помещения tп=+10С; температура наружного воздуха tн=-29С. Рассмотрим узел 1 Рис. 8. Толщина оконных стекол равна 0,002 м; толщина воздушной прослойки =0,10м. Анализ результатов расчета позволяет сделать следующие выводы: при нестационарном процессе уже через час в конструкции устанавливается распределение температурных полей, эквивалентное стационарному процессу; уменьшение толщины воздушной прослойки до 48 мм ведет к промерзанию конструкции, на поверхности внутреннего оконного стекла температура равна - 0,7С, что приводит к образованию конденсата и последующему намораживанию слоя льда. |
Рассмотрим узел 2 Рис. 8. Толщина несущей части стены из силикатного кирпича 1=0,380 м; толщина ограждающей части стены из силикатного кирпича 3=0,120 м; толщина утеплителя из пенополистирола 2=0,140 м.
Анализ результатов расчета позволяет сделать следующие выводы:
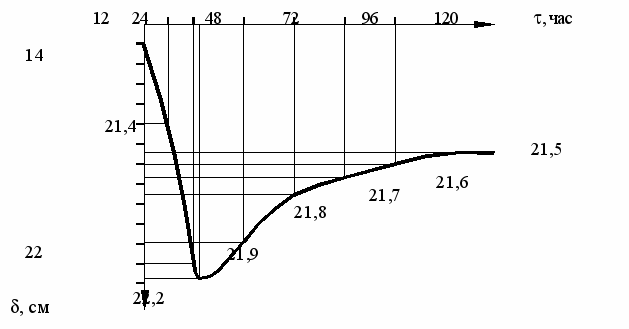
1. Если принять температуру фронта промерзания tф=0С, то уже через час нестационарного процесса в ограждающий слой кладки фронт промерзания проникает на глубину 3,2 см, через 2 часа - на 6,6 см, через 2 часа 32 минуты слой 3 промерзает полностью, и в процесс охлаждения начинает вовлекаться слой 2. Через три часа процесса фронт промерзания продвинется в тело конструкции на 13 см, через 4 часа - на 15 см, через 5 часа - на 16,7 см, через 6 часов - на 18,1 см, через 12 часов на 21,4 см, через 1 сутки - на 22,1 см, через 1сутки и 10 минут отмечена максимальная глубина промерзания конструкции - 22,2 см, далее фронт промерзания начинает отступать и двигаться к внешней поверхности ограждения, и через 5 суток значение температуры практически выходит на уровень стационарного режима, а глубина промерзания составляет 21,6 см.
2. Глубина промерзания при регулярном режиме составляет 21,6 см, а фактическая глубина промерзания превышает ее на 0,6 см.
3
 . Чем ниже начальная температура слоев и больше их влажность, тем быстрее и глубже в тело конструкции продвигается фронт промерзания (Рис. 9 и 10).
. Чем ниже начальная температура слоев и больше их влажность, тем быстрее и глубже в тело конструкции продвигается фронт промерзания (Рис. 9 и 10).