Методические указания по лабораторным занятиям По дисциплине

Вид материала

Методические указания

Содержание 1. Краткие характеристики лабораторных занятий Оценка. Формирует необходимые представления о методах решения задач линейного программирования. Время выполнения заданий Решение задачи Рисунок 5 - Вставка формулы СУММПРОИЗВ в ячейки таблицы 2, 3 Рисунок 6 – Поиск решения Тема 2. Решение транспортных задач в Excel Поиск решения Оценка. Формирует необходимые представления о методах получения уравнений регрессии. Время выполнения заданий График нормальной вероятности. Расходы на рекламу по телевидению Метки; - Выходной интервал Оценка. Формирует необходимые представления о методах получения уравнений регрессии и производственных функций. Время выполнения Варианты индивидуальных заданий Оценка. Формирует необходимые представления о структуре и содержании межотраслевого баланса. Время выполнения заданий Решение задачи

Подобный материал:

• Методические указания по лабораторным занятиям По дисциплине Базы данных Для специальности, 364.77kb.
• Методические указания к лабораторным занятиям (Стоматология), 640.88kb.
• Методические указания по лабораторным занятиям По дисциплине, 487.31kb.
• Методические указания к лабораторным занятиям для студентов Vкурса специальности «Агрономия», 1655.23kb.
• Методические указания к лабораторным занятиям по дисциплине "Автоматизированный бухучет, 580kb.
• Методические указания к лабораторным занятиям и самостоятельной работе студентов, 490.78kb.
• Методические указания к лабораторным занятиям по дисциплинам «Методика региональных, 252.37kb.
• Методические указания к лабораторным работам по дисциплине «Материаловедение и ткм», 215.09kb.
• Методические указания по лабораторным работам По дисциплине, 803.46kb.
• Методические указания по лабораторным работам По дисциплине, 929.67kb.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Тихоокеанский государственный университет


Институт экономики и управления

Кафедра Экономическая кибернетика


Методические указания по лабораторным занятиям


По дисциплине Математическое моделирование в экономике


Для специальности 080301.65 «Коммерция (торговое дело)»

(ускоренное)


Методические указания разработаны в соответствии с составом УМКД


Методические указания разработала Макарова О.А. _____________


Методические указания утверждены на заседании кафедры,

протокол № ______ от «___» _______________ 200__ г.

Зав. кафедрой _________ «___» ______________ 200__ г. Пазюк К.Т.


Методические указания по лабораторным занятиям по дисциплине «Математическое моделирование в экономике» включают тематику лабораторных заданий, выполняемых студентами под контролем преподавателя или самостоятельно во время аудиторных занятий.


Методические указания рассмотрены и утверждены на заседании УМКС и рекомендованы к изданию

протокол № ______ от «___» _______________ 200__ г.

Председатель УМКС _______ «___» ______________ 200__ г.

Директор института _________ «___» ____________ 200__ г. Зубарев А.Е.


Введение


Изучение дисциплины «Математическое моделирование в экономике» имеет цель формирования у студентов специальности 080301.65 «Коммерция" (Торговое дело)» теоретических знаний и умений в области практического использования экономико-математических методов, развитие способности к логическому и алгоритмическому мышлению.

Основные задачи курса:

- на примерах математических моделей в экономике продемонстрировать студентам действие математических законов, специфику моделирования;

- научить студентов приемам исследования и решения математически сформулированных задач;

- выработать у студентов умение анализировать полученные результаты;

- сформировать у будущих специалистов теоретические знания и практические навыки по применению математического моделирования для исследования сложных экономических систем, а также построения надежных моделей экономических процессов с целью обоснования принимаемых решений;

- привить студентам навыки самостоятельного изучения литературы по практическому применению математических методов.

Студенты должны получить базовые знания и навыки математического моделирования. Они должны уметь применять их в моделировании экономических процессов. В данном курсе студенты должны освоить методы математического программирования.

Курс основан на знаниях, полученных студентами в области экономической теории, статистики, линейной алгебры и математического анализа и др.

Изучение курса «Математическое моделирование в экономике» проводится в форме лекции, практических и лабораторных занятий.

Практические занятия по дисциплине проводятся в форме решения задач.

Основная цель лабораторных занятий - углубленное изучение проблем, затронутых в лекционном курсе, и отработка навыков в применении изучаемых методов моделирования с использованием современного программного обеспечения персональных компьютеров.

В качестве базового информационно-программного инструментария на лабораторных работах предлагается воспользоваться ППП Excel. По завершении изучения каждой темы проводится тестирование.

Завершается изучение дисциплины «Математическое моделирование в экономике» сдачей зачета.

1. Краткие характеристики лабораторных занятий

Тема 1. Решение задач линейного программирования в Excel

Задание. Методы решения задач линейного программирования.

Исполнение. Решение задач линейного программирования с помощью инструмента «Поиск решения».

Оценка. Формирует необходимые представления о методах решения задач линейного программирования.

Время выполнения заданий: 4 часа.


Методические указания.


Задание: студентам необходимо решить задачу 1, используя данные методические указания, задачу 2 – решить самостоятельно по аналогии с задачей 1. Условие задачи 2 одинаково для всех студентов, независимо от варианта.

Условие задачи 1: Фирма выпускает 2 вида мороженного: сливочное и шоколадное. Для изготовления используются 2 исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженного и суточные запасы исходных продуктов даны в таблице.

Исходный продукт	Расход исходных продуктов на 1 кг мороженного		Запас, кг
	Сливочное	Шоколадное
Молоко	0.8	0.5	400
Наполнители	0.4	0.8	365

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженное превышает спрос на шоколадное мороженное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженное не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженного 16 ден.ед., шоколадного - 14 ден.ед. Определить количество мороженого каждого вида, которое должна производить фирма, чтобы доход от реализации продукции был максимальным.


Решение задачи:

1. Составляем математическую модель задачи.
   

Вводим обозначения (переменные величины):

х ₁ – суточный объем выпуска сливочного мороженного, кг;

х ₂ - суточный объем выпуска шоколадного мороженного, кг

Целевая функция:

f = 16 х ₁ + 14 х ₂→max

при ограничениях:

0.8 х ₁ + 0.5 х ₂ ≤ 400 (ограничение по молоку);

0.4 х ₁ + 0.8 х ₂ ≤ 365 (ограничение по наполнителям);

х ₁ + х ₂ ≤ 100 (рыночное ограничение по спросу);

х ₂ ≤ 350 (рыночное ограничение по спросу);

х ₁ ≥ 0, х ₂ ≥ 0

Данная задача является задачей линейного программирования (ЗЛП), так как целевая функция и ограничения линейны. ЗЛП можно решить: графическим методом, симплекс-методом, с помощью EXCEL.

2. Для решения ЗЛП с помощью EXCEL строим три таблицы с исходными данными на основании математической модели задачи (рисунок 1)
   

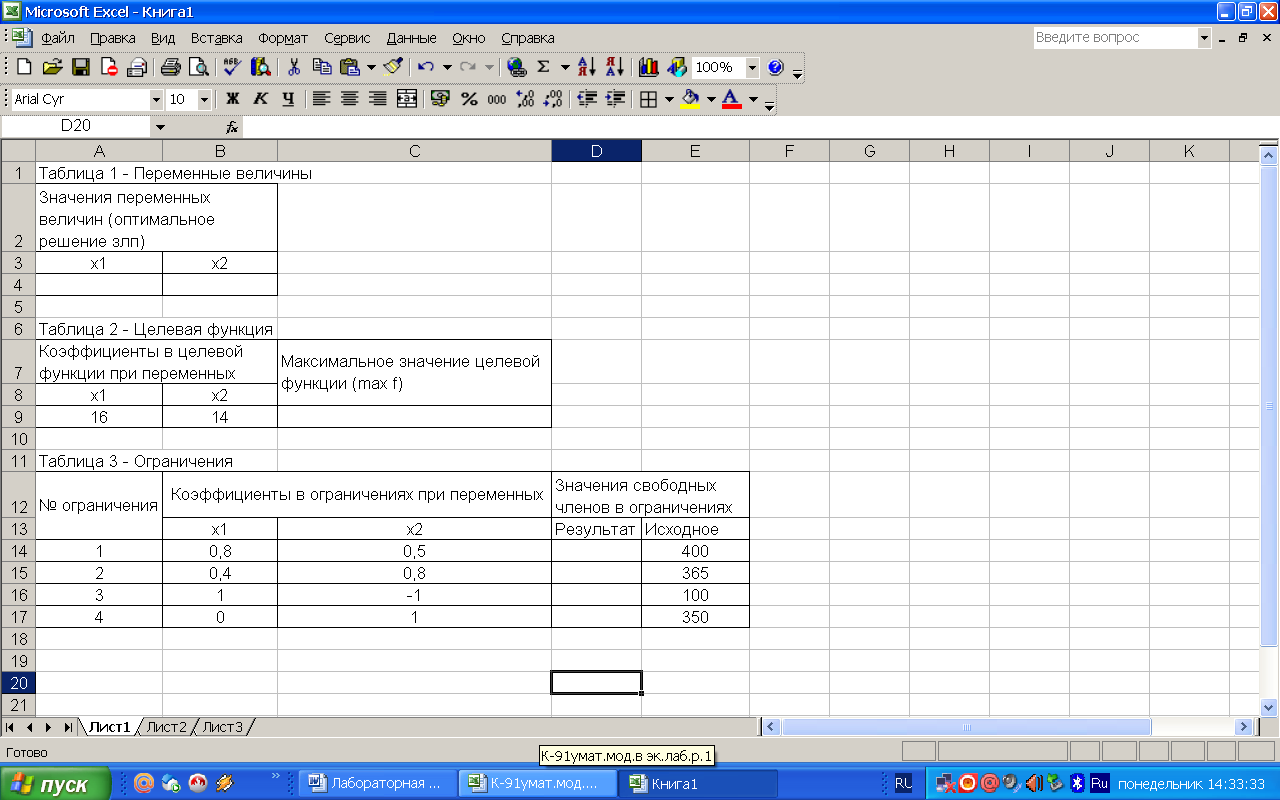
Рисунок 1 – Таблицы с исходными данными

В ячейки С9, D14-D17 вставляем функцию СУММПРОИЗВ (Вставка – Функция – Математические – СУММПРОИЗВ). Массив1 для каждой ячейки это коэффициенты при переменных из таблицы 2 таблицы 3 соответственно. Массив2 – это ячейки значения переменных величин таблицы 1 (рисунок 2, 3, 4, 5).



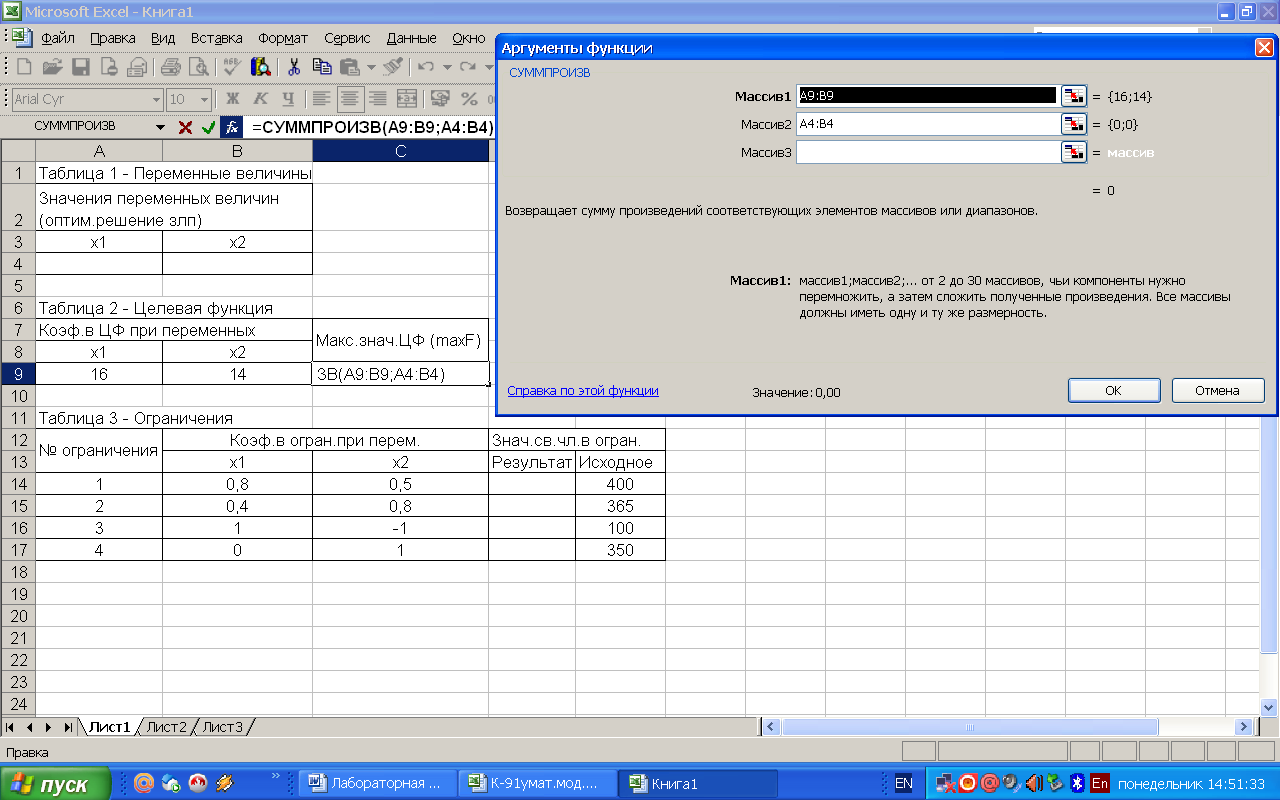
Рисунок 2 – Вставка формулы СУММПРОИЗВ в ячейку таблицы 2




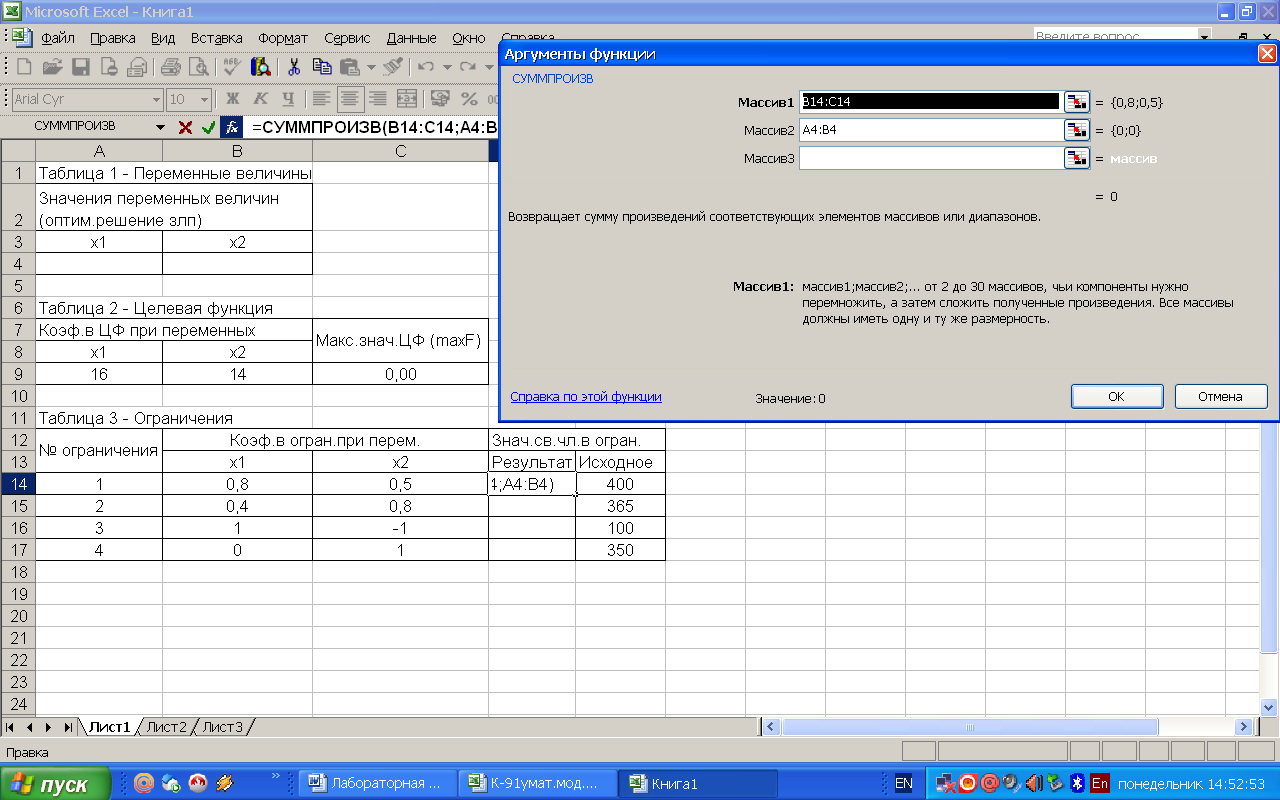
Рисунок 3 – Вставка формулы СУММПРОИЗВ в ячейку таблицы




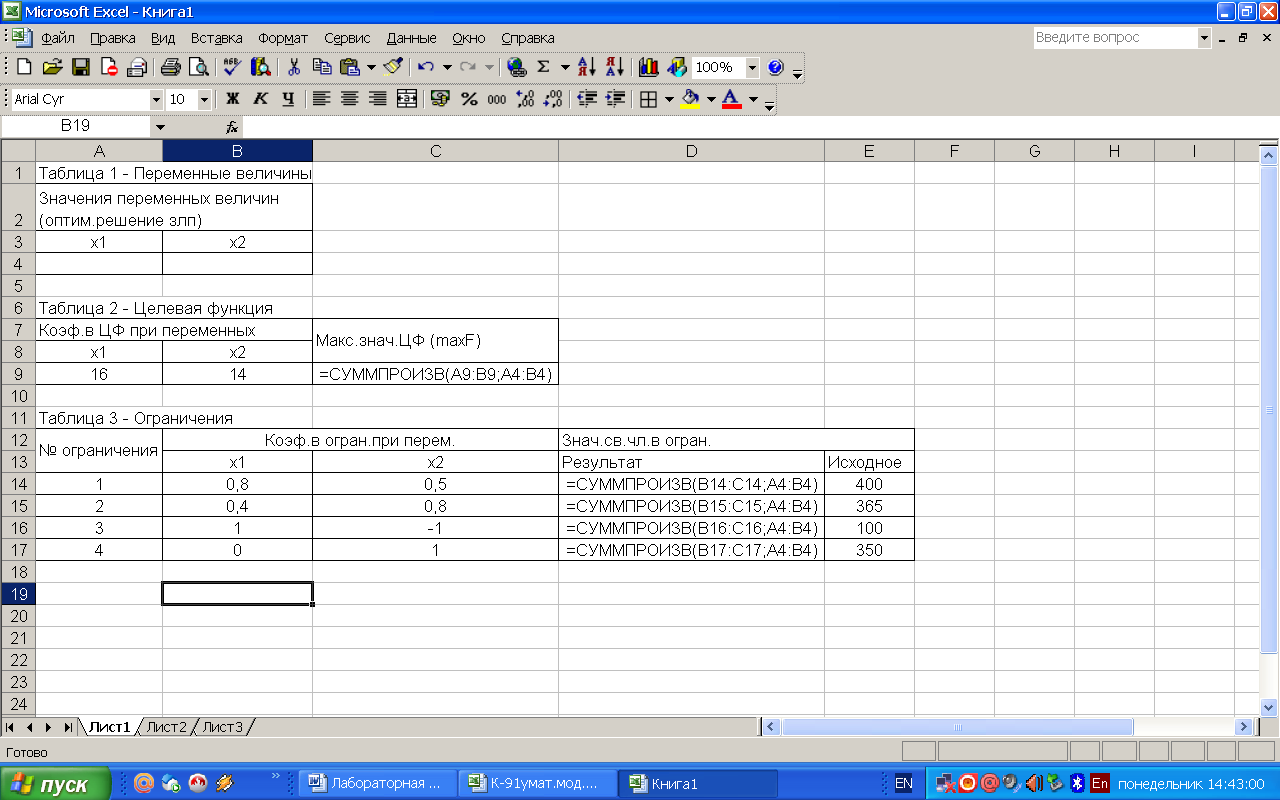
Рисунок 4 - Вставка формулы СУММПРОИЗВ в ячейки таблицы 2, 3




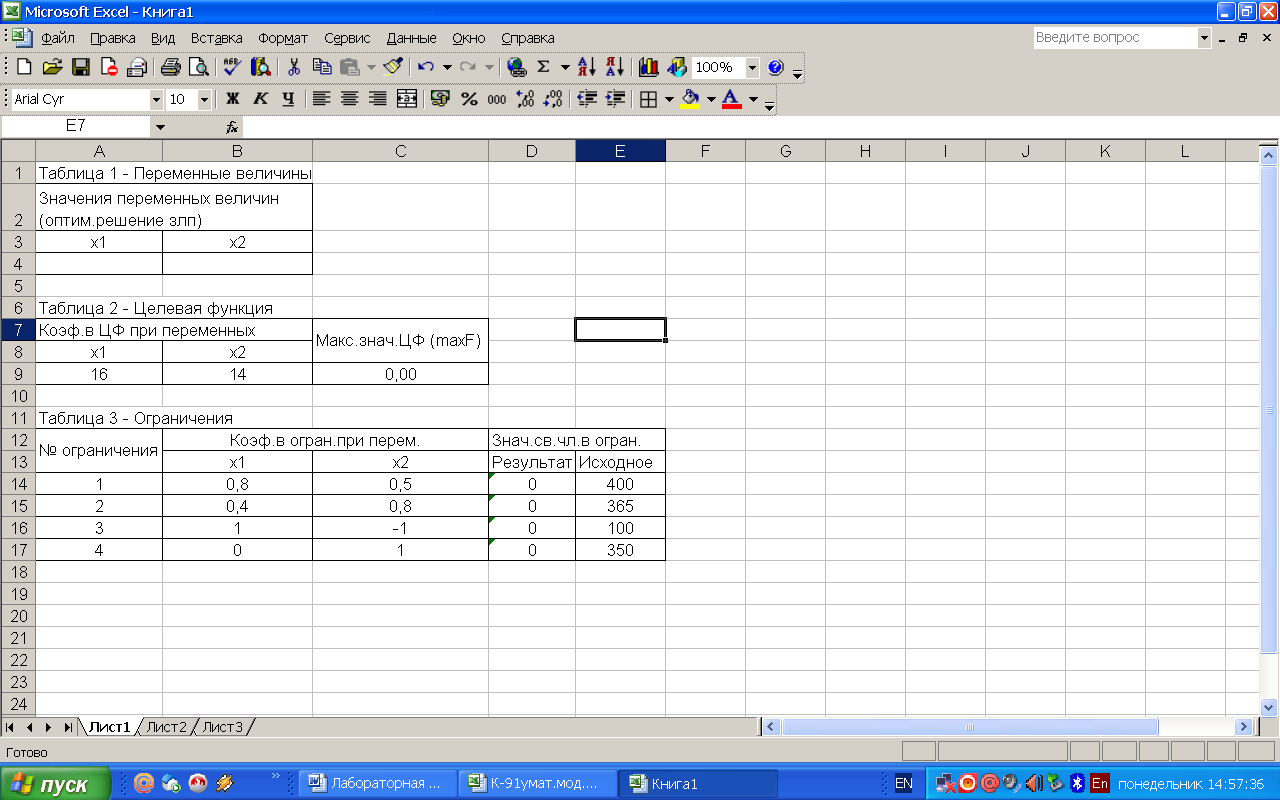
Рисунок 5 - Вставка формулы СУММПРОИЗВ в ячейки таблицы 2, 3


Далее выделяем ячейку С9 и находим значения переменных х₁, х₂ и максимальное значение целевой функции с помощью поиска решений (Сервис – Поиск решения) – рисунок 6.



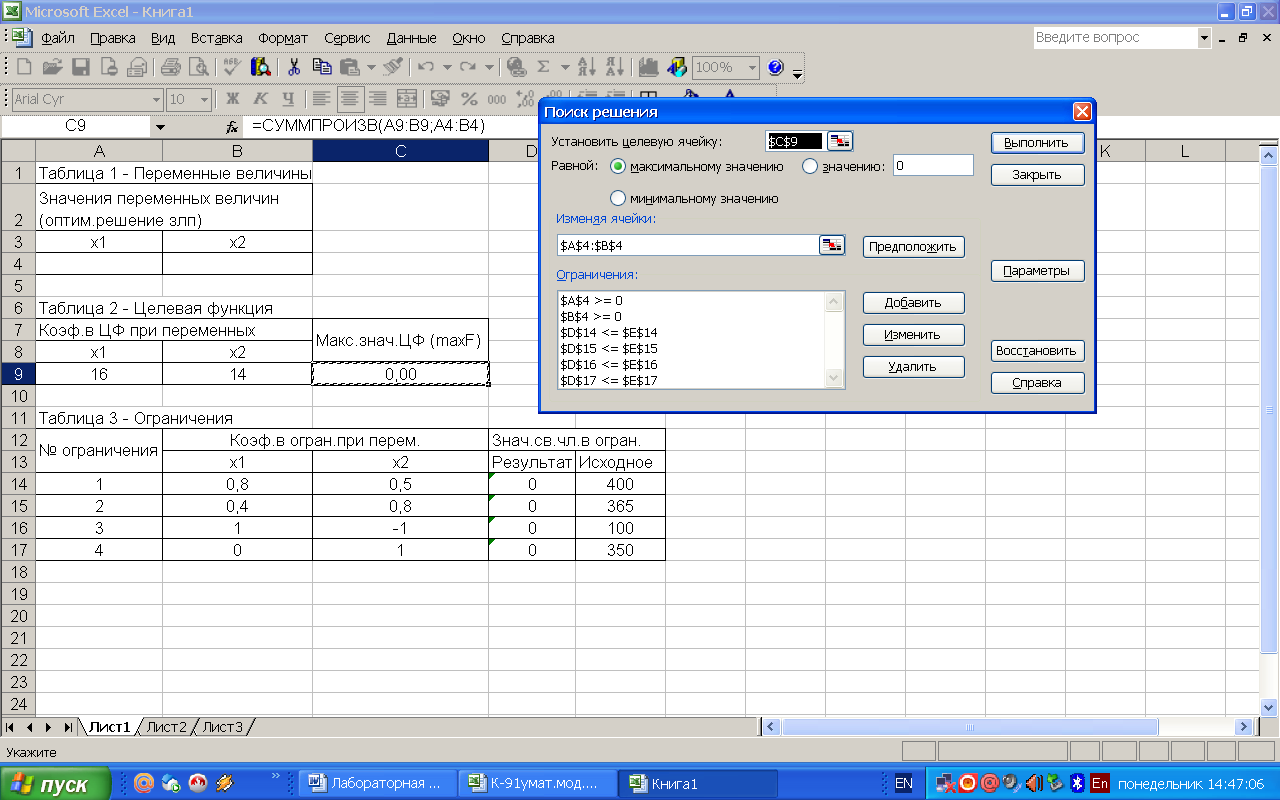
Рисунок 6 – Поиск решения


После того, как окно поиска решение заполнено необходимыми данными, нужно нажать Выполнить и решение будет найдено, его необходимо сохранить (рисунок 7).



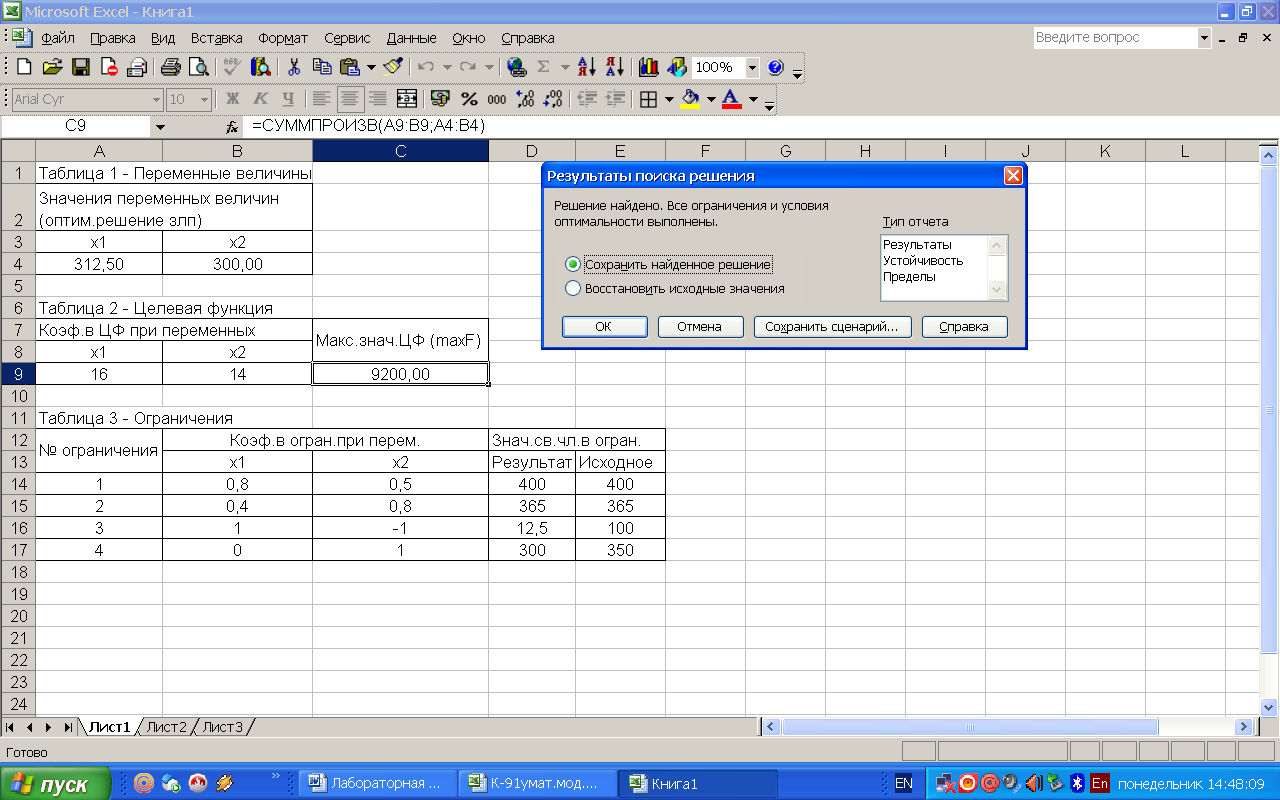
Рисунок 7 – Результаты поиска решений

В результате решения получили х₁^* = 312.5кг, х₂^* = 300кг, max а = 9200 ден.ед. Все ограничения выполнены.

Ответ: максимальный доход фирмы от реализации продукции составит 9200 ден.ед. при выпуске 312,5кг сливочного и 300кг шоколадного мороженного.

Условие задачи 2: Предприятие рекламирует свою продукцию с использованием четырех источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 усл.ед., в расчете на 1 усл.ед., затраченную на рекламу. На рекламу выделено 50000 усл.ед. Администрация предприятия не намерена тратить на телевидение более 40% (20000 усл.ед), а на радио и газеты – более 50% (25000 усл.ед) от общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?


Тема 2. Решение транспортных задач в Excel

Задание. Методы решения специальных задач линейного программирования.

Исполнение. Решение транспортных задач с помощью инструмента «Поиск решения».

Оценка. Формирует необходимые представления о методах решения специальных задач линейного программирования.

Время выполнения заданий: 3 часа.


Пример. На складах А1, А2, АЗ имеются запасы товаров в ко­личествах 90. 400 и 110 т соответственно. Грузополучатели В1, В2, ВЗ должны получить эти товары в количествах 130, 300, 1(50 т соответ­ственно. Требуется найти такой вариант перевозки грузов, при кото­ром сумма затрат на перевозки будет минимальной. Расходы по пере­возке 1 г грузов в условных единицах приведены в таблице.

Грузополучатели	Склад А1	Склад А2	Склад АЗ
В1	2	5	2
В2	4	1	5
ВЗ	3	6	8

Решение:

Математическая модель

Введем следующие обозначения:

X₁₁— количество товара, перевозимое грузополучателю B1 со склада А1;

X₁₂ — количество товара, перевозимое грузополучателю B1 со склада А2;

X₁₃— количество товара, перевозимое грузополучателю В1 со склада АЗ;

Х₂₁— количество товара, перевозимое грузополучателю В2 со склада А1;

X₂₂ - количество товара, перевозимое грузополучателю В2 со склада А2;

X₂₃— количество товара, перевозимое грузополучателю В2 со склада АЗ;

X₃₁— количество товара, перевозимое грузополучателю ВЗ со склада А1;

Х₃₂ - количество товара, перевозимое грузополучателю ВЗ со склада А2;

Х₃₃— количество товара, перевозимое грузополучателю ВЗ со склада АЗ.


Тогда целевая функция будет иметь вид

L = 2х₁₁+ 5х₁₂ + 2 х₁₃ + 4 х₂₁ + х₂₂+ 5 х₂₃ +3 х₃₁ + 6 х₃₂ + 8 х₃₂ → min

При ограничениях:

x₁₁+ х₁₂ + x₁₃ = 140 - груз, привезенный грузополучателю В1со всех складов

x₂₁+ х₂₂ + x₂₃ = 300 - груз привезенный, грузополучателю В2 со всех складов

x₃₁₊ х₃₂ + x₃₃ = 160 - груз, привезенный грузополучателю ВЗ со всех складов

x₁₁₊ х₂₁ + x₃₁= 90 - груз, отгруженный со склада А1

х₁₂ + х₂₂ + х₃₂ = 400 - груз, отгруженный со склада А2

х₁₃ + х₂₃ + х₃₃ = 90 - груз, отгруженный со склада АЗ

х₁₁≥0; х₁₂≥0; х₁₃≥0;

х₂₁≥0; х₂₂≥0; х₂₃≥0;

х₃₁≥0; х₃₂≥0; х₃₃≥0.

Представим математическую модель на рабочем-листе в виде, изображенном на рисунок 1, записывая в ячейку В9 формулу функ­ции цели, а в ячейки В11 - В16 формулы ограничений.

В диалоговом окне Поиск решения в соответствующих полях ус­тановим адрес целевой ячейки, адрес диапазона, содержащего подби­раемые параметры, введем все ограничения, установим переключатель Минимальному значению (рисунок 2, 3, 4).

После выполнения вычислений будет получен результат, представленный на рисунке 5. Минимальные затраты на перевозку грузов со складов потребителям при полученном плане перевозок составят 1360 у.е.



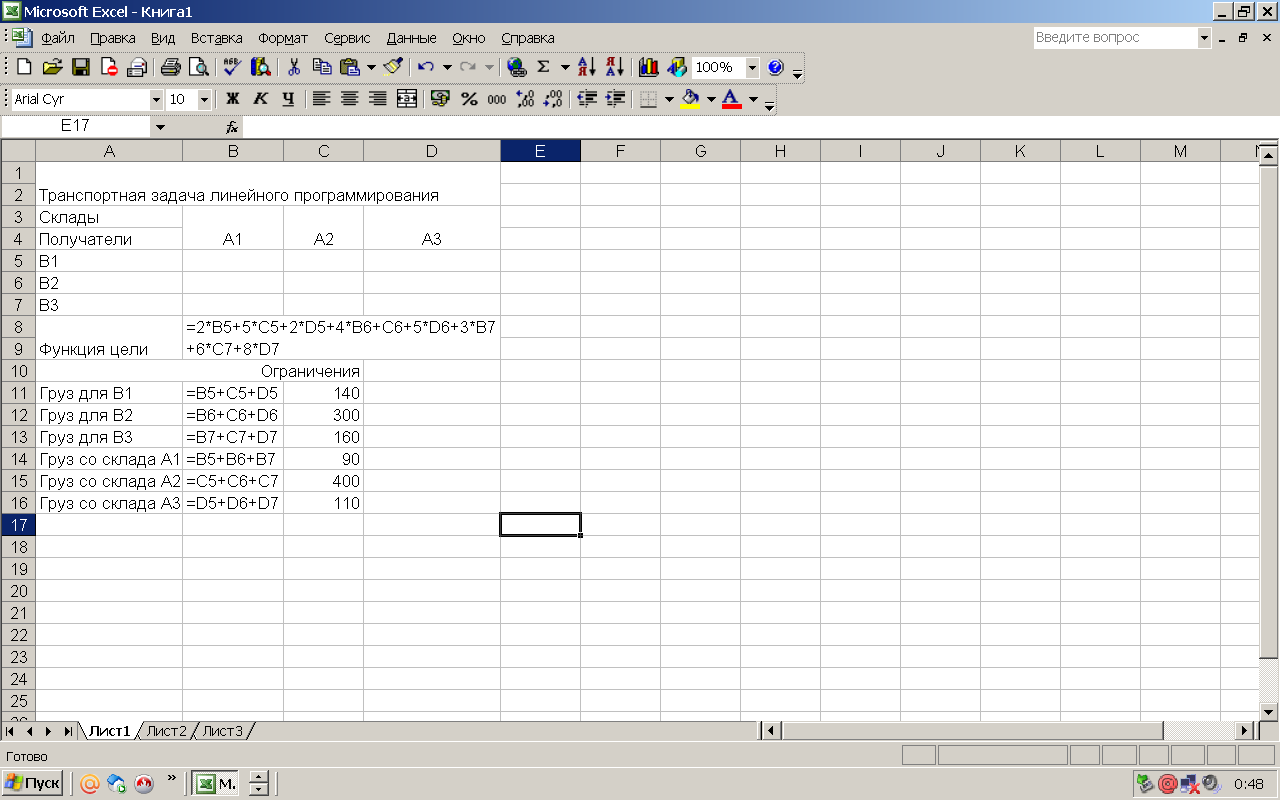
Рисунок 1




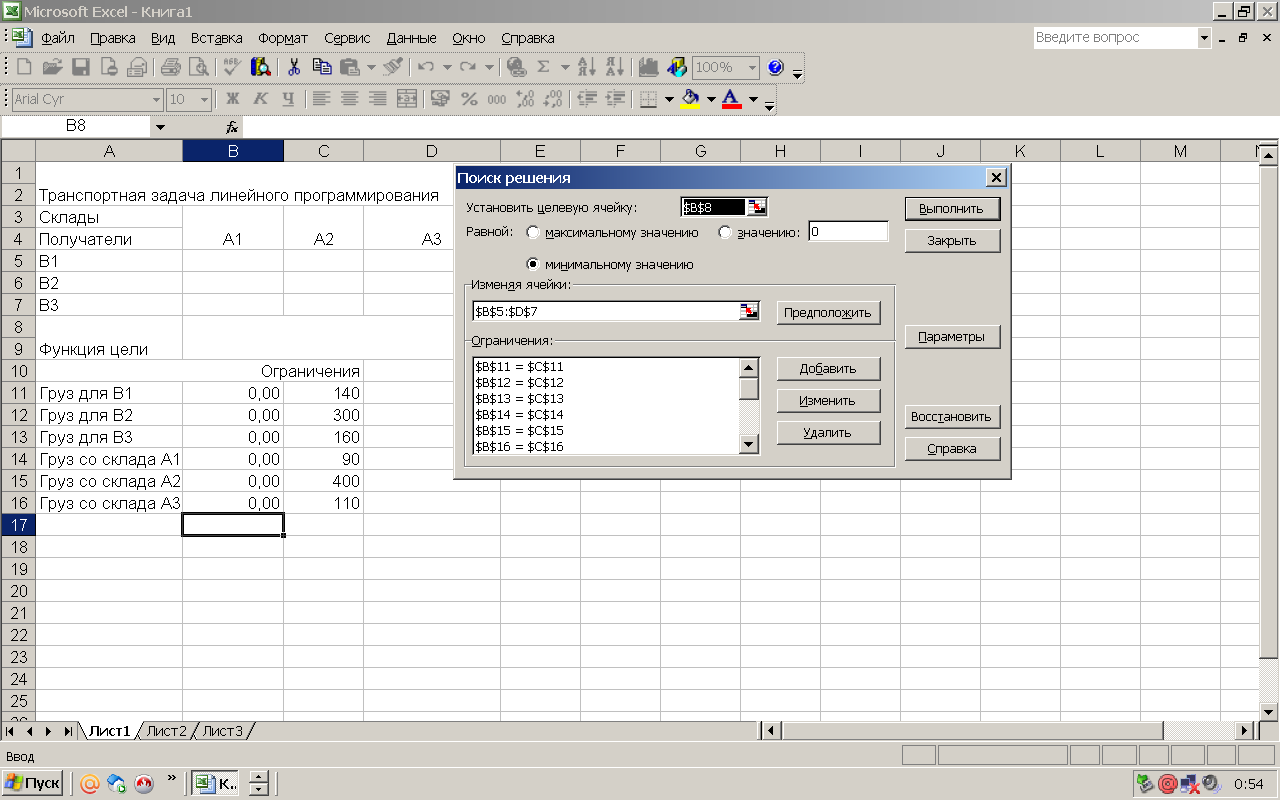
Рисунок 2




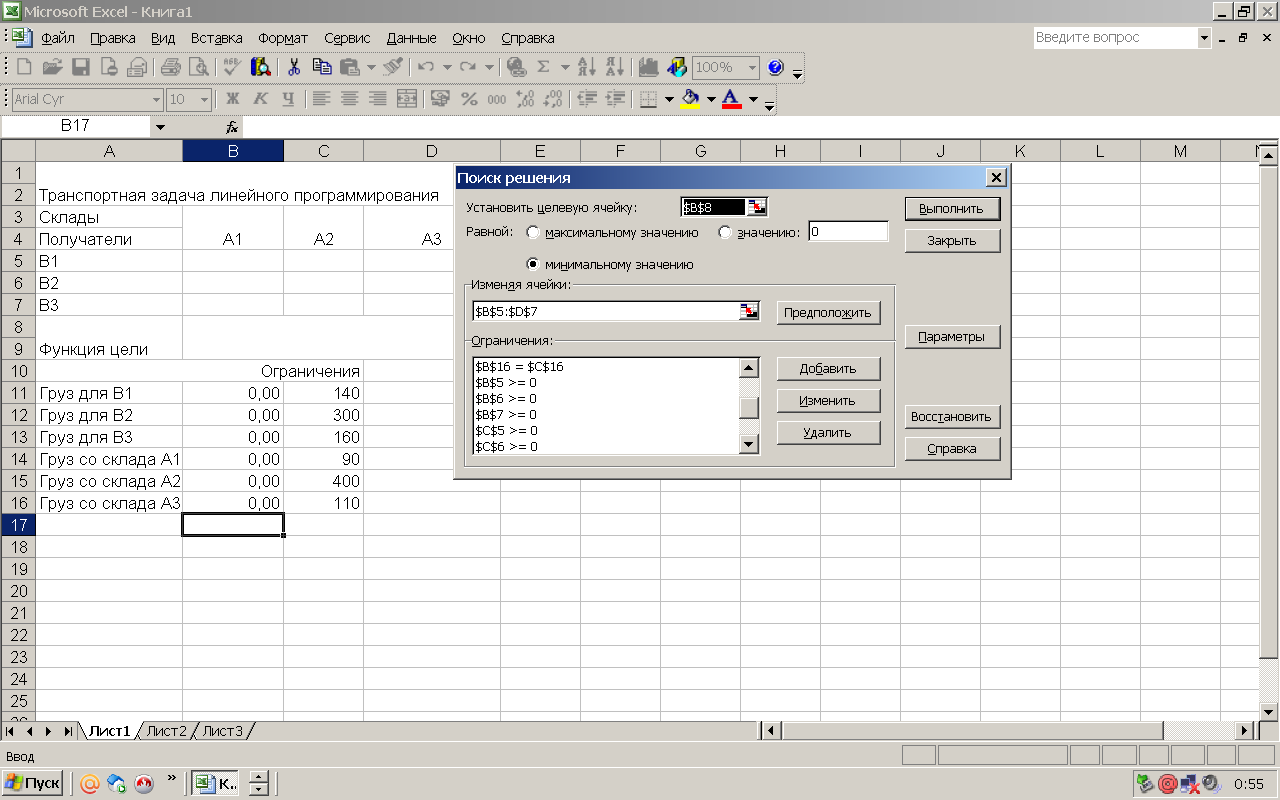
Рисунок 3




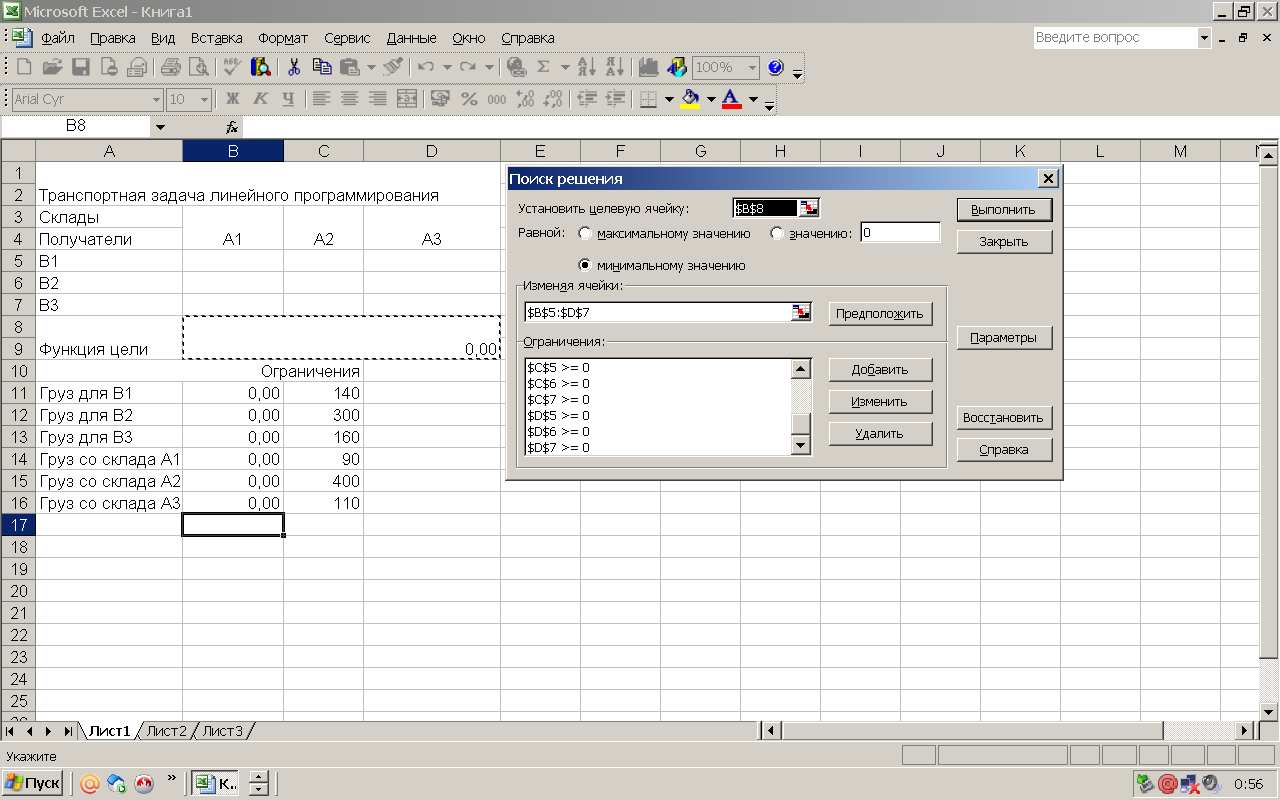
Рисунок 4



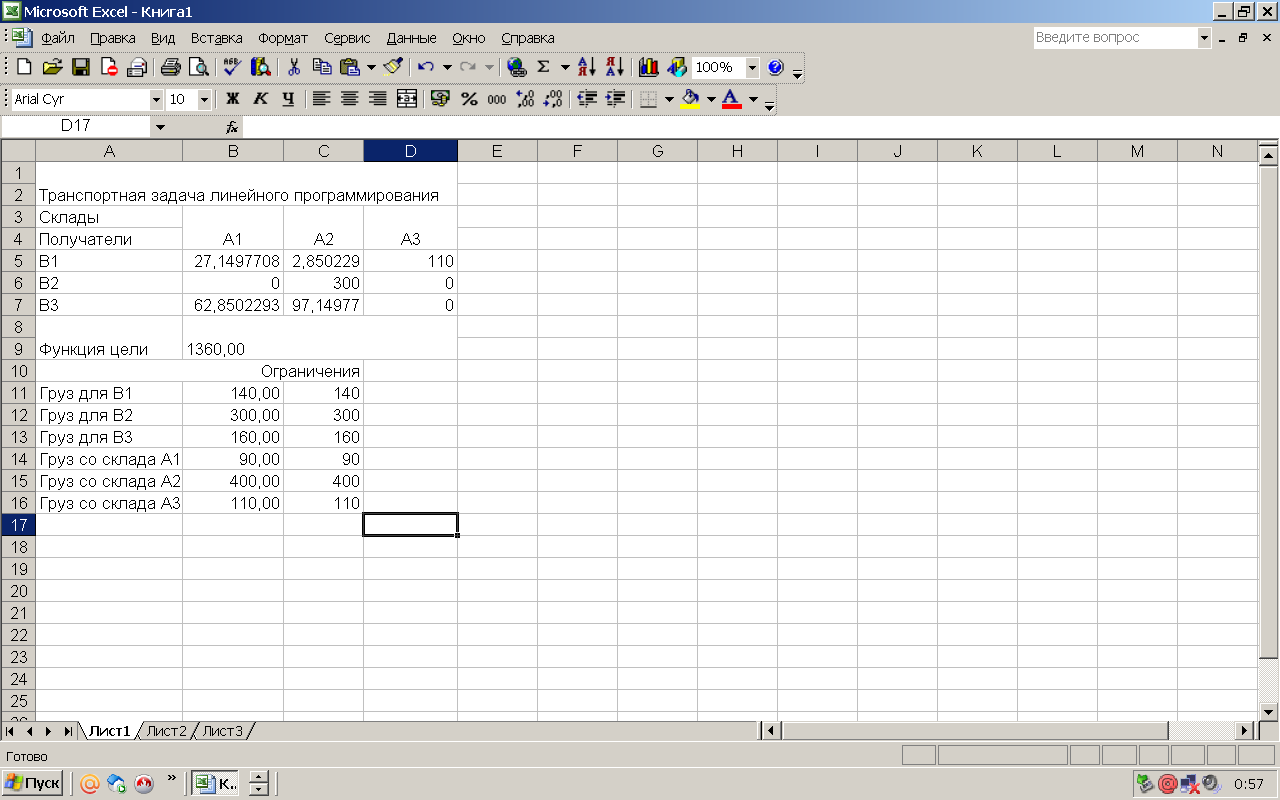
Рисунок 5


Тема 3. Технология решения задач регрессионного анализа в Excel

Задание. Уравнение линейной регрессии.

Исполнение. Построить уравнение линейной регрессии с помощью инструмента Пакета анализа «Регрессия».

Оценка. Формирует необходимые представления о методах получения уравнений регрессии.

Время выполнения заданий: 3 часа.

Регрессия позволяет проанализировать воздействие на какую-либо зависимую переменную одной или более независимых переменных и позволяет установить аналитическую фор­му (модель) этой зависимости в виде аппроксимирующего полинома.

Если рассматривается зависимость между одной зависимой пе­ременной у и несколькими независимыми х₁, х₂, ..., х_п, то речь идет о множественной линейной регрессии. В этом случае уравнение рег­рессии имеет вид

у = а₀ + а₁х₁ + а₂х₂+...+ а_пх_п,

где а₁, а₂ ... а_п - коэффициенты при независимых переменных, которые нужно

вычислить (коэффициенты регрессии);

а_о — константа.

При построении регрессионной модели важнейшими моментами являются оценка ее адекватности (эффективности) и значимости, на основании которых можно судить о возможности применения в прак­тике полученной модели.

Мерой оценки адекватности регрессионной модели является коэффициент детерминации R² (R-квадрат), который определяет, с ка­кой степенью точности полученное уравнение регрессии аппроксими­рует исходные данные.

Значимость регрессионной модели оценивается с помощью кри­терия Фишера (F-критерия). Если величина F-критерия значима (р < 0,05), то регрессионная модель является значимой.

В табличном процессоре можно аппроксимировать эксперимен­тальные данные линейным уравнением до 16-го порядка у = а₀ + а₁х₁ + а₂х₂+...+ а₁₆х₁₆.

Для вычисления коэффициентов регрессии служит инструмент Регрессия, который можно включить следующей последовательностью операций.

1. Выполнить команду Сервис/Анализ данных.
   
2. В раскрывшемся окне диалога Анализ данных выбрать из спис­ка строку Регрессия — раскроется окно диалога Регрессия.
   
3. В группе Входные данные в поле Входной интервал у указать адресную ссылку на диапазон, содержащий значения зависимой пере­менной, а в поле Входной интервал X — ссылку на диапазон, содержа­щий значения независимых переменных, т.е. переменных, влияние которых на зависимую переменную у оценивается. Установить фла­жок Метки, если исходная таблица имеет названия столбцов и фла­жок Константа-ноль, если а₀ = 0.
   

В группе Параметры выхода указать адресную ссылку на ячейку рабочего листа, которая будет являться верхней левой ячейкой резуль­тирующей таблицы.

Если необходимо получить визуальную картинку отличия экс­периментальных точек от предсказанных регрессионной моделью, то установить флажок График подбора.

Если нужно получить график нормальной вероятности, то уста­новить флажок График нормальной вероятности.

В выходном диапазоне после выполнения вычислений отобража­ются результаты дисперсионного анализа, коэффициенты регрессии, стандартная погрешность вычисления у, среднеквадратичные откло­нения, количество наблюдений, стандартные погрешности для коэф­фициентов.

Значения коэффициентов регрессии размещаются в столбце Коэффициенты:

• у — пересечение а₀;
  
• x₁ — коэффициент а₁;
  
• х₂ — коэффициент а₂ и т.д.
  

В столбце Р-Значение содержится оценка достоверности отличия соответствующих коэффициентов от нуля. Если Р > 0,05, то коэффи­циент можно считать нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую пере­менную.

Значение R-квадрат определяет, с какой степенью точности рег­рессионное уравнение будет аппроксимировать экспериментальные данные. Если R-квадрат > 0,95, то точность аппроксимации высокая. При 0,8
Кроме инструмента Регрессия в табличном процессоре для полу­чения параметров уравнения регрессии есть функция ЛИНЕЙН и функция ТЕНДЕНЦИЯ для получения значения у в требуемых точках.

Пример. Имеются статистические данные о затратах, свя­занных с рекламой по телевидению, с рекламой в метро и объеме реали­зации продукции в рублях, приведенные в таблице.

Затраты на рекламу но телевидению (руб.)	Затраты па рекламу в метро (руб.)	Объем реализации (руб.)
125850	20000	1850000
260500	21000	2500000
150000	22000	1900000
300000	21000	3000000
280000	24000	2600000
290000	23000	2700000
140000	20000	1900000

Требуется найти регрессионные коэффициенты для независимых переменных Расходы на рекламу по телевидению и Расходы на рекламу в метро на объем реализации продукции и построить уравнение регрессии.

Решение:

1. На рабочем листе в диапазон А1:С8 введем данные приведен­ной таблицы.
   
2. Включим инструмент Регрессия.
   

3.В открывшемся диалоговом окне Регрессия установим пара­метры как показано на рисунке 1.

- Входной интервал у — диапазон С1:С8;

- Входной интервал х — диапазон А1:В8;

- Флажок Метки;

- Выходной интервал — адрес D1;

- Флажок График нормальной вероятности;

- Флажок График остатков.

После щелчка на кнопке ОК в диапазон D1:L21 будет выведен результат регрессионного анализа (рисунок 2).




Рисунок 1

Полученные результаты и их интерпретация

• Коэффициент детерминации R-квадрат - 0,974641 (аппрокси­мация высокая).
  
• Значимость F = 0,000643 (р < 0,05 — регрессионная модель зна­чима).
  
• У-пересечение a₀⁼ 2102438,6
  
• a₁ = 6,4004 — коэффициент при независимой переменной За­траты на рекламу по телевидению.
  
• а₂ = -54,068 — коэффициент при независимой переменной За­траты на рекламу в метро.
  

С учетом полученных данных функциональная зависимость ве­личины прибыли от затрат на рекламу запишется в виде полинома у = 2102438,6 + 6,4004х₁ - 54,068х₂,

где х₁ — величина затрат на рекламу по телевидению;

x₂ — величина затрат на рекламу в метро.

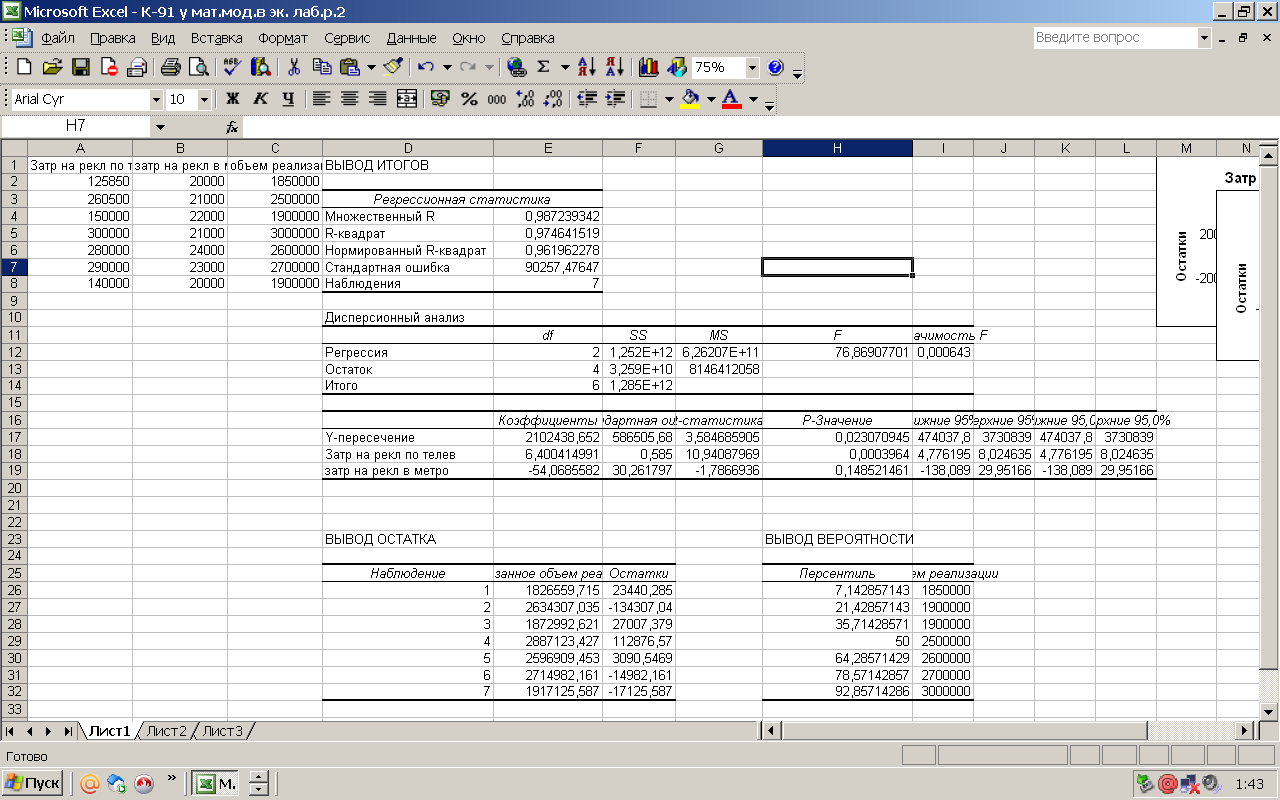
Рисунок 2