Контрольная работа по дисциплине «Теоретические основы информатики» направление 050200. 62 Физико-математическое образование (бакалавр), профиль подготовки «Информатика»

Вид материала

Контрольная работа

Подобный материал:

• Рабочая программа по дисциплине: математический анализ направление, 531.3kb.
• График учебного процесса направление 050200 Физико-математическое образование профиль, 52.92kb.
• Учебно- методический комплекс учебной дисциплины дпп. 04"Теоретические основы информатики", 530.12kb.
• Программа вступительных испытаний для лиц, поступающих в магистратуру на направление, 220.49kb.
• Курс по направлению 050200. 62 «Физико-математическое образование» профиль «Математика», 48.27kb.
• Учебно-методический комплекс курса по выбору (опд) Направление подготовки 050202., 311kb.
• Учебная программа дисциплины опд. Р. 05. Основы дискретной математики Направление:, 113.76kb.
• Рабочая учебная программа по дисциплине «Технологии и методики обучения информатике», 457.47kb.
• Программа вступительного испытания по дисциплине Физика с теорией и методикой обучения, 388.78kb.
• Учебно-методический комплекс учебной дисциплины сдм. 02 «программирование» подготовки, 879.43kb.

Государственное образовательное учреждение

высшего профессионального образования

«Тобольская государственная социально-педагогическая академия

им. Д.И. Менделеева»


Кафедра информатики, ТиМОИ


КОНТРОЛЬНАЯ РАБОТА


по дисциплине «Теоретические основы информатики»

направление 050200.62 – Физико-математическое образование (бакалавр), профиль подготовки «Информатика»

физико-математический факультет

отделение заочного обучения

III курс, 6 семестр

2010-2011 уч. год


Составил: ст. преподаватель

кафедры информатики, ТиМОИ

Лудова О.М.


Тобольск – 2011

Вариант-1


1. Выполнить перевод чисел из одной системы счисления в другую:

1. 110101001010₂ → Х₈
   
2. 1001011001,01₂ → Х₁₀
   
3. 5948₁₀ → Х₁₆
   

2. Получить двоичный код числа Z = 82₁₀ и преобразовать его в код Грея Z_G.


3. Преобразовать код Грея Z_G = 10101000101100 в двоичный код.


4. Используя методику Шеннона-Фано провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,09; p(z₂) = 0,15; p(z₃) = 0,24; p(z₄) = 0,01; p(z₅) = 0,26; p(z₆) = 0,07; p(z₇) = 0,16; p(z₈) = 0,02.

Вычислить среднее число разрядов на знак.


5. Используя алгоритм Хаффмена провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,09; p(z₂) = 0,15; p(z₃) = 0,24; p(z₄) = 0,01; p(z₅) = 0,26; p(z₆) = 0,07; p(z₇) = 0,16; p(z₈) = 0,02.

Вычислить среднее число разрядов на знак.


6. Получить двоичный код числа Z = 37₁₀ и определить для него код Хемминга.


7. Определить значение числа, переданного с использованием кода Хемминга 1010001011010, если при передаче имела место однократная ошибка.


8. Построить таблицу переходов и граф переходов для машины Тьюринга, заданной программой:

q₁ a → q₂ R, q₁ b→ R, q₁ 0→ q₆ L, q₂ a → q₃ c R, q₂ b → q₄ c R, q₃ a → a R, q₃ b → q₄ a R, q₃ 0 → q₅ a L, q₄ a → q₃ b R, q₄ b → b R, q₄ 0 → q₅ b L, q₅ b → L, q₅ c → q₁ a R, q₆ a → L, q₆ b → L, q₆ c → a L, q₆ 0 → q₀ R.

Применить машину Тьюринга из задания 1 к следующим начальным конфигурациям и определить заключительные конфигурации:

1. bbaba
   
2. abbbaab
   
3. abaaba
   

9. Составить программу машины Тьюринга, вычисляющей функцию
   

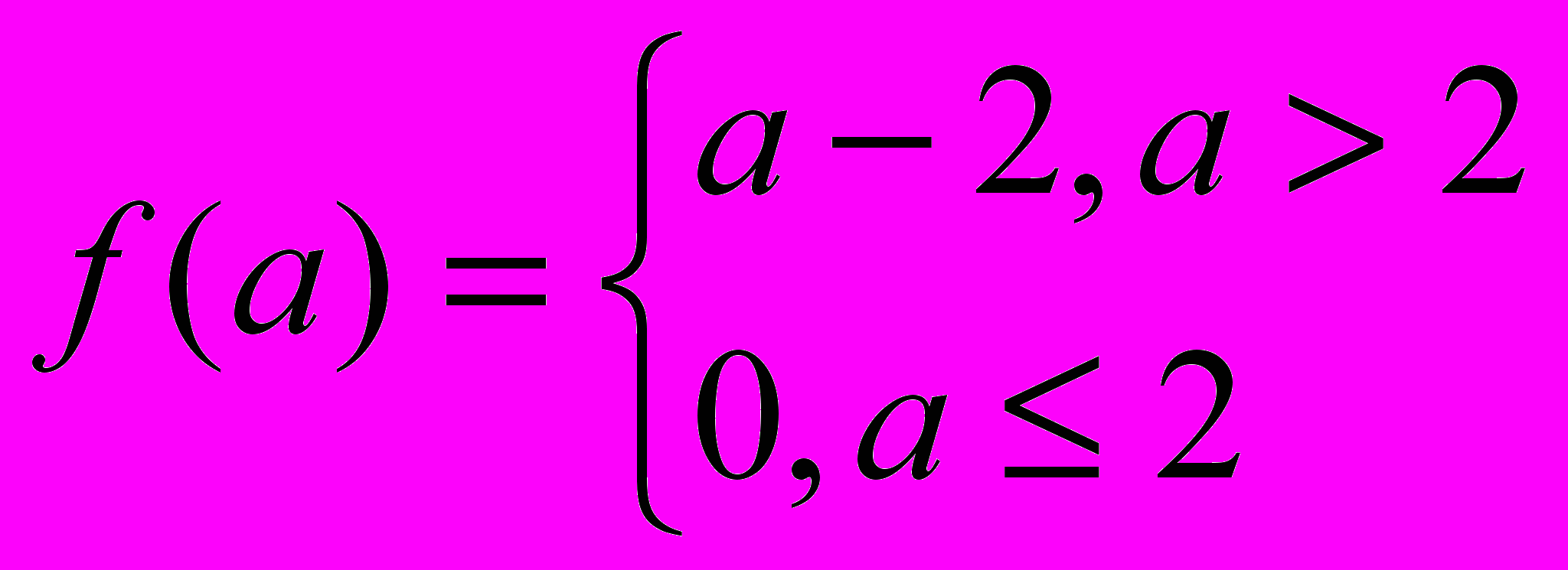
и проиллюстрировать ее работу.


10. Докажите, что одноместная функция f(x) принадлежит классу примитивно рекурсивных функций: f(x) = x


11. Докажите, что двухместная функция f(x, y) принадлежит классу примитивно рекурсивных функций: f(x, y) = x∙(y + 1)


12. Построить нормальный алгоритм Маркова для вычисления функции f(x) = x – 1 в двоичной системе счисления.


Вариант-2


1. Выполнить перевод чисел из одной системы счисления в другую:

1. 5А4D7₁₆ → Х₈
   
2. 4657₁₀ → Х₈
   
3. 1101001101,011₂ → Х₁₀
   

2. Получить двоичный код числа Z = 74₁₀ и преобразовать его в код Грея Z_G.


3. Преобразовать код Грея Z_G = 00110110010101101 в двоичный код.


4. Используя методику Шеннона-Фано провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,12; p(z₂) = 0,01; p(z₃) = 0,08; p(z₄) = 0,19; p(z₅) = 0,23; p(z₆) = 0,02; p(z₇) = 0,31; p(z₈) = 0,04.

Вычислить среднее число разрядов на знак.


5. Используя алгоритм Хаффмена провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,12; p(z₂) = 0,01; p(z₃) = 0,08; p(z₄) = 0,19; p(z₅) = 0,23; p(z₆) = 0,02; p(z₇) = 0,31; p(z₈) = 0,04.

Вычислить среднее число разрядов на знак.


6. Получить двоичный код числа Z = 46₁₀ и определить для него код Хемминга.


7. Определить значение числа, переданного с использованием кода Хемминга 1110010100110010, если при передаче имела место однократная ошибка.


8. Построить таблицу переходов и граф переходов для машины Тьюринга, заданной программой:

q₁ 0 → q₅ R, q₂ a→ R, q₂ b→ R, q₂ 0 → q₃ 1 R, q₂ 1 → R, q₃ a → L, q₃ b → L, q₃ c → q₅ R, q₃ 0 → q₀, q₃ 1 → L, q₄ a → 0 L, q₄ b → 0 L, q₄ c → 0 L, q₄ 0 → R, q₄ 1 → q₀ L, q₅ a → q₂ c R, q₅ b → R, q₅ 0 → q₃ L, q₅ 1 → q₄ L.

Применить машину Тьюринга из задания 1 к следующим начальным конфигурациям и определить заключительные конфигурации:

1. 0aaaaa
   
2. 0aaababa
   
3. 0bbbbb
   

9. Составить программу машины Тьюринга, вычисляющей функцию

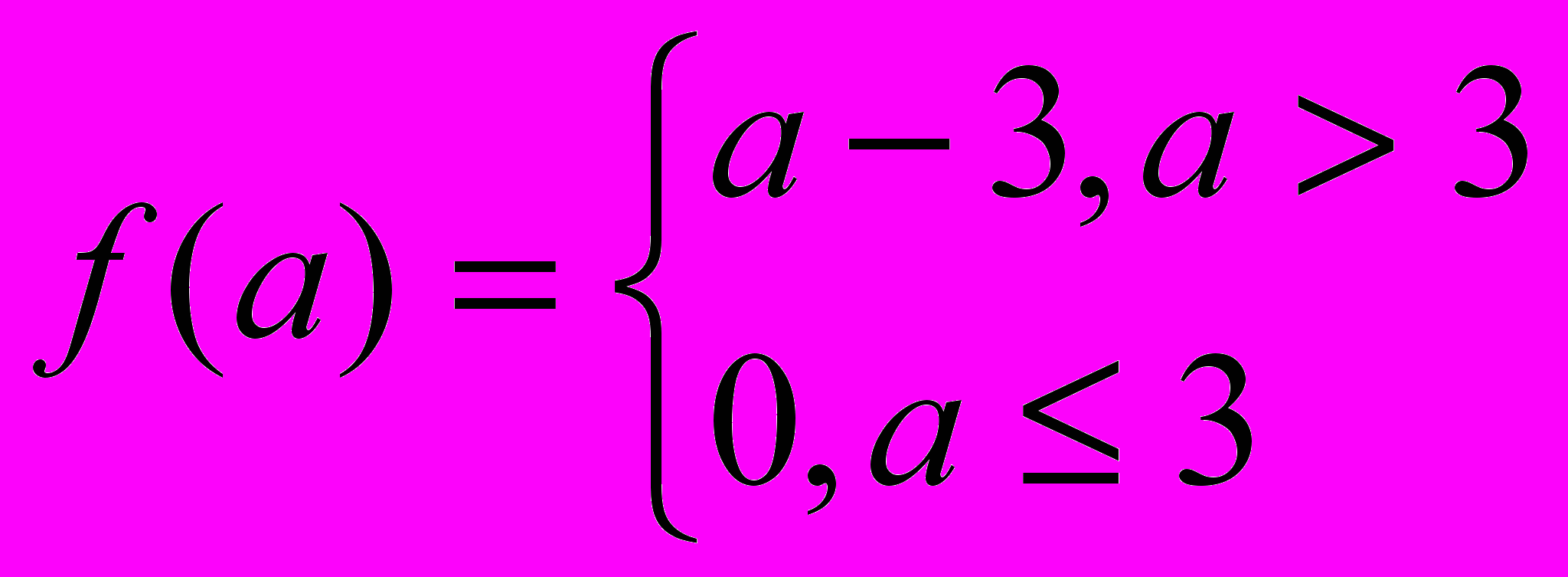
и проиллюстрировать ее работу.


10. Докажите, что одноместная функция f(x) принадлежит классу примитивно рекурсивных функций: f(x) = x + 5


11. Докажите, что двухместная функция f(x, y) принадлежит классу примитивно рекурсивных функций: f(x, y) = x + y + 2


12. Построить нормальный алгоритм Маркова для вычисления функции f(x) = x – 1 в восьмеричной системе счисления.


Вариант-3


1. Выполнить перевод чисел из одной системы счисления в другую:

1. 3208₁₀ → Х₂
   
2. 100011010,11₂ → Х₁₀
   
3. 61523₈ → Х₁₆
   

2. Получить двоичный код числа Z = 91₁₀ и преобразовать его в код Грея Z_G.


3. Преобразовать код Грея Z_G = 01001101100100 в двоичный код.


4. Используя методику Шеннона-Фано провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,05; p(z₂) = 0,13; p(z₃) = 0,20; p(z₄) = 0,15; p(z₅) = 0,22; p(z₆) = 0,07; p(z₇) = 0,08; p(z₈) = 0,10.

Вычислить среднее число разрядов на знак.


5. Используя алгоритм Хаффмена провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,05; p(z₂) = 0,13; p(z₃) = 0,20; p(z₄) = 0,15; p(z₅) = 0,22; p(z₆) = 0,07; p(z₇) = 0,08; p(z₈) = 0,10.

Вычислить среднее число разрядов на знак.


6. Получить двоичный код числа Z = 29₁₀ и определить для него код Хемминга.


7. Определить значение числа, переданного с использованием кода Хемминга 110100110011101, если при передаче имела место однократная ошибка.


8. Построить таблицу переходов и граф переходов для машины Тьюринга, заданной программой:

q₁ a → q₂ R, q₁ b→ R, q₁ 0→ q₆ L, q₂ a → q₃ c R, q₂ b → q₄ c R, q₃ a → a R, q₃ b → q₄ a R, q₃ 0 → q₅ a L, q₄ a → q₃ b R, q₄ b → b R, q₄ 0 → q₅ b L, q₅ b → L, q₅ c → q₁ a R, q₆ a → L, q₆ b → L, q₆ c → a L, q₆ 0 → q₀ R.

Применить машину Тьюринга из задания 1 к следующим начальным конфигурациям и определить заключительные конфигурации:

1. baaab
   
2. aababbb
   
3. bbaba
   

9. Составить программу машины Тьюринга, вычисляющей функцию

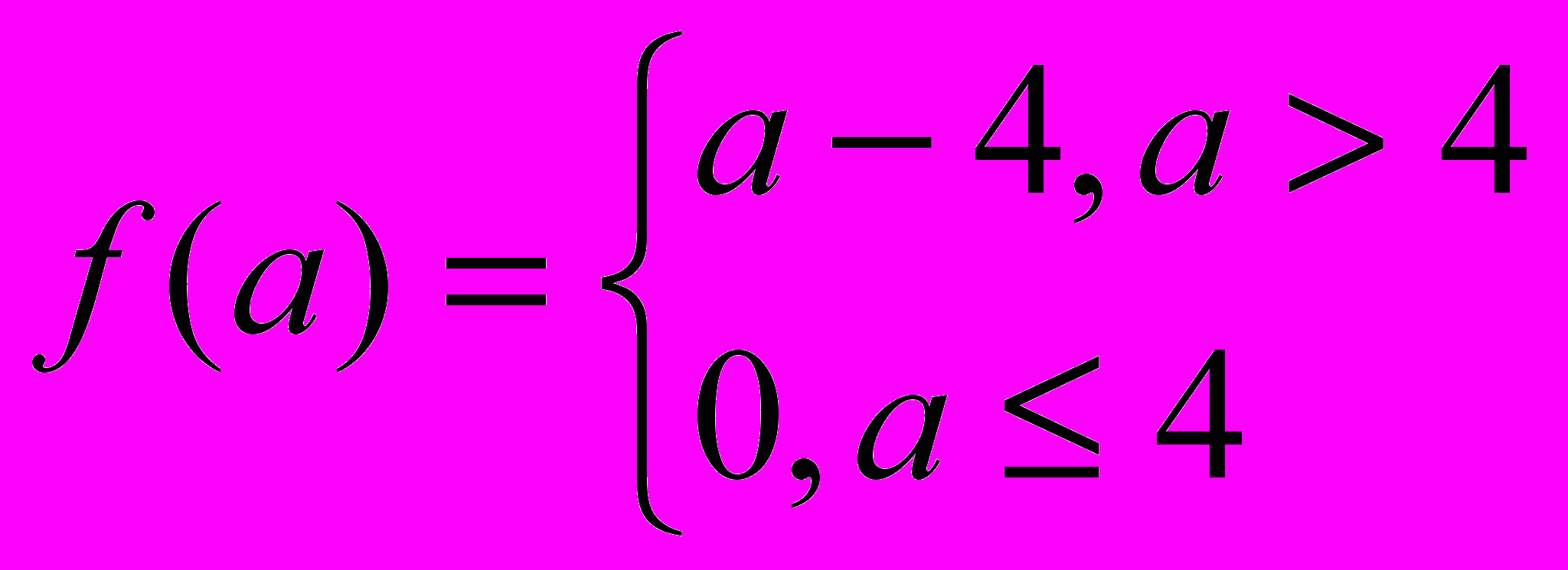
и проиллюстрировать ее работу.


10. Докажите, что одноместная функция f(x) принадлежит классу примитивно рекурсивных функций: f(x) = 2∙x + 1


11. Докажите, что двухместная функция f(x, y) принадлежит классу примитивно рекурсивных функций: f(x, y) = x + 4∙y


12. Построить нормальный алгоритм Маркова для вычисления функции f(x) = x – 1 в пятеричной системе счисления.


Вариант-4


1. Выполнить перевод чисел из одной системы счисления в другую:

1. 1001110100,101₂ → Х₁₀
   
2. 26073₈ → Х₂
   
3. 4103₁₀ → Х₁₆
   

2. Получить двоичный код числа Z = 85₁₀ и преобразовать его в код Грея Z_G.


3. Преобразовать код Грея Z_G = 10001011001010 в двоичный код.


4. Используя методику Шеннона-Фано провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,15; p(z₂) = 0,13; p(z₃) = 0,20; p(z₄) = 0,14; p(z₅) = 0,12; p(z₆) = 0,07; p(z₇) = 0,08; p(z₈) = 0,11.

Вычислить среднее число разрядов на знак.


5. Используя алгоритм Хаффмена провести эффективное кодирование группы из восьми элементов, имеющих следующие характеристики:

p(z₁) = 0,15; p(z₂) = 0,13; p(z₃) = 0,20; p(z₄) = 0,14; p(z₅) = 0,12; p(z₆) = 0,07; p(z₇) = 0,08; p(z₈) = 0,11.

Вычислить среднее число разрядов на знак.


6. Получить двоичный код числа Z = 53₁₀ и определить для него код Хемминга.


7. Определить значение числа, переданного с использованием кода Хемминга 01101001100110, если при передаче имела место однократная ошибка.


8. Построить таблицу переходов и граф переходов для машины Тьюринга, заданной программой:

q₁ 0 → q₅ R, q₂ a→ R, q₂ b→ R, q₂ 0 → q₃ 1 R, q₂ 1 → R, q₃ a → L, q₃ b → L, q₃ c → q₅ R, q₃ 0 → q₀, q₃ 1 → L, q₄ a → 0 L, q₄ b → 0 L, q₄ c → 0 L, q₄ 0 → R, q₄ 1 → q₀ L, q₅ a → q₂ c R, q₅ b → R, q₅ 0 → q₃ L, q₅ 1 → q₄ L.

Применить машину Тьюринга из задания 1 к следующим начальным конфигурациям и определить заключительные конфигурации:

1. 0abbaaba
   
2. 0bbabaab
   
3. 0aaaaaaab
   

9. Составить программу машины Тьюринга, вычисляющей функцию

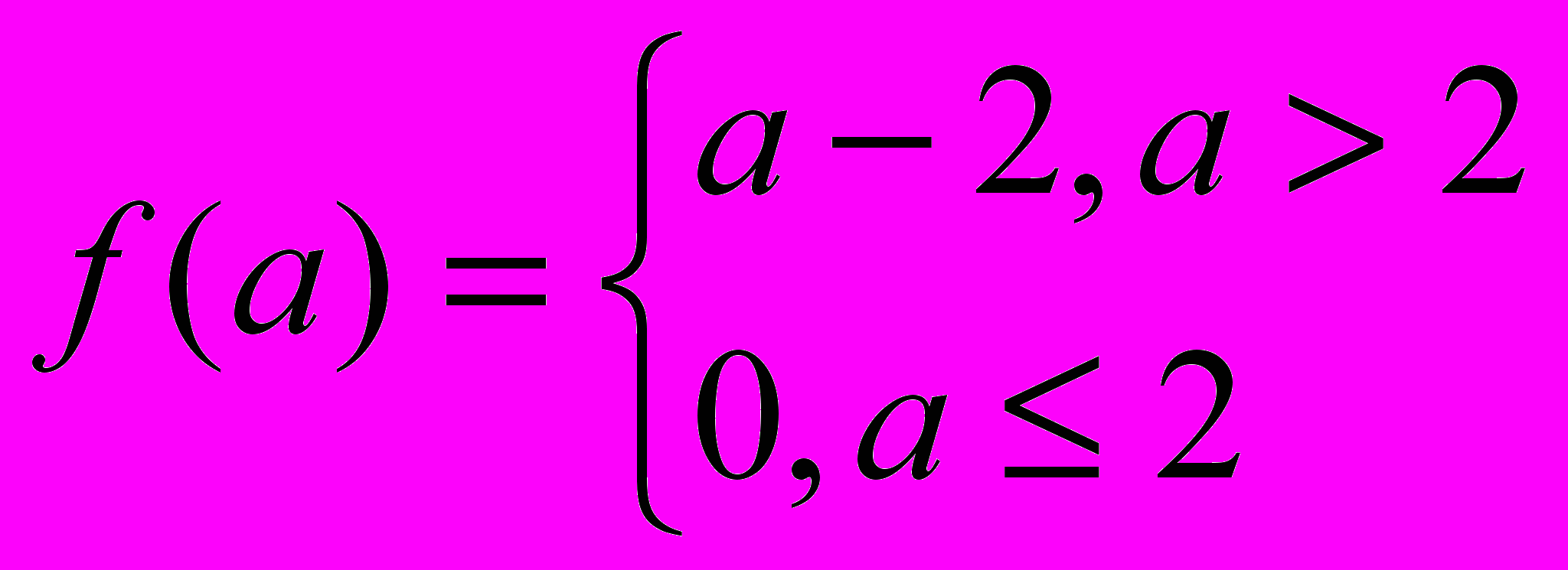
и проиллюстрировать ее работу.


10. Докажите, что одноместная функция f(x) принадлежит классу примитивно рекурсивных функций: f(x) = 4∙x


11. Докажите, что двухместная функция f(x, y) принадлежит классу примитивно рекурсивных функций: f(x, y) = (x + 1)∙y


12. Построить нормальный алгоритм Маркова для вычисления функции f(x) = x – 1 в десятичной системе счисления.