Программа вступительного экзамена в магистратуру по специальности 521602 «Математические методы анализа экономики»

Вид материала

Содержание

521602 – «Математические методы анализа экономики»
В первой части
Во второй части
Соответствие содержания дисциплин, включенных в настоящую программу государственным образовательным стандартам подготовки бакала
Экзаменационные билеты включают три теоретических вопроса и две задачи
I. дисциплины, их основное содержание и рекомендуемая литература
Рекомендуемая литература по информатике
II. ОСНОВНЫЕ СВЕДЕНИЯ ПО МАТЕМАТИКЕ: понятия, свойства, методы

Подобный материал:

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ УПРАВЛЕНИЯ И РЕГИОНАЛЬНОЙ ЭКОНОМИКИ

УТВЕРЖДАЮ		УТВЕРЖДАЮ
Проректор ВолГУ по учебной работе, профессор		Декан факультета управления и региональной экономики, профессор
_________________________С.Г.Сидоров		_______________________А.Э.Калинина
_________________________2009 г.		_______________________2009 г.

ПРОГРАММА

вступительного экзамена в магистратуру по специальности

521602 – «Математические методы анализа экономики»

Утверждена
на заседании кафедры математических методов и информатики в экономике

28 апреля 2009 г.

Протокол № 8

Заведующая кафедрой ММИЭ, д.э.н, проф. Л.Ю. Богачкова

Настоящая программа состоит из двух частей.

В первой части перечислены включенные в программу дисциплины, к которым относятся «Математика», «Экономика», «Информатика», приведены их основное содержание и рекомендуемая литература.

Во второй части указаны основные сведения по математике (понятия, формулы, свойства, методы), необходимые для успешного решения задач, включаемых в экзаменационные билеты.

Объем знаний и степень владения материалом, описанным в программе, соответствуют необходимому минимуму знаний, определенному государственными образовательными стандартами для бакалавров по направлениям 080100 – «Экономика», 010100 – «Математика», 010500 – «ссылка скрыта», как показано в табл. 1. Допускается также грамотное использование сведений, выходящих за рамки данной программы, но при этом от абитуриента требуются исчерпывающие пояснения к его действиям.

Таблица 1.

Соответствие содержания дисциплин, включенных в настоящую программу государственным образовательным стандартам подготовки бакалавров

Дисциплина, включенная в настоящую программу	Направление подготовки бакалавров, определяющее содержание дисциплины
Математика	080100 – «Экономика»
Экономика	010100 – «Математика», 010500 – «ссылка скрыта»
Информатика	080100 – «Экономика»

Экзаменационные билеты включают три теоретических вопроса и две задачи. Теоретические вопросы относятся к сферам экономики (два вопроса) и информатики (один вопрос); задачи – к различным областям математики, например: первая задача по математическому анализу, а вторая – по теории вероятностей.

На вступительном экзамене в магистратуру по специальности 521602 – «Математические методы анализа экономики» абитуриент должен показать:

а) знание теоретических основ экономической теории, базовых принципов, положений и моделей микро- и макроэкономики;

б) знакомство с основными положениями наиболее широко используемых разделов информатики, а также с тенденциями их развития; осведомленность о современных информационных технологиях, применяемых в экономике и управлении; наличие навыков работы с ПЭВМ;

в) уверенное владение математическими знаниями из областей математического анализа, линейной алгебры и аналитической геометрии, теории вероятностей и математической статистики, предусмотренными данной программой; умение применять их при решении задач.

I. ДИСЦИПЛИНЫ, ИХ ОСНОВНОЕ СОДЕРЖАНИЕ И РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Математика

1.1. Математический анализ

Понятие множества. Операции над множествами. Понятие окрестности точки. Функциональная зависимость. Графики основных элементарных функций. Предел числовой последовательности. Предел функции. Непрерывность функции в точке. Свойства числовых множеств и последовательностей. Глобальные свойства непрерывных функций. Производная и дифференциал. Основные теоремы о дифференцируемых функциях и их приложения. Выпуклость функции. Неопределенный интеграл. Несобственные интегралы. Точечные множества в N – мерном пространстве. Функции нескольких переменных, их непрерывность. Производные и дифференциалы функций нескольких переменных. Классические методы оптимизации. Дифференциальные уравнения первого и второго порядка.

1.2. Линейная алгебра и элементы аналитической геометрии

Системы линейных уравнений. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве. Определители. Системы векторов, ранг матрицы. N – мерное линейное векторное пространство. Линейные операторы и матрицы. Собственные векторы линейных операторов. Евклидово пространство. Квадратичные формы. Системы линейных неравенств. Линейные задачи оптимизации.

1.3. Теория вероятностей и математическая статистика

Основные понятия теории вероятностей. Вероятностное пространство. Случайные величины и способы их описания. Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях. Закон распределения вероятностей для функций от известных случайных величин. Неравенство Чебышева. Закон больших чисел и его следствие. Особая роль нормального распределения: центральная предельная теорема. Цепи Маркова и их использование в моделировании социально-экономических процессов. Статистическое оценивание и проверка гипотез, статистические методы обработки экспериментальных данных.

Рекомендуемая литература по математике

Основная литература

Высшая математика для экономистов./ Под ред. Н.Ш.Кремера. – Москва: Юнити, 2003.
Гмурман В.Е.. Теория вероятностей и математическая статистика – М., 2003.
Ермаков В.И.. Общий курс высшей математики для экономистов – М., 2000.
Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М.: ВШ, 1982. – Ч. 1,2.
Колесников А.Н. Краткий курс математики для экономистов. – М.: Инфра-М, 2000.
Красс М.С. Математика для экономических специальностей. – М.: Дело, 2002.
Кремер Н.Ш. и др., Исследование операций в экономике. М.: ЮНИТИ, 1997.
Кудрявцев В.А., Демидович Б.П.. Краткий курс высшей математики: Учебное пособие для ВУЗ-ов. М.: Наука, 1989.
Малыхин В.И. Математика в экономике. – М.: ИНФРА-М, 1999.
Мироненко Е.С.. Высшая математика – М., 1998.
Практикум по высшей математике для экономистов / Под ред. Н.Ш.Кремера. – Москва: Юнити, 2003.
Общий курс высшей математики для экономистов / Под редакцией В.И. Ермакова. – М.: ИНФРА-М, 2000. – 656 с.
Солодовников А.С. Бабайцев В.А., Браилов А.В. Математика в экономике. – М.: Финансы и статистика, 1998
Солодовников А.С.. Теория вероятностей – М., 1983.
Таха Х. Введение в исследование операций, в 2х т., 1985.

Дополнительная литература

Агапов Г.И.. Задачник по теории вероятностей. М., 1986.
Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
Андрухаев Х.М. Сборник задач по теории вероятностей – М., 1985.
Вагнер Г. Основы исследования операций. В 3-х т., 1972–1973.
Ватюкова О.Ю., Зайцева Е.Е., Зайцева Ю.В., Пономарева Л.В., Черкунова Н.А.. Математика (математический анализ). – Волгоград, Изд-во ВолГУ, 2007.
Ватюкова О.Ю., Черкунова Н.А., Сборник задач по линейной алгебре для студентов экономических специальностей, 2007г
Ватюкова О.Ю., Черкунова Н.А., Сборник задач по теории вероятностей для студентов экономических специальностей, 2007г.
Вентцель Е. . Исследование операций. Задачи, принципы, методология. – М.: Наука, 1988.
Гнеденко Б.В. Курс теории вероятностей.  М., 2000.
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: Дело и Сервис, 2001.
Экономико-математические методы и модели / под ред. Кузнецова А.В., 1999.
Экономико-математические методы и прикладные модели / под ред. Федосеева В.В., 1999.

2. Экономика

2.1. Введение в экономическую теорию.

Блага. Потребности, ресурсы. Экономический выбор. Экономические отношения. Экономические системы. Основные этапы развития экономической теории. Методы экономической теории.

2.2. Микроэкономика.

Рынок. Спрос и предложение. Потребительские предпочтения и предельная полезность. Факторы спроса. Индивидуальный и рыночный спрос. Эффект дохода и эффект замещения. Эластичность. Предложение и его факторы. Закон убывающей предельной производительности. Эффект масштаба. Виды издержек. Фирма. Выручка и прибыль. Принцип максимизации прибыли. Предложение совершенно-конкурентной фирмы и отрасли. Эффективность конкурентных рынков. Рыночная власть. Монополия. Монополистическая конкуренция. Олигополия. Антимонопольное регулирование. Спрос на факторы производства. Рынок труда. Спрос и предложение труда. Заработная плата и занятость. Рынок капитала. Процентная ставка и инвестиции. Рынок земли. Рента. Общее равновесие и благосостояние. Распределение доходов. Неравенство. Внешние эффекты и общественные блага. Роль государства.

2.3. Макроэкономика.

Национальная экономика как целое. Кругооборот доходов и продуктов. ВВП и способы его измерения. Национальный доход. Располагаемый личный доход. Индексы цен. Безработица и ее формы. Инфляция и ее виды. Экономические циклы. Макроэкономическое равновесие. Совокупный спрос и совокупное предложение. Стабилизационная политика. Равновесие на товарном рынке. Потребление и сбережения. Инвестиции. Государственные расходы и налоги. Эффект мультипликатора. Бюджетно-налоговая политика. Деньги и их функции. Равновесие на денежном рынке. Денежный мультипликатор. Банковская система. Денежно-кредитная политика. Экономический рост и развитие. Международные экономические отношения. Внешняя торговля и торговая политика. Платежный баланс. Валютный курс. Особенности переходной экономики России. Приватизация. Формы собственности. Предпринимательство. Теневая экономика. Рынок труда. Распределение и доходы. Преобразования в социальной сфере. Структурные сдвиги в экономике. Формирование открытой экономики.

Рекомендуемая литература по экономике

Основная литература

Гальперин В.М., Игнатьев С.М., Моргунов В. И. Микроэкономика: В 2-х т. / Общ. ред. В.М.Гальперина. СПб.: Экономическая школа, 1994: T.I; 1998: Т.2.
Гребенников П.И., Леусский А.И., Тарасевич Л.С. Микроэкономика/ Общ. ред. Л.С.Тарасевича. СПб.: Изд-во СПбУЭФ, 1996.
Пиндайк Р.С., Рубинфельд Д.Л. Микроэкономика. М.: Дело, 2000.
Агапова Т.А., Серегина С.Ф. Макроэкономика: Учебник / Под общ. ред. А.В. Сидоровича: МГУ им. М.В. Ломоносова — М.: Изд-во «Дело и сервис», 2001.
Лэйард Р. Макроэкономика. Курс лекций для российских читателей. М., Джон Уэйли энд Санз, 1994.
Макконнелл, К. Р. Экономикс: принципы, проблемы и политика. В 2 т. / К.Р. Макконнелл, С.Л. Брю: пер. с англ. – М.: Республика, 1992.
Мэнкью Н.Г. Макроэкономика. М.: Изд-во Моск. ун-та, 1994.
Самуэльсон П., Нордхаус В. Экономика. 16-е изд. Пер с англ. – М.: Вильямс, 2000.
Самуэльсон, П. А. Основания экономического анализа / П.А. Самуэльсон / Пер. с англ. – СПб.: – 2002. – 604 с.
Самуэльсон, П. А. Экономика. В2 т. Т. 2. / П.А. Самуэльсон: пер. с англ. – М.: – МГП «АЛГОН», ВНИИСИ, 1992. – 415 с.
Тарасевич Л.С., Гальперин В.М., Гребенников П.И., Леусский А.И., Макроэкономика: Учебник / Общая редакция Л.С. Тарасевича. — СПб.: Изд-во СПбГУЭФ, 1999.
Фишер, С. Экономика/ С. Фишер, Р. Дорнбуш, Р. Шмалензи: пер. с англ. – М.: Дело ЛТД, 1993.– 864 с.

Дополнительная литература

50 лекций по микроэкономике: в 2х т. СПб.: Экон. школа. 2000.
Богачкова Л.Ю. Математические аспекты микроэкономики: Часть I. Элементы количественного анализа конъюнктуры индивидуального конкурентного рынка: Учебное пособие/ Под ред. О.В.Иншакова. — Волгоград: Изд-во ВолГУ, 1997.
Вэриан Хэл Р. Микроэкономика. Промежуточный уровень. Современный подход. М.: ЮНИТИ, 1997.
Шагас Н.Л., Туманова Е.А. Макроэкономика-2. Долгосрочный аспект: Учебное пособие. – М.: Экономический факультет МГУ, ТЕИС, 1999.
Шагас Н.Л., Туманова Е.А. Макроэкономика-2. Краткосрочный аспект: Учебное пособие. – М.: Экономический факультет МГУ, ТЕИС, 1999.

3. Информатика

Понятие информации, общая характеристика процессов сбора, передачи, обработки и накопления информации; технические и программные средства реализации информационных процессов; офисное программное обеспечение; разработка текстовых документов; финансово-экономические расчеты в электронных таблицах; базы данных; прикладное программное обеспечение в экономике; локальные и глобальные сети ЭВМ. Методы защиты информации.

Рекомендуемая литература по информатике

Основная литература

Симонович С.В. Информатика. Базовый курс: Учебник для вузов. 2-е изд. 2004 г., 640 с.
Косарев В.П. Экономическая информатика: Учебник для вузов экономических специальностей. Издание 2 Издательство: Финансы и статистика, 2004. – 592 с.
Степанов А. Н Информатика 4-е издание Издательство: СПб.: Питер. – 2006. – 684 с.
Соболь Б.В., Галин А.Б., Панов Ю.В. и др. Информатика: учебник: Феникс. – 2007. – 446 с.

Дополнительная литература

Соболь Б.В., Галин А.Б., Панов Ю.В. и др. Информатика: учебник: Феникс. – 2007.
Аржаник А.В. Microsoft Office. Практикум [Электронный ресурс]: электронный учебник по дисциплине «Информатика» / А.В. Аржаник, А.В. Ля-мин; СПбГИТМО(ТУ), ЦДО. – СПб. : СПбГИТМО(ТУ). – Режим доступа: ссылка скрыта
Ковырялова Т.Н. Информатика [Электронный ресурс]: учебно-методическое пособие. Ч. 1. Информационно-логические основы работы ЭВМ / Т.Н. Ковырялова; Международный университет бизнеса и новых технологий. – 2-е изд., испр. и доп.– Ярославль: МУБиНТ, 2003. – Режим доступа: ссылка скрыта
Лаздин А.В. Основы вычислительной техники [Электронный ресурс]: электронный учебник / А.В. Лаздин; СПбГИТМО(ТУ). – СПб.: СПбГИТМО(ТУ). – Режим доступа: ссылка скрыта

II. ОСНОВНЫЕ СВЕДЕНИЯ ПО МАТЕМАТИКЕ: понятия, свойства, методы

1. Математика

1.1. Математический анализ

Свойства и график функции .
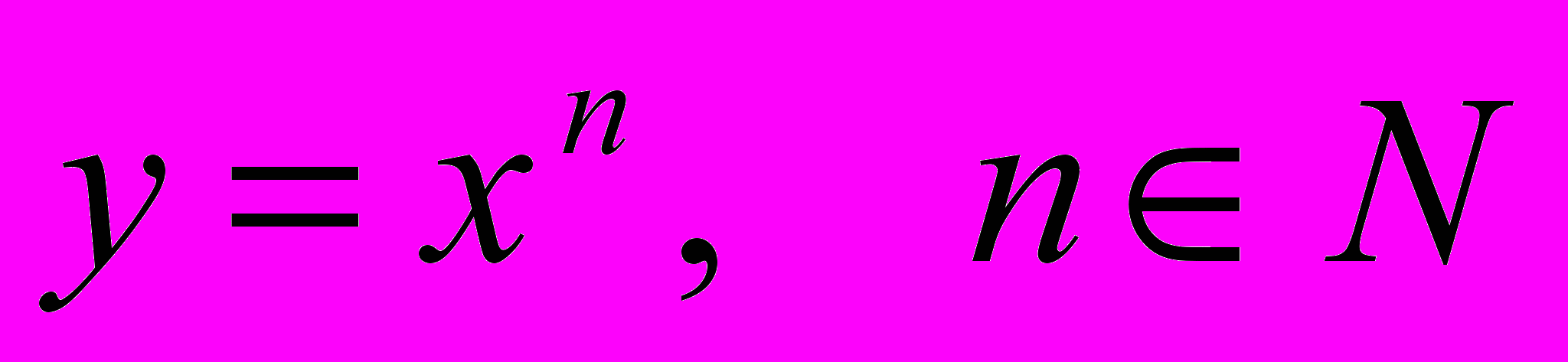Свойства и график функции .
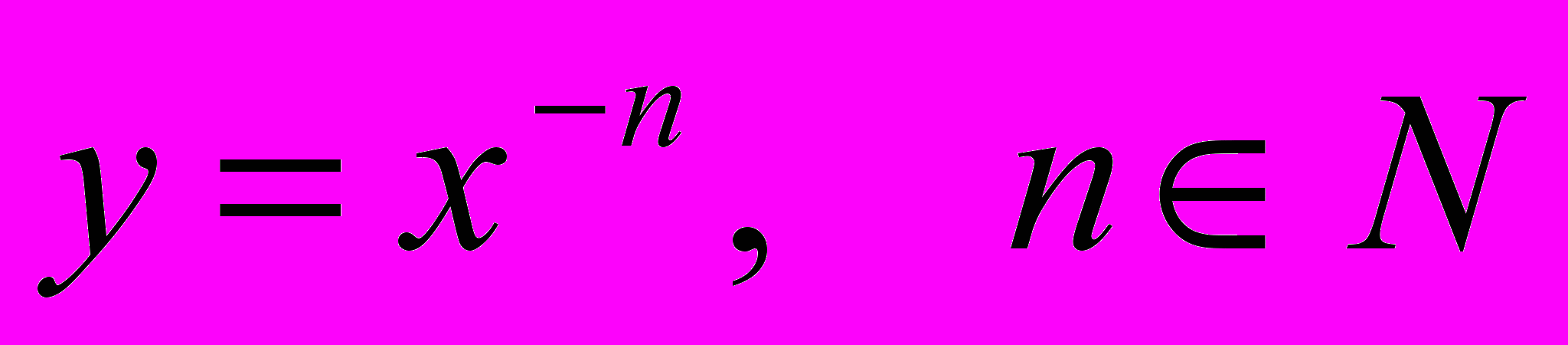Свойства и график функции .
Свойства и график функции .
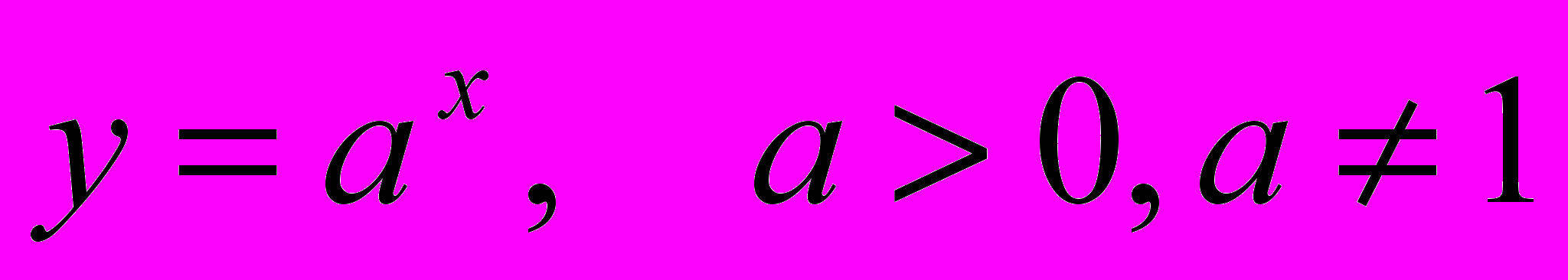Свойства и график функции .
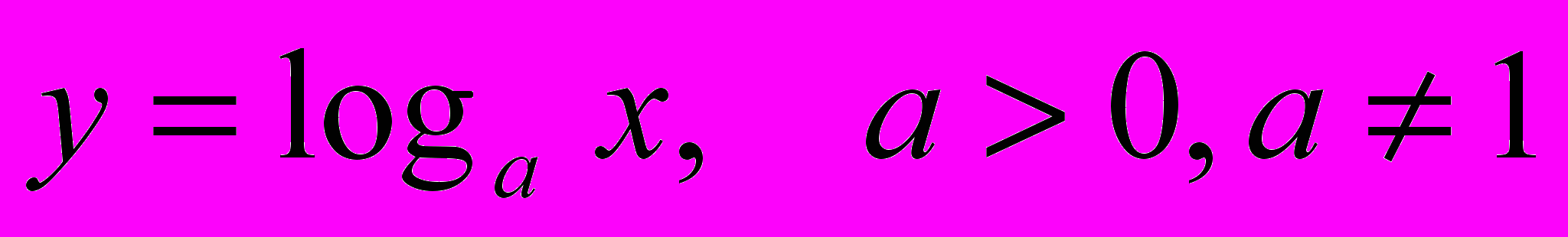Свойства и график функции .
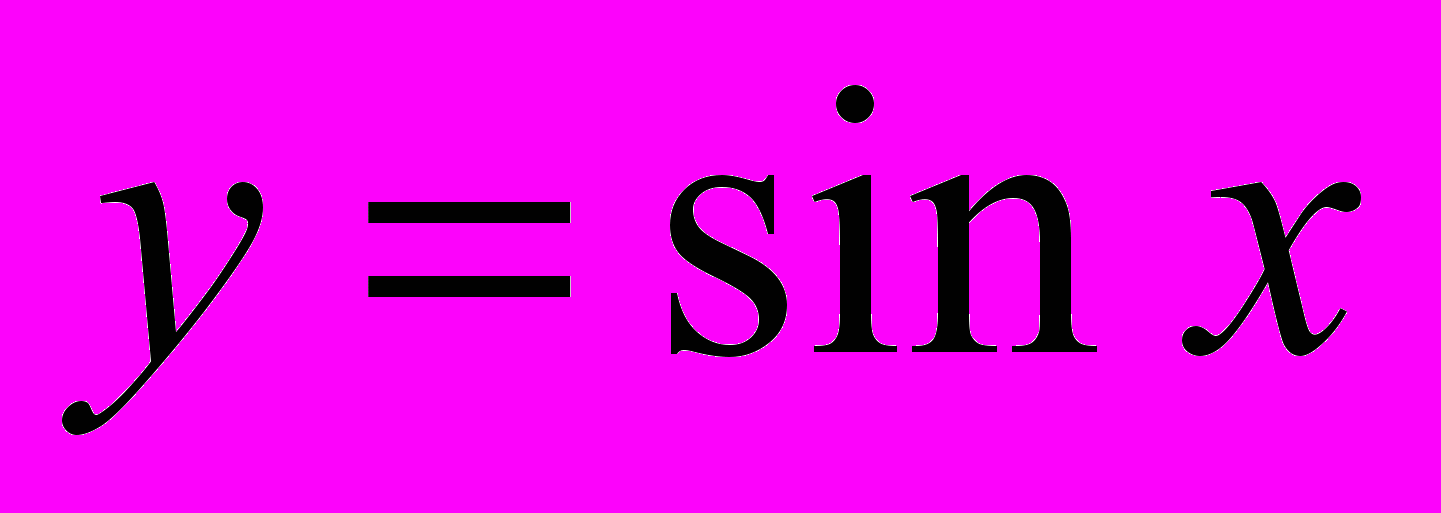Свойства и график функции .
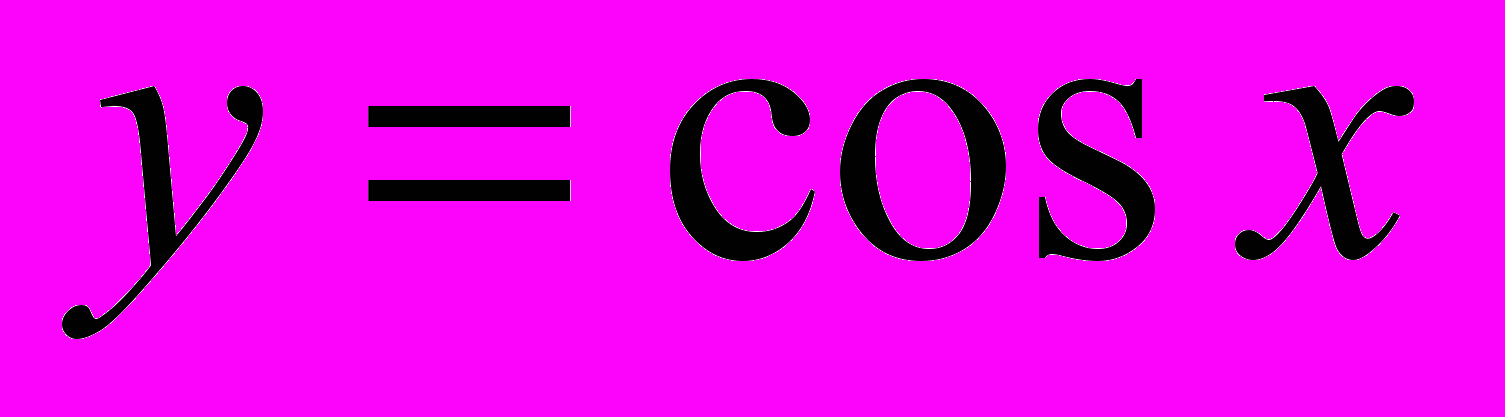Свойства и график функции .
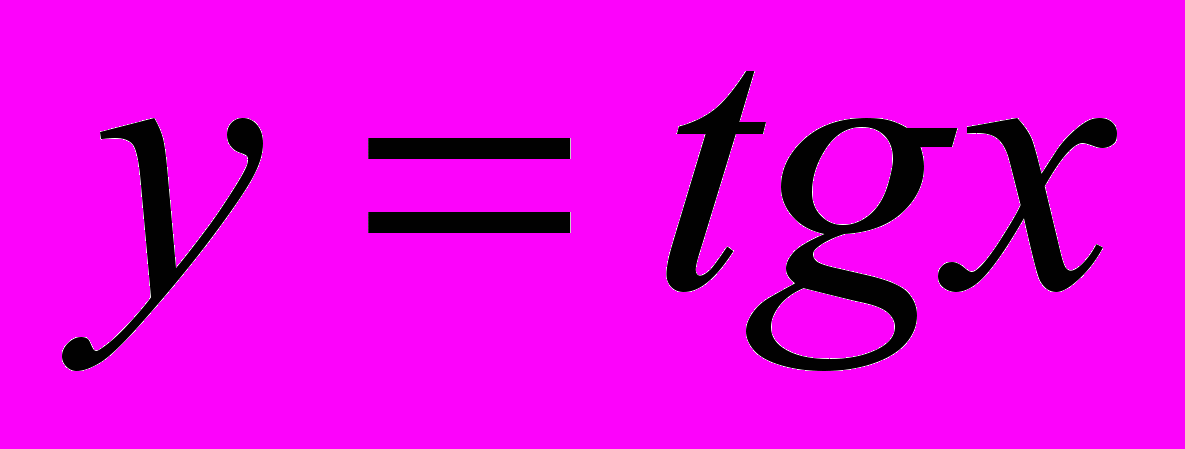Свойства и график функции .
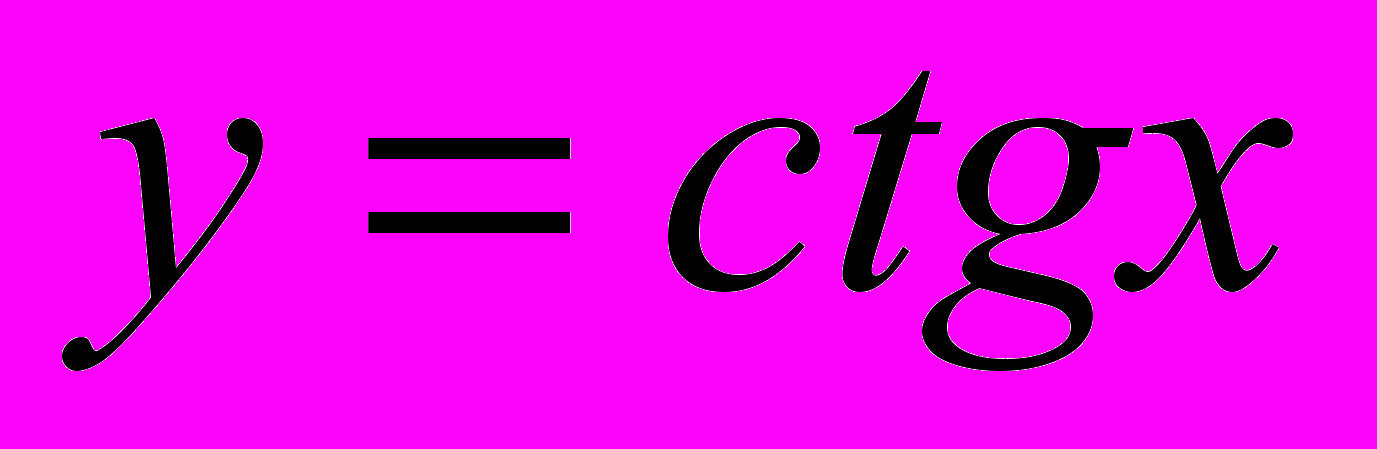Понятие сложной функции. Графики сложных функций.
Понятие обратной функции.
Преобразование графиков функций. Графики функций , , , .
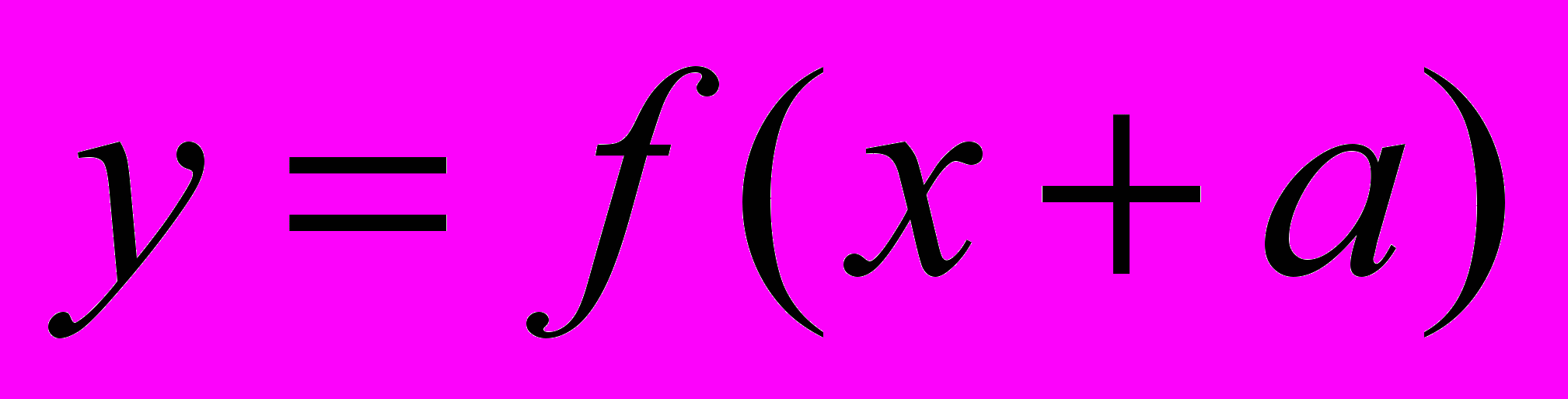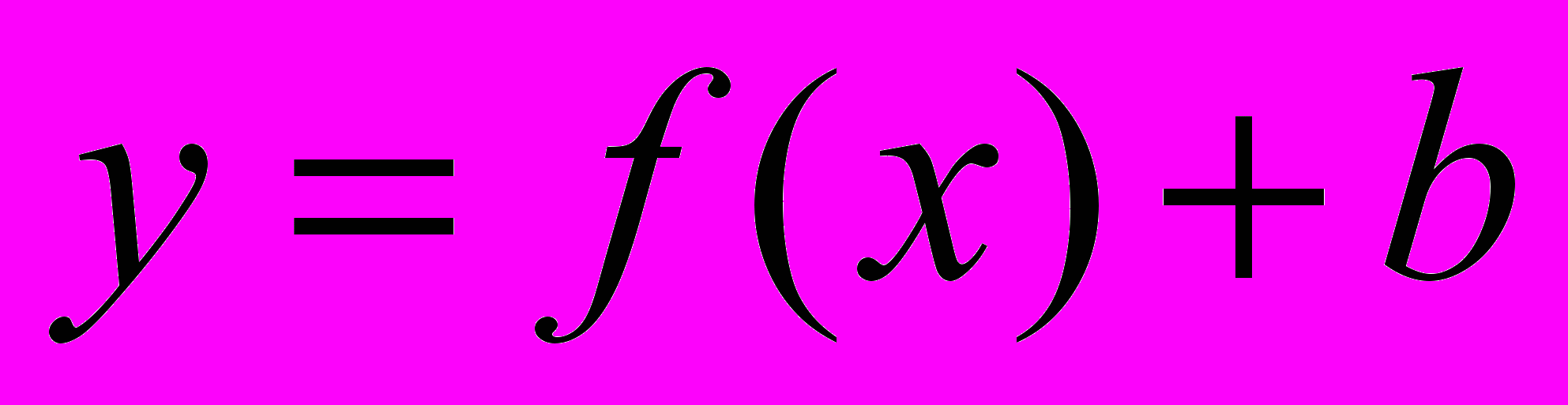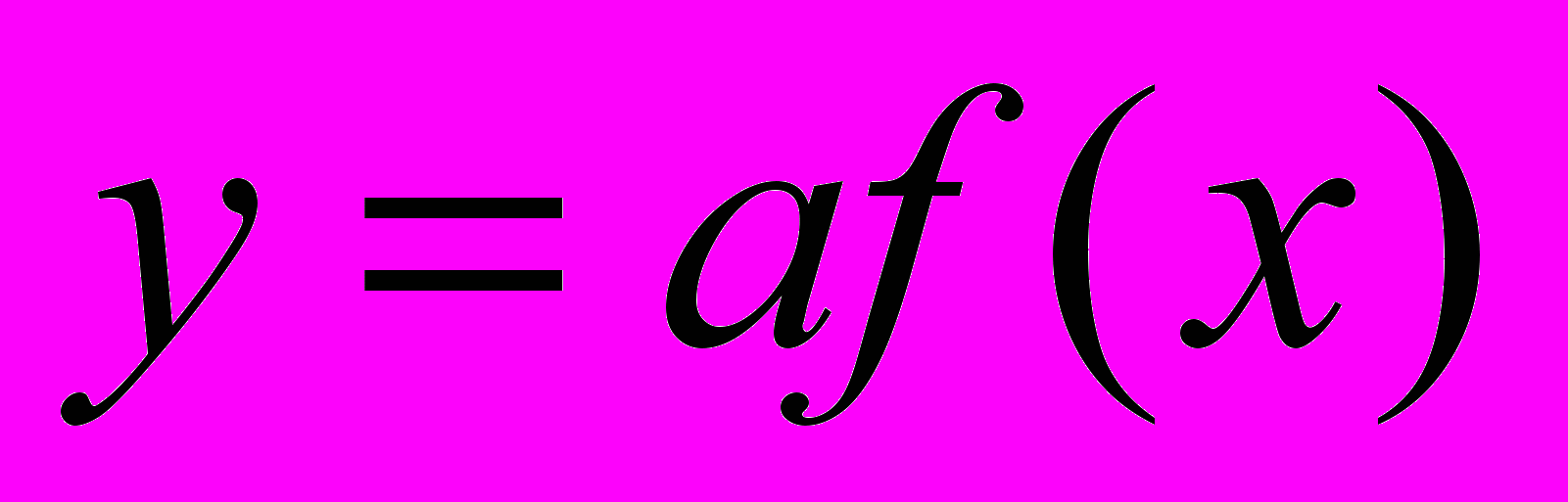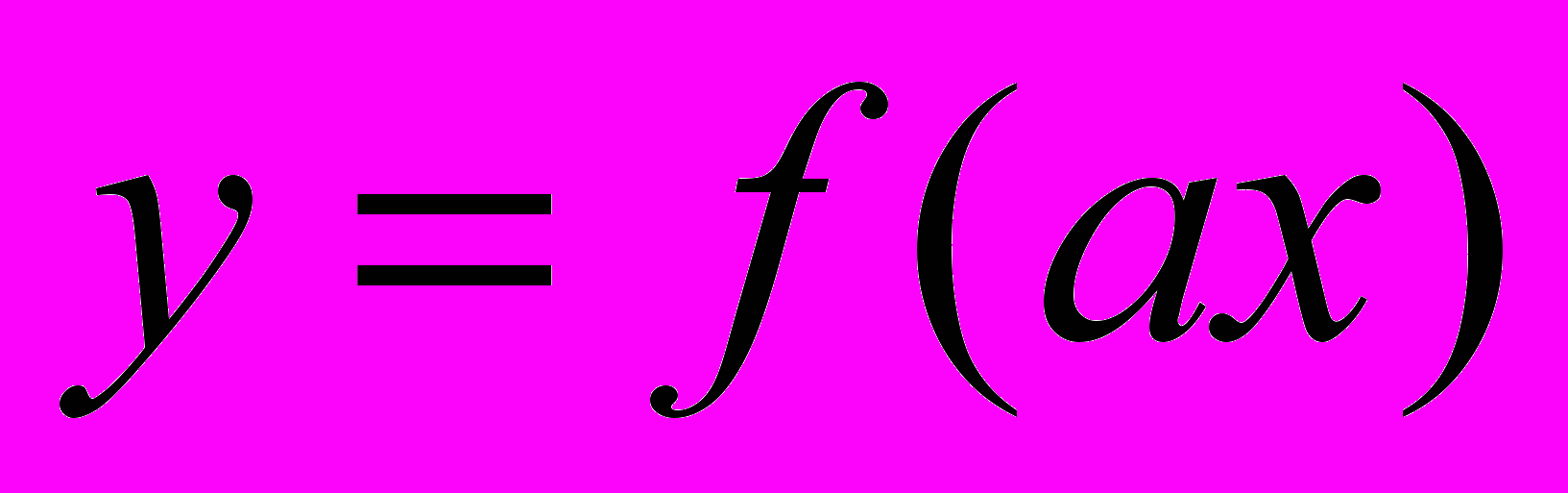Преобразование графиков функций. Графики функций , , , .
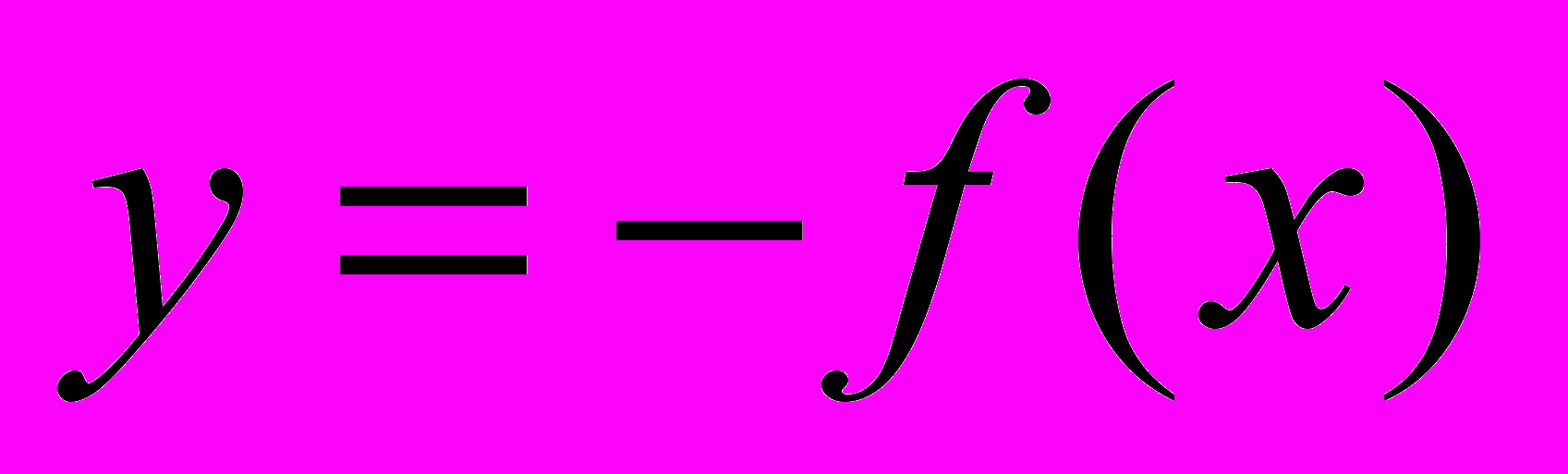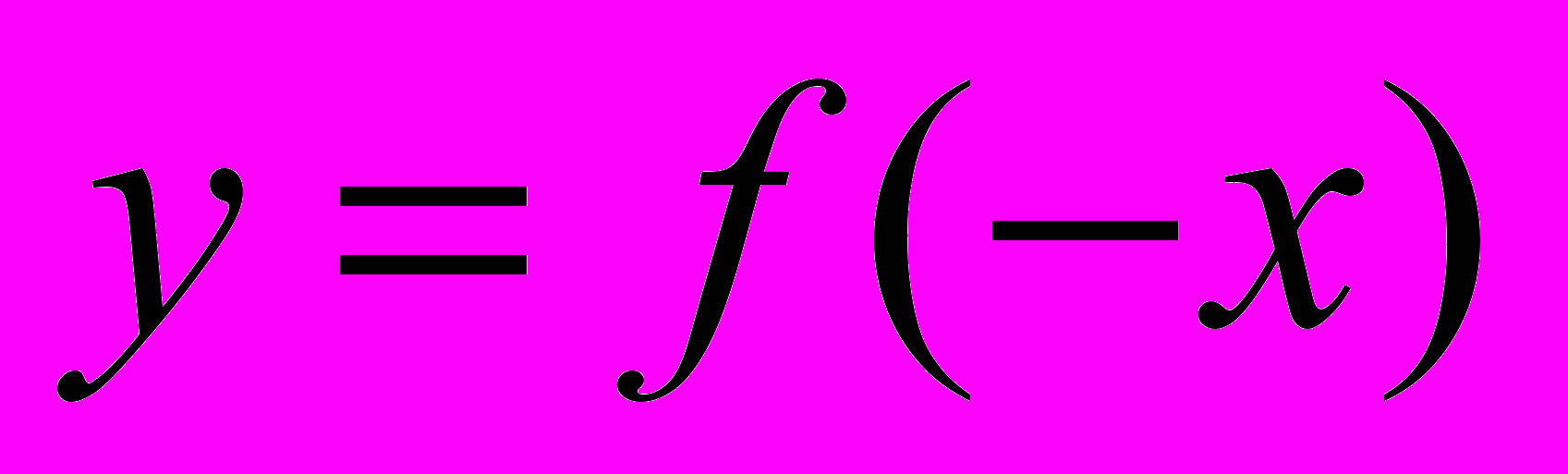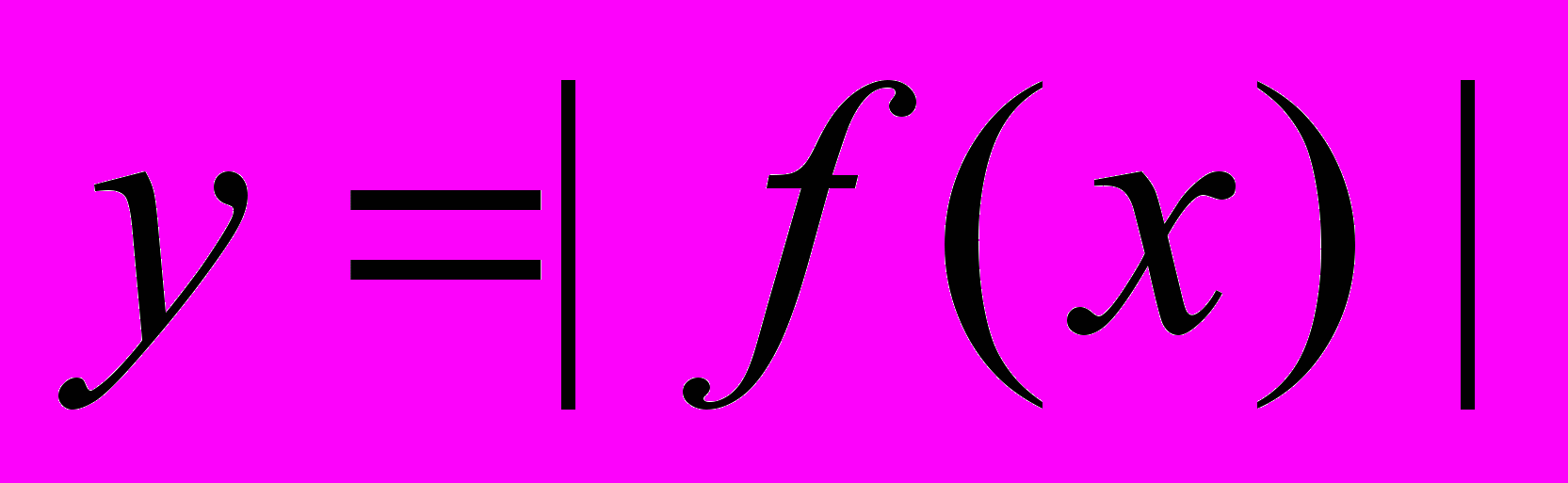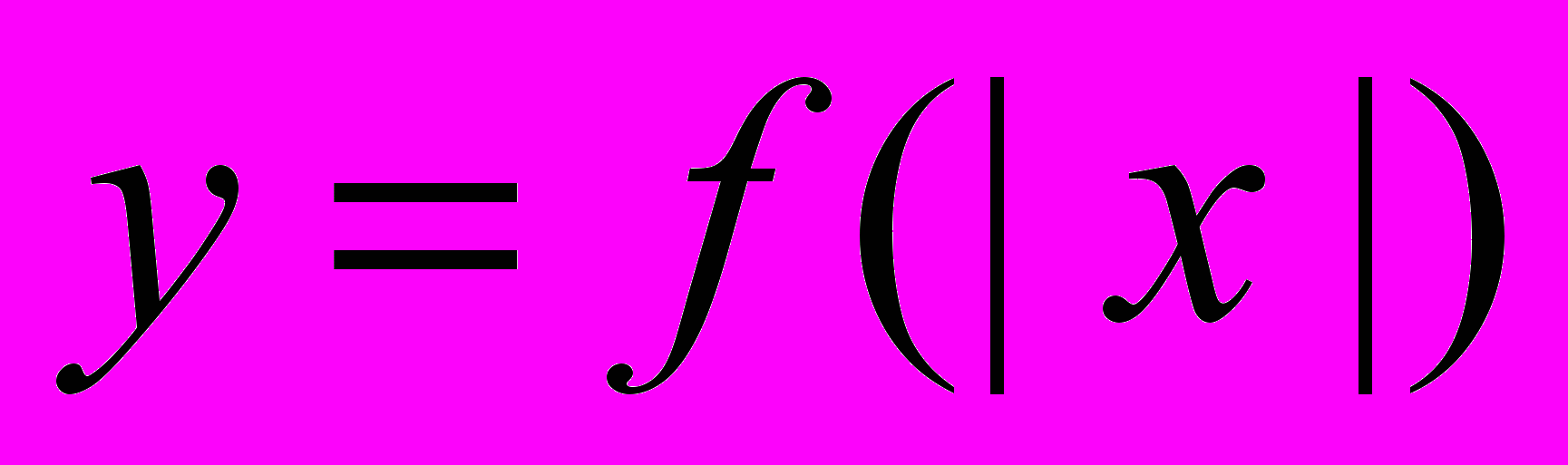Понятие числовой последовательности. Предел числовой последовательности. Свойства пределов последовательностей.
Предел функции в бесконечности.
Пределы функций слева и справа. Предел функции в точке.
Бесконечно малые величины и их свойства.
Бесконечно большие величины и их свойства.
Пределы суммы, разности, произведения и частного.
Предел сложной функции. Теорема о двух милиционерах.
Первый замечательный предел.
Второй замечательный предел. Задача о непрерывном начислении процентов.
Понятие непрерывности функции.
Классификация точек разрыва.
Свойства функций непрерывных на отрезке.
Определение производной. Примеры вычисления производной по определению.
Геометрический смысл производной (задача о касательной).
Экономический смысл производной.
Производная суммы двух функций.
Производная произведения двух и нескольких функций.
Производная частного двух функций.
Производная логарифмической функции.
Производная показательной функции.
Производная степенной функции.
Производная функции .
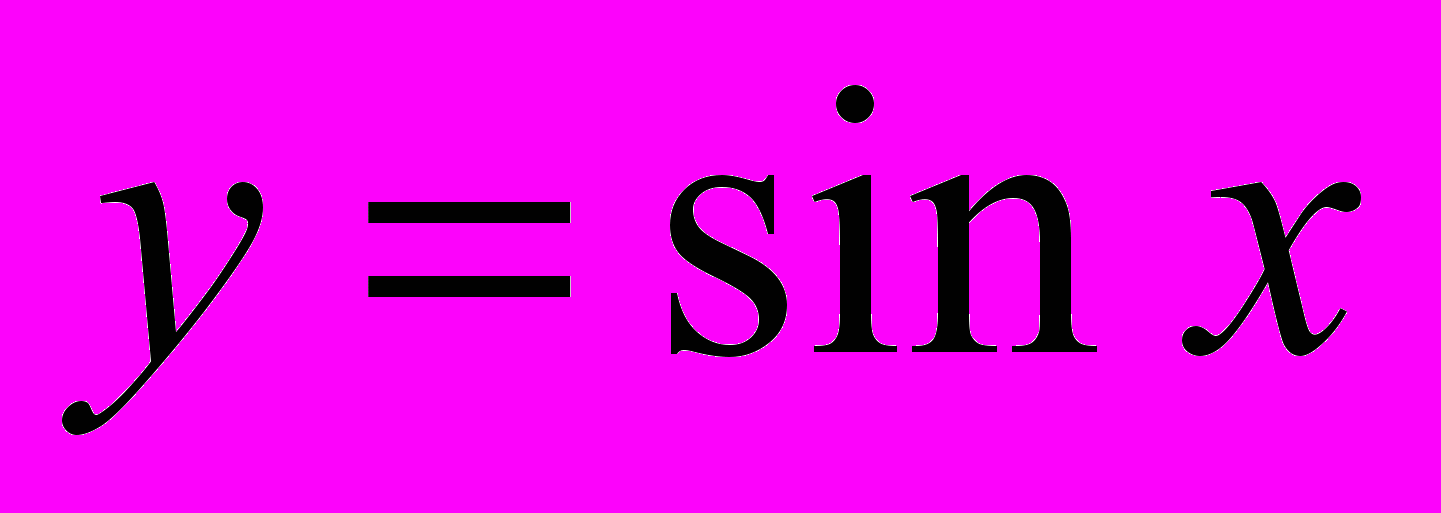Производная функции .
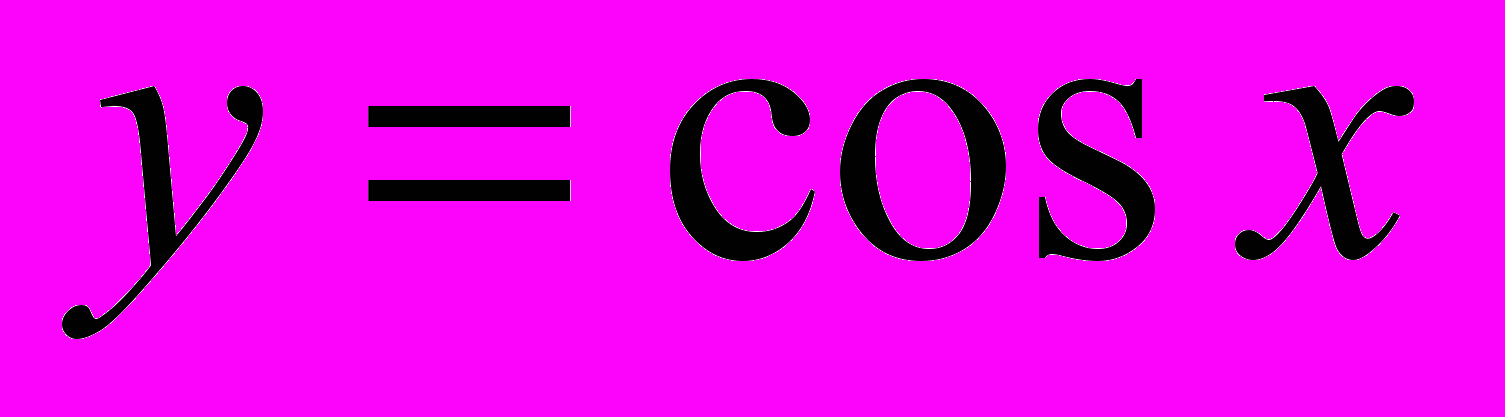Производная функции .
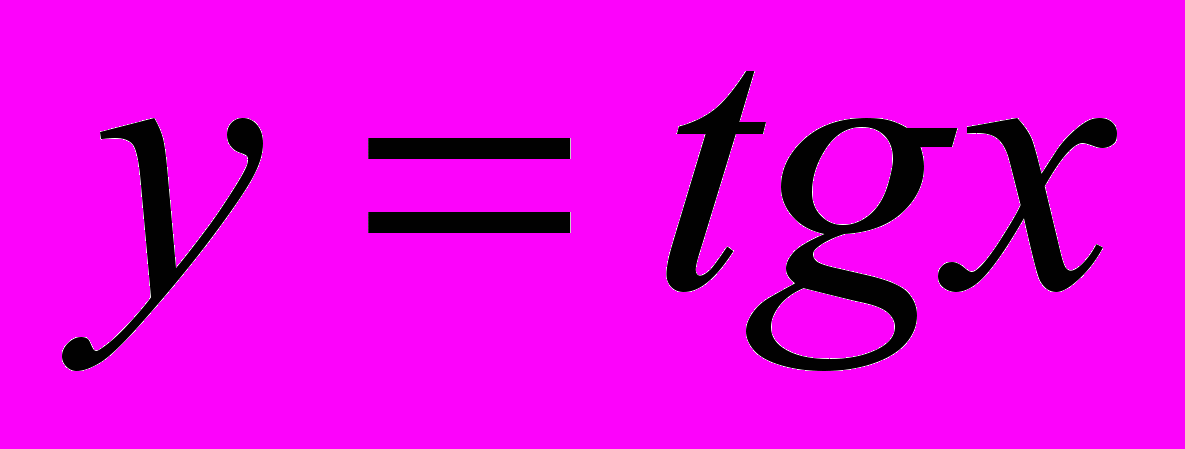Производная функции .
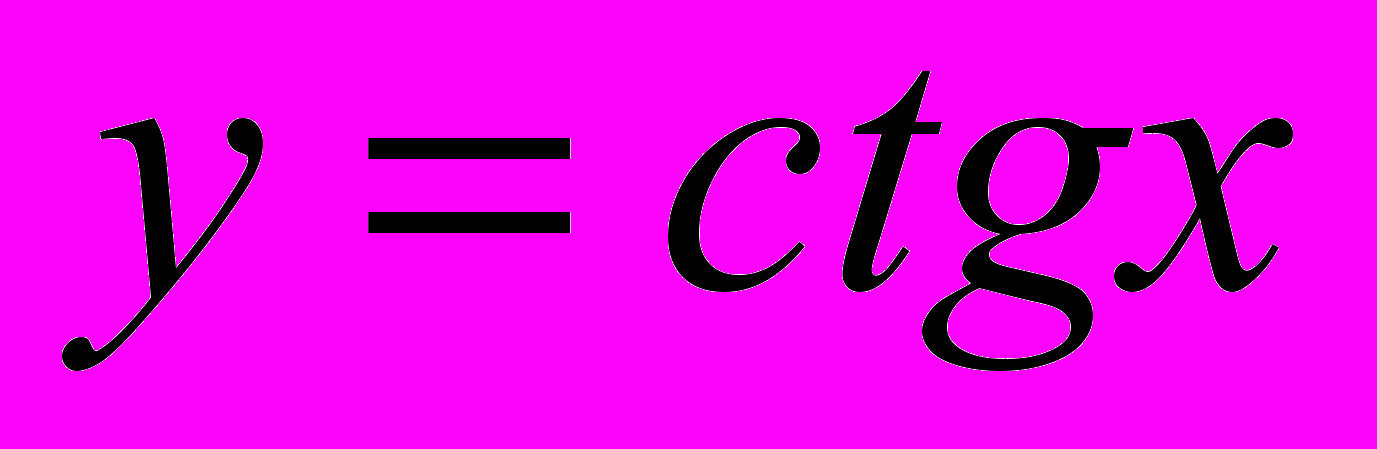Понятие производных высших порядков.
Предельные величины в экономике.
Понятие эластичности функции и ее связь с производной.
Эластичность произведения и частного двух функций.
Достаточные условия возрастания и убывания функции.
Понятие экстремума функции. Необходимое и достаточные условия экстремума.
Наибольшее и наименьшее значения функции на отрезке.
Выпуклость функции и точки перегиба.
Асимптоты графика функции.
Правило Лопиталя.
Понятие дифференциала функции и его свойства.
Применение дифференциала для приближенных вычислений.
Понятие функции нескольких переменных.
График функции двух переменных. Линии уровня.
Понятие частных производных первого и второго порядка.
Понятие градиента и дифференциала функции двух переменных.
Частные производные для анализа эластичностей в экономике.
Частные производные для анализа полезностей в экономике. Кривые безразличия.
Частные производные для анализа производственных функций в экономике. Кривые безразличия производства.

Необходимое и достаточные условия экстремума функции двух переменных.

Понятие точки условного экстремума функции двух переменных. Метод подстановки для нахождения условного экстремума.
Графический метод для нахождения условного экстремума.
Метод множителей Лагранжа для нахождения условного экстремума.
Понятия первообразной и неопределенного интеграла (с примерами).
Свойства неопределенного интеграла.
Табличные интегралы: , , , , , , , , , , , , .
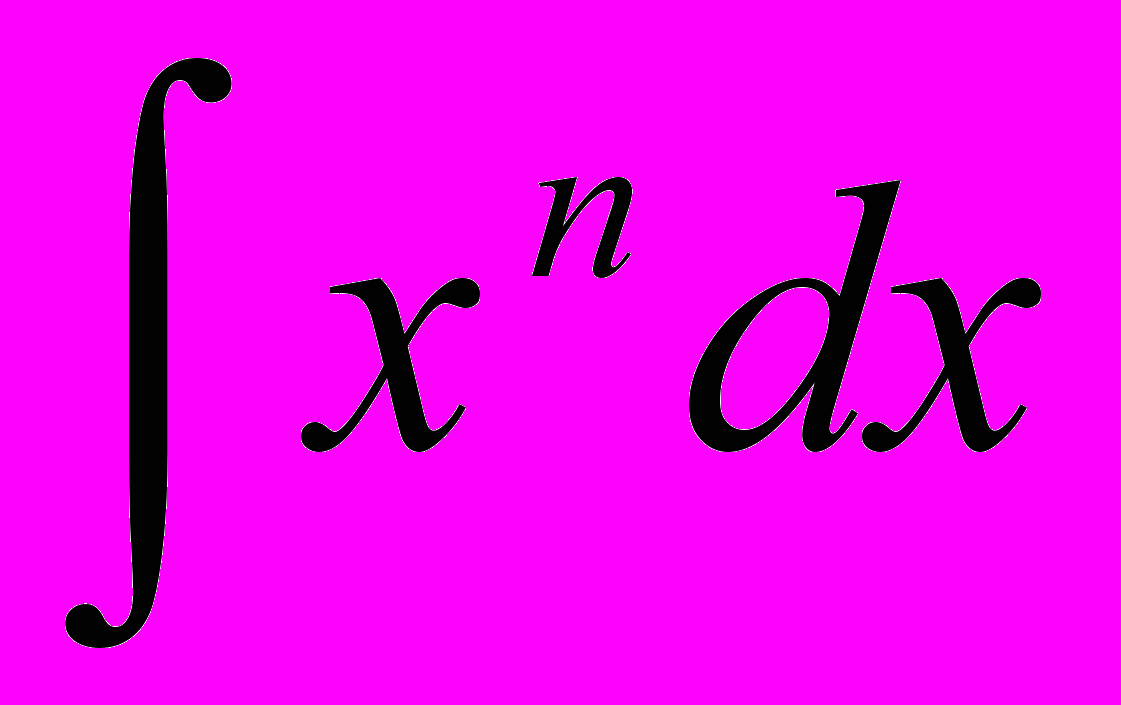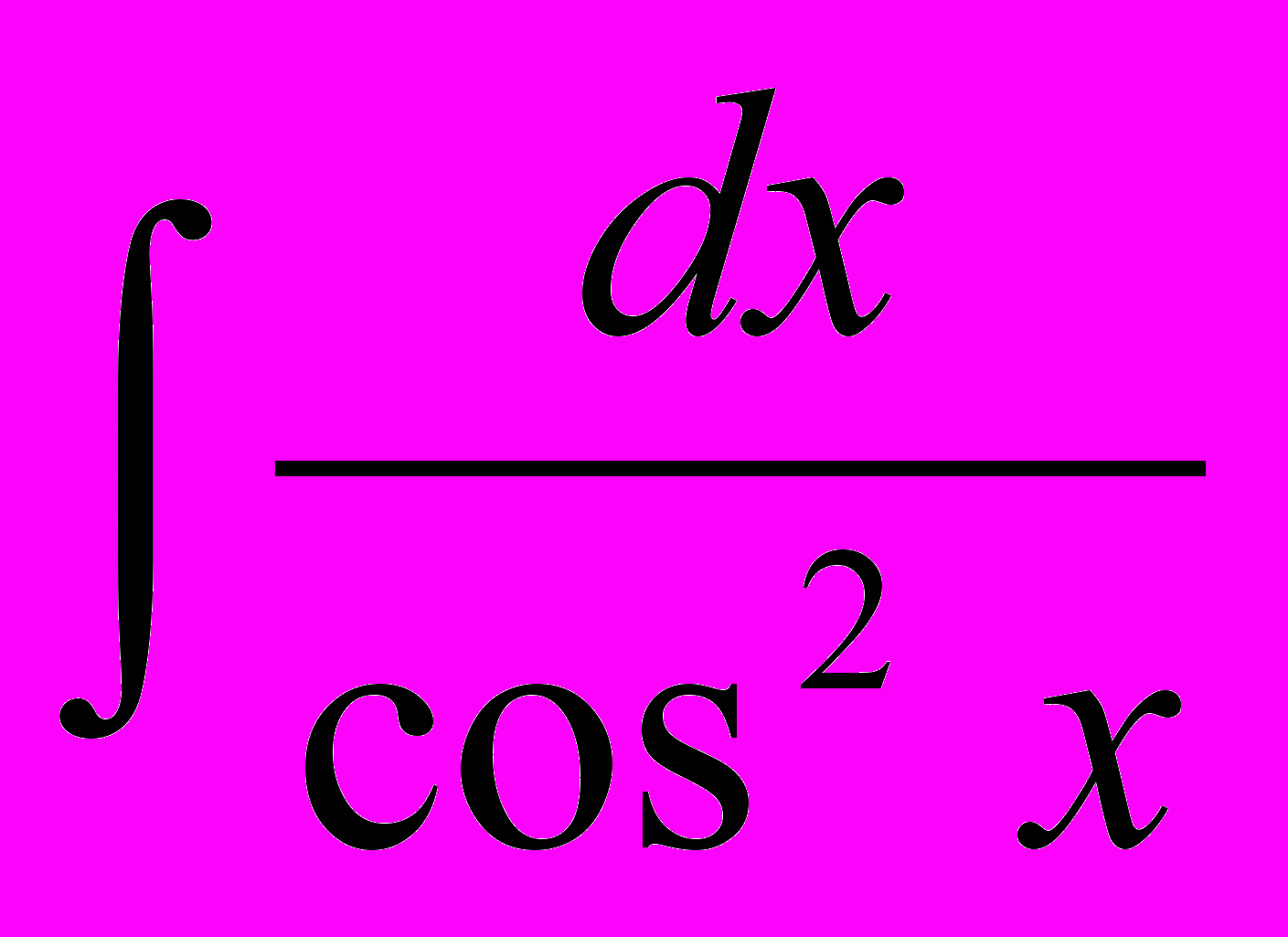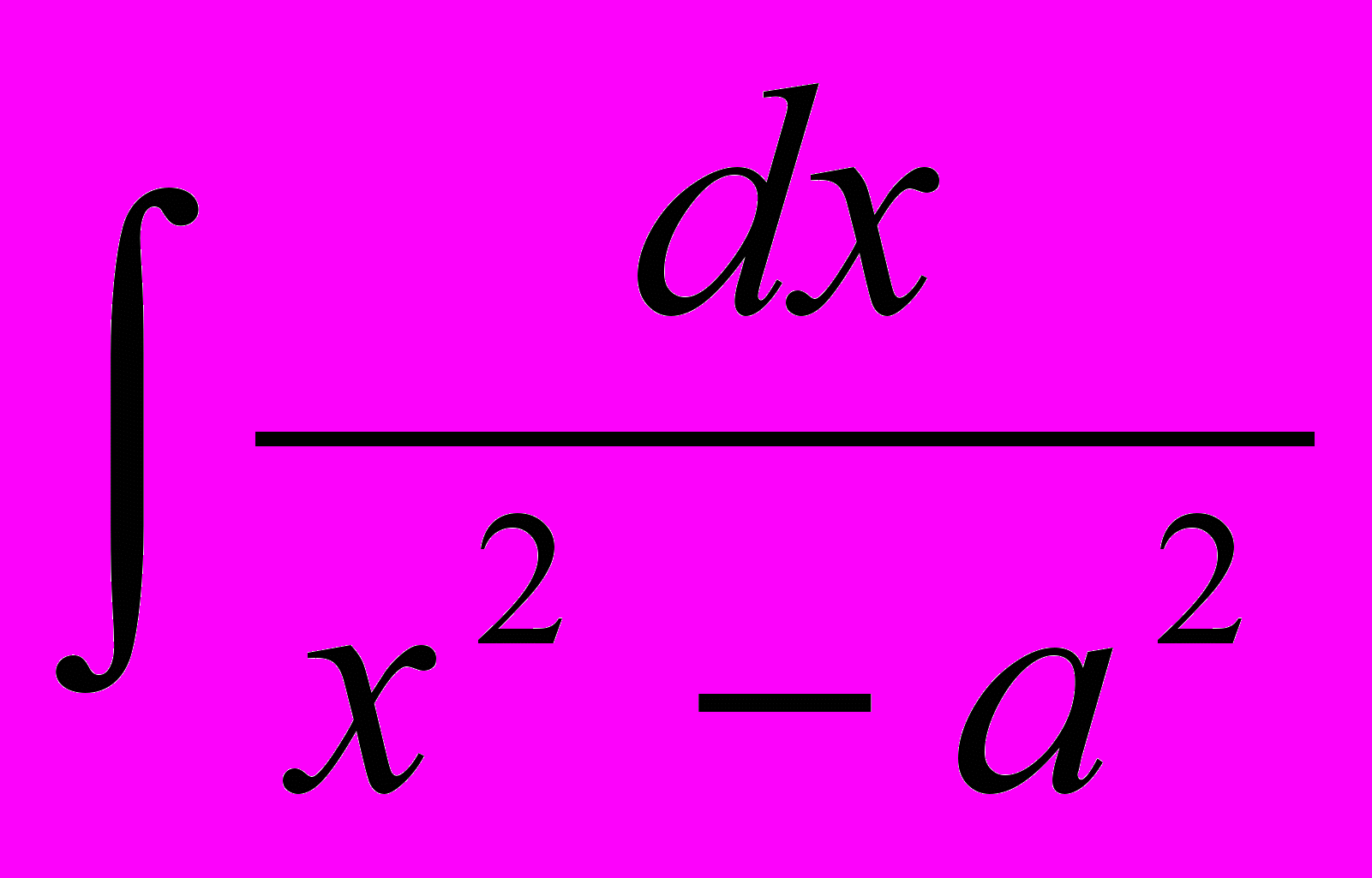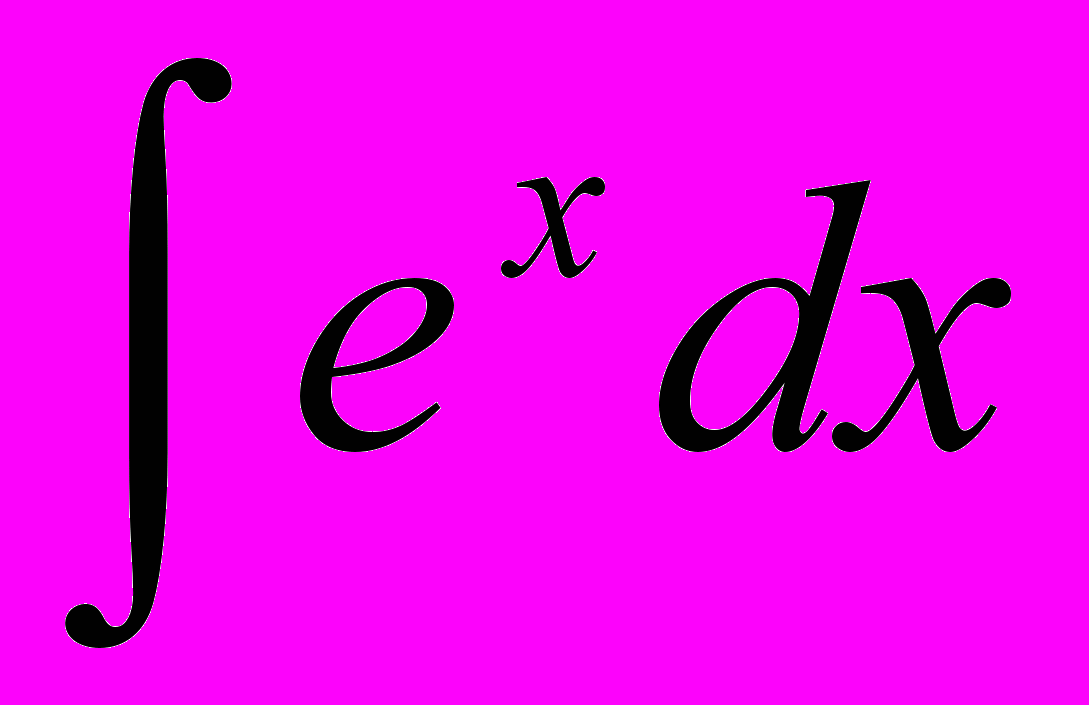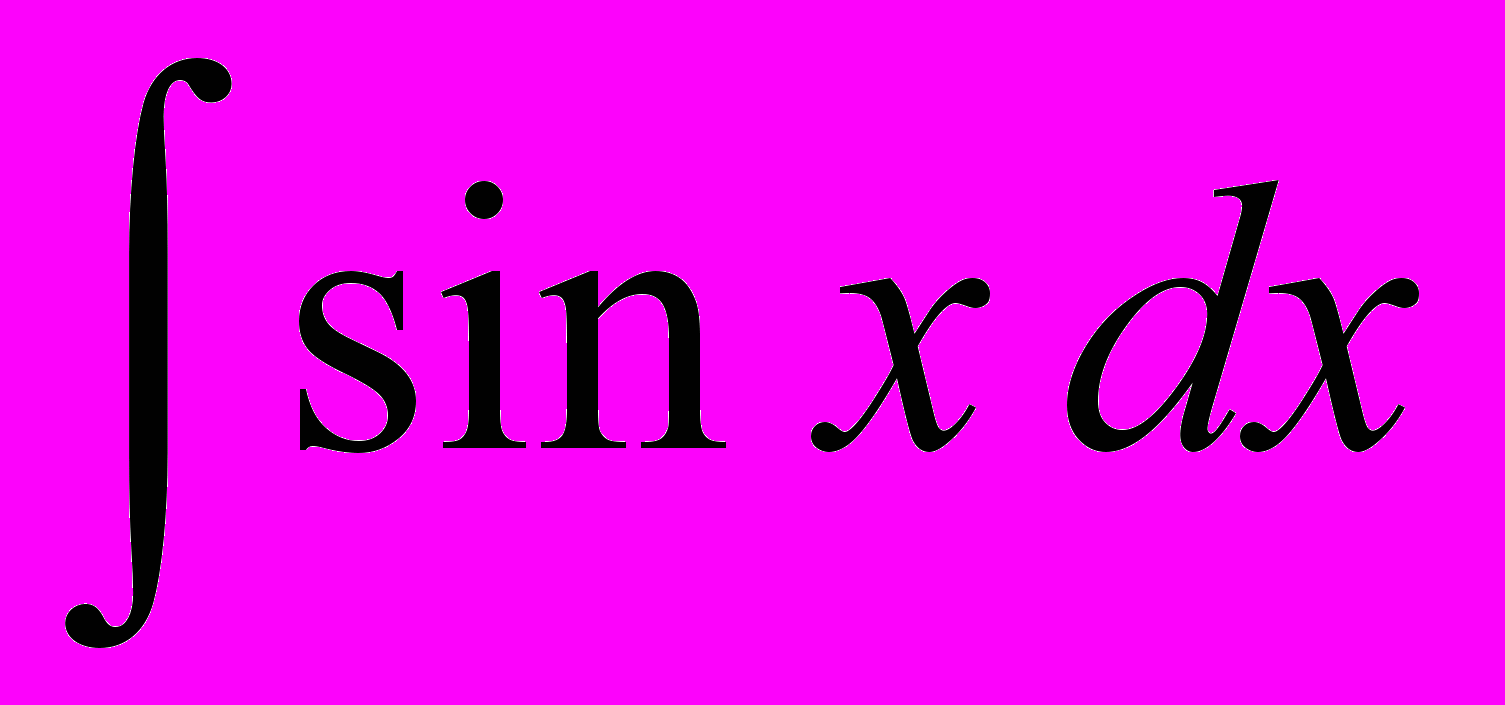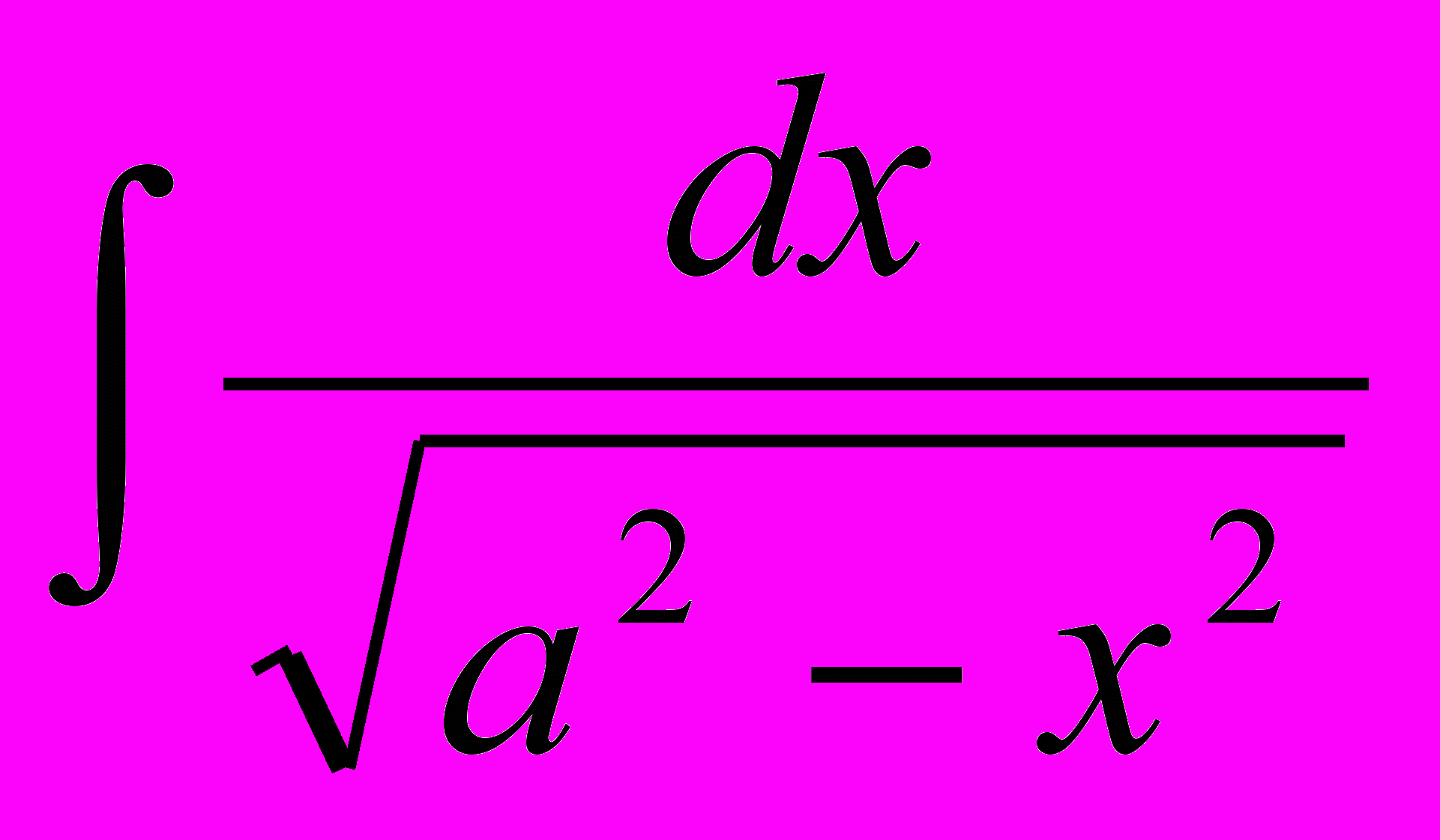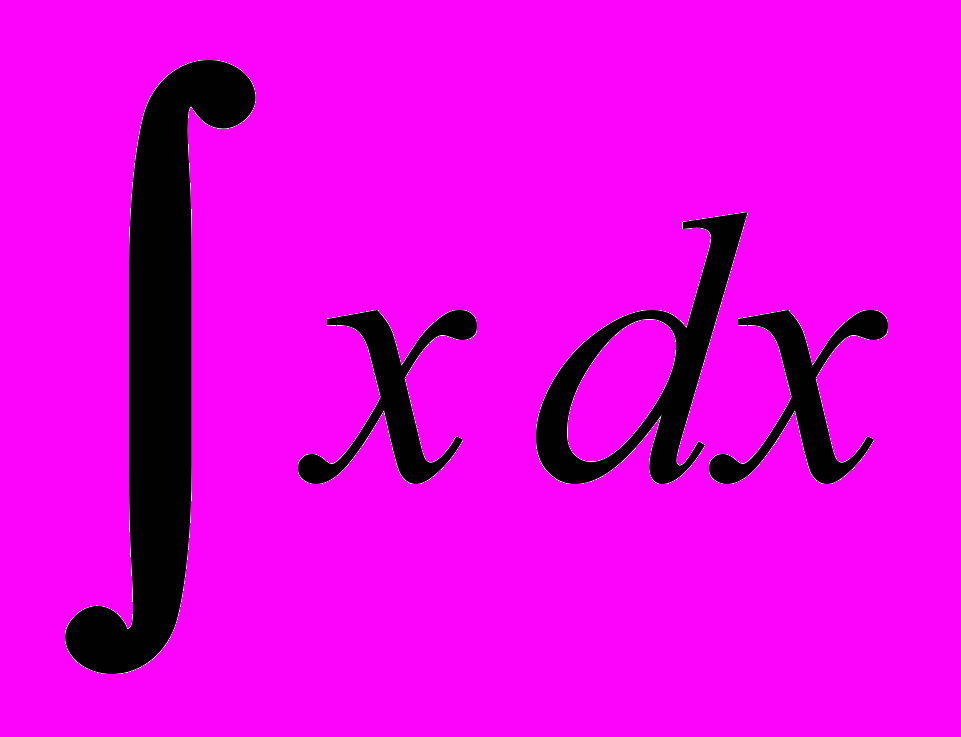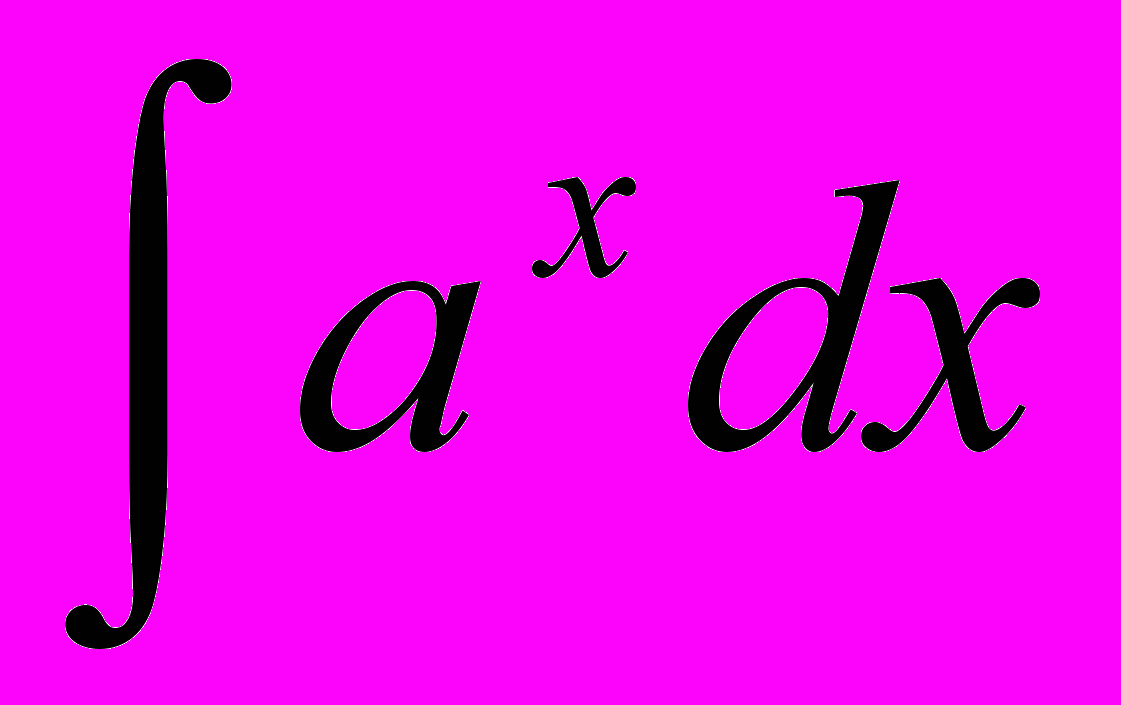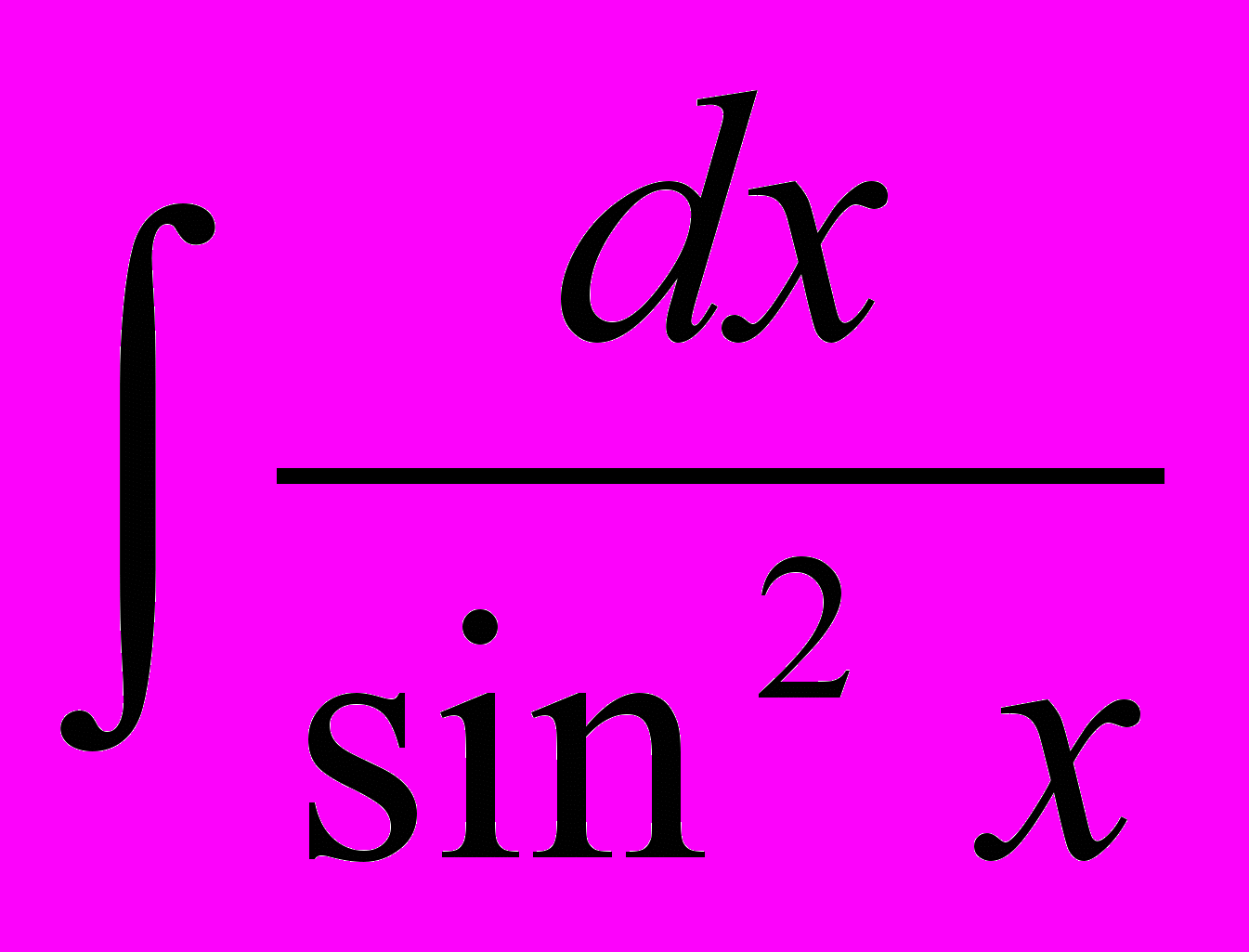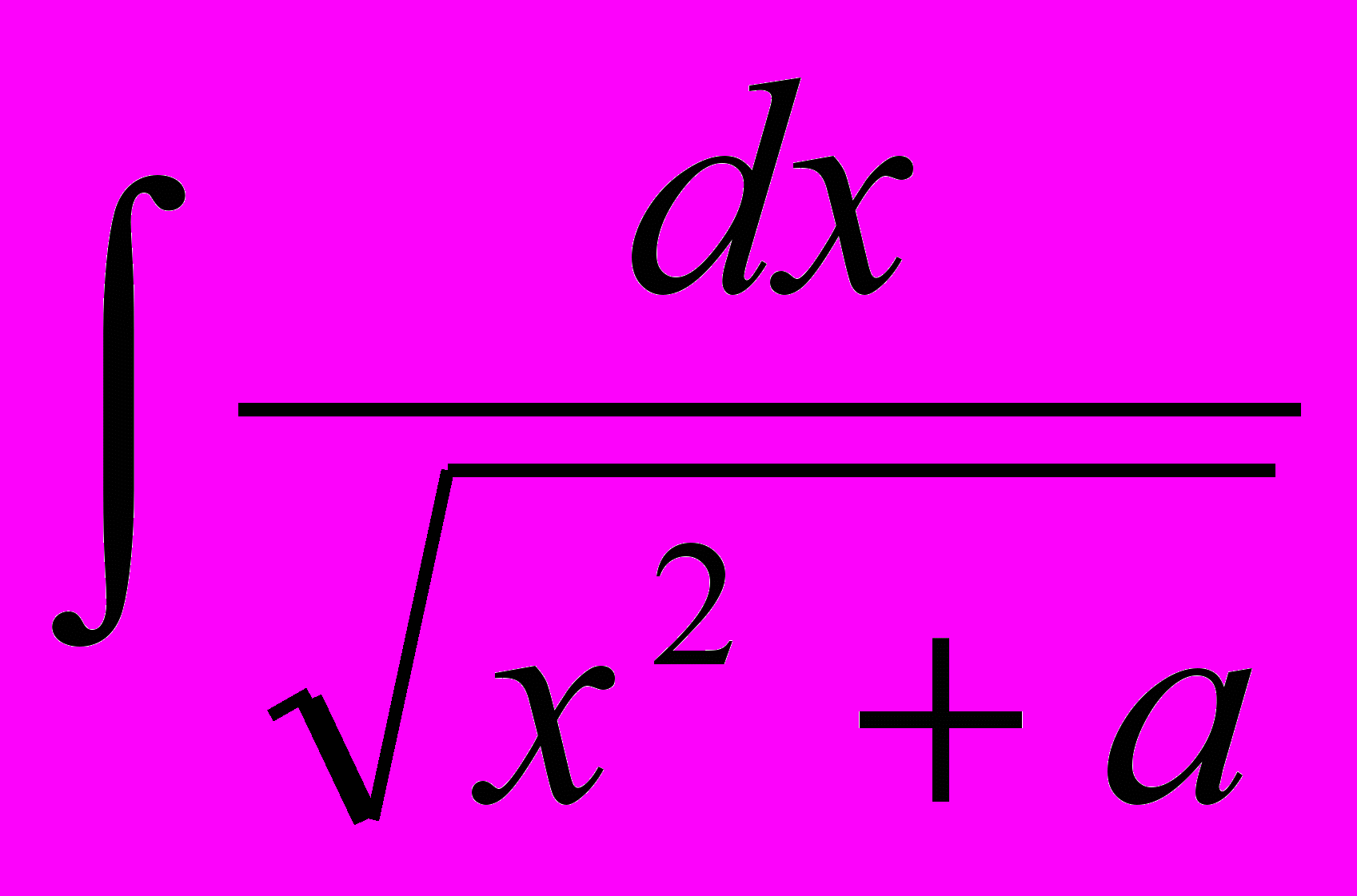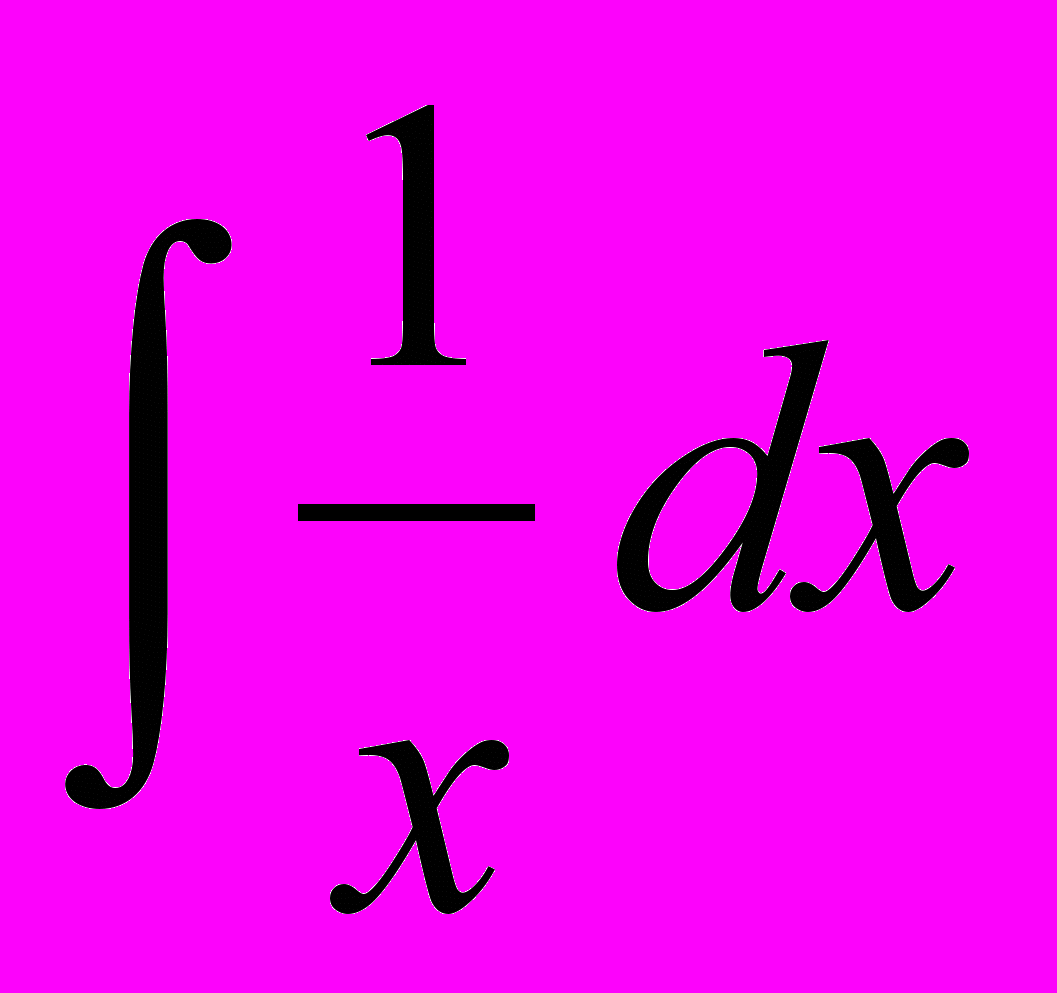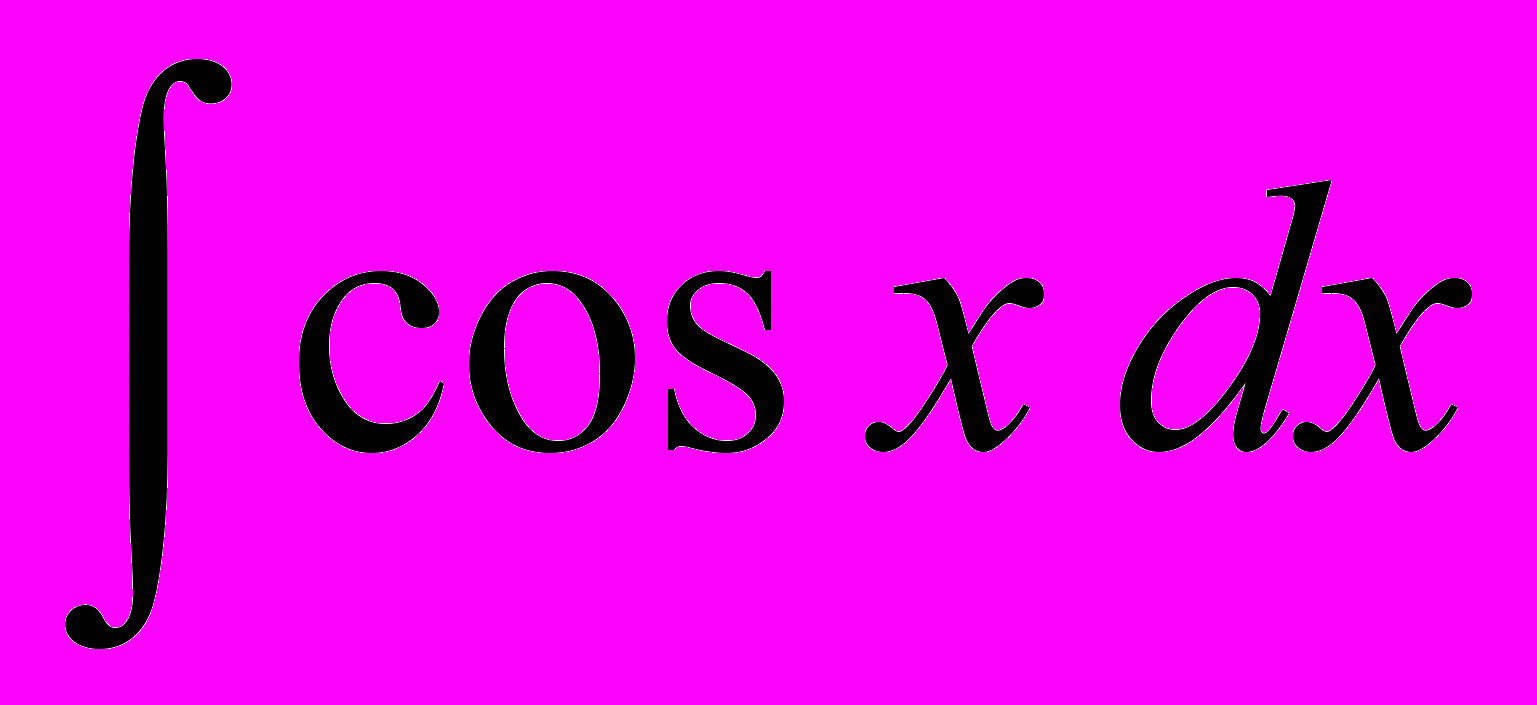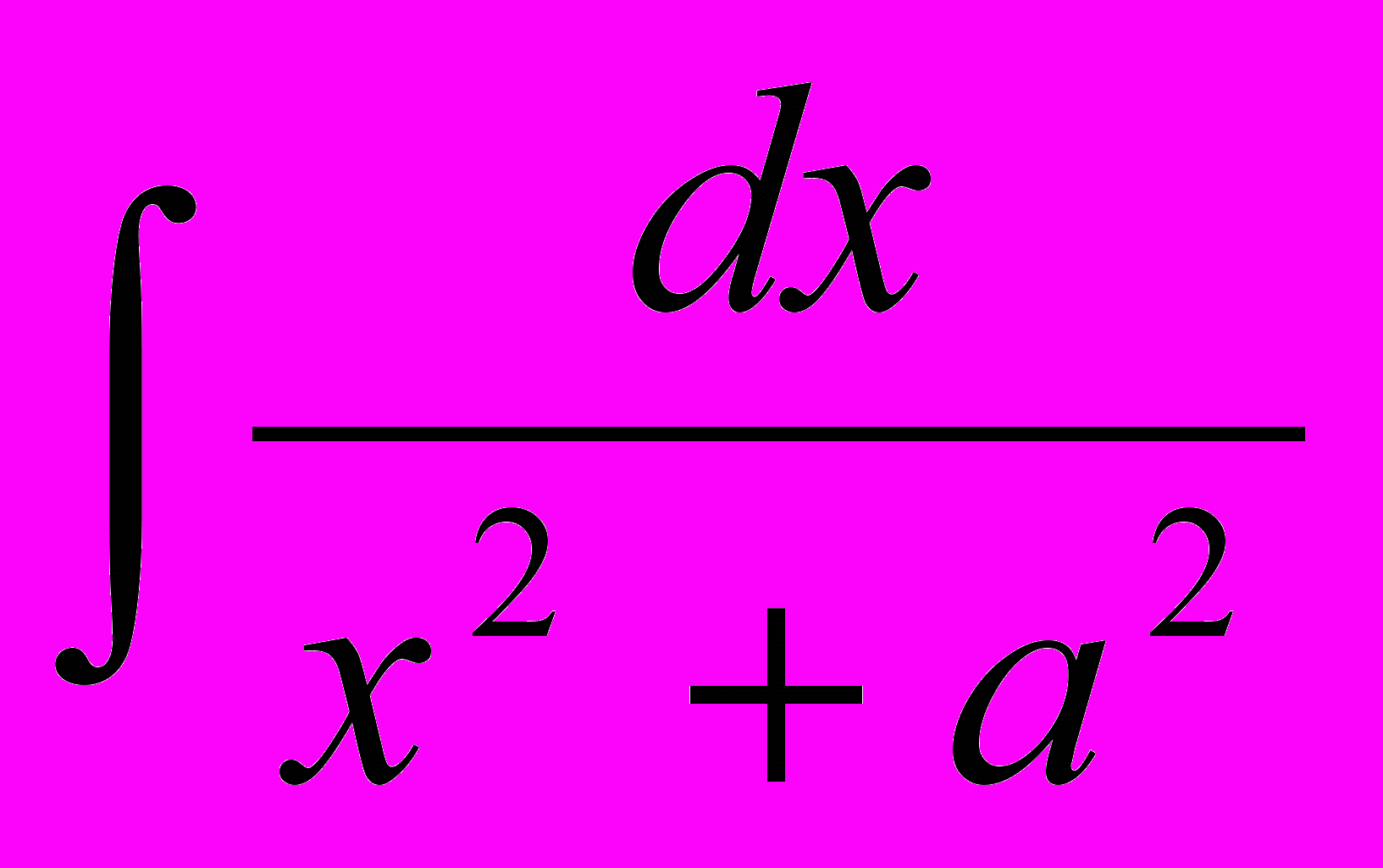Метод замены переменных для вычисления неопределенного интеграла.
Вычисление интегралов вида .
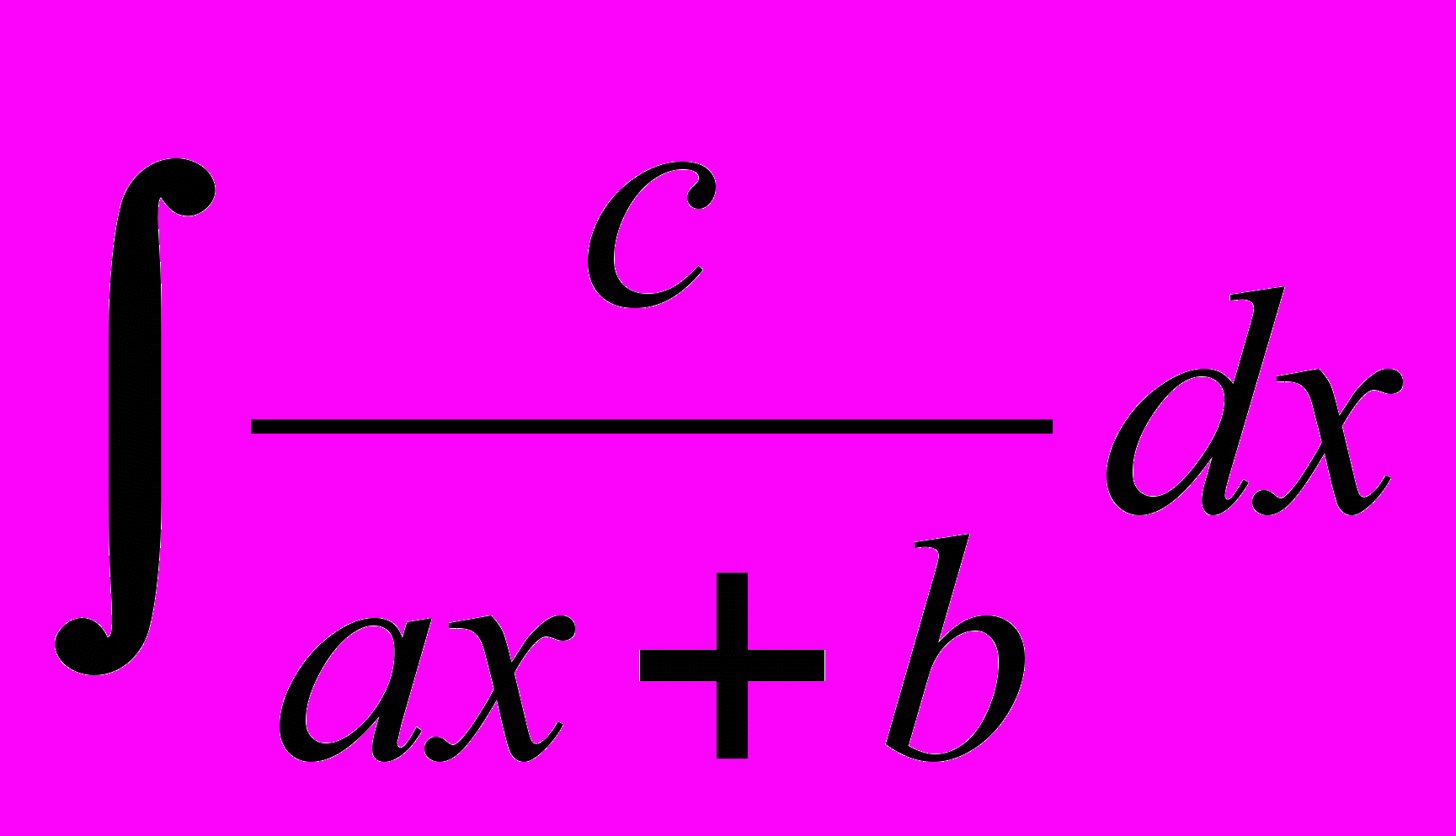Вычисление интегралов вида .
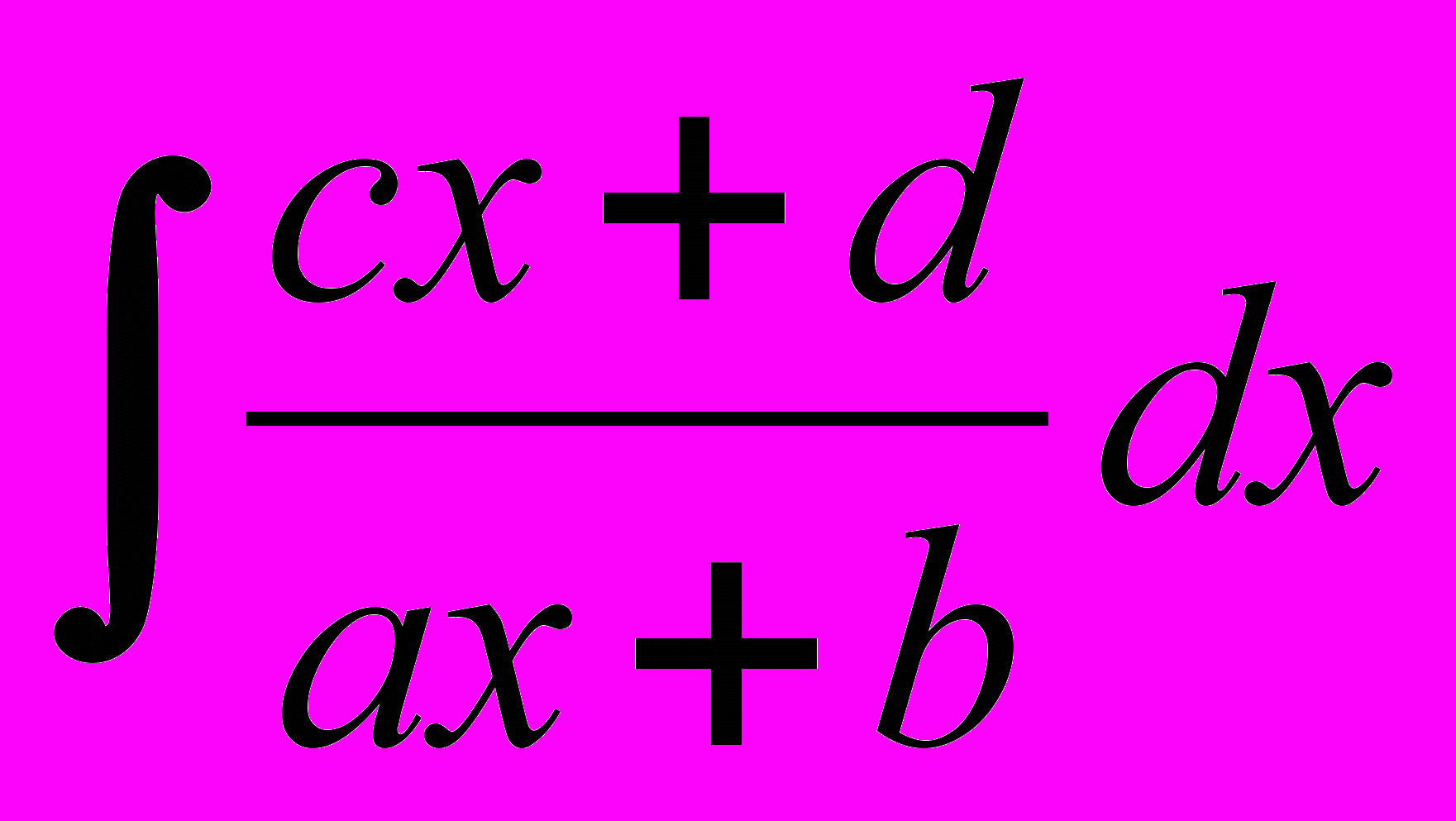Вычисление интегралов вида .
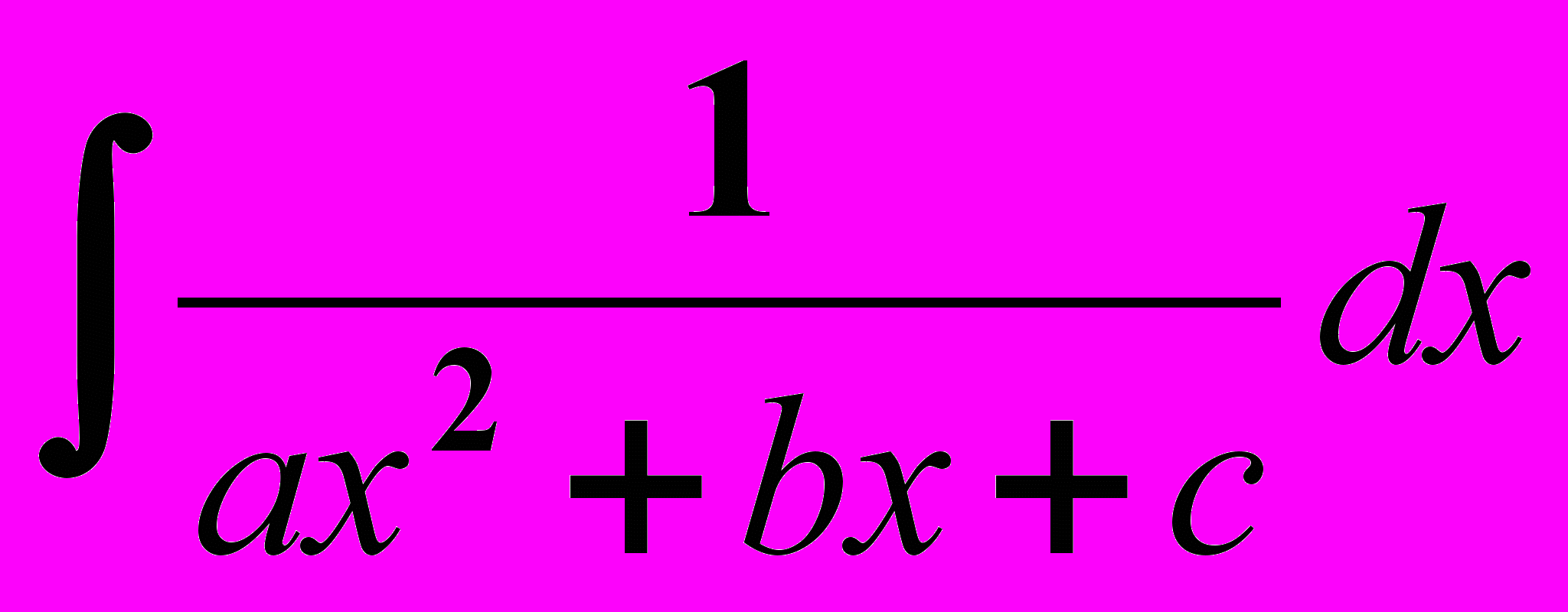Вычисление интегралов вида .
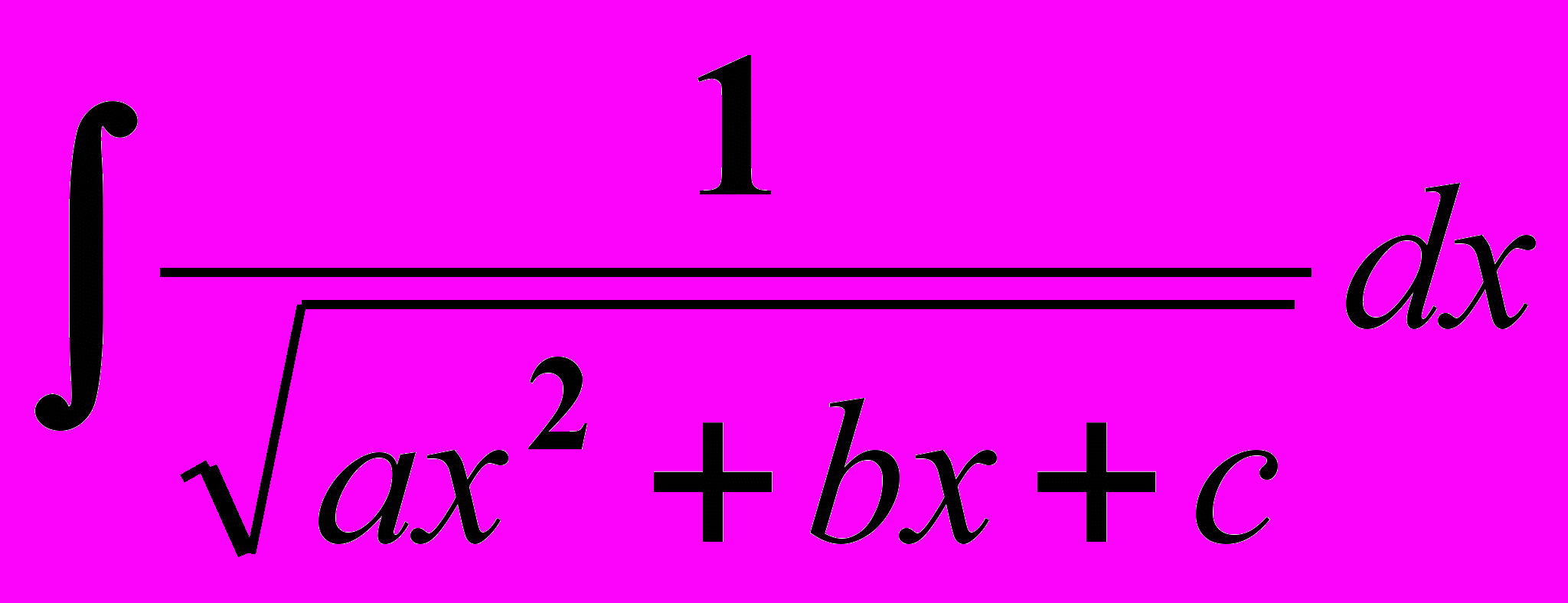Вычисление интегралов вида , .
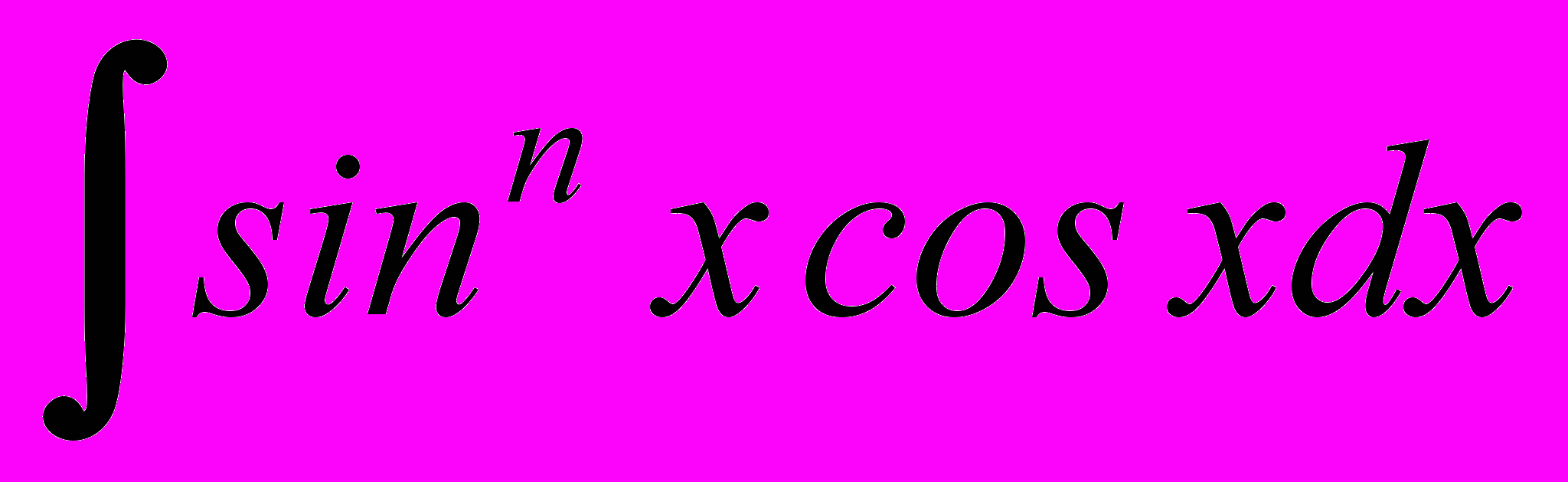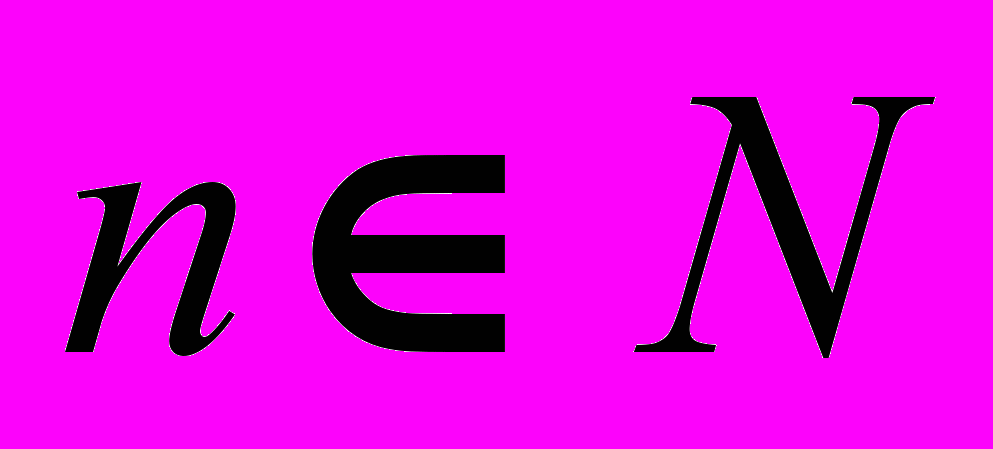Вычисление интегралов вида , .
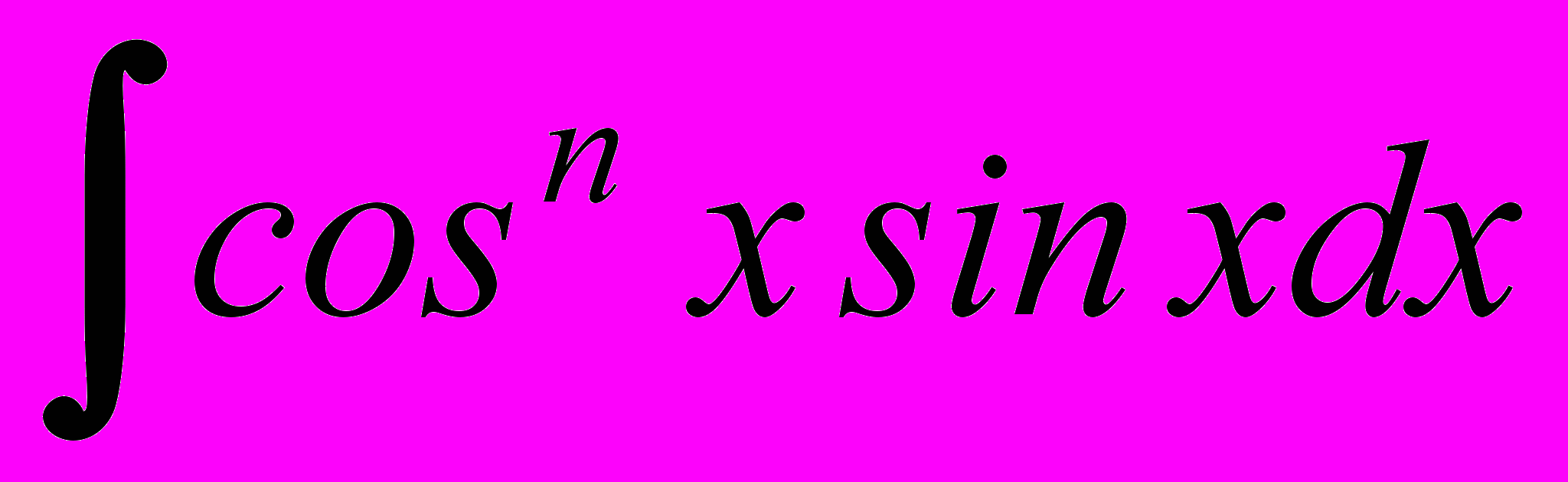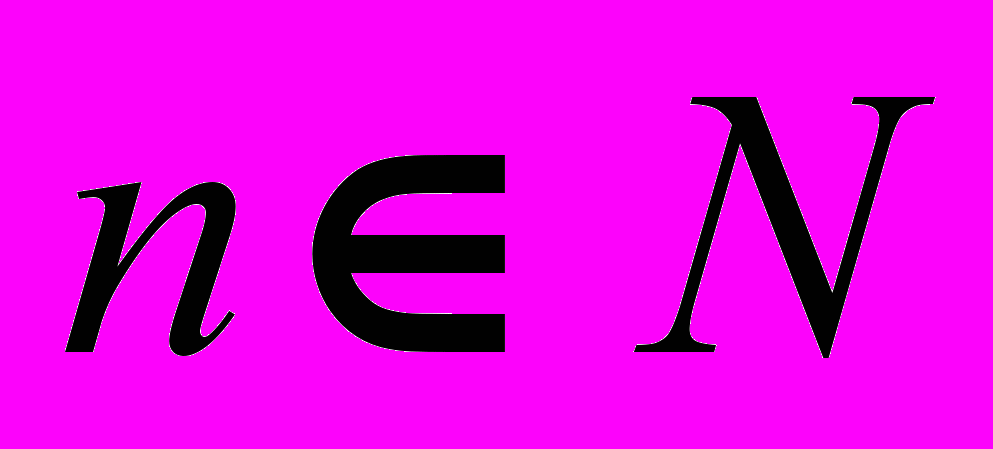Метод интегрирования по частям для вычисления неопределенного интеграла.
Вычисление интегралов вида , .
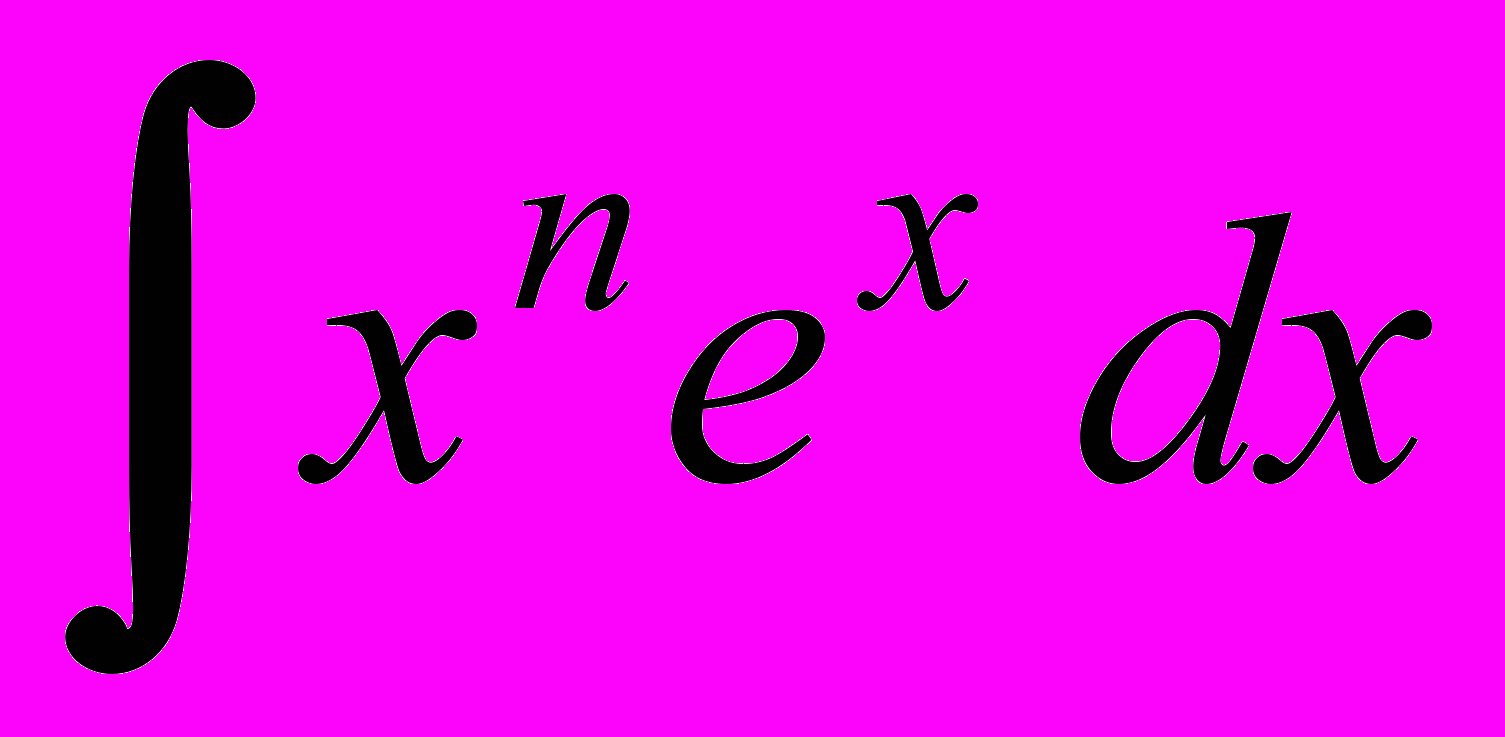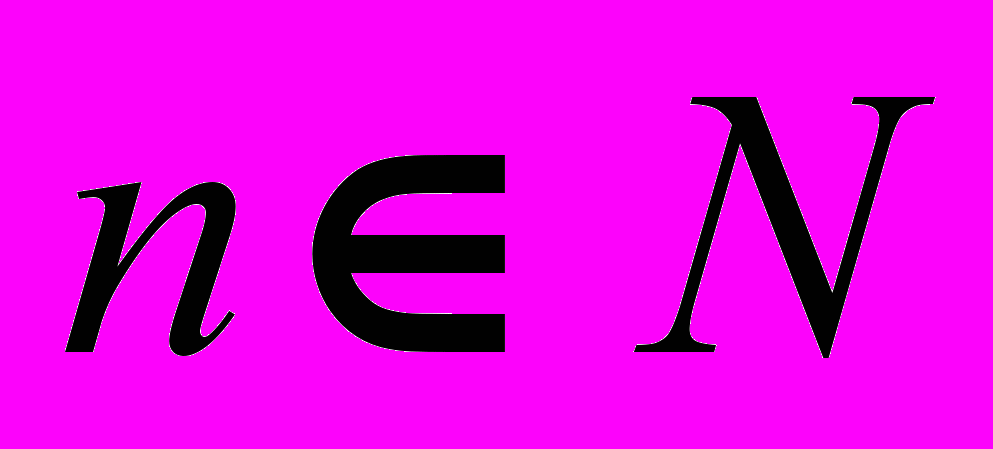Вычисление интегралов вида , .
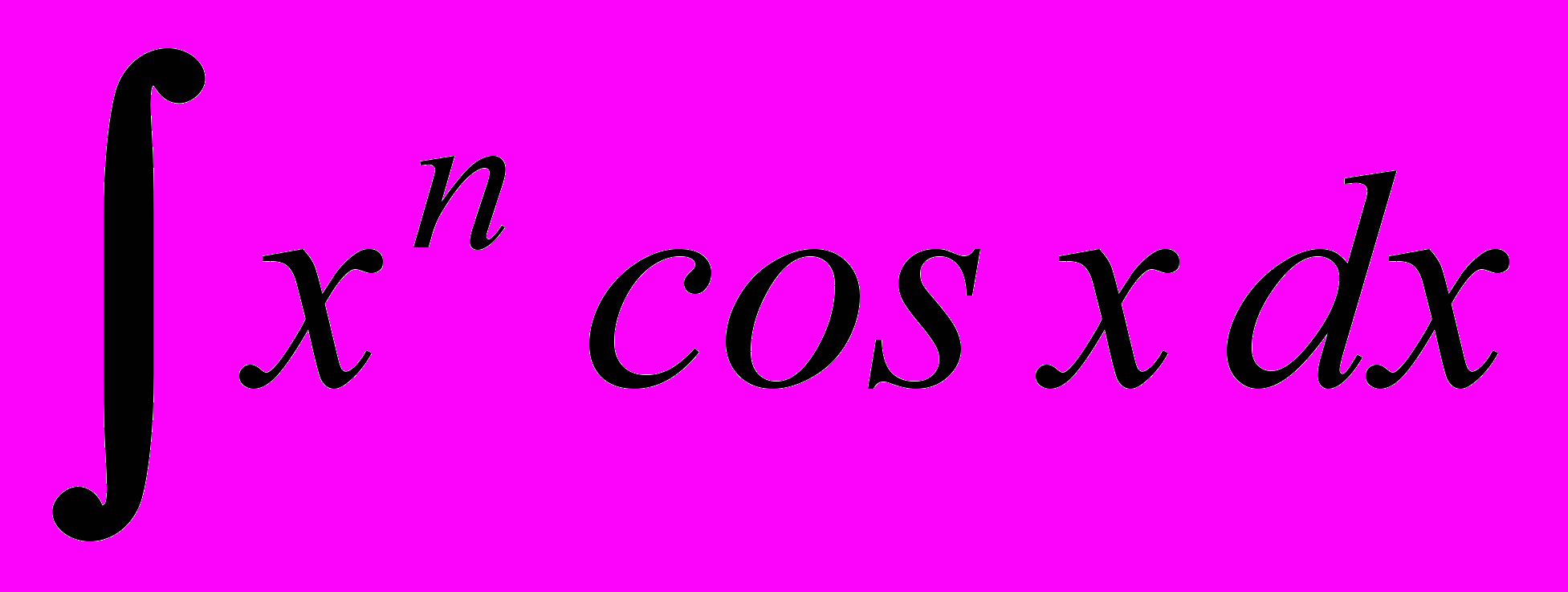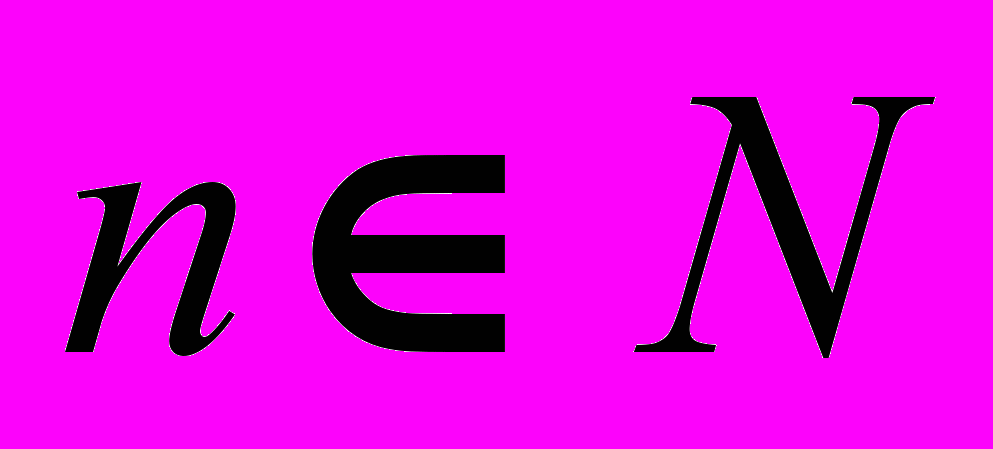Вычисление интегралов вида , .
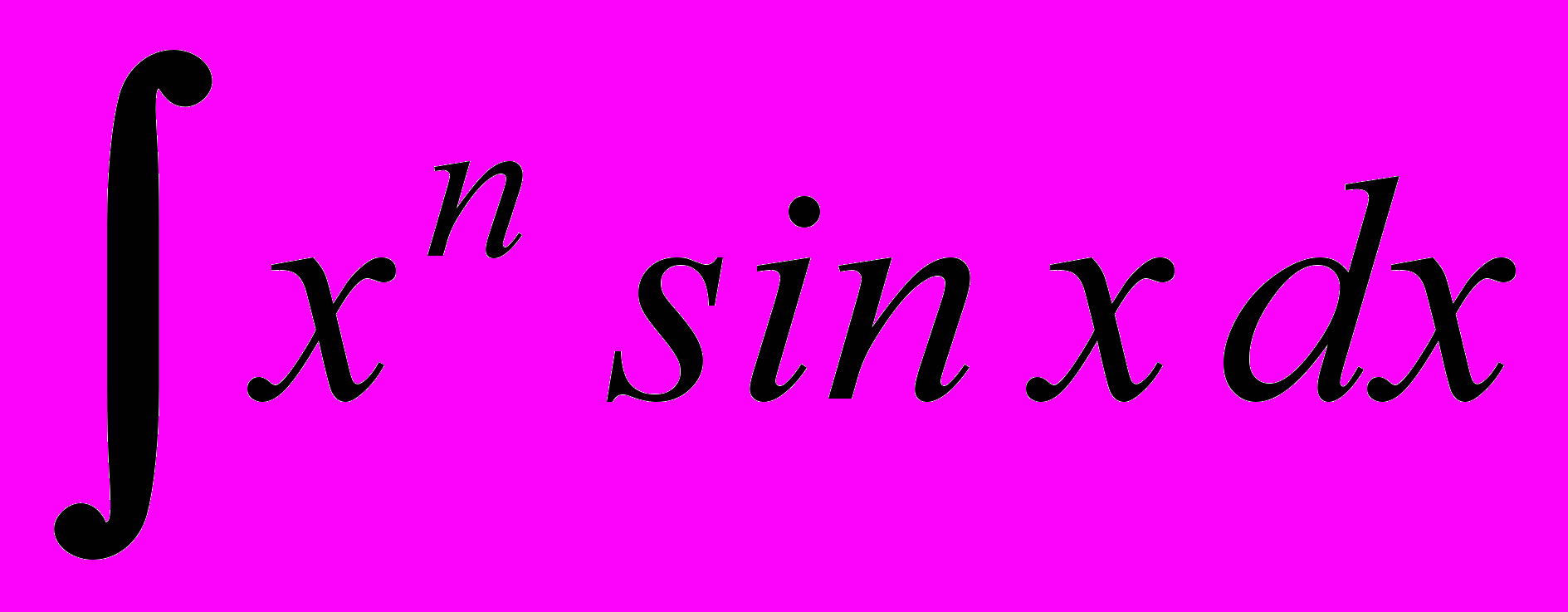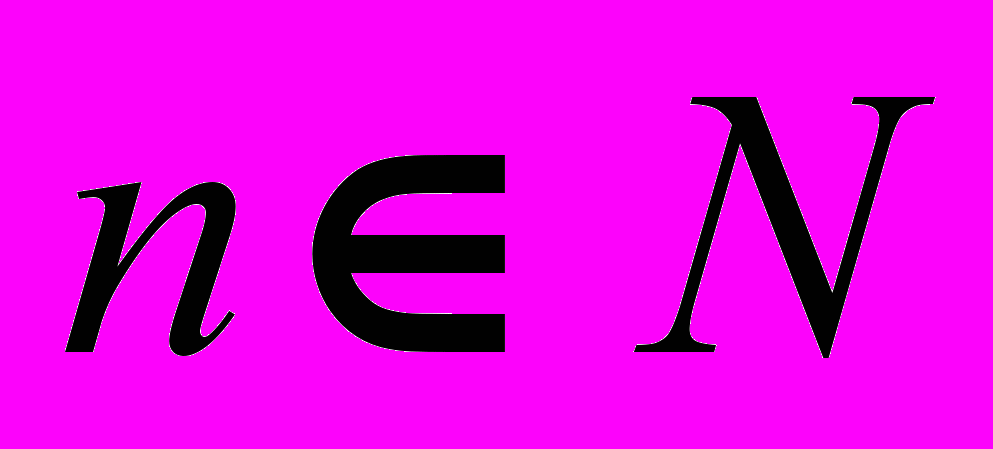Вычисление интегралов вида , , .
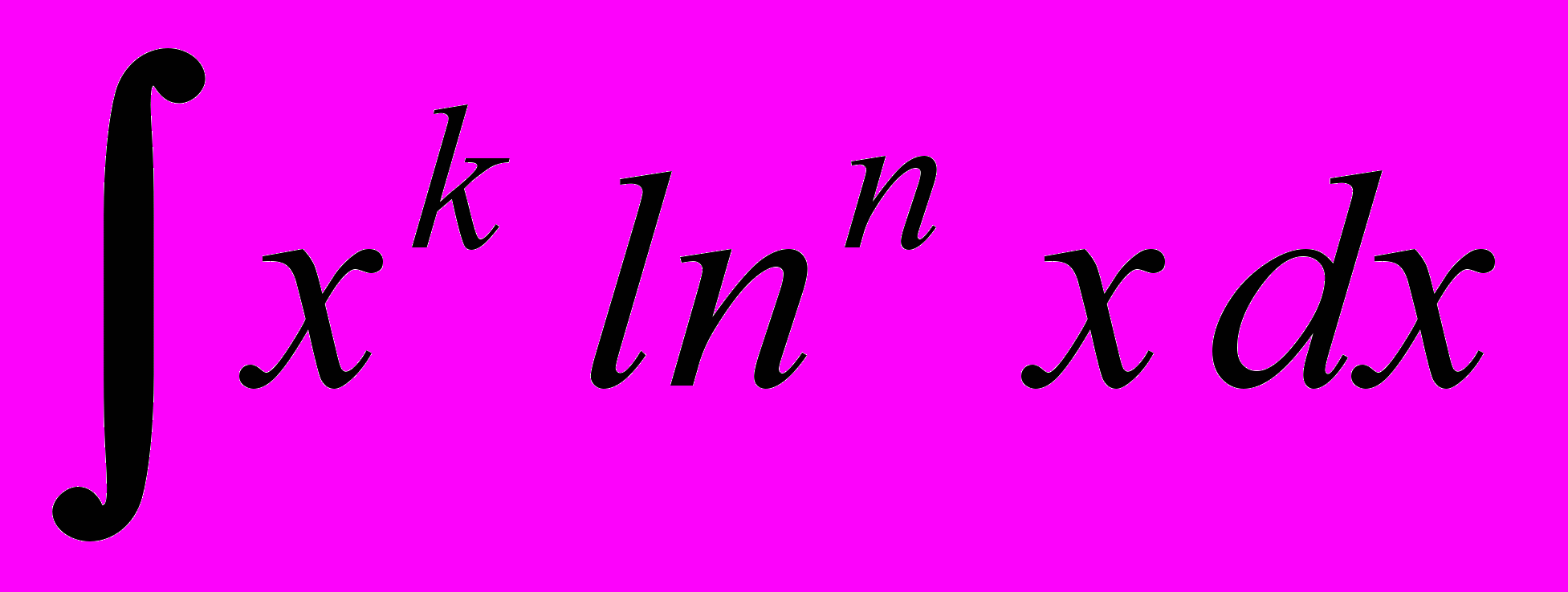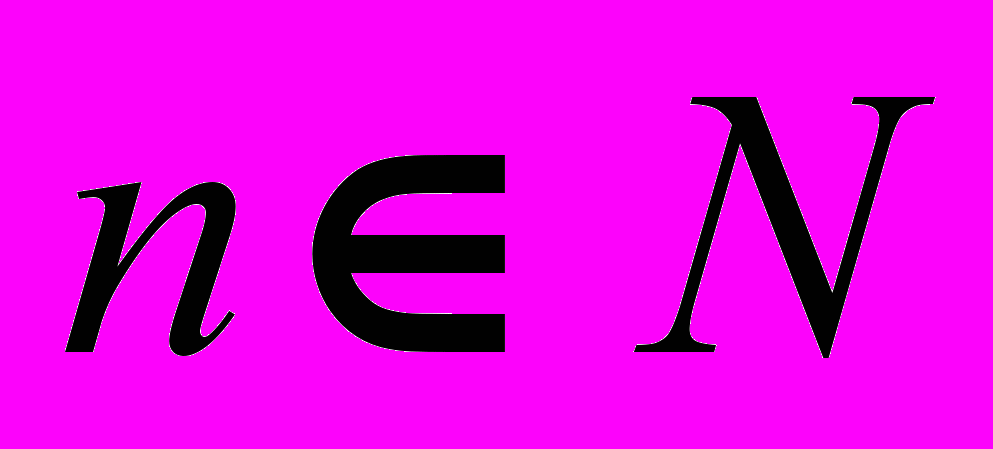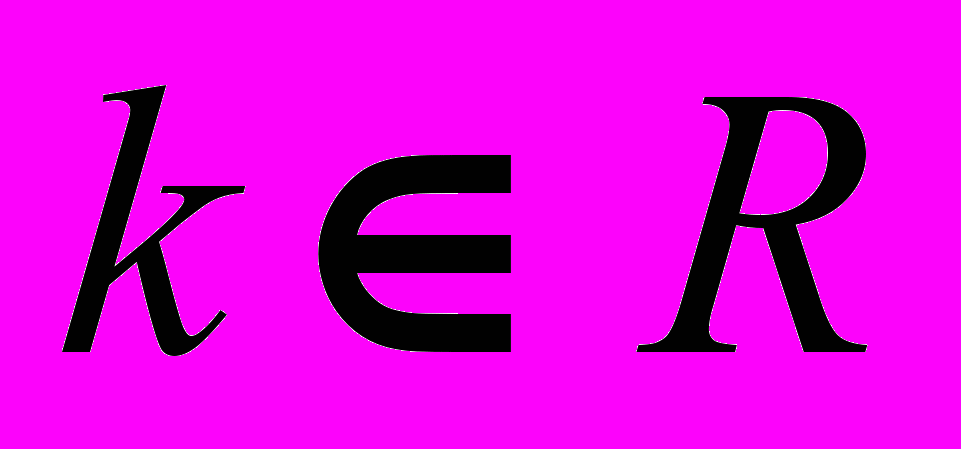Понятие определенного интеграла. Геометрический смысл определенного интеграла.
Свойства определенного интеграла.
Теорема о среднем.
Формула Ньютона-Лейбница.
Вычисление площадей плоских фигур.
Приложения определенного интеграла в экономической теории: понятие излишка потребителя.
Понятие дифференциального уравнения, общего и частного решения, интегральной кривой
Неполные дифференциальные уравнения первого порядка вида .
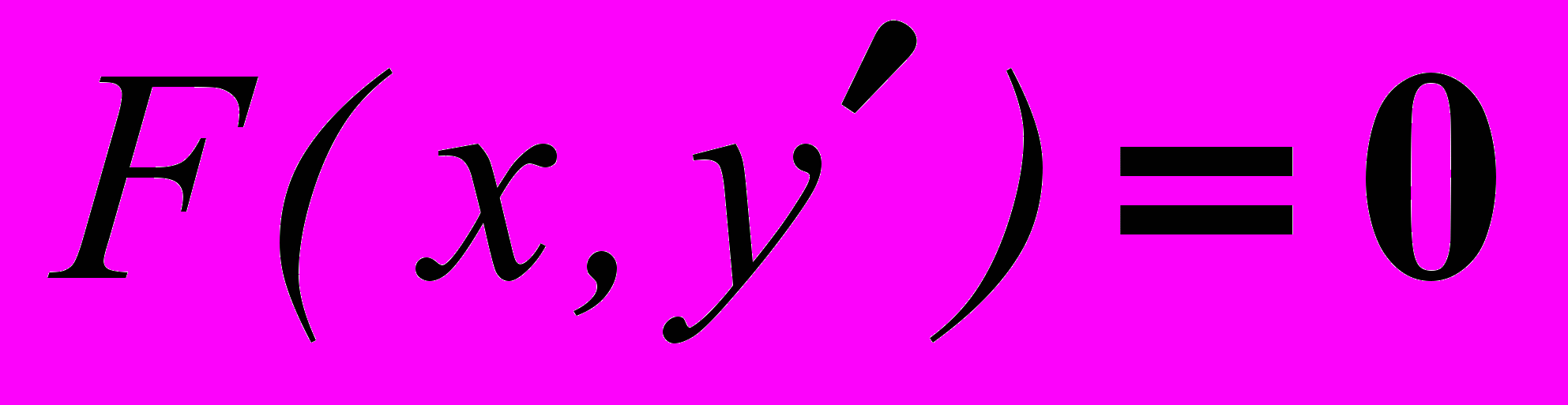Неполные дифференциальные уравнения второго порядка вида .
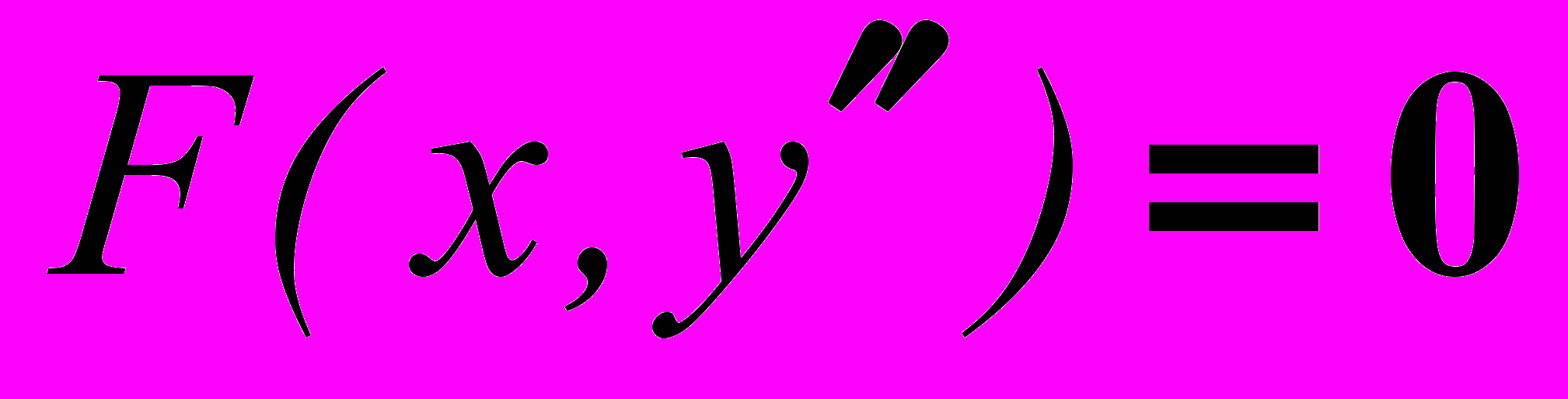Дифференциальные уравнения первого порядка с разделяющимися переменными.
Однородные дифференциальные уравнения первого порядка.

1.2. Линейная алгебра и элементы аналитической геометрии

Линейные уравнения.
Уравнения прямой на плоскости.
Условия параллельности и перпендикулярности прямых.
Расстояние от точки до прямой.
Кривые второго порядка: окружность и эллипс
Кривые второго порядка: гипербола и парабола.
Прямая и плоскость в пространстве.
Матрицы. Основные определения. Виды матриц.
Операции над матрицами. Умножение матрицы на число. Сложение матриц. Разность двух матриц. Произведение матриц. Свойства операций над матрицами.
Определители квадратных матриц. Определители матриц второго и третьего порядков.
Миноры и алгебраические дополнения к элементам матрицы.
Свойства определителей.
Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Алгоритм вычисления обратной матрицы. Свойства невырожденных матриц.
Системы линейных уравнений.
Нахождение решения системы линейных уравнений с помощью обратной матрицы.
Нахождение решения системы линейных уравнений по формулам Крамера.
Метод Гаусса.
Системы векторов. N – мерное линейное векторное пространство.
Собственные числа и собственные вектора матриц и линейных операторов.
Матрицы и квадратичные формы.
Системы линейных неравенств.
Линейные задачи оптимизации.
Основные определения и задачи линейного программирования.
Симплексный метод.
Теория двойственности.

1.3. Теория вероятностей и математическая статистика

Случайные события. Достоверное событие.
Классическое определение вероятности.
Сочетание. Размещение. Перестановка.
Основные свойства вероятности.
Геометрическая вероятность.
Несовместные события. Сумма событий. Произведение событий.
Теорема сложения вероятностей несовместных событий.
Условная вероятность. Пример. Независимые события.
Теоремы умножения вероятностей двух зависимых и независимых событий.
Совместные события. Теорема сложения вероятностей двух совместных событий.
Формула полной вероятности.
Формула Байеса.
Схема Бернулли. Формула Бернулли.
Локальная теорема Лапласа.
Интегральная теорема Лапласа.
Поток событий. Формула Пуассона.
Дискретная величина. Закон распределения дискретной случайной величины. Многоугольник распределения.
Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
Дисперсия дискретной случайной величины. Свойства дисперсии. Среднее квадратичное отклонение.
Функция распределения случайной величины, её свойства.
Плотность распределения случайной величины, её свойства.
Закон распределения вероятностей для функций от случайных величин с известным распределением.
Равномерное распределение.
Показательное распределение.
Нормальное распределение.
Неравенство Чебышева.
Закон больших чисел и его следствия.
Особая роль нормального распределения: центральная предельная теорема.
Цепи Маркова и их использование в моделировании социально-экономических процессах.
Выборочный метод. Задачи математической статистики.
Генеральная и выборочная совокупности.
Характеристики вариационного ряда: среднее, дисперсия, среднеквадратичное отклонение, мода, медиана.
Эмпирическая функция распределения и гистограмма частот.
Точечные оценки параметров распределения.
Интервальные оценки параметров распределения.
Основная и альтернативная гипотезы. Ошибки первого и второго рода. Мощность критерия.
Проверка гипотезы о среднем нормального распределения.
Проверка гипотезы о равенстве средних двух нормально распределенных совокупностей.
Проверка гипотезы о дисперсии нормального распределения.
Проверка гипотезы о равенстве дисперсий двух нормально распределенных совокупностей.
Выборочный коэффициент корреляции и его свойства.
Модель парной линейной регрессии.
Оценивание параметров модели парной линейной регрессии.

Blog

Программа вступительного экзамена в магистратуру по специальности 521602 «Математические методы анализа экономики»

Содержание