Программа курса опирается на знания, полученные студентами-психологами в рамках следующих дисциплин

Вид материала

Содержание

Десятибальная оценка
II. Содержание программы.
2.1. Основные понятия математической статистики.
2.2. Числовые характеристики одномерных распределений.
2.3. Числовые меры парной взаимосвязи случайных величин.
2.4. Типы данных, четыре уровни измерений.
2.5. Многомерные методы описания данных.
3.1. Основные распределения, используемые при проверке гипотез в психологических исследованиях.
3.2. Проверка статистических гипотез. Алгоритмы проверки наиболее часто используемых гипотез.
4.1. Основные понятия.
4.2. Непараметрические критерии для связанных выборок.
4.3. Непараметрические критерии для несвязанных выборок.
4.4. Многофункциональные критерии. Угловой 
5.1. Алгоритмы математической обработки данных при различных схемах проведения исследования.
5.2. Обработка данных на компьютере.
Iii. тематика заданий по различным видам текущего контроля
Пример задания для контрольной работы
IV. Экзаменационные вопросы
Базовые учебники
VI. Тематический план курса
...
Полное содержание

Подобный материал:

I. Пояснительная записка.

Требования к студентам

Программа курса опирается на знания, полученные студентами-психологами в рамках следующих дисциплин:

Высшая математика
Общая психология

Аннотация

Курс "Математические методы в психологии" даёт студентам знания, необходимые для корректной постановки психологического (социологического) исследования и обработки его результатов, ориентирован на выработку у студентов навыков адекватного применения алгоритмов статистической обработки к данным психологического тестирования.

Данный курс теснее всего связан с курсами "Высшая математика", "Психологическая диагностика", "Экспериментальная психология" и необходим студентам для написания курсовых и дипломных работ.

Особое внимание в курсе уделяется формированию у студентов практических навыков обработки данных психологического исследования – все алгоритмы представления и обработки данных прорабатываются студентами на материале, полученном в специально для этой цели организованном тестировании.

Продолжительность курса

Продолжительность курса "Математические методы в психологии" – 40 часов, из них 20 часов – лекции и 20 часов – практические занятия.

В самостоятельную работу студента по освоению дисциплины входит:

чтение и анализ основной и дополнительной литературы из приводимого списка;
решение домашних примеров и задач;
выполнение контрольной работы.

Цель курса

Цель курса "Математические методы в психологии" – дать студентам знания, необходимые для корректной постановки психологического (социологического) исследования и обработки его результатов, выработать у студентов навыки адекватного применения алгоритмов статистической обработки данных.

Учебная задача дисциплины

В результате изучения дисциплины студент должен:

иметь представление

о значении и месте математических методов в психологии как науки;
о методологии проведения психологического исследования и обработке его результатов;
об основных сферах приложения математических методов в различных направлениях психологии;

знать

основные понятия и формулы теории вероятностей;
основные алгоритмы описательной статистики;
методы проверки значимости наиболее часто используемых в психологии параметров;
основные алгоритмы параметрической и непараметрической статистик;
основные алгоритмы многомерной статистики;

уметь

решать вероятностные задачи;
применять на практике основные алгоритмы описательной статистики;
применять на практике методы проверки значимости наиболее часто используемых в психологии параметров;
корректно использовать алгоритмы параметрической и непараметрической статистик;
корректно планировать психологическое (социологическое) исследование.

Формы работы студентов:

Лекционные и практические занятия, проработка литературы по применению математических методов в психологии, проведение самостоятельных исследований и обработка полученных данных, написание контрольной работы.

Виды контроля:

текущий контроль: оценивается самостоятельная работа студентов на практических занятиях, выполнение домашних заданий и контрольной работы;
итоговый контроль: осуществляется в форме зачета.

Результирующая оценка рассчитывается по накопительной системе за работу в течение всего курса:

активная работа на практических занятиях (0,1);
выполнение домашних работ (0,2);
защита контрольной работы – (0,4);
зачет (0,3).

Итоговая оценка проставляется в зачетную ведомость.

Знания студентов оцениваются по десятибалльной системе:

от 4 до 10 баллов – экзаменационный балл,

от 1 до 3 баллов – неаттестация предмета.

Результирующая экзаменационная оценка по курсу определяется по 10-ти и 5-ти бальной системах через следующее соотношение:

Десятибальная оценка	Пятибальная оценка
1,2, 3 – неудовлетворительно	Неудовлетворительно
4 – почти удовлетворительно	Удовлетворительно
5 – удовлетворительно	Удовлетворительно
6 – почти хорошо	Хорошо
7 – хорошо	Хорошо
8 – почти отлично	Отлично
9 – отлично
10 – блестяще

II. Содержание программы.

Тема 1. Введение, основные понятия теории вероятностей.

Особенности описаний объектов, явлений в психологии.
1. Отличие психологических описаний от описаний объектов в естественных науках. Основные теоретические модели психологии и их характеристика: качественный уровень описания, субъективность, фрагментарность. Случайность психологических явлений.
Основные понятия теории вероятностей.
1. Теория вероятностей как аппарат математического описания случайных явлений.
2. Понятие события, детерминированные и случайные события. Частота, частость, вероятность события. Классификация случайных событий: простые и сложные, совместные и несовместные, зависимые и независимые события. Вероятность суммы и произведения событий. Полная система событий, формула полной вероятности. Формула Байеса. Примеры психологических задач на определение вероятностей событий.

Тема 2. Описательная статистика.

2.1. Основные понятия математической статистики.

Способы представления распределений.

Случайная величина, генеральная совокупность, выборка, распределение. Табличное, графическое, аналитическое представление распределений. Таблица приведенных данных, интервал квантования, алгоритм построения гистограммы и кумуляты.

2.2. Числовые характеристики одномерных распределений.

Меры положения – мода, медиана, математическое ожидание; меры разброса – дисперсия, стандартное отклонение, коэффициент вариации; мера скошенности – коэффициент асимметрии. Их свойства и способы вычисления.

2.3. Числовые меры парной взаимосвязи случайных величин.

Корреляционный анализ: диаграмма рассеивания, ковариация, коэффициент линейной корреляции Пирсона; его вычисление и свойства; корреляционная матрица, корреляционная плеяда.
Двумерный регрессионный анализ. Понятие о линейной и нелинейной регрессии. Алгоритм построения простой линейной регрессии. Факторная и остаточная дисперсии, коэффициент детерминации.
Однофакторный дисперсионный анализ. Назначение, виды, основное уравнение ДА, структура итоговой таблицы, психологическая интерпретация.

2.4. Типы данных, четыре уровни измерений.

Понятие измерения, уровни измерений.

Шкала наименований: коэффициент φ парной (четырехклеточной) сопряженности Пирсона, коэффициент C многоклеточной сопряженности Пирсона.

Шкала порядка: шкала рангов, коэффициент ρ ранговой корреляции Спирмена, рангово-бисериальный коэффициент корреляции r_r_b.

Шкала интервалов, метрическая шкала: точечно-бисериальный коэффициент корреляции r_pb.

2.5. Многомерные методы описания данных.

Классификация многомерных методов по их назначению.

Множественный регрессионный анализ.
1. Назначение МРА, общий вид уравнения множественной линейной регрессии. Коэффициент множественной корреляции. Представление уравнения множественной линейной регрессии в z-значениях, стандартные β-коэффициенты регрессии, их свойства. Коэффициент множественной детерминации. Методы компьютерной обработки: стандартный и пошаговый.
Факторный анализ.
1. Назначение; латентная переменная, виды ФА.
2. Модель главных компонент, её геометрическая интерпретация. Представление исходной корреляционной матрицы R через матрицу компонентных нагрузок A: R=A• A′. Собственные векторы и собственные значения, их интерпретация. Выбор числа факторов.
3. Матрица факторных нагрузок, её структура. Мощность фактора. Общность и характерность переменной, их смысл.
4. Простая факторная структура (принцип Терстоуна) и вращение факторов, геометрическая интерпретация. Критерий варимакс. Процедура ФА и методы компьютерной обработки.

Кластерный анализ.
1. Назначение, основные понятия (кластер, меры сходства, дендрограмма). Меры расстояния: Евклидово расстояние, "метрика города". Основные методы кластерного анализа: метод одиночной связи (метод "ближайшего соседа"), метод полных связей (метод "дальнего соседа"), метод средней связи, их психологическая интерпретация. Методы компьютерной обработки.

Тема 3. Индуктивная параметрическая статистика.

3.1. Основные распределения, используемые при проверке гипотез в психологических исследованиях.

Нормальное распределение.
1. Биноминальное распределение, схема испытаний Бернулли. Аппроксимирующая формула Муавра. Z-преобразование, единичное нормальное распределение, его свойства. Таблица стандартизованного единичного нормального распределения. Понятие квантилей распределения.
χ², t и F-распределения, их конструирование.
1. Графики χ², t и F-распределений, их свойства. Понятие степени свободы. Таблицы χ², t и F-распределений и их практическое применение.

3.2. Проверка статистических гипотез. Алгоритмы проверки наиболее часто используемых гипотез.

Статистики и параметры. Алгоритм проверки статистических гипотез, нулевая и альтернативная гипотезы, доверительная вероятность, ошибки первого и второго рода.
Частные случаи проверки гипотез, наиболее часто используемых в психологии:
1. достоверность различий средних значений и дисперсий двух выборок, значимость различных мер взаимосвязи случайных величин:

Тема 4. Непараметрическая статистика.

4.1. Основные понятия.

Параметрические и непараметрические критерии: сравнительная характеристика, возможности и ограничения. Связанные и несвязанные выборки.

4.2. Непараметрические критерии для связанных выборок.

Критерий знаков G: характеристика, ограничения, алгоритм вычисления, проверка значимости.

Критерий Т Вилкоксона: характеристика, ограничения, алгоритм вычисления, проверка значимости.

4.3. Непараметрические критерии для несвязанных выборок.

Критерий U Манна-Уитни: характеристика, ограничения, алгоритм вычисления, проверка значимости.

Критерий Q Розенбаума: характеристика, ограничения, алгоритм вычисления, проверка значимости.

4.4. Многофункциональные критерии. Угловой ^-критерий Фишера.

Общая характеристика многофункциональных критериев. Эффект, виды эффектов. Угловой ^-критерий Фишера: назначение, ограничения, геометрическая интерпретация, алгоритм вычисления, проверка значимости.

Тема 5. Алгоритмы математической обработки данных при различных схемах проведения исследования. Обработка данных на компьютере.

5.1. Алгоритмы математической обработки данных при различных схемах проведения исследования.

Исследование одной выборки:
- описание данных:
  - построение гистограмм распределений признаков;
  - определение числовых характеристик распределений – М_о, М, D, s, As;
  - вычисление парных коэффициентов корреляции признаков - j, r, r - и проверка их значимости, корреляционный анализ;
  - регрессионный анализ, построение линейной регрессии на «внешние» признаки;
  - многомерные методы описания данных (множественный регрессионный анализ, дисперсионный анализ, дискриминантный анализ, факторный анализ, кластерный анализ).
- проверка значимости изменений (при двух и более срезах):
  - сравнение средних по критериям t, G, Т;
  - сравнение корреляционных матриц, уравнений регрессии, структур признаков, определенных через использование многомерных методов.
Исследование двух (нескольких) выборок.
- описание данных формально аналогично описанию данных в предыдущем случае.
- проверка значимости различий между выборками:
  - сравнение средних по критериям t, U, Q;

сравнение корреляционных матриц, уравнений регрессии, структур признаков, определенных через использование многомерных методов.

5.2. Обработка данных на компьютере.

Анализ данных на компьютере. Математико-статистическая обработка результатов исследования с использованием компьютерных пакетов Statistica, SPSS, Statgrafic. Возможности и ограничения конкретных компьютерных методов обработки данных.

Стандарты обработки данных. Нормативы представления результатов анализа данных в научной психологии.

Математическое моделирование и средства построения моделей: классификации, латентных структур, семантических пространств и т.п. Модели индивидуального и группового поведения. Моделирование когнитивных процессов и структур. Проблема искусственного интеллекта. Нетрадиционные методы моделирования.

III. ТЕМАТИКА ЗАДАНИЙ ПО РАЗЛИЧНЫМ ВИДАМ ТЕКУЩЕГО КОНТРОЛЯ

Примеры задач для практических занятий и домашних заданий

По теме "Теория вероятностей"

Задачи – на определение вероятности сложного события,

на формулу полной вероятности,
на формулу Байеса.

Примеры задач:

Используемые в медицине тесты естественной классификации обычно состоят из четырех изображений объектов, один из которых "лишний". Сколько раз нужно предъявить испытуемому такой тест, чтобы на 99% быть уверенным в неслучайности правильного выполнения всех предъявлений?
Вероятность диагностики заболевания при одном тестировании равна ¾. Какова вероятность обнаружения заболевания при трех тестированиях?
Компьютерная система экзаменационного тестирования содержит два набора вопросов. В одном наборе 5 трудных и 25 легких, в другом – 20 трудных и 10 легких вопросов. Как следует задать вероятности выбора одного и другого наборов, чтобы уравнять для каждого экзаменующегося предъявление на экране дисплея трудных и легких вопросов?
Имеется 6 тестов профотбора. Вероятность правильного ответа на них в данной выборке претендентов равна, соответственно: на первый тест – 0.7,

на второй – 0.4,
на третий – 0.5,
на четвертый – 0.3,
на пятый – 0.2,
на шестой – 0.1.

В результате укороченного тестирования только по одному случайно выбранному тесту один из претендентов был отобран. Какова вероятность того, что ему достался i-тый тест? (всего возможно 6 вариантов этой задачи, в которых i = 1 ¸ 6).

* В условиях задач могут быть заданы различные числовые значения для разных вариантов задания.

По теме "Параметрическая статистика"

По таблице исходных данных, где i – номер индивида,

i	X₁	X₂	X₃
1
2
…
N

N – размер выборки,

X₁ и X₂ – психологические признаки,

X₃ – "внешний" критерий,

требуется:

построить гистограммы признаков,
рассчитать коэффициенты корреляции r_1,3 и r_2,3 и определить их значимость,
построить линейные регрессии на Х₃,
дать психологическую интерпретацию полученным результатам.

* Для повышения мотивации студентов данные исходной таблицы берутся из предварительного тестирования самих студентов по нетрудоемким тестам (например, по тесту "Логические ряды" из батареи Амтхауэра), а в качестве "внешнего" критерия может служить самооценка успешности студентов в их учебе.

* Предлагается N вариантов задания, получаемых путем исключения из исходной таблицы данных одного из индивидов.

По теме "Непараметрическая статистика"

По таблице исходных данных проверить значимость уровневых различий между признаками Х₁ и Х₂ по критериям знаков G и Вилкоксона Т для связанных выборок.

* Предлагается N вариантов задания, получаемых путем исключения из исходной таблицы данных одного из индивидов.

Пример задания для контрольной работы

Цель контрольной работы: формирование у студентов навыков использования основных методов и приёмов обработки данных психологического исследования и интерпретации его результатов.

Порядок выполнения контрольной работы:

Составление таблицы исходных данных проведённого психологического исследования.

i x_j – тестируемые признаки j – номер признака m – количество признаков i – порядковый номер индивида n – размер выборки	x₁	x₂	… x_j…	x_m
1			…….
2			…….
…	…	…	…….	…
n			…….
			…….

Построение гистограмм распределений признаков (состав признаков задаётся преподавателем).

Порядок построения гистограммы:

составление таблицы упорядоченных данных

m_i – частота i–го значения признака x_j p_i=m_i/n-частость (выборочная вероятность) i–го значения признака x_j x_j	m_i	p_i
(x_j)_min
…
(x_j)_max

построение палочковой диаграммы,
определение "нулевой" точки: (x_j)₀=(x_j)_min– _ (где_-начальный интервал квантования),
выбор интервала квантования 
построение гистограммы.

Вычисление коэффициентов линейной корреляции Пирсона (состав признаков задаётся преподавателем).

1) вычисление промежуточных данных по таблице

i	x_i	y_i	(x_i-M_x)	(y_i-M_y)	(x_i-M_x)²	(y_i-M_y)²	(x_i-M_x)·(y_i-M_y)
1
2
…	…	…	…	…	…	…	…
n
			0	0

M_x=x_i/n

M_y=y_i/n

D_x=(x_i-M_x)²/n

D_y=(y_i-M_y)²/n

COV_xy=[(x_i-M_x)·(y_i-M_y)]/n

2) вычисление коэффициентов линейной корреляции

Пирсона: r_xy= COV_xy/(_x∙_y)

3) проверка значимости коэффициентов линейной корреляции Пирсона

по t – критерию Стьюдента.

Построение простой линейной прогрессии (признаки задаются преподавателем).

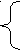y = a·x + b

a = r_xy· _x/_y

b = M_y- a·M_x

Определение значимости уровневых различий между признаками по t – критерию Стьюдента, G-критерию знаков, T-критерию Вилкоксона (признаки задаются преподавателем).
Психологическая интерпретация полученных результатов.

IV. Экзаменационные вопросы

Особенности описаний объектов, явлений, изучаемых в психологии; их отличия от описаний объектов естественных наук.
Модели, используемые в психологии (структурные, вероятностные, информационные).
Отличие измерений в психологии от измерений в естественных науках.
Адекватность применения теории вероятностей и математической статистики для описания объектов, явлений, изучаемых в психологии.
Событие, классификация событий; примеры психологических событий.
Совместные и несовместные события. Вероятность суммы событий. Примеры задач из психологии.
Зависимые и независимые события. Вероятность произведения событий. Примеры задач из психологии.
Полная группа событий. Формула полной вероятности. Примеры задач из психологии.
Объект и предмет математической статистики. Адекватность аппарата математической статистики для планирования и обработки психологических данных.
Описательная и индуктивная статистика.
Распределение случайных величин. Формы представления распределений.
Построение гистограммы полученных в эксперименте данных.
Числовые характеристики распределения одной случайной величины.
Типы данных. Четыре типа шкал. Примеры из психологии.
Числовые характеристики, используемые для описания данных, измеренных в номинальной шкале.
Числовые характеристики, используемые для описания данных, измеренных в порядковой шкале.
Числовые характеристики, используемые для описания данных, измеренных в интервальной шкале.
Меры взаимосвязи двух случайных величин.
Числовые характеристики парной взаимосвязи. Коэффициент линейной корреляции Пирсона, его вывод и характеристика.
Числовые характеристики парной взаимосвязи. Коэффициент детерминации, его вывод и характеристика.
Числовые характеристики парной взаимосвязи. Коэффициент ранговой корреляции Спирмена, его характеристика.
Коэффициент парной сопряженности, его характеристика.
Линейная регрессия, ее применение в психологии.
Факторный анализ, основные понятия: фактор, ротация, факторный вес. Итоговая таблица, интерпретация факторов.
Кластерный анализ, его характеристика.
Дисперсионный анализ, его характеристика.
Нормальное распределение, его роль в статистике и в психологии. Z – преобразование и таблица единичного нормального распределения.
Нормализация данных, назначение и процедура. Применение в психологии.
Проверка статистических гипотез. Виды гипотез: нулевая и альтернативная.
Основные статистические критерии, используемые в психологии.
Параметрические и непараметрические критерии, их сравнительная характеристика.
t–критерий Стьюдента, его таблица и использование.
t–критерий Стьюдента, его использование для измерения уровня достоверности различия средних значений признака.
χ²- критерий, его таблица и использование.
Непараметрические критерии, общая характеристика.
Связанные и несвязанные выборки, адекватные им статистические критерии.
Связанные выборки, критерий знаков G.
Связанные выборки, критерий Вилкоксона Т.
Несвязанные выборки, критерий Манна-Уитни U.
Несвязанные выборки, критерий Розенбаума Q.

V. Учебно-методическое обеспечение

Литература:

Базовые учебники

Наследов А.Д. Математические методы психологического исследования. – СПб: Речь, 2004.
Сидоренко Е.В. Методы математической обработки в психологии. - СПб: СПЦ, 1996.

Основная литература:

Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. - М., Прогресс, 1976.
Ермолаев О.Ю. Математическая статистика для психологов. – М.: МПСИ, 2002.
Наследов А.Д. Многомерные методы математической обработки в психологии. – СПб: СПГУ, 1998.
Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. – М., 1982.
Суходольский Г.В. Основы математической статистики для психологов. - Л.: ЛГУ, 1996.
Тарасов С.Г. Основы применения математических методов в психологии. – СПб: СПГУ, 1998.

Дополнительная литература:

Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. - М., 1975.
Боровиков В.П. Программа STATISTICA для студентов и инженеров. – М., 2001.
Бюль А., Цёфель П. SPSS: искусство обработки информации. – М., СПб, Киев, 2002.
Годфруа Ж. Что такое психология. Том 2. - М., 1996.
Калинин С.И. Компьютерная обработка данных для психологов. – СПб: Речь, 2002.
Куликов Л.В. Введение в психологическое исследование. - СПб., 1994.
Немов Р.С. Психология. Книга 3. - М., 1995.

VI. Тематический план курса

Наименование разделов и тем	Кол-во часов			Всего часов
Наименование разделов и тем	Лекции	Практи-ческие занятия	Самостоя-тельная работа	Всего часов
Тема 1. Введение, основные понятия теории вероятностей.	1	2	3	6
Раздел 2. Описательная статистика.
2.1. Основные понятия математической статистики. Способы представления распределений.	2	2	5	9
2.2. Числовые характеристики одномерных распределений.	2	2	5	9
2.3. Числовые меры парной взаимосвязи случайных величин.	2	3	5	10
2.4. Типы данных, четыре уровни измерений.	2	2	5	9
2.5. Многомерные методы описания данных.	2	-	5	7
Тема 3. Индуктивная параметрическая статистика.
3.1. Основные распределения, используемые при проверке гипотез в психологических исследованиях.	1	2	5	8
3.2. Проверка статистических гипотез. Алгоритмы проверки наиболее часто используемых гипотез.	1	2	5	8
Тема 4. Непараметрическая статистика.
4.1. Основные понятия.	1	-	5	6
4.2. Непараметрические критерии для связанных выборок.	1	2	5	8
4.3. Непараметрические критерии для несвязанных выборок.	1	2	5	8
4.4. Многофункциональные критерии. Угловой j^*-критерий Фишера.	1	1	5	7
Тема 5. Алгоритмы математической обработки данных при различных схемах проведения исследования. Обработка данных на компьютере.
5.1. Алгоритмы математической обработки данных при различных схемах проведения исследования.	1	-	5	6
5.2. Обработка данных на компьютере.	2	-	5	7
Итого:	20	20	68	108

Автор программы: ____________________ /Раскин В.Н./

Blog

Программа курса опирается на знания, полученные студентами-психологами в рамках следующих дисциплин

Содержание

Базовые учебники