Бражникова Ирина Митрофановна, методист Центра моудпо оценки качества образования Швецова Ольга Алексеевна, учитель математики моу лицея №6 пояснительная записка

Вид материала

Пояснительная записка

Содержание Пояснительная записка Цель программы Учебно-тематический план Из науки о числах. III. Решение логических задач Тема 3. Принцип крайнего элемента. Применение принципа крайнего элемента при решении логических задач.Тема 4. Материально-техническое обеспечение Методическое обеспечение программы Методы и приемы Различные системы счисления Из науки о числах Решение логических задач Геометрические задачи Математические игры и соревнования

Подобный материал:

• Дмитриева Ирина Ивановна, заместитель директора по увр, учитель математики и информатики,, 757.21kb.
• Т. В. Лушина положение о системе оценки качества образования в моу сош №3г. Пушкино, 117.54kb.
• Хмелёва Наталья Алексеевна заместитель директора по увр моу г. Гатчины «Начальная общеобразовательная, 147.03kb.
• Роль межпредметных связей курса химии со школьными курсами математики и физики в повышении, 148.88kb.
• Дундукова Татьяна Алексеевна Учитель математики Романчева Ирина Викторовна Учитель, 11.44kb.
• Петрова Светлана Семеновна, учитель математики моу гимназия №1 г. Чебоксары Научный, 47.37kb.
• Организационно-педагогические условия функционирования педагогической технологии исследования, 304.79kb.
• Фейгина Евгения Алексеевна, Методист моу дод «цит» Г. Кировск 2010 содержание содержание, 534.9kb.
• Характеристика внутришкольной системы оценки качества образования, 41.64kb.
• Чиркова Ирина Александровна Тропина Ольга Алексеевна Никитина Татьяна Михайловна Парамонова, 4079.82kb.

Комитет образования администрации Тамбова

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ЛИЦЕЙ №29


ПРОГРАММА

дополнительного образования


«Живая математика»


Тамбов

2008


Допущено

комитетом образования

администрации города Тамбова


Авторы: КЛОЧКОВА ИРАИДА ИВАНОВНА, учитель математики, МОУ

лицей № 29


КОБЗАРЬ ОКСАНА ПЕТРОВНА, учитель математики, МОУ лицей № 29


ЧИЖУНОВА МАРИНА НИКОЛАЕВНА, учитель математики,

МОУ лицей № 29


Рецензенты:

1. 
   Бражникова Ирина Митрофановна, методист Центра МОУДПО оценки качества образования
   
2. Швецова Ольга Алексеевна, учитель математики МОУ лицея № 6
   

Пояснительная записка


Математика- это язык, на котором говорят не только наука и техника, математика – это язык человеческой цивилизации. Она практически проникла во все сферы человеческой жизни. Современное производство, компьютеризация общества, внедрение современных информационных технологий требует математической грамотности. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.

Математическое образование вносит свой вклад в формирование общей культуры человека. Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений.

Первоначальные математические познания должны входить с самых ранних лет в наше образование и воспитание. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью.

Дополнительная образовательная программа «Живая математика» рассчитана на учащихся шестых классов (11-12 лет), склонных к занятиям математикой и желающих повысить свой математический уровень.

Программа «Занимательная математика» является частью интеллектуально-познавательного направления дополнительного образования и расширяет содержание программ общего образования.


Цель программы – способствовать воспитанию интереса учащихся к математике и развитию их математических способностей.


Образовательные задачи:

• углубление и расширение знаний учащихся по математике
  
• привитие интереса учащимся к математике
  
• активизировать познавательную деятельность
  
• показать универсальность математики и её место среди других наук.
  

Воспитательные задачи:

• воспитание культуры личности
  
• воспитание отношения к математике как к части общечеловеческой культуры
  
• воспитание понимания значимости математики для научно – технического прогресса
  
• воспитание настойчивости, инициативы, чувства ответственности, самодисциплину.
  

Развивающие задачи:

• развитие ясности и точности мысли, критичность мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
  
• формирование математического кругозора, исследовательских умений учащихся.
  

Программа содержит материал, как занимательного характера, так и дополняющий, расширяющий программу общеобразовательной школы по математике. Большое внимание в программе уделяется исто­рии математики и рассказам, каким-то образом связанным с математикой (задача «о кенигсбергских мостах», запись цифр и чисел у других народов, математические фокусы, ребусы и др.), выполнению самостоятельных заданий творческого характера (составить рассказ, фокус, задачу с использованием изученных матема­тических свойств.), изучению раз­личных арифметических методов решения задач (метод ре­шения «с конца», составление высказываний, отрицаний высказываний, составление графов и др.). Уделяется внимание рассмотрению геометрического ма­териала, развитию пространственного воображения. Такое «ран­нее» рассмотрение некоторых тем (даже без строгих матема­тических доказательств) способствует в дальнейшем более глубокому их усвоению. Некоторый материал дается с доказательством (посиль­ным для ребят). Школьники начинают познавать задачи на доказательство, что очень хорошо развивает логику и способ­ствует развитию умения доказывать теоремы и находить пути решения в задачах на доказательство.

На занятиях предполагается использовать наглядный материал, возможности новых информационных технологий и технических средств обучения.

Новизна данной программы заключается в ее четкой логической структуре, гармоничном сочетании строгих математических фактов и занимательности. Программа дополнительного образования «Живая математика» для шестиклассников является логическим продолжением программы «Занимательная математика» для пятиклассников и входит в общий курс для 5-11 классов дополнительного математического лицейского образования. В тоже время программа «Живая математика» является самостоятельным курсом, отличительной особенностью которого является универсальность знаний, умений и навыков, полученных в результате ее прохождения.

Программа «Живая математика» рассчитана на один год обучения

(72 часа).

Курс является открытым. В него можно добавлять новые фрагменты, развивать тематику или заменять какие-либо разделы другими. Главное, чтобы они были небольшими по объёму, интересными для учащихся, соответствовали их возможностям.

Основными формами проведения занятий могут являться: комбинированные тематические занятия, практикумы по решению задач, конкурсы по решению математических задач.

Изложение материала может осуществляться с использованием традиционных словесных и наглядных методов: рассказ, беседа, демонстрация видеоматериалов, наглядного материала, различного оборудования.

При проведении занятий целесообразно использовать основные положения и принципы культурологического подхода. Существенное значение имеет проведение дискуссий, выполнение учениками индивидуальных заданий, подготовка сообщений. Ведущее место при проведении занятий должно быть уделено задачам. Однако это не исключает теоретическое ознакомление учащихся с новым материалом при изучении каждой очередной темы.

Занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.

В процессе работы по программе преподаватель может с учетом математического развития учащихся сокращать или увеличивать время на изучение определенной темы.

Итогом реализации программы «Живая математика» могут служить: успешные выступления кружковцев в городском конкурсе «Математическая регата», международной математической игре-конкурсе «Кенгуру», создание предпосылок для успешных выступлений кружковцев на олимпиадах всех уровней.


Учебно-тематический план

№	Раздел	Тема	Кол-во часов
			Теория	Практика	Всего
1	Различные системы счисления	Тема1. Вводное занятие. История появления числа. Различные системы счисления. Тема 2. Двоичная система счисления. Тема 3. 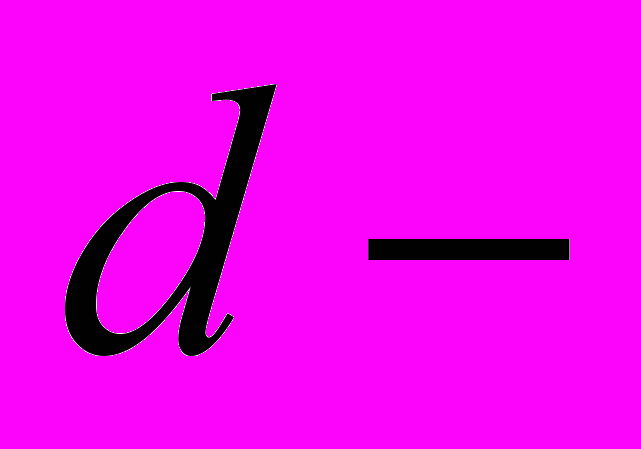системы счисления.	1 1 1	1 2 3	2 3 4
2	Из науки о числах.	Тема 1. Из истории дробей. Пропорции. Тема 2. Кто придумал отрицательные и положительные числа и зачем они нужны? Тема 3. Простые и составные числа. Тема 4. Признаки делимости. Тема 5. Наибольший общий делитель и наименьшее общее кратное.	1 1 1 1 1	1 1 2 3 1	2 2 3 4 2
3	Решение логических задач	Тема 1. Принцип Дирихле. Тема 2. Методы решения нестандартных логических задач. Тема 3. Принцип крайнего элемента. Тема 4. Поиск инварианта.	1 1 1 1	3 5 1 1	4 6 2 2
4	Геометрические задачи	Тема 1. Из истории геометрии. Тема 2. Графы. Тема 3. Геометрические задачи на разрезания. Тема 4. Замечательные кривые. Тема 5. Симметрия. Тема 6.Геометрические узоры.	1 1 1 1 1 1	1 2 3 3 1 1	2 3 4 4 2 2
5	Математические игры и соревнования	Тема 1. Комбинации и расположения. Тема 2. Выигрышные стратегии. Тема 3. Числовые ребусы. Тема 4.Игры на шахматной доске. Тема 5. Исчезновение фигур. Тема 6. Решение задач международной математической игры-конкурса «Кенгуру»	1 1 1	3 2 2 1 2 6	4 2 3 2 2 6
		ИТОГО:	21	51	72

Краткое содержание разделов


I. Различные системы счисления


Тема1. Вводное занятие. История появления числа. Различные системы счисления.

Понятие о системах счисления. Развитие систем счисления. Различные системы счисления.


Тема 2. Двоичная система счисления.

Понятие о двоичной системе счисления. Перевод из двоичной системы счисления в десятичную и обратно. Сложение и вычитание в двоичной системе счисления. Умножение и деление в двоичной системе счисления.


Тема 5. 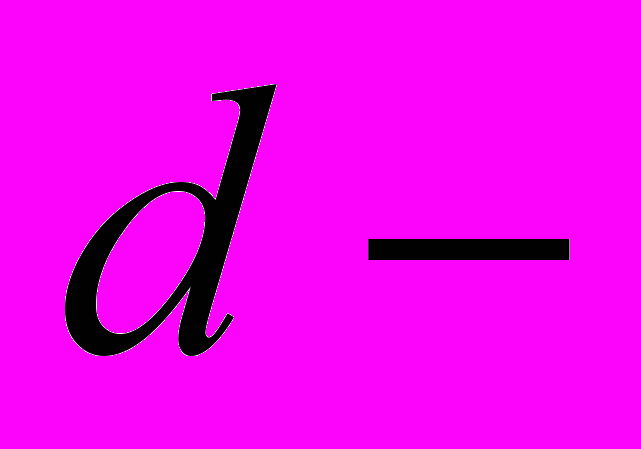системы счисления.

Троичная, пятеричная, восьмеричная системы счисления. Перевод из этих систем счисления в десятичную и обратно.


II. Из науки о числах.


Тема 1. Из истории дробей. Пропорции.

Дроби. Понятие о цепных дробях. Из истории дробей. Цепные дроби и календарь. Решение задач на все действия с дробями. Пропорции.


Тема 2. Кто придумал отрицательные и положительные числа и зачем они нужны?

Из истории положительных и отрицательных чисел. Арифметика «Диофанта».


Тема 3. Простые и составные числа.

Простые, составные, совершенные, дружественные числа, числа – «близнецы». Решето Эратосфена.


Тема 4. Признаки делимости.

Признаки делимости на 3 и 9 с доказательством.

Признаки делимости на 11 и 19. Решение задач с использованием этих и других признаков делимости.


Тема 5. Наибольший общий делитель и наименьшее общее кратное.

Взаимно простые числа. Остатки. Решение задач с использованием наибольшего общего делителя и наименьшего общего кратного. Алгоритм Евклида. Из истории математики: Евклид.


III. Решение логических задач


Тема 1. Принцип Дирихле.

Применение принципа Дирихле для решения задач.


Тема 2. Методы решения нестандартных логических задач.

Метод перебора. Метод поиска родственных задач. Метод «причесывания задач» (или «Можно считать, что…». Метод доказательства «от противного». Обратный ход (метод решения с конца. Метод «круги Эйлера».


Тема 3. Принцип крайнего элемента.

Применение принципа крайнего элемента при решении логических задач.


Тема 4. Поиск инварианта.

Перестановки. Раскраски. Четность (нечетность) и остаток от деления.


IV. Геометрические задачи


Тема 1. Из истории геометрии.

Биографические сведения об учёных: Фалес, Эратосфен, Архимед, Пифагор.


Тема 2. Графы.

Основные понятия и определения. Кратчайшие расстояния. Проблема четырех красок. Из истории математики: Л. С. Понтрягин.


Тема 3. Геометрические задачи на разрезания.

Решение геометрических задач на разрезания и переклеивания.


Тема 4. Замечательные кривые.

Эллипс. Гипербола. Парабола. Конус. Спираль Архимеда. Синусоида. Кардиоида. Циклоида. Гипоциклоиды.


Тема 5. Симметрия.

Применение симметрии для решения задач.


Тема 6. Геометрические узоры.

Правильные фигуры. Паркеты, бордюры, орнаменты.


V.Математические игры и соревнования


Тема1. Комбинации и расположения.

Решение простейших комбинаторных задач. Понятие « факториала». Перестановки.

Тема 2. Выигрышные стратегии.

Практические задачи на раздел имущества при затруднительных обстоятельствах.


Тема 3. Числовые ребусы.

Приемы решения числовых ребусов. Восстановление знаков действий. Перестановка и зачеркивание цифр.


Тема 4. Игры на шахматной доске.

Шахматные головоломки. Комбинаторика на шахматной доске.


Тема 5. Исчезновение фигур.

Парадоксы с линиями, с площадью. Парадокс шахматной доски. Числа Фибоначчи.


Тема 6. Решение задач международной математической игры-конкурса « Кенгуру».


Предполагаемые результаты обучения


знать

• различные системы счисления, приемы перевода числа из десятичной системы счисления в другие системы счисления и обратно;
  
• понятия простого и составного числа, совершенных, дружественных чисел;
  
• признаки делимости на 3 и 9, 4 и 25, 8 и 125, 11 и 19 и др.;
  
• понятия наибольшего общего делителя и наименьшего общего кратного;
  
• алгоритм Евклида;
  
• принцип Дирихле;
  
• принцип крайнего элемента;
  
• понятие инварианта;
  
• методы решения нестандартных логических задач;
  
• понятие графа;
  
• виды замечательных кривых;
  
• понятие симметрии, ее виды;
  

уметь

• переводить числа из десятичной системы счисления в двоичную, пятеричную, восьмеричную и обратно;
  
• производить действия сложения и вычитания, умножения и деления в двоичной системе счисления;
  
• определять простые и составные числа, раскладывать составные числа на простые множители;
  
• использовать различные признаки делимости при решении задач;
  
• находить наибольший общий делитель и наименьшее общее кратное чисел и использовать их при решении задач;
  
• использовать различные приемы решения логических задач
  
• решать геометрические задачи на разрезание, простейшие задачи на графы;
  
• строить замечательные кривые;
  
• решать задачи с использованием понятия симметрии, строить бордюры, орнаменты;
  
• решать числовые ребусы, показывать математические фокусы; играть в различные игры на шахматной доске.
  

• решать задачи международной математической игры-конкурса
  

« Кенгуру».


Для реализации программы «Живая математика» необходимо:

Материально-техническое обеспечение	Методическое и дидактическое обеспечение
Учебный кабинет, учебные столы, стулья, компьютеры, принтер, сканер, интерактивная доска, медиапроектор, классная доска, мел.	-Подборка информационной и справочной литературы; -Обучающие и справочные электронные издания; - Доступ в Интернет

Методическое обеспечение программы

№	Название раздела	Формы занятий	Методы и приемы	Дидактический материал, техническое оснащение	Формы подведения итогов
1	Различные системы счисления	Комбинированные тематические занятия Практикумы по решению задач	Беседа, рассказ, объяснение, решение задач, практическая работа, доклады	Конспект занятий, презентация, компьютер, медиапроектор, интерактивная доска.	Устный опрос Разбор задач, заданных на дом
2	Из науки о числах	Комбинированные тематические занятия Практикумы по решению задач	Беседа, рассказ, объяснение, решение задач, самостоятельная работа, групповая работа, доклады.	Конспект занятий, презентация, компьютер, медиапроектор, интерактивная доска.	Устный опрос Разбор задач, заданных на дом Подготовка докладов по истории математики
3	Решение логических задач	Комбинированные тематические занятия Практикумы по решению задач Конкурсы по решению математических задач	Рассказ, объяснение, беседа, создание ситуации новизны, актуальности, успеха, эвристический метод, решение задач, самостоятельная работа, проведение конкурсов, мозговой штурм	Конспект занятий, презентация, компьютер, медиапроектор, интерактивная доска.	Устный опрос Разбор задач, заданных на дом
4	Геометрические задачи	Комбинированные тематические занятия Практикумы по решению задач Конкурсы по решению математических задач Практическое занятие по изготовлению бордюров, орнаментов.	Рассказ, объяснение, беседа, создание ситуации новизны, актуальности, успеха, эвристический метод, решение задач, доклады, самостоятельная работа, проведение конкурсов, практическая деятельность групповая.	Конспект занятий, презентация, компьютер, медиапроектор, интерактивная доска.	Устный опрос Разбор задач, заданных на дом Подготовка докладов по истории математики Изготовление бордюров, орнаментов.
5	Математические игры и соревнования	Практикум по решению задач Конкурсы по решению математических задач	Решение задач, проведение игр, проведение конкурсов.	Конспект занятий, компьютеры, медиапроектор, интерактивная доска.	Участие кружковцев в лицейской олимпиаде, городской «Математической регате», международной математической игре-конкурсе «Кенгуру»

Литература для учителя:


1. Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная работа с учениками 5-6 классов. - М.: Просвещение,2005 .

2. Журналы «Квант», 1976-2008 гг.

3. Журналы «Математика в школе», 1980-2008.

4. Кордемский Б.А. Увлечь школьников математикой. - М.: Просвещение, 1981.

5. Мерлин А.В., Мерлина Н.И. Задачи для внеклассной работы по мате­матике (5-11 классы): Учеб. пособие, 2-е изд., испр. и доп. Чебоксары: Изд-во Чуваш, ун-та, 2002.

6. Пчелинцев ФА., Чулков П.В. Математика. 5-6 классы. Уроки мате­матического мышления с решениями и ответами. 2-е изд., испр. М.: Издат-школа, 2000. .

7. Руденко В.Н., Бахурин ГЛ., Захарова ГЛ. Занятия математического кружка в 5-м классе. М.: Издательский дом «Искатель», 1999.

8. Смыкалова Е.В. Дополнительные главы по математике для учащихся 6 класса. СПб.: СМИО Пресс, 2001.

9. СпивакА.В. Математический кружок. 6-7 классы. М.: Посев, 2003.

10. Степанов В.Д. Активизация внеурочной работы по матема­тике в средней школе. - М.: Просвещение, 2001.

11. Чименгирова Л., Спиридонова Б. Играя, учимся математике. - М.: Просвещение, 1993.

12. Фарков А.В. Математические кружки в школе. – М. Айрис-пресс, 2007

13.Фарков А.В. Математические олимпиады в школе. 5-11 классы. 3-е изд., испр. и доп. М.:.Айрис-пресс, 2004.

14.Фарков А.В. Олимпиадные задачи по математике и методы их решения. М.: Народное образование, 2003.

15. Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного круж­ка. 5-6 кл. М.: Изд-во НЦ ЭНАС, 2003.

16. Шуба М.Ю. Занимательные задания в обучении математике. -М.: Просвещение, 1996.

17. Шустеф Ф.М. Материал для внеклассной работы по матема­тике. - Минск, 1968.

18. Яковлев А.Я. Леонард Эйлер. - М.: Просвещение, 1983.


Литература для учащихся:


1. Абдрашитов Б.М., Абдрашитов Т.М., Шлихунов В.Н. Учи­тесь мыслить нестандартно. - М.: Просвещение, 1996.

2. Алееницкий Н.Н., Сахаров И.П. Забавная арифметика. - М., 2005.

3. Асарина Е.Ю., Фрид М.Е. Математика выводит из лабирин­та. - М.: Контекст, 1997.

4. Бабинская И.Л. Задачи математических олимпиад. - М.: Наука, 2006.

5. Баврин И.И., Фрибус Е.А. Старинные задачи. - М.: Просвещение, 1994.

6. Белл Э.Т. Творцы математики. - М.: Просвещение, 1979.

7. Беррондо М. Занимательные задачи. - М.: Мир, 1971.

8. Екимова МЛ., Кукин Г.П. Задачи на разрезание. М.: МЦНМО, 2002.

9. Игнатьев Е.И. В царстве смекалки. М.: Наука, Главная редакция физико-математической литературы, 1979.

10. Клименко Д.В. Задачи по математике для любознательных. -М.: Просвещение, 1991.

11. Кордемский Б.А. Великие жизни в математике. - М.: Про­свещение, 1995.

12. Леман И. Увлекательная математика. - М.: Знание, 1985.

13. Лоповок Л.М. Математика на досуге: Кн. для учащихся средн. школь­ного возраста. М.: Просвещение, 1981.

14. Минковский В.Л. За страницами учебника математики. - М.: Просвещение, 2005.

15. Нагибин Ф.Ф., Канин E.G. Математическая шкатулка. - М.: Просвещение, 1988.

16. Семенов Е.Е. Изучаем геометрию. - М.: Просвещение, 1987.

17. СпивакА.В. Тысяча и одна задача по математике: Кн. для учащихся 5-7 кл. М.: Просвещение, 2002.

18. Чистяков В.Д. Исторические задачи. - М: Просвещение, 2002.

19. Чистяков В.Д. Рассказы о математике. -. М: Просвещение, 2001.